Abstract
Several phenomena in nature are subjected to the interaction of various physical parameters, which, if these latter are well known, allow us to predict the behavior of such phenomena. In most cases, these physical parameters are not exactly known, or even more these are unknown, so identification techniques could be employed in order to estimate their values. Systems for which their inputs and outputs vary both temporally and spatially are the so-called distributed parameter systems (DPSs) modeled through partial differential equations (PDEs). The way in which their parameters evolve with respect to time may not always be known and may also induce undesired behavior of the dynamics of the system. To reverse the above, the well-known adaptive boundary control technique can be used to estimate the unknown parameters assuring a stable behavior of the dynamics of the system. In this work, we focus our attention on the design of an adaptive boundary control for a parabolic type reaction–advection–diffusion PDE under the assumption of unknown parameters for both advection and reaction terms and Robin and Neumann boundary conditions. An identifier PDE system is established and parameter update laws are designed following the certainty equivalence approach with a passive identifier. The performance of the adaptive Neumann stabilizing controller is validated via numerical simulation.
1. Introduction
A large number of physical phenomena in nature can be modeled by partial differential equations (PDEs) like those in the field of engineering, physics, or chemical sciences since these disciplines encompass the study of phenomena such as electromagnetic field, acoustics, fluid flow, heat transfer, strength of materials, chemical reactions and concentration, mechanical vibrations, among other like logistics, flocking behavior, or even disease spreading. These phenomena have interactions between different variables and parameters for which it becomes necessary to correlate them into a mathematical model through the use of fundamental laws of nature, like those about conservation of energy, mass, and momentum. Due to the interaction between variables and parameters and by the way in which they vary both temporally and spatially, such processes are known as distributed parameter systems (DPSs). An essential feature of the DPSs is that they are infinite-dimensional systems that lead to PDEs for which, in some scenarios, it is possible to use a reduction methodology to transform the system into a finite-dimensional ordinary differential equation (ODE) in order to simplify the DPS making it more accurate for a specific application.
The PDEs are classified into three main categories, namely, the parabolic type, elliptic type, and hyperbolic type, according to the properties that each equation may have. Each one of these latter are used to describe the behavior of different phenomena, e.g., parabolic PDEs mainly describe heat transfer and diffusion processes, elliptic PDEs describe steady state behavior for systems like electrostatic fields, and the hyperbolic type are associated with vibrations or wave phenomena [1]. Unlike an ODE, where the solution leads to finding a specific state, the solution from a PDE lead us to find a family of functions due to its infinite-dimensional nature becoming necessary to establish certain conditions that help us to find the family of solutions inside a domain; such conditions are the so-called boundary conditions, namely, Dirichlet, Neumann, and Robin conditions, which ensures the well-posedness of the PDE [2].
In many DPSs, the physical parameters are unknown because these vary as the dynamics of the system evolve over time. From control theory, a recurrent approach has been widely used for estimation of unknown parameters from finite-dimensional systems, namely, the adaptive control technique, which has been extended to the control of infinite-dimensional PDEs. The adaptive control technique for PDEs successfully contribute to estimating the unknown parameters assuring the convergence to their true values. Depending on the location of the sensors and actuators, the control of PDEs can be performed either in the domain or at the boundary.
Some of the first works conducting studies of convergence of the estimation error to zero in DPSs were reported in [3,4,5]. These works were focused on the design of a model reference adaptive control (MRAC) for different types of PDEs. First, attempts on the development of a robust methodology to the design of adaptive controllers in the boundary of PDEs systems was reported in [6] to the Burgers’ equation case when considering unknown viscosity as well as that for an axially moving string system in [7]; for both cases, the adaptive laws were designed through the Lyapunov’s direct method. An adaptive boundary controller for a parabolic PDE, containing an unknown destabilizing parameter affecting the interior of the domain, was developed in [8]. In [9,10], it was shown how adaptive boundary control problems for unstable parabolic PDEs of infinite relative degree were solved via output feedback approach. In [11], the first adaptive controllers for parabolic PDEs with actuation at the boundary and spatially-varying parameters were introduced. In this latter work, the Lyapunov’s direct method was used in the design of adaptive laws guaranteeing convergence to zero for the estimation and parametric errors. The most relevant contributions for adaptive boundary control of parabolic PDEs through a backstepping approach were reported in [12,13,14]. The backstepping approach was used to establish an explicit expression for the kernel gain applied to the control law. The control law is then modified substituting the unknown parameters by their estimates. Parameter update (adaptive) laws were designed through the Lyapunov’s technique for the establishment of the parameter identifier assuring convergence to zero of the estimation error. In [15,16], adaptive boundary control laws were developed for wave equations, namely hyperbolic type PDEs. In [17], the design of a nonlinear adaptive controller, using the Lyapunov’s technique, for a hyperbolic PDE model representing crowd dynamics was reported. A system of a reaction–advection–diffusion (R–A–D) PDE of a parabolic type with a distributed input subject to an arbitrarily large and unknown time-delay was considered in [18]; although the control was not applied at the boundary, the main contribution lies with the need to compensate unfavorable effects on communication delays. The trend in this latter work was directed in the sense of [19,20], which addresses the development of control designs for coupled PDEs systems of hyperbolic and parabolic type, respectively.
Adaptive boundary control for PDEs has been positioned as an effective tool for estimation of the dynamic behavior of the state and unknown parameters from infinite-dimensional systems; the control signal is actuated at the boundary so as not to be intrusive in the domain under the fact that placement of sensors and actuators within the system becomes unfeasible [21,22].
In [23], adaptive boundary control design methods, namely, the Lyapunov’s method, and certainty equivalence approaches with passive and swapping identifiers, were shown. Backstepping controllers for boundary control of PDEs, previously designed and explicitly parametrized in physical parameters of the respective plants to be controlled, were considered as nominal controllers in the development of such adaptive control schemes. In that work, the certainty equivalence approach with passive identifier was used for the design of an adaptive boundary controller for a two-dimensional (2D) R–A–D PDE system having Dirichlet boundary conditions with actuation in one of them. In addition, authors claim that these adaptive control methods can be extended to R–A–D PDE systems in 2D and 3D as well as to systems with spatially varying (functional) parametric uncertainties and to other types of boundary conditions. Moreover, an adaptive boundary control design method via the output–feedback approach was shown, where authors also claim that this method can be applied to general R–A–D PDE systems. In [24], an adaptive boundary controller via Lyapunov’s method for a R–A–D PDE system with unknown diffusion and advection parameters having Dirichlet boundary conditions was designed. In addition, the design of an adaptive boundary control via certainty equivalence approach with passive identifiers for a 3D R–A–D system and Dirichlet boundary conditions was included. Moreover, the certainty equivalence approach but with swapping identifiers was used to the design of an adaptive boundary controller for a R–A–D system having Dirichlet boundary conditions.
In the field of control for nonlinear PDEs, there is so much to explore. The study of the backstepping methodology is motivated from its potential for nonlinear PDEs. For some of the problems that have been addressed, the nonlinearity appears in the PDE in such a way that it does not affect stability, i.e., the choice of a Lyapunov function was simple, as it was to the case for the Burgers’ equation in [6,25,26,27]. Problems of most practical interest and mathematically challenging are those with boundary control and with in-domain nonlinearities. The design of nonlinear feedback laws for this latter kind of systems is a complex task. An approach which consists in spatial discretization of a nonlinear PDE plant to the development of an optimal feedback law for the resulting ODE system was introduced in [28]. However, this proposal would entail the problem of the curse of dimensionality. The feedback linearization approach has been considered for PDEs but using spatial discretization or some ways of ODE model reduction. It is well known that a bound of the numerical solution is crucial in the establishment of stability and convergence for a fully discrete scheme applied to nonlinear PDEs. The analysis for stability and convergence of the pseudospectral (Fourier collocation) method, coupled with a variety of specially designed time-stepping methods of up to fourth order, for the numerical solution of a 3D viscous Burgers’ equation with periodic boundary conditions was carried out in [29]. The major advantage of the pseudospectral method is that it is easier to implement and very efficient due to the fast Fourier transform. The ease of implementation comes from the fact that the pseudospectral approach avoids some difficulties when evaluating 3D nonlinear terms. In that work, the inverse inequality approach is avoided, which is a classical way to obtain such a bound and leads to a restriction on the time-step in terms of the spatial grid size, which can be prohibitive in two or three dimensions.
In this work, we try with a non-previously exposed case where the adaptive boundary control methodology is used for the control of a parabolic type R–A–D PDE when assuming unknown constant parameters for the reaction and advection terms and both Robin and Neumann type boundary conditions. We focus our attention on reaching convergence to zero for the estimation error by designing adaptive laws that estimate the unknown parameters where the adaptive controller signal is actuated in one of the boundaries. Our work is motivated from [24,28], where the adaptive boundary control design for the R–A–D PDE system considered here has been left as an open problem.
This paper is organized as follows: In Section 2, the properties for function spaces are summarized. In Section 3, the R–A–D PDE system is described. In addition, a Neumann stabilizing controller previously designed, in a work of our own, for the class of PDE system considered here is shown. The identifier PDE and estimation error PDE are properly established through Section 4 and Section 5, respectively. In Section 6, parameter update (adaptive) laws are designed following the certainty equivalence approach with passive identifier. The performance of the adaptive boundary controller is shown in Section 7. Some concluding remarks are given at the end of the manuscript.
2. Function Spaces
Let us denote by an open set of with boundary . Assume that either is Lipschitz or is of class for . The generic point of is denoted by . The Lebesgue measure on is denoted by .
Let us denote by (resp. or ) the space of real continuous functions on (resp. the space of k times continuously differentiable functions on ), (resp. ) represents the space of real continuous functions on (resp. the space of k times continuously differentiable functions on ). Let us denote by the spaces of real functions on with a compact support in .
For , is the space of real functions on which are for the Lebesgue measure. It is a Banach space for the norm
For , is the space of measurable and bounded real functions on . It is also a Banach space for the norm
For , is a Hilbert space for the scalar product
with the corresponding norm denoted by
Let us denote by , , the Sobolev space of functions u in whose distribution derivatives of order less than or equal to s are in . It is a Banach space for the norm
where , , is the notation for the partial differential derivatives of a function u, , , and .
For , and this is a Hilbert space for the scalar product
Let us consider the Sobolev spaces which contain and . The closure of in (resp. ) is denoted by (resp. ). In particular,
which are Hilbert spaces for the scalar product
For a bounded , the Poincaré inequality
implies that is a Hilbert space for the scalar product
and that the corresponding norm
is equivalent to the norm induced by [30].
3. Reaction–Advection–Diffusion (R–A–D) Equation
The R–A–D PDE model deals with the time evolution of concentration of species in a flowing medium. The adaptive boundary control methodology to be applied in this work for stabilizing a certain class of R–A–D PDE requires of the prior design a backstepping-based boundary control law (nominal backstepping controller) [23,24] that achieves the stabilization objective.
Let us consider the R–A–D system
where is a function defined in , b and are known constant coefficients. The system has a Robin condition imposed at the boundary as well as a Neumann actuation signal applied on the other one boundary . Here, , , and are the diffusion, advection and reaction terms, respectively. This last term is the one that causes instability in the system for or it behaves as a stable system otherwise. The R–A–D PDE system (13)–(15) represents a hypothetical simple case developed in one spatial dimension and rectangular coordinates.
A Neumann stabilizing controller for the system (13)–(15) was designed in [31], via the previously mentioned backstepping approach, which is given by
when considering the heat equation
as a target system, where “exp” stands for the Euler exponential constant, the parameter is given as , and , stands for modified Bessel functions of the first and second kind, respectively. The Neumann stabilizing controller (16) is applied in the boundary condition (15) assuring the stabilization of the system even if the parameter is large enough. It must be noticed that the stabilizing control law (16) was designed in [31] under the assumption that the parameters b and from the system (13)–(15) are known.
4. Identifier PDE
Let us now consider that the constant parameters b and of the system (13)–(15) are unknown and that it is still desired to stabilize the system.
We begin the analysis of our case study by introducing the auxiliary system
This auxiliary system (20)–(22) is called identifier PDE. Notice here that the identifier PDE employs a copy of the original R–A–D PDE and one additional nonlinear term along with its boundary conditions. In this identifier PDE, we employ the notation to denote the estimate of a function or from a parameter, so that and are the estimate parameters. The nonlinear additional term within the identifier is , where is an arbitrary constant, is the so-called error signal or estimation error, and is the squared -norm of . The -norm is defined by
This identifier PDE will help us with obtaining the estimation error, which, during the adaptation process, should be gradually reduced until it becomes equal to zero as time progresses. The stabilizing control signal for the system (20)–(22) is the same as (16), but the constant parameters b, are being replaced by their estimates and , respectively, i.e.,
where .
5. Estimation Error PDE
In order to be able to approximate the value of the unknown parameters b and from (13)–(14), we need to establish an expression capable of comparing the estimated parameters , from (20)–(21) with their real values; this expression is the so-called estimation error PDE. Let us consider the estimation error
Taking the derivative of (25) with respect to time, it yields
Then, the first and second space derivatives from (25), i.e., the first and second derivative with respect to x, are given by
Rearranging (29) results in
Now, introducing the notation to refer to the difference between the real and estimated parameters, regarding (25) and (28), and considering the -norm from (23), we obtain
where and are the parameter estimation errors, i.e.,
To determine the boundary conditions in terms of the estimation error, let us first consider (27) along with (14) and (21), and, evaluating them at ,
Repeating the previous process for (15) and (22) evaluated at yields
6. Parameter Update Laws
Up to this point, we have established three PDE systems: the unstable R–A–D PDE (13)–(15) with unknown parameters b and , the identifier PDE (20)–(22) with parametric estimates and , and the estimation error PDE (31)–(35) which contains the preceding systems via estimation error (25). In what follows, we will prove that the system (31)–(35) is bounded and square integrable in time in the sense of the -norm (23).
Let us consider the Lyapunov function
and its time derivative given by
where since these are constants and . From (31), (37) becomes
Using integration by parts on some terms of (38) along with boundary conditions (34)–(35) and regarding the -norm (23), we get
From the adaptive control theory [32], we need to get rid of those terms that do not allow for ensuring that (38) is negative definite. In order to achieve this latter, the following adaptive laws (also known as parameter update laws) are chosen:
which, when replaced in (38), causes the last five terms be cancelled, yielding
which implies
Now, according to (36), we can see that and as well as the term are all bounded functions.
Certain properties can be achieved from (41) if we integrate it, with respect to time, by setting t from zero to infinity, i.e.,
and accordingly to (42)
from which and are square integrable functions of time, i.e., , .
In the manner described above, it has been proved that the system (20)–(22) effectively estimates and which converge to the true parameters b and via adaptive laws (39)–(40), allowing for the dynamics of the system (20)–(22) also converge with that from (13)–(15). Then, the following lemma can be stated.
From Lemma 1, although the stability of the identifier has been proven, the proof for closed-loop stability of the whole adaptive boundary control scheme designed here can be carried out along the same lines as in [24].
In Figure 1, a block diagram is shown to illustrate the adaptive control scheme for the R–A–D PDE system (13)–(15).
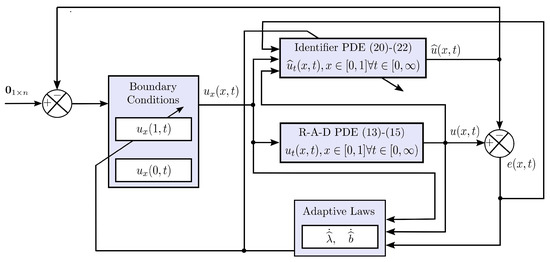
Figure 1.
Adaptive boundary control scheme for the R–A–D PDE system (13)–(15).
7. Simulation Results
In this section, we discuss the simulation results from the dynamics in the closed loop of the adaptive Neumann stabilizing controller. The main objective is to show the convergence to zero for the estimation error (25) as a function of time and that the estimated parameters and converge to their true values as time progresses. The simulation is set to and along with initial condition . A built-in function in MATLAB with a previous finite discretization in space process to solve a resulting parabolic PDE system, consisting of the R–A–D PDE system (13)–(15) and identifier PDE (20)–(22), is implemented. Figure 2 shows the dynamics of the R–A–D PDE system with adaptive Neumann control at the boundary while Figure 3 shows the progression in time of the identifier PDE. The dynamics from the identifier PDE are very similar to that from the R–A–D PDE system. Figure 4 clearly shows how the estimation error (25) converges to zero almost immediately after starting the process. In Figure 5, we can see the effort of the control signal (24), where the parametric estimates and actively affect its behavior as they are computed at each time interval. Figure 6 and Figure 7 show the progression of convergence over time of the estimated parameters and versus their true values, respectively. The performance of the adaptive Neumann stabilizing control scheme but for parameters set to and and initial condition is shown from Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.
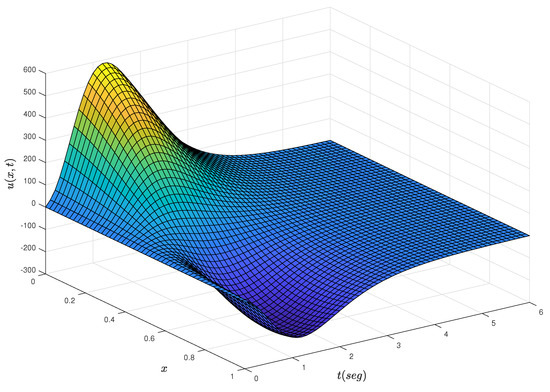
Figure 2.
Dynamics in closed-loop of the adaptive boundary controller.
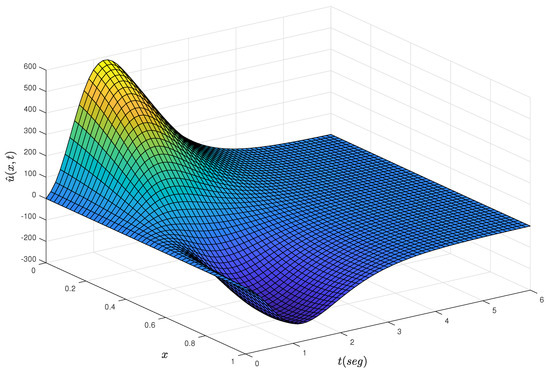
Figure 3.
Dynamics of the identifier PDE.
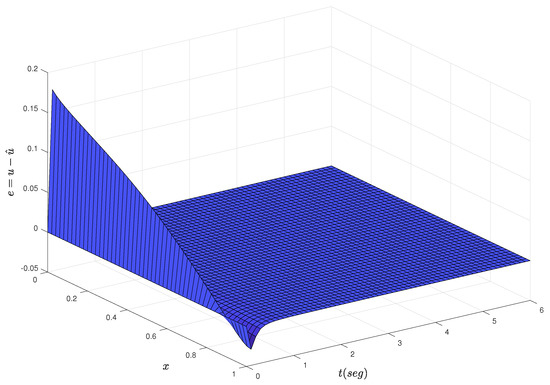
Figure 4.
Convergence to zero of the estimation error.
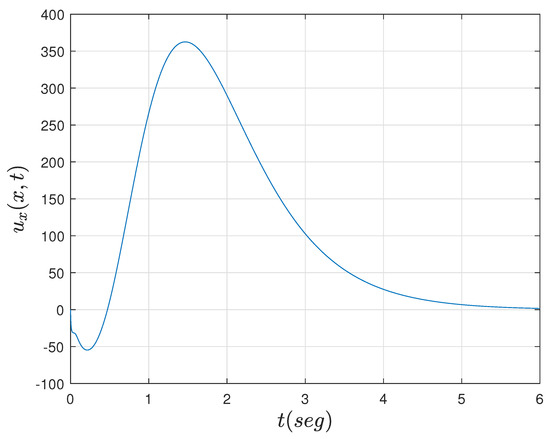
Figure 5.
Control effort of the adaptive Neumann stabilizing controller.
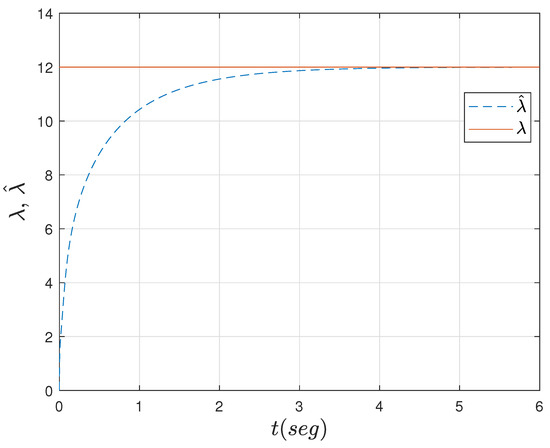
Figure 6.
Progression of the convergence for .
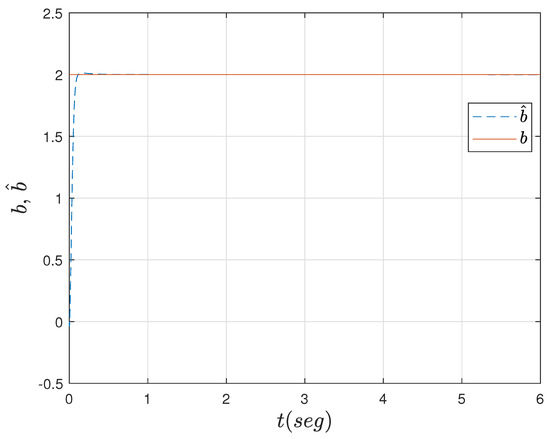
Figure 7.
Progression of the convergence for .
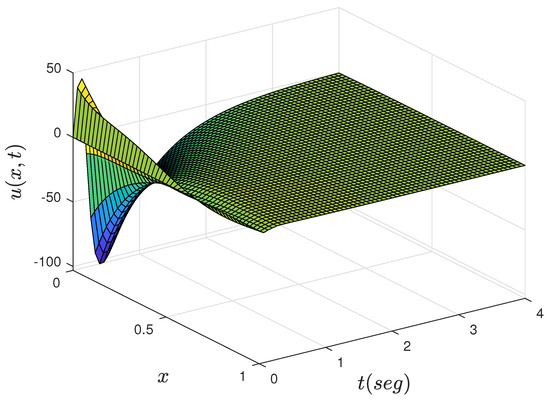
Figure 8.
Performance in closed-loop of the adaptive Neumann stabilizing controller.
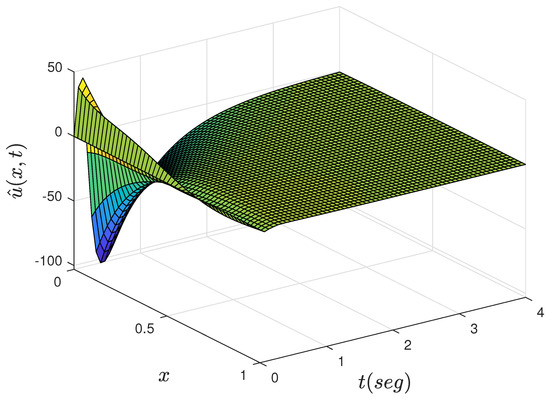
Figure 9.
Dynamics of the identifier PDE.
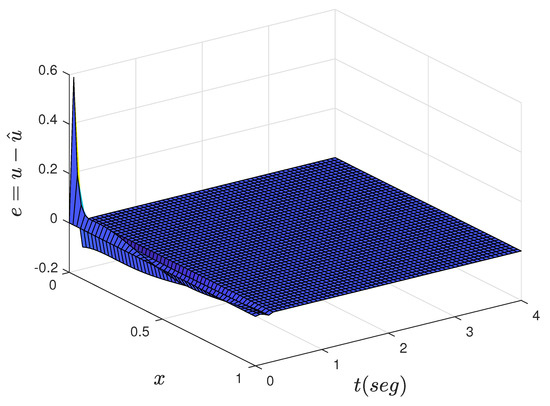
Figure 10.
Dynamics of the estimation error.
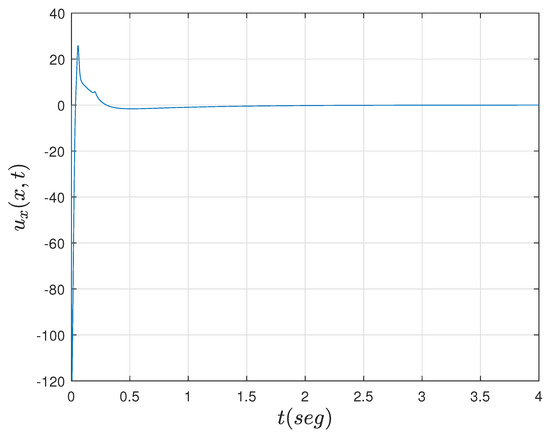
Figure 11.
Control effort of the adaptive Neumann stabilizing controller.
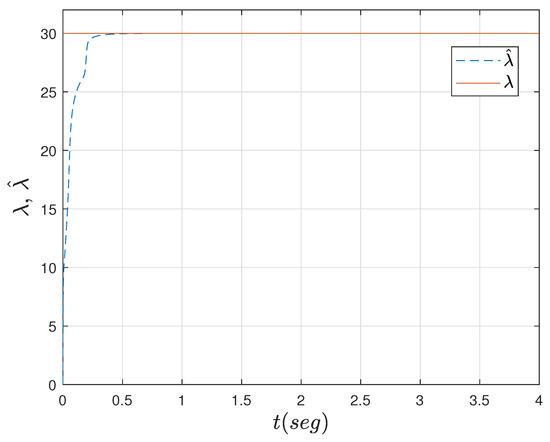
Figure 12.
Progression of the convergence for .
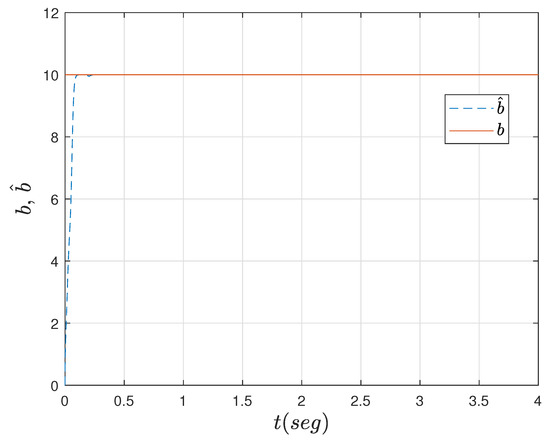
Figure 13.
Progression of the convergence for .
8. Conclusions
In this work, an adaptive Neumann stabilizing controller is designed to a certain class of an R–A–D PDE system under the assumption of unknown constant parameters to the reaction and advection terms along with combined boundary conditions of both Robin and Neumann type. The performance of the adaptive boundary controller is evaluated via numerical simulation. Simulation results from the convergence to zero for the estimation error as well as the convergence of the parametric estimates to their true (assumed as unknowns but constant) values show that the backstepping-based adaptive boundary control scheme, particularly the certainty equivalence design with passive identifier, also works well with this certain class of PDE system. As future work, the design of an adaptive Neumann stabilizing controller could be explored to try with boundary control of coupled R–A–D PDE systems with spatially-varying coefficients, or having the same diffusivity parameter, but with both Robin and Neumann boundary conditions or to extend our proposal to the case of distributed actuation and unknown input delay.
Author Contributions
Conceptualization, O.F.M.-G. and F.J.; methodology, O.F.M.-G. and F.J.; software, O.F.M.-G. and F.J.; validation, F.J.; formal analysis, O.F.M.-G. and F.J.; investigation, O.F.M.-G. and F.J.; data curation, O.F.M.-G. and F.J.; visualization, O.F.M.-G. and F.J.; writing—original draft preparation, O.F.M.-G. and F.J.; writing—review and editing, F.J.; supervision, F.J.; resources, F.J.; funding acquisition, F.J.; project administration, F.J. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Tecnológico Nacional de México (TecNM) under project 11472.21-P and, partially, under Grant No. 34064 from the EDD 2020 program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by CONACYT, México, through Grant No. 456010.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DPSs | Distributed Parameters Systems |
| ODEs | Ordinary Differential Equations |
| PDEs | Partial Differential Equations |
| R–A–D | Reaction–Advection–Diffusion |
References
- Evans, L.C. Partial Differential Equations, 2nd ed.; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Strauss, W.A. Partial Differential Equations: An Introduction, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Hong, K.S.; Bentsman, J. Direct Adaptive Control of Parabolic Systems: Algorithm Synthesis and Convergence and Stability Analysis. IEEE Trans. Autom. Control 1994, 39, 2018–2033. [Google Scholar] [CrossRef]
- Orlov, Y.V. Model Reference Adaptive Control of Distributed Parameter Systems. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 10–12 December 1997; pp. 263–268. [Google Scholar]
- Böhm, M.; Demetriou, M.A.; Reich, S.; Rosen, I.G. Model Reference Adaptive Control of Distributed Parameter Systems. SIAM J. Control Optim. 1998, 36, 33–81. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.J.; Krstic, M. Adaptive control of Burgers’ equation with unknown viscosity. Int. J. Adapt. Control Signal Process. 2001, 15, 745–766. [Google Scholar] [CrossRef]
- Fung, R.F.; Wu, J.W.; Lu, P.Y. Adaptive Boundary Control of an Axially Moving String System. J. Vib. Acoust. 2002, 124, 435–440. [Google Scholar] [CrossRef]
- Krstić, M. Lyapunov Adaptive Stabilization of Parabolic PDEs-Part I: A Benchmark for Boundary Control. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 3164–3169. [Google Scholar]
- Krstić, M. Lyapunov Adaptive Stabilization of Parabolic PDEs-Part II: Output Feedback and Other Benchmark Problems. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 3170–3175. [Google Scholar]
- Smyshlyaev, A.; Krstić, M. Output–Feedback Adaptive Control for Parabolic PDEs with Spatially Varying Coefficients. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 3099–3104. [Google Scholar]
- Smyshlyaev, A.; Krstić, M. Lyapunov Adaptive Boundary Control for Parabolic PDEs with Spatially Varying Coefficients. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 41–48. [Google Scholar]
- Smyshlyaev, A.; Krstić, M. Adaptive boundary control for unstable parabolic PDEs-Part II: Estimation-based designs. Automatica 2007, 43, 1543–1556. [Google Scholar] [CrossRef]
- Smyshlyaev, A.; Krstić, M. Adaptive boundary control for unstable parabolic PDEs-Part III: Output feedback examples with swapping identifiers. Automatica 2007, 43, 1557–1564. [Google Scholar] [CrossRef]
- Krstić, M.; Smyshlyaev, A. Adaptive Boundary Control for Unstable Parabolic PDEs—Part I: Lyapunov Design. IEEE Trans. Autom. Control 2008, 53, 1575–1591. [Google Scholar] [CrossRef]
- He, W.; Ge, S.S. Robust adaptive boundary control of a vibrating string under unknown time-varying disturbance. IEEE Trans. Control Syst. Technol. 2011, 20, 48–58. [Google Scholar] [CrossRef]
- Krstić, M. Adaptive Control of Anti-stable Wave PDE Systems: Theory and Applications in Oil Drilling. In Proceedings of the 11th IFAC International Workshop on Adaptation and Learning in Control and Signal Processing, Caen, France, 3–5 July 2013; pp. 432–439. [Google Scholar]
- Wadoo, S.A. Adaptive Control of a Hyperbolic Partial Differential Equation System with Uncertain Parameters. In Proceedings of the 15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012; pp. 608–612. [Google Scholar]
- Wang, S.; Diagne, M.; Qi, J. Adaptive Control of Reaction–Advection–Diffusion PDEs with Distributed Actuation and Unknown Input Delay. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 4509–4514. [Google Scholar]
- Aamo, O.M. Disturbance Rejection in 2 × 2 Linear Hyperbolic Systems. IEEE Trans. Autom. Control 2013, 58, 1095–1106. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y. Adaptive stabilization for a class of uncertain coupled parabolic equations. Int. J. Control 2018, 93, 2469–2479. [Google Scholar] [CrossRef]
- Morris, K. Control of Systems Governed by Partial Differential Equations in the Control Handbook, 2nd ed.; Levine, W.S., Ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Morris, K.A. Controller Design for Distributed Parameter Systems; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Krstic, M.; Smyshlyaev, A. Boundary Control of PDEs: The Backstepping Approach in the Control Handbook, 2nd ed.; Levine, W.S., Ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Smyshlyaev, A.; Krstic, M. Adaptive Control of Parabolic PDEs; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Krstic, M. On global stabilization of Burgers’ equation by boundary control. Syst. Control Lett. 1999, 37, 123–142. [Google Scholar] [CrossRef]
- Balogh, A.; Krstic, M. Burgers’ equation with nonlinear boundary feedback: H1 stability, well posedness, and simulation. Math. Probl. Eng. 2000, 6, 189–200. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.J.; Krstic, M. Backstepping boundary control of Burgers’ equation with actuator dynamics. Syst. Control Lett. 2000, 41, 291–303. [Google Scholar] [CrossRef]
- Krstic, M.; Smyshlyaev, A. Boundary Control for PDEs: A Course on Backstepping Designs; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Gottlieb, S.; Wang, C. Stability and convergence analysis of fully discrete Fourier collocation spectral method for 3D viscous Burgers’ equation. J. Sci. Comput. 2012, 53, 102–128. [Google Scholar] [CrossRef]
- Temam, R. Infinite-Dimensional Dynamical Systems in Mechanics and Physics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Cruz-Quintero, E.; Jurado, F. Boundary Control for a Certain Class of Reaction–Advection–Diffusion System. Mathematics 2020, 8, 1854. [Google Scholar] [CrossRef]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).