On the Convergence of the Benjamini–Hochberg Procedure

Abstract

The Benjamini–Hochberg procedure is one of the most used scientific methods up to date. It is widely used in the field of genetics and other areas where the problem of multiple comparison arises frequently. In this paper we show that under fairly general assumptions for the distribution of the test statistic under the alternative hypothesis, when increasing the number of tests, the power of the Benjamini–Hochberg procedure has an exponential type of asymptotic convergence to a previously shown limit of the power. We give a theoretical lower bound for the probability that for a fixed number of tests the power is within a given interval around its limit together with a software routine that calculates these values. This result is important when planning costly experiments and estimating the achieved power after performing them.

1. Introduction

In many modern studies scientists perform the same statistical test on many objects, e.g., genes or single-nucleotide polymorphisms. The number of these objects could be very large, say millions, resulting in a multiple comparison issue. This is due to the fact that even under the null hypothesis we expect some of these tests to have p-values below a predetermined significance level $\alpha$. There are various techniques to overcome this problem with the Benjamini–Hochberg method [1] being the most used. Given $\alpha$, for a set of m p-values, the method rejects the tests corresponding to the smallest k p-values, where k is the largest index such that $p_{\left(k\right)}\le k\alpha /m$. The method controls the FDR (false discovery rate) in a sense that the expected proportion of false discoveries out of all discoveries (rejected hypotheses) is not more than $\alpha$ when the tests are independent as shown in the original paper [1]. In some cases, rather than finding the cutoff index for rejecting tests, the so-called Benjamini–Hochberg-adjusted p-values are used; these are the p-values transformed by the formula on the right-hand side of the above inequality and truncated at 1.

In the field of genetics it is used in many software packages, for example, DESeq2 [2], edgeR [3], cuffdiff [4], GenomeStudio (Illumina). It is also often used when studying various types of images, e.g., PET or CT [5], fMRI [6], or astrophysical [7].

Despite the fact that there are improved methods either in terms of weaker assumptions, e.g., dependency or better statistical power, e.g., [8,9,10], the Benjamini–Hochberg method is one of the most cited scientific articles, determined to be 59th most cited article in [11]. We should underline that in this work we are not interested in improving the Benjamini–Hochberg method, but rather than that in inferring about the statistical power of the original method as it is the most used one in practice. Moreover, article [12] shows that no correction of the standard methods is needed in certain cases even when there is some degree of dependence among the tests. See Section 5 for more information and related work.

Calculating the statistical power, that is the probability of correctly rejecting the null when the alternative hypothesis is true, is an important task when designing scientific studies. For example it allows us to estimate the required sample size, and therefore the budget needed to perform the experiment, in order to make sure that we have a reasonable chance of detecting the objects for which there is indeed a difference between the two groups. After performing the study, it allows us to determine whether we have found a relatively large proportion of significant objects.

For practical applications we are interested not only in the limit of the statistical power as shown in previous works (see Section 5), but also in the speed of convergence to that limit. The speed of convergence would allow us to find the probability that the statistical power is within a given range around its limit. Consequently this would allow us to calculate the probability that the statistical power is above a pre-determined threshold, typically 80%. In cases when this probability is relatively low, one would have to increase the sample size in order to have more favorable parameters of the Beta distribution that models the p-values under the alternative hypothesis.

In more detail, in this work we show that under natural condition, that we call (M), the convergence is exponential and give explicit expression of the constants involved in the asymptotics. That condition allows the usage of suitable Beta distributions amongst others. The relationship between our condition and the non-criticality condition in [13] will be discussed below. Condition (M) allows us to find a lower bound for the probability that for fixed parameters of the model the power is within given interval around that asymptotic limit. In this sense our work can be understood as a tool which can be used in the planning of the experiment and which complements [14], another article by the authors of [15], which deals with a variety of questions, such as estimation of the proportion of significant tests, the effect of the sample size to the quality of results, etc.

2. Main Results and Their Proofs

2.1. Some Preliminary Notation

Let $X_1,X_2,\cdots ,X_m,m\in {\mathbb{N}}^{+},$ with ${\mathbb{N}}^{+}=\left\{1,2,\cdots \right\}$, be independent random variables that are defined on a common probability space $\left(\Omega ,\mathcal{F},\mathbb{P}\right)$. For some $1\le m_0<m$ the random variables ${\left(X_j\right)}_{j\le m_0}$ are assumed to have a common cumulative distribution function (c.d.f.) F, whereas ${\left(X_j\right)}_{m_0<j\le m}$ are assumed to have a common c.d.f. G. In this work we set F to be the c.d.f. of the uniform random variable on $\left(0,1\right)$ and let for the time being G be any continuous c.d.f. We note that even if G is discrete, one can always approximate it with a suitable continuous distribution. We also work with the condition that $\frac{m_0}{m}=\gamma \in \left(0,1\right)$ is fixed and set $m_1:=m-m_0\in \left(0,m\right)$, which is strictly non-binding since we develop exponential bounds that are valid with different degree of accuracy for any fixed $m_0,m$ and the respective ratio $\frac{m_0}{m}$. It will be usually the case that $\gamma$ is larger than $1/2$ as the first $m_0$ random variables represent the non-significant observations. If $X_m^{\left(i\right)},i\le m,$ is i-th order statistics of $X_1,X_2,\cdots ,X_m$ then for a fixed level of rejection $\alpha \in \left(0,1\right)$, the Benjamini–Hochberg procedure declares significant the first $R_m$ order statistics, where

$$R_m=max\left\{i:X_m^{\left(i\right)}\le \alpha \frac{i}{m}\right\}.$$

(1)

The truly non-significant tests have c.d.f F and the truly significant tests possess c.d.f. G. It is well known from [15] (1.2) that for $x\in \left(0,1\right)$ we can express the event $\left\{R_m\ge mx\right\}$ in the following fashion

$$\left\{\frac{R_m}{m}\ge x\right\}=\left\{\underset{t\in A_{\alpha }\left(m,x\right)}{max}\frac{H_m\left(t\right)-t}{t}\ge \frac{1}{\alpha }-1\right\},$$

(2)

where $H_m\left(t\right)=\frac{1}{m}{\sum }_{j=1}^m{\mathbb{I}}_{\left\{X_j\le t\right\}}$ is the empirical c.d.f. of $X_1,X_2,\cdots ,X_m$ and

$$A_{\alpha }\left(m,x\right)=\left\{\frac{k}{m}\alpha :\lceil mx\rceil \le k\le m\right\},$$

(3)

where $\lceil y\rceil =min\left\{m\in {\mathbb{N}}^{+}:m\ge y\right\}$ is the ceiling function. We can express $H_m$ as

$$H_m\left(t\right)=\frac{\gamma }{m_0}\sum _{j=1}^{m_0}{\mathbb{I}}_{\left\{X_j\le t\right\}}+\frac{\left(1-\gamma \right)}{m_1}\sum _{j=m_0+1}^m{\mathbb{I}}_{\left\{X_j\le t\right\}}=\gamma F_{m_0}\left(t\right)+\left(1-\gamma \right)G_{m_1}\left(t\right),$$

where $F_{m_0}$ is the empirical c.d.f. of $X_1,X_2,\cdots ,X_{m_0}$ and $G_{m_1}$ is the empirical c.d.f. of $X_{m_0+1},\cdots ,X_m$. Therefore a simple rearrangement yields that

$$\frac{H_m\left(t\right)-t}{t}=\gamma \frac{F_{m_0}\left(t\right)-t}{t}+\left(1-\gamma \right)\frac{G_{m_1}\left(t\right)-G\left(t\right)}{t}+\left(1-\gamma \right)\frac{G\left(t\right)-t}{t}.$$

(4)

2.2. General Inequalities and Information concerning the Distribution of $R_m$

We introduce the function $c\left(ϵ\right)=(1+ϵ)ln\left(1+ϵ\right)-ϵ,\mathrm{for}ϵ>0,$ which is investigated in Proposition A1 in Appendix A. Then the following inequalities hold true.

Proposition 1.

For any distribution function T with $T\left(\alpha x\right)>0$ and empirical cumulative distribution function $T_n(·)=\frac{1}{n}{\sum }_{j=1}^n{\mathbb{I}}_{\left\{X_j\le ·\right\}}$, where ${\left(X_j\right)}_{j\ge 1}$ are i.i.d. random variables with c.d.f. T, any $k,m\in {\mathbb{N}}^{+}$, any $\alpha ,x,\rho \in \left(0,1\right)$ and $A_{\alpha }(x,m)$ as in (3) above, we have, for every $ϵ>0$, that

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\rho \underset{t\in A_{\alpha }(m,x)}{max}\left|\frac{T_k\left(t\right)-T\left(t\right)}{t}\right|>ϵ\right)\hfill \\ \hfill & \le 2min\left\{m(1-x)e^{-k{inf}_{t\in A_{\alpha }(m,x)}T\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)},e^{-2\frac{k}{{\rho }^2}{\left(ϵ\alpha x\right)}^2}\right\}\hfill \\ \hfill & :=K_T(x,m,k,\rho ,ϵ,\alpha ).\hfill \end{array}$$

(5)

Finally, if $T\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)$ as a function of t is non-decreasing on $\left[\alpha x,\alpha \right)$ we get that

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\rho \underset{t\in A_{\alpha }(m,x)}{max}\left|\frac{T_k\left(t\right)-T\left(t\right)}{t}\right|>ϵ\right)\hfill \\ \hfill & \le 2min\left\{m(1-x)e^{-kT\left(\alpha x\right)c\left(\frac{ϵ}{\rho }\frac{\alpha x}{T\left(\alpha x\right)}\right)},e^{-2\frac{k}{{\rho }^2}{\left(ϵ\alpha x\right)}^2}\right\}=K_T(x,m,k,\rho ,ϵ,\alpha ).\hfill \end{array}$$

(6)

Remark 1.

Let us compute $K_T$ when $T\left(t\right)=F\left(t\right)=t$ for $t\in \left(0,1\right)$. Then $T\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)=tc\left(\frac{ϵ}{\rho }\right)$ is non-decreasing in t and substituting in the right-hand side of (6) we deduct that

$$K_F(x,m,k,\rho ,ϵ,\alpha )=2min\left\{m(1-x)e^{-k\alpha xc\left(\frac{ϵ}{\rho }\right)},e^{-2\frac{k}{{\rho }^2}{\left(ϵ\alpha x\right)}^2}\right\}.$$

(7)

Remark 2.

Given that $c\left(ϵ\right)\ge min\left(1,\frac{{ϵ}^2}{2e}\right)$, see Proposition A1 we may eradicate the dependence on the function c in $K_T$, see (5) by providing an upper bound for it:

$$\begin{array}{cc}\hfill & K_T(x,m,k,\rho ,ϵ,\alpha )\le \hfill \\ \hfill & 2min\left\{m(1-x)e^{-kmin\left(T\left(\alpha x\right),{inf}_{t\in A_{\alpha }(m,x)}\frac{{ϵ}^2}{{\rho }^2}\frac{t^2}{2eT\left(t\right)}\right)},e^{-2\frac{k}{{\rho }^2}{\left(ϵ\alpha x\right)}^2}\right\}.\hfill \end{array}$$

(8)

Remark 3.

Inspecting the proof below one easily discovers that for computational purposes it is better to use the sharper estimate

$$\mathbb{P}\left(\rho \underset{t\in A_{\alpha }(m,x)}{max}\left|\frac{T_k\left(t\right)-T\left(t\right)}{t}\right|>ϵ\right)\le 2min\left\{\sum _{t\in A_{\alpha }(m,x)}{e}^{-kT\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)},e^{-2\frac{k}{{\rho }^2}{\left(ϵ\alpha x\right)}^2}\right\}.$$

(9)

For theoretical purposes the bounds stated in the theorem are more suitable.

Proof of Proposition 1.

The second part of the minimum (5) follows from the Dvoretsky–Kiefer–Wolfowitz inequality, see [16], which gives, for any $x,ϵ>0$ that

$$\begin{array}{cc}\hfill \mathbb{P}\left(\rho \underset{t\in A_{\alpha }(m,x)}{max}\left|\frac{T_k\left(t\right)-T\left(t\right)}{t}\right|>ϵ\right)& \le \mathbb{P}\left(\rho \underset{t\in \left(\alpha x,\alpha \right)}{sup}\left|\frac{T_k\left(t\right)-T\left(t\right)}{t}\right|>ϵ\right)\hfill \\ \hfill & \le \mathbb{P}\left(\underset{t\in \left(\alpha x,\alpha \right)}{sup}\left|T_k\left(t\right)-T\left(t\right)\right|>\frac{ϵ\alpha x}{\rho }\right)\hfill \\ \hfill & \le 2e^{-2k\frac{{\left(ϵ\alpha x\right)}^2}{{\rho }^2}}.\hfill \end{array}$$

(10)

In Proposition A1 we use the function $c\left(ϵ\right)=\left(1+ϵ\right)ln\left(1+ϵ\right)-ϵ$. The first part of the minimum of (5) is immediate from Proposition A1 since $k{T}_k\left(t\right)={\sum }_{j=1}^k{\mathbb{I}}_{\left\{X_j\le t\right\}}$ is binomially distributed with parameters k and $T\left(t\right)=\mathbb{P}\left(X_1\le t\right)$, and thus

$$\begin{array}{cc}\hfill \mathbb{P}\left(\rho \underset{t\in A_{\alpha }(m,x)}{max}\left|\frac{T_k\left(t\right)-T\left(t\right)}{t}\right|>ϵ\right)& \le \sum _{t\in A_{\alpha }(m,x)}\mathbb{P}\left(|k{T}_k\left(t\right)-kT\left(t\right)|>\frac{ϵt}{\rho T\left(t\right)}kT\left(t\right)\right)\hfill \\ \hfill & \le 2\sum _{t\in A_{\alpha }(m,x)}{e}^{-kT\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)}\hfill \\ \hfill & \le 2|A_{\alpha }(m,x)|e^{-k{inf}_{t\in A_{\alpha }(m,x)}T\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)}\hfill \\ \hfill & \le 2m(1-x)e^{-k{inf}_{t\in A_{\alpha }(m,x)}T\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)},\hfill \end{array}$$

where we have used the fact that the number of elements in $A_{\alpha }(m,x)$ is bounded from above as follows $|A_{\alpha }(m,x)|\le m(1-x).$ Next, (6) is deduced from the assumption that $T\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)$ as a function of t is non-decreasing on $\left[\alpha x,\alpha \right)$ and the simple fact $A_{\alpha }(m,x)\subseteq \left[\alpha x,\alpha \right)$.  □

Applying Proposition 1 with $T=F$ and $T=G$ and respectively $m_0=m\gamma$ and $m_1=m(1-\gamma )$ and $\rho =\gamma$ and $\rho =1-\gamma$ we can confirm from (4) the proof of Theorem 3.1 in [15] in the sense that we have the convergence in probability

$$\underset{m\to \infty }{lim}\underset{t\in \left\{\alpha \frac{\lceil mx\rceil }{m},\cdots ,\alpha \frac{m-1}{m},\alpha \right\}}{max}\frac{H_m\left(t\right)-t}{t}\stackrel{\mathbb{P}}{=}\left(1-\gamma \right)\underset{\left[\alpha x,\alpha \right]}{sup}\frac{G\left(t\right)-t}{t}=:u_{\alpha ,\gamma }\left(x\right).$$

(11)

Clearly, $u_{\alpha ,\gamma }:\left[0,1\right]\mapsto \mathbb{R}$, with $u_{\alpha ,\gamma }\left(1\right)=\frac{G\left(\alpha \right)-\alpha }{\alpha }$, is a non-increasing function on $\left(0,1\right]$. Denote

$${\underline{x}}_{\alpha ,\gamma }^{\beta }=inf\{x\in \left(0,1\right):u_{\alpha ,\gamma }\left(x\right)\le \frac{1}{\beta }-1\},\alpha ,\beta \in \left(0,1\right),$$

(12)

and

$${\overline{x}}_{\alpha ,\gamma }^{\beta }=inf\{x\in \left(0,1\right):u_{\alpha ,\gamma }\left(x\right)<\frac{1}{\beta }-1\},\alpha ,\beta \in \left(0,1\right).$$

(13)

Since $u_{\alpha ,\gamma }$ is non-increasing we have that ${\overline{x}}_{\alpha ,\gamma }^{\beta }\ge {\underline{x}}_{\alpha ,\gamma }^{\beta }$. Therefore from relations (2) and (4) we can easily get that

$$\begin{array}{cc}\hfill & \underset{m\to \infty }{lim}\mathbb{P}\left(\frac{R_m}{m}\ge x\right)=1,\mathrm{for}x<{\underline{x}}_{\alpha ,\gamma }^{\alpha }\hfill \\ \hfill & \underset{m\to \infty }{lim}\mathbb{P}\left(\frac{R_m}{m}\ge x\right)=0,\mathrm{for}x>{\overline{x}}_{\alpha ,\gamma }^{\alpha }.\hfill \end{array}$$

(14)

We can provide more precise information about probabilities of the type $\mathbb{P}\left(\frac{R_m}{m}<x\right)$ in the general case. In the sequel we use ${\mathbb{I}}_{\left\{A\right\}}$ for the indicator function of the set A.

Proposition 2.

We have for any $ϵ>0$ and $x\in \left(0,1\right)$ that

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\frac{R_m}{m}<x\right)\ge 1-K_F(x,m,m_0,\gamma ,ϵ,\alpha )-K_G(x,m,m_1,1-\gamma ,ϵ,\alpha )\hfill \\ \hfill & -{\mathbb{I}}_{\left\{\left(1-\gamma \right){max}_{t\in A_{\alpha }(x,m)}\frac{G\left(t\right)-t}{t}\ge \frac{1}{\alpha }-1-2ϵ\right\}}.\hfill \end{array}$$

(15)

Proof. 

Using successively (2), (4) and (10) with $\rho =\gamma ,k=m_0=\gamma m$ for the probability involving $F_{m_0}$ and $\rho =1-\gamma ,k=m_1=\left(1-\gamma \right)m$ for the expression concerning $G_{m_1}$, we arrive at the inequalities

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\frac{R_m}{m}<x\right)=1-\mathbb{P}\left(\frac{R_m}{m}\ge x\right)\hfill \\ \hfill & =1-\mathbb{P}\left(\left\{\underset{t\in A_{\alpha }(x,m)}{max}\frac{H_m\left(t\right)-t}{t}\ge \frac{1}{\alpha }-1\right\}\right)\hfill \\ \hfill & \ge 1-\mathbb{P}\left(\gamma \underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{F_{m_0}\left(t\right)-t}{t}\right|>ϵ\right)-\mathbb{P}\left(\left(1-\gamma \right)\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{G_{m_1}\left(t\right)-G\left(t\right)}{t}\right|>ϵ\right)\hfill \\ \hfill & -{\mathbb{I}}_{\left\{\left(1-\gamma \right){max}_{t\in A_{\alpha }(x,m)}\frac{G\left(t\right)-t}{t}\ge \frac{1}{\alpha }-1-2ϵ\right\}}\times \hfill \\ \hfill & \times \mathbb{P}\left(\underset{t\in A_{\alpha }(x,m)}{max}\left(\gamma \left|\frac{F_{m_0}\left(t\right)-t}{t}\right|,\left|(1-\gamma )\frac{G_{m_1}\left(t\right)-G\left(t\right)}{t}\right|\right)\le ϵ\right)\hfill \\ \hfill & \ge 1-K_F(x,m,m_0,\gamma ,ϵ,\alpha )-K_G(x,m,m_1,1-\gamma ,ϵ,\alpha )\hfill \\ \hfill & -{\mathbb{I}}_{\left\{\left(1-\gamma \right){max}_{t\in A_{\alpha }(x,m)}\frac{G\left(t\right)-t}{t}\ge \frac{1}{\alpha }-1-2ϵ\right\}}.\hfill \end{array}$$

(16)

We only note that in the last expression of the first inequality above we have used that once the dependence on $F_{m_0},G_{m_1}$ is estimated away, the remaining term is deterministic and thus the indicator function appears.  □

2.3. Condition (M)

In view of the fact that Theorem 3.1 in [15] holds, the limit in probability, that is $\underset{m\to \infty }{lim}\frac{R_m}{m}=x_{\alpha ,\gamma }$ exists if and only if ${\underline{x}}_{\alpha ,\gamma }^{\alpha }={\overline{x}}_{\alpha ,\gamma }^{\alpha }=x_{\alpha ,\gamma }$. We shall therefore restrict our attention only to the case when for fixed $\alpha$ we have that the function $\frac{G\left(t\right)-t}{t}$ is decreasing on $\left(0,\alpha \right]$. In this case we have from (11) that

$$u_{\alpha ,\gamma }\left(x\right)=(1-\gamma )\frac{G\left(\alpha x\right)-\alpha x}{\alpha x}.$$

(17)

If in addition $\underset{t\to 0}{lim}\frac{G\left(t\right)-t}{t}=\infty$ then

$$x_{\alpha ,\gamma }^{\beta }:={\underline{x}}_{\alpha ,\gamma }^{\beta }={\overline{x}}_{\alpha ,\gamma }^{\beta },\mathrm{for}\mathrm{any}\beta <1,$$

(18)

and if $\beta =\alpha$ then we set $x_{\alpha ,\gamma }:=x_{\alpha ,\gamma }^{\alpha }.$ From now on we work under this condition which we call condition (M) and which is synthesized as follows.

Definition 1.

We say that condition (M) holds for fixed $\alpha \in \left(0,1\right)$ if and only if $H\left(t\right):=\frac{G\left(t\right)-t}{t}$ is decreasing on $\left(0,\alpha \right]$ with $\underset{t\to 0}{lim}H\left(t\right)=\infty$.

Remark 4.

As mentioned in [17], “[u]nder the alternative hypothesis, the p-values will have a distribution that has high density for small p-values and the density will decrease as the p-values increase”. Therefore when modeling the p-values under the alternative hypothesis with a Beta distribution, $B(a,b)$, its parameters should be so that $a<1$ and $b\ge 1$. Note that condition (M) also holds when $b<1$ and $a<(1-2\alpha )/(1-\alpha )$, although that case should not happen for well-behaved statistical procedures.

Remark 5.

Note that in our context Equation (2.2) of [13] translates to ${\alpha }_{*}={inf}_{u>0}\{u/G\left(u\right)\}$ and as it is mentioned there, the asymptotic of the Benjamini–Hochberg procedure exhibits a very different behavior on the regions $\alpha \in \left(0,{\alpha }_{*}\right)$ and $\alpha >{\alpha }_{*}$. In the same paper it is demonstrated that when $G\left(t\right)/t\to 0$ then the overwhelming proportion of discoveries will be amongst the non-significant features. Under our assumptions it is always true that ${\alpha }_{*}=0$ and therefore we are always in the second regime, for which [13] provides a law of the iterated logarithm for $R_n$, see Theorem 2.2 of [13]. In more detail it is shown that the precise estimate

$$\underset{n\to \infty }{lim\; sup}\pm \frac{R_n-x_{\alpha ,\gamma }}{\sqrt{nlog\left(log\left(n\right)\right)}}=\frac{\sqrt{x_{\alpha ,\gamma }\left(1-x_{\alpha ,\gamma }\right)}}{1-\alpha G^{\prime }\left(x_{\alpha ,\gamma }\right)}$$

holds true.

A very interesting contribution is made in Theorems 3.1 and 3.2 in [18]. The author finds a Donsker-type of convergence for the so-called threshold procedures, which are essentially functionals on the empirical functions $H_m\left(t\right)$ which recover, for example, the false discovery rate, see Theorem 3.2 in [18]. This implies a convergence rate $1/\sqrt{n}$ in $|R_n/n-x_{\alpha ,\gamma }|$ and is applicable in a variety of other examples. Moreover, their results go beyond the scope of the Benjamini–Hochberg procedure and capture different procedures some of which are of higher power than the Benjamini–Hochberg procedure. In the particular case of the Benjamini–Hochberg procedure, however, we know from [15] that the probabilities of the events $\left\{|\frac{R_n}{n}-x_{\alpha ,\gamma }|\le \beta x_{\alpha ,\gamma }\right\}$ and of $\left\{|\frac{S_n}{n}-x_{\alpha ,\gamma }\frac{1-\alpha \gamma }{1-\gamma }|\le \beta x_{\alpha ,\gamma }\frac{1-\alpha \gamma }{1-\gamma }\right\}$, where $S_n/n$ is the power of that procedure, converge to 1. Our Theorems 1 and 3 strengthen this by showing that the speed of convergence is of an exponential order. As discussed earlier, this allows a direct estimate on the probability that $S_n/n$ is in a prescribed interval.

Remark 6.

We note that upon the validity of condition (M) it is impossible that G has atoms on $\left(0,\alpha \right)$ as otherwise if $\mathbf{a}\in \left(0,\alpha \right)$ is an atom then

$$\underset{t\downarrow \mathbf{a}}{lim}H\left(t\right)=H\left(\mathbf{a}\right)>\underset{t\uparrow \mathbf{a}}{lim}H\left(t\right)=H(\mathbf{a}-),$$

which leads to a contradiction with the assumption that H is decreasing. Thus, our initial requirement that G is continuous is included in condition (M). This also means that H is continuous on $\left(0,\alpha \right)$ and thus ${\underline{x}}_{\alpha ,\gamma }^{\beta }={\overline{x}}_{\alpha ,\gamma }^{\beta }=x_{\alpha ,\gamma }^{\beta }$.

We then have the following elementary lemma.

Lemma 1.

Condition (M) is valid for fixed $\alpha \in \left(0,1\right)$ if G has on $\left(0,\alpha \right)$ a density $g=G^{\prime }$ satisfying $\underset{x\to 0}{lim}g\left(x\right)=g\left(0\right)=\infty$ and $tg\left(t\right)-G\left(t\right)<0$ on $\left(0,\alpha \right)$. The latter is satisfied if, for example, $g^{\prime }\left(t\right)<0$ on $\left(0,\alpha \right)$.

Proof. 

From the assumptions it is clear that on $\left(0,\alpha \right)$

$$\begin{array}{cc}\hfill \frac{dH\left(t\right)}{dt}& =\frac{\left(g\left(t\right)-1\right)t-{\int }_0^t\left(g\left(s\right)-1\right)ds}{t^2}<0\hfill \\ \hfill & \iff tg\left(t\right)-G\left(t\right)<0.\hfill \end{array}$$

Furthermore, since $\underset{t\to 0}{lim}\frac{G\left(t\right)}{t}=g\left(0\right)=\infty$ we conclude that $\underset{t\to 0}{lim}H\left(t\right)=\infty$. Thus the first part of the proof is settled. Clearly, $tg\left(t\right)-G\left(t\right)<0$ if $g^{\prime }\left(t\right)<0$ on $\left(0,\alpha \right)$ and the overall proof is thus completed.  □

The next lemma ensures an easier expression for $K_G$, see (5) and (6), provided condition (M) holds.

Lemma 2.

Let condition (M) hold for G and $m_1=m(1-\gamma )$. Then we have that

$$\begin{array}{cc}\hfill K_G^{\mathbf{M}}\left(x,m,1-\gamma ,ϵ,\alpha \right)& =K_G(x,m,m_1,1-\gamma ,ϵ,\alpha )\hfill \\ \hfill & =2min\left\{m(1-x)e^{-m(1-\gamma )G\left(\alpha x\right)c\left(\frac{ϵ}{1-\gamma }\frac{\alpha x}{G\left(\alpha x\right)}\right)},e^{-2\frac{m}{\left(1-\gamma \right)}{\left(ϵ\alpha x\right)}^2}\right\}.\hfill \end{array}$$

(19)

The same holds for the c.d.f. of the uniform distribution F. In particular if $\gamma >1/2$ then

$$\begin{array}{cc}\hfill K_F^{\mathbf{M}}\left(x,m,\gamma ,ϵ,\alpha \right)& =K_F(x,m,m_0,\gamma ,ϵ,\alpha )\hfill \\ \hfill & =2min\left\{m(1-x)e^{-m\gamma \alpha xc\left(\frac{ϵ}{\gamma }\right)},e^{-2\frac{m}{\gamma }{\left(ϵ\alpha x\right)}^2}\right\}.\hfill \end{array}$$

(20)

Remark 7.

Under condition (M) we have that $G\left(t\right)c\left(d\frac{t}{G\left(t\right)}\right)$ is non-decreasing on $\left(0,\alpha \right)$, for any $d>0$, since $\frac{t}{G\left(t\right)}$ is non-decreasing on $\left(0,\alpha \right)$ and c is increasing on $\left(0,\infty \right)$, see Proposition A1. Hence the function $K_G^{\mathbf{M}}\left(x,m,1-\gamma ,ϵ,\alpha \right)$ is decreasing in x as long as the other parameters stay fixed. The same is valid for $K_F^{\mathbf{M}}$.

Proof of Lemma 2.

The proof is immediate from (6) since under condition (M) we have that the function $G\left(t\right)c\left(\frac{ϵ}{1-\gamma }\frac{t}{G\left(t\right)}\right)$ is non-decreasing on $\left(0,\alpha \right)$, see Remark 7. We just note that by definition $m_1=m(1-\gamma )$ and we have employed this for k in (6) to derive (19). Finally, (20) follows from (7).  □

2.4. Theoretical Bounds on the Distribution of $R_m$ under Condition ( M)

If condition (M) holds we have the identity equivalent to (17)

$$\underset{t\in A_{\alpha }(x,m)}{max}H\left(t\right)=\frac{G\left(\alpha \frac{\lceil mx\rceil }{m}\right)-\alpha \frac{\lceil mx\rceil }{m}}{\alpha \frac{\lceil mx\rceil }{m}}=H\left(\alpha \frac{\lceil mx\rceil }{m}\right)$$

(21)

and with $\beta =\alpha$ relation (18) together with (12) and (13) gives that

$$\frac{1}{\alpha }-1=(1-\gamma )H\left(\alpha x_{\alpha ,\gamma }\right)=\left(1-\gamma \right)\left(\frac{G\left(\alpha x_{\alpha ,\gamma }\right)-\alpha x_{\alpha ,\gamma }}{\alpha x_{\alpha ,\gamma }}\right).$$

(22)

Let $\beta >0$ and denote using (21)

$$\begin{array}{cc}\hfill m_G(x,\beta ,\alpha ,\gamma ):& =inf\{k\in {\mathbb{N}}^{+}:\underset{m\ge k}{max}{\mathbb{I}}_{\left\{\left(1-\gamma \right){max}_{t\in A_{\alpha }(x,m)}H\left(t\right)\ge \beta \right\}}=0\}\hfill \\ \hfill & =inf\{k\in {\mathbb{N}}^{+}:\underset{m\ge k}{max}{\mathbb{I}}_{\left\{\left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\ge \beta \right\}}=0\}.\hfill \end{array}$$

(23)

We then have the following key result:

Theorem 1.

Let condition (M) hold for given G and fixed $\alpha \in \left(0,1\right)$ with $G\left(\alpha \right)<1$. Fix $\gamma \in \left(0,1\right)$. Recall from (18) that $x_{\alpha ,\gamma }={\underline{x}}_{\alpha ,\gamma }^{\alpha }={\overline{x}}_{\alpha ,\gamma }^{\alpha }$. Then $\underset{m\to \infty }{lim}\frac{R_m}{m}=x_{\alpha ,\gamma }\in \left(0,1\right)$. Moreover, for any $x\in \left(x_{\alpha ,\gamma },1\right)$, $\exists ϵ\left(x\right)$ such that for any $0\le ϵ\le ϵ\left(x\right)$ the inequality $\left(1-\gamma \right)H\left(\alpha x\right)<\frac{1}{\alpha }-1-2ϵ$ holds and then for any $m\ge m_G(x,\frac{1}{\alpha }-1-2ϵ,\alpha ,\gamma )$ we have that

$$\begin{array}{cc}\hfill \mathbb{P}\left(\frac{R_m}{m}\le x\right)& \ge 1-K_F^{\mathbf{M}}(x,m,\gamma ,ϵ,\alpha )-K_G^{\mathbf{M}}(x,m,1-\gamma ,ϵ,\alpha ).\hfill \end{array}$$

(24)

Finally, for any $x\in \left(0,x_{\alpha ,\gamma }\right)$, $\exists ϵ\left(x\right)$ such that for any $0\le ϵ\le ϵ\left(x\right)$ the inequality $\left(1-\gamma \right)H\left(\alpha x\right)>\frac{1}{\alpha }-1+2ϵ$ holds and then for any $m\ge m_G(x,\frac{1}{\alpha }-1+2ϵ,\alpha ,\gamma )$

$$\begin{array}{cc}\hfill \mathbb{P}\left(\frac{R_m}{m}<x\right)& \le K_F^{\mathbf{M}}(x,m,\gamma ,ϵ,\alpha )+K_G^{\mathbf{M}}(x,m,1-\gamma ,ϵ,\alpha ).\hfill \end{array}$$

(25)

Remark 8.

It seems important to evaluate or approximate $m_G(x,\frac{1}{\alpha }-1-2ϵ,\alpha ,\gamma )$ with say $m^{\prime }$ so that (24) is valid beyond this estimate, that is for $m\ge m^{\prime }$. If $H_d:={inf}_{t\in \left(0,\alpha \right)}\left|H^{\prime }\left(t\right)\right|>0$, since $\alpha x<\alpha \frac{\lceil mx\rceil }{m}$, $1>x>x_{\alpha ,\gamma }$ and H is decreasing on $\left(0,\alpha \right)$ we get using 22 in the first relation

$$\begin{array}{cc}\hfill \frac{1}{\alpha }-1& =(1-\gamma )H\left(\alpha x_{\alpha ,\gamma }\right)=\left(1-\gamma \right)\left(H\left(\alpha x_{\alpha ,\gamma }\right)-H\left(\alpha x\right)\right)+\left(1-\gamma \right)H\left(\alpha x\right)\hfill \\ \hfill & \ge \left(1-\gamma \right)H_d\alpha \left(x-x_{\alpha ,\gamma }\right)+\left(1-\gamma \right)H\left(\alpha x\right).\hfill \end{array}$$

However, if $\left(1-\gamma \right)H_d\alpha \left(x-x_{\alpha ,\gamma }\right)>2ϵ$ we get from the last observation that

$$\begin{array}{cc}\hfill \left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)& \le \left(1-\gamma \right)H\left(\alpha x\right)\le \frac{1}{\alpha }-1-\left(1-\gamma \right)H_d\alpha \left(x-x_{\alpha ,\gamma }\right)\hfill \\ & <\frac{1}{\alpha }-1-2ϵ=\frac{1}{{\alpha }_{ϵ}}\hfill \end{array}$$

for any $m\ge 1$ and therefore if $\left(1-\gamma \right)\alpha H_d\left(x-x_{\alpha ,\gamma }\right)>2ϵ$ then

$$m_G(x,\frac{1}{\alpha }-1-2ϵ,\alpha ,\gamma )=inf\{k\in \mathbb{N}:\underset{m\ge k}{max}{\mathbb{I}}_{\left\{\left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\ge \frac{1}{\alpha }-1-2ϵ\right\}}=0\}=1.$$

and (24) is always valid. Of course various similar and more precise estimates can be achieved, but these are beyond the scope of this work.

Remark 9.

Considering Remark 3 the inequalities (24) and (25) can be improved for computational purposes by using as an upper bound the expression

$$2min\left\{\sum _{t\in A_{\alpha }(m,x)}{e}^{-kT\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)},e^{-2\frac{k}{{\rho }^2}{\left(ϵ\alpha x\right)}^2}\right\}$$

for $K_T^{\mathbf{M}},T=G,F$ with $k=m_1,m_0;\rho =1-\gamma ,\gamma$ respectively.

Remark 10.

We point out that in our setting $\underset{m\to \infty }{lim}\frac{R_m}{m}>0$ and there have been a number of works that attempt to offer FDR even under weak dependence structure between the random variables following the uniform distribution or ${\left(X_j\right)}_{j\le m_0}$. We point out, for example, to [19]. There is an interesting contribution, see [20], which discusses difficulties in controlling FDR under weak dependence in the case when $\underset{m\to \infty }{lim}\frac{R_m}{m}=0$.

Proof of Theorem 1.

Under condition (M) we have that ${\underline{x}}_{\alpha ,\gamma }^{\alpha }={\overline{x}}_{\alpha ,\gamma }^{\alpha }:=x_{\alpha ,\gamma }$, see (18). Clearly, $x_{\alpha ,\gamma }\in \left(0,1\right)$ since $u_{\alpha ,\gamma }\left(0\right)=\infty$ and $u_{\alpha ,\gamma }\left(1\right)=\frac{G\left(\alpha \right)-\alpha }{\alpha }<\frac{1}{\alpha }-1$, see (17), and by assumption $G\left(\alpha \right)<1$. The fact that $\underset{m\to \infty }{lim}\frac{R_m}{m}=x_{\alpha ,\gamma }\in \left(0,1\right)$ follows from Theorem 3.1 in [15]. Henceforth, it remains to show (24) and (25). The former thanks to (16) and (19) follows for any $m\ge m_G(x,\frac{1}{\alpha }-1-2ϵ,\alpha ,\gamma ),$ if $m_G(x,\frac{1}{\alpha }-1-2ϵ,\alpha ,\gamma )<\infty$, since then

$${\mathbb{I}}_{\left\{\left(1-\gamma \right){max}_{t\in A_{\alpha }(x,m)}\frac{G\left(t\right)-t}{t}\ge \frac{1}{\alpha }-1-2ϵ\right\}}={\mathbb{I}}_{\left\{\left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\ge \frac{1}{\alpha }-1-2ϵ\right\}}=0.$$

However, since $\underset{m\to \infty }{lim}\alpha \frac{\lceil mx\rceil }{m}=\alpha x$, $x>x_{\alpha ,\gamma }$ and H decreasing on $\left(0,\alpha \right)$, then

$$\underset{m\to \infty }{lim}\left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)=\left(1-\gamma \right)H\left(\alpha x\right)<\left(1-\gamma \right)H\left(\alpha x_{\alpha ,\gamma }\right)=\frac{1}{\alpha }-1.$$

Thus, for all $ϵ$ small enough, we conclude that $\left(1-\gamma \right)H\left(\alpha x\right)<\frac{1}{\alpha }-1-2ϵ$ and thus $m_G(x,\frac{1}{\alpha }-1-2ϵ,\alpha ,\gamma )<\infty$, see (23). Hence, (24) follows.

To prove (25) for any $x\in \left(0,x_{\alpha ,\gamma }\right)$ we work with the complement event, that is $\left\{\frac{R_m}{m}\ge x\right\}$. Similarly as in (16) and utilizing (4) and (21) we get that on the event

$$\left\{\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{F_{m_0}\left(t\right)-t}{t}\right|\le \frac{ϵ}{\gamma };\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{G_{m_1}\left(t\right)-G\left(t\right)}{t}\right|\le \frac{ϵ}{1-\gamma }\right\}$$

we have that ${max}_{t\in A_{\alpha }(x,m)}\frac{H_m\left(t\right)-t}{t}\ge \left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)-2ϵ$ and therefore

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\frac{R_m}{m}\ge x\right)\ge \hfill \\ \hfill & \mathbb{P}\left(\frac{R_m}{m}\ge x;\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{F_{m_0}\left(t\right)-t}{t}\right|\le \frac{ϵ}{\gamma };\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{G_{m_1}\left(t\right)-G\left(t\right)}{t}\right|\le \frac{ϵ}{1-\gamma }\right)\hfill \\ \hfill & \ge \mathbb{P}\left(\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{F_{m_0}\left(t\right)-t}{t}\right|\le \frac{ϵ}{\gamma };\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{G_{m_1}\left(t\right)-G\left(t\right)}{t}\right|\le \frac{ϵ}{1-\gamma }\right)\hfill \\ \hfill & \times {\mathbb{I}}_{\left\{\left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\ge \frac{1}{\alpha }-1+2ϵ\right\}}.\hfill \end{array}$$

Again as $\frac{\lceil mx\rceil }{m}\to x<x_{\alpha ,\gamma }$ and $H\left(\alpha x\right)>H\left(\alpha x_{\alpha ,\gamma }\right)$ we conclude that for all $ϵ$ small enough the inequality $(1-\gamma )H\left(\alpha x\right)\ge \frac{1}{\alpha }-1+2ϵ$ holds and we have that

$$\underset{m\to \infty }{lim}{\mathbb{I}}_{\left\{\left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\ge \frac{1}{\alpha }-1+2ϵ\right\}}=1.$$

(26)

From Proposition 1, the expressions for $K_F^{\mathbf{M}},K_G^{\mathbf{M}}$ in Lemma 2 and the independence of ${\left(X_j\right)}_{j\le m_0}$ and ${\left(X_j\right)}_{m\ge j>m_0}$ we have that

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{F_{m_0}\left(t\right)-t}{t}\right|\le \frac{ϵ}{\gamma };\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{G_{m_1}\left(t\right)-G\left(t\right)}{t}\right|\le \frac{ϵ}{1-\gamma }\right)\hfill \\ \hfill & =\mathbb{P}\left(\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{F_{m_0}\left(t\right)-t}{t}\right|\le \frac{ϵ}{\gamma }\right)\mathbb{P}\left(\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{G_{m_1}\left(t\right)-G\left(t\right)}{t}\right|\le \frac{ϵ}{1-\gamma }\right)\hfill \\ \hfill & \ge \left(1-K_F^{\mathbf{M}}(x,m,\gamma ,ϵ,\alpha )\right)\left(1-K_G^{\mathbf{M}}(x,m,1-\gamma ,ϵ,\alpha )\right).\hfill \end{array}$$

and we conclude the proof of the theorem via the now trivial relations

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\frac{R_m}{m}<x\right)=1-\mathbb{P}\left(\frac{R_m}{m}\ge x\right)\hfill \\ \hfill & \le 1-\mathbb{P}\left(\frac{R_m}{m}\ge x;\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{F_{m_0}\left(t\right)-t}{t}\right|\le \frac{ϵ}{\gamma };\underset{t\in A_{\alpha }(x,m)}{max}\left|\frac{G_{m_1}\left(t\right)-G\left(t\right)}{t}\right|\le \frac{ϵ}{1-\gamma }\right)\hfill \\ \hfill & \le 1-\left(1-K_F^{\mathbf{M}}(x,m,\gamma ,ϵ,\alpha )\right)\left(1-K_G^{\mathbf{M}}(x,m,1-\gamma ,ϵ,\alpha )\right)\times \hfill \\ \hfill & \times {\mathbb{I}}_{\left\{\left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\ge \frac{1}{\alpha }-1+2ϵ\right\}}\hfill \end{array}$$

(27)

and an appeal to (26).  □

For practical reasons and especially for the accompanying software routine it is optimal to choose $ϵ$ in Theorem 1 as large as possible. The latter is due to fact that the bounds for $K_F^{\mathbf{M}},K_G^{\mathbf{M}}$, see (19) and (20), are decreasing in $ϵ$. Since in practical computations m is usually available, it is then beneficial to choose the largest $ϵ$ as a function in $x,m$ in a way that the previous theorem holds. In this direction we have the following result:

Theorem 2.

Under the conditions of Theorem 1 and $m\in {\mathbb{N}}^{+},x\in \left(x_{\alpha ,\gamma },1\right)$ fixed we have that

$$\begin{array}{cc}\hfill \mathbb{P}\left(\frac{R_m}{m}\le x\right)& \ge 1-K_F^{\mathbf{M}}(x,m,\gamma ,{ϵ}_G,\alpha )-K_G^{\mathbf{M}}(x,m,1-\gamma ,{ϵ}_G,\alpha ),\hfill \end{array}$$

(28)

where

$$\begin{array}{cc}\hfill {ϵ}_G& =ϵ(x,m)=\frac{1}{2}\left(\frac{1}{\alpha }-1\right)-\frac{1-\gamma }{2}H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\hfill \\ \hfill & =\frac{1-\gamma }{2}\left(H\left(\alpha x_{\alpha ,\gamma }\right)-H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\right).\hfill \end{array}$$

(29)

Similarly, if $m\in \mathbb{N},x\in \left(0,x_{\alpha ,\gamma }\right)$ are fixed and $\frac{\lceil mx\rceil }{m}<x_{\alpha ,\gamma }$ then

$$\begin{array}{cc}\hfill \mathbb{P}\left(\frac{R_m}{m}<x\right)& \le K_F^{\mathbf{M}}(x,m,\gamma ,{ϵ}_G,\alpha )+K_G^{\mathbf{M}}(x,m,1-\gamma ,{ϵ}_G,\alpha ),\hfill \end{array}$$

(30)

where

$$\begin{array}{cc}\hfill {ϵ}_G& =ϵ(x,m)=\frac{1-\gamma }{2}H\left(\alpha \frac{\lceil mx\rceil }{m}\right)-\frac{1}{2}\left(\frac{1}{\alpha }-1\right)\hfill \\ \hfill & =\frac{1-\gamma }{2}\left(H\left(\alpha \frac{\lceil mx\rceil }{m}\right)-H\left(\alpha x_{\alpha ,\gamma }\right)\right).\hfill \end{array}$$

(31)

Proof. 

To show (28) with ${ϵ}_G$ as in (29) it suffices to show that for the chosen ${ϵ}_G$ and the given $m,x$ we have that

$${\mathbb{I}}_{\left\{\left(1-\gamma \right){max}_{t\in A_{\alpha }(x,m)}\frac{G\left(t\right)-t}{t}\ge \frac{1}{\alpha }-1-2ϵ\right\}}=0$$

in (16). However, as condition (M) holds, then

$$\underset{t\in A_{\alpha }(x,m)}{max}\frac{G\left(t\right)-t}{t}=\underset{t\in A_{\alpha }(x,m)}{max}H\left(t\right)=H\left(\alpha \frac{\lceil mx\rceil }{m}\right)$$

and we see that ${ϵ}_G$ is the maximal possible choice such that

$${\mathbb{I}}_{\left\{\left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\ge \frac{1}{\alpha }-1-2ϵ\right\}}=0.$$

For the second part of (29) we only recall that $\left(1-\gamma \right)H\left(\alpha x_{\alpha ,\gamma }\right)=\frac{1}{\alpha }-1$, see (22). The rest of the theorem, that is (30) and (31), follows in a similar fashion from (27) wherein the expression of (31) is the maximal $ϵ$ such that for the fixed $m,x\in \left(0,x_{\alpha ,\gamma }\right)$

$${\mathbb{I}}_{\left\{\left(1-\gamma \right)H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\ge \frac{1}{\alpha }-1+2ϵ\right\}}=1.$$

We only note that in this instance we need to have that $x<\frac{\lceil mx\rceil }{m}<x_{\alpha ,\gamma }$, which is part of the assumptions of the theorem.  □

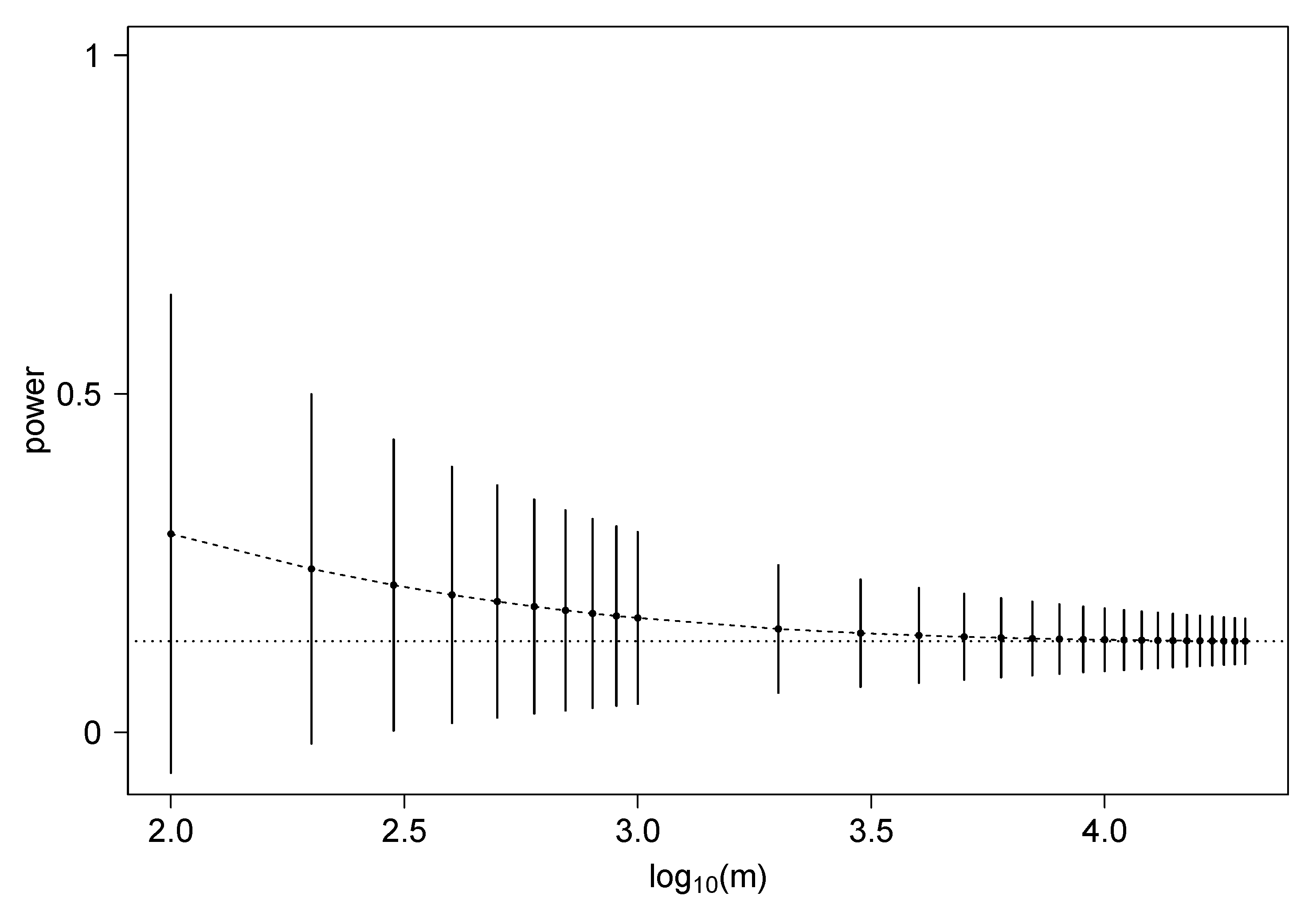
2.5. Exponential Convergence to the Theoretical Limit of the Power of the Benjamini–Hochberg Procedure

We proceed by studying the question about the power of the test. It is clear that if we denote by

$$S_m=\sum _{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha \frac{R_m}{m}\right\}},$$

(32)

where ${\left(X_j\right)}_{1\le j\le m_1}$ are i.i.d. with c.d.f G then

$$S_m^{*}=\frac{S_m}{m_1}$$

(33)

is the proportion of tested elements that we have correctly identified as significant or the power of the test. If one wishes to understand the behavior of $S_m^{*}$ with the increase of m one ought to decouple its dependence on $\frac{R_m}{m}$ in (32). Theorem 1 aids in this matter. We note that if we choose $x_1<\underset{m\to \infty }{lim}\frac{R_m}{m}=x_{\alpha ,\gamma }<x_2$, see (18) for the definition of $x_{\alpha ,\gamma }$, then from Theorem 1 we have for every

$$m\ge max\left\{m_G(x_1,\frac{1}{\alpha }-1-2ϵ,\alpha ,\gamma );m_G(x_2,\frac{1}{\alpha }-1+2ϵ,\alpha ,\gamma )\right\}:=m^{*}(x_1,x_2,ϵ,\alpha ,\gamma )$$

with $ϵ\le min\left\{ϵ\left(x_1\right),ϵ\left(x_2\right)\right\}$ that

$$\begin{array}{cc}\hfill \mathbb{P}\left(\frac{R_m}{m}\in \left[x_1,x_2\right]\right)& =\mathbb{P}\left(\frac{R_m}{m}\le x_2\right)-\mathbb{P}\left(\frac{R_m}{m}<x_1\right)\hfill \\ \hfill & \ge 1-\left(K_F^{\mathbf{M}}(x_2,m,\gamma ,ϵ,\alpha )+K_G^{\mathbf{M}}(x_2,m,1-\gamma ,ϵ,\alpha )\right)\hfill \\ \hfill & -\left(K_F^{\mathbf{M}}(x_1,m,\gamma ,ϵ,\alpha )+K_G^{\mathbf{M}}(x_1,m,1-\gamma ,ϵ,\alpha )\right).\hfill \end{array}$$

(34)

Then we can formulate the following fundamental result that offers exponential bounds on the convergence of $S_m^{*}$.

Theorem 3.

Let condition (M) be valid and assume the notation of Theorem 1. Let next $x_{\alpha ,\gamma }\in \left(x_1,x_2\right)\subset \left(0,1\right)$. Then there exists $m^{*}=m^{*}(x_1,x_2,ϵ,\alpha ,\gamma )$ and ${ϵ}^{*}=ϵ(x_1,x_2)$ such that for any $m\ge m^{*}$ and any $ϵ\le {ϵ}^{*}$

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\frac{1}{m_1}\sum _{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha x_1\right\}}\le S_m^{*}\le \frac{1}{m_1}\sum _{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha x_2\right\}}\right)\hfill \\ \hfill & \ge 1-\left(K_F^{\mathbf{M}}(x_1,m,\gamma ,ϵ,\alpha )+K_G^{\mathbf{M}}(x_1,m,1-\gamma ,ϵ,\alpha )\right)\hfill \\ \hfill & -\left(K_F^{\mathbf{M}}(x_2,m,\gamma ,ϵ,\alpha )+K_G^{\mathbf{M}}(x_2,m,1-\gamma ,ϵ,\alpha )\right).\hfill \end{array}$$

(35)

Clearly, the random variables ${\sum }_{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha x\right\}}$ are Binomial with parameters $m_1$ and $G\left(\alpha x\right)=\mathbb{P}\left(X_1\le \alpha x\right)$. Henceforth,

$$\underset{m\to \infty }{lim}{S}_m^{*}=G\left(\alpha x_{\alpha ,\gamma }\right)=x_{\alpha ,\gamma }\frac{1-\alpha \gamma }{1-\gamma }.$$

(36)

Moreover, for any $\eta \in \left(0,1\right)$ with $m,ϵ$ as above, we have that

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\left(1-\eta \right)G\left(\alpha x_1\right)\le S_m^{*}\le \left(1+\eta \right)G\left(\alpha x_2\right)\right)\hfill \\ \hfill & \ge 1-\left(K_F^{\mathbf{M}}(x_1,m,\gamma ,ϵ,\alpha )+K_G^{\mathbf{M}}(x_1,m,1-\gamma ,ϵ,\alpha )\right)\hfill \\ \hfill & -\left(K_F^{\mathbf{M}}(x_2,m,\gamma ,ϵ,\alpha )+K_G^{\mathbf{M}}(x_2,m,1-\gamma ,ϵ,\alpha )\right)\hfill \\ \hfill & -e^{-mc\left(\eta \right)(1-\gamma )G\left(\alpha x_1\right)}-e^{-mc\left(\eta \right)(1-\gamma )G\left(\alpha x_2\right)}\hfill \end{array}$$

(37)

where $c\left(\eta \right)=(1+\eta )ln\left(1+\eta \right)-\eta ,\eta >0,$ is considered in Proposition A1.

Remark 11.

We note that (36) has been proved in Corollary 3.3 in [15], but here we offer some exponential bounds on this convergence.

Proof of Theorem 3.

The proof of (35) follows immediately from (32), (34) and the considerations thereabout since

$$\mathbb{P}\left(\frac{1}{m_1}\sum _{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha x_1\right\}}\le S_m^{*}\le \frac{1}{m_1}\sum _{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha x_2\right\}}\right)\ge \mathbb{P}\left(\frac{R_m}{m}\in \left[x_1,x_2\right]\right).$$

(38)

The fact that ${\sum }_{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha x\right\}}$ is Binomial with parameters $m_1$ and $G\left(\alpha x\right)=\mathbb{P}\left(X_1\le \alpha x\right)$ is straightforward which with the help of (35) and

$$\begin{array}{cc}\hfill & \underset{m\to \infty }{lim}\left(K_F^{\mathbf{M}}(x_1,m,\gamma ,ϵ,\alpha )+K_G^{\mathbf{M}}(x_1,m,1-\gamma ,ϵ,\alpha )\right)\hfill \\ \hfill & +\underset{m\to \infty }{lim}\left(K_F^{\mathbf{M}}(x_2,m,\gamma ,ϵ,\alpha )+K_G^{\mathbf{M}}(x_2,m,1-\gamma ,ϵ,\alpha )\right)=0\hfill \end{array}$$

prove (36). Indeed, the strong law of large numbers gives almost surely that

$$\underset{m_1\to \infty }{lim}\frac{1}{m_1}\sum _{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha x\right\}}=G\left(\alpha x\right)$$

and from (35) $\underset{m\to \infty }{lim}{S}_m^{*}=G\left(\alpha x_{\alpha ,\gamma }\right)$. Next, from (22) we get that

$$H\left(\alpha x_{\alpha ,\gamma }\right)=\frac{G\left(\alpha x_{\alpha ,\gamma }\right)-\alpha x_{\alpha ,\gamma }}{\alpha x_{\alpha ,\gamma }}=\frac{1-\alpha }{\alpha }$$

and henceforth $G\left(\alpha x_{\alpha ,\gamma }\right)=x_{\alpha ,\gamma }\frac{1-\alpha \gamma }{1-\gamma }.$ The latter is the limit on the right-hand side of (36). The very last relation, that is (37), follows again from (35) and an application of Proposition A1 which yields in our case with $m_1=m\left(1-\gamma \right)$ the bounds

$$\mathbb{P}\left(\frac{1}{m_1}\sum _{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha x_2\right\}}\ge \left(1+\eta \right)G\left(\alpha x_2\right)\right)\le e^{-c\left(\eta \right)(1-\gamma )mG\left(\alpha x_2\right)}$$

and

$$\mathbb{P}\left(\frac{1}{m_1}\sum _{j=1}^{m_1}{\mathbb{I}}_{\left\{X_j\le \alpha x_1\right\}}\le \left(1-\eta \right)G\left(\alpha x_1\right)\right)\le e^{-c\left(\eta \right)(1-\gamma )mG\left(\alpha x_1\right)}.$$

This concludes the proof.  □

As in the case of $\frac{R_m}{m}$ we state a more practical version of Theorem 3 which is aimed to compute the largest $ϵ$ for fixed $m,x_1,x_2$. It is in the spirit of Theorem 2.

Theorem 4.

Let condition (M) be valid and assume the notation of Theorem 2. Let $m\in {\mathbb{N}}^{+}$ be fixed. Let next $x_{\alpha ,\gamma }\in \left(x_1,x_2\right)\subset \left(0,1\right)$ and $x_1$ is such that $\frac{\lceil m{x}_1\rceil }{m}<x_{\alpha ,\gamma }$. Finally, let $\eta \in \left(0,1\right)$ be fixed. Then with

$$\begin{array}{cc}\hfill {ϵ}_1& =ϵ(x_1,m)=\frac{1}{2}\left(\frac{1}{\alpha }-1\right)-\frac{1-\gamma }{2}H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\hfill \\ \hfill & =\frac{1-\gamma }{2}\left(H\left(\alpha x_{\alpha ,\gamma }\right)-H\left(\alpha \frac{\lceil mx\rceil }{m}\right)\right),\hfill \end{array}$$

(39)

and

$$\begin{array}{cc}\hfill {ϵ}_2& =ϵ(x_2,m)=\frac{1-\gamma }{2}H\left(\alpha \frac{\lceil mx\rceil }{m}\right)-\frac{1}{2}\left(\frac{1}{\alpha }-1\right)\hfill \\ \hfill & =\frac{1-\gamma }{2}\left(H\left(\alpha \frac{\lceil mx\rceil }{m}\right)-H\left(\alpha x_{\alpha ,\gamma }\right)\right)\hfill \end{array}$$

(40)

we have that

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\left(1-\eta \right)G\left(\alpha x_1\right)\le S_m^{*}\le \left(1+\eta \right)G\left(\alpha x_2\right)\right)\hfill \\ \hfill & \ge max\{1-\left(K_F^{\mathbf{M}}(x_1,m,\gamma ,{ϵ}_1,\alpha )+K_G^{\mathbf{M}}(x_1,m,1-\gamma ,{ϵ}_1,\alpha )\right)\hfill \\ \hfill & -\left(K_F^{\mathbf{M}}(x_2,m,\gamma ,{ϵ}_2,\alpha )+K_G^{\mathbf{M}}(x_2,m,1-\gamma ,{ϵ}_2,\alpha )\right)\hfill \\ \hfill & -e^{-mc\left(\eta \right)(1-\gamma )G\left(\alpha x_1\right)}-e^{-mc\left(\eta \right)(1-\gamma )G\left(\alpha x_2\right)};0\}\hfill \end{array}$$

(41)

and $c\left(\eta \right)=(1+\eta )ln\left(1+\eta \right)-\eta$ is considered in Proposition A1. For a one-sided bound we get the inequality

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\left(1-\eta \right)G\left(\alpha x_1\right)\le S_m^{*}\right)\hfill \\ \hfill & \ge max\{1-K_F^{\mathbf{M}}(x_1,m,\gamma ,{ϵ}_1,\alpha )-K_G^{\mathbf{M}}(x_1,m,1-\gamma ,{ϵ}_1,\alpha )-e^{-mc\left(\eta \right)(1-\gamma )G\left(\alpha x_1\right)};0\}.\hfill \end{array}$$

(42)

Remark 12.

Noting Remark 9 we see that the expressions involving $K_F^{\mathbf{M}},K_G^{\mathbf{M}}$ can be substituted with

$$2min\left\{\sum _{t\in A_{\alpha }(m,x)}{e}^{-kT\left(t\right)c\left(\frac{ϵ}{\rho }\frac{t}{T\left(t\right)}\right)},e^{-2\frac{k}{{\rho }^2}{\left(ϵ\alpha x\right)}^2}\right\},$$

where T is either F or G.

Proof of Theorem 4.

The proof is immediate but we note that the assumption $\frac{\lceil m{x}_1\rceil }{m}<x_{\alpha ,\gamma }$ and the choice of ${ϵ}_1,{ϵ}_2$ are such that Theorem 2 applies to the right-hand side of (38), which yields an inequality identical to (35). The rest is as in the proof of Theorem 3.  □

3. Workflow

In this section we consider the case when the non-uniform distribution of ${\left(X_j\right)}_{m_0<j\le m}$ is Beta with parameters $a,b$, that is $G\left(·,a,b\right)$ is the cdf of $B(a,b)$, where $a<1$ and $b>1$ are taken so that condition (M) is satisfied. In this case Lemma 1 is valid and condition (M) holds since elementary calculations yield that $g_{a,b}^{\prime }<0$ on $(0,\alpha )$ and $\underset{x\to 0}{lim}{g}_{a,b}\left(x\right)=\infty$, where $g_{a,b}$ is the probability density function of $B(a,b)$.

For a given number of hypotheses m, level of significance $\alpha$ and proportion of significant hypotheses $\gamma$, we are interested in finding a theoretical bound for the probability that the power is between a number l and 1, where of course only $l<G(\alpha x_{\alpha ,\gamma },a,b)$ makes sense to be considered. We shall only provide a step by step description of the implementation and we shall refrain from developing a particular, explicit theoretical example for given values of $a,b$ since the latter involves tedious, non-instructive and lengthy computations. We proceed with describing the workflow that has been implemented numerically in R:

• we calculate $x_{\alpha ,\gamma }$ by solving numerically Equation (22) wherein $G(·)=G\left(·,a,b\right)$;
• using the value of $x_{\alpha ,\gamma }$, we calculate the power limit of $S_m^{*}$, see (33), i.e., $G(\alpha x_{\alpha ,\gamma },a,b)$, according to (36);
• for given $l<G(\alpha x_{\alpha ,\gamma },a,b)$, any given $\eta$ and $x_1$ is such that $\frac{\lceil m{x}_1\rceil }{m}<x_{\alpha ,\gamma }$ we have an estimate based on (42), that is

  $$\begin{array}{cc}\hfill & \mathbb{P}\left(\left(1-\eta \right)G\left(\alpha x_1\right)\le S_m^{*}\right)\hfill \\ \hfill & \ge max\{1-K_F^{\mathbf{M}}(x_1,m,\gamma ,{ϵ}_1,\alpha )-K_G^{\mathbf{M}}(x_1,m,1-\gamma ,{ϵ}_1,\alpha )-\hfill \\ \hfill & -e^{-mc\left(\eta \right)(1-\gamma )G\left(\alpha x_1,a,b\right)};0\};\hfill \end{array}$$
• fixing $\eta$ we attempt to solve (numerically) in $x_1$ the equation

  $$l=\left(1-\eta \right)G\left(\alpha x_1,a,b\right);$$
• if $\frac{\lceil m{x}_1\rceil }{m}<x_{\alpha ,\gamma }$ then (42) represents a valid theoretical lower bound, that is

  $$\begin{array}{cc}\hfill p\left(\eta \right)& =max\{1-K_F^{\mathbf{M}}(x_1,m,\gamma ,{ϵ}_1,\alpha )-K_G^{\mathbf{M}}(x_1,m,1-\gamma ,{ϵ}_1,\alpha )-\hfill \\ \hfill & -e^{-mc\left(\eta \right)(1-\gamma )G\left(\alpha x_1,a,b\right)};0\}\hfill \end{array}$$

  with $\mathbb{P}\left(l\le S_m^{*}\right)\ge p\left(\eta \right);$
• finally, we optimize $p\left(\eta \right)$ in $\eta$ and choose ${\eta }^{*}$ so that the estimated probability bound is the largest, that is $\mathbb{P}\left(l\le S_m^{*}\right)\ge {sup}_{\eta \in \left(0,1\right)}p\left(\eta \right)=p\left({\eta }^{*}\right).$

4. Results

The following Table 1, Table 2, Table 3 and Table 4 give empirical results for some values of $m,a,b,\gamma$. We have included different cases for the real power limit—taking large, moderate and small values. In all cases the significance level is $\alpha =0.05$. These tables also show the empirical probability based on numerical simulations with 1 million repetitions. Empirical probability of 1 means that no simulation repetition had power lower than l. Theoretical probability of 0 or empty value of ${\eta }^{*}$ indicate that some of the conditions of the method were not met.

Table 1. Simulation results for B(0.1, 100), number genes = 20,000, proportion significant = 0.1, real power limit = 0.940359.

Lower Bound l	Empirical Probability	Theoretical Estimate $\mathit{p}\left({\mathit{\eta }}^{*}\right)$	${\mathit{\eta }}^{*}$
0.750	1.000	1.000	0.098
0.760	1.000	1.000	0.097
0.770	1.000	1.000	0.096
0.780	1.000	1.000	0.096
0.790	1.000	1.000	0.095
0.800	1.000	1.000	0.095
0.810	1.000	1.000	0.094
0.820	1.000	1.000	0.094
0.830	1.000	1.000	0.093
0.840	1.000	1.000	0.093
0.850	1.000	0.999	0.085
0.860	1.000	0.996	0.078
0.870	1.000	0.985	0.068
0.880	1.000	0.952	0.058
0.890	1.000	0.873	0.048
0.900	1.000	0.714	0.037
0.910	1.000	0.476	0.027
0.920	1.000	0.204	0.016
0.930	0.967	0.018	0.005
0.940	0.550	0.000

Table 2. Simulation results for B(0.25, 2), number genes = 20,000, proportion significant = 0.1, real power limit = 0.233737.

Lower Bound l	Empirical Probability	Theoretical Estimate $\mathit{p}\left({\mathit{\eta }}^{*}\right)$	${\mathit{\eta }}^{*}$
0.190	1.000	0.779	0.105
0.200	0.997	0.434	0.072
0.210	0.972	0.000	0.001
0.220	0.868	0.000	0.001
0.230	0.626	0.000	0.001

Table 3. Simulation results for B(0.1, 2), number genes = 20,000, proportion significant = 0.1, real power limit = 0.620014.

Lower Bound l	Empirical Probability	Theoretical Estimate $\mathit{p}\left({\mathit{\eta }}^{*}\right)$	${\mathit{\eta }}^{*}$
0.500	1.000	1.000	0.119
0.510	1.000	1.000	0.117
0.520	1.000	1.000	0.116
0.530	1.000	1.000	0.115
0.540	1.000	0.999	0.106
0.550	1.000	0.996	0.097
0.560	1.000	0.979	0.081
0.570	1.000	0.926	0.067
0.580	1.000	0.786	0.052
0.590	0.994	0.521	0.036
0.600	0.953	0.189	0.02
0.610	0.803	0.000	0.001
0.620	0.511	0.000

Table 4. Simulation results for B(0.1, 10), number genes = 20,000, proportion significant = 0.1, real power limit = 0.755055.

Lower Bound l	Empirical Probability	Theoretical Estimate $\mathit{p}\left({\mathit{\eta }}^{*}\right)$	${\mathit{\eta }}^{*}$
0.600	1.000	1.000	0.109
0.610	1.000	1.000	0.108
0.620	1.000	1.000	0.107
0.630	1.000	1.000	0.106
0.640	1.000	1.000	0.105
0.650	1.000	1.000	0.105
0.660	1.000	1.000	0.104
0.670	1.000	0.999	0.096
0.680	1.000	0.995	0.085
0.690	1.000	0.980	0.074
0.700	1.000	0.934	0.062
0.710	1.000	0.821	0.049
0.720	0.999	0.608	0.037
0.730	0.991	0.309	0.024
0.740	0.924	0.048	0.009
0.750	0.693	0.000	0.001

Larger sample size would result in a smaller parameter a of the Beta distribution, thus squeezing the distribution towards 0 and increasing the statistical power and its theoretical estimates, e.g., as in Table 2 and Table 3.

We have carried out numerical simulations for many values of the parameters and based on the results it appears that the theoretical bound works well when l is not close to the real power limit $lG(\alpha x_{\alpha ,\gamma },a,b)$. Link to our R code is provided in the Supplementary Materials section.

Interestingly, when m increases and all other parameters are kept fixed, the expected power decreases for most values of m. This is shown in the following Figure 1. Perhaps this is due to the fact that the set for which we take the maximum in (2) increases its size for most values of m (unless the ceiling function jumps).

Figure 1. Empirical results when the p-values under the alternative hypothesis have $B(0.5,100)$ distribution and the proportion of alternative tests is $2\%$. The x-axis shows the common logarithm of the number of tests m. The y-axis shows the empirical power. The dots depict the mean of the empirical power, the vertical lines are of length one standard deviation below and above the mean. The dotted line shows the asymptotic power.

We note that as expected when either a is closer to 1 or/and $\gamma$ is smaller then the theoretical estimates are getting significantly worse. This is natural as the closer the alternative distribution gets to the uniform the harder is to distinguish that the respective random variable X originates from it. The same is valid if the lower bound l is very close to the true limit and it is harder to account for the possible error. All these points reflect natural restrictions when one deals with universal, theoretical bounds, which are seemingly conducted in an optimal way.

5. Discussion

5.1. Related Work

There are a number of results concerning the statistical power of the Benjamini–Hochberg procedure that relate to our result. Paper [15] discusses different properties of the procedure and shows that when increasing the number of tests m, while keeping the underlying distributions and the proportion of true significant tests the same, the statistical power under some conditions converges to a limit that can be found as a solution of a particular equation, see (3.8) of Corollary 3.3 of that article. A step forward is made in [13] wherein it is shown that the proportions related to the power of the test obey even a law of the iterated logarithm. Other notable contributions amongst others include the papers [18] which deal with various properties of the Benjamini–Hochberg procedure, including a Donsker-type of convergence. They are discussed in more detail in Remark 5. We wish to highlight explicitly that to our knowledge there are no bounds, albeit conservative, for the probability to uncover a given proportion of the truly significant tests (that is $S_n/n$) with respect to the limit of $S_n/n$, as n goes to infinity. We achieve this by evaluating the speed of convergence, whereas the results under more general assumptions, including under weak dependence between the tests, consider limit results. This does not allow for the derivation of any concrete intervals, depending solely on the set of parameters, which give a certain probability for the proportion of correctly identified significant tests.

While we argue below that for genetic studies the assumption of independence is not binding at all, we wish to mention some achievements under the weak dependence assumption since it is natural to pursue as a future development the extension of our results to this scenario. The limit for the power of the Benjamini–Hochberg procedure is proved in [15]. An interesting contribution is [12] which shows that for a large number of tests the FDR is controlled even when there is some degree of dependence between the test statistics. A conservative estimator for the proportion of false nulls among the hypotheses (the quantity $1-\gamma$ in our work) is found (the proof there uses the Dvoretsky–Kiefer–Wolfowitz inequality [16], as we do for different purposes in our work). Then the estimator is used in a plug-in procedure in order to boost the power of the procedure while keeping the FDR controlled. An estimator for $\gamma$ may precede the application of our procedure.

We are not interested in improving the procedure itself, but rather than that in estimating the power of the original procedure, that as we mentioned in the Introduction section, is the most widely used among the similar procedures.

As mentioned in [20], the results in [12] assume that $R_n/n$ is asymptotically larger than zero, where $R_n$ is the number of rejected tests out of all n tests (the R notation is consistent with ours through this work). A counterexample is given of a case in which $R_n/n$ converges asymptotically to zero with positive probability and in which the FDR is larger than $\alpha$. Such situation does not appear to be relevant to the RNA-seq data used for single-step differential expression methods that prompted our work. Moreover, paper [12] is concerned with controlling the FDR rather than estimates of the power, which is the scope of our work in which we are interested in the power of the procedure that the scientists predominantly use, regardless of whether the FDR is controlled.

5.2. Considerations about Our Work

Because this is the first result of this exact type that we are aware of, we start our considerations under independence assumption. We want to point out that, as mentioned above, there are more general results under convergence, but they do not include explicit bounds for given set of parameters. The independence assumption holds approximately in the case of RNA-seq expression level analysis, where there are groups of genes that are correlated within the group, but most pairs of genes are weakly or not correlated. Even in the case of weak dependence, having real-world RNA-seq expression data, one cannot reliably estimate or replicate the dependence unless the sample size is much larger than the one of the currently available datasets. In addition, more complicated assumptions for the structure of dependence would make the numerical procedure impossible to set up as there would be too many parameters in the input and these parameters cannot be easily estimated for small sample sizes that are typical for RNA-seq experiments.

Theoretical results under more complicated assumptions for the dependence could be a subject of a follow-up studies. Numerical simulations of RNA-seq data under different basic types of weak dependencies could also be considered in subsequent studies.

It is important to also emphasize that our considerations differ from the basic situations in which the statistical power is studied. In a case of a simple test the statistical power is typically considered as a function of the sample size. However, in a case of a complex tests such as the ones cited above, often it is not possible to estimate the distribution of the test statistic, even for a single test in the multiple comparison setup. In order to be able to model a general setup we model the test statistic under the alternative hypothesis using the Beta family of distributions. In order to use our current results, one would first have to approximately or exactly estimate the parameters of the Beta distribution as function of the sample size of the particular test. Because such estimates are test-specific and cannot be studied in general, this would be a subject of another article. One would also have to estimate the proportion of significant tests and, having achieved that, one would apply our results for that proportion and those parameters of the Beta distribution, taking into account the possible values of the number of tests. For example, in the differential expression analysis methods, mentioned above, the sample size corresponds to the number of individuals and the number of tests may correspond to the number of genes.