Multiple Loop Fuzzy Neural Network Fractional Order Sliding Mode Control of Micro Gyroscope
Abstract
:1. Introduction
- (1)
- By adding fractional terms to the sliding surface, the memory characteristics of the fractional calculus operator are used to enhance the continuity of sliding mode control. The switching gain is optimized for the purpose of weakening the system chattering. The designed fractional sliding surface has higher robustness and higher tracking accuracy; meanwhile, the tracking error converges to zero in a finite period of time.
- (2)
- The combination of the fuzzy system and neural network is used to estimate the upper bound of lumped parameter uncertainty, and the true value is replaced by the estimated value as the gain of switching law. Two feedbacks are added to the structure of fuzzy neural control, which has the characteristic of dynamic mapping and can smooth the output of the neural network.
2. Dynamic Analysis of Micro Gyroscope
3. Fractional-Order Sliding Mode Controller
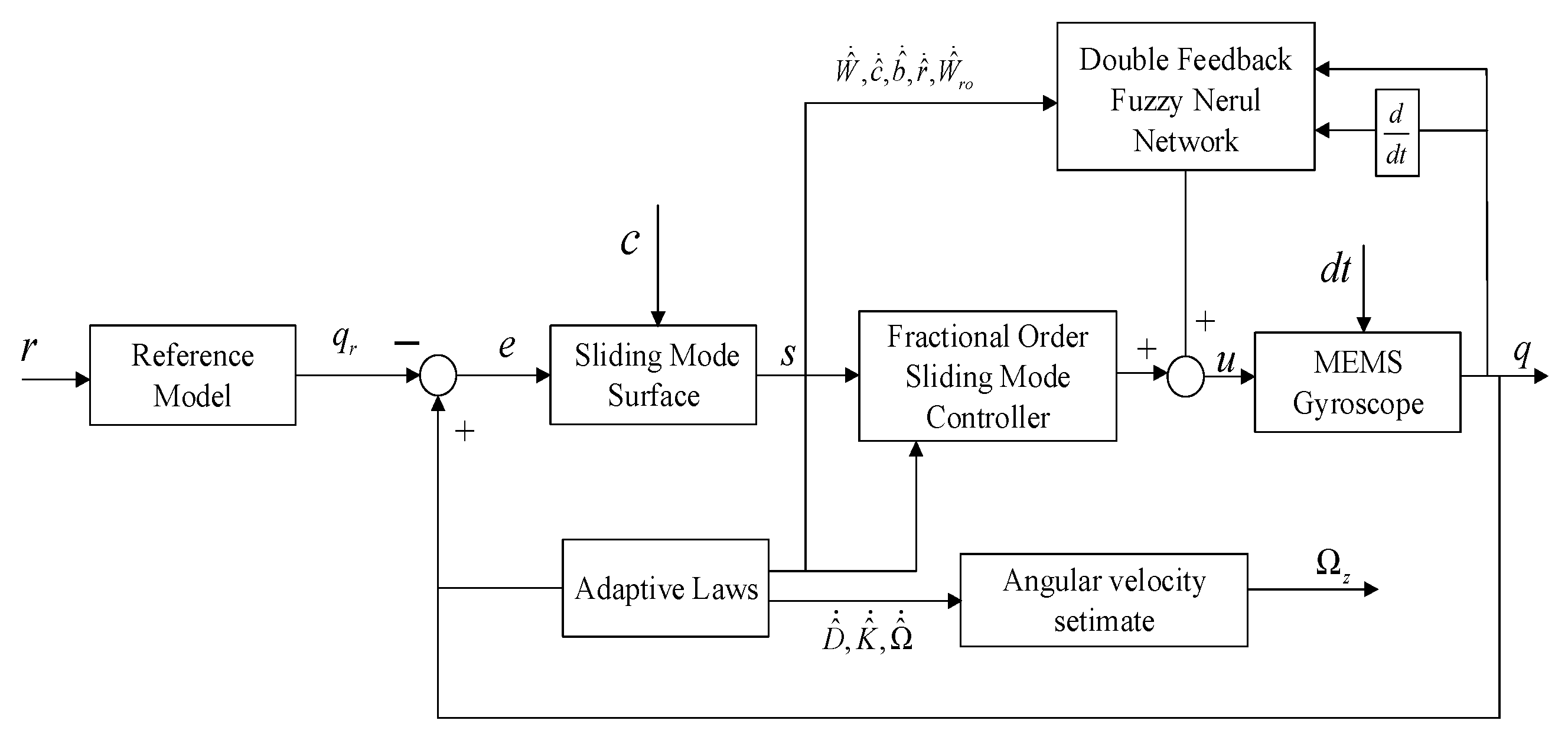
4. Adaptive Double Feedback Fuzzy Neural Network Fractional-Order Sliding Mode Controller
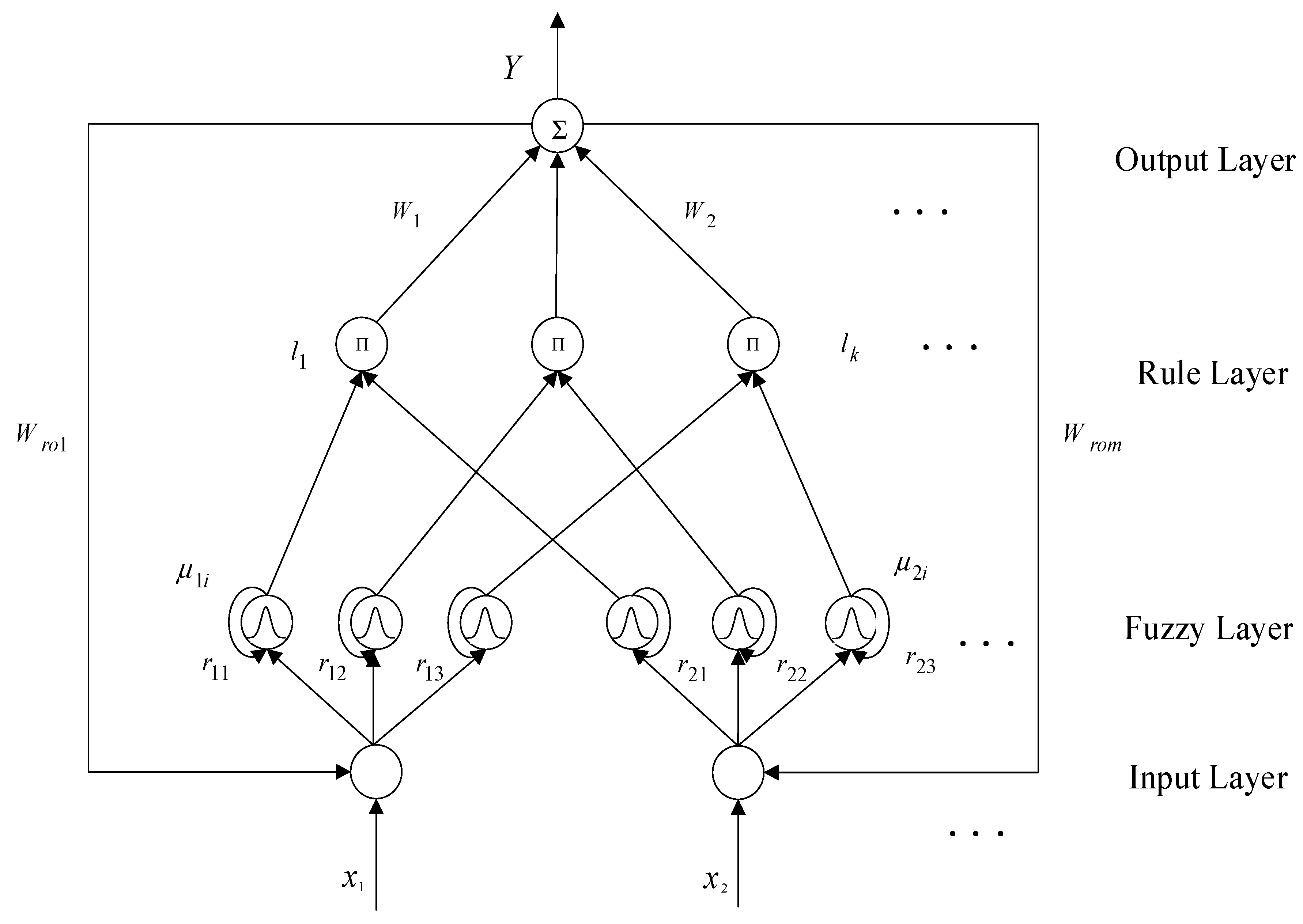
4.1. Double Feedback Fuzzy Neural Network
4.2. Design and Stability of the Adaptive Double Feedback Fuzzy Neural Network Fractional-Order Sliding Mode Controller
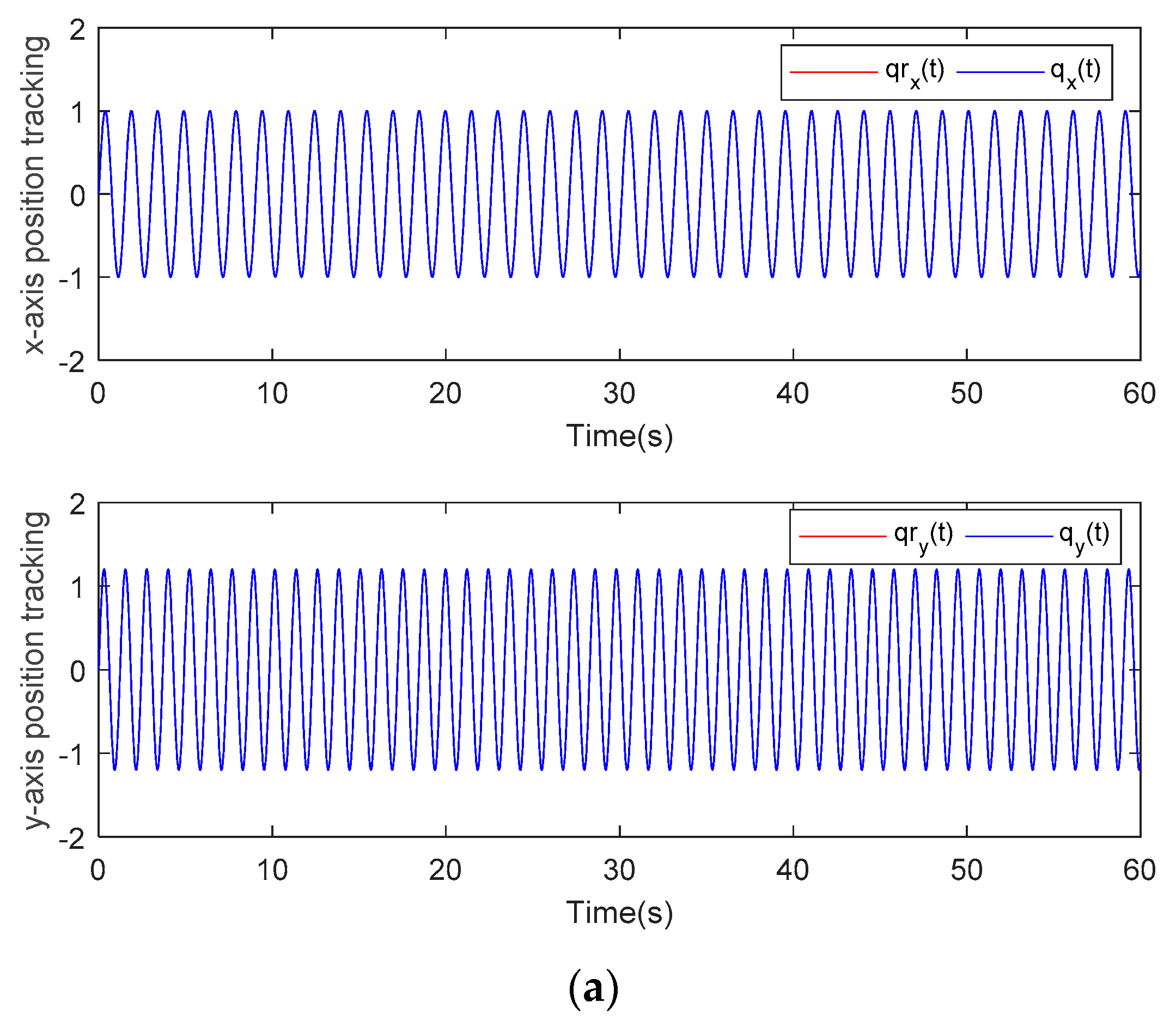
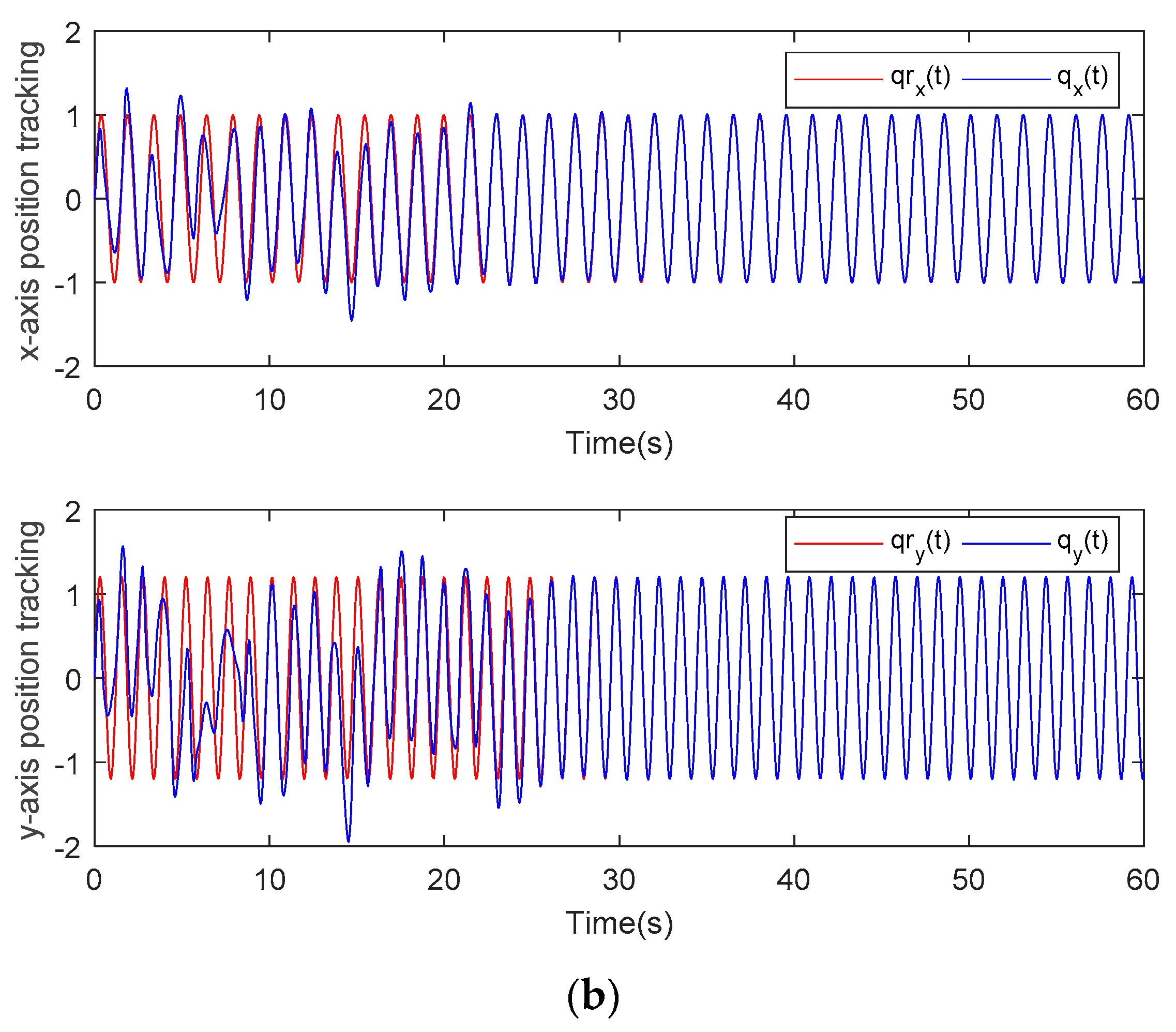
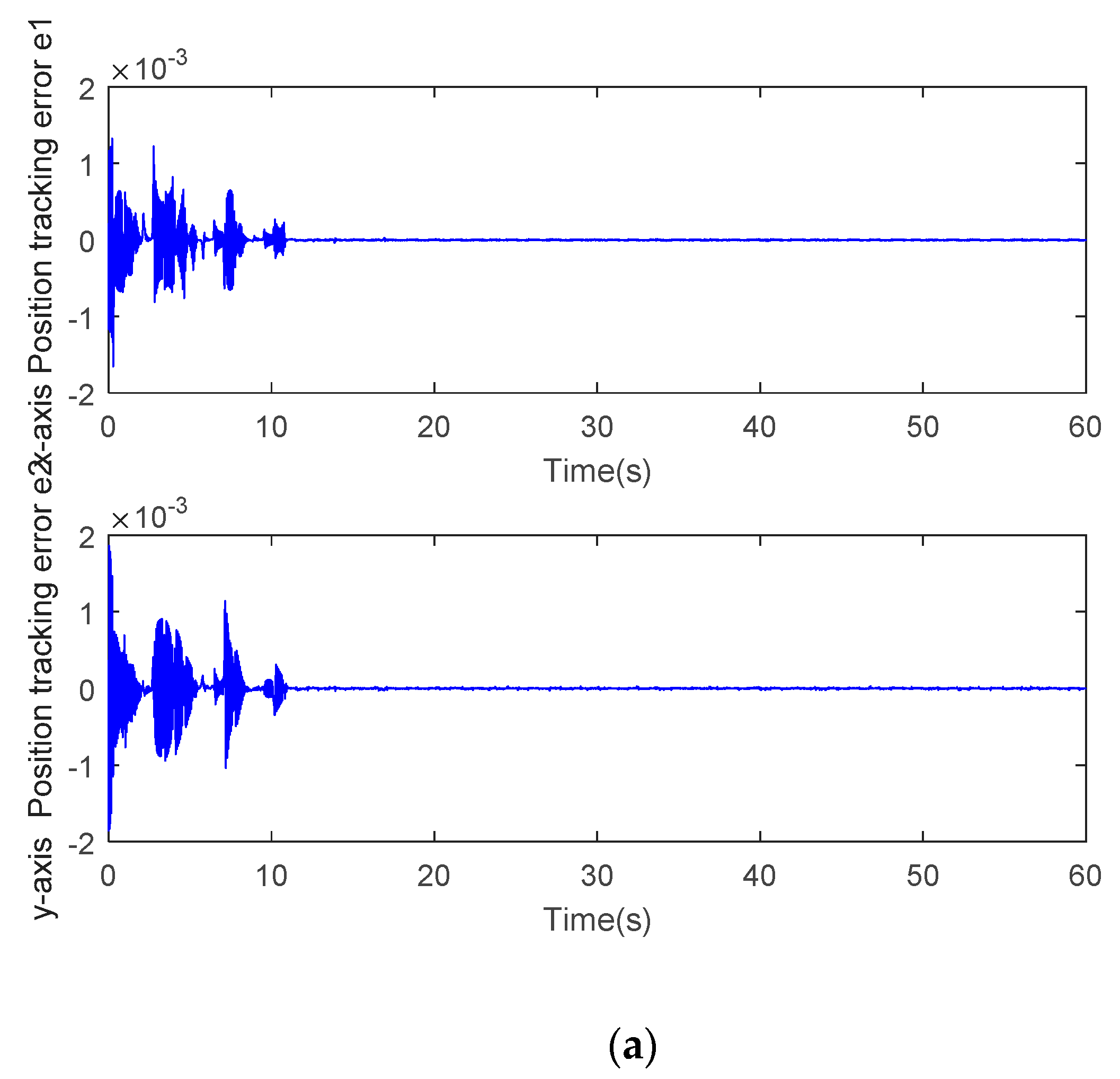
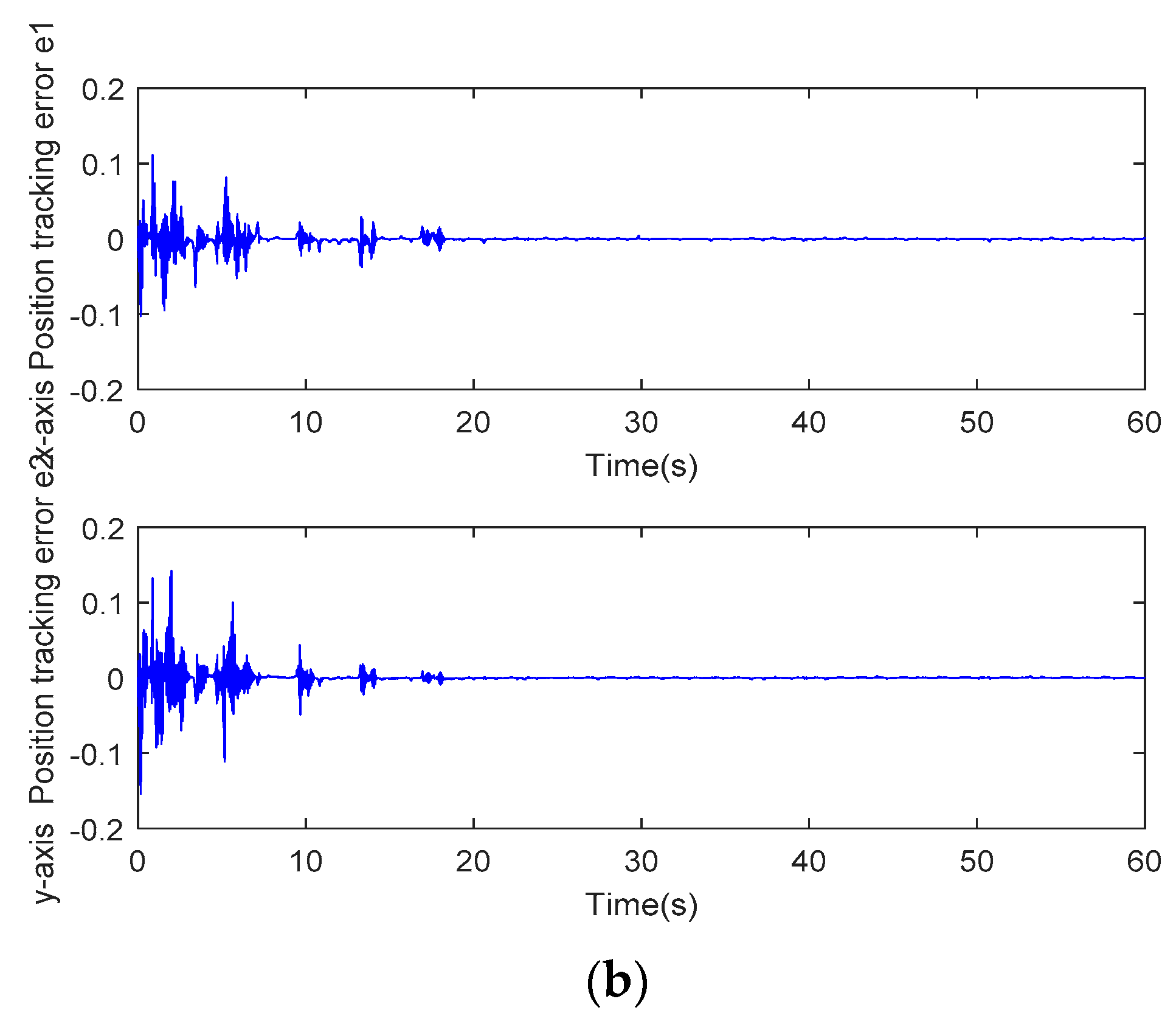
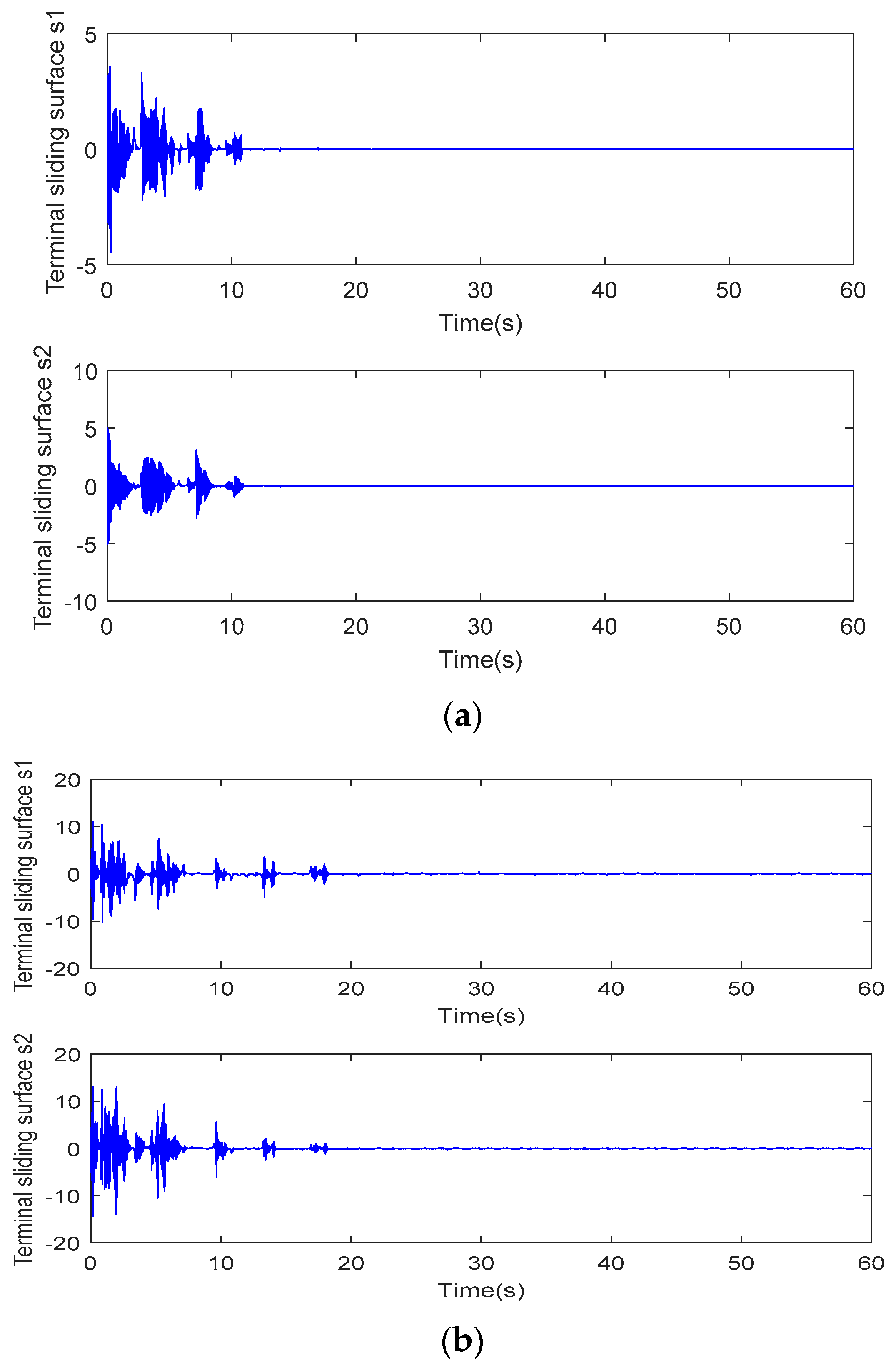
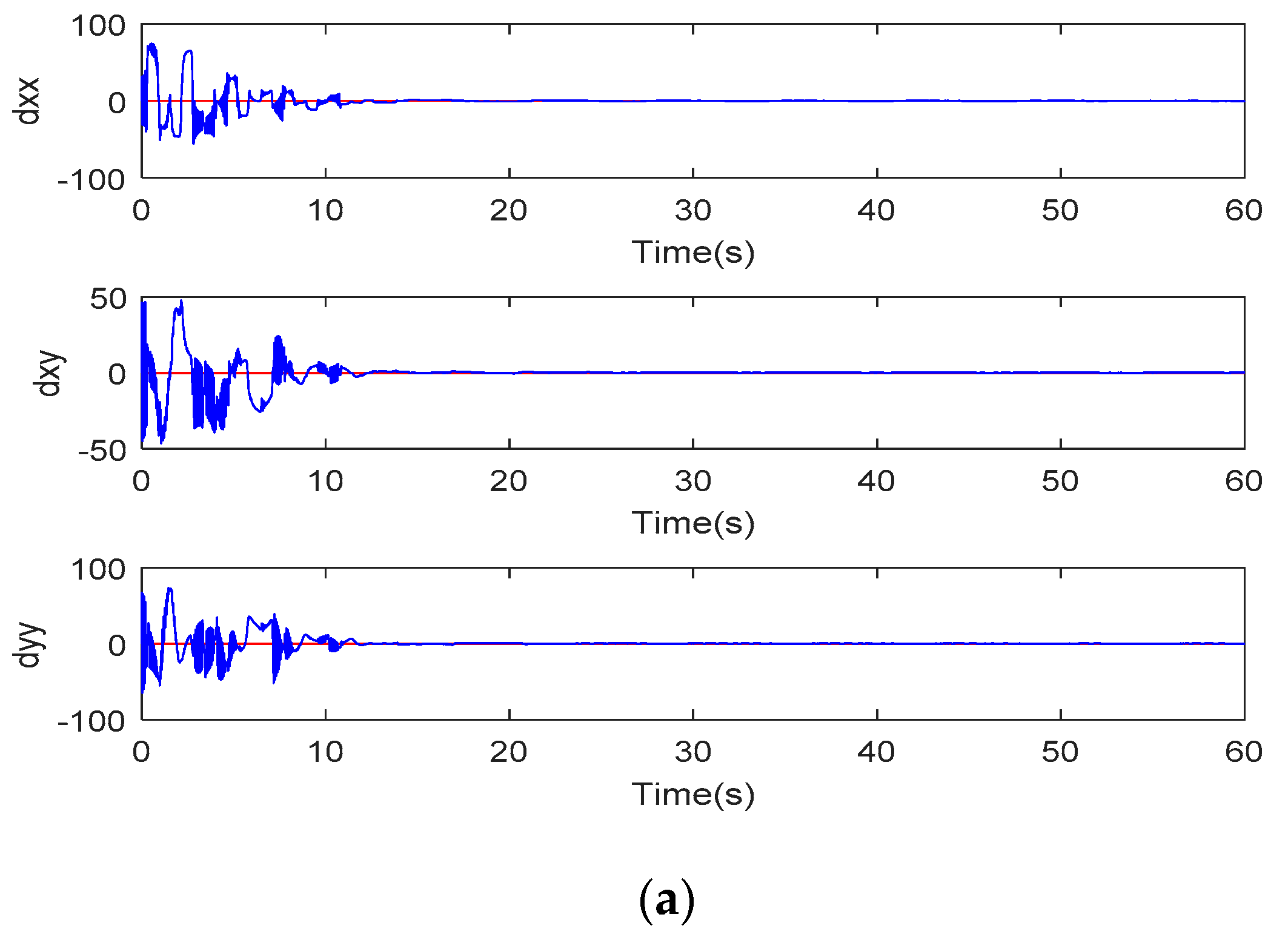
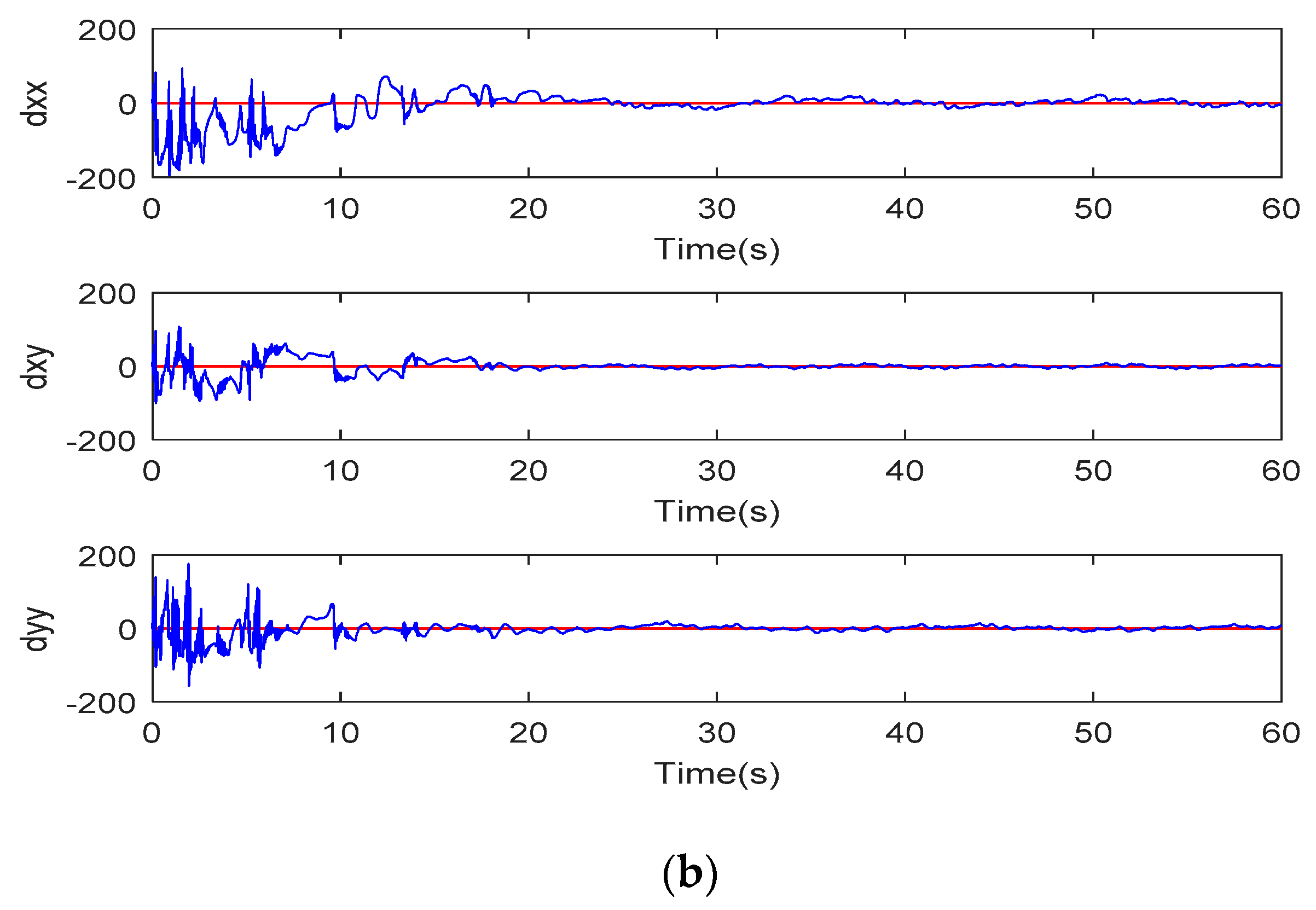
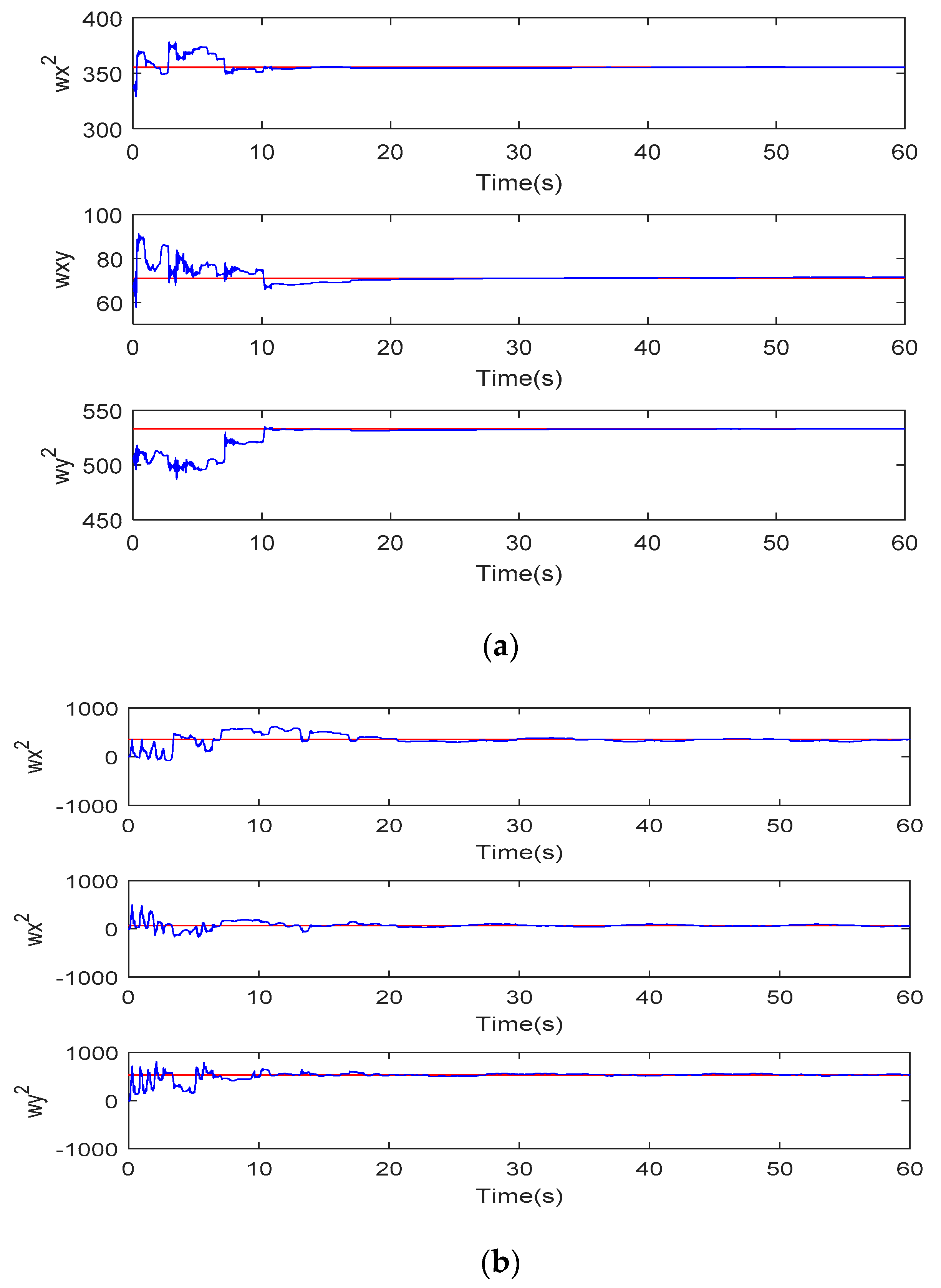
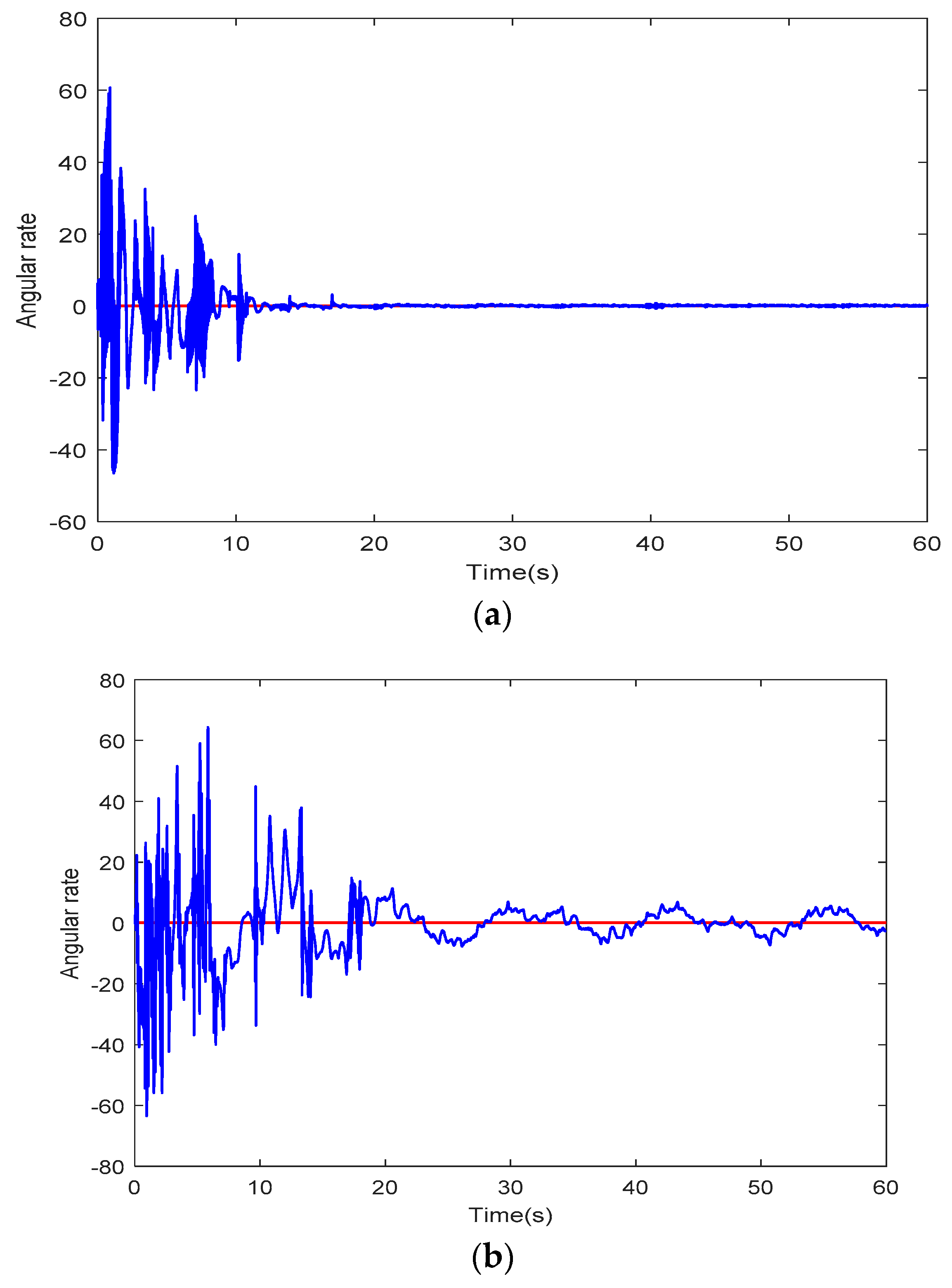
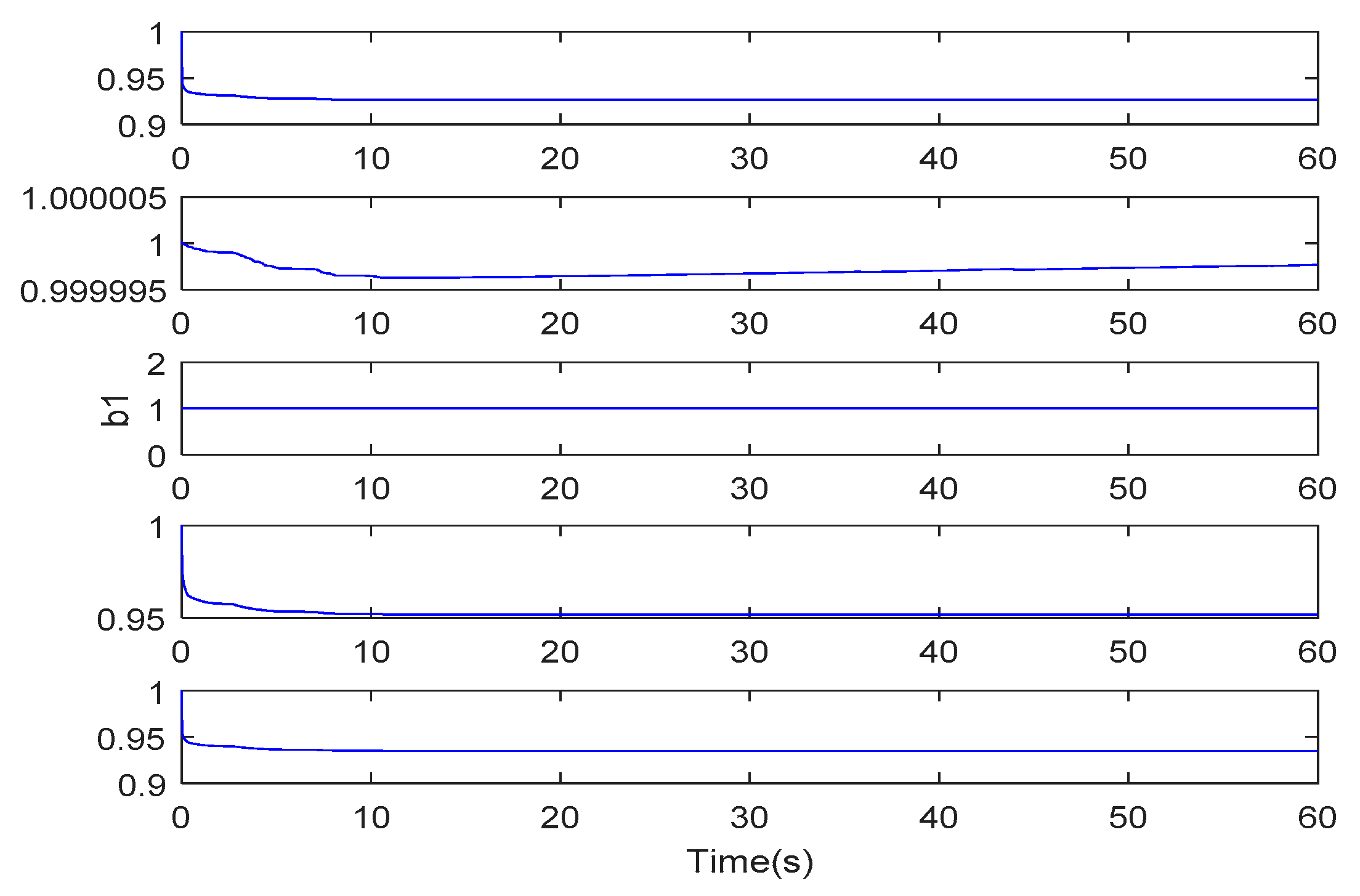
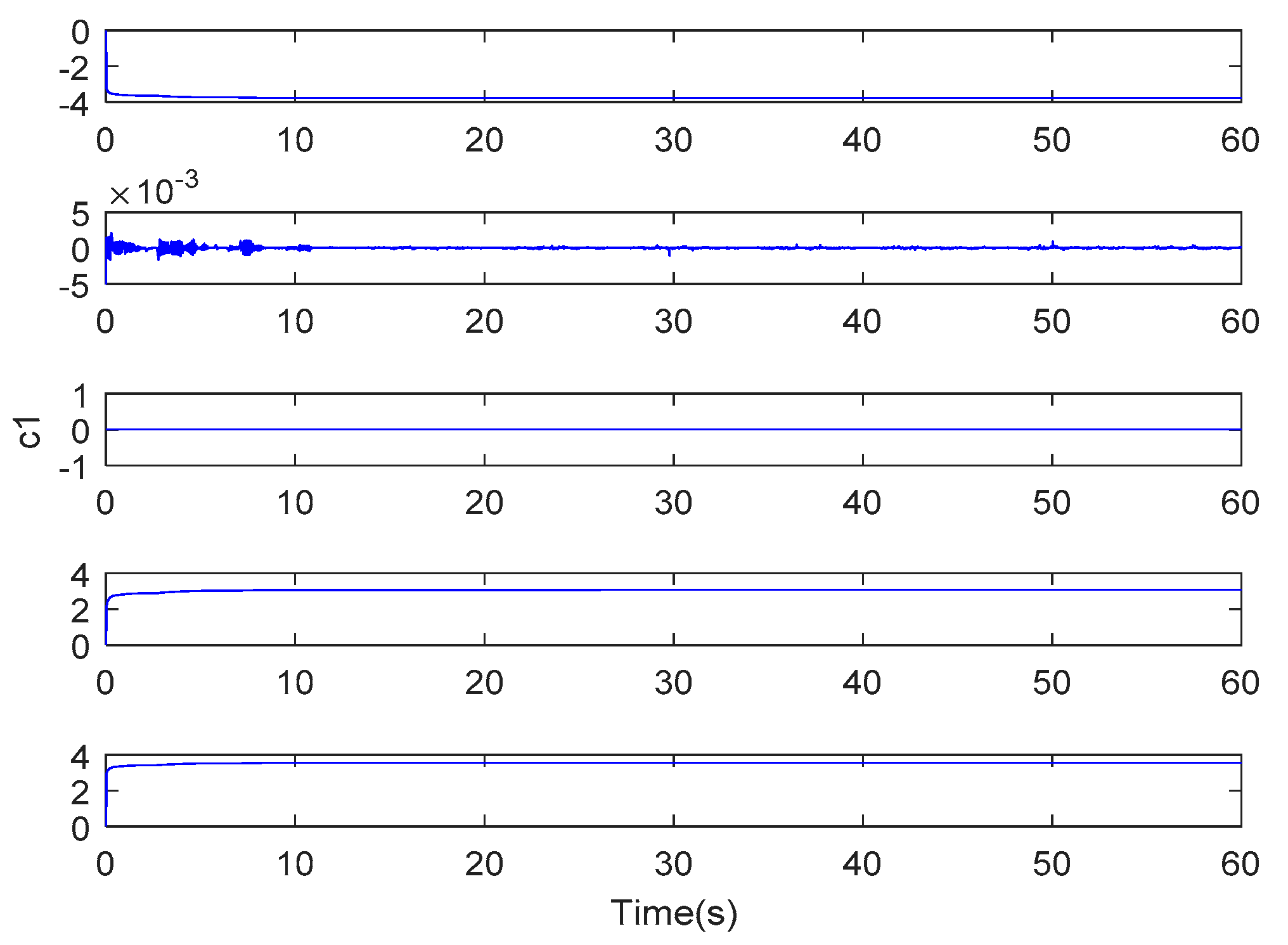
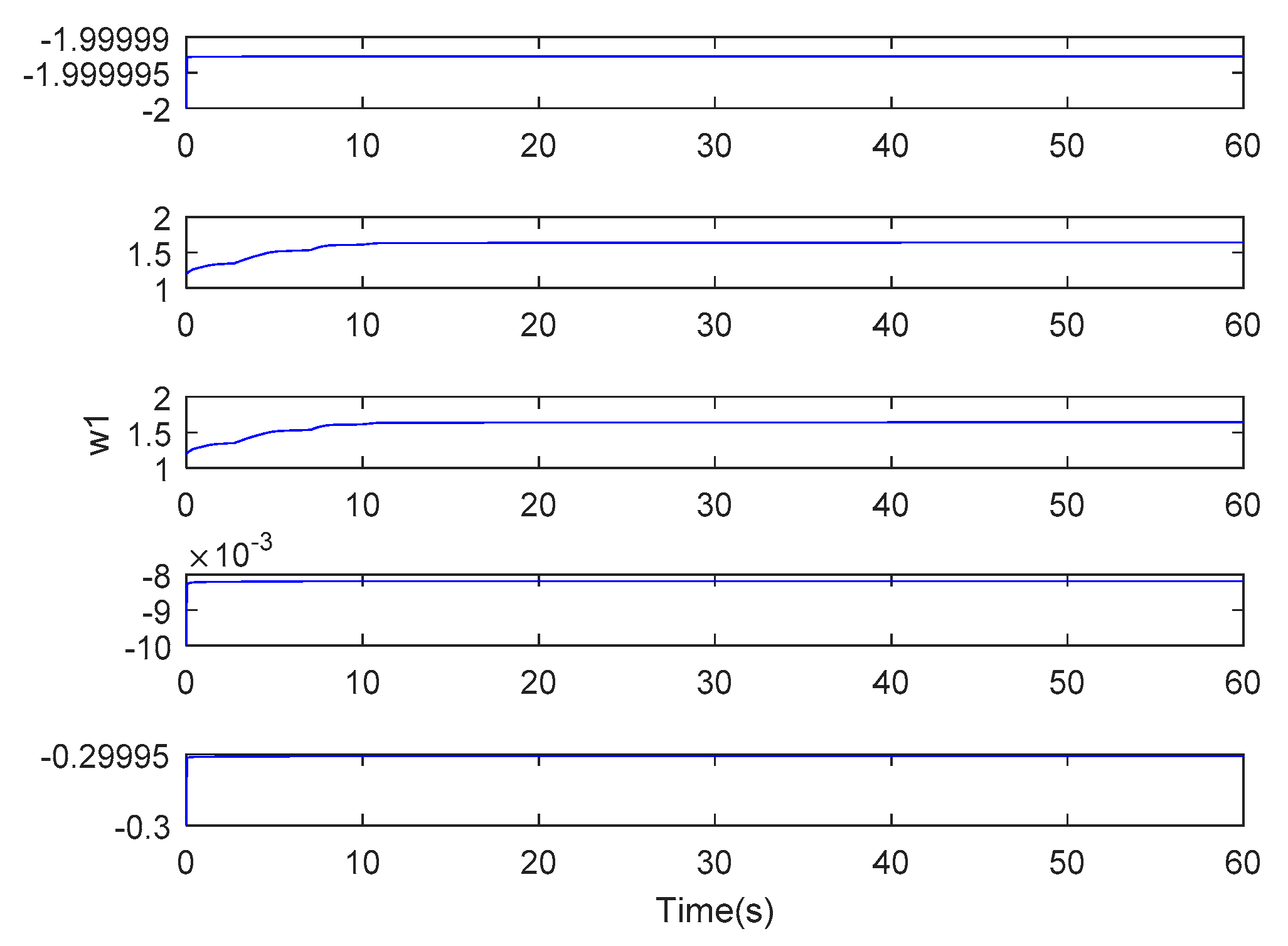
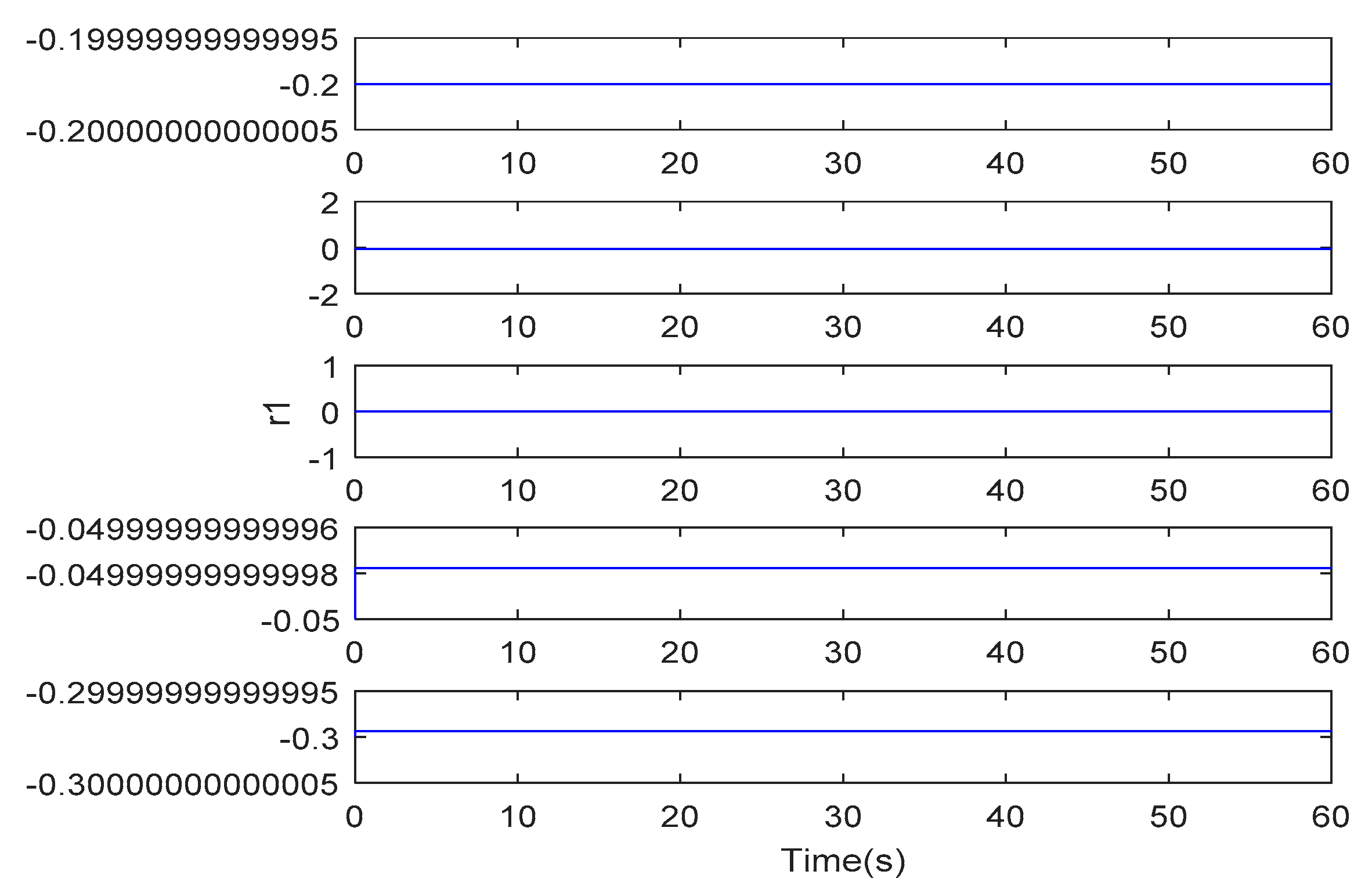
5. Simulation Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koruba, Z.; Garus, J. Dynamics and Control of a Gyroscope- Stabilized Platform in a Ship Anti-Aircraft Rocket Missile Launcher. Solid State Phenom. 2013, 196, 124–139. [Google Scholar] [CrossRef]
- Lahdenoja, O.; Hurnanen, T.; Iftikhar, Z.; Nieminen, S.; Knuutila, T.; Saraste, A.; Kiviniemi, T.; Vasankari, T.; Airaksinen, J.; Pänkäälä, M.; et al. Atrial Fibrillation Detection via Accelerometer and Gyroscope of a Smartphone. IEEE J. Biomed. Health Inform. 2018, 22, 108–118. [Google Scholar] [CrossRef] [PubMed]
- Xia, D.; Kong, L.; Hu, Y.; Ni, P. Silicon microgyroscope temperature prediction and control system based on BP neural network and Fuzzy-PID control method. Meas. Sci. Technol. 2015, 26, 25101. [Google Scholar] [CrossRef]
- He, C.; Zhao, Q.; Huang, Q.; Liu, D.; Yang, Z.; Zhang, D.; Yan, G. A MEMS Vibratory Gyroscope with Real-Time Mode-Matching and Robust Control for the Sense Mode. IEEE Sens. J. 2015, 15, 2069–2077. [Google Scholar] [CrossRef]
- Montoya–Cháirez, J.; Santibáñez, V.; Moreno–Valenzuela, J. Adaptive Control Schemes Applied to a Control Moment Gyroscope of 2 degrees of Freedom. Mechatronics 2019, 57, 73–85. [Google Scholar] [CrossRef]
- Fei, J.; Feng, Z. Adaptive Fuzzy Super-Twisting Sliding Mode Control for Microgyroscope. Complexity 2019, 2019, 6942642. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Q.; Lü, X.; Sui, J.-J. Adaptive Perturbation Compensation for Micro-electro-mechanical systems Tri-axial Gyroscope. Control Theory Appl. 2014, 31, 451–457. [Google Scholar]
- Fei, J.; Wang, Z.; Liang, X.; Feng, Z.; Xue, Y. Fractional Sliding Mode Control for Micro Gyroscope Based on Multilayer Recurrent Fuzzy Neural Network. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Wang, Z.; Fei, J. Fractional-Order Terminal Sliding Mode Control Using Self-Evolving Recurrent Chebyshev Fuzzy Neural Network for MEMS Gyroscope. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Pratama, M.; Lu, J.; Anavatti, S.; Lughofer, E.; Lim, C. An incremental meta-cognitive-based scaffolding fuzzy neural network. Neurocomputing 2015, 171, 89–105. [Google Scholar] [CrossRef]
- Tang, J.; Liu, F.; Zou, Y. An Improved Fuzzy Neural Network for Traffic Speed Prediction Considering Periodic Characteristic. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2340–2350. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, R.; Li, S.; He, W.; Shi, Z. Composite Neural Learning-Based Nonsingular Terminal Sliding Mode Control of MEMS Gyroscopes. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1375–1386. [Google Scholar] [CrossRef]
- Fei, J.; Wang, H.; Fang, Y. Novel Neural Network Fractional-Order Sliding-Mode Control with Application to Active Power Filter. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–11. [Google Scholar] [CrossRef]
- Hou, S.; Fei, J. A Self-Organizing Global Sliding Mode Control and Its Application to Active Power Filter. IEEE Trans. Power Electron. 2019, 35, 7640–7652. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Tong, S. Finite-time adaptive fuzzy output feedback dynamic surface control for MIMO non-strict feedback systems. IEEE Trans. Fuzzy Syst. 2019, 27, 96–110. [Google Scholar] [CrossRef]
- Li, Y.; Qu, F.; Tong, S. Observer-based fuzzy adaptive finite time containment control of nonlinear multi-agent systems with input-delay. IEEE Trans. Cybern. 2021, 51, 126–137. [Google Scholar] [CrossRef]
- Fang, Y.; Fei, J.; Cao, D. Adaptive Fuzzy-Neural Fractional-Order Current Control of Active Power Filter with Finite-Time Sliding Controller. Int. J. Fuzzy Syst. 2019, 21, 1533–1543. [Google Scholar] [CrossRef]
- Fei, J.; Chen, Y.; Liu, H.; Fang, Y. Fuzzy Multiple Hidden Layer Recurrent Neural Control of Nonlinear System Using Terminal Sliding Mode Controller. IEEE Trans. Cybern. 2021, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Faa-Jeng, L.; Shih-Gang, C.; Che-Wei, H. Intelligent Backstepping Control Using Recurrent Feature Selection Fuzzy Neural Network for Synchronous Reluctance Motor Position Servo Drive System. IEEE Trans. Fuzzy Syst. 2019, 27, 413–427. [Google Scholar]
- Fei, J.; Liu, L. Real-Time Nonlinear Model Predictive Control of Active Power Filter Using Self-Feedback Recurrent Fuzzy Neural Network Estimator. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Fei, J.; Chen, Y. Fuzzy Double Hidden Layer Recurrent Neural Terminal Sliding Mode Control of Single-Phase Active Power Filter. IEEE Trans. Fuzzy Syst. 2020. [Google Scholar] [CrossRef]
- Lin, F.; Chen, S.; Shuyu, K. Robust dynamic sliding-mode control using adaptive RENN for magnetic levitation system. IEEE Trans. Neural Netw. 2009, 20, 938–951. [Google Scholar] [PubMed]
- Fei, J.; Liang, X. Adaptive Backstepping Fuzzy-Neural-Network Fractional Order Control of Microgyroscope Using Nonsingular Terminal Sliding Mode Controller. Complexity 2018, 2018, 5246074. [Google Scholar] [CrossRef] [Green Version]
- Zhong, F.; Li, H.; Zhong, S. An SOC estimation approach based on adaptive sliding mode observer and fractional order equivalent circuit model for lithium-ion batteries. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 127–144. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, X.; Zhao, D.; Zhao, G.; Guan, X. Fractional order sliding mode controller design for antilock braking systems. Neurocomputing 2013, 111, 122–130. [Google Scholar] [CrossRef]
- Majidabad, S.; Shandiz, H.; Hajizadeh, A. Nonlinear fractional-order power system stabilizer for multi-machine power systems based on sliding mode technique. Int. J. Robust Nonlinear Control 2015, 25, 1548–1568. [Google Scholar] [CrossRef]
- Delghavi, M.; Shoja-Majidabad, S.; Yazdani, A. Fractional-Order Sliding-Mode Control of Islanded Distributed Energy Resource Systems. IEEE Trans. Sustain. Energy 2016, 7, 1482–1491. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Parameters | Values |
|---|---|
| Order | RMSE of x-Axis Tracking Error | RMSE of y-Axis Tracking Error |
|---|---|---|
| 0.1 | 4.1396 × 10−4 | 4.8700 × 10−4 |
| 0.2 | 4.136 × 10−4 | 4.8663 × 10−4 |
| 0.5 | 4.1355 × 10−4 | 4.8639 × 10−4 |
| 0.7 | 4.1351 × 10−4 | 4.8630 × 10−4 |
| 0.9 | 4.1209 × 10−4 | 4.8423 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Chen, F.; Fei, J. Multiple Loop Fuzzy Neural Network Fractional Order Sliding Mode Control of Micro Gyroscope. Mathematics 2021, 9, 2124. https://doi.org/10.3390/math9172124
Fang Y, Chen F, Fei J. Multiple Loop Fuzzy Neural Network Fractional Order Sliding Mode Control of Micro Gyroscope. Mathematics. 2021; 9(17):2124. https://doi.org/10.3390/math9172124
Chicago/Turabian StyleFang, Yunmei, Fang Chen, and Juntao Fei. 2021. "Multiple Loop Fuzzy Neural Network Fractional Order Sliding Mode Control of Micro Gyroscope" Mathematics 9, no. 17: 2124. https://doi.org/10.3390/math9172124
APA StyleFang, Y., Chen, F., & Fei, J. (2021). Multiple Loop Fuzzy Neural Network Fractional Order Sliding Mode Control of Micro Gyroscope. Mathematics, 9(17), 2124. https://doi.org/10.3390/math9172124





