1. Introduction
In 1967, Ehrlich [
1] introduced one of the most famous iterative methods for calculating all zeros of a polynomial simultaneously. It has a third order of convergence (if all zeros of the polynomial are simple). Historical notes and recent convergence results on Ehrlich’s method can be found in [
2,
3].
In 1977, Nourein [
4] constructed a fourth-order improved Ehrlich method by combining Ehrlich’s iterative function with Newton’s iterative function. Nowadays this method is known as
Ehrlich’s method with Newton’s correction. The convergence and computational efficiency of this method have been studied by many authors (see [
5,
6,
7,
8,
9] and references therein). The latest convergence results for Ehrlich’s method with Newton’s correction can be seen in [
9].
In 2019, Proinov, Ivanov and Petković [
10] introduced and studied a fifth-order
Ehrlich’s method with Halley’s correction which is obtained by combining Ehrlich’s iterative function with Halley’s one [
11]. In the same year, Machado and Lopes [
12] studied the convergence of the sixth-order
Ehrlich’s Method with King’s correction which is obtained by combination of Ehrlich’s iteration function and King’s family [
13].
In this paper, combining the Ehrlich method with an arbitrary iteration function, we construct and study a new family of iterative methods for finding all the roots of a given polynomial simultaneously. We provide a local and semilocal convergence of the iterative methods of the new family. The results generalize previous results about some particular methods of the family [
2,
7,
8,
9,
10].
The paper is structured as follows:
Section 2 contains some notations that are used throughout the paper. In
Section 3, we introduce the new family of iterative methods. In
Section 4, we present a local convergence result (Theorem 2) of first kind for the iterative methods of the new family.
Section 5 contains some special cases of Theorem 2. In
Section 6, we prove a local convergence result (Theorem 4) of second kind for the new iterative methods.
Section 7 contains some special cases of Theorem 4.
In
Section 8, we provide a semilocal convergence result (Theorem 6) with computer verifiable initial conditions.
Section 9 presents four special cases of Theorem 6.
Section 10 provides some numerical experiments to show the applicability of Theorem 6. The paper ends with a conclusion section.
2. Notations
Throughout this paper, we use the following notations.
stands for a valued field with a nontrivial absolute value
,
denotes a vector space over
. As usual, the vector space
is endowed with the product topology. In addition,
is equipped with a norm
defined by
In addition,
is endowed with a vector valued norm (cone norm)
with values in
defined by
assuming that the real vector space
is equipped with coordinate-wise partial ordering ⪯ defined as follows
Here and throughout the paper,
. Furthermore, we define on
a binary relation
by
Throughout this paper stands for the set of all vectors in with pairwise distinct coordinates.
Given
p with
, we always denote by
q the conjugate exponent of
p, that is
q is defined by means of
For the sake of brevity, for given integer
and
, we use the following notation
Let us note that a and b satisfy the inequalities and .
We define the function
by
In addition, we define the function
by
We assume by definition that
. For an integer
and
, we define the function
as follows:
As usual, we denote by
the ring of polynomials over
. A vector
is called a
root vector of a polynomial
of degree
if and only if
where
. It is obvious that
f possesses a root vector in
if and only if it splits over
.
4. Local Convergence of First Kind
In this section, we present a local convergence result (Theorem 2) of first kind for the iterative methods of the family (
5). This result generalizes, improves and complements some results of Proinov [
2], Proinov and Vasileva [
9], Proinov, Ivanov and Petković [
10], Machado and Lopes [
12], Milovanović and Petković [
16], Kyurkchiev and Tashev [
17], Wang and Zhao [
18], Petković, Herceg and Ilić [
7], Petković, Petković and Rančić [
8] and Kyurkchiev and Andreev [
19].
Let
be a polynomial of degree
which has
n simple zeros in
and let
be a root vector of
f. In this section we study the local convergence of the iterative methods (
5) with respect to the function of initial conditions
defined by
Lemma 1 ([
15]).
Let , , and be three vectors such thatIf is a vector with pairwise distinct coordinates, then for all , we havewhere is defined by (13). Definition 3 ([
20,
21]).
Let J be an interval on containing 0. A function is called quasi-homogeneous of exact degree if it satisfies the following two conditions:- (i)
- (ii)
Definition 4 ([
21,
22]).
A function is called an iteration function of first kind
at a point if there exists a quasi-homogeneous function of exact degree such that for each vector with , the following conditions are satisfied:where the function is defined by (13). The function ϕ is said to be control function of F. The following general convergence theorem plays an important role in this section.
Theorem 1 ([
21,
22]).
Let be an iteration function of first kind at a point with a control function of exact degree and let be an initial approximation of ξ such thatwhere the function is defined by (
13).
Then the Picard iterationis well defined and converges to ξ with Q-order and with error estimateswhere . Besides, we have the following estimate for the asymptotic error constant: Lemma 2. Let be a polynomial of degree which has only simple zeros in , be a root vector of f, and let be an iteration function. Suppose is a vector such that for some . Thenwhere is defined by Proof. Taking into account that
is a root vector of
f and the fact that
for some
, we obtain
From (
5) and (
22), we get
which completes the proof. □
Let
be a quasi-homogeneous function of exact degree
. We define the functions
and
A as follows
where
a is defined by (
1). Furthermore, we define a function
by
where the interval
is defined by
It easy to show that
is an interval on
containing 0 and such that
It can be easily seen that A is positive and strictly decreasing on and is quasi-homogeneous of exact degree on .
Lemma 3. Let be a polynomial of degree which has only simple zeros in and be a root vector of f. If is an iteration function of first kind at ξ with control function of exact degree , then defined by (
5)
is an iteration function of first kind at ξ with control function defined by (
24)
of degree . Proof. Let
be an iteration function of first kind at
with control function
of exact degree
. Suppose that
is a vector such that
. According to Definition 4, we must prove that
First we prove that
. It follows from (
25) that
, and so
and
. Therefore, taking into account that
is an iteration function of first kind at
with control function
, we conclude by Definition 4 that
and
Hence, the inequality (
14) is satisfied with
and
. Then from Lemma 1 taking into account that
and (
26), we obtain
for all
. Consequently,
. Now, let
for some
. According to (
7), it remains to prove that
From (
22), we conclude that (
29) holds if and only if
, where
is defined in (
21). Applying Lemma 1 with
and
, and taking into account that
, we get
By (
21), (
28), (
30), Hölder’s inequality, and taking into account that
, we get the following estimate:
which yields
. Hence,
.
Now, we have to prove the second condition of (
27) which is equivalent to the following inequalities:
Let
be fixed. If
, then
and so (
32) becomes an equality. Suppose
. From Lemma 2 and the estimate (
31), we obtain
which completes the proof. □
The following theorem is the first main result of this paper.
Theorem 2 (Local convergence of first kind for Ehrlich’s method with correction). Let be a polynomial of degree which has n simple zeros in , be a root vector of f, be an iteration function of first kind at ξ with control function of exact degree . Suppose is an initial approximation satisfying the following conditions:where the function E is defined by (
13)
, the real function B is defined byand a is defined by(
1).
Then the iterative method (
5)
is well defined and converges to ξ with Q-order and with the following error estimates: for all , where and the function ϕ is defined by (
24).
Besides, we have the following estimate for the asymptotic error constant: Proof. It follows from Theorem 1 and Lemma 3 that under the initial condition
the iteration (
5) is well defined and converges to
with
Q-order
and with estimates (
35) and (
36). It is easy to see that the initial condition (
37) is equivalent to (
33) which completes the proof. □
5. Local Convergence of First Kind: Special Cases
In this section, we consider several consequences of Theorem 2.
The following convergence result for Ehrlich’s method (see Definition 2(i)) was proved by Proinov [
2] with the exception of the
Q-convergence and the estimate of the asymptotic constant. It improves previous results of Milovanović and Petković [
16], Kyurkchiev and Tashev [
17] and Wang and Zhao [
18].
Corollary 1 (Local convergence of first kind for Ehrlich’s method [2]).Let be a polynomial of degree which has n simple zeros in , be a root vector of f and . Suppose is an initial approximation satisfyingwhere the function E is defined by (
13)
, and a and b are defined by (
1).
Then Ehrlich’s method is well defined and converges Q-cubically to ξ with error estimatesfor all , where and the function ϕ is defined byBesides, we have the following estimate for the asymptotic error constant: Proof. Ehrlich’s method is a member of the family (
5) with
. Obviously,
is an iteration function of first kind at
with control function
defined by
of exact degree
. It follows from (
34) that
. Now it is easy to see that Theorem 2 coincides with Corollary 1 for Ehrlich’s method. This completes the proof. □
The next convergence result for Ehrlich’s method with Newton’s correction (see Definition 2(iii)) was proved by Proinov and Vasileva [
9] with the exception of the
Q-convergence and the estimate of the asymptotic constant. This result improves previous results of Petković, Herceg and Ilić [
7] and Petković, Petković and Rančić [
8].
Corollary 2 (Local convergence of first kind for the EN method [9]). Let be a polynomial of degree which has n simple zeros in , be a root vector of f. Suppose is an initial approximation satisfying the following condition:where the function E is defined by (
13)
and the function is defined byThen Ehrlich’s method with Newton’s correction is well defined and converges to ξ with Q-order and with the following error estimates:where and the function ϕ is defined byBesides, we have the following estimate for the asymptotic error constant: Proof. It is known that Newton’s iteration function (
10) is an iteration function of first kind at
with control function
defined by
with exact degree
(see Lemma 4.4 of [
23]). Then it follows from Theorem 2 that the conclusions of the corollary hold under the initial conditions
It can be shown that
for all
. Hence, the first condition of (
46) can be omitted, which completes the proof. □
The following convergence result for Ehrlich’s method with Halley’s correction (see Definition 2(v)) is an improved version of Corollary 5.1 of Proinov, Ivanov and Petković [
10]. It gives sharper error estimates,
Q-convergence and an estimate of the asymptotic constant.
Corollary 3 (Local convergence of first kind for the EH method [10]).Let be a polynomial of degree which has only simple zeros in , be a root vector of f. Suppose is an initial approximation satisfyingwhere the function is defined by (
13).
In the case and , we assume that the inequality (
47)
is strict. Then Ehrlich’s method with Halley’s correction is well defined and converges to ξ with Q-order and with error estimatesfor all , where and the function ϕ is defined byBesides, we have the following estimate for the asymptotic error constant: Proof. It is known that Halley’s iteration function (
12) is an iteration function of first kind at
with control function
defined by (
49) of exact degree
(see Lemma 4.5 of [
24]), where
Then it follows from Theorem 2 that the claims of the lemma hold under the initial conditions
where the function
B is defined by (
34) with
defined by (
49). It remains to prove that
satisfies both conditions (
52). The first condition follows trivially from
and the second one follows from
,
and the fact that
only in the case
and
. This completes the proof. □
We end this section with a convergence result for a family of iterative methods which was constructed by Kyurkchiev and Andreev [
19] (see also Proinov and Vasileva [
25]). Before formulating the result, we introduce two more definitions.
Definition 5 (Kyurkchiev and Andreev [
19]).
Let be a polynomial of degree . Define a sequence of iteration functions as follows: Definition 6. We define a sequence of functions recursively by setting andand a is defined by (
1).
The next result is an improved version of a result of Proinov and Vasileva [
25]. It gives the same domain of convergence but sharp error estimates,
Q-convergence and an estimate of the asymptotic constant. In addition, it improves the previous result of Kyurkchiev and Andreev [
19].
Corollary 4 (Local convergence of first kind for Kyurkchiev–Andreev’s family [9]). Let be a polynomial of degree which has only simple zeros in , be a root vector of f and . Suppose is an initial approximation satisfyingwhere the function is defined by (
13)
and a and b are defined by (
1).
Then N-th Kyurkchiev-Andreev’s iterative method is well defined and converges to ξ with Q-order and error estimatesfor all , where and the function is defined by Definition 6. Besides, we have the following estimate for the asymptotic error constant: Proof. It can easily be proved that for every integer :
is a quasi-homogeneous of exact degree on and ;
is an iteration function of first kind at with control function defined by (this statement follows from Lemma 3).
for all
, where
B is defined by (
34).
Then the conclusions of the corollary follow immediately from Theorem 2. □
6. Local Convergence of Second Kind
In this section, we provide a local convergence result (Theorem 4) of second kind for the iterative methods of the family (
5). This result generalizes some results of Proinov [
2] and Proinov and Vasileva [
9].
Let
be a polynomial of degree
which splits over
, and let
be a root vector of the polynomial
f. In this section, we study the local convergence of the iterative methods (
5) with respect to the function of initial conditions
defined by
Lemma 4 ([
25]).
Let , , and be three vectors such thatIf is a vector with pairwise distinct coordinates, then for all , we havewhere is defined by (57). Definition 7 ([
21,
22]).
A function is called an iteration function of second kind
at a point if there exists a nonzero quasi-homogeneous function of exact order such that for each vector with , the following conditions are satisfied:where the function is defined by (
57).
The function β is said to be control function
of F. The following general convergence theorem plays an important role in this section.
Theorem 3 ([
21,
22]).
Let be an iteration function of second kind at a point with control function of exact degree and let be an initial approximation with distinct coordinates such thatwhere the function is defined by (
57),
the function is defined byand b is defined by (
1).
Then ξ is a fixed point of F with distinct coordinates and the Picard iteration (
17)
is well defined and converges to ξ with Q-order and with error estimateswhere , and the functions ψ and ϕ are defined by Let
be an iteration function of second kind at a point
with control function
of exact degree
. We define the function
by
Using the functions
and
, we define the function
by
and the function
by
where
a is defined by (
1) and the interval
is defined by
It easy to show that
is an interval in
containing 0 and
It can be proved that:
In accordance to Theorem 3, we define the real functions
and
as follows:
where
a and
b are defined by (
1).
Lemma 5. Suppose is a polynomial of degree which has n simple zeros in and is a root vector of f. Let be an iteration function of second kind at ξ with control function of exact degree . Then defined by (
5)
is an iteration function of second kind at ξ with control function of exact degree , where β is defined by (
63).
Proof. The proof is carried out in the same way as the proof of Lemma 3 using Definition 7 and Lemma 4 instead of Definition 4 and Lemma 1, respectively. □
Now we can state the second main result of this paper.
Theorem 4 (Local convergence of second kind for Ehrlich’s method with correction). Let be a polynomial of degree which has n simple zeros in , be a root vector of f, be an iteration function of second kind at ξ with control function of exact degree . Suppose is an initial approximation satisfying the following conditions:where the function E is defined by (
57)
, the real function B is defined bywith defined by (
61)
and a and b defined by (
1).
Then the iterative method (
5)
is well defined and converges to ξ with Q-order and with the following error estimatesfor all , where , , and ψ and ϕ are defined by (67) and (68), respectively. Proof. It follows from Theorem 3 and Lemma 5 that under the initial condition
the iteration (
5) is well defined and converges to
with
Q-order
and with error estimates (
71). Taking into account that
for
, where
A is defined by (
62), we can prove that
which implies that the initial conditions (
69) and (
72) are equivalent. This completes the proof. □
8. Semilocal Convergence
In this section, we prove a semilocal convergence result for the iterative methods of the family (
5). The result is a generalization of Theorem 11 of Proinov and Vasileva [
9].
Throughout this and the next section, we assume that is an algebraically closed valued field.
Let
be a polynomial of degree
. In this section, we study the semilocal convergence of the iterative methods (
5) with respect to the function of initial conditions
defined by
where the function
is defined by
and
is the leading coefficient of
f.
The next theorem plays a dual role in our paper. In this section we will use it to transform Theorem 4 into a semilocal result, and in the next section we will use it as a stopping criterion.
Theorem 5 ([
26], Theorem 5.1).
Suppose is a polynomial of degree and is a vector with distinct coordinates such thatwhere a is defined by (
1)
and the function is defined by (
79).
Then f has only simple zeros and there exists a root vector of f such that:- (i)
,
- (ii)
,
where the function E is defined by (57) and the real functions are defined as follows: Let us note that the functions
and
h defined by (
82) are strictly increasing on the interval
.
The following definition allows us to formulate our semilocal convergence results more compactly.
Definition 8. Let be an iteration function, and let J be a quasi-homogeneous function of exact degree . We say that Φ is an iteration function of second kind with control function ω if for every root vector of every polynomial of degree which has distinct zeros in , Φ is an iteration function of second kind at ξ with control function ω.
In
Table 1 are given some iteration functions in
with control function
on an interval
J of exact degree
m. According to Theorem 3, the
Q-order of these iteration functions is
. In the table, the real numbers
and
are defined by
The next theorem is our third main result in this paper.
Theorem 6 (Semilocal convergence of Ehrlich’s method with correction). Suppose f is a polynomial of degree in and is an iteration function of second kind with control function of exact degree . Let be an initial approximation with distinct coordinates satisfying the following condition:where μ is defined by (
81)
, the functions , h and B are defined by (
79), (
82)
and (
70)
respectively. Then f has only simple zeros and the iterative method (
5)
is well defined and converges to a root vector of f with Q-order . Proof. Let
a and
b be defined by (
1) and the function
E be defined by (
57). We note that the function
h is strictly increasing on
and the function
B is strictly decreasing on
. It follows from Theorem 5 and the first condition of (
84) that
f has only simple zeros and there exists a root vector
of
f such that:
From this and the second inequality of (
84), we conclude that both sides of the inequality
belong to the interval
. Then we obtain
It follows from (
85), (
86) and the second condition of (
84) that
satisfies the initial conditions (
69). Then it follows from Theorem 4 that iterative method (
5) is well defined and converges to
with
Q-order
. This complete the proof. □
9. Semilocal Convergence: Special Cases
In this section, we present four special cases of Theorem 6. Namely, we study the semilocal convergence of the iterative methods which are introduced in Definition 2. The initial conditions of each corollary is a simplified but equivalent form of the initial conditions (
84) of Theorem 6.
Throughout this and the next section, we define the functions
and
h by (
79) and (
82), respectively. In addition, we use the function
g defined on the interval
as follows:
where
a is defined by (
1). The function
g is the inverse of the function
h. It was introduced in [
26] to obtain important consequences of Theorem 5.
We begin this section with a semilocal convergence result for Ehrlich’s method with Weierstrass’ correction (see Definition 2(ii)).
Corollary 7 (Semilocal convergence of EW method). Let be a polynomial of degree and be an initial approximation with distinct coordinates satisfyingwhere μ is defined by (
81)
and the function B is defined by (
70)
with ω defined in the first row of Table 1. Then f has only simple zeros and Ehrlich’s method with Weierstrass’ correction is well defined and convergent to a root vector of f with Q-order . Proof. Weierstrass’ iteration function (
9) is an iteration function of second kind with control function
defined in the first row of
Table 1. Note that
is quasi-homogeneous of exact degree
on the interval
. Hence, the proof follows immediately from Theorem 6. □
The next semilocal convergence result for Ehrlich’s method with Newton’s correction (see Definition 2(iii)) coincides with Theorem 11 of Proinov and Vasileva [
9].
Corollary 8 (Semilocal convergence of EN method [9]). Let be a polynomial of degree and be an initial approximation with distinct coordinates satisfyingwhere the function g is defined by (
87)
and the function B is defined bywhere a and b are defined by (
1).
Then f has only simple zeros and Ehrlich’s method with Newton’s correction is well defined and convergent to a root vector of f with Q-order . Proof. Newton’s iteration function (
10) is an iteration function of second kind with control function
defined in the second row of
Table 1. The function
is quasi-homogeneous of exact degree
on the interval
. It is easy to show that
where
is defined by (
81). Then it follows that the first two conditions of (
84) are equivalent to the first condition of (
89) which completes the proof. □
The following corollary is a semilocal convergence result for Ehrlich’s method with Ehrlich’s correction (see Definition 2(iv)).
Corollary 9 (Semilocal convergence of EE method). Let be a polynomial of degree and is an initial approximation with distinct coordinates such thatwhere μ is defined by (
81)
and the function B is defined by (
70)
with ω defined in the third row of Table 1. Then f has only simple zeros and Ehrlich’s method with Ehrlich’s correction is well defined and converges to a root vector of f with Q-order . Proof. Ehrlich’s iteration function (
11) is an iteration function of second kind with control function
defined in the third row of
Table 1. Note that
is quasi-homogeneous of exact degree
on the interval
, where
is defined by (
83). For every
, we have
This implies that the second condition of (
84) holds, which completes the proof. □
We end this section with a semilocal convergence result for Ehrlich’s method with Halley’s correction (see Definition 2(v). This result improves Corollary 6.2 of Proinov, Ivanov and Petković [
10].
Corollary 10 (Semilocal convergence of EH method). Let be a polynomial of degree and is an initial approximation with distinct coordinates such thatwhere ν is defined by (
83)
, the function g is defined by (
87)
and the functions B is defined by (
70)
with ω defined in the fourth row of Table 1. Then f has only simple zeros in and Ehrlich’s method with Halley’s correction is well defined and convergent to a root vector of f with Q-order . Proof. Halley’s iteration function (
12) is an iteration function of second kind with control function
defined in the fourth row of
Table 1. The function
is quasi-homogeneous of exact degree
on the interval
, where
is defined by (
83). It is easy to check that
, where
a is defined by (
1), Then we have
where
is defined by (
81). From this we conclude that the first two conditions of (
84) are equivalent to the first condition of (
91) which completes the proof. □
10. Numerical Experiments
Let
be a polynomial of degree
. Starting from an initial approximation
, we generate an iterative sequence
by an iterative method of the family (
5). The main purpose of this section is to show that Theorem 6 can be used for computer proof that an iterative method of family (
5) is convergent under the initial condition
. In the examples below, we apply Theorem 6 with
.
It follows from Theorem 6 that if there exists an integer
s such that
then
f has only simple zeros and the iterative sequence
is convergent to a root vector of the polynomial
f with
Q-order
.
The convergence criterion (
92) can be used for any iterative method of the family (
5). However, in the conducted numerical experiments we study the following methods:
Ehrlich’s method with Weierstrass’ correction (EW);
Ehrlich’s method with Newton’s correction (Nourein’s method) (EN);
Ehrlich’s method with Ehrlich’s correction (EE);
Ehrlich’s method with Halley’s correction (EH).
These are defined in Definition 2. It follows from Corollaries 7–10 that for these methods, the convergence criterion (
92) takes the following simpler equivalent form:
where
for the EW and EE methods,
for the EN method,
for the EH method, where .
In accordance to Theorem 5(i), we use the following stopping criterion:
which guarantees that zeros of
f are calculated with accuracy
.
We consider three monic polynomials
f of degree
taken from [
6,
28]. In each example, we choose very crude initial approximation
with coordinates
randomly in the square
For each example, we exhibit the following values:
r – the order of convergence of the corresponding iterative method;
s – the smallest nonnegative integer that satisfies the convergence criterion (
93);
– the guaranteed accuracy for the approximation ;
k – the smallest nonnegative integer that satisfies stopping criterion (
94);
– the guaranteed accuracy for the approximation ;
– the guaranteed accuracy for the approximation .
In order to be able to see that the convergence-criterion (
93) is satisfied, we also show the quantities
and
.
In the figures below, we present the trajectories of the approximations
in the complex plane
, where
k is the smallest nonnegative integer that satisfies the stopping criterion (
94). Besides, the roots of the polynomial
f are presented with red points, and the initial approximations are presented with blue points.
We use CAS Wolfram Mathematica 12 to implement the corresponding algorithms and to present approximations of higher accuracy.
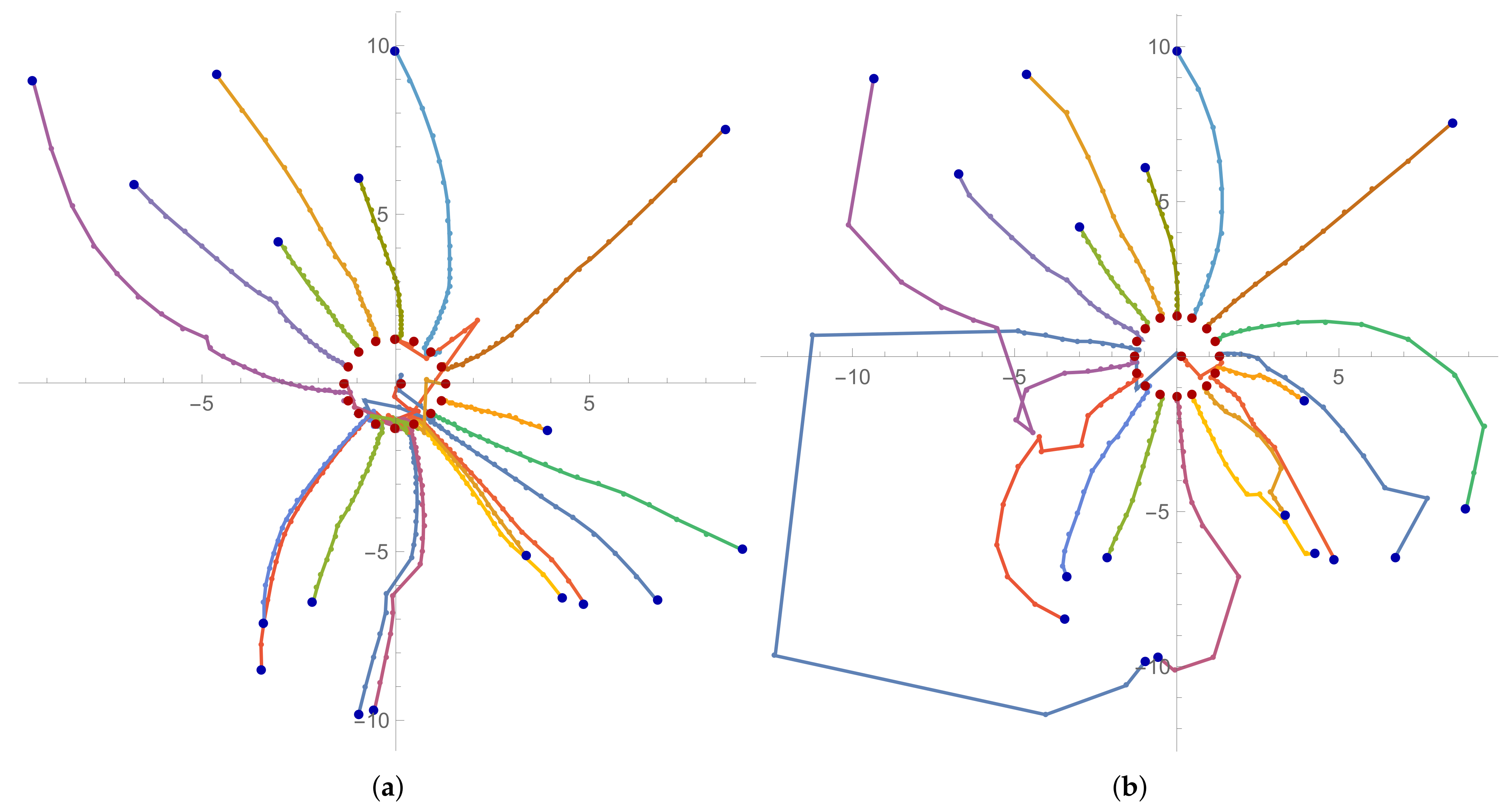
Example 1. Let us consider Mignotte’s polynomial of the form , ([28]), that is,Our random initial approximation for this example is In
Table 2, we present the numerical results for Example 1. For instance, for Ehrlich’s method with Newton’s correction (EN) it is seen that the convergence criterion (
93) is satisfied for
and that the stopping criterion (
94) is satisfied for
. Besides, at the 35th iteration each of the roots of the polynomial (
96) is calculated with a guaranteed accuracy of
and at 36th iteration the zeros of
f are calculated with an accuracy of
.
In
Figure 1 are presented the trajectories of the approximations (
95) for the EW and EN methods for Example 1. The trajectories of the approximations (
95) for the EE and EH methods for Example 1 are presented in
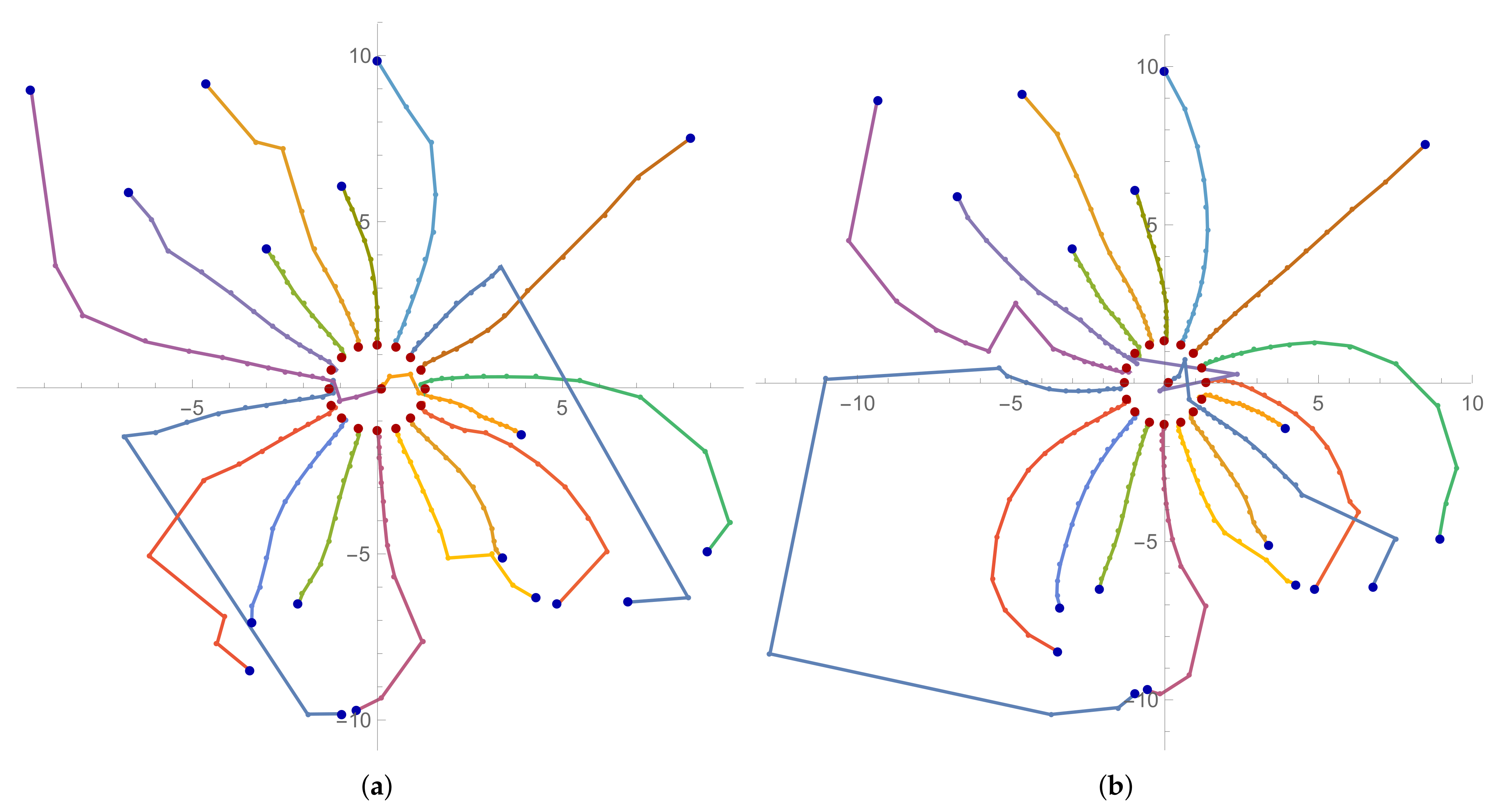
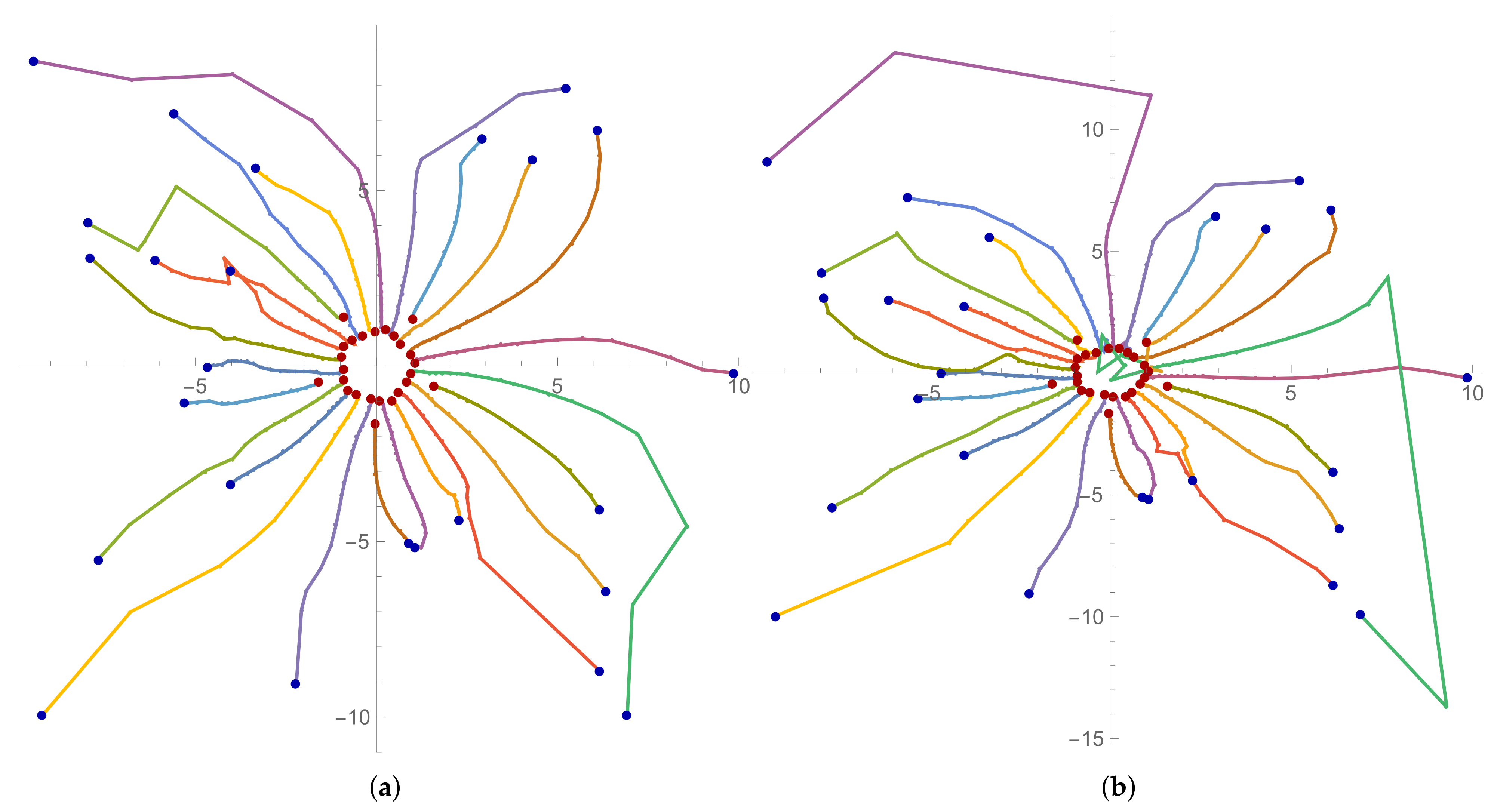
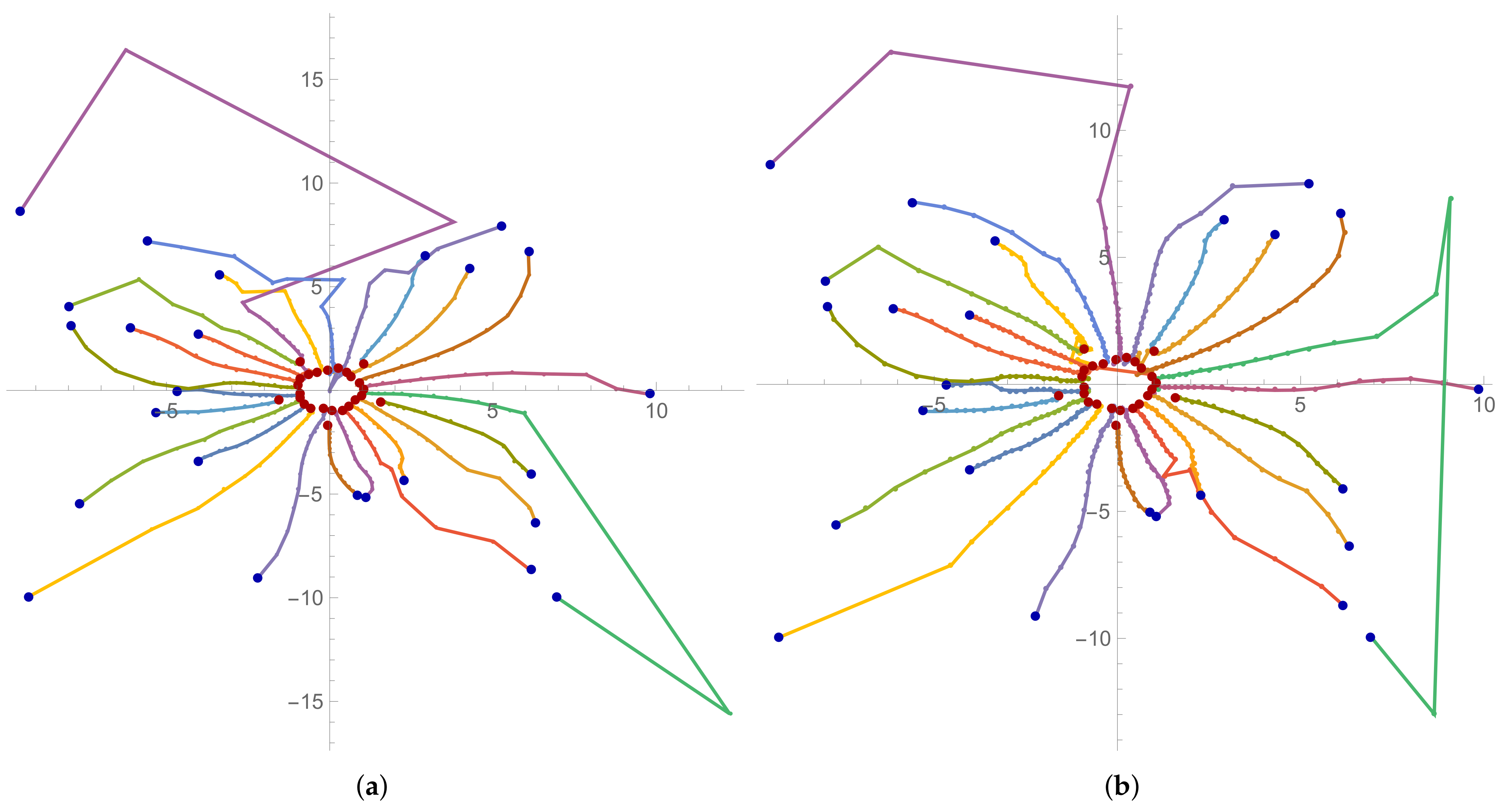
Figure 2. Interesting trajectories can be seen. Some of them go a long way, others a shorter one, but each of them finds exactly one root of the polynomial.
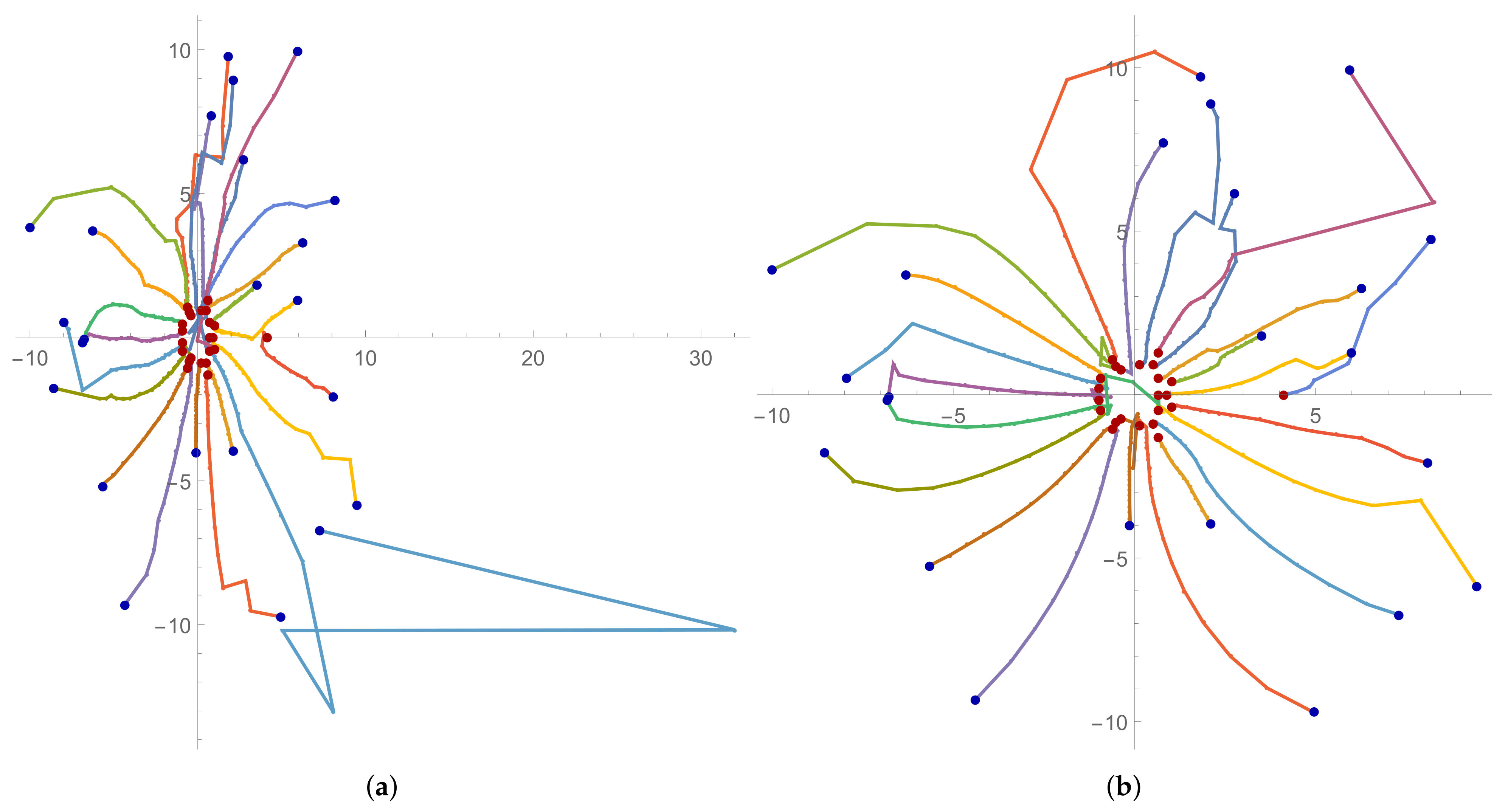
Example 2. Following [6], we consider the following polynomial with random-integer coefficients from the interval and with the randomly chosen signs: -4.6cm0cm Our random initial approximation for Example 2 is -4.6cm0cm Table 3 presents numerical results for Example 2. For instance, for Ehrlich’s method with Weierstrass’ correction (EW) it can be seen that the convergence criterion (
93) is satisfied for
and that the accuracy criterion (
94) is satisfied for
. In addition, at 45th iteration each of the roots of the polynomial is calculated with a guaranteed accuracy of
.
In
Figure 3 and
Figure 4, one can see the trajectories (
95) of the approximations of the EW, EN, EE and EH methods for Example 2. For instance, in
Figure 3a we can see trajectories of the approximations of the EW method for the first 44 iterations
. Here we observe an interesting phenomenon: one of the trajectories goes in the opposite direction of the roots and after moving away quite far it changes its direction by moving horizontally, then it goes in the opposite direction of the roots again, but finally it turns back and finds its root.
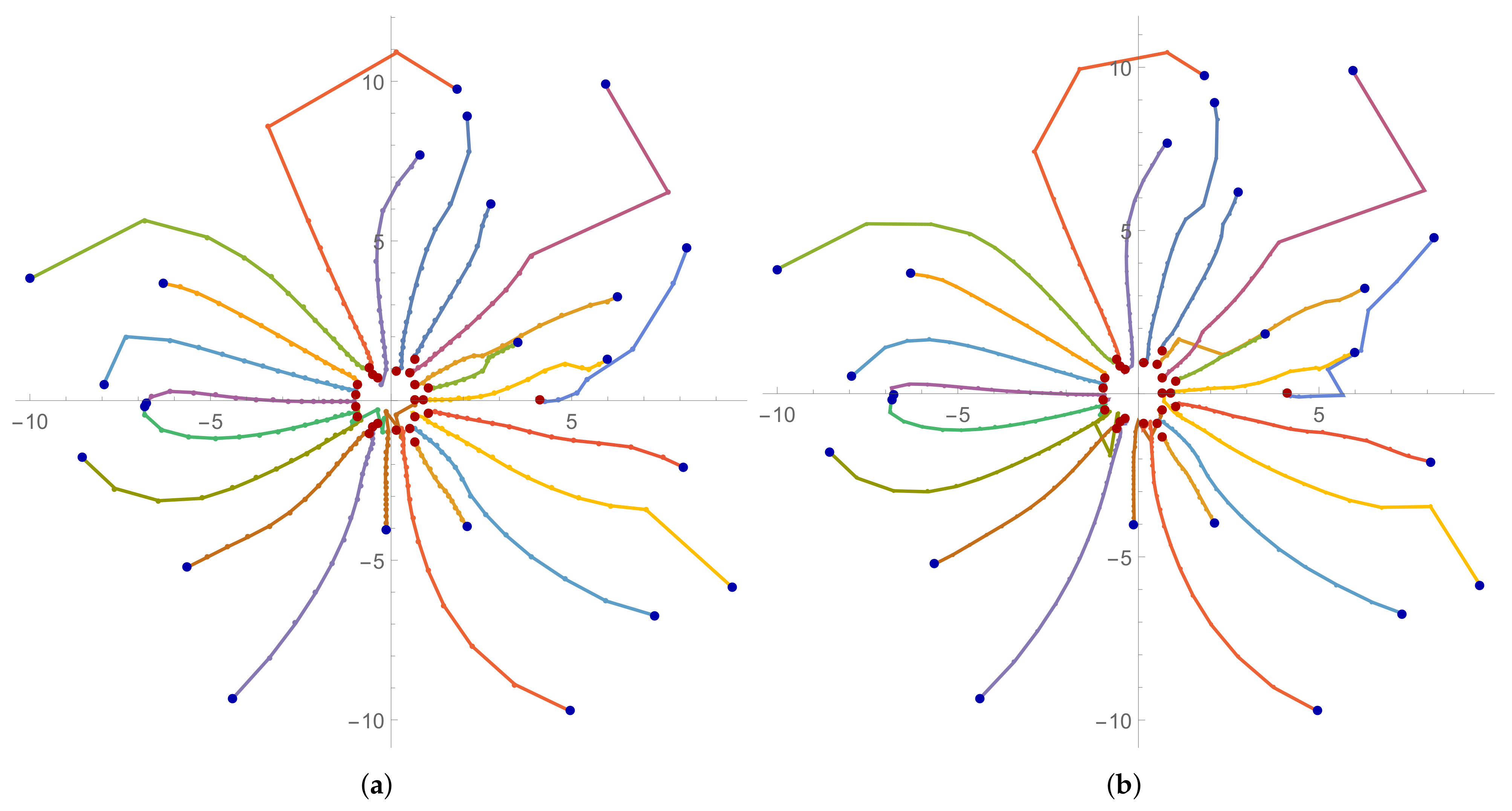
Example 3. In this example, we consider the following polynomial with complex coefficients ([6]): Our random initial approximation for Example 3 is -4.6cm0cm The numerical results for Example 3 are given in
Table 4. For instance, for Ehrlich’s method with Halley’s correction (EH) it is seen that the convergence criterion (
93) is satisfied for
and that the stopping criterion (
94) is satisfied for
, which means that the preset accuracy
is reached at 30th iteration. Moreover, the table shows that, at 30th iteration it is guarantees an accuracy of
and at 31th iteration, it guarantees that each of the roots of the polynomial is calculated with a guaranteed accuracy of
.
In
Figure 5 and
Figure 6, one can see the trajectories (
95) of the approximations of the EW, EN, EE and EH methods for Example 3. We again observe extremely interesting and strange trajectories.
It can be seen from
Table 2,
Table 3 and
Table 4 that, in all experiments, Theorem 6 guarantees that each of the considered iterative methods of the family (
5) is convergent under the given very rough initial approximation. In addition, we see on which iteration the preset accuracy is reached. Let us pay attention to the interesting fact that in each example Ehrlich’s method with Ehrlich’s correction (EE) needs the least iterations to satisfy convergence and accuracy criteria.
One can see from
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6 that some initial points during iterating are not going to the nearest zero. Moreover, for the same polynomial and same initial approximation for different methods, some initial points during iterating go to a different zero of the polynomial.