Numerical Investigation of Fuzzy Predator-Prey Model with a Functional Response of the Form Arctan(ax)
Abstract
1. Introduction
2. Basic Concepts
3. The Models
3.1. Fuzzy Initial Conditions
3.2. Fuzzy Parameters
- (1)
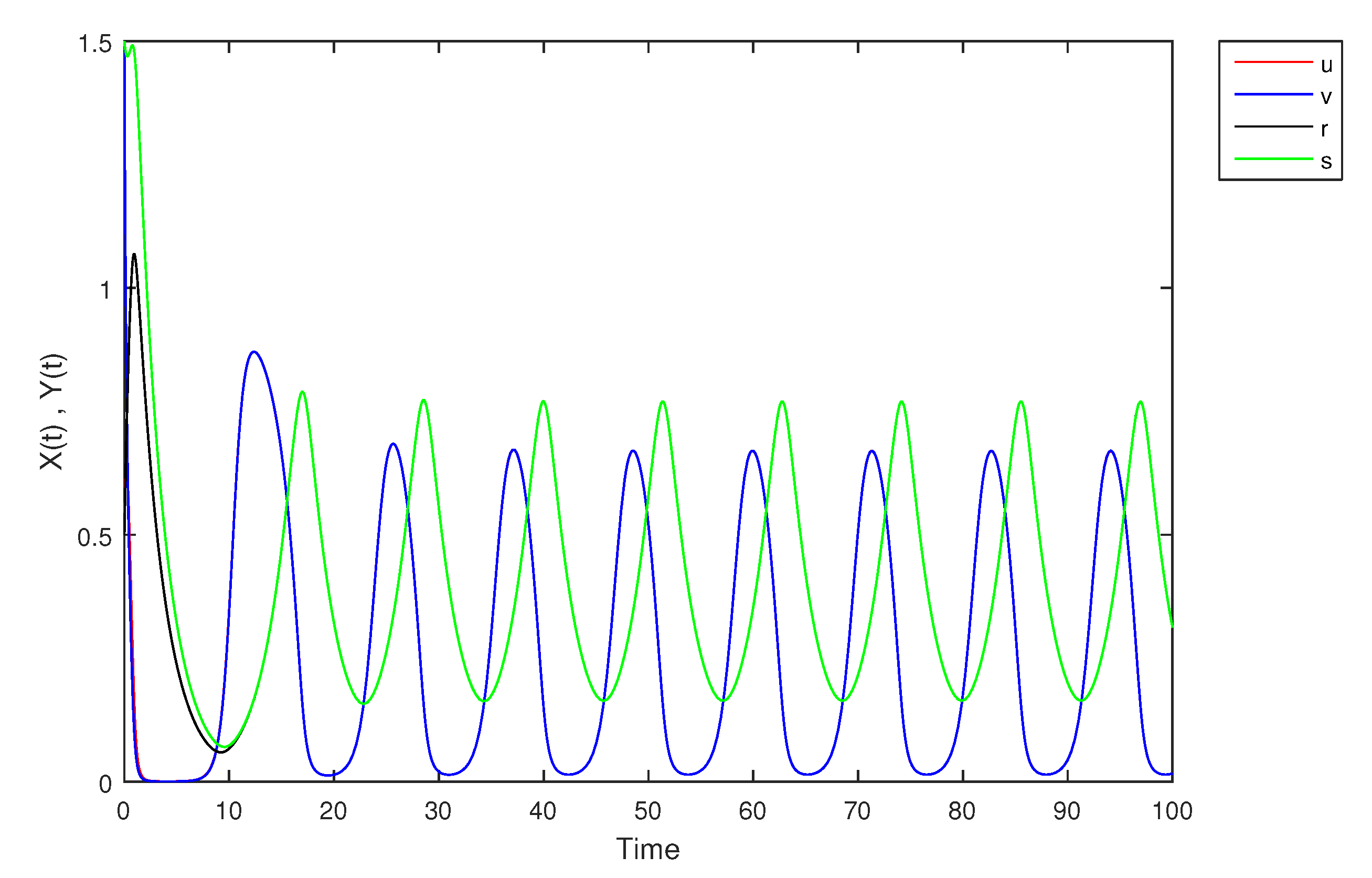
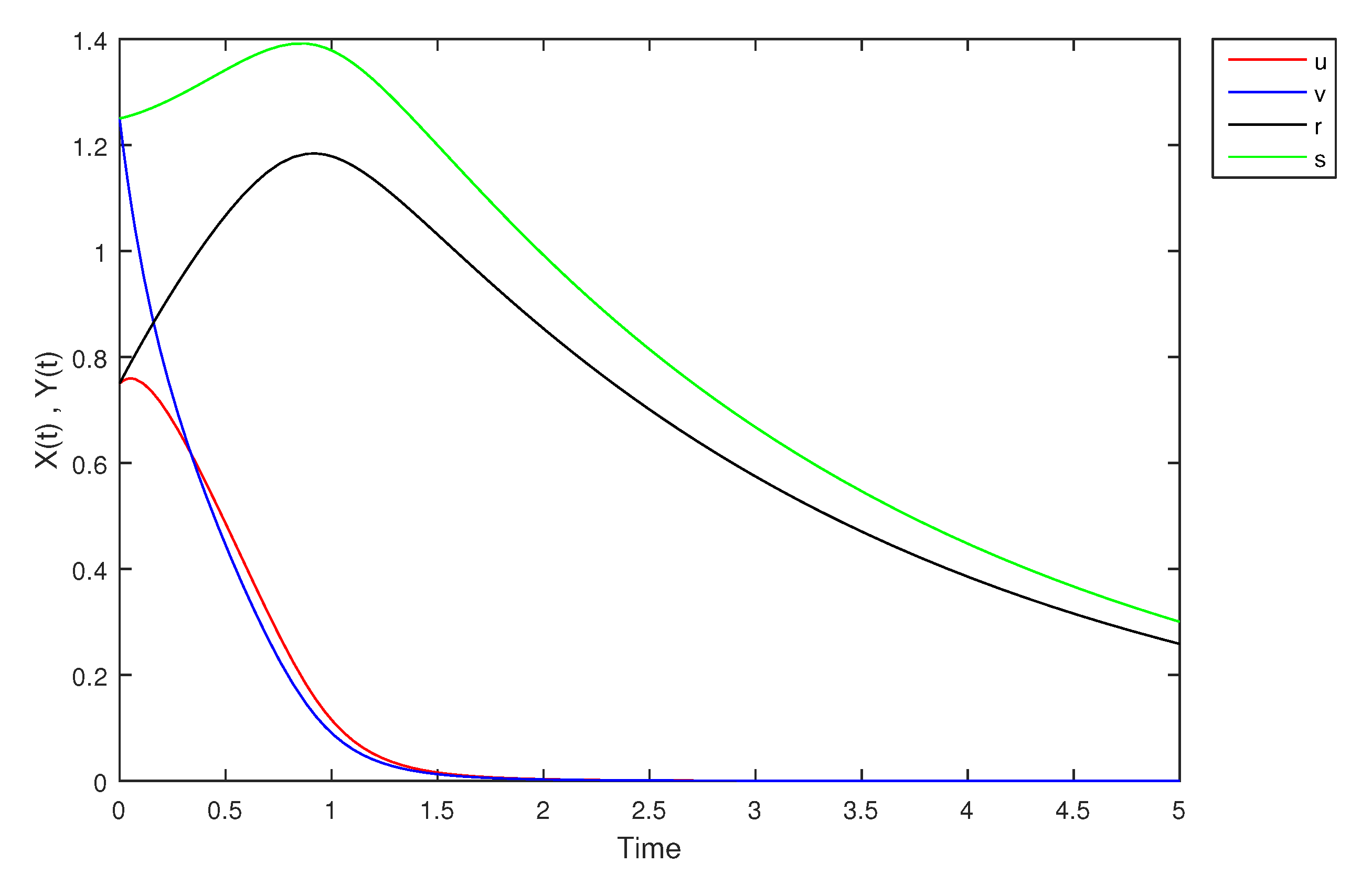
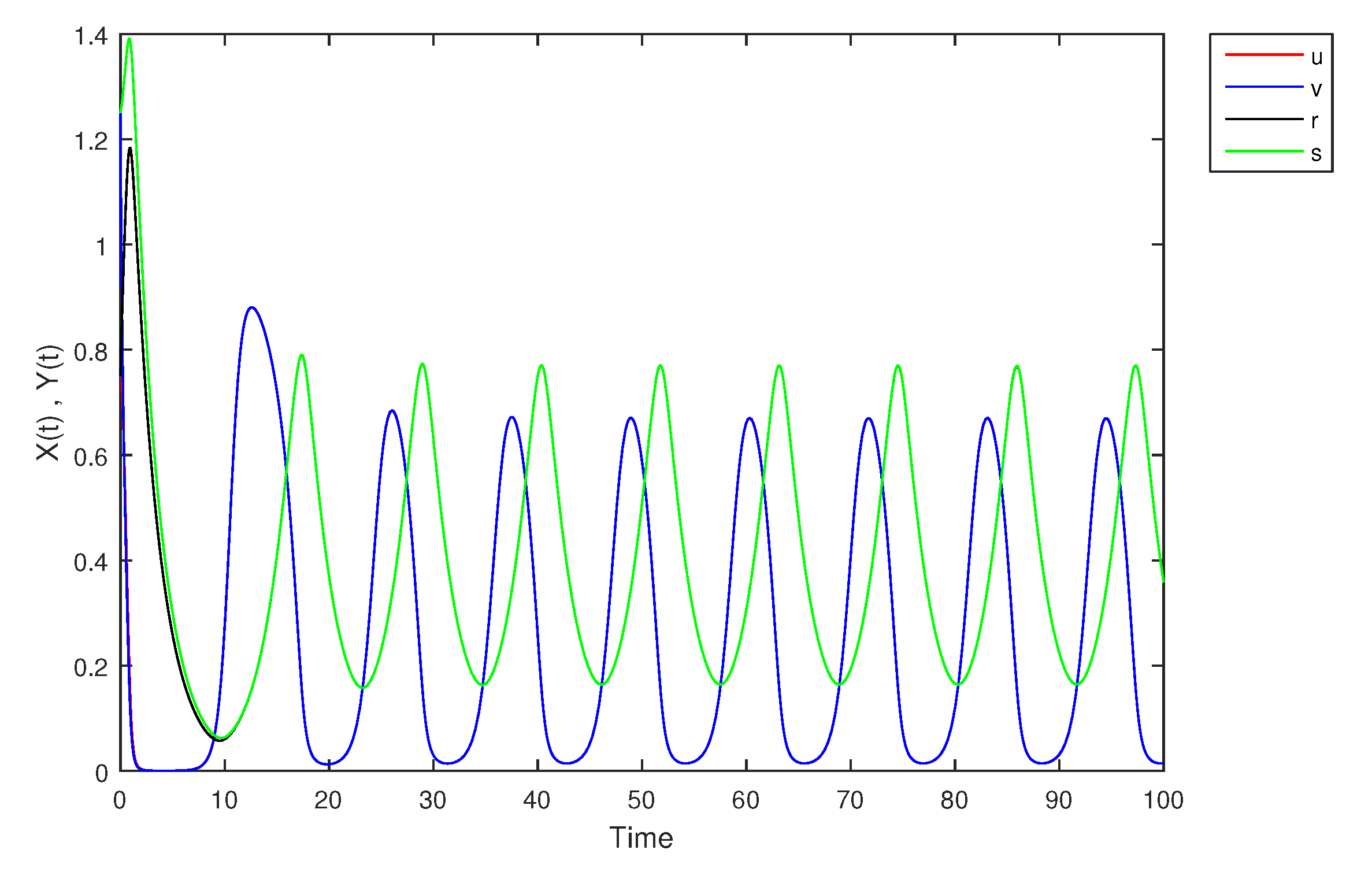
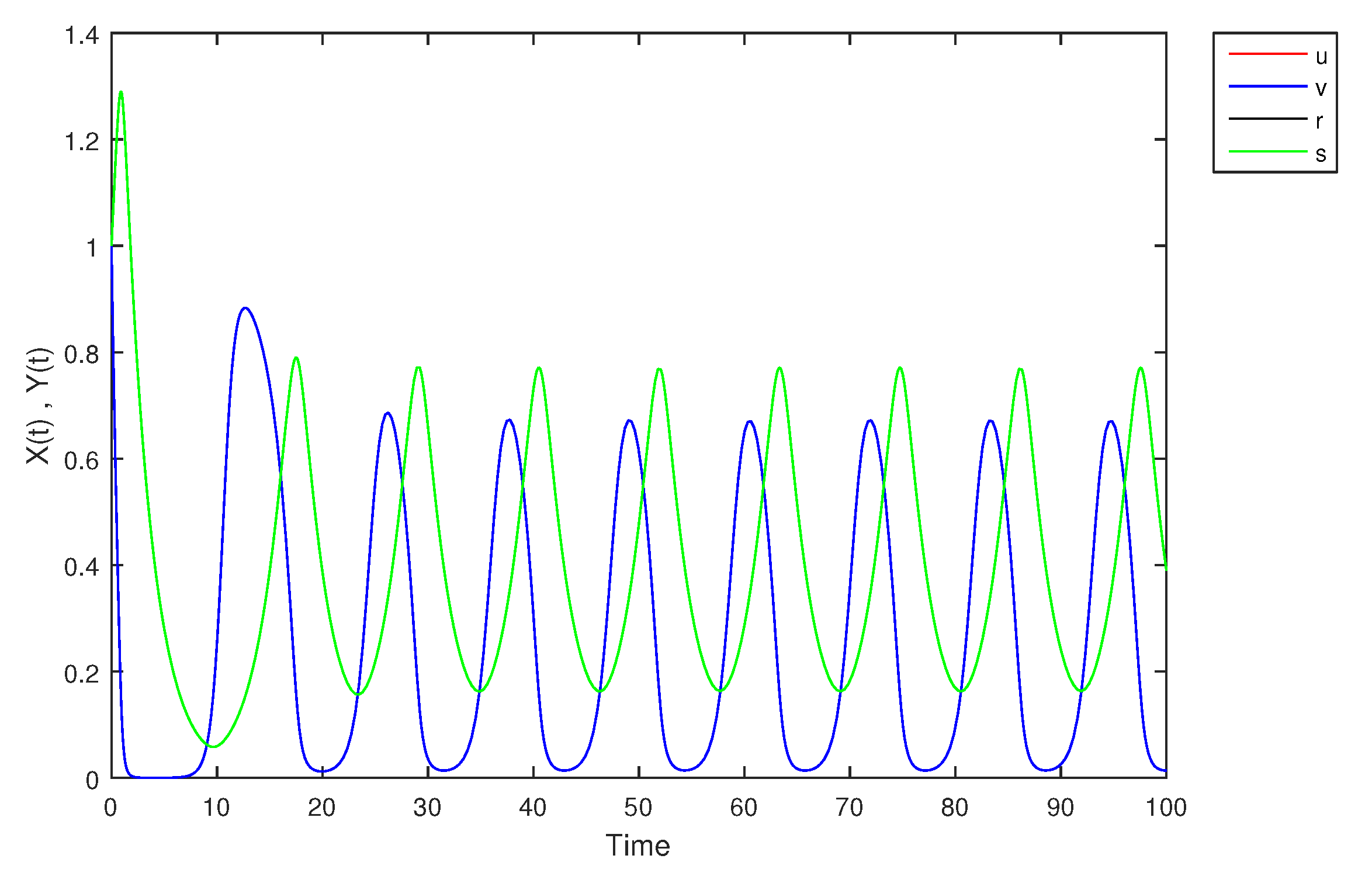
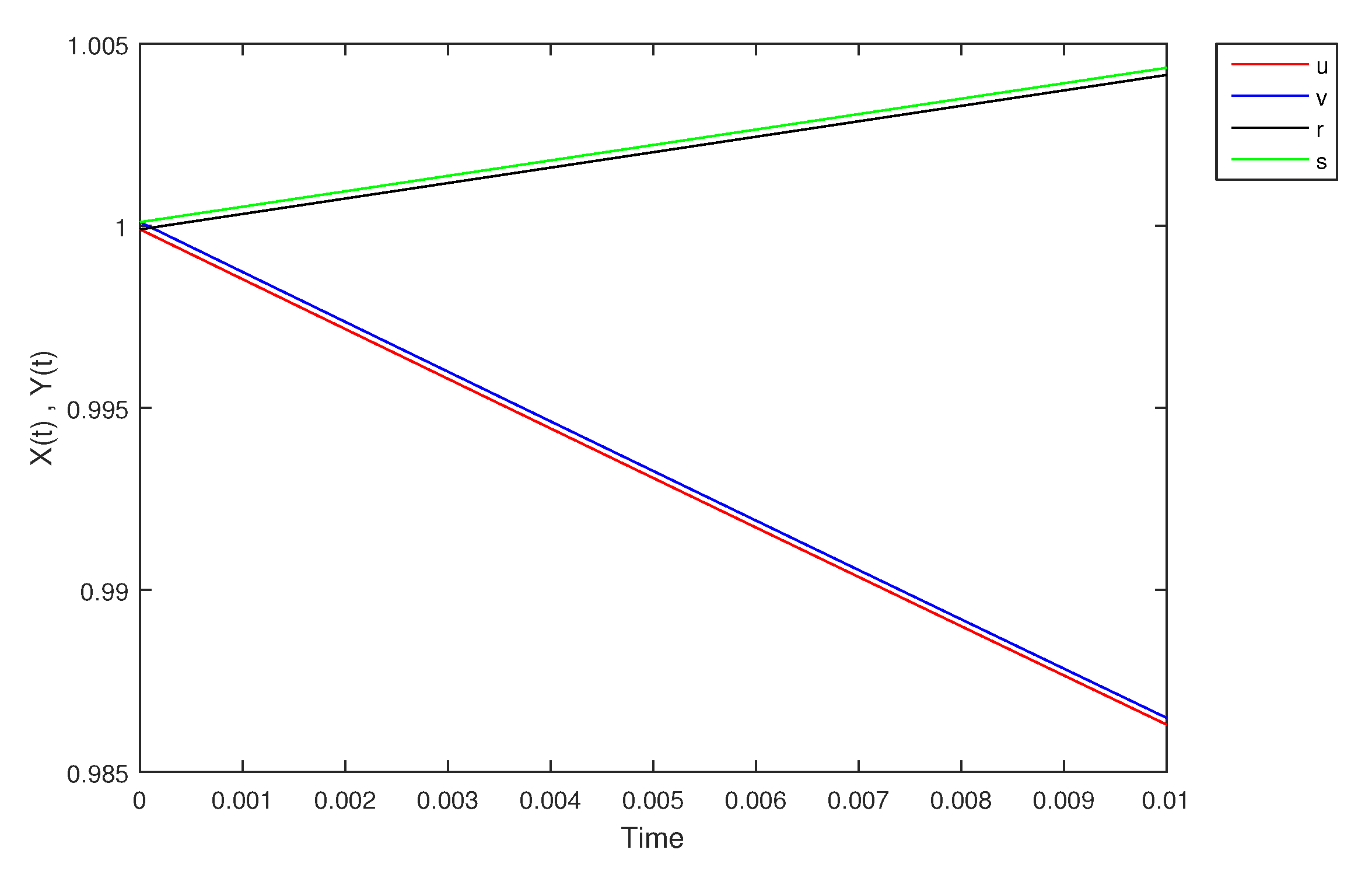
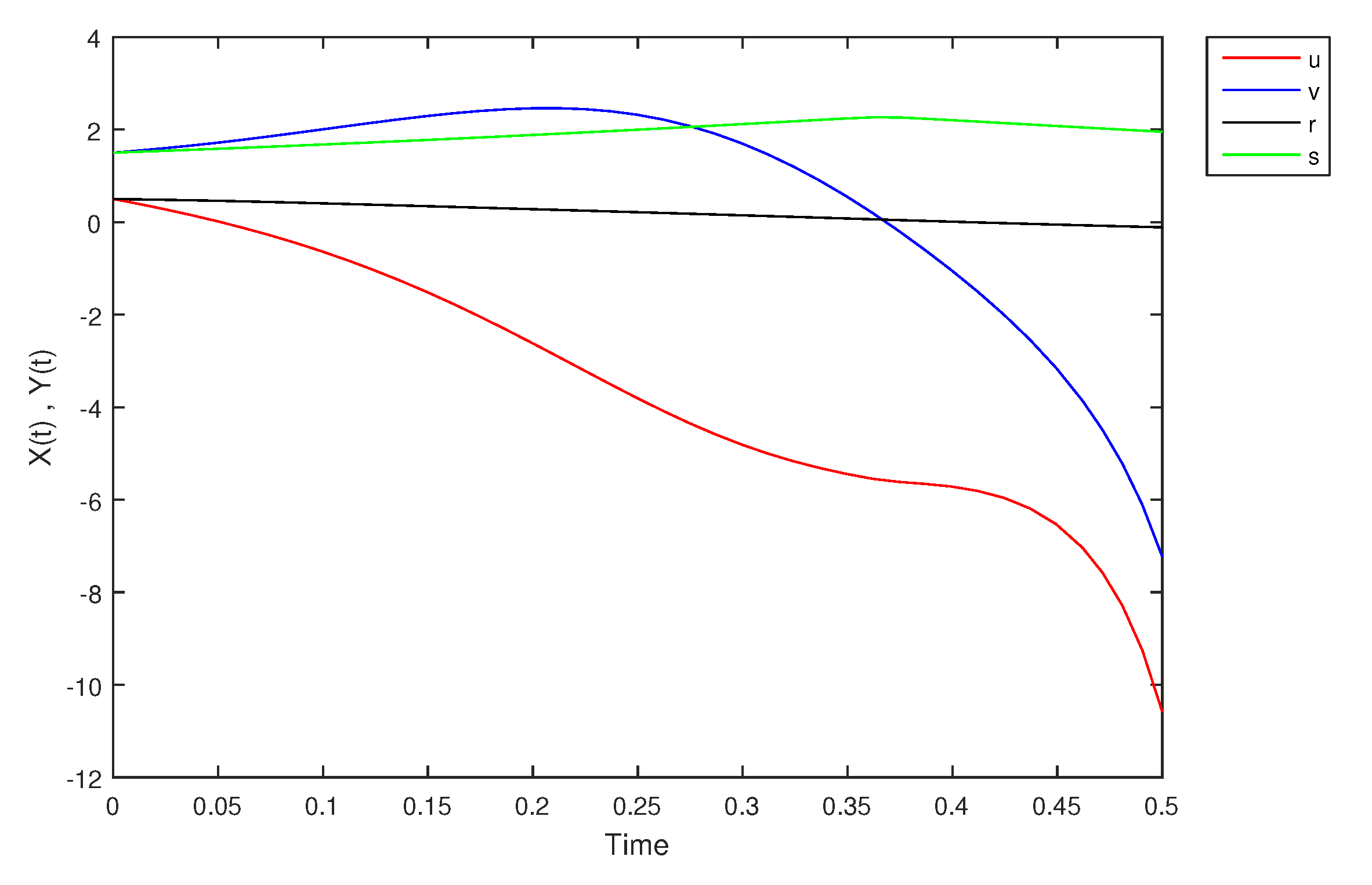
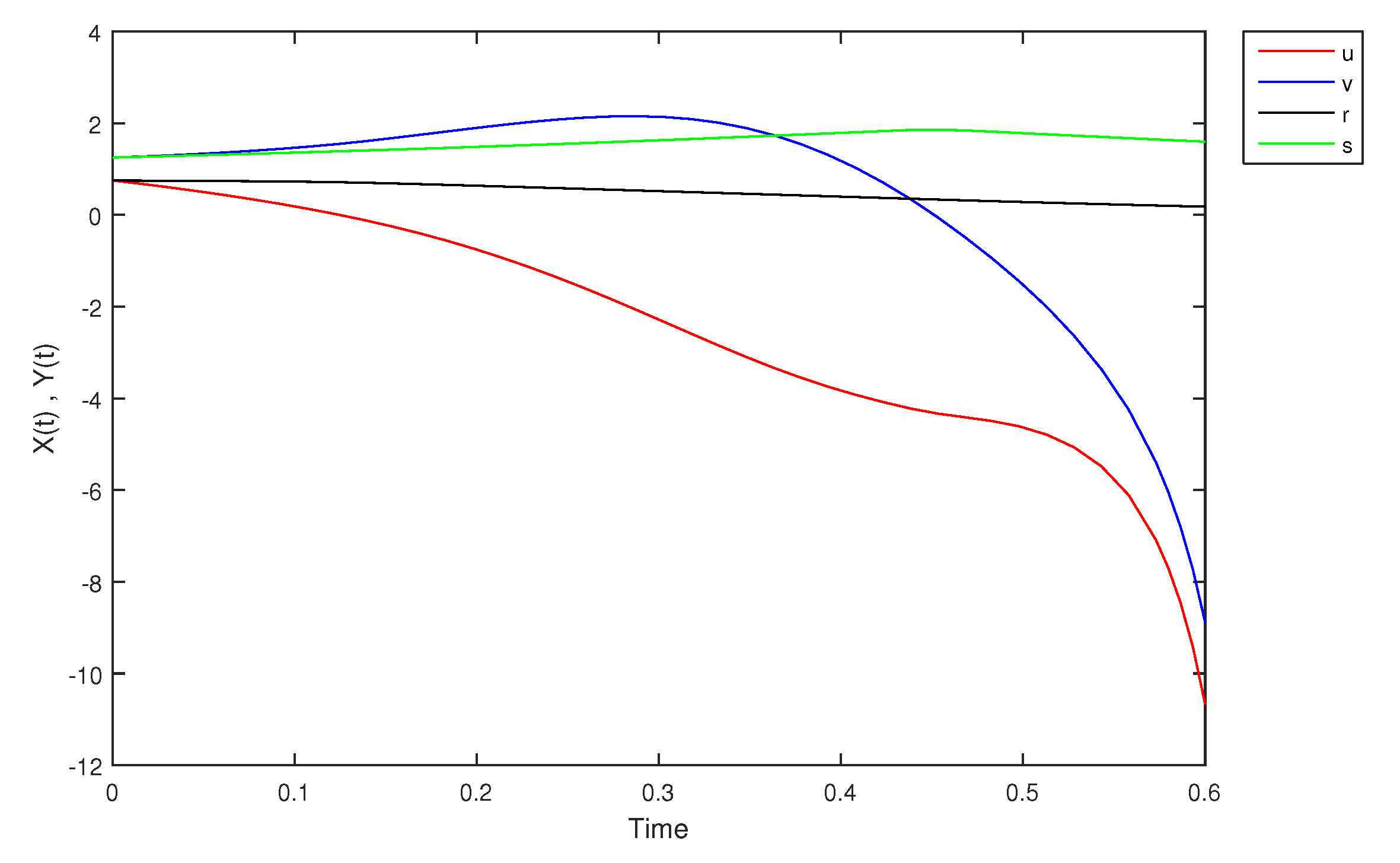
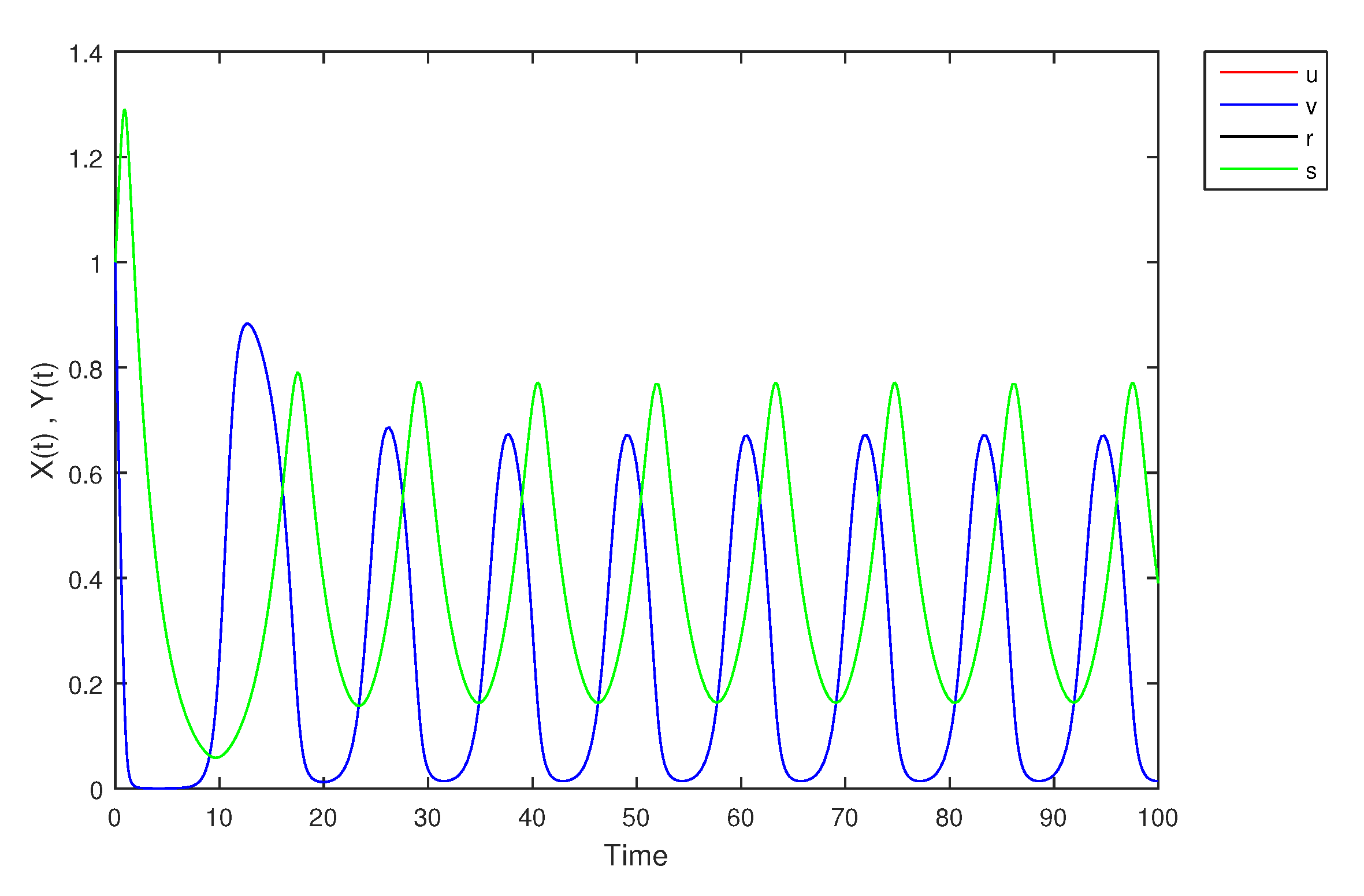
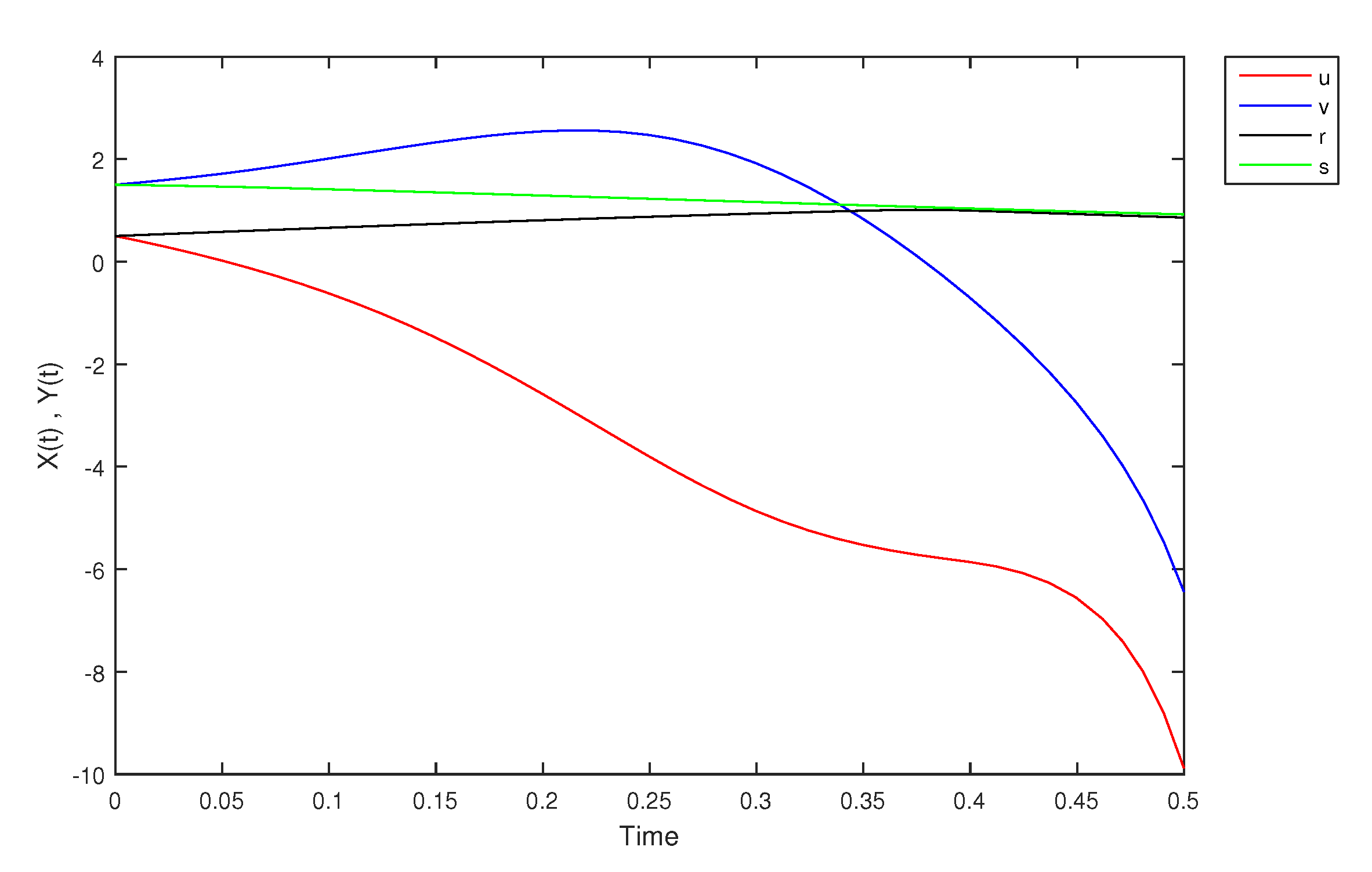
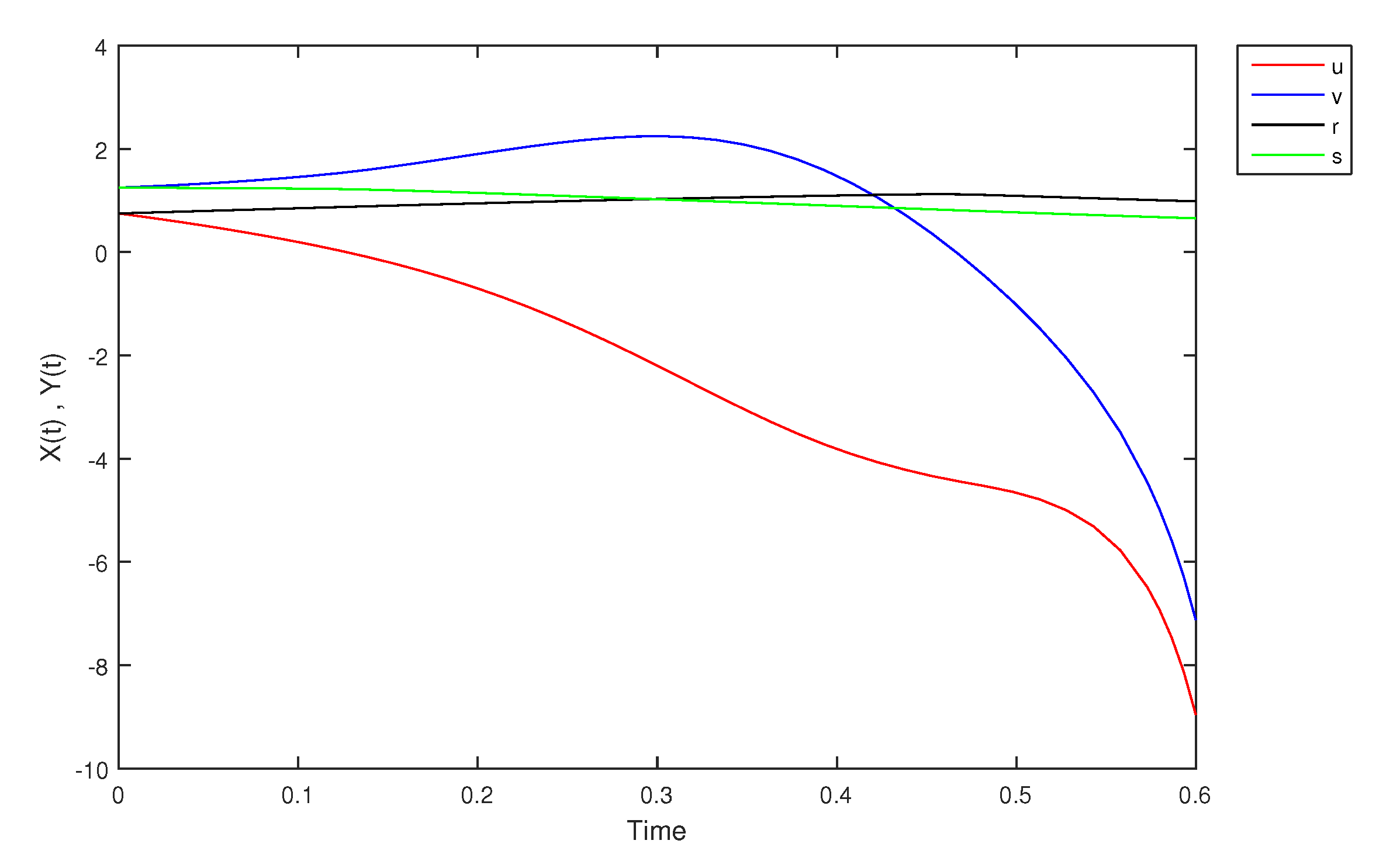
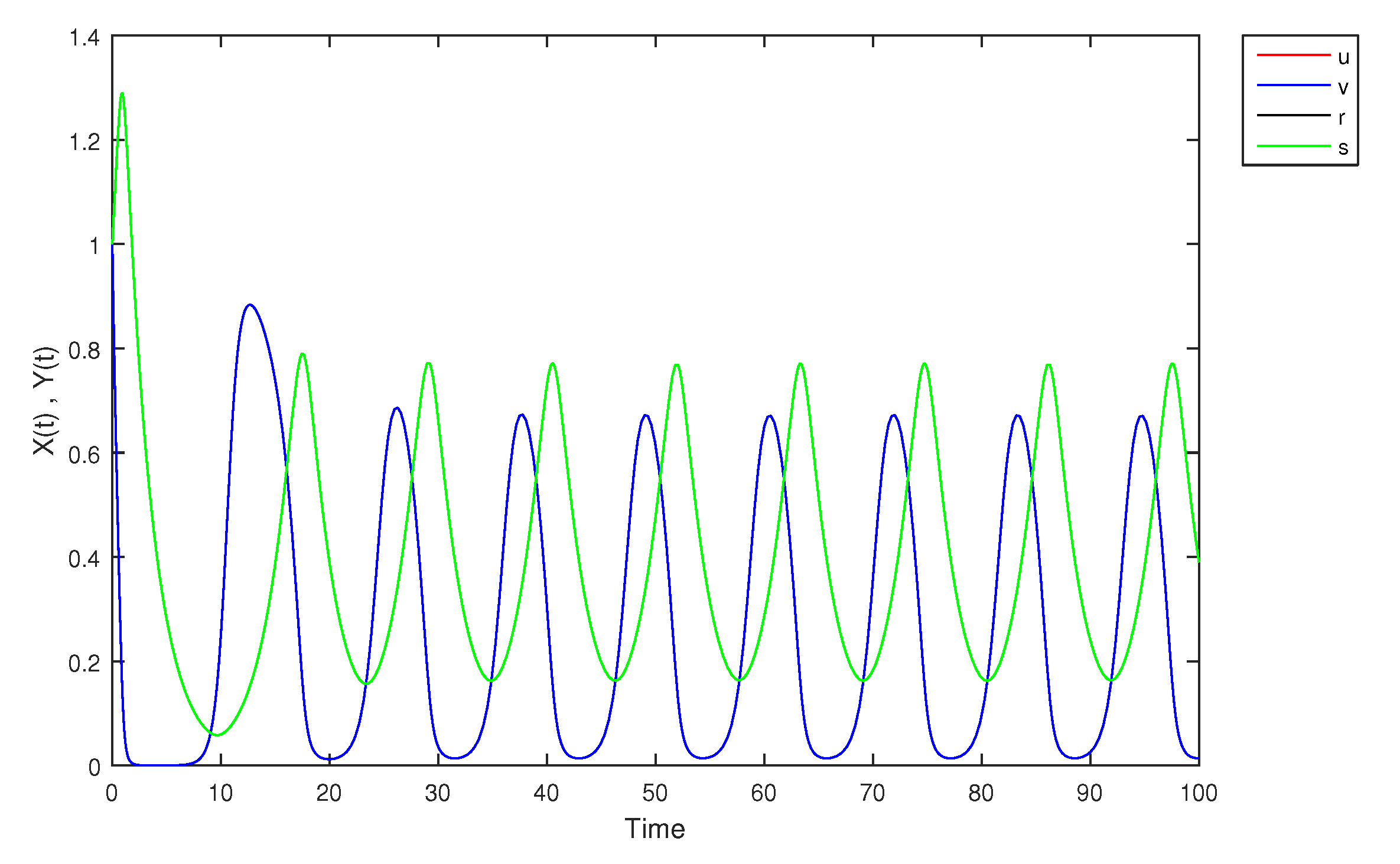
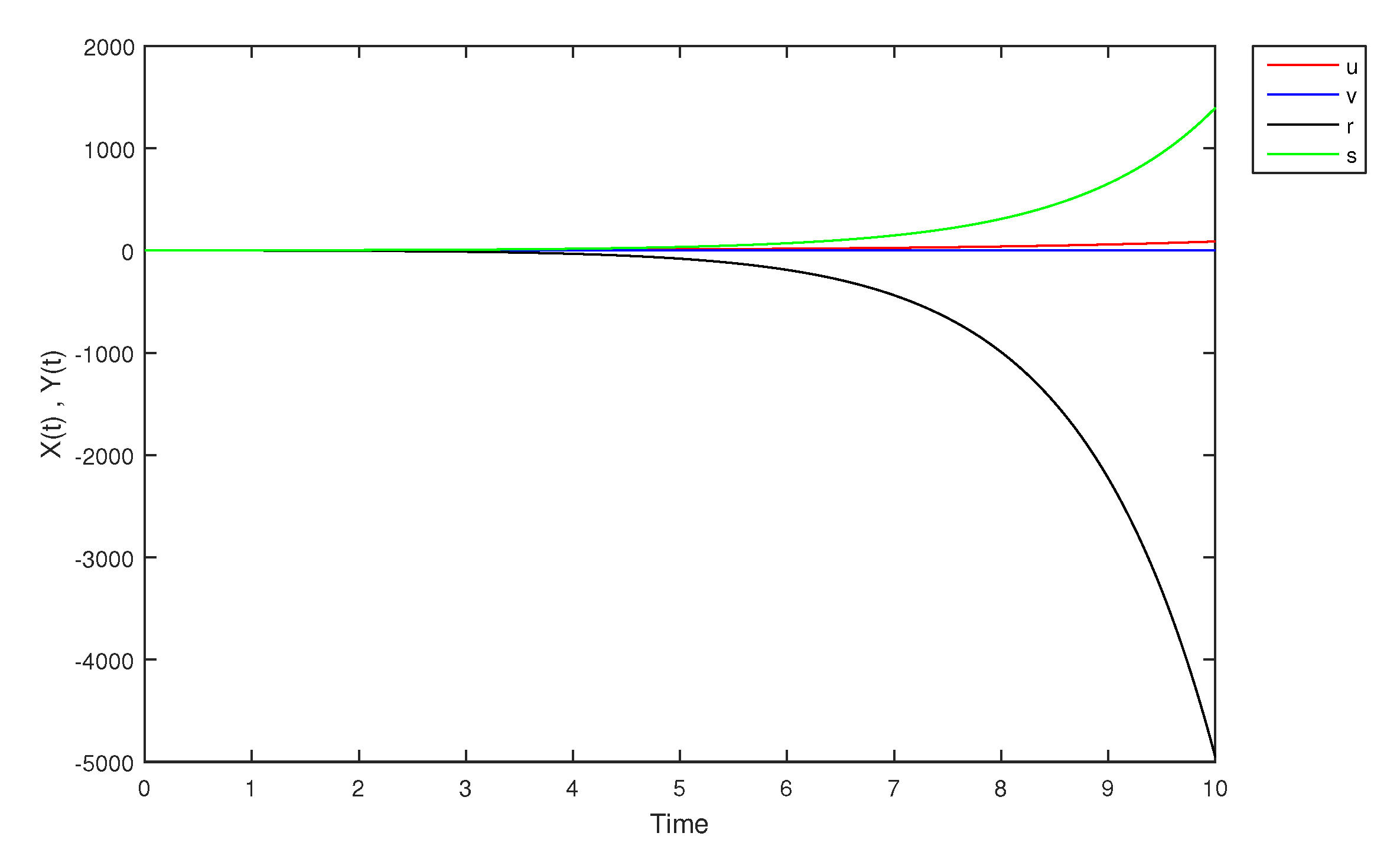
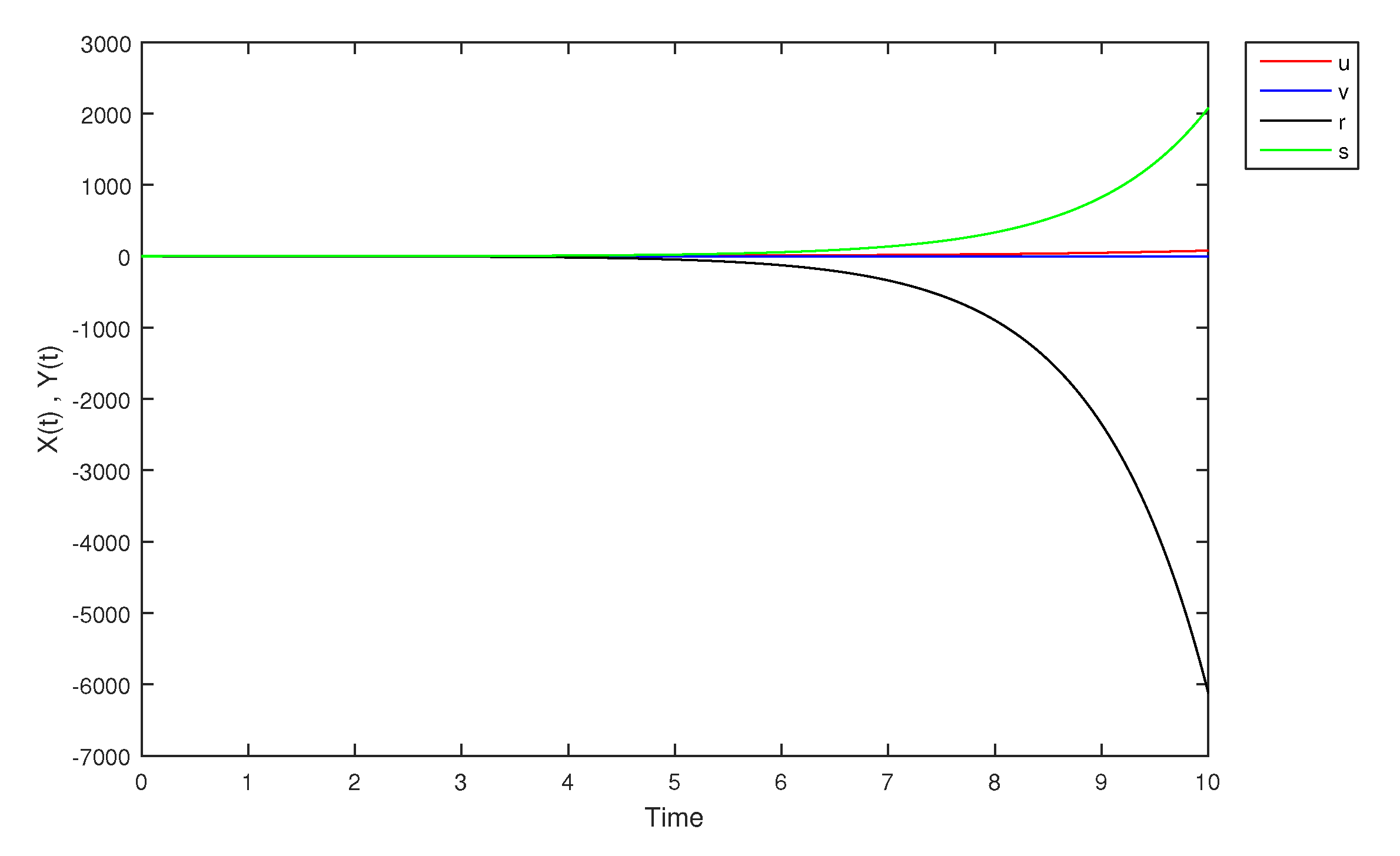
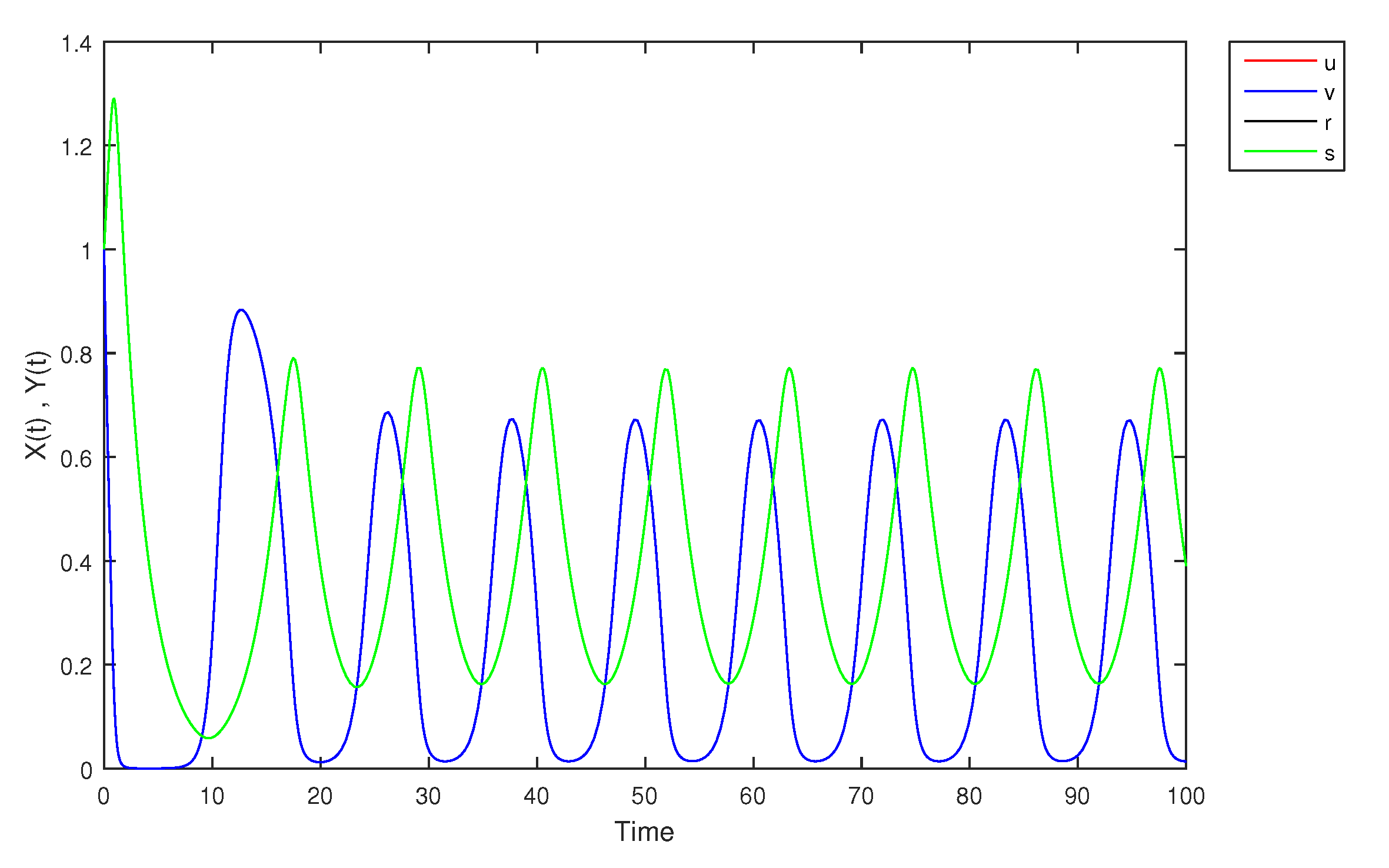
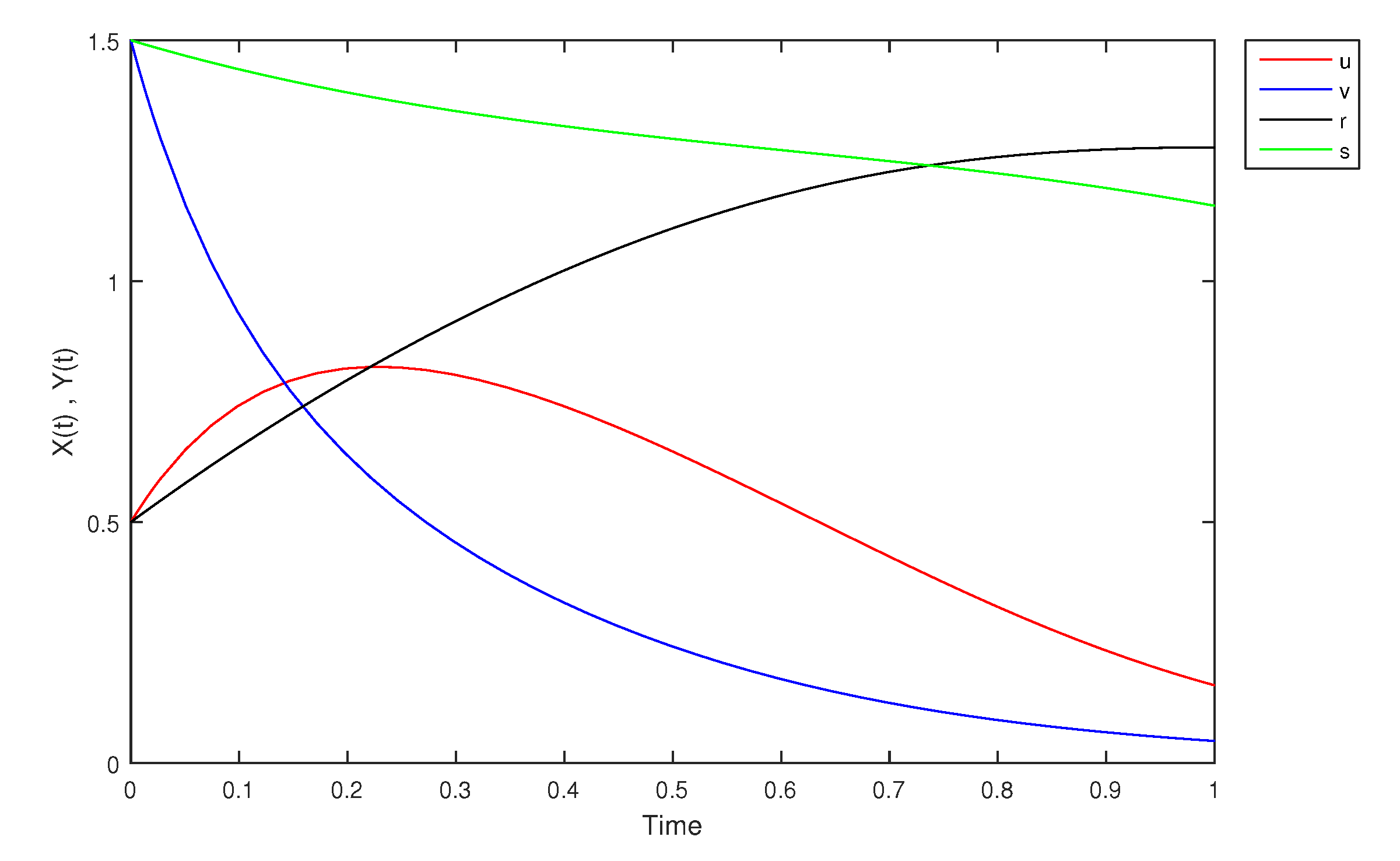
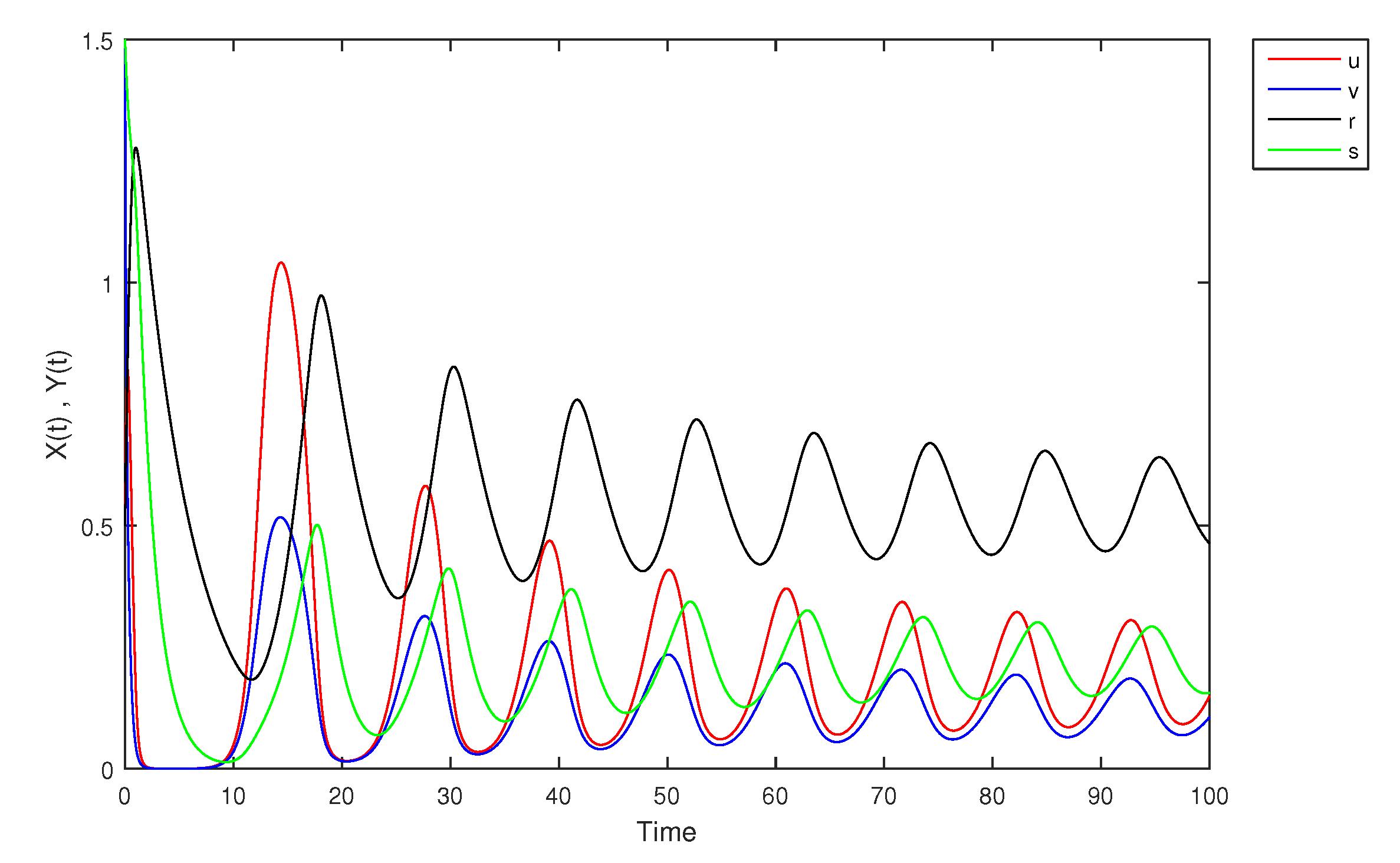
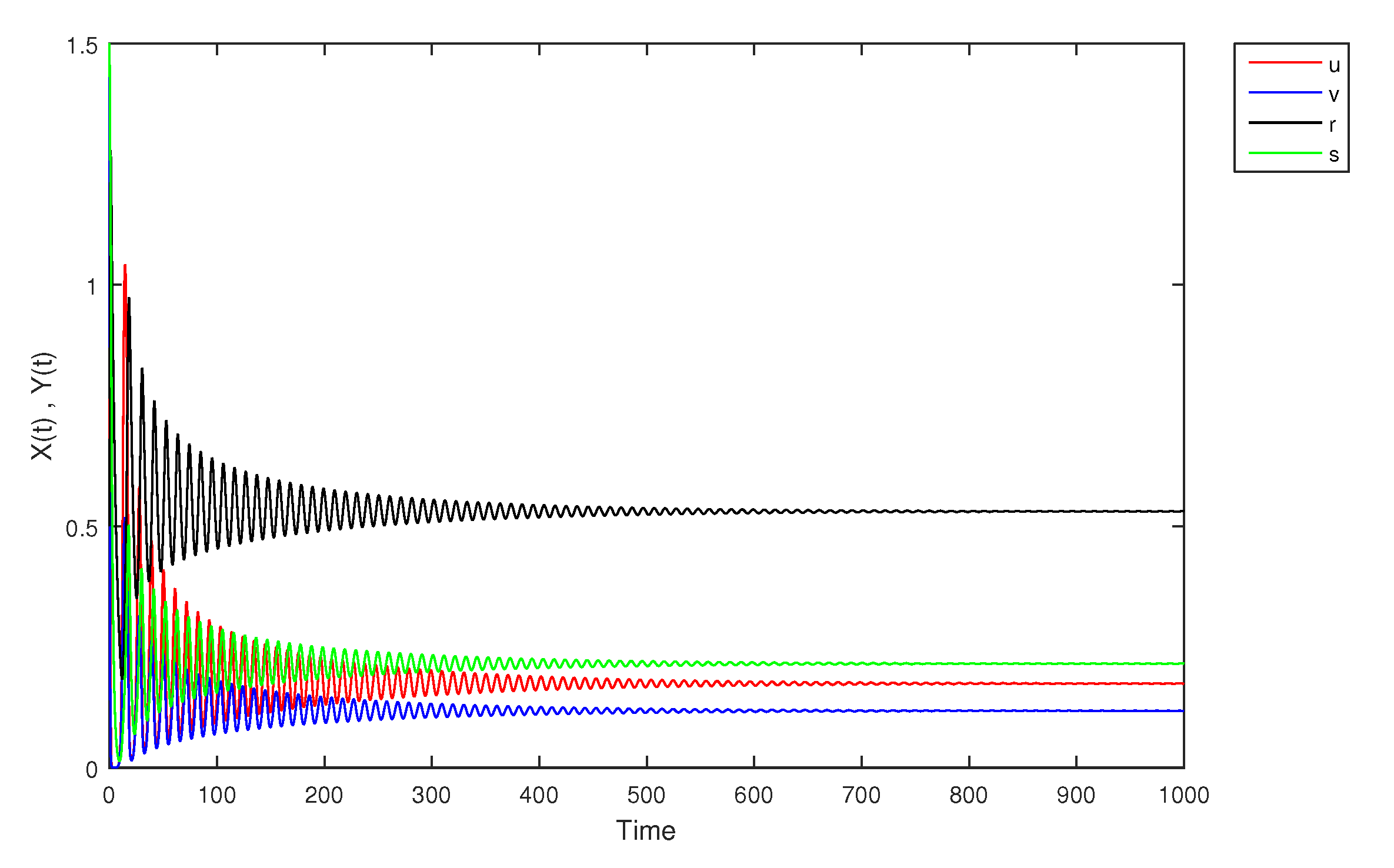
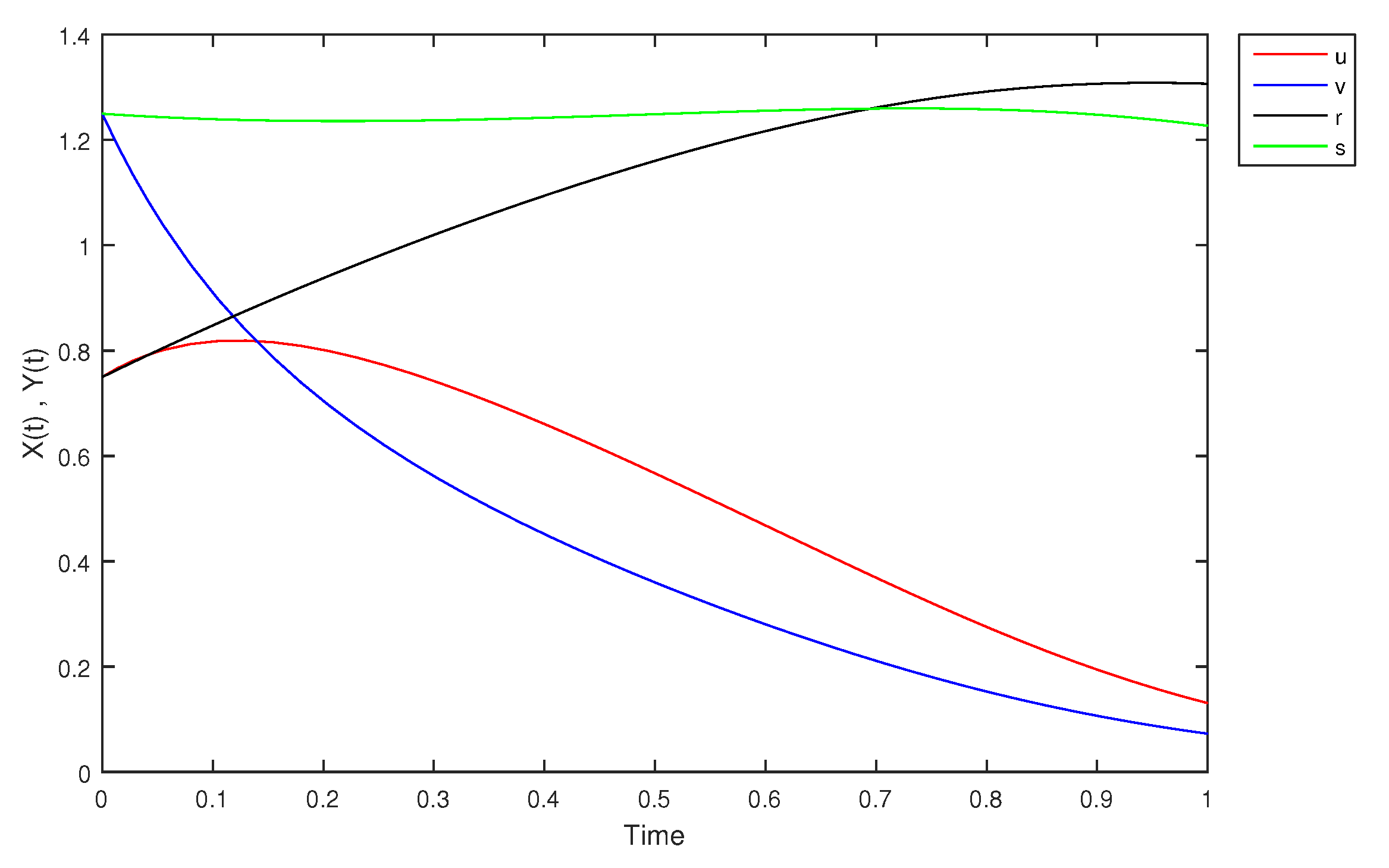
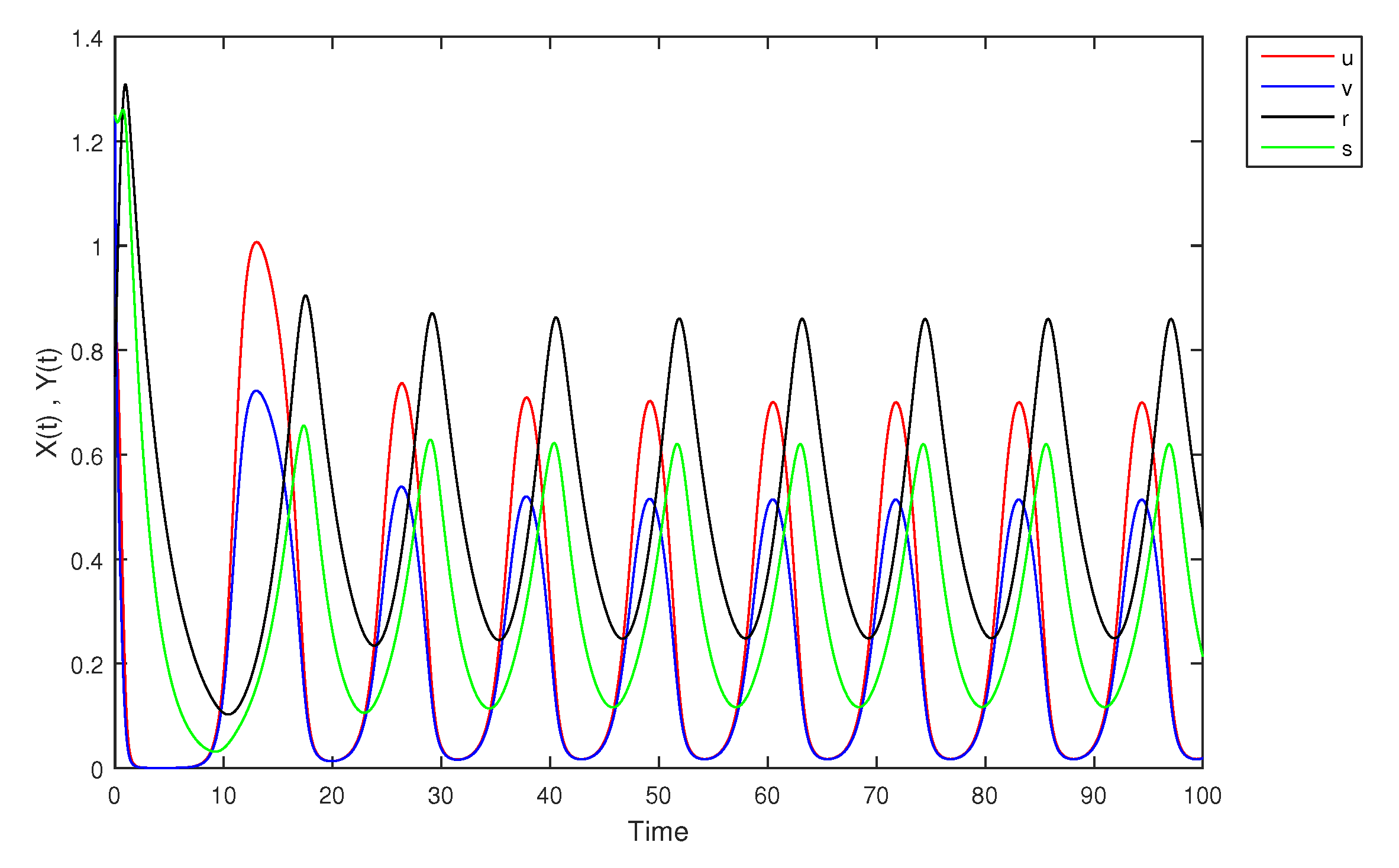
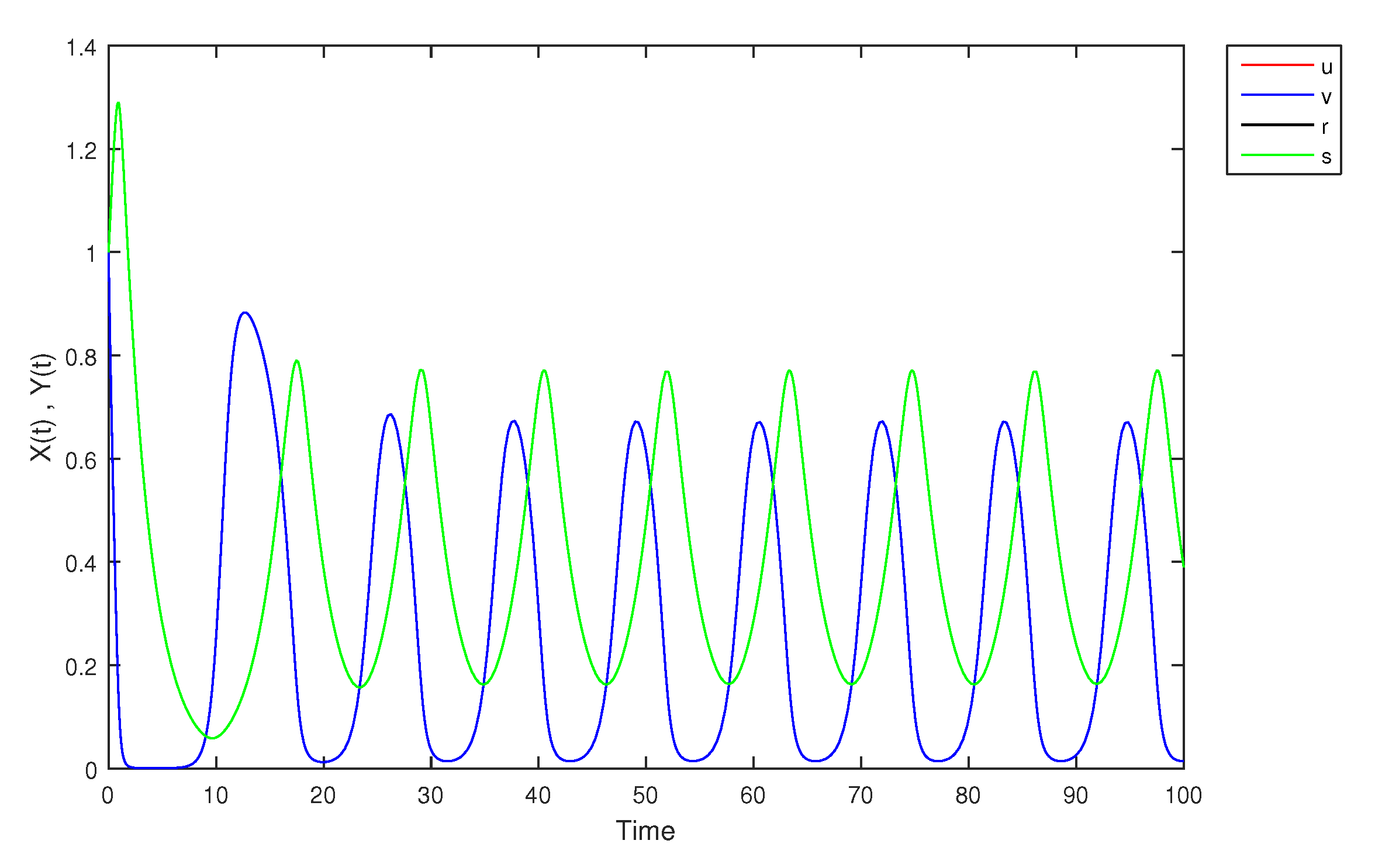
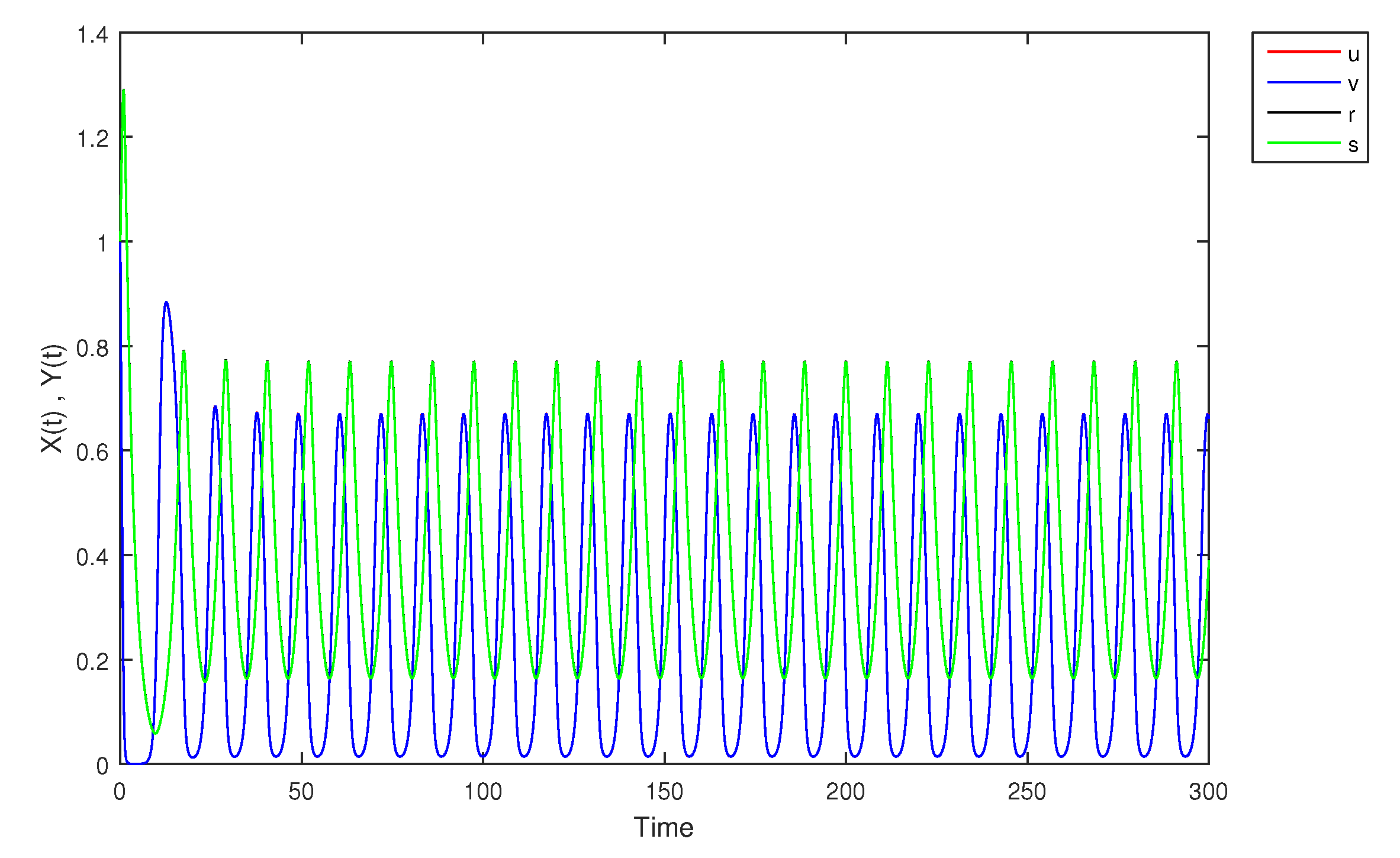
- If X and Y are (1)-differentiable, then we have the following model:The equilibrium points of (9) areAt , the solution is shown in Figure 17:At -level = 0.5, the solution is shown in Figure 18:At -level = 1, the solution is shown in Figure 19:
- (2)
- If X is (1)-differentiable and Y is (2)-differentiable, then we have the following model:At -level = 0, the solution is shown in Figure 20:At -level = 0.5, the solution is in Figure 21:At -level = 1, the solution is shown in Figure 22:
- (3)
- If X is (2)-differentiable and Y is (1)-differentiable, then we have the following model:At -level = 0, the solution is shown in Figure 23:At -level = 0.5, the solution is shown in Figure 24:At -level = 1, the solution is shown in Figure 25:
- (4)
- If X and Y are (2)-differentiable, then we have the following model:
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bede, B.; Gal, G.S. Generalizations of differentiability of fuzzy number valued functions with applications to fuzzy differential equations. Fuzzy Sets Syst. 2005, 151, 581–599. [Google Scholar] [CrossRef]
- Bede, B.; Stefanini, L. Solution of Fuzzy Differential Equations with Generalized Differentiability Using LU-Parametric Representation; Atlantis Press: Atlantis, France, 2011. [Google Scholar]
- Bede, B.; Stefanini, L. Generalized differentiability of fuzzy-valued function. Fuzzy Sets Syst. 2012, 230, 119–141. [Google Scholar] [CrossRef]
- Cano, Y.C.; Flores, H.R. On new solutions of fuzzy differential equations. Chaos Solitons Fractals 2008, 38, 112–119. [Google Scholar] [CrossRef]
- Gomes, L.T.; Barros, L.C. A note on the generalized difference and the generalized differentiability. Fuzzy Sets Syst. 2015, 280, 142–145. [Google Scholar] [CrossRef]
- Pirzada, U.M.; Vakaskar, D.C. Existence of Hukuhara differentiability of fuzzy-valued functions. J. Indian Math. 2017, 84, 239–254. [Google Scholar] [CrossRef]
- Stefanini, L. A generalization of Hukuhara difference for interval and fuzzy arithmetic. Fuzzy Sets Syst. 2008, 161, 1564–1584. [Google Scholar] [CrossRef]
- Bede, B.; Gal, S.G. Solutions of fuzzy differential equations based on generalized differentiability. Commun. Math. Anal. 2010, 9, 22–41. [Google Scholar]
- Ortega, N.R.; Sallum, P.C.; Massad, E. Fuzzy Dynamical Systems in Epidemic Modeling. Kybernetes 2000, 29, 201–218. [Google Scholar] [CrossRef]
- Ahmad, M.Z.; Baets, B. A Predator-Prey Model with Fuzzy Initial Populations. In Proceedings of the 13th IFSA World Congress and 6th EUSFLAT Conference, Lisbon, Portugal, 20–24 July 2009; pp. 1311–1314. [Google Scholar]
- Ahmad, M.Z.; Hasan, M.K. Modeling of Biological Populations Using Fuzzy Differential Equations. Intern. J. Mod. Physic Conf. Ser. 2012, 9, 354–363. [Google Scholar] [CrossRef]
- Ghanaie, Z.A.; Moghadam, M. Solving fuzzy differential equations by Runge-Kutta method. J. Math. Comput. Sci. 2011, 2, 295–306. [Google Scholar]
- Ma, M.; Friedman, M.; Kandel, A. Numerical solutions of fuzzy differential equations. Fuzzy Sets Syst. 1999, 105, 133–138. [Google Scholar] [CrossRef]
- Attili, B. The Shooting Method for Solving Second Order Fuzzy Two-Point Boundary Value Problems. Intern. J. Appl. Math. 2019, 32, 663–676. [Google Scholar] [CrossRef][Green Version]
- Attili, B. Initial Value Methods for the Numerical Simulation of Fuzzy Two-Point Boundary Value Problems using General Linear Method. Intern. J. Fuzzy Syst. Appl. 2021, 10, 94–126. [Google Scholar]
- Mallak, S.; Bedo, D.A. Fuzzy Comparison Method for Particular Fuzzy Numbers. J. Mahani Math. Res. Cent. 2013, 3, 1–14. [Google Scholar]
- Akin, O.; Oruc, O. A Prey Predator Model with Fuzzy Initial Values. Hacet. J. Math. Stat. 2012, 4, 387–395. [Google Scholar]
- Mizukoshi, M.T.; Barros, L.C.; Bassanezi, R.C. Stability of Fuzzy Dynamic Systems. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2009, 17, 69–83. [Google Scholar] [CrossRef]
- Peixoto, M.S.; Barros, L.C.; Bassanezi, R.C. Predator-Prey Fuzzy Model. Ecol. Model 2008, 214, 39–44. [Google Scholar] [CrossRef]
- Attili, B.; Mallak, S. Existence of Limit Cycles in A Predator-Prey System with a Functional Responce of the Form Arctan(ax). Commun. Math. Anal. 2006, 1, 27–33. [Google Scholar]
- Pereira, C.M.; Cecconello, M.S.; Bassanezi, R.C. Prey-Predator Model Under Fuzzy Uncertanties. In Fuzzy Information Processing. NAFIPS 2018. Communications in Computer and Information Science; Barreto, G., Coelho, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 831. [Google Scholar]
- Barzinji, K. Numerical Solution of Fuzzy Delay Predator-Prey System. Intern. J. Math. Anal. 2017, 11, 595–603. [Google Scholar] [CrossRef]
- Banerjee, M.; Mukherjee, N.; Volpert, V. Prey-Predator Model with a Nonlocal Bistable Dynamics of Prey. Mathematics 2018, 6, 41. [Google Scholar] [CrossRef]
- Pal, D.; Mahapatra, G.S.; Samanta, G.P. Stability and bionomic analysis of fuzzy prey–predator harvesting model in presence of toxicity: A dynamic approach. Bull. Math. Biol. 2016, 78, 1493–1519. [Google Scholar] [CrossRef] [PubMed]
- Yavuz, M.; Sene, N. Stability Analysis and Numerical Computation of the Fractional Predator–Prey Model with the Harvesting Rate. Fractal Fract. 2020, 4, 35. [Google Scholar] [CrossRef]
- Yu, X.; Yuan, S.; Zhang, T. About the optimal harvesting of a fuzzy predator–prey system: A bioeconomic model incorporating prey refuge and predator mutual interference. Nonlinear Dyn. 2018, 94, 2143–2160. [Google Scholar] [CrossRef]
- Pal, D.; Mahapatra, G.S.; Mahato, S.K.; Samanta, G.P. A Mathematical Model of A Prey-Predator Type Fishery in the Presence of Toxicity With Fuzzy Optimal Harvisting. J. Appl. Math. Inform. 2020, 38, 13–36. [Google Scholar] [CrossRef]
- Thota, S. A Mathematical Study on a Diseased Prey-Predator Model with Predator Harvesting. Asian J. Fuzzy Appl. Math. 2020, 8, 16–21. [Google Scholar] [CrossRef]
- Zimmerman, H.J. Fuzzy Set Theory and Its Applications, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Mallak, S.; Bedo, D. Particular Fuzzy Numbers and a Fuzzy Comparison Method between Them. Intern. J. Fuzzy Math. Syst. 2013, 2, 113–123. [Google Scholar]
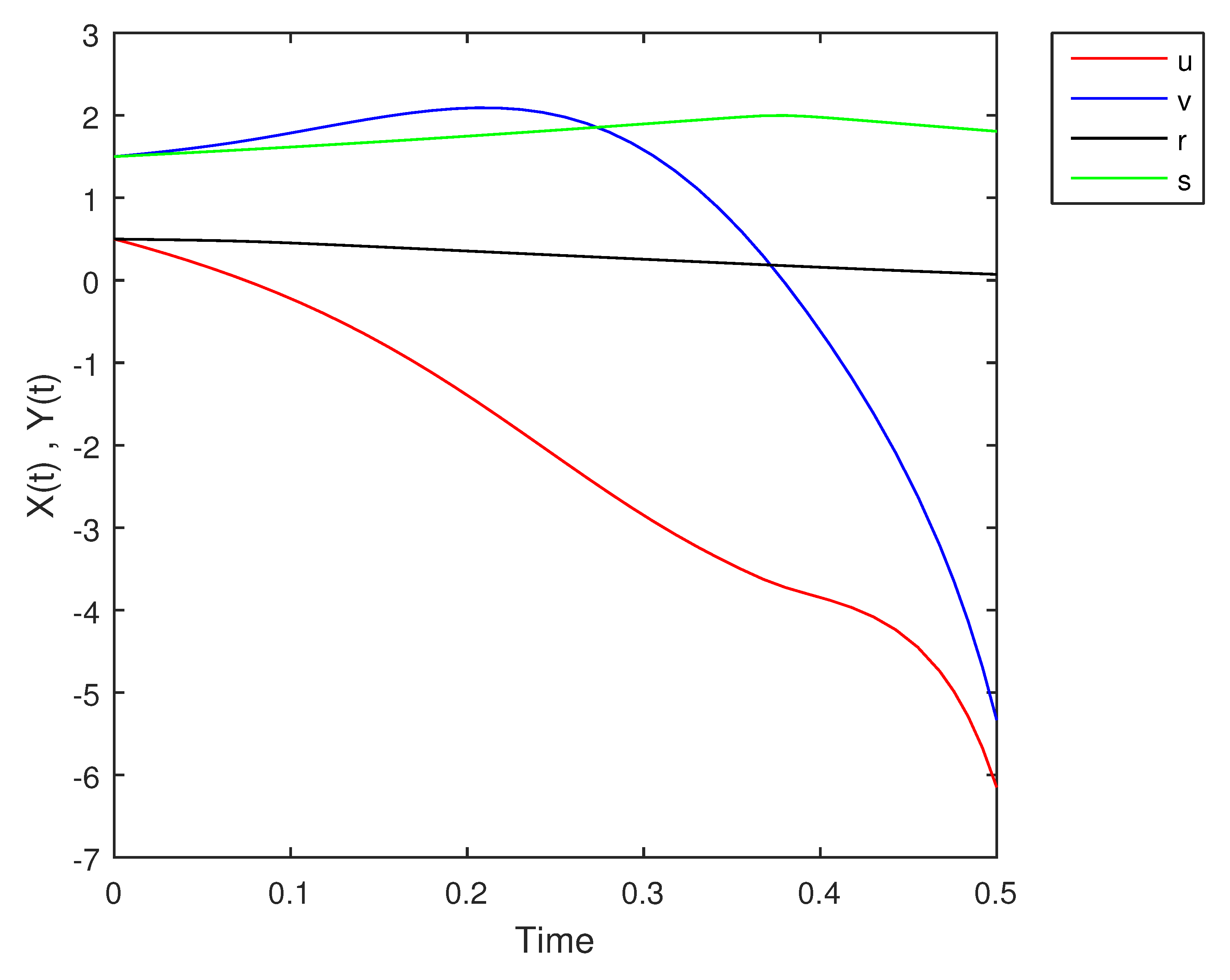

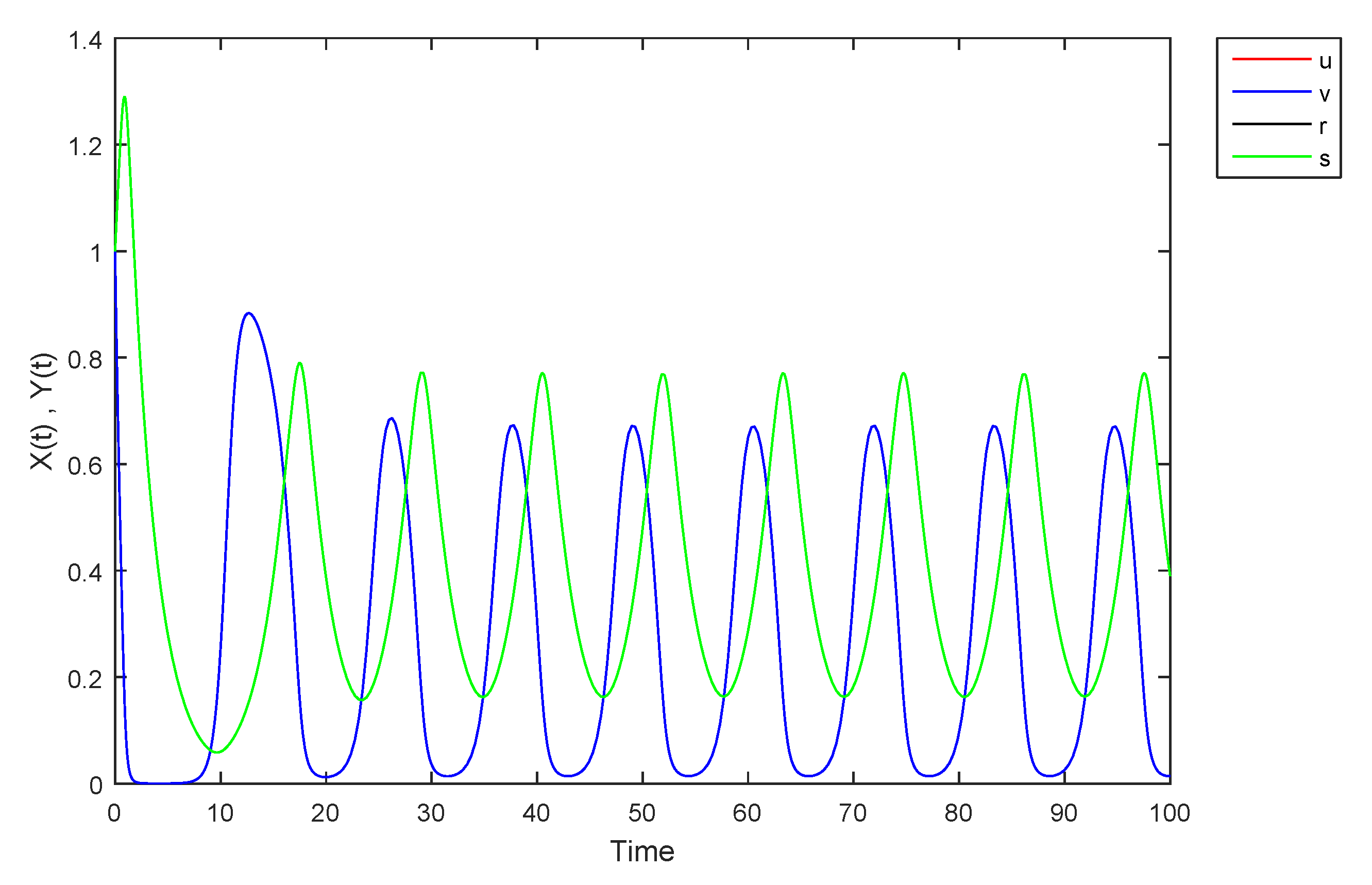

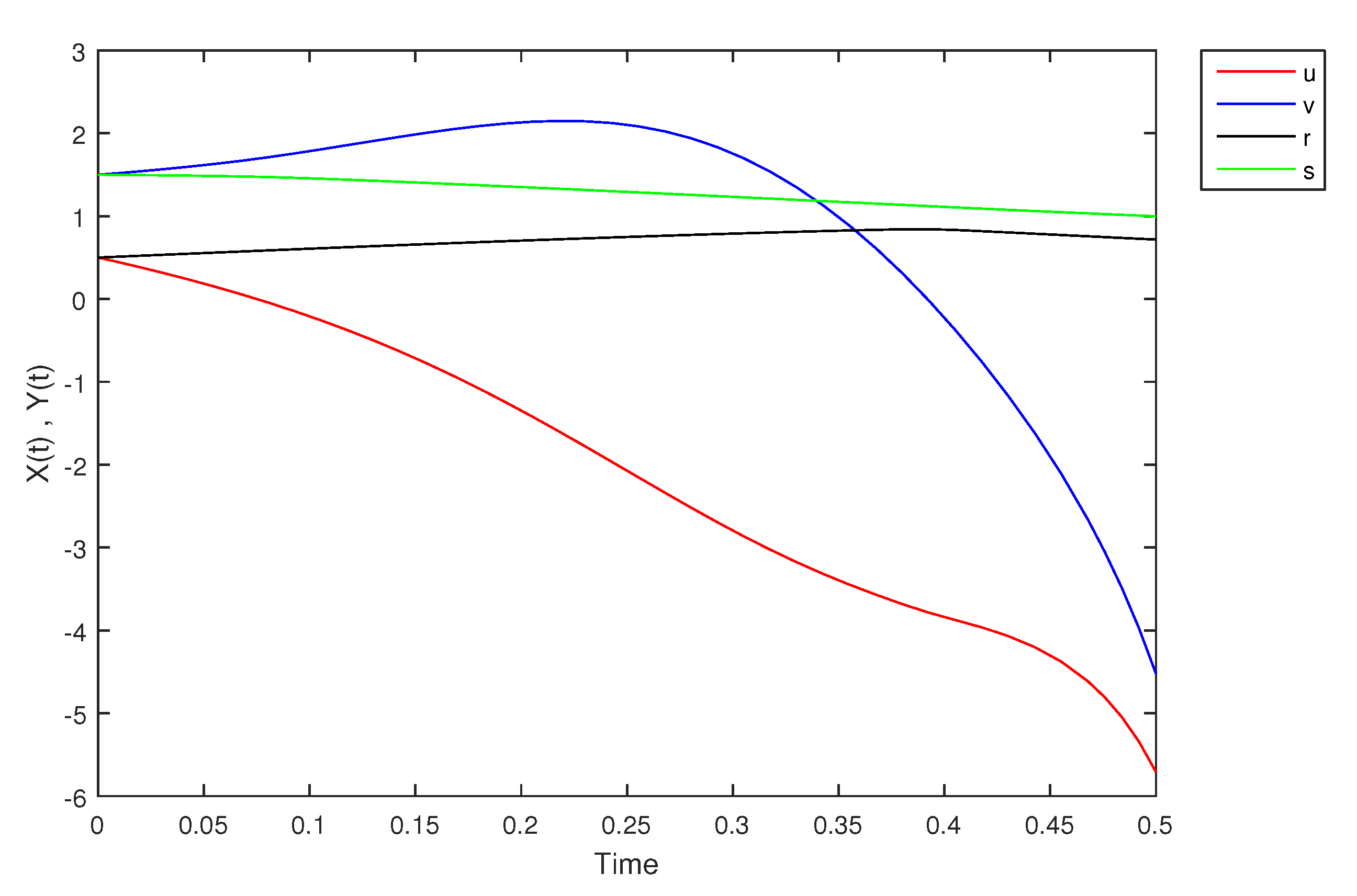
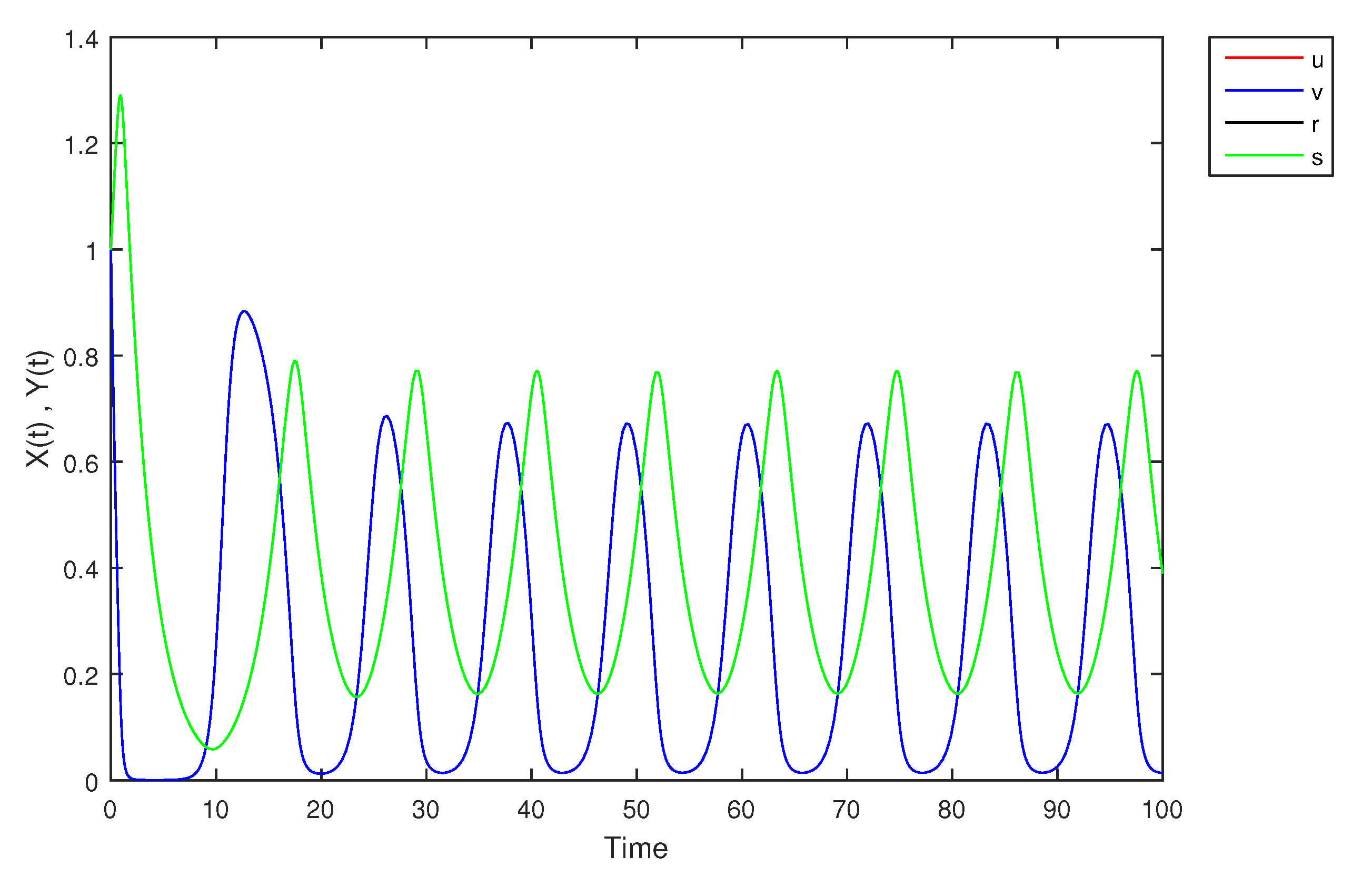
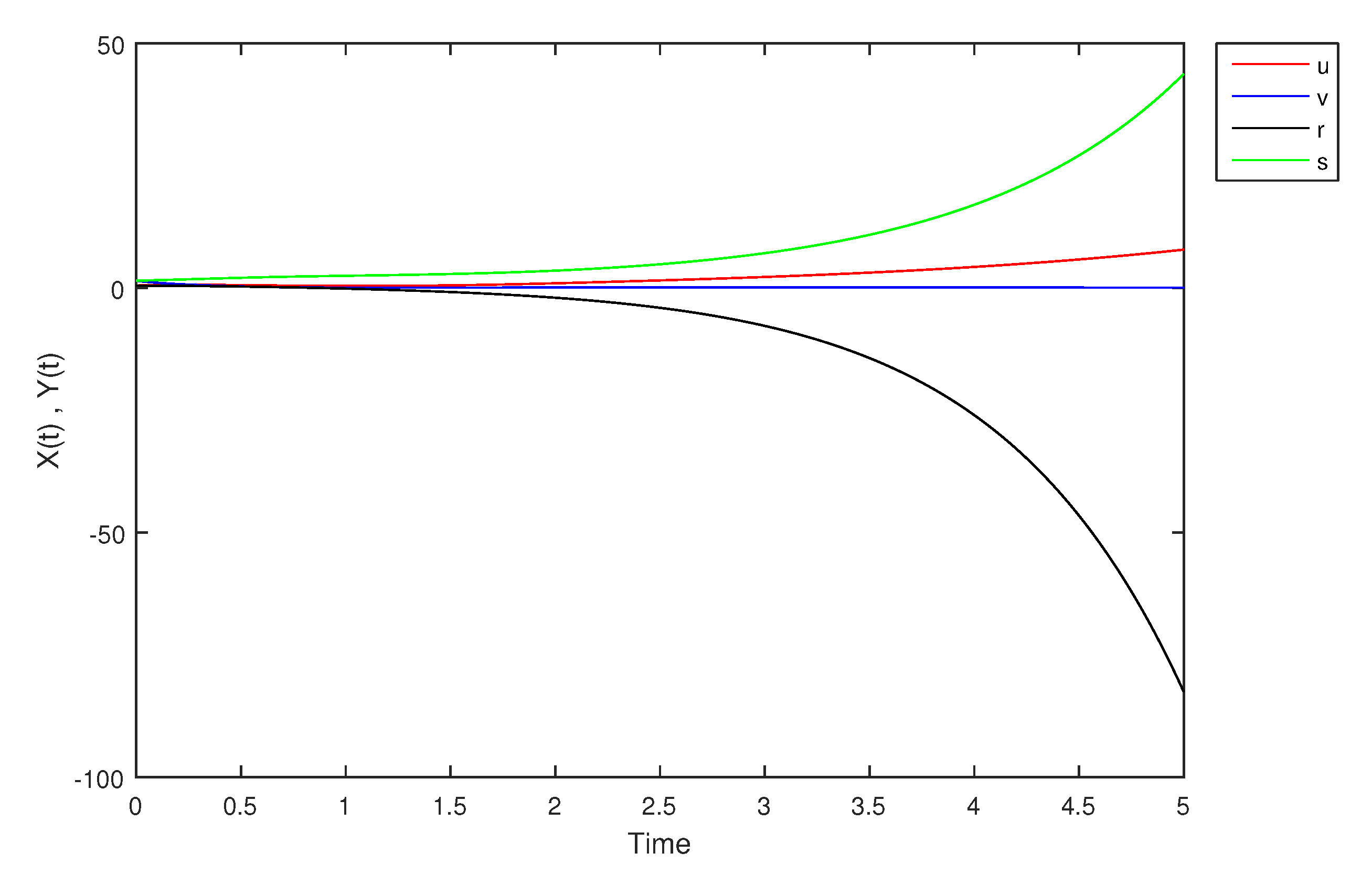
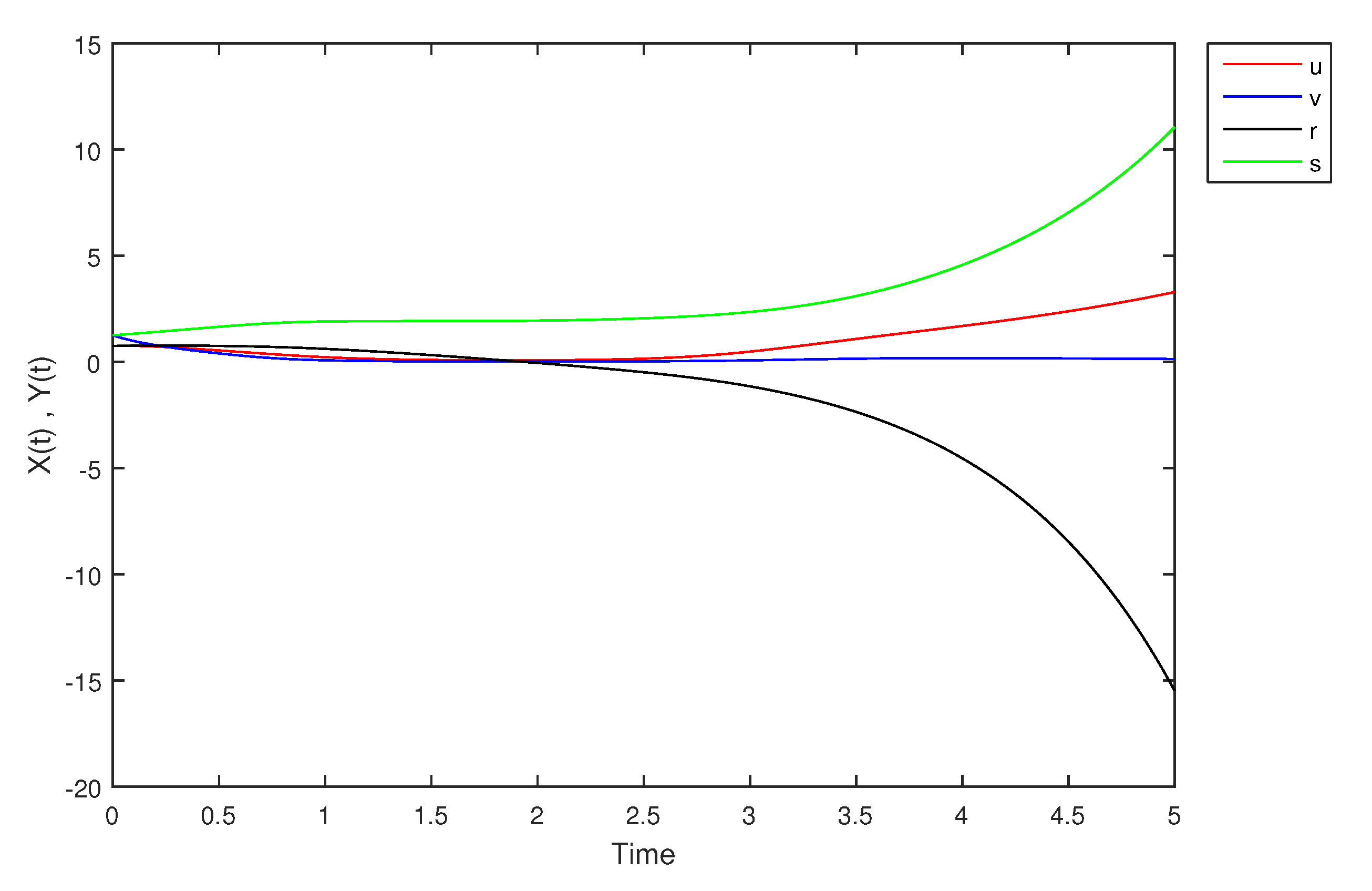
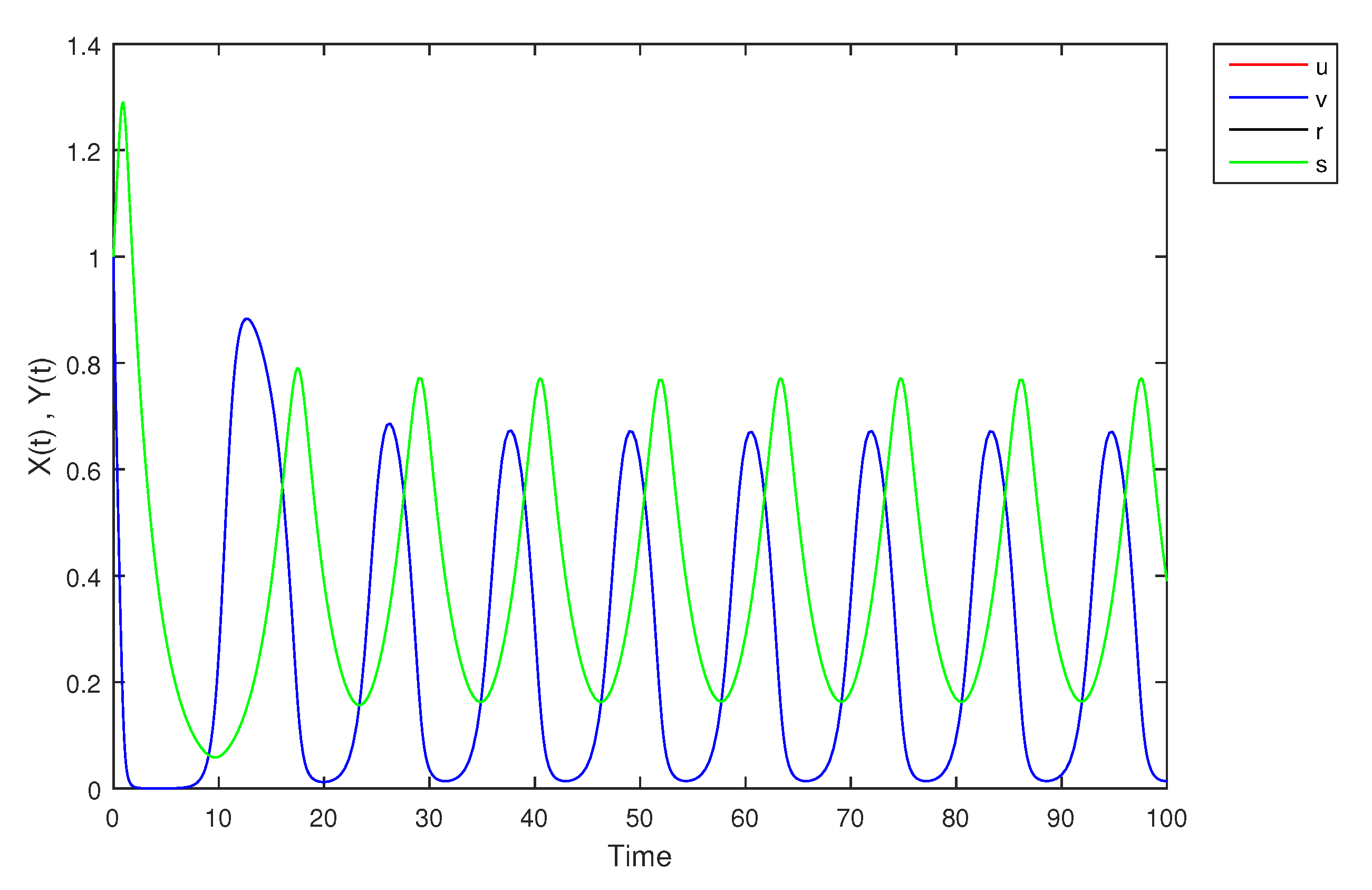
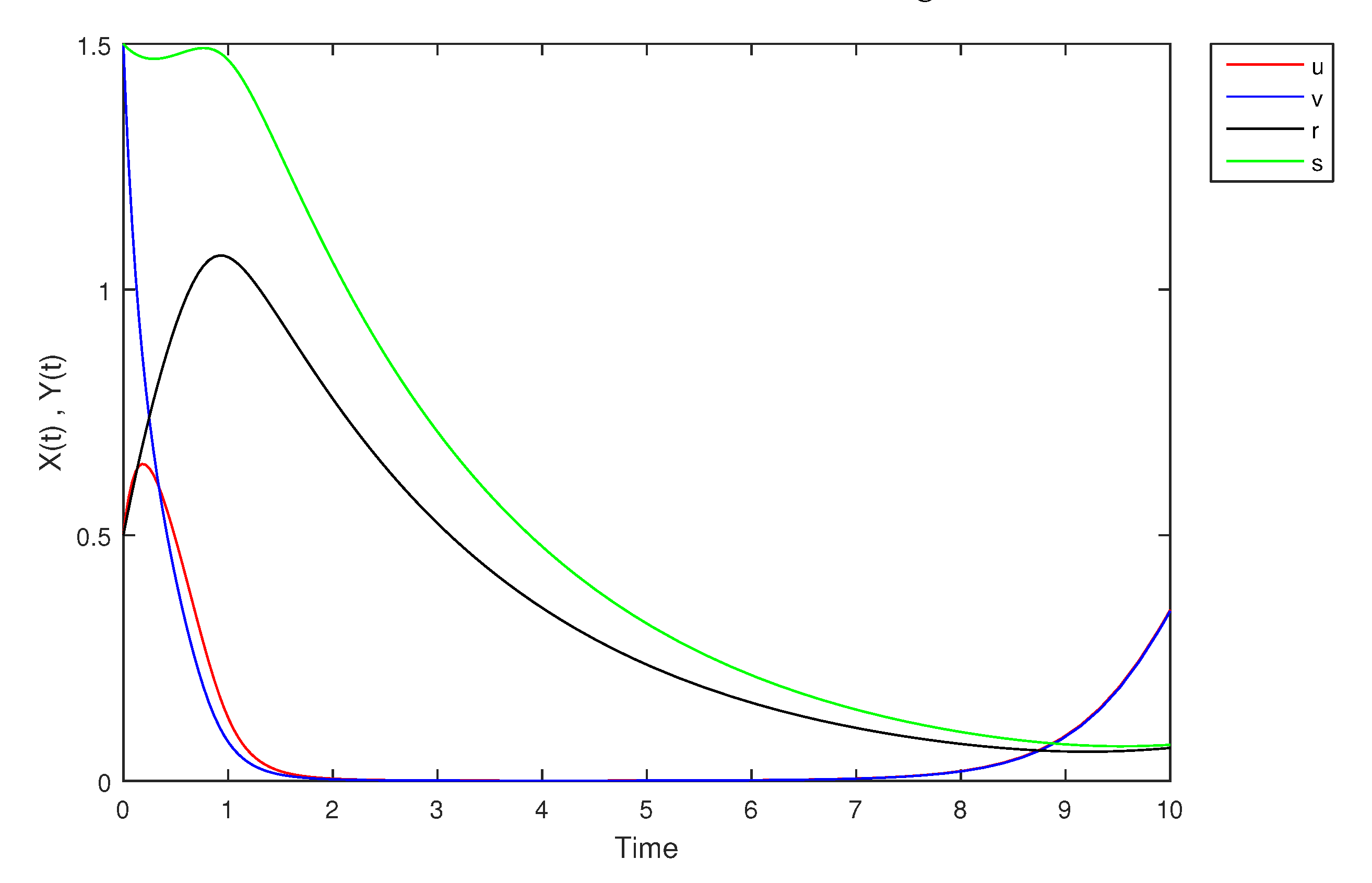


| Time | ||||
|---|---|---|---|---|
| 0.00 | 0.5000 | 1.5000 | 0.5000 | 1.5000 |
| 0.05 | 0.1826 | 1.6173 | 0.4846 | 1.5563 |
| 0.10 | −0.2220 | 1.7863 | 0.4525 | 1.6160 |
| 0.15 | −0.7446 | 1.9743 | 0.4049 | 1.6798 |
| 0.20 | −1.3939 | 2.0889 | 0.3550 | 1.7480 |
| 0.25 | −2.1298 | 2.0063 | 0.3049 | 1.8203 |
| 0.30 | −2.8510 | 1.5822 | 0.2552 | 1.8961 |
| 0.35 | −3.4498 | 0.7150 | 0.2061 | 1.9726 |
| 0.40 | −3.8465 | −0.6121 | 0.1580 | 1.9774 |
| 0.45 | −4.3524 | −2.3905 | 0.1131 | 1.8927 |
| 0.50 | −6.1491 | −5.3338 | 0.0719 | 1.8069 |
| Time | ||||
|---|---|---|---|---|
| 0.00 | 0.7500 | 1.2500 | 0.7500 | 1.2500 |
| 0.05 | 0.5664 | 1.2846 | 0.7534 | 1.2888 |
| 0.10 | 0.3465 | 1.3510 | 0.7533 | 1.3295 |
| 0.15 | 0.0756 | 1.4562 | 0.7440 | 1.3724 |
| 0.20 | −0.2693 | 1.6206 | 0.7084 | 1.4181 |
| 0.25 | −0.7169 | 1.8064 | 0.6560 | 1.4674 |
| 0.30 | −1.2786 | 1.9369 | 0.6004 | 1.5205 |
| 0.35 | −1.9297 | 1.9132 | 0.5446 | 1.5772 |
| 0.40 | −2.5952 | 1.6137 | 0.4895 | 1.6372 |
| 0.45 | −3.1783 | 0.9376 | 0.4353 | 1.6989 |
| 0.50 | −3.6292 | −0.1595 | 0.3822 | 1.7393 |
| 0.55 | −3.9949 | −1.6588 | 0.3319 | 1.6669 |
| 0.60 | −5.0673 | −3.8682 | 0.2852 | 1.5879 |
| Time | ||||
|---|---|---|---|---|
| 0.0 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 5.0 | 0.0004 | 0.0004 | 0.2800 | 0.2800 |
| 10.0 | 0.2536 | 0.2536 | 0.0598 | 0.0598 |
| 15.0 | 0.7375 | 0.7375 | 0.3892 | 0.3892 |
| 20.0 | 0.0123 | 0.0123 | 0.3867 | 0.3867 |
| 25.0 | 0.5572 | 0.5572 | 0.2186 | 0.2186 |
| 30.0 | 0.0359 | 0.0359 | 0.6595 | 0.6595 |
| 35.0 | 0.1821 | 0.1821 | 0.1628 | 0.1628 |
| 40.0 | 0.3046 | 0.3046 | 0.7312 | 0.7312 |
| 45.0 | 0.0441 | 0.0441 | 0.1979 | 0.1979 |
| 50.0 | 0.6131 | 0.6131 | 0.4784 | 0.4784 |
| 55.0 | 0.0163 | 0.0163 | 0.3125 | 0.3125 |
| 60.0 | 0.6503 | 0.6503 | 0.2871 | 0.2871 |
| 65.0 | 0.0173 | 0.0173 | 0.5135 | 0.5135 |
| 70.0 | 0.3583 | 0.3583 | 0.1827 | 0.1827 |
| 75.0 | 0.1017 | 0.1017 | 0.7595 | 0.7595 |
| 80.0 | 0.0953 | 0.0953 | 0.1683 | 0.1683 |
| 85.0 | 0.4766 | 0.4766 | 0.6195 | 0.6195 |
| 90.0 | 0.0258 | 0.0258 | 0.2402 | 0.2402 |
| 95.0 | 0.6657 | 0.6657 | 0.3817 | 0.3817 |
| 100.0 | 0.0140 | 0.0140 | 0.3900 | 0.3900 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallak, S.; Farekh, D.; Attili, B. Numerical Investigation of Fuzzy Predator-Prey Model with a Functional Response of the Form Arctan(ax). Mathematics 2021, 9, 1919. https://doi.org/10.3390/math9161919
Mallak S, Farekh D, Attili B. Numerical Investigation of Fuzzy Predator-Prey Model with a Functional Response of the Form Arctan(ax). Mathematics. 2021; 9(16):1919. https://doi.org/10.3390/math9161919
Chicago/Turabian StyleMallak, Saed, Doa’a Farekh, and Basem Attili. 2021. "Numerical Investigation of Fuzzy Predator-Prey Model with a Functional Response of the Form Arctan(ax)" Mathematics 9, no. 16: 1919. https://doi.org/10.3390/math9161919
APA StyleMallak, S., Farekh, D., & Attili, B. (2021). Numerical Investigation of Fuzzy Predator-Prey Model with a Functional Response of the Form Arctan(ax). Mathematics, 9(16), 1919. https://doi.org/10.3390/math9161919






