Electromagnetic Devices with Moving Parts—Simulation with FEM/BEM Coupling
Abstract
:1. Introduction
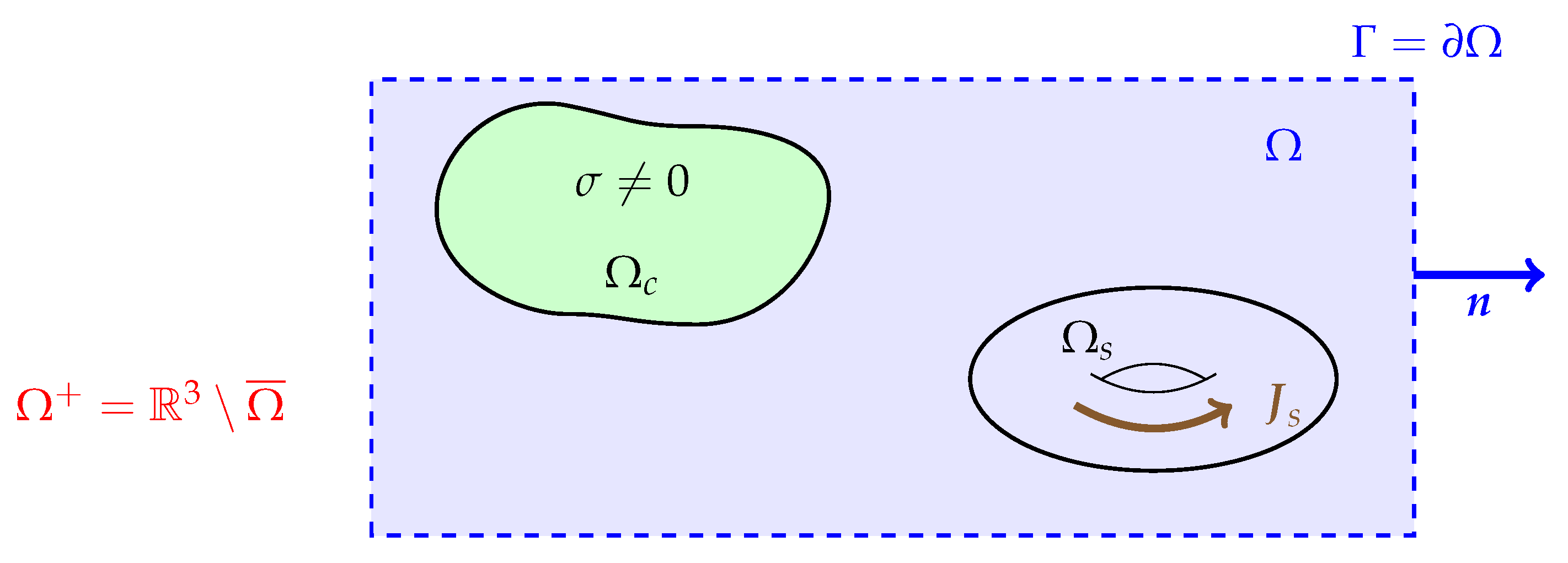
2. Continuous Formulation
2.1. Eddy-Current Model
2.2. Weak Form
- 1.
- Perfect electric conductor (PEC) boundary conditions imply (and therefore ). In this case, one usually makes use of the function space , that is the subspace of (12) with vanishing on the boundary. Application of the weighted-residual method in this subspace does not yield any boundary term.
- 2.
- Perfect magnetic conductor (PMC) boundary conditions state , which means that the boundary term can be dropped from Equation (19).
- 3.
- Dirichlet-to-Neumann maps allow for a (global) functional relation between and . In this case, the boundary term is either approximated by absorbing or asymptotic boundary conditions or represented accurately by means of boundary integral equations as in the following. For an overview of these techniques, see [9].
2.3. Boundary Integral Equations
3. Discretisation
3.1. Cohomologies
3.2. Spatial Discretisation
3.3. Time Integration
3.4. Newton Method
4. Solution of Linear System of Equations
- The matrix , that is, the linearisation of at , has a large kernel due to the fact that . In case there are non-conducting regions, or in other words , this deficiency carries over to the entire top-left block of the system matrix. In case of a direct solver, one would need to classify the degrees of freedom on the finite element mesh and eliminate the redundant ones, see [13]. For iterative solvers, on the other hand, careful preconditioning is needed as discussed below.
- The matrices , , and are fully populated. This implies a quadratic complexity for storage and cost of matrix-vector products. Since a direct solution is complicated from the onset—see the previous point—it can be ruled out completely when considering its cubic complexity due to the boundary element matrices. In case of an iterative solution, only the actions of these matrices on a given vector need to be calculated.
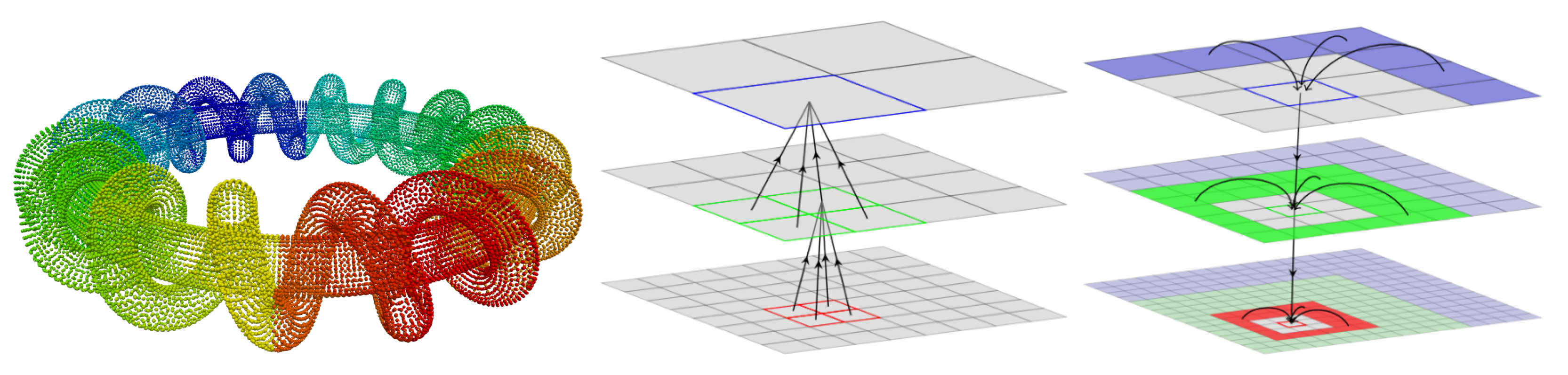
4.1. Fast Multipole Method
4.2. Preconditioning
5. Force Computation
6. Results
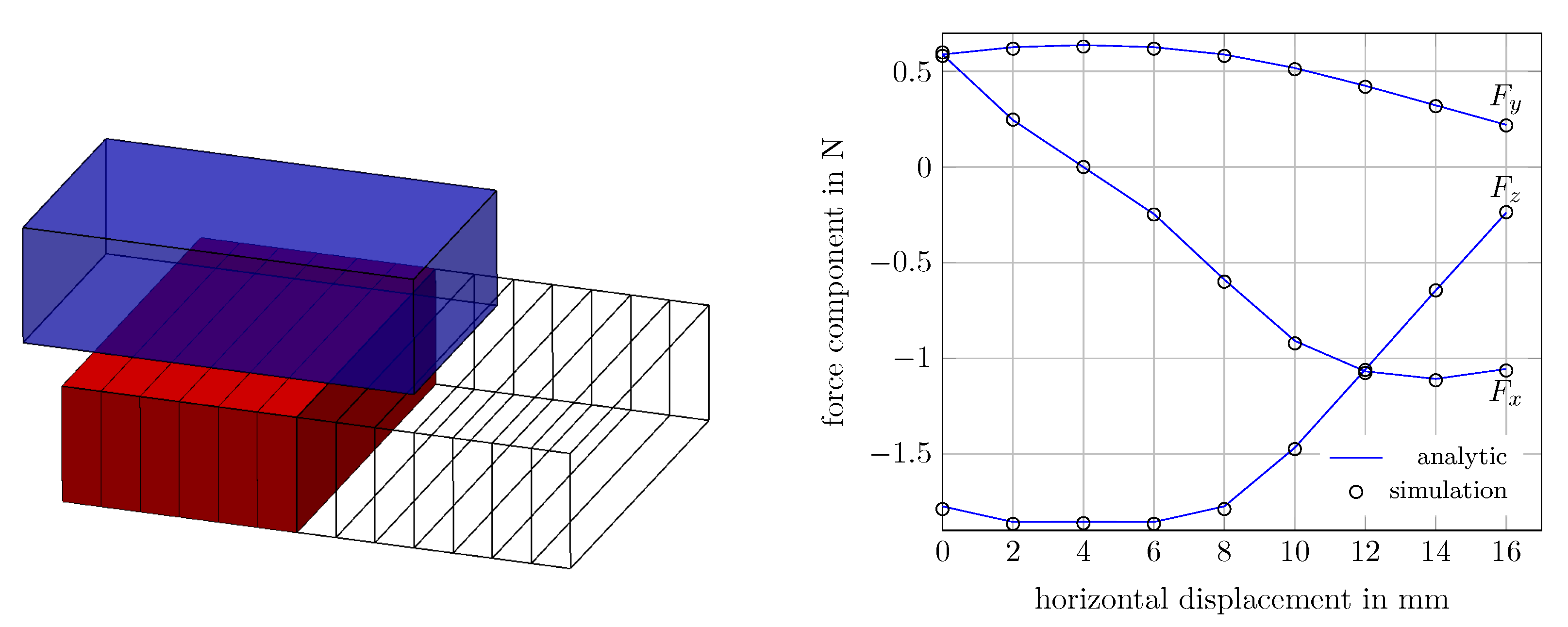
6.1. Force between Permanent Magnets
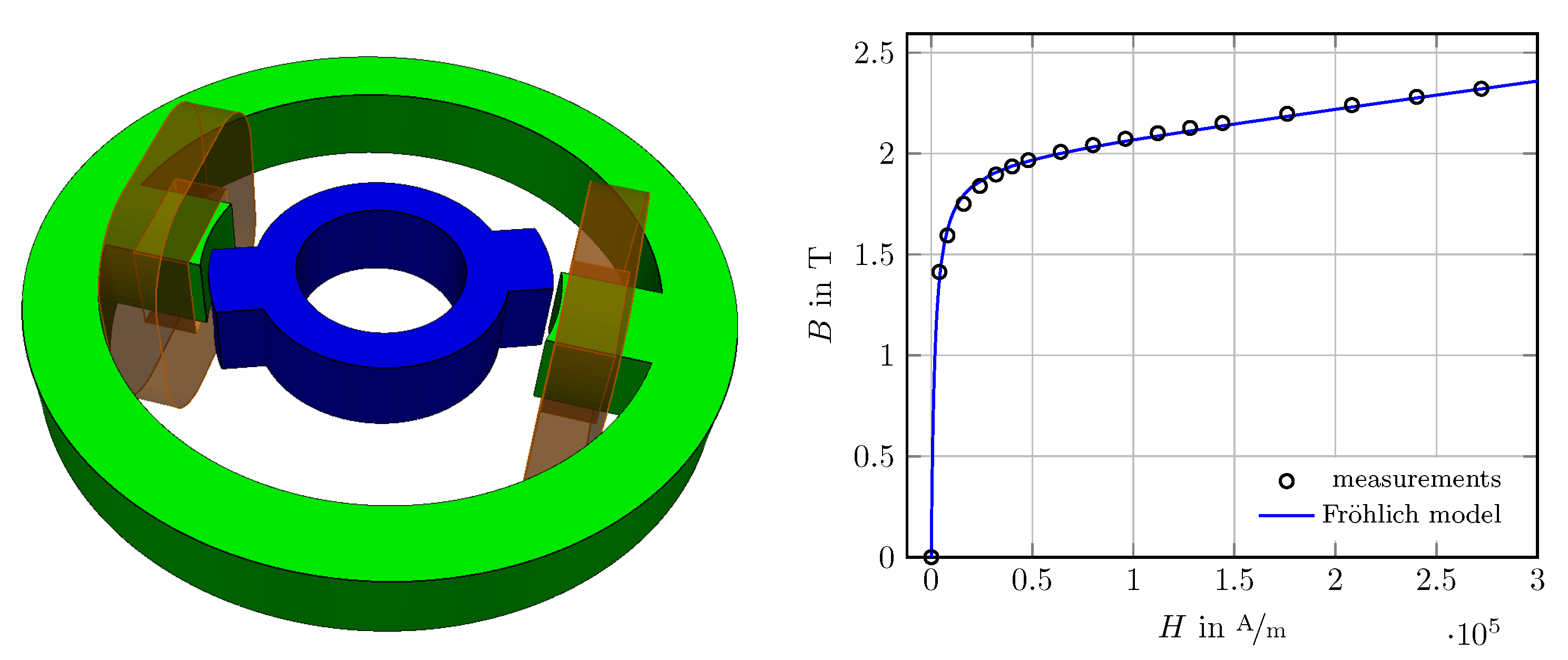
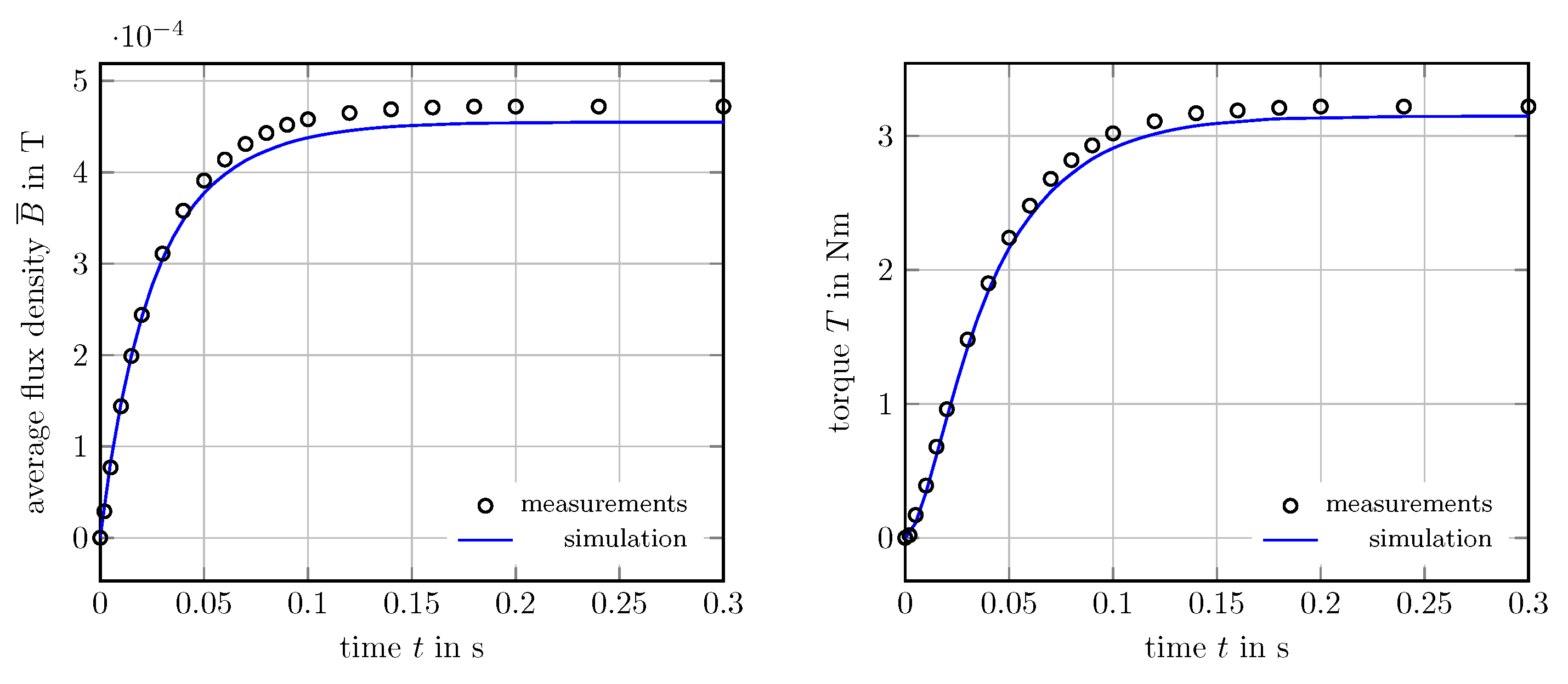
6.2. TEAM 24
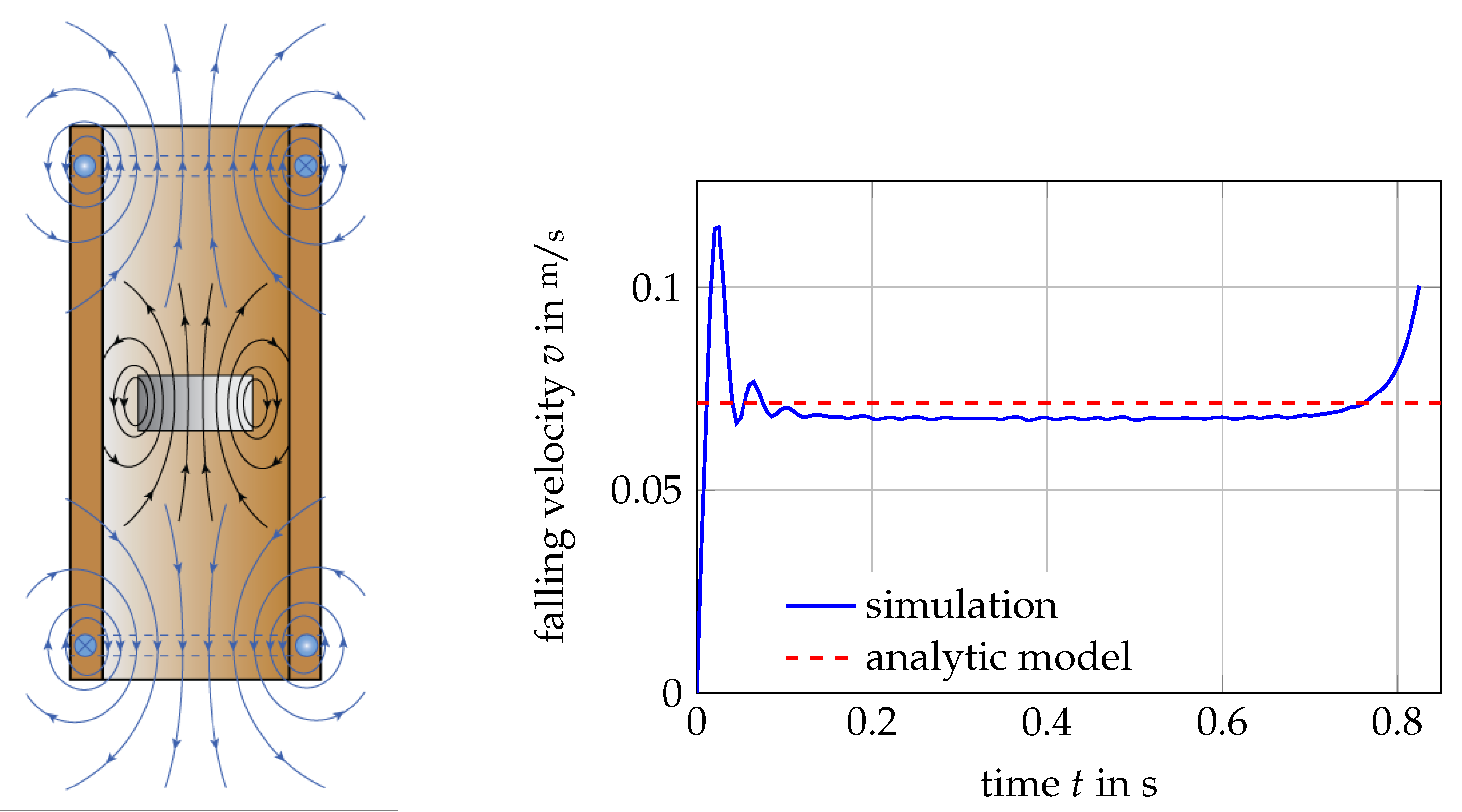
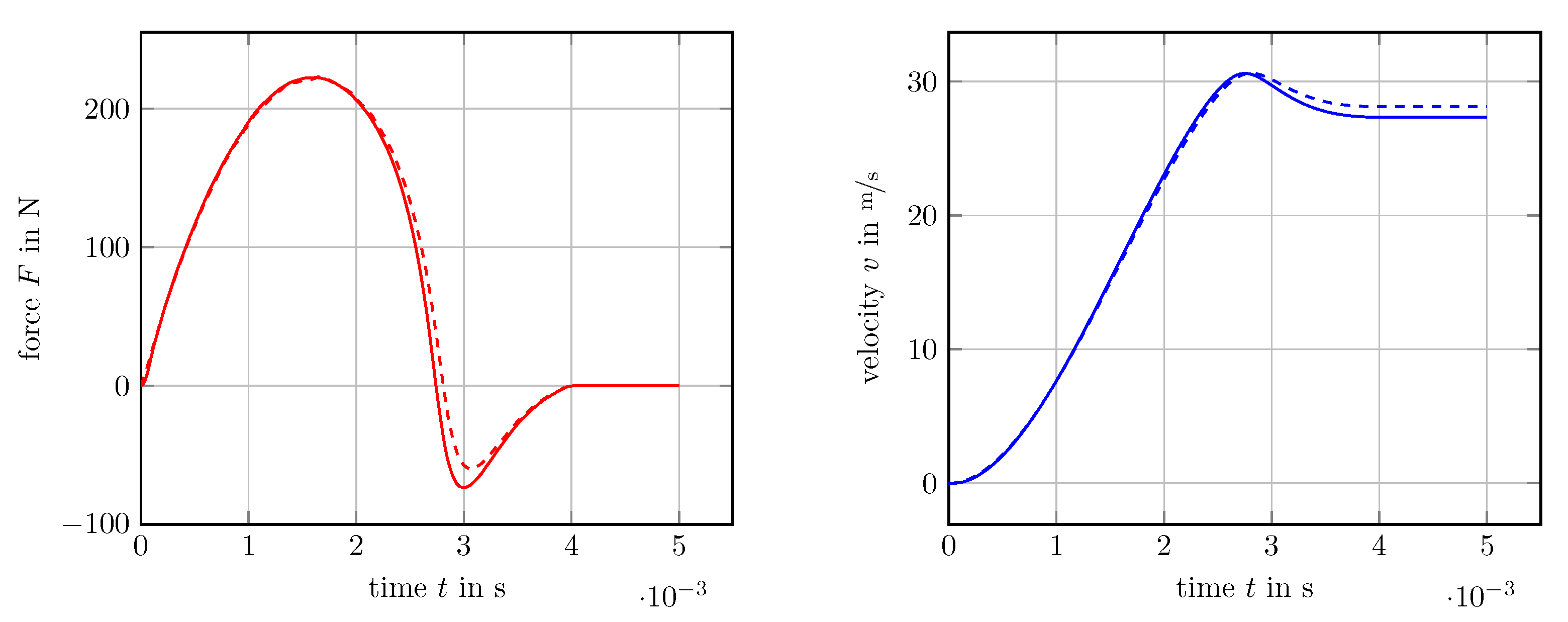
6.3. Eddy-Current Brake
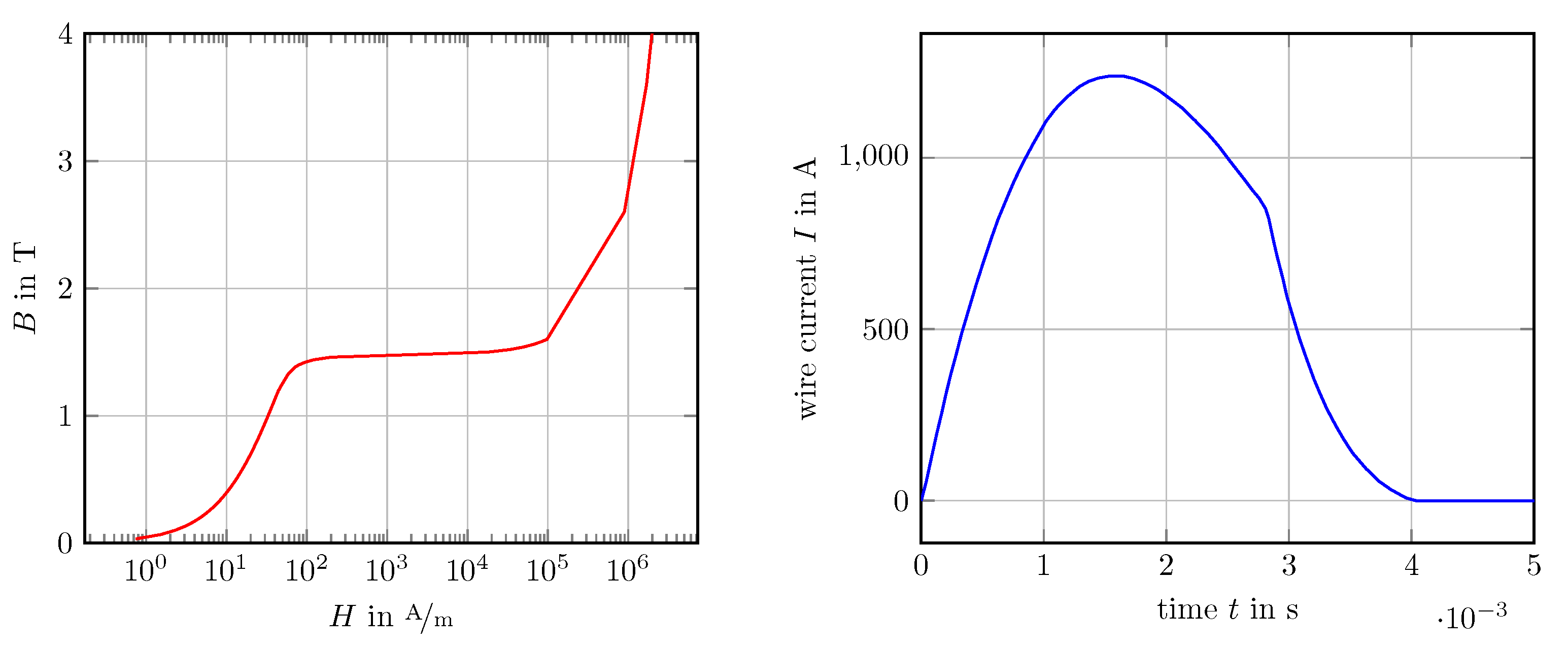
6.4. Electromagnetic Launcher
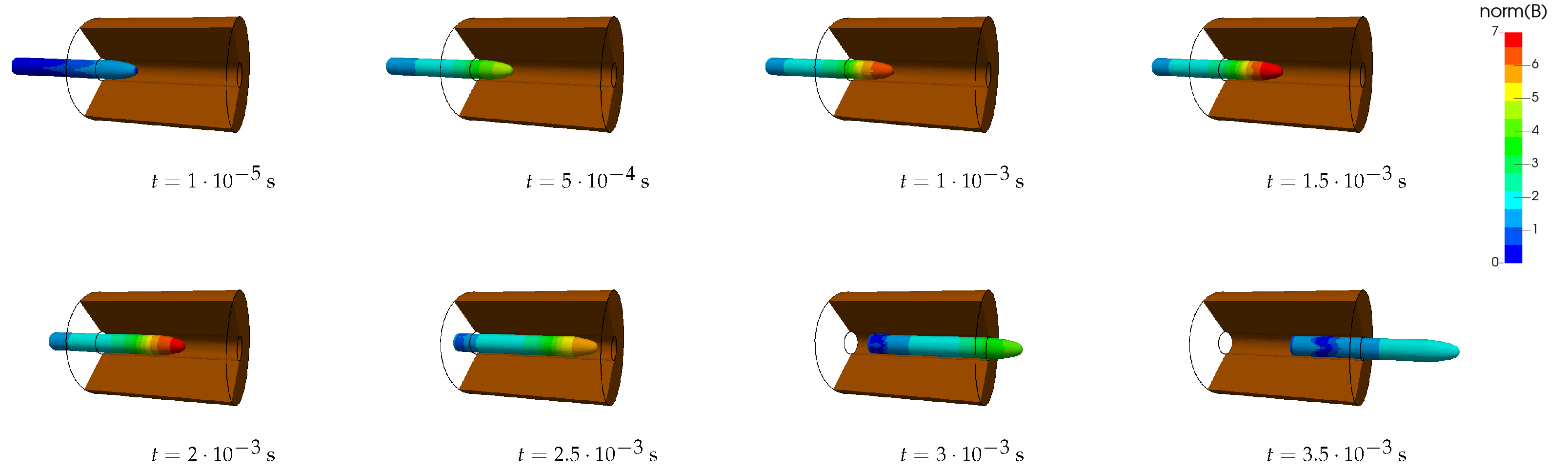
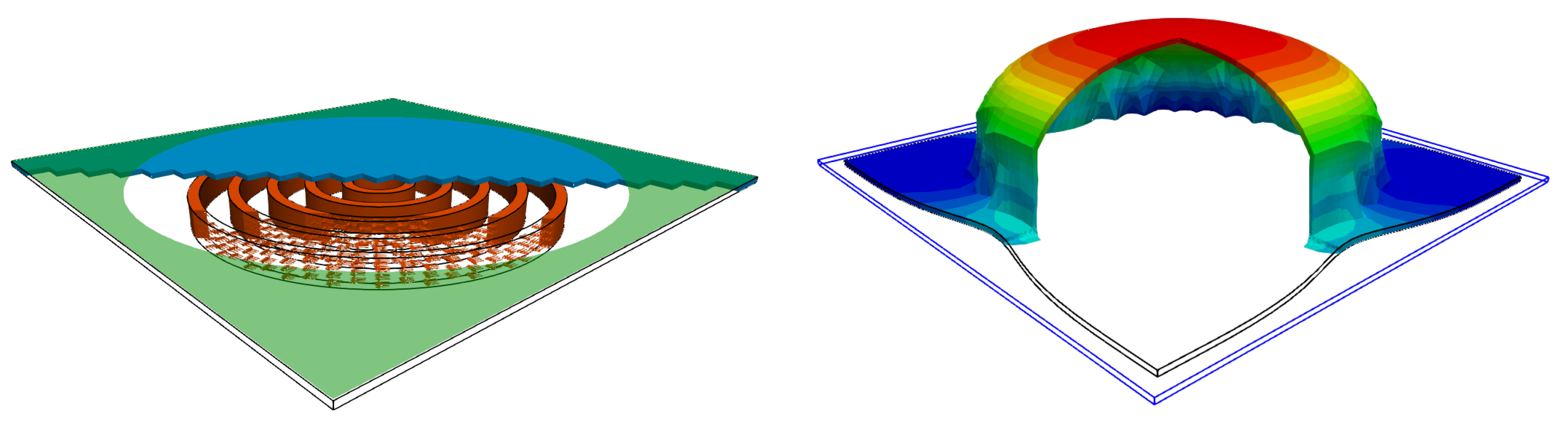
6.5. Magnetic Metal Forming
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sauter, S.A.; Schwab, C. Boundary Element Methods; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zienkiewicz, O.; Kelly, D.; Bettess, P. The coupling of the finite element method and boundary solution procedures. Int. J. Numer. Methods Eng. 1977, 11, 355–375. [Google Scholar] [CrossRef]
- Johnson, C.; Nédélec, J. On the coupling of boundary integral and finite element methods. Math. Comput. 1980, 35, 1063–1079. [Google Scholar] [CrossRef]
- Bossavit, A.; Verite, J.C. A mixed FEM-BIEM method to solve 3-D eddy-current problems. IEEE Trans. Magn. 1982, 18, 431–435. [Google Scholar] [CrossRef]
- Kuhn, M.; Steinbach, O. Symmetric coupling of finite and boundary elements for exterior magnetic field problems. Math. Methods Appl. Sci. 2002, 25, 357–371. [Google Scholar] [CrossRef]
- Hiptmair, R. Symmetric coupling for eddy current problems. SIAM J. Numer. Anal. 2002, 40, 41–65. [Google Scholar] [CrossRef] [Green Version]
- Hiptmair, R.; Sterz, O. Current and voltage excitations for the eddy current model. Int. J. Numer. Model. Electron. Netw. Devices Fields 2005, 18, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Monk, P. Finite Element Methods for Maxwell’s Equations; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Chen, Q.; Konrad, A. A review of finite element open boundary techniques for static and quasi-static electromagnetic field problems. IEEE Trans. Magn. 1997, 33, 663–676. [Google Scholar] [CrossRef]
- Ern, A.; Guermond, J.L. Theory and Practice of Finite Elements; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 159. [Google Scholar]
- Hiptmair, R.; Ostrowski, J. Generators of H1(Γh,) for Triangulated Surfaces: Construction and Classification. SIAM J. Comput. 2002, 31, 1405–1423. [Google Scholar] [CrossRef]
- Moré, J.J.; Thuente, D.J. Line search algorithms with guaranteed sufficient decrease. ACM Trans. Math. Softw. TOMS 1994, 20, 286–307. [Google Scholar] [CrossRef]
- Manges, J.B.; Cendes, Z.J. A generalized tree-cotree gauge for magnetic field computation. IEEE Trans. Magn. 1995, 31, 1342–1347. [Google Scholar] [CrossRef]
- Greengard, L.; Rokhlin, V. A new version of the fast multipole method for the Laplace equation in three dimensions. Acta Numer. 1997, 6, 229–269. [Google Scholar] [CrossRef]
- Ruge, J.W.; Stüben, K. Algebraic multigrid. In Multigrid Methods; SIAM: Philadelphia, PA, USA, 1987; pp. 73–130. [Google Scholar]
- Steinbach, O.; Wendland, W.L. The construction of some efficient preconditioners in the boundary element method. Adv. Comput. Math. 1998, 9, 191–216. [Google Scholar] [CrossRef]
- Hiptmair, R.; Xu, J. Nodal auxiliary space preconditioning in H(curl) and H(div) spaces. SIAM J. Numer. Anal. 2007, 45, 2483–2509. [Google Scholar] [CrossRef]
- Henrotte, F.; Hameyer, K. A theory for electromagnetic force formulas in continuous media. IEEE Trans. Magn. 2007, 43, 1445–1448. [Google Scholar] [CrossRef]
- Kielhorn, L.; Rüberg, T.; Zechner, J. Simulation of electrical machines: A FEM-BEM coupling scheme. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 1540–1551. [Google Scholar] [CrossRef] [Green Version]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Akoun, G.; Yonnet, J.P. 3D analytical calculation of the forces exerted between two cuboidal magnets. IEEE Trans. Magn. 1984, 20, 1962–1964. [Google Scholar] [CrossRef]
- Vokoun, D.; Beleggia, M.; Heller, L.; Šittner, P. Magnetostatic interactions and forces between cylindrical permanent magnets. J. Magn. Magn. Mater. 2009, 321, 3758–3763. [Google Scholar] [CrossRef]
- Allen, N.; Rodger, D. Description of TEAM Workshop Problem 24: Nonlinear time-transient rotational test rig. In Proceedings of the TEAM Workshop in the Sixth Round; 1996; pp. 57–60. Available online: http://www.compumag.org/jsite/images/stories/TEAM/problem24.pdf (accessed on 30 May 2021).
- Trutt, F.C.; Erdelyi, E.A.; Hopkins, R.E. Representation of the magnetization characteristic of DC machines for computer use. IEEE Trans. Power Appar. Syst. 1968, 665–669. [Google Scholar] [CrossRef]
- Levin, Y.; da Silveira, F.L.; Rizzato, F.B. Electromagnetic braking: A simple quantitative model. Am. J. Phys. 2006, 74, 815–817. [Google Scholar] [CrossRef] [Green Version]
- Leubner, K.; Laga, R.; Doležel, I. Advanced model of electromagnetic launcher. Power Eng. Electr. Eng. 2015, 13, 223–229. [Google Scholar] [CrossRef]
- Baltzis, K. The FEMM Package: A Simple, Fast, and Accurate Open Source Electromagnetic Tool in Science and Engineering. J. Eng. Sci. Technol. Rev. 2008, 1, 83–89. [Google Scholar] [CrossRef]
- Psyk, V.; Risch, D.; Kinsey, B.L.; Tekkaya, A.E.; Kleiner, M. Electromagnetic forming—A review. J. Mater. Process. Technol. 2011, 211, 787–829. [Google Scholar] [CrossRef]
- Simo, J.C. Numerical analysis and simulation of plasticity. Handb. Numer. Anal. 1998, 6, 183–499. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rüberg, T.; Kielhorn, L.; Zechner, J. Electromagnetic Devices with Moving Parts—Simulation with FEM/BEM Coupling. Mathematics 2021, 9, 1804. https://doi.org/10.3390/math9151804
Rüberg T, Kielhorn L, Zechner J. Electromagnetic Devices with Moving Parts—Simulation with FEM/BEM Coupling. Mathematics. 2021; 9(15):1804. https://doi.org/10.3390/math9151804
Chicago/Turabian StyleRüberg, Thomas, Lars Kielhorn, and Jürgen Zechner. 2021. "Electromagnetic Devices with Moving Parts—Simulation with FEM/BEM Coupling" Mathematics 9, no. 15: 1804. https://doi.org/10.3390/math9151804
APA StyleRüberg, T., Kielhorn, L., & Zechner, J. (2021). Electromagnetic Devices with Moving Parts—Simulation with FEM/BEM Coupling. Mathematics, 9(15), 1804. https://doi.org/10.3390/math9151804





