Solving High-Dimensional Problems in Statistical Modelling: A Comparative Study †
Abstract
:1. Introduction
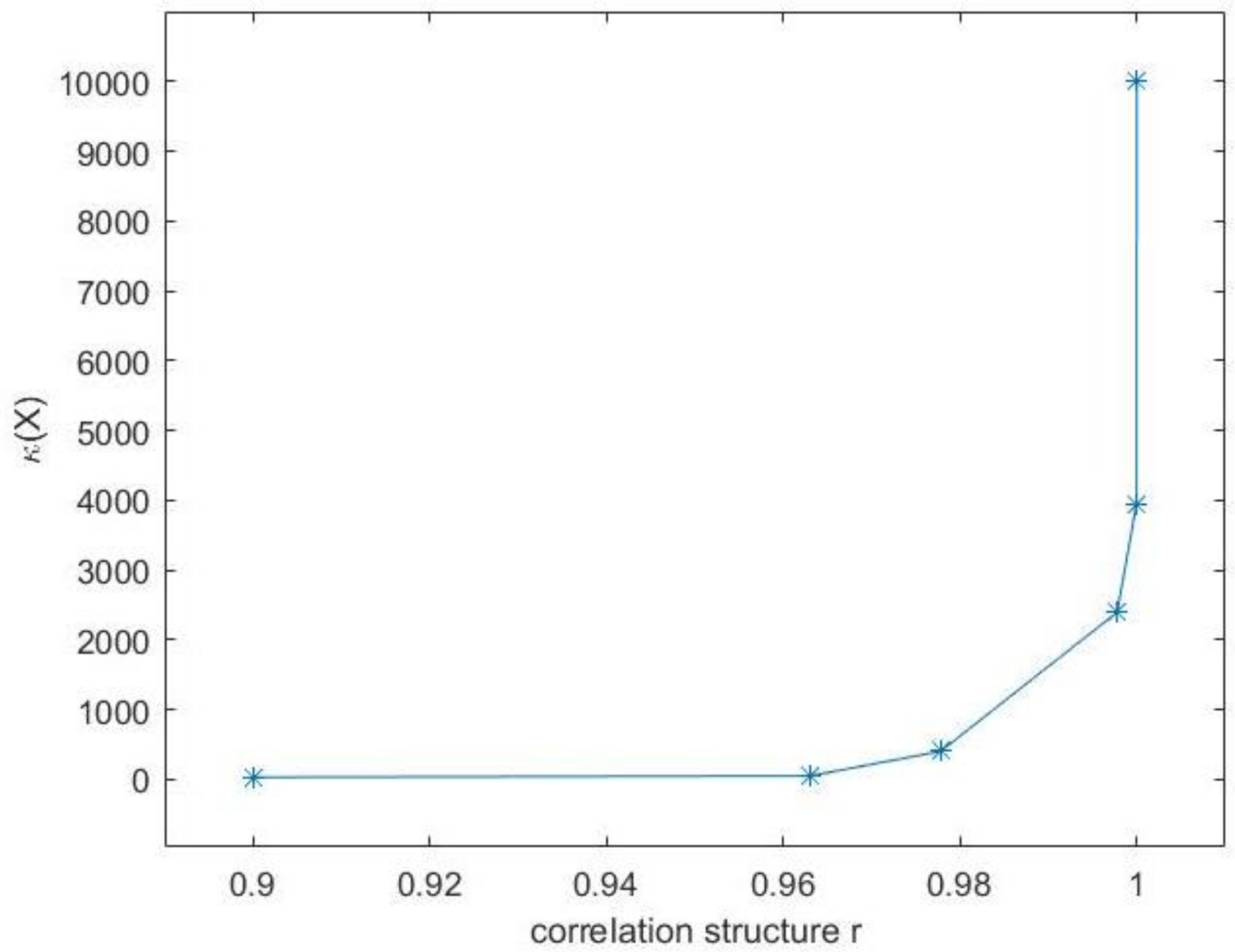
- Estimation of the regression parameter .From numerical linear algebra point of view, the statistical model (1) can be considered as an underdetermined system. This kind of system has infinitely many solutions. The first way to determine the desired vector is to keep the solution with the minimum norm. This solution is referred to as minimum norm solution (MNS), [1] (p. 264). Another way of solving these problems is based on regularisation techniques. Specifically, these methods allow us to solve a different problem which has a unique solution and thus to estimate the desired vector . One of the most popular regularisation methods is Tikhonov regularization, [2]. Another regularization technique which is used is the - regularization, [3,4].It is of major importance to decide whether problem (1) can be solved directly in the least squares sense or regularisation is required. Therefore, we describe a way of choosing the appropriate method for solving (1) for design matrices with correlated covariates. For these matrices we study extensively their properties. We prove that as the correlation of the covariates increases, the generalised condition number of the design matrix increases as well and thus the design matrix becomes ill-conditioned.
- To ascertain the most important factors of the statistical model.Variable selection is a major issue in solving high-dimensional problems. By means of variable selection we refer to the specification of the important variables (active factors) in the linear regression model, i.e., the variables which play a crucial role in the model. The rest of the variables (inactive factors) can be omitted.We deal with the variable selection in supersaturated designs (SSDs) which are fractional factorial designs in which the run size is less than the number of all the main effects. In this class of designs, the columns of X, except the first column, have elements ±1. The symbols 1 and are usually utilised to denote the high and low level of each factor, respectively. The correlation of SSDs is usually small, i.e., . The analysis of SSDs is a main issue in Statistics. Many methods for analysing these designs have been proposed. In [5], a Dantzig selector was introduced. Recently, a sure independence screening method has been applied in a model selection method in SSDs [6], and a support vector machine recursive feature elimination method for feature selection [7]. In our study, as we want to retain sparsity in variable selection, we adopt the - regularisation and the SVD principal regression method, [8], in order to determine the most important factors of the statistical model.
2. Methods Overview
2.1. Minimum Norm Solution
| Algorithm 1: Computation of MNS via . |
| Inputs: Design matrix , , Response vector Output: MNS solution − Compute the of X, i.e., − Compute the solution |
2.2. The Discrete Picard Condition
2.3. Regularisation Techniques
2.3.1. Tikhonov Regularisation
| Algorithm 2: Discrepancy principle. |
| Inputs: Design matrix , , Response vector Error norm Output: Regularisation parameter − Compute the of X, i.e., − Set − Choose such that , over a given grid of . |
2.3.2. - Regularisation
3. Design Matrix with Correlated Covariates
3.1. Correlated Covariates with Same Variance and Correlation
- 1.
- , if ,
- 2.
- , if or,
- 3.
- , if .
3.2. Highly Correlated Covariates with Different Variance and Correlation
3.3. Numerical Implementation
| Algorithm 3: Simulation scheme. |
 |
4. Variable Selection in SSDs
- Model 1:
- Model 2:
- Model 3:
- Model 1:
- Model 2:
- Model 3:
5. Conclusions
- Regularisation should be applied only if the given data set satisfies the discrete Picard condition. In this case, the choice of the regularisation parameter can be uniquely chosen by applying the discrepancy principle method.
- The regression parameter can be satisfactory estimated by the MNS if the design matrix is not highly correlated but in case of highly correlated data matrices we have to adopt regularisation techniques. The quality of the derived estimation of is assessed by the computation of .
- In variable selection, where sparse solutions are needed, SVD regression or - regularisation can be used. When only few factors of the experiment are needed to be specified (maybe only the most important), SVD regression may be preferable since it avoids regularisation and the troublesome procedure of defining the regularisation parameter. The quality of the variable selection which is proposed by the estimation methods is assessed by the evaluation of Type I and II error rates.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Datta, B.N. Numerical Linear Algebra and Applications, 2nd ed.; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Tikhonov, A.N. On the solution of ill-posed problems and the method of regularization. Dokl. Akad. Nauk SSSR 1963, 151, 501–504. [Google Scholar]
- Huang, G.; Lanza, A.; Morigi, S.; Reichel, L.; Sgallari, F. Majorization-minimization generalized Krylov subspace methods for ℓp-ℓq optimization applied to image restoration. BIT Numer. Math. 2017, 57, 351–378. [Google Scholar] [CrossRef]
- Buccini, A.; Reichel, L. An ℓ2-ℓq regularization method for large discrete ill-posed problems. J. Sci. Comput. 2019, 78, 1526–1549. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. The Dantzig Selector: Statistical Estimation When p is much larger than n. Ann. Stat. 2007, 35, 2313–2351. [Google Scholar]
- Drosou, K.; Koukouvinos, C. Sure independence screening for analyzing supersaturated designs. Commun. Stat. Simul. Comput. 2019, 48, 1979–1995. [Google Scholar] [CrossRef]
- Drosou, K.; Koukouvinos, C. A new variable selection method based on SVM for analyzing supersaturated designs. J. Qual. Technol. 2019, 51, 21–36. [Google Scholar] [CrossRef]
- Georgiou, S.D. Modelling by supersaturated designs. Comput. Stat. Data Anal. 2008, 53, 428–435. [Google Scholar] [CrossRef]
- Yagola, A.G.; Leonov, A.S.; Titarenko, V.N. Data errors and an error estimation for ill-posed problems. Inverse Probl. Eng. 2002, 10, 117–129. [Google Scholar] [CrossRef]
- Winkler, J.R.; Mitrouli, M. Condition estimation for regression and feature selection. J. Comput. Appl. Math. 2020, 373, 112212. [Google Scholar] [CrossRef] [Green Version]
- Hansen, P.C. The discrete picard condition for discrete ill-posed problems. BIT 1990, 30, 658–672. [Google Scholar] [CrossRef]
- Hansen, P.C. Rank-Deficient and Discrete Ill-Posed Problems; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Hansen, P.C. The L-curve and its use in the numerical treatment of inverse problems. In Computational Inverse Problems in Electrocardiology, Advances in Computational Bioengineering 4; WIT Press: Southampton, UK, 2000; pp. 119–142. [Google Scholar]
- Golub, G.H.; Meurant, G. Matrices, Moments and Quadrature with Applications; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Kluwer: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Koukouvinos, C.; Lappa, A.; Mitrouli, M.; Roupa, P.; Turek, O. Numerical methods for estimating the tuning parameter in penalized least squares problems. Commun. Stat. Simul. Comput. 2019, 1–22. [Google Scholar] [CrossRef]
- Koukouvinos, C.; Jbilou, K.; Mitrouli, M.; Turek, O. An eigenvalue approach for estimating the generalized cross validation function for correlated matrices. Electron. J. Linear Algebra 2019, 35, 482–496. [Google Scholar] [CrossRef]
- Liu, Y.; Dean, A. k-Circulant supersaturated designs. Technometrics 2004, 46, 32–43. [Google Scholar] [CrossRef]
- Li, R.; Lin, D.K.J. Analysis Methods for Supersaturated Design: Some Comparisons. J. Data Sci. 2003, 1, 249–260. [Google Scholar] [CrossRef]
- Cesa, M.; Campisi, B.; Bizzotto, A.; Ferraro, C.; Fumagalli, F.; Nimis, P.L. A Factor Influence Study of Trace Element Bioaccumulation in Moss Bags. Arch. Environ. Contam. Toxicol. 2008, 55, 386–396. [Google Scholar] [CrossRef] [PubMed]
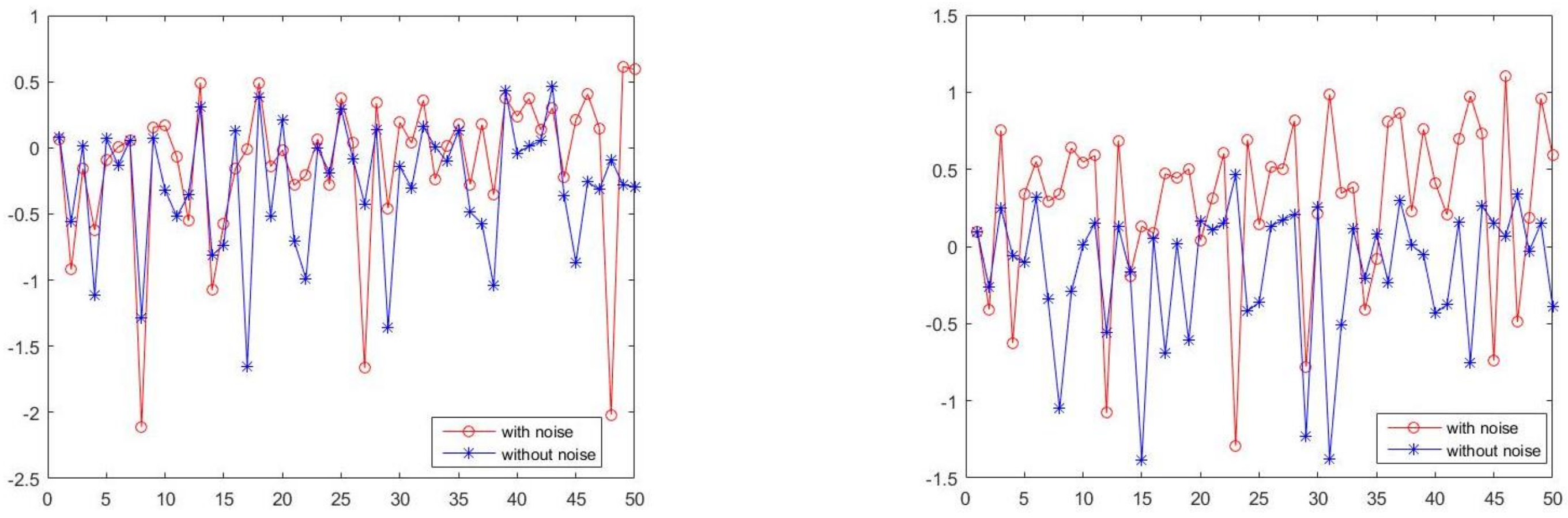

| r | Method | MSE () | ||
|---|---|---|---|---|
| 0.5 | 0.25 | MNS | ||
| Tikhonov | [1, 10] | |||
| - | [] | |||
| 0.5 | 1.0 | MNS | ||
| Tikhonov | [1, 10] | |||
| - | [] | |||
| 0.9 | 0.25 | MNS | ||
| Tikhonov | [1, 10] | |||
| - | [0.1, 10] | |||
| 0.9 | 1.0 | MNS | ||
| Tikhonov | [1, 10] | |||
| - | [0.1, 10] | |||
| 0.999 | 0.25 | MNS | 4.4474 | |
| Tikhonov | [1, 10] | 1.774 | ||
| - | [] | |||
| 0.999 | 1.0 | MNS | 2.0129 | |
| Tikhonov | [1, 10] | 1.0456 | ||
| - | [0.1, 10] |
| r | Method | MSE () | ||
|---|---|---|---|---|
| 0.9 | 0.25 | MNS | ||
| Tikhonov | [1, 10] | |||
| - | [] | |||
| 0.9 | 1.0 | MNS | ||
| Tikhonov | [1, 10] | |||
| - | [] | |||
| 0.999 | 0.25 | MNS | 3.5306 | |
| Tikhonov | [1, 10] | 1.0022 | ||
| - | [0.1, 10] | |||
| 0.999 | 1.0 | MNS | 1.1970 | |
| Tikhonov | [1, 10] | |||
| - | [0.1, 10] |
| r | Method | MSE () | ||
|---|---|---|---|---|
| [0.27, 0.91] | [0.19, 1.17] | MNS | ||
| Tikhonov | [1, 10] | |||
| - | [0.1, 10] | |||
| [−0.32, 0.85] | [0.13, 2.32] | MNS | ||
| Tikhonov | [1, 10] | |||
| - | [0.1, 10] | |||
| [0.06, 0.91] | [0.42, 1.93] | MNS | ||
| Tikhonov | [1, 10] | |||
| - | [0.1, 10] |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | + | + | - | - | - | + | + | + | + | + | - | - | - | + | + | - | - | + | - | - | - | + | 133 |
| + | - | - | - | - | - | + | + | + | - | - | - | + | + | + | - | + | - | - | + | + | - | - | 62 |
| + | + | - | + | + | - | - | - | - | + | - | + | + | + | + | + | - | - | - | - | + | + | - | 45 |
| + | + | - | + | - | + | - | - | - | + | + | - | - | + | + | - | + | + | + | - | - | - | - | 52 |
| - | - | + | + | + | + | - | + | + | - | - | - | - | + | + | + | - | - | + | - | + | + | + | 56 |
| - | - | + | + | + | + | + | - | + | + | + | - | + | + | - | + | + | + | + | + | + | - | - | 47 |
| - | - | - | - | + | - | - | + | - | + | - | + | + | - | + | + | + | + | + | + | - | - | + | 88 |
| - | + | + | - | - | + | - | + | - | + | - | - | - | - | - | - | - | + | - | + | + | + | - | 193 |
| - | - | - | - | - | + | + | - | - | - | + | + | - | + | - | + | + | - | - | - | - | + | + | 32 |
| + | + | + | + | - | + | + | + | - | - | - | + | + | + | - | + | - | + | - | + | - | - | + | 53 |
| - | + | - | + | + | - | - | + | + | - | + | - | + | - | - | - | + | + | - | - | - | + | + | 276 |
| + | - | - | - | + | + | + | - | + | + | + | + | - | - | + | - | - | + | - | + | + | + | + | 145 |
| + | + | + | + | + | - | + | - | + | - | - | + | - | - | - | - | + | - | + | + | - | + | - | 130 |
| - | - | + | - | - | - | - | - | - | - | + | + | + | - | - | - | - | - | + | - | + | - | - | 127 |
| Method | Intercept | |
|---|---|---|
| - | 6.11 | −1.13 |
| SVD Regression | 102.7857 | −36.0341 |
| Model | Method | Type I | Type II |
|---|---|---|---|
| Model 1 | - | 0.23 | 0.56 |
| SVD Regression | 0.15 | 0.74 | |
| Model 2 | - | 0.00 | 0.00 |
| SVD Regression | 0.05 | 0.00 | |
| Model 3 | - | 0.00 | 0.27 |
| SVD Regression | 0.07 | 0.33 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | - | - | - | - | - | - | + | + | - | - | - | + | - | + | + | + | - | + | + | + |
| + | + | + | - | - | - | - | - | - | - | + | + | - | - | - | + | - | + | + | + | - |
| + | + | - | + | + | + | - | - | - | - | - | - | - | + | + | - | - | - | + | - | + |
| + | - | + | + | + | - | + | + | + | - | - | - | - | - | - | - | + | + | - | - | - |
| - | - | - | + | - | + | + | + | - | + | + | + | - | - | - | - | - | - | - | + | + |
| - | + | + | - | - | - | + | - | + | + | + | - | + | + | + | - | - | - | - | - | - |
| - | - | - | - | + | + | - | - | - | + | - | + | + | + | - | + | + | + | - | - | - |
| + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + |
| Model | Method | Type I | Type II |
|---|---|---|---|
| Model 1 | - | 0.00 | 0.00 |
| SVD Regression | 0.08 | 0.00 | |
| Model 2 | - | 0.39 | 0.13 |
| SVD Regression | 0.08 | 0.67 | |
| Model 3 | - | 0.39 | 0.45 |
| SVD Regression | 0.17 | 0.80 |
| Method | Main Effects | Second-Order Interactions | Third-Order Interactions |
|---|---|---|---|
| - | Fe, Zn | Al/Hg, As/Pb, | Al/As/Mn, Al/Cr/Zn, |
| Cd/Mn, Mn/Ni | As/Cd/Fe, As/Cd/Mn, | ||
| Cr/Mn/Zn, Cu/Hg/Mn | |||
| Fe/Hg/Ni, Fe/ Ni/Pb | |||
| SVD Regression | Zn | As/Pb, Cd/Mn, | |
| Fe/Mn, Fe/Zn, | |||
| Mn/Ni, Pb/Zn |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choudalakis, S.; Mitrouli, M.; Polychronou, A.; Roupa, P. Solving High-Dimensional Problems in Statistical Modelling: A Comparative Study. Mathematics 2021, 9, 1806. https://doi.org/10.3390/math9151806
Choudalakis S, Mitrouli M, Polychronou A, Roupa P. Solving High-Dimensional Problems in Statistical Modelling: A Comparative Study. Mathematics. 2021; 9(15):1806. https://doi.org/10.3390/math9151806
Chicago/Turabian StyleChoudalakis, Stamatis, Marilena Mitrouli, Athanasios Polychronou, and Paraskevi Roupa. 2021. "Solving High-Dimensional Problems in Statistical Modelling: A Comparative Study" Mathematics 9, no. 15: 1806. https://doi.org/10.3390/math9151806
APA StyleChoudalakis, S., Mitrouli, M., Polychronou, A., & Roupa, P. (2021). Solving High-Dimensional Problems in Statistical Modelling: A Comparative Study. Mathematics, 9(15), 1806. https://doi.org/10.3390/math9151806






