Abstract
Let M be a compact d-dimensional Riemannian manifold without a boundary. Given a compact set , we study the set of distances from the set E to a fixed point . This set is , where is the Riemannian metric on M. We prove that if the Hausdorff dimension of E is greater than , then there exist many such that the Lebesgue measure of is positive. This result was previously established by Peres and Schlag in the Euclidean setting. We give a simple proof of the Peres–Schlag result and generalize it to a wide range of distance type functions. Moreover, we extend our result to the setting of chains studied in our previous work and obtain a pinned estimate in this context.
1. Introduction
The celebrated Falconer distance conjecture (see e.g., [1,2]) says that if the Hausdorff dimension of a compact set , , is greater than , then the Lebesgue measure of the distance set is positive. The best known results are due to Wolff in two dimension [3] and Erdogan [4] in higher dimensions. They proved that Lebesgue measure of the distance set is positive if the Hausdorff dimension of E is greater than . When , Orponen ([5]) proved that in under the additional assumption that is Ahlfors–David regular, if the Hausdorff dimension of E is greater than 1, then the packing dimension of the distance set is 1.
An interesting variant of the Falconer distance problem is obtained by pinning the distance set. More precisely, given , let . Once again, the question is, how large does the Hausdorff dimension of E need to be to ensure that the Lebesgue measure of is positive for some x in E. Peres and Schlag ([6]) proved that the conclusion holds if the Hausdorff dimension of , , is greater than . While the Peres–Schlag method, which relies on non-linear projection theory, is flexible and powerful, it is not particularly well-suited to the study of chains we undertake in this paper. Instead, we employ a rather direct approach that is suitable for a wide range of distance type functions.
For , E a compact subset of for some , we consider
where is continuous. Further, if F is the set of points where is not infinitely differentiable, then we assume that is such that
where denotes the closure of a set A, and denotes the Hausdorff dimension of E. It follows then that if is a Frostman measure of exponent (see, for instance, Ref. [7] page 18 for the construction of Frostman measures), then is a Frostman measure of exponent , and so is -a.e. infinitely differentiable and -a.e. satisfies
Remark 1.
If, for instance, , then the gradient is undefined on the set . If , then vanishes on the set . In either example, the troublesome set has dimension at most d. Recalling that , it follows that , and so, for each of these examples, condition (3) is violated on a set of whose dimension is strictly less than that of .
Remark 2.
To simplify matters, one may simply assume that we are working in a compact neighborhood of a point on which the function ϕ is infinitely differentiable, and on which both and .
We also assume throughout that satisfies the non-vanishing Monge–Ampere determinant assumption:
does not vanish on the set , .
Our main results are the following.
Theorem 1.
Let E be a compact subset of where , and let be defined as in (1) above, with ϕ, as described on page 2, satisfying (2) and (4). Suppose that the Hausdorff dimension of E is greater than . Then
In particular, if for some , and if μ is a Frostman measure on E of exponent , then for μ-a.e. , where denotes the -dimensional Hausdorff measure of E.
Corollary 1.
Let E be a closed subset of a compact d-dimensional, , Riemannian manifold M without a boundary and let ρ denote the Riemannian metric on M. Suppose that the Hausdorff dimension of E is greater than . Then
In particular, if for some , then for μ-a.e. , where μ is a Frostman measure of exponent and denotes the -dimensional Hausdorff measure of E.
Corollary 1 follows from Theorem 1 by observing that in local coordinates, the Riemannian metric on a compact manifold without a boundary satisfies the assumptions (3) and (4). See, for example, the Remark on the bottom of page 191 and top of page 192 in [8].
Remark 3.
As the reader will see, the method of proof of Theorem 1 is very flexible. For example, assumption on the Monge–Ampere determinant can be easily replaced by a weaker condition on the rank of the Monge–Ampere matrix. More precisely, the only thing required to obtain a non-trivial result is Sobolev bound for some for the generalized Radon transform
where ψ is a smooth cut-off function and is a smooth surface measure on the set
It is also important to note that in this case of the Euclidean metric, , the only analytic input our proof uses is the fact that the operator
where σ is the Lebesgue measure on the sphere, maps to . This is, of course, just equivalent to the well-known stationary phase estimate (see, e.g., [8])
1.1. Pinned Chains
Our methods also yield a result for pinned chains in thin subsets of Euclidean space. Let E be a compact subset of , , and define a k-chain in E with gaps by
In the special case that is the Euclidean distance, it is shown in [9] that if the Hausdorff dimension of a set is greater than , then the k-dimensional Lebesgue measure
Moreover, it is shown that under this assumption has non-empty interior.
We now extend this result to show that has positive k-dimensional Lebesgue measure for a large set of x to be quantified.
Theorem 2.
Let E be a compact subset of , and let as in (8). Suppose that the Hausdorff dimension of E is greater than . Then
In particular, if for some , then for μ-a.e. , where μ is a Frostman measure of exponent and denotes the -dimensional Hausdorff measure of E.
Corollary 2.
Let E be a compact subset of a compact d-dimensional, , Riemannian manifold M without a boundary and let be defined as in (8), where ϕ is replaced by ρ, the Riemannian metric on M. Suppose that the Hausdorff dimension of E is greater than . Then
In particular, if , then the k-dimensional Lebesgue measure of , denoted by , is positive for μ a.e. , where μ is a Frostman measure of exponent satisfying .
Corollary 2 follows from Theorem 2 in the same way Corollary 1 follows from Theorem 1.
Remark 4.
Since this paper appeared on the Arxiv, several interesting developments have taken place. Bochen Liu ([10]) proved that if the Hausdorff dimension of a compact set , , is greater than , then there exists , such that the Lebesgue measure of is positive. In two dimensions this threshold was further lowered to by Guth, the first listed author of this paper, Ou and Wang in [11]. Shmerkin [12] proved that if so that , where denotes the packing dimension of A, then for all x outside of a set of dimension at most 1. In the realm of chains, with the Euclidean metric, Bochen Liu lowered the dimensional threshold to in [13]. Once again, his method can be used to lower this threshold further to in view of [14]. Some interesting improvements on the size of the exceptional set of x’s for which the pinned distance set is small were obtained by Bochen Liu in [15]. Simon and the second listed author of this paper studied the interior of pinned distance sets corresponding to Cartesian products of Cantor sets in [16], as well as more general pinned distance sets for sets E of the critical dimension in [17]. In addition see [18,19] for further results on the interior of pinned distance sets corresponding to geometric configurations.
1.2. A General Pinning Scheme
While we do not study the pinning problem in full generality in this paper, we outline the basic general mechanism in this subsection and work out a few examples. For the sake of simplicity we work with the Euclidean distance, but the arguments work equally well with functions satisfying (1) and (3). Define the edge map
and let denote the number of non-zero values taken on by .
Given a compact set , a positive integer and an edge map , we define the k-point configuration to be the set of vectors with entries where , . In this way, we may naturally view . For example, the chain set from the previous subsection corresponds to the edge function , , , and 0 otherwise.
To illustrate the general pinning process, we begin with a 2-chain and pin the middle vertex. More precisely, we have
and the rest of the values of . Since we are pinning the middle vertex, we are looking at the set
Following the argument for pinned chains below in this context, and relabelling the coordinates, we see that proving that the two-dimensional Lebesgue measure of is positive, we must estimate
To put it another way, after relabelling the coordinates, we are led to consider , where if and , and 0 otherwise. This is a four vertex star with the center at . This instantly leads to an interesting estimate because estimation of (12) leads to an estimate of the underlying operator (see (23) below), instead of the bound required to prove Theorems 1 and 2. In this case integration in t is helpful, in view of Mockenhaupt–Seeger–Sogge local smoothing estimates.
In general, in order to study the pinned version of , where the st vertex is pinned (which we can always arrange by relabeling), we are led to consider , where if , , and if and .
A slightly more complicated situation is described in Figure 1 above. In this case and otherwise. Denote this configuration by , which is precisely what is depicted on the left hand side of Figure 1. If we pin the vertex and apply our method, we arrive at the configuration depicted on the right hand side of Figure 1.
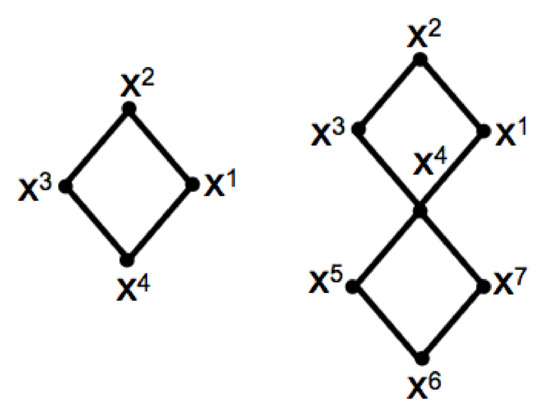
Figure 1.
The pinned necklace reduces to the consideration of two necklaces sharing the pinned point.
Our method also allows us to pin two or more vertices. We shall undertake a systematic study of the pinned configurations in a subsequent paper.
2. Proof of Theorem 1
2.1. Basic Reductions
Let denote a Frostman measure on E of exponent satisfying so that
(See, for example, [7] page 18 for the construction of such measures.)
Define the measure on by the relation
Applying Cauchy–Schwarz we see that (formally)
If we could make sense of the right hand side and show that
we could conclude that
for -a.e. , and plugging this into (15) would show that for -a.e. .
In order to prove the more precise estimate (5) we will show that if is a compactly supported Borel measure such that
for some , then
if
The conclusion (5) is recovered by taking to be a Frostman measure on a subset of E.
Remark 5.
The expression on the left hand side of (17), excluding the integration in t, is precisely the quantity that arises in the study of geometric hinges, first explored by the second listed author in her thesis and later studied systematically in the case in [9] and [20].
Remark 6.
One need not restrict attention to studying for . More generally, our proof techniques extend to show that if of sufficiently large dimension, then for a.e.
We now make the setup rigorous. We first address the problem set of points in (2). Let be a smooth cut-off function which equals 1 on , where N is a small open neighborhood of the set of points being measured in Equation (2). By the regularity of the measure (see [21], Theorem 2.18) and by assumption (2), we can choose N so that is arbitrarily small. Further, assume that vanishes on the closed set in Equation (2).
Next, modify the definition of given in (14) as follows: Set
The plan is as follows. We will show that, for this modified measure , the desired upper bound in (17) holds (where the expression in (17) is made formal in Lemma 1). Regarding the lower bound in Equation (15), while it no longer necessarily holds that is a probability measure, we observe that is a sufficient substitute, and we now show that (in (18)) can be chosen so that for all but a -“tiny” set of x. Indeed, let and assume that N is a small open neighborhood of the set of points being measured in Equation (2) chosen so that . Let denote those points of N that have the first coordinate equal to a fixed . By Chebyshev’s inequality,
Set . Note that and, if , then , and so, since is equal to 1 on , we have
and is a non-zero measure. The formal argument following (14) thus yields that for -almost every , the set has positive Lebesgue measure. Finally, since was arbitrary, this establishes that for -almost every , has positive Lebesgue measure.
Turning to the next reduction, we will prove (17) for , where is a smooth cut-off function, and . The following Lemma provides a self-contained proof that this is sufficient. Alternatively, note that converges to as measures and hence as distributions. Moreover, if , where C is independent of , then by Banach–Alaoglu we obtain that is absolutely continuous with respect to Lebesgue measure and has density in
Lemma 1.
Suppose that
independently of ϵ, where ψ is a smooth cut-off function and is defined in (18). Then carries an density for λ-almost every . This would imply that, for λ-almost every x, the Lebesgue measure of is positive.
To prove the Lemma, let be a smooth cut-off function, supported in the ball of radius 2, identically equal to 1 in the ball of radius 1, centered at the origin, with . Let . Observe that by the definition of (see (18)),
Plugging this expression into (19), it follows that
independently of .
Going back to (18), we see that
We want to show that carries an -density for -a.e. . To this end, it is enough to show that for every ,
independently of . This expression equals
and the bound follows from (21). This completes the proof of Lemma 1.
We have shown that the proof of Theorem 1 would follow if we could establish the estimate (17) with (defined in (18)) replaced by , where is a smooth cut-off function. We now reduce this estimate to an operator bound. Set
where is the same as in the statement of the Theorem.
The estimate (17) would follow instantly from the operator bound
under the assumption . Here, the constant C is uniform over t in a compact set and independent of , and equals for an arbitrary t in a fixed compact set. This is where we now turn our attention.
2.2. Proof of the Operator Bound
We prove estimate (23) by showing that, for ,
Let and be smooth cut-off functions such that is supported in the ball , is supported in the annulus , and .
Define , the classical Littlewood–Paley projection (see, for instance, [22] (pp. 241–243)), by the relation
and in general, for ,
Let . Then
This equation would probably benefit from a few words of explanation. Indeed, is trivially continuous and, thus, in the sense, , if were in , and then denotes inner product in , so the can be taken out of the inner product. This is indeed what happens, except that one has to make sense of and , which are not in , since the measures and are typically singular with respect to the Lebesgue measure.
In order to do that, instead of and , consider and (since has already been used as a parameter for regularization). Then these new measures are absolutely continuous with respect to the Lebesgue measure and we can consider and which are continuous and compactly supported. Now we can run the whole argument of the proof below, and obtain (23) for the measures and . Now note that by Fubini, for any F continuous and compactly supported,
Recall that if F is continuous and compactly supported, uniformly. Thus, by the dominated convergence Theorem we have that, as ,
On the other hand we claim that, for all x, as , . Indeed, fix x and note that is then a continuous function in y with compact support. Then the same reasoning as (25) and (26) shows that as ,
As a consequence, by Fatou’s Lemma, the same reasoning as (25) and (26) for , and duality, we obtain (23) (for the measures and , as stated), and for f continuous and compactly supported, which, by density, yields (23) in full generality.
Returning to (24), we consider the sum over , for a large integer K to be determined, and over separately.
Lemma 2.
Let K be a positive integer. Then there exists a positive constant, dependent on K, so that
Lemma 3.
With the notation above, there exists a positive integer K such that
To prove Lemma 2, we note that since the support of in the frequency side is contained in that of , we can add these in front of the left hand term:
We only consider the second term above, the first and the third being similar. Then we have that
for sufficiently small.
We shall need the following Lemma from [9] (Lemma 2.5). We shall give a proof below for the sake of completeness.
Lemma 4.
Let λ be a compactly supported Borel measure such that for some . Suppose that . Then for ,
To prove Lemma 4, note that the left hand side of (30) can be re-written (see e.g., Proposition 8.5 in [3]) as
where We apply Schur’s test (see Lemma 7.5 in [3]) to verify that there exists a constant so that if , then
To complete the proof of Lemma 4, we need only verify that Schur’s test applies. Observe that
and assuming without loss of generality that the diameter of the support of is at most 1,
We recall that and conclude that the quantity above is bounded above when . This completes the proof of Lemma 4.
Applying Lemma 4 shows that the first term on the right hand side in (29) is uniformly bounded. To handle the second term, we shall need the following classical result similar to the results obtained in [23] where the notion of rotational curvature is explicitly introduced, as well as Corollary 6.2.3 on page 173 in [8]. Since the result is not precisely covered by these references, we sketch the proof of Theorem 3 in the Appendix A below.
Theorem 3.
The presence of implies there exist constants such that the square of the second term in the summand of (29) is bounded by
By Theorem 3, and recalling that , the right hand side is bounded by
It easily follows from Lemma 4 that
for sufficiently small.
Inserting this back into (31) we obtain
The geometric series converges precisely when thus completing the proof of Lemma 2.
To complete the proof of Theorem 1, it remains to prove Lemma 3 and Lemma 4. These proofs can be found in the next two subsections.
2.3. Proof of Lemma 3
(See, for example, [24], for similar arguments). Use Fourier inversion to write
where is times the indicator function of the interval .
Recalling that , we have
where
We now give an upper bound on the modulus of G in the regime that and .
Lemma 5.
Suppose that and . Then there exists a so that if , then for each positive integer M, there exists a positive constant so that
We give the proof of this Lemma momentarily. Returning to the calculation above, we multiply both sides of (32) by to see that
Inserting the estimate from Lemma 5 and integrating in s, we bound (33) above in absolute value by
where M will be taken sufficiently large momentarily.
After applying Cauchy–Schwarz, we use Lemma 4 to bound this expression above by
for sufficiently small.
At last,
for an sufficiently small.
Summing in the previous display yields convergence of the geometric series, for an M chosen sufficiently large, thus proving the Lemma.
2.4. Proof of Lemma 5
We prove the first inequality in the statement of the Lemma, and the second follows by taking an M sufficiently large. We first compute the critical points of the phase function for
The critical points occur when
We may assume that there exists positive constants so that
where the lower bound follows from the non degeneracy assumption in (3) coupled with the assumption that has compact support.
We argue that if , , and j and k are sufficiently separated, then both equations in (35) cannot both simultaneously hold for in the support of . Let us first take care of the scenario when . If , then we may at least assume that either or , and the Lemma follows by repeated integration by parts. Assume then that .
If both equations in (35) were to hold, then it would follow that
This is clearly false if , , and j and k are sufficiently separated. We conclude then that there exists so that if , then the integrand of G is supported away from critical points.
Assuming then that , it follows that for each in the support of that either
Fix in the support of , and assume the first inequality in (36) holds. Let denote the coordinate such that is maximal. It follows that .
Next, we cover the compact support of by finitely many open neighborhoods about a finite collection of points and obtain a finite collection of coordinates , so that is maximal and, for each , . In the case that the second equation in (36) holds for some , we choose the neighborhood and coordinate in an analogous way.
Next, choose a partition of unity, , subordinate to the open cover so that . Now, we can write
where
For fixed, we see that is an eigenvector of the differential operator
Integrating by parts M times, we conclude that
We interpret this estimate in three separate cases: , , and .
If , then
Similarly, if , then
In either of the first two cases, if ,
which in turn is if .
In the case that , then the second inequality in (36) holds (otherwise ), and we can repeat the argument above to conclude that in this case,
Now, consider the case when . In this regime, we claim that the second equality in (35) cannot hold. Indeed, if the second equality in (35) held, then . However, then note that if , , and , then both and cannot both simultaneously hold.
Thus, when we can repeat the argument above (for the second inequality in (36)), and we are only left with the case that both and hold. But again, if , , and , then both and cannot both simultaneously hold.
In all cases, we see that if , , and , then
Recalling the is a finite sum of such terms (see (37)), the proof of the Lemma 5 is complete.
3. Proof of Theorem 2
As before, let be a Frostman measure supported on E. Recall that this means that
for and we can make as close to as we want.
Let as in (8), and define the measure on by the relation
Applying Cauchy–Schwarz we see that (formally)
As in the proof of Theorem 1, the strategy is to establish the bound
and conclude that
for -a.e. . Plugging this into (41) shows that for -a.e. .
In order to prove the more precise estimate (10) we will show that if is a compactly supported Borel measure such that
for some , then
if
The conclusion (10) is recovered by taking to be a Frostman measure on a subset of E.
We prove (43) by following the same basic reductions found in the proof of Theorem 1. Begin by more carefully defining the measure in (40) by introducing a product of smooth cut-off functions which avoid the problem set for the function (this is done in an analogous way to that in (18) and the following discussion). Next, let be a smooth cut-off function, supported in the ball of radius 2 and identically equal to 1 in the ball of radius 1 centered at the origin, with . Let . Then by the definition of the measure given in (40),
Let be a smooth cut-off function. Since the integration in t is compact owing to the compactness of E, we can throw in for free. Squaring and integrating with respect to , we obtain
It follows that in order to bound
it suffices to set equal the following set
and show that
independently of .
Letting , the operator as in (22), bounding the expression above reduces to bounding the following from above by a constant independent of t in a compact set and
We repeatedly apply the mapping property in (23) k times with to see that this expression is bounded above when and .
Author Contributions
All authors contributed equally to the conceptual work of this article. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the NSA Grant H98230-15-1-0319 (A.I.), the Simons Foundation Grant 523555 (K.T.), and grants DMS- 1056965 (US NSF), MTM2010-16232, MTM2015-65792-P (MINECO, Spain) (I.U.-T.).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Allan Greenleaf for graciously sharing his expertise of Fourier integral operators and for many illuminating discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Sketch of Proof of Theorem 3
We outline the proof of Theorem 3, where the estimates are uniform in t as well as . Fix t in a compact subset of the positive real line, and let be as in (22). For simplicity, we denote by T. T has Schwartz kernel
Note that each is rapidly decreasing. For the estimates, the important thing to note for the estimate is that the family of , as ranges over , is bounded in the symbol class . This implies that any of the Frechet seminorms is uniformly bounded.
The Schwartz kernel of is
where
Note that depends on t but, as the comments below show, only as a parameter in which everything is uniform, so t is suppressed in the notation. Observe that
As in the standard proof of the composition of FIOs (transverse intersection calculus, see e.g., [25]), one divides this integral for into three pieces: , , .
Step One: For a suitable that only depends on and on the support of (independent of t), it holds that on the region , the first term in the expression in (A1) dominates, so . Hence, one may integrate by parts in y some large number, N, times, and then integrate out in y (compact) and (bounded by ) and finally in , yielding a continuous function of x and z. However, one could first have differentiated any number of times in x and z and then carried this out. This process yields a function of x and z with all derivatives uniform in T and . In more detail, each differentiation in the x or z variables brings down powers of and , respectively; that is, for any multi-indices and , applying yields and applying yields . The integral in y is of the form
where . So, is an eigenfunction of the differential operator
One next integrates in (and since , one at most picks up ) and then integrates in to arrive at a function of x and z which we see is integrable by taking .
When for suitable, t-independent , the argument is also handled as above.
Step Two: Consider the case when . We homogenize the variable y by letting where denotes the norm of . This makes the phase function
Since satisfies the rotational curvature condition, the general composition calculus for FIO (and its proof, see e.g., [25]) applies: one is guaranteed that this phase function parametrizes the diagonal canonical relation, which means that the operator is a DO and the oscillatory integral can be rewritten using any other phase function that parametrizes the diagonal, such as . Furthermore, any finite number of seminorms of the amplitude only depend on a finite number of seminorms of the amplitude one is starting with, which is the times the Jacobian factor from above. Note that, on the region in question, is bounded in for . Standard proofs of boundedness of DOs only depend on a finite number of seminorms of the amplitude (see e.g., [25]) since all of these are bounded uniformly in t and , one arrives at the desired uniform boundedness. That is, the standard phase function for the Schwartz kernel of a DO is . Combining this with a symbol of order m and integrating gives an operator of order m.
However, if is another phase function (with the dimension of not necessarily equal to d, although it turns out that it can not be any less than d) which parametrizes the diagonal canonical relation in , then Hormander’s invariance of phase ([8], Section 3.2) states that can also be written as an oscillatory integral using the phase , but with a possibly different order for the needed symbol.
When one takes the third piece of the oscillatory integral for the kernel of , and homogenizes the y variable to (see [25] for the homogenization in y), then turns into such a phase , where . The new phase function parametrizes a canonical graph (again, see [25]). Because the rotation curvature condition implies that (i) the composition is covered by the transverse intersection calculus and (ii) the composition of the canonical relation corresponding to T with its transpose relation is the diagonal relation in , it follows that is a DO.
All of the steps of computing its symbol with respect to the standard phase for a DO from the symbol of the original operator are continuous with respect to the topology on the symbol classes. Moreover, the estimates in the proof for -Sobolev estimate for DOs only depend on a finite number of semi-norms of the symbols. The fact that the operator norm estimates for DOs only depend on a finite number of seminorms of the amplitude can be found in ([26], Section 18.6, see also [22], Chapter 7). The argument in Stein is based on the standard phase function for a DO, but inspection shows that the proof (based on integration by parts) works for any phase parametrizing the diagonal.
References
- Falconer, K.J. On the Hausdorff dimensions of distance sets. Mathematika 1986, 32, 206–212. [Google Scholar] [CrossRef]
- Mattila, P. Geometry of Sets and Measures in Euclidean Spaces; Cambridge University Press: Cambridge, UK, 1995; Volume 44. [Google Scholar]
- Wolff, T. Lectures on Harmonic Analysis; Łaba, S.C., Ed.; University Lecture Series; American Mathematical Society: Providence, RI, USA, 2003; Volume 29. [Google Scholar]
- Erdogan, B. A bilinear Fourier extension theorem and applications to the distance set problem. IMRN 2006, 23, 2411. [Google Scholar]
- Orponen, T. On the distance sets of Ahlfors David-regular sets. Adv. Math. 2017, 307, 1029–1045. [Google Scholar] [CrossRef]
- Peres, Y.; Schlag, W. Smoothness of Projections, Bernoulli Convolutions, and the Dimension of Exceptions. Duke Math. J. 2000, 102, 193–251. [Google Scholar] [CrossRef]
- Mattila, P. Fourier Analysis and Hausdorff Dimension; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Sogge, C. Fourier Integrals in Classical Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; Volume 210. [Google Scholar]
- Bennett, M.; Iosevich, A.; Taylor, K. Finite chains inside thin subsets of Rd. Anal. PDE 2016, 9, 579–614. [Google Scholar] [CrossRef][Green Version]
- Liu, B. An L2-identity and pinned distance problem. Geom. Funct. Anal. 2019, 29, 283–294. [Google Scholar] [CrossRef]
- Guth, L.; Iosevich, A.; Ou, Y.; Wang, H. On Falconer’s distance set problem in the plane. Invent. Math. 2020, 219, 779–830. [Google Scholar] [CrossRef]
- Shmerkin, P. On the Hausdorff dimension of pinned distance sets. Isr. J. Math. 2019, 230, 949–972. [Google Scholar] [CrossRef]
- Liu, B. Improvement on 2-chains inside thin subsets of Euclidean space. J. Geom. Anal. 2019, 29, 3520–3539. [Google Scholar] [CrossRef]
- Du, X.; Zhang, R. Sharp L2 estimate of Schrödinger maximal function in higher dimensions. Ann. Math. 2019, 189. [Google Scholar] [CrossRef]
- Liu, B. Hausdorff dimension of distance sets and the L2 method. Proc. Am. Math. Soc. 2020, 148, 333–341. [Google Scholar] [CrossRef]
- Simon, K.; Taylor, K. Interior of sums of planar sets and curves. Math. Proc. Camb. Philos. Soc. 2020, 168, 119–148. [Google Scholar] [CrossRef]
- Simon, K.; Taylor, K. Dimension and measure of sums of planar sets and curves. arXiv 2017, arXiv:1707.01407. [Google Scholar]
- Greenleaf, A.; Iosevich, A.; Taylor, K. On k-point configurations with nonempty interior, to appear. arXiv 2021, arXiv:2005.10796. [Google Scholar]
- Greenleaf, A.; Iosevich, A.; Taylor, K. Configuration Sets with Nonempty interior. J Geom. Anal. 2021, 31, 6662–6680. [Google Scholar] [CrossRef]
- Iosevich, A.; Krause, B.; Sawyer, E.; Taylor, K.; Uriarte-Tuero, I. Maximal operators: Scales, curvature and the fractal dimension. Anal. Math. 2019, 45, 63–86. [Google Scholar] [CrossRef]
- Rudin, W. Real and Complex Analysis, 3rd ed.; McGraw-Hill Book CO.: New York, NY, USA, 1987. [Google Scholar]
- Stein, E.M. Harmonic Analysis; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Phong, D.; Stein, E. Hilbert integrals, singular integrals and Radon transforms I. Acta Math. 1986, 157, 99–157. [Google Scholar] [CrossRef]
- Eswarathasan, S.; Iosevich, A.; Taylor, K. Fourier integral operators, fractal sets, and the regular value theorem. Adv. Math. 2011, 228, 2385–2402. [Google Scholar] [CrossRef]
- Duistermaat, J. Fourier Integral Operators, Progress in Mathematics; Birkhäuser Boston, Inc.: Boston, MA, USA, 1996; Volume 130. [Google Scholar]
- Hormander, L. The Analysis of Linear Partial Differential Operators, III; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).