Abstract
The current work aims to investigate how to utilize rough set theory for generating a set of rules to investigate the combined effects of heat and mass transfer on entropy generation due to MHD nanofluid flow over a vertical rotating frame. The mathematical model describing the problem consists of nonlinear partial differential equations. By applying suitable transformations these equations are converted to non-dimensional form which are solved using a finite difference method known as “Runge-Kutta Fehlberg (RKF-45) method”. The obtained numerical results are depicted in tabular form and the basics of rough sets theory are applied to acquire all reductions. Finally; a set of generalized classification rules is extracted to predict the values of the local Nusselt number and the local Sherwood number. The resultant set of generalized classification rules demonstrate the novelty of the current work in using rough sets theory in the field of fluid dynamics effectively and can be considered as knowledge base with high accuracy and may be valuable in numerous engineering applications such as power production, thermal extrusion systems and microelectronics.
1. Introduction
The study of Hydromagnetic fluid flow problems has attracted the attention of relatively few researchers. However, the analysis of such flows finds application in different areas such as polymer technology, Meteorology, the field of earth science, MHD generators, metal purification, geothermal energy extractions and flow meters. Mabood et al. [1] had studied the influence of variable fluid properties on heat transfer in MHD Casson fluid melts over a moving surface in a porous medium in the presence of the radiation. Nagy et al. [2] investigated the effects of hall currents and rotation on a generalized Hartmann flow and heat transfer. Sato [3] has studied the Hall effect in the viscous flow of ionized gas between parallel plates under transverse magnetic field. Some other studies also explored this issue [4,5,6,7,8,9,10]. It is noted that all the previously mentioned papers considered the models of a conventional fluid flow of an electrically conducting fluid; while fluids with the inclusion of solid particles in millimeter or micrometer sizes (nanofluid) have a quite different behavior from that of the traditional fluid in various vital aspects.
Nanofluids became a theme with considerable interest during the final decade due to their ability to improve the heat transfer rate in engineering suits. Nanofluids have wide utilities in solar receiver, nuclear reactor, cars and manufacturing cooling; tumefaction therapy and other fields. Mabood et al. [11] have studied the effects of hybrid nanoparticles on several physical quantities in a water-based hybrid nanofluid involved in a steady and fully developed forced convective flow generated over a stretched surface. Opanuga et al. [12] investigated the influence of Hall current and suction/injection on a steady, viscous, incompressible and electrically conducting third grade fluid past a semi-infinite plate with entropy generation. Ferdows et al. [13], Zahra et al. [14], Rashad et al. [15], Chamkha et al. [16] and Nabwey [17] investigate the MHD flow of a dissipative nanofluid for different flow configuration assuming that the nanoparticles contain gyrotactic microorganisms. Nabwey [18] studied the steady free convection of nanofluid has in occurrence of magnetic field. Mahdy et al. [19] point out the MHD mixed convection stagnation-point flow with entropy generation analysis due to Casson nanofluid around a rotating sphere. Chamkha et al. [20], Tlili et al. [21] and El-Kabeir et al. [22] studied the boundary layer flow and heat transfer characteristics of nanofluid flowing in the presence of radiation. More flow patterns can be found in [23,24,25,26,27,28]. In recent years, the study of Chemical reactions effects on heat and mass transfer with radiation effects has been one of the most appealing cases due to its various engineering applications and hydrometallurgical industries. Various studies had been carried out by the scholars to investigate this issue. For example, Srinivasacharya and Reddy [29] studied Chemical reaction and radiation effects on mixed convection heat and mass transfer over a vertical plate in power-law fluid saturated porous medium. Yusuf et al. [30] investigated the influence of thermal radiation on the magnetohydrodynamic flow of a Williamson nanofluid over a stretching sheet with chemical reaction.
Rough sets theory (RST) is one of the most successful approximations based on mathematical model to deal the imprecision and uncertainty present in knowledge [31]. Various heuristic algorithms are proposed based on rough set theory, also several approaches based on rough set theory and other theories are studied to generate decision rules and reduce dataset dimensionality. For example, Nabwey [32] introduced a hybrid approach based on rough set methodology and a fuzzy inference system to extract classification rules, in [33] also introduced a methodology for building knowledge base for heat transfer rate on free convection over a vertical flat plate embedded in a porous medium. Ref. [34] investigated how to use RST for analyzing the impact of viscoelastic and micropolar parameters on Hiemenz flow. A combination of RST and grey System was introduced in [35,36] for extracting decision rules. Shaaban et al. [37,38,39,40] proposed several methods and techniques for generating classification rules based on rough sets theory and apply it in different applications. Nabwey [41,42,43] investigate how to use the principles of RST in the medical field such as diagnosis of heart disease, predicting the primary site of metastatic adenocarcinoma cancer and prediction of wart treatment. For more engineering applications, see [44,45,46,47,48].
The main objective of this article is to generate a set of rules to investigate combined effects of heat and mass transfer on entropy generation due to MHD nanofluid flow over a vertical rotating frame based on rough set theory. The governing partial differential equations (PDEs) describing the problem are transformed to dimensionless nonlinear partial differential equations. Then, their numerical solutions are found. Finally, the rough sets theory is applied to generate some classification rules to predict the different behaviors of relevant parameters on the local Nusselt number and local Sherwood number. The proposed method put this work in a different position where we can obtain the values of local Nusselt number and local Sherwood number at any values of the parameters under consideration and determine the most important parameters that affect the values of local Nusselt number and local Sherwood number.
2. The Mathematical Framework
Mabood et al. [49] investigated a problem considering the incompressible and time-dependent magnetohydrodynamic convective flow of Sodium alginate-Fe3O4 based Brinkman type nanofluid, which is examined in a vertical rotating frame as shown in Figure 1 with the following assumptions:
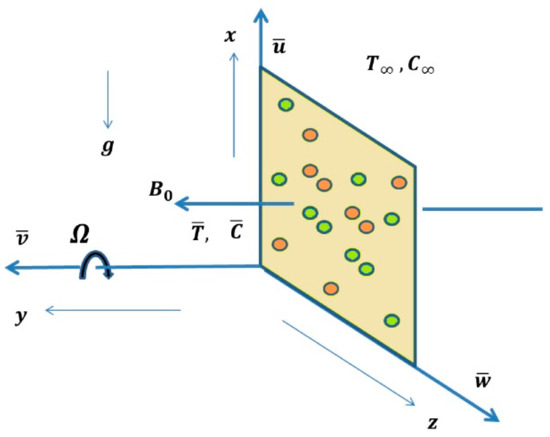
Figure 1.
The coordinate system and schematic diagram of the problem.
- Consider the physical quantities depend only on y.
- A magnetic field of constant strength is introduced in a direction parallel to y-axis in the direction of the fluid flow.
- The system spins about the normal axis with an angular velocity .
- assume that there exists a homogenous chemical reaction of first-order with rate constant between the diffusing species and the fluid.
Hence, the mathematical model which describes the governing equations of the flow by taking the effects of thermal radiation and chemical reaction into consideration can be constructed mathematically as:
Subject to:
where, A is constant with dimension 1/s and shows the amplitude [50] and;
Now, it is required to convert Equations (1)–(5) to dimensionless form, and this is accomplished by using the following transformations:
and define the new variables as:
where represent the functions which depend on the thermo-physical properties of the base fluid and nanoparticles. It should be noted that, to understand the flow features of the fluid flow; a special case will be taken, namely, uniformly accelerated the movement of the plate, i.e., where ξ is dimensionless constant [50].
The final form of the mathematical model can be written as:
Subject to the following initial and boundary conditions [50]:
The most significant parameters for this paper are the local Nusselt number and the local Sherwood number, and can be written as:
And their formulas in dimensionless form are:
The equation for entropy generation rate per unit volume can be constructed mathematically as follows:
The dimensionless number for entropy generation can be written as:
Bejan number () can be introduced in dimensionless form as:
The next stage is to find solution of the Equations (9)–(12) subject to the boundary conditions in (13), it is solved numerically by using finite-difference scheme known as “Runge-Kutta Fehlberg (RKF-45) method”. The numerical results are reported in Table 1 and Table 2 which represent the decision tables for local Nusselt number and local Sherwood number , respectively [49].

Table 1.
Decision Table of local Nusselt number for various values of , Nr and at .

Table 2.
Decision Table of Sherwood number for various values of , and at .
Now, the principles of rough sets theory will be applied to detect the essential relationships within the given data (in Table 1 and Table 2), compute all the reductions and extracting the final classification rules. The flow chart shown in Figure 2, illustrates the basic steps of extracting the generalized rules to predict the value of local Nusselt number and local Sherwood number for various values of the physical parameters under consideration. These main four steps can be explained briefly as follows:
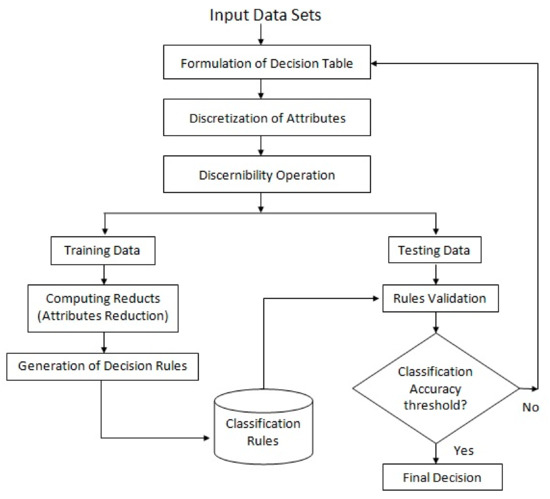
Figure 2.
The flow chart of generating classification rules.
- Formulation of the Decision table
The starting point of rough set theory (Pawlak, 1982) is an information system (called a decision table) which contains data about objects of interest characterized in terms of some attributes (condition and decision attributes). In this work, Table 1 and Table 2 represent the decision tables for the problem under consideration.
- Discretization of attributes
The key issue in the pre-processing stage of rough set is the discretization of continuous attributes process. It can be considered as transferring the continuous domain into the corresponding integer domain. There are many methods for finding suitable breakpoints in attribute values interval. In this work the algorithm “rough sets with Boolean reasoning discretization” was used.
- Reduction of attributes
It is the most important Process; the key issue is to reduce redundant information while maintaining the indiscernibility relation. There are many methods to obtain the reductions such as attribute reduction based on discernibility matrix, based on heuristic information and based on evolutionary computation.
- Extracting the Decision Rules
The next step is to split the data into training and test datasets (around 70–30%). The training set is the one that we use to learn the relationship between independent variables and the target variable. This relationship is captured as a set of rules. The results are considered satisfactory if classification accuracy threshold is obtained.
3. Results and Discussion
A software called ROSETTA, which is an RST analysis toolkit, will be used during this stage, where the algorithm “rough sets with Boolean reasoning discretization” will be used to discretize the data of Table 1 and Table 2. The results of this process shown in Table 3 and Table 4, It should be noted that * means do not care condition; Finally, the rough set reduction technique is applied to find the minimal subsets of attributes (reductions) which describe all the concepts in the decision tables without any loss.

Table 3.
The discretized decision table of Table 1.

Table 4.
The discretized decision table of Table 2.
Table 5 shows the generated classification rules to represent the effect of some parameters such as the volume fraction parameter , Brinkman parameter and thermal radiation parameter on the local Nusselt number and can be considered as base knowledge for . Figure 3 display the effects of the Brinkman parameter and the Hall current parameter (m) on the local Nusselt number. It is observed that the higher rate of heat transfer from the moving fluid to the wall occurs with larger values of the Brinkman parameter . The Effect of Eckert number and Magnetic parameter on the local Nusselt number are investigated in Figure 4. It is noticed that an increase in reduce . The physical explanation of this issue is that an increase in corresponds to upsurge in the thermal field via dissipation, hence, boosting the heat transfer rate.

Table 5.
The generated rules to predict the value of local Nusselt number .
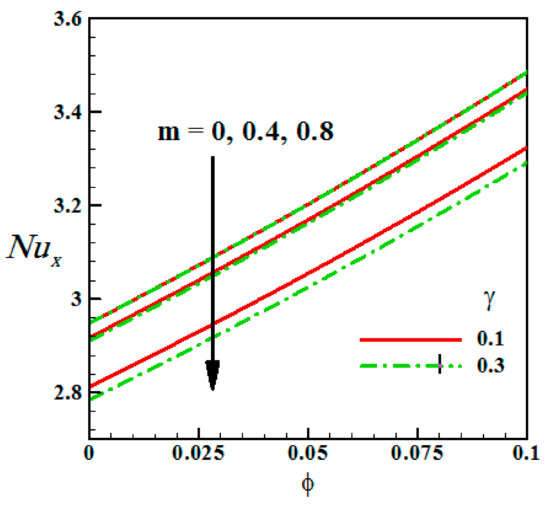
Figure 3.
Variation of local Nusselt number with for different values of and m.
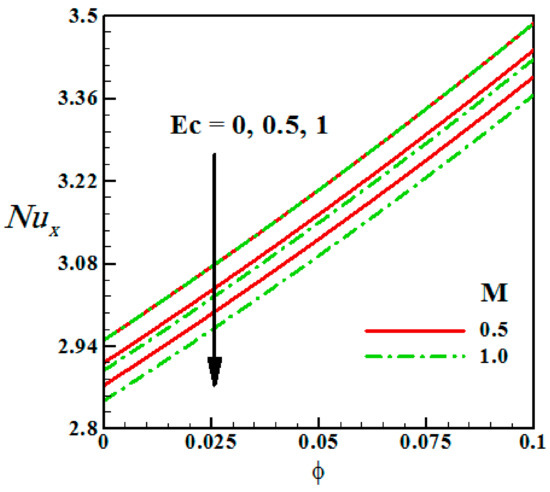
Figure 4.
Effect of Eckert number and Magnetic parameter on the local Nusselt number .
The generated classification rules, shown in Table 6, represent the effects of some parameters such as the volume fraction parameter , Schmidt number and chemical reaction parameter on the local Sherwood number and can be considered as base knowledge for . Figure 5 elucidates the impact of the Schmidt number and chemical reaction parameter on the Sherwood number . It is observed that with a rise in the concentration gradient, mass transport increases for increasing values of both and .

Table 6.
The generated rules to predict the value of Sherwood number .
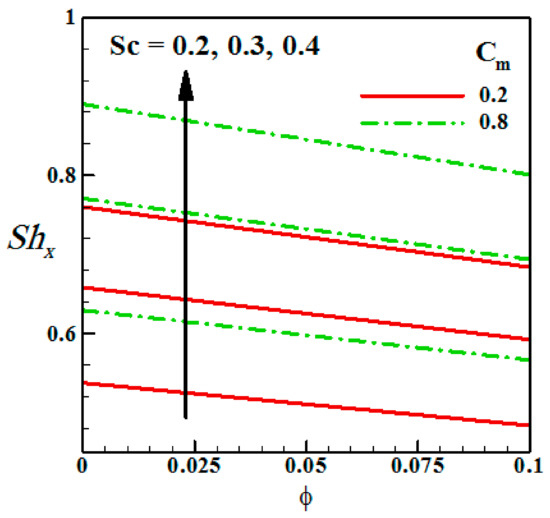
Figure 5.
Variation of local Sherwood number with for different values of and .
Through the numerical results and by the aid of Figure 6 and Figure 7 some physical facts and axioms can be proven as follows:
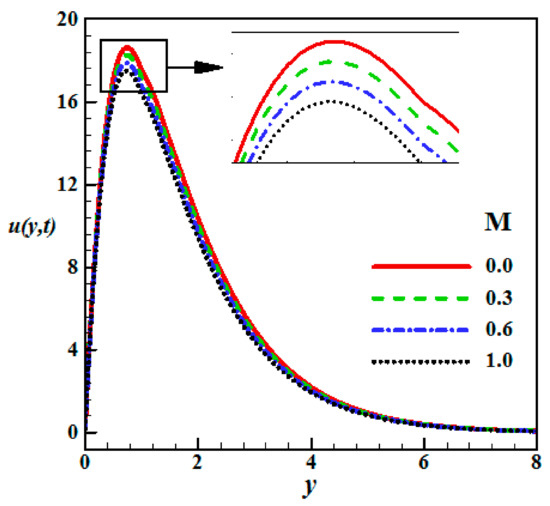
Figure 6.
Impact of the magnetic parameter (M) on the velocity of the liquid.
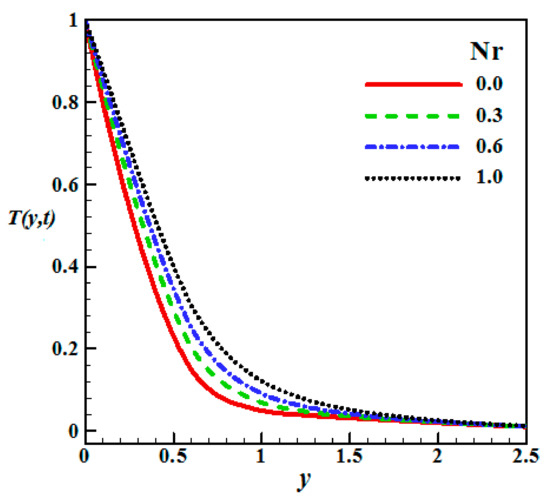
Figure 7.
Impact of the radiation parameter (Nr) on the Temperature.
- Figure 6 shows the impact of the magnetic field parameter on the dimensionless velocity . It is noticed that increasing values of leads to deceleration of the dimensionless velocity . The physical explanation of this issue is that as the magnetic field is applied; a resistance force opposing the fluid motion is generated, therefore causing a decrease in the velocity of the liquid.
- Figure 7 displays the influence of the radiation parameter Nr on the dimensionless temperature, where an enhancement in the temperature profile occurred at all the points in the presence of thermal radiation. The physical explanation of this issue is that bigger estimations of Nr generate more heat into the fluid leading to a rise in the temperature.
- The chemical reaction parameter decreases the heat transfer coefficient but increases the mass transfer rate. Increase in the values of implies more interaction of species concentration with the momentum boundary layer and less interaction with thermal boundary layer. Hence, chemical reaction parameter has more significant effect on Sherwood number than it does on Nusselt number.
In order to determine the accuracy of the obtained results and test the effectiveness of the proposed methodology; the results of local Nusselt number were compared with the previous literature, particularly Mabood et al. [49] as shown in Table 7. From this comparison we conclude that there is an excellent agreement and the accuracy of the proposed method is high.

Table 7.
Comparison of the local Nusselt number for various values of , Nr, .
The obtained results show the basic advantages of the proposed methodology that it is feasible, reasonable and it has important theoretical significance and practical value for artificial intelligence and data mining. While, the limitations of the proposed method can be stated as follows:
- It can only deal with discrete databases. However, in the real-life applications databases are numerical; therefore, the continuous data need to be discretized before attribute reduction by using one of the following methods: discretization based on information entropy, box method for equal frequency, discretization based on cluster analysis. The discretization process leads to information loss. Therefore, it is desirable to develop an efficient method which can deal with numerical databases directly.
- It depends upon the principles of equivalence relations. however, in real life applications equivalence relations are relatively not suitable; so, it is required to find a way to make the relations less significant by removing one or more of the three requirements of an equivalence relation.
4. Conclusions
This work investigated how to use rough set theory in the field of fluid dynamics; which opens new horizons for rough sets theory. A methodology based on rough sets theory for generating a set of classification rules to predict the value of local Nusselt number and local Sherwood number to investigate the combined effects of heat and mass transfer on entropy generation due to MHD nanofluid flow over a vertical rotating frame was introduced. The main results of the current work can be summarized as follow:
- This research clarifies that the proposed rule induction approach based on rough sets theory is a unique and viable posterior classification approach to extract knowledge
- The local Nusselt number increases with an increase in the volume fraction of nanoparticles and the radiation parameter.
- An increase in magnetic parameter, Brinkman parameter and Eckert number reduce the local Nusselt number.
- With a rise in the concentration gradient, mass transport increases to increase the value of .
- Higher values of the magnetic field parameter cause decrease in the velocity of the liquid and gradual drop in the secondary velocity w(y, t) is noticed.
- The chemical reaction parameter decreases the heat transfer coefficient but increases the mass transfer rate.
- The chemical reaction parameter has more significant effect on Sherwood number than it does on Nusselt number.
- As the radiation parameter (Nr) increases more heat is produced into the fluid and consequently increases the temperature.
The obtained results demonstrate that the current work has important theoretical significance and practical value for artificial intelligence and data mining; giving an opportunity for the researchers to conducting studies for developing new mathematical methods based on multidiscipline for the service of society. The proposed technique may be valuable in many engineering applications such as solar receiver, biomedical applications, heat exchangers, industrial cooling medium and can be considered as knowledge base. To overcome the drawbacks of the proposed methodology an extension work of using rough sets with other intelligent systems such as neural networks, fuzzy approaches and so forth, will be considered in the future work.
Author Contributions
Investigation, S.I.A. and H.A.N.; Methodology, S.I.A. and H.A.N.; Software, S.I.A.; Supervision, H.A.N.; Writing—original draft, S.I.A. and H.A.N.; Writing—review & editing, H.A.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| x, y and z | The Cartesian Coordinates (m) |
| The x, yand z-components of the velocity field (m/s) | |
| Magnetic field strength (T) | |
| Angular velocity (1/s) | |
| g | Acceleration due to gravity (m/s2) |
| Thermal conductivity of the base fluid (W m−1 K−1) | |
| Thermal conductivity of nanofluid (W m−1 K−1) | |
| Thermal conductivity of nanoparticles (W m−1 K−1) | |
| Viscosity of the base fluid (kg m−1 s−1) | |
| Dynamic Viscosity of the nanofluid (kg m−1 s−1) | |
| Density of the base fluid (kg/m3) | |
| Density of the nanofluid (kg/m3) | |
| heat capacitance of base fluid | |
| heat capacitance of nanofluid | |
| Kinematic viscosity (m2 s−1) | |
| material parameter of Brinkman type fluid | |
| Concentration (kg/m2) | |
| electrical conductivity of base fluid | |
| electrical conductivity of nanofluid | |
| t | Time (s) |
| dimensionless constant | |
| Temperature (k) | |
| temperature far from the frame (k) | |
| Concentration far from the frame (kg/m2) | |
| specific heat due to constant pressure (J kg−1 K−1) | |
| Hall current parameter | |
| Schmidt number | |
| Diffusive constant parameter (m2 s−1) | |
| Brinkman parameter | |
| Ideal gas constant (J K−1 mol−1) | |
| Temperature difference (k) | |
| Concentration difference (kg/m2) | |
| Thermal Grashof number | |
| Solutal Grashof number | |
| Effective Prandtl number | |
| Prandtl number | |
| Radiation parameter | |
| Eckert number | |
| Magnetic parameter | |
| Chemical reaction parameter | |
| Reynolds number | |
| the characteristic entropy | |
| volume fraction parameter | |
| Non dimensional rotation parameter | |
| Nusselt number | |
| Sherwood number | |
| The wall shear stress | |
| the heat transfer rate | |
| the rate of mass transfer |
References
- Mabood, F.; Abdel-Rahman, R.G.; Lorenzini, G. Effect of melting heat transfer and thermal radiation on Casson fluid flow in porous medium over moving surface with magnetohydrodynamics. J. Eng. Thermophys. 2016, 25, 536–547. [Google Scholar] [CrossRef]
- Nagy, T.; Demendy, Z. Effects of Hall currents and Coriolis force on Hartmann flow under general wall conditions. Acta Mech. 1995, 113, 77–91. [Google Scholar] [CrossRef]
- Sato, H. The Hall effect in the viscous flow of ionized gas between parallel plates under transverse magnetic field. J. Phys. Soc. Jpn. 1961, 16, 1427–1433. [Google Scholar] [CrossRef]
- Mabood, F.; Abdel-Rahman, R.G.; Lorenzini, G. Numerical study of unsteady Jeffery fluid flow with magnetic field effect and variable fluid properties. J. Therm. Sci. Eng. Appl. 2016, 8, 041003. [Google Scholar] [CrossRef]
- Mabood, F.; Lorenzini, G.; Pochai, N.; Shateyi, S. Homotopy analysis method for radiation and hydrodynamic-thermal slips effects on MHD flow and heat transfer impinging on stretching sheet. Defect Diffus. Forum 2018, 388, 317–327. [Google Scholar] [CrossRef]
- Krishna, M.V.; Bharathi, K.; Chamkha, A.J. Hall effects on MHD peristaltic flow of Jeffrey fluid through porous medium in a vertical stratum. Interfacial Phenom. Heat Transf. 2018, 6, 253–268. [Google Scholar] [CrossRef]
- Muthucumaraswamy, R.; Prema, K.M.A. Hall effects on flow past an exponentially accelerated infinite isothermal vertical plate with mass diffusion. J. Appl. Fluid Mech. 2016, 9, 889–897. [Google Scholar] [CrossRef]
- Krishna, M.V.; Swarnalathamma, B.V.; Chamkha, A.J. Investigations of Soret, Joule and Hall effects on MHD rotating mixed convective flow past an infinite vertical porous plate. J. Ocean Eng. Sci. 2019, 4, 263–275. [Google Scholar] [CrossRef]
- Krishna, M.V.; Chamkha, A.J. Hall and ion slip effects on MHD rotating flow of elastico-viscous fluid through porous medium. Int. Commun. Heat Mass Transf. 2020, 113, 104494. [Google Scholar] [CrossRef]
- Krishna, M.V.; Reddy, G.S.; Chamkha, A.J. Hall effects on unsteady MHD oscillatory free convective flow of second grade fluid through porous medium between two vertical plates. Phys. Fluids 2018, 30, 1–9. [Google Scholar]
- Mabood, F.; Yusuf, T.A.; Khan, W.A. Cu–Al2O3–H2O hybrid nanofluid flow with melting heat transfer, irreversibility analysis and nonlinear thermal radiation. J. Therm. Anal. Calorim. 2020, 141, 1–12. [Google Scholar] [CrossRef]
- Opanuga, A.A.; Gbadeyan, J.A.; Okagbue, H.I.; Agbolla, O.O. Hall current and suction/injection effects on the entropy generation of third-grade fluid. Int. J. Adv. Appl. Sci. 2018, 5, 108–115. [Google Scholar] [CrossRef]
- Ferdows, M.; Khairy, Z.; Rashad, A.M.; Nabwey, H.A. MHD Bioconvection Flow and Heat Transfer of Nanofluid through an Exponentially Stretchable Sheet. Symmetry 2020, 12, 692. [Google Scholar] [CrossRef]
- Zahra, A.; Khan, S.U.; Waqas, H.; Nabwey, H.A.; Tlili, I. Utilization of second order slip, activation energy and viscous dissipation consequences in thermally developed flow of third grade nanofluid with gyrotactic microorganisms. Symmetry 2020, 12, 309. [Google Scholar]
- Rashad, A.M.; Nabwey, H.A. Gyrotactic mixed bioconvection flow of a nanofluid past a circular cylinder with convective boundary condition. J. Taiwan Inst. Chem. Eng. 2019, 99, 9–17. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Nabwey, H.A.; Abdelrahman, Z.M.A.; Rashad, A.M. Mixed bioconvective flow over a wedge in porous media drenched with a nanofluid. J. Nanofluids 2019, 8, 1692–1703. [Google Scholar] [CrossRef]
- Nabwey, H.A. Feasibility of Rough Sets Theory in Predicting Heat Transfer Performance in Thermally Developed Flow of Third Grade Nanofluid with Gyrotactic Microorganisms. J. Nanofluids 2020, 9, 66–74. [Google Scholar] [CrossRef]
- Nabwey, H.A. A revised model of “Steady laminar natural convection of nanofluid under the impact of magnetic field on 2-D cavity with radiation” [AIP advances 9, 065008 (2019); https://doi.org/10.1063/1.5109192]. Therm. Sci. 2020, 24, 421–425. [Google Scholar] [CrossRef] [Green Version]
- Mahdy, A.; Chamkha, A.J.; Nabwey, H.A. Entropy analysis and unsteady MHD mixed convection stagnation-point flow of Casson nanofluid around a rotating sphere. Alex. Eng. J. 2020, 59, 1693–1703. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Modather, M.; L-Kabeir, S.M.M.E.; Rashad, A.M. Radiative effects on boundary-layer flow of a nanofluid on a continuously moving or fixed permeable surface. Recent Pat. Mech. Eng. 2012, 5, 176–183. [Google Scholar] [CrossRef]
- Tlili, I.; Sandeep, N.; Reddy, M.G.; Nabwey, H.A. Effect of radiation on engine oil-TC4/NiCr mixture nanofluid flow over a revolving cone in mutable permeable medium. Ain Shams Eng. J. 2020, 11, 1255–1263. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.M.; Chamkha, A.J.; Rashad, A.M. Effect of thermal radiation on non-Darcy natural convection from a vertical cylinder embedded in a nanofluid porous media. J. Porous Media 2014, 17, 269–278. [Google Scholar] [CrossRef] [Green Version]
- Gorla, R.; El-Kabeir, S.M.M.; Rashad, A.M. Heat transfer in the boundary layer on a stretching circular cylinder in a nanofluid. J. Thermophys. Heat Transf. 2011, 25, 183–186. [Google Scholar] [CrossRef]
- Imran, N.; Javed, M.; Sohail, M.; Phatiphat, T.; Nabwey, H.A.; Tlili, I. Utilization of hall current and ions slip effects for the dynamic simulation of peristalsis in a compliant channel. Alex. Eng. J. 2020, 59, 3609–3622. [Google Scholar] [CrossRef]
- Khan, N.; Nabwey, H.A.; Hashmi, M.S.; Khan, S.U.; Tlili, I. A theoretical analysis for mixed convection flow of Maxwell fluid between two infinite isothermal stretching disks with heat source/sink. Symmetry 2020, 12, 62. [Google Scholar] [CrossRef] [Green Version]
- Chamkha, A.J.; Rashad, A.M.; Alsabery, A.I.; Abdelrahman, Z.M.A.; Nabwey, H.A. Impact of partial slip on magneto-ferrofluids mixed convection flow in enclosure. J. Therm. Sci. Eng. Appl. 2020, 12, 1–13. [Google Scholar] [CrossRef]
- Chamkha, A.; Yassen, R.; Ismael, M.A.; Rashad, A.M.; Salah, T.; Nabwey, H.A. MHD Free Convection of Localized Heat Source/Sink in Hybrid Nanofluid-Filled Square Cavity. J. Nanofluids 2020, 9, 1–12. [Google Scholar] [CrossRef]
- Mahdy, A.; Hady, F.M.; Nabwey, H.A. Unsteady homogeneous-heterogeneous reactions in MHD nanofluid mixed convection flow past a stagnation point of an impulsively rotating sphere. Therm. Sci. 2019, 388. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Reddy, G.S. Chemical reaction and radiation effects on mixed convection heat and mass transfer over a vertical plate in power-law fluid saturated porous medium. J. Egypt. Math. Soc. 2016, 24, 108–115. [Google Scholar] [CrossRef] [Green Version]
- Yusuf, T.A.; Adesanya, S.O.; Gbadeyan, J.A. Entropy generation in MHD Williamson nanofluid over a convectively heated stretching plate with chemical reaction. Heat Transf. 2020, 49, 1982–1999. [Google Scholar] [CrossRef]
- Pawlak, Z. On learning—A rough set approach. In Symposium on Computation Theory; Springer: Berlin/Heidelberg, Germany, 1984; pp. 197–227. [Google Scholar]
- Nabwey, H.A. A Hybrid Approach for Extracting Classification Rules Based on Rough Set Methodology and Fuzzy Inference System and Its Application in Groundwater Quality Assessment. In Advances in Fuzzy Logic and Technology; Springer: Cham, Switzerland, 2017; pp. 611–625. [Google Scholar]
- Nabwey, H.A.; Modather, M.; Abdou, M. Rough set theory based method for building knowledge for the rate of heat transfer on free convection over a vertical flat plate embedded in a porous medium. In Proceedings of the International Conference on Computing, Communication and Security (ICCCS), Pointe aux Piments, Mauritius, 4–5 December 2015; pp. 1–8. [Google Scholar]
- Nabwey, H.A. Rough set approach for analyzing the effect of viscoelastic and micropolar parameters on hiemenz flow in hydromagnetics. Int. J. Eng. Res. Technol. 2020, 13, 170–180. [Google Scholar] [CrossRef]
- Nabwey, H.A. An approach based on Rough Sets Theory and Grey System for Implementation of Rule-Based Control for Sustainability of Rotary Clinker Kiln. Int. J. Eng. Res. Technol. 2019, 12, 2604–2610. [Google Scholar]
- Nabwey, H.A.; El-Paoumy, M.S. An integrated methodology of rough set theory and grey system for extracting decision rules. Int. J. Hybride Inf. Technol. 2013, 6, 57–65. [Google Scholar]
- Shaaban, S.M.; Nabwey, H.A. A decision tree approach for steam turbine-generator fault diagnosis. Int. J. Adv. Sci. Technol. 2013, 51, 59–66. [Google Scholar]
- Shaaban, S.M.; Nabwey, H.A. A probabilistic rough set approach for water reservoirs site location decision making. In International Conference on Computational Science and Its Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 358–372. [Google Scholar]
- Shaaban, S.M.; Nabwey, H.A. Rehabilitation and reconstruction of asphalts pavement decision making based on rough set theory. In International Conference on Computational Science and Its Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 316–330. [Google Scholar]
- Shaaban, S.M.; Nabwey, H.A. Transformer fault diagnosis method based on rough set and generalized distribution table. Int. J. Intell. Eng. Syst. 2012, 5, 17–24. [Google Scholar] [CrossRef]
- Nabwey, H.A. An intelligent mining model for medical diagnosis of heart disease based on rough set data analysis. Int. J. Eng. Res. Technol. 2020, 13, 355–363. [Google Scholar] [CrossRef]
- Nabwey, H.A. A Mathematical Methodology for Predicting the Primary Site of Metastatic adenocarcinoma Cancer based on Rough Set Theory. Int. J. Eng. Res. Technol. 2020, 13, 427–432. [Google Scholar] [CrossRef]
- Nabwey, H.A. A Methodology Based on Rough Set Theory and Hypergraph for the Prediction of Wart Treatment. Int. J. Eng. Res. Technol. 2020, 13, 552–559. [Google Scholar] [CrossRef]
- Mohamed, H.A. A probabilistic rough set approach to rule discovery. In International Conference on Ubiquitous Computing and Multimedia Applications; Springer: Berlin/Heidelberg, Germany, 2011; pp. 55–65. [Google Scholar]
- Nabwey, H.A. Identification of short circuit fault location in voltage source inverters based on rough set theory. Int. J. Eng. Res. Technol. 2020, 13, 929–937. [Google Scholar] [CrossRef]
- Pathak, H.K.; George, R.; Nabwey, H.A.; El-Paoumy, M.S.; Reshma, K.P. Some generalized fixed point results in ab-metric space and application to matrix equations. Fixed Point Theory Appl. 2015, 1, 1–17. [Google Scholar]
- Mohamed, H.A. An Algorithm for Mining Decision Rules Based on Decision Network and Rough Set Theory. In International Conference on Ubiquitous Computing and Multimedia Applications; Springer: Berlin/Heidelberg, Germany, 2011; pp. 44–54. [Google Scholar]
- Nabwey, H.A. A method for fault prediction of air brake system in vehicles. Int. J. Eng. Res. Technol. 2020, 13, 1002–1008. [Google Scholar] [CrossRef]
- Mabood, F.; Yusuf, T.A.; Rashad, A.M.; Khan, W.A.; Nabwey, H.A. Effects of Combined Heat and Mass Transfer on Entropy Generation due to MHD Nanofluid Flow over a Rotating Frame. CMC 2021, 66, 575–587. [Google Scholar]
- Ali, F.; Aamina, B.; Khan, I.; Sheikh, N.A.; Saqib, M. Magnetohydrodynamic flow of brinkman-type engine oil based MoS2-nanofluid in a rotating disk with hall effect. Int. J. Heat Technol. 2017, 4, 893–902. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).