1. Introduction
Current trends in the teaching of mathematics reveal that the extensive mathematical education community has reached a consensus on how to improve the teaching of the subject. One such trend emphasizes the importance of problem solving and modeling (see, for instance, [
1,
2]). To “know mathematics” is supposed to include the competence of using mathematics in and applying it to real-life extra-mathematical situations. In some countries, this recent trend has led to competence-based curricula including inquiry and modeling competences. This is the case, for instance, of the modeling competency, as explained by Blum [
1]. A wide range of international studies, such as the TIMSS study [
3] or the Programme for International Students Assessment (PISA) [
4,
5], provide significant recommendations with regard to integrating inquiry and modeling competences in school curricula.
A variety of approaches and research projects related to how to foster inquiry-based learning (IBL) in mathematics education also attach considerable importance to problem solving and modeling processes. For instance, the PRIMAS international project aimed at implementing inquiry-based methodologies in mathematics and science classrooms as well as in teacher education [
6,
7]. As highlighted by Maass and Engeln ([
7], p. 3), the teaching of modeling within this project’s framework equates to adopting an inquiry approach in realistic contexts.
Several research studies on the likely relationship between mathematical modeling and inquiry—for instance, Niss [
8], (focuses on the connections between the processes of pre-mathematization and inquiry; or Stillman and Brown [
9], who analyze the notion of “implemented anticipation” [
8] in the modeling cycle, are regarded as closely related processes that should be combined. Some authors even consider modeling as a particular way to approach inquiry-based teaching and learning of mathematics, as stated in Artigue and Blomhoj [
10]. They believe that the similarity with the modeling cycles is striking and state the following: “we see a trans-disciplinary structure of a dynamical inquiry process behind both processes”. In line with what they say, we assume that working with modeling in mathematics, as in other subjects, can thus lead to gaining a valuable insight into inquiry as a general process using different implementations in diverse disciplines and contexts.
For the past few years, our research team has been working on the implementation of inquiry projects in interdisciplinary contexts, involving the subjects of mathematics and history. Through the analysis of different case studies, it was observed that the students often developed mathematical modeling cycles at specific moments during their inquiry process [
11,
12,
13]. Consequently, one open question that emerged from these works is about how the students developed inquiry together with mathematical modeling.
However, these commonalities between modeling and inquiry have not been examined in depth nor have they been clearly conceptualised. This led us to gain a deeper understanding of how both processes, inquiry and modeling, are interrelated. This paper aims at contributing to the understanding of the relationships between both processes, especially when used in an interdisciplinary context, such as archaeology, to develop inquiry and mathematical modeling. With this purpose in mind, the following objectives of this article were established: (1) to analyze the presence of the processes of inquiry and mathematical modeling in the implementation of an interdisciplinary teaching sequence, aiming to look for the coincidences, concatenations and synergies between both processes; and (2) to elaborate an integrated proposal for the joint analysis of both processes in the implementation of teaching sequences in interdisciplinary contexts.
To accomplish these objectives, we start by presenting a review of some dominant conceptualizations of modeling and inquiry. Then, we make our theoretical position on inquiry and mathematical modeling explicit. Next, the implementation of an interdisciplinary teaching sequence is analyzed from each of these two processes. Finally, as one of the main results of this research, we present a proposal of a model that integrates both processes for the analysis of interdisciplinary teaching sequences that aims to promote inquiry and modeling. Some final considerations derived from the analysis of the implementation and potentialities of the integrative model are highlighted in the last section. We hope that this integrative model will become a useful tool to, on the one hand, describe the possible learning paths of students and, on the other hand, to design teaching sequences to promote mathematical modeling and inquiry in a dialectical relationship. Finally, based on the literature review we have done, this integrated view of the inquiry and mathematical modeling is represented as a new contribution to the research field of mathematical modelling in mathematics education.
5. Analysis of the Didactic Sequence Based on Inquiry and Modeling Processes
In the first session, the students were introduced to the initial problem, which was related to the discovery ten years ago of Roman ruins in the center of Badalona by the team of archaeologists of the Badalona Museum. According to archaeological research [
38], these ruins belonged to an old building in the Roman city of
Baetulo—the Roman name for Badalona. The activities were structured along certain questions that facilitated the students to progress within the cycle of inquiry. The students were asked to find out what type of public building the Roman ruins belonged to. The teachers suggested the main questions of the project described below.
The students worked with real data from the beginning of the project. For example, to introduce the project, the teachers showed the students how to locate and study the area of the city where the ruins were discovered by using Google Maps and Badalona’s urban geo-portal. Managing these real local data was important for some teams in order to formulate their initial working hypotheses about what kind of building the ruins could correspond to.
The main initial question that initiated and motivated the inquiry was: What lies behind these ruins? After a group discussion, the students agreed that the problem formulation (and the task formulation) of the real situation had to be specified as: What type of Roman building could the Roman ruins correspond to? [I1] and [Ma].
Faced with this question, the students proposed that the ruins could correspond to, for instance, a theater, a circus, an amphitheater, a basilica, baths, a pantheon, a temple, etc. The students then focused on searching historical information to look for possible answers [I2] about the kind of roman construction this building could be. Different kinds of explanations [sub-process to justify the choice of building] could be provided, but the most satisfactory ones in the school context were related to taking into account the shape of the building. For example, the students deduced that “if the ruins correspond to an ellipse, the building could be an amphitheater; or, if it is a semicircle it could be a theater; or, if a section of its perimeter was rectangular, it could have been a circus, etc.” [Mb]. The rest of the possible buildings that have a regular polygonal layout were rejected, as it turned out the wall was curvilinear.
To work on the justification and validation of these hypotheses, the students worked with a new set of questions and their corresponding answers, which meant going back a few steps in the cycle of inquiry. The teachers, following the students’ comments and their firsts hypotheses, proposed working on these questions: What geometrical shapes could fit into the building’s partial wall discovered by the archaeologists (a 1.5-m-high curvilinear wall)?
The students knew that the wall was curvilinear, as they refer to it using the archaeological report available on the blog. They thus hypothesized [I3] that the Roman wall had been part of a curved building [Mb], such as a (semi-circular) theater, an (elliptical) amphitheater or a circus (as a part of its semi-circular floor). Different questions arose that were further specified as follows: How can we find out the original shape of the discovered wall?
To validate their hypotheses, the students worked on defining an action plan [I4] with the help of the history and mathematics teachers to determine the original shape of the remnants of the curved wall. To do this, the students undertook a range of mathematically orientated actions. To find out whether the Roman wall was part of an ellipse or a circumference, in order to look for possible answers [I2]), the students went to a public square near their school where the teachers had drawn the shape of the Roman wall on the ground using the archaeological information available. In this activity, the students developed mathematical modeling because they tried to find a geometrical model that would fit a representation of the original wall. First of all, the students tried to graphically fit the drawn wall into an ellipse using a manual method. Two students of group 10 were then placed at the foci (determined by trial and error) of the possible ellipse, each holding the end of a rope. A ring, which could move along the rope, was used. A third student held on to the ring to keep the rope tight at all times while following the trajectory of the drawn wall. This process of data collection [I5], mathematization [Mc] mathematical systematization [Md] analysis and interpretation [Me] was repeated several times as the students changed the location of the foci of the ellipse to be able to follow the wall drawn on the ground and to try to validate the model [Mf] and [I6] the results geometrically. The students encountered numerous difficulties to fit the shape of the wall into an ellipse, basically because it was not easy to draw such a large ellipse. Considering the dimensions of the wall represented on the floor of the square, the radius of the ellipses had to be at least 16 m long. Moreover, it was not easy for the students to visualize the wall’s curved shape, as it looked more like straight line than part of an ellipsis or a circumference. The students concluded that the wall could not possibly be part of an ellipse. A student from inquiry team 8 drew an ellipse on the floor and justified the following [Mb]: “If it really was an ellipse, it could only be the flatter part, the middle part, because if it was this part (pointing toward the vertex of an imaginary ellipse she was drawing with her finger), it wouldn’t be curved enough”. Another student added: “But … It could be a part of a big circumference, right? There were buildings that were round, don’t you remember? We should try to find out if this shape has a center
Once the ellipse hypothesis was rejected, the students continued looking for answers [I2] and tried to fit the wall into a circumference by aligning its center and radius. To collect new data, to mathematize, systematize, analyze and interpret them [I5], [Mc], [Md] and [Me], the inquiry teams used different methods of construction. First, when the students remembered that all the points of a circumference are at the same distance from its center, they tried to find the center by testing possible centers through trial and error [Mc] and [Md]. As this was unsuccessful, they tried again by using plaster to draw some of the tangents at different points of the wall. They drew a perpendicular to these tangents (using a large ruler and a wooden square) to find the center at their intersection to then be able to determine the radius ([Mc] and [Md]). Teams 6 and 10 opted for a different strategy: they drew two bisections at three points of the arch of the wall using a rope and plaster to mark them. They found the center at the midpoint of the bisector and thus concluded that the wall belonged to a circular building ([Mc] and [Md]). The teachers encouraged the students to measure the radius—16 m—and to draw the complete semi-circumference on the square [I5]. The students decided to ‘draw’ it placing some classmates side-by-side at a distance of 16 m to the center of the circumference. The students realized that the perimeter of the building was enormous. A student said: “It was bigger than our school! And … how many people fit in it? A lot of people, right?” [Me]. At this stage of the activity, it is observed that all the inquiry teams completed a mathematical modeling cycle and they managed to develop the initial strategies to work on the validation of the initial hypothesis formulated ([Mf] and [I6]) testing the geometrical models that best fit the simulation of the Roman ruins and rejecting those that do not fit. The use the students gave to the tangible construction of the geometrical model was an important contribution in order to progress in the modeling and inquiry cycle. At this point of the inquiry, almost all the teams concluded that the wall fit into a circumference.
Given the fact that the question of having to discover what kind of curve the wall could fit into was complex, the historical context of the situation played a central role. The students look for answers [I2], collect and interpret [I5] data from the historical context, that is, from the information found about the reported shape of the Roman building, the information from the archaeological report, etc. This historical context allowed the students to formulate and work on the most plausible hypotheses [I3]. Indeed, the number of possible curves was limited to the forms used in public Roman constructions (an ellipse or circumference and their defining elements). Moreover, the students could select (systematization [Mb]) the most relevant and mathematizable [Mc] data based on limited information. Limiting the wide variety of possible models to fit the shape of the ruins, thanks to the historical context and the answers found, allowed the students to make the problem accessible to them and to put into practice some mathematical knowledge easily available to them.
Once the students validated [I6] and [Mf] that the wall fit into a circumference, two possible types of buildings were historically possible: a (semi-circular) theater or a circus (with a semi-circular floor layout on one side and a rectangular one on the other). To determine which of these two options the building could correspond to [I2], the students went back to the information provided by the historical data about the size and area [I5], which helped them discard one of the options.
At this point, students considered two new hypotheses (a theater or a circus), problematized by the following questions: In Roman times, what were theaters actually like? What about circuses? Do we have the necessary data to sketch their layout?
The students needed to know more about Roman architecture. The teachers decided to talk about the work “De Architectura” by Marcus Vitruvius (a free English version of “The Ten Books on Architecture” by Vitruvius is available online 19 July 2021:
http://www.gutenberg.org/files/20239/20239-h/20239-h.htm#Page_137 but we use the Spanish version available on the blog (see endnote 1)) (c. 80-70 BCE-15 BCE) that describes the construction rules for a range of public Roman buildings, detailing their parts, proportions, etc. By doing so, the students could
look for possible answers [I2].
After presenting this external resource, the students decided to try to validate the hypothesis of a theater. They planned the actions to be carried out and started by systematizing [Mb] and mathematizing [Mc] the data collected during the inquiry (data from the archaeological report, historical data, data from the site’s location, data from the previous modeling cycle developed, etc.), interpreting them [Me] according to the rules of Vitruvius on theater building with the help of the teachers. At this stage, the students started a modeling cycle that consisted of building a geometrical model of a Roman theater by following the construction method recommended by Vitruvius.
The students had a Spanish translation of the facsimile in the blog of the project, where the method for the construction of a Roman theater model was explained. The students also had a document on the blog, prepared by the participant-researcher, which helped them to reproduce Vitruvius’ method by using GeoGebra (considering it could be difficult for the students to set it up using Geogebra). Nevertheless, they quickly learned how to use the program. Moreover, they resorted to images of ancient Roman theaters they found on the Internet in order to understand and visualize their forms and likely sizes.
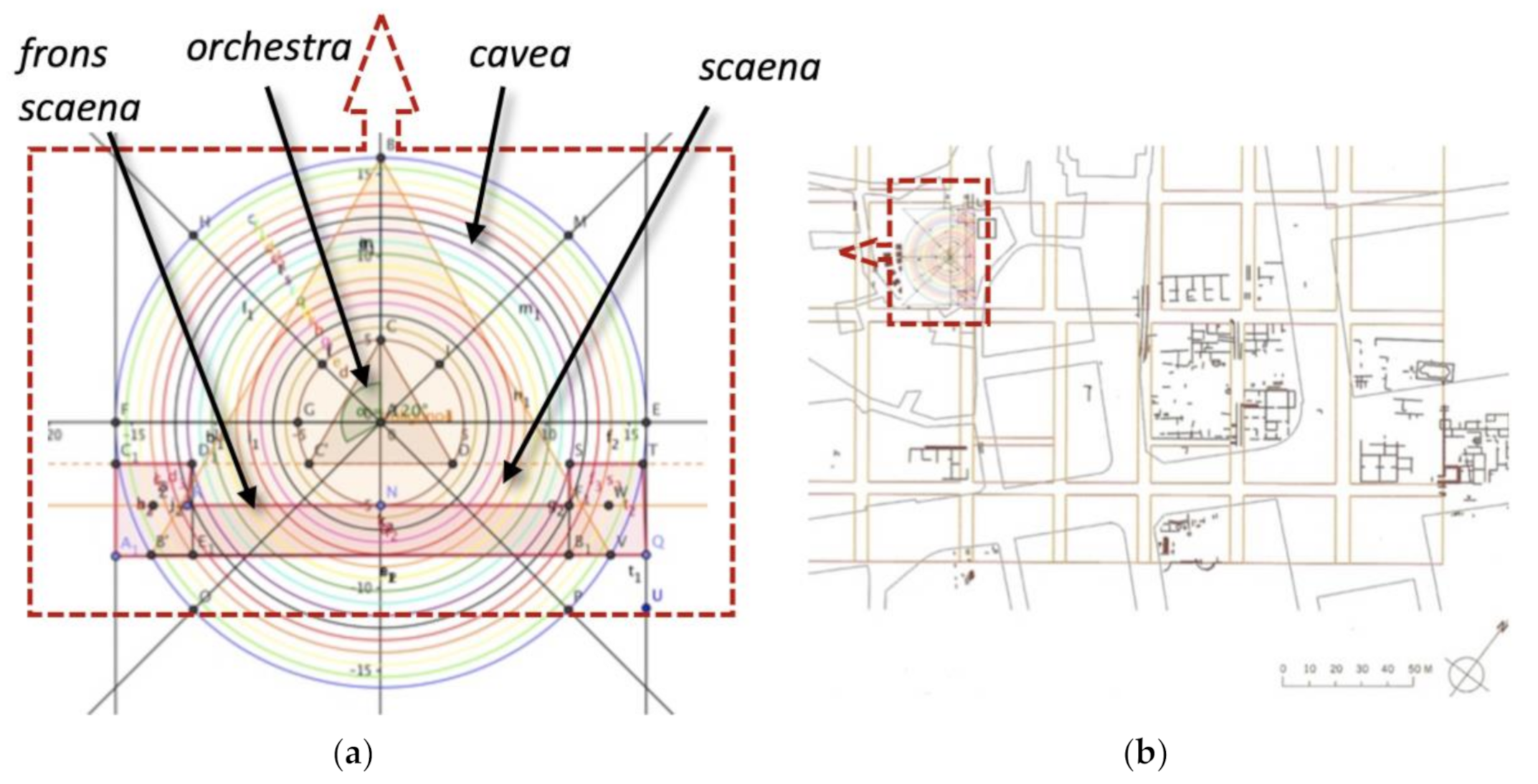
This whole process concluded with the construction of several geometric models of the
Baetulo theater that each research team built (see
Figure 4a). The models were adjusted and simulated using the information provided by Vitruvius’ canon of proportions as well as the measurements the students had gathered and shared in the class with the other teams.
Regarding the work developed by Group 8, they distinguished the main parts of a Roman theater, which were: the cavea (tiered seating space for spectators), the orchestra (semicircular space for the musicians, between the bleachers and the stage), the frons scaena (decorated stage background to which actors had access) and the stage (rectangular space in front of the stage background). The cavea, which was shaped like a semicircle, was the grandstand where the spectators used to sit. It was enclosed by an external semicircular wall. Group 8 assumed that the fragment of the curvilinear wall found in the ruins was a part of this wall bordering the cavea.
Group 8 followed the procedure described in
Figure 4, when they built and simulated their model with GeoGebra. As shown in
Figure 4, they distinguished the different parts to propose different models fitting each part. Firstly, group 8 estimated the radius of the semicircle to be 16 m, as was concluded in the first part of the activity carried out at the square near the school. The students drew the outer semicircular shape of a part of the theater. Then, following the classical rules of construction, which indicated to give to the
orchestra part of the building a value of 5 m, they drew it. They subsequently simulated the
frons scaena and the
scaena, which corresponds to a polygon that closes the perimeter of the theater on the opposite side. They extended two straight lines tangent to the semicircle of the outer perimeter of the
cavea, drawing a perpendicular to both, as shown in
Figure 4. Next, they drew, between the external circumference (corresponding to the
cavea) and the internal one (corresponding to the
orchestra), other circumferences distanced at 0.74 m (equivalent to 2.5 feet), which corresponds to the classical proportions of construction. Group 8 correctly interpreted that each of these circumferences represented one tier (or terrace) in the
cavea (or bleacher) where Roman citizens sat to watch the performance.
Once the model was built using GeoGebra, the teachers asked some new questions to help the students reject the hypothesis of the circus and validate the hypothesis of the theater: Does the built model fit properly into the dimensional layout of the area where the ruins were found? How can we evaluate how well it fits?
To answer these questions, the students superimposed a simulation of the theater they had drawn using GeoGebra onto the archaeological site plan (which showed the details and contours of the ruins) adapting the scale and checking whether the contours fit or not.
Figure 4b shows the proposal of group 8. This group, like others in the class, pivoted their model until they thought the theater simulation was in an appropriate position according to what was shown on the real map. In other words, the students thought it necessary to
validate ([Mf] and [I6]) the model simulation with respect to reality, in this case the real map.
The fact that the GeoGebra model fit the site plan did not validate (or disprove) the hypothesis of the circus. Since the process of fitting the model meant it had to be reduced or enlarged beyond its form, it was necessary to check if the resulting model continued to meet the characteristics of a Roman theater set out by Vitruvius, such as its location (theater exits had to be placed next to city squares) or (that had to continue to comply with several building rules after applying the scale of the map to the building). The students performed these checks appropriately, obtaining the answer to the questions proposed by the teachers and, consequently, validating the hypothesis that the wall might have belonged to a Roman theater.
At this point of the inquiry, the students were asked to compare their conclusions with the results obtained by the team of archaeologists of the local museum so as to validate their answers and processes followed with external experts [I6]. To this end, a meeting was scheduled with the main archaeologist, P. Padrós, who was responsible for the discovery of the real ruins. Each team prepared some questions to interview her. The students’ questions were about the archaeologist’s discoveries to check their own results. She answered all the questions and showed interest in the students’ work.
She also offered new historical information on the theater in the city of Baetulo, such as the estimated population in the first century before the common era (BCE) when the theater was already in operation, the location of the city wall and its gates in relation to the theater, etc. One of the gates was located close by, supposedly so the theater could welcome people from neighboring towns.
Thanks to the archaeologist’s new contributions and after sharing this information, the students were able to answer the inquiry’s initial and main question. They argued that the Roman wall belonged to a Roman theater, which meant the inquiry could be considered as concluded. However, the archaeologist had sparked off new questions related to the details of her team’s current research process and this led to a new cycle of inquiry. For example, the students wanted to calculate the capacity of their theater model to re-evaluate it, checking whether it coincided with that obtained by the archaeological experts. This means that the situation was again problematized ([I1] and [Ma]) and new questions were posed: What was the theater’s occupant capacity? How many people could it hold?
A new cycle of inquiry was initiated to look for possible answers regarding the occupant capacity of the theater [I2]. Baetulo’s population (approximate data provided by the archaeologist) was taken into account to formulate new hypotheses [I3] on the theater’s maximum occupancy to meet the needs of the inhabitants of Baetulo. Historical data were collected to estimate the number of inhabitants out of the total population that would usually have gone to the theater: for example, what type of performances were planned, to which audience were the performances addressed—only to adults or to children, to what social classes, etc. In this way, a hypothesis was formulated only based, like in the first stage, on inquiry processes of historical content looking for information about other similar Roman theaters in Spain, such as Pollentia (in Mallorca) or theaters in Málaga.
To validate their hypotheses, the students devised an
action plan [I4] based on completing the model built in the second stage of the previous cycle with a drawing of the essential details (such as stands, stairs, access, evacuation corridors, etc.) to calculate the number of seats. They continually took the proportions recommended by Vitruvius into account. Group 8, for instance, counted how many rows there were present in their model. They had considered a total of 15 rows (see
Figure 4a). Then, using their model, they calculated the approximate length of each of the semicircles that represented a stand of the
cavea. With this information, they estimated how many people could sit in the theater, assuming that two people could be seated in 1 square meter.
This meant a new model had to be prepared to systematize [Mb] the data, to mathematize [Mc] them, to analyze [Md] them, and obtain new results to be validated based on the real archaeological context. The students performed a graphical analysis of the resulting new model [Me], based on the determining elements of the theater’s capacity (number of stands, distance between stands, space between spectators, location, number of stairs and entrances, etc.). Several groups made some adjustments with regard to the capacity. For instance, they took into account that it was likely that the first stand was reserved for senators and other important people in the city and that they were therefore supposed to have more space to sit there. Again, historical and archaeological data were enriched by mathematical data, and vice versa. Both kinds of data and models had to be combined to obtain relevant answers.
The model that emerged from this second modeling process based on the new archaeological and historical data and Vitruvius’ rules enabled quantifying the theater’s capacity. All the inquiry teams obtained similar results on the approximation of this capacity, which oscillated between 878 and 1100 spectators. This result, together with the new model, was interpreted and validated [Me] with respect to the real work of the experts, the archaeologists. The students, guided by their history teacher, concluded that the theater seemed to be able to hold more spectators than expected, taking into account Baetulo’s population at that time. This exceeded the students’ initial hypothesis. However, taking into account the information provided by the archaeologist of the museum, this result was consistent with the fact that the theater welcomed inhabitants from neighboring towns. Finally, once all the inquiry teams had shared their work, the students drew up their inquiry report with the aim of communicating their results and providing their answers to the questions posed throughout the process [I7]. During this collective process, new questions emerged that could have led to new cycles of inquiry, accompanied by new modeling processes, but mainly due to time constraints, it could not be further extended. At the end of the implementation, for instance, some questions emerged about if the way to inquire into the Roman theater model here studied could help to model and explain other ruins found around the world.
7. Conclusions
To analyze inquiry processes and modeling processes we could use either one of the pre-existing analytical models for each type of process, which correspond to specific conceptualizations of what inquiry and modeling consist of, could be used. However, the models proposed for inquiry do not consider some important processes characteristic of mathematical modeling, such as the mathematization or the systematization processes. Consequently, none of these models allowed us to adopt an integrative approach concerning inquiry and modeling developed when students are involved in open-disciplinary and ground-breaking teaching projects. We thus aimed at building an integrative model, presented in this paper, that integrates all these aspects and that enables us to perform the joint analysis of inquiry and modeling within the empirical context of our implementation.
To do so, first, we adopted the proposal put forward by Blomhøj [
20] to analyze the mathematical modeling processes and the model formulated by Sala Sebastià [
28] for the inquiry processes. We then used these two models to analyze the presence of these processes in the implementation of an interdisciplinary teaching sequence, which was designed for students to develop inquiry. Our aim was also to look for coincidences, concatenations and synergies, established between both processes.
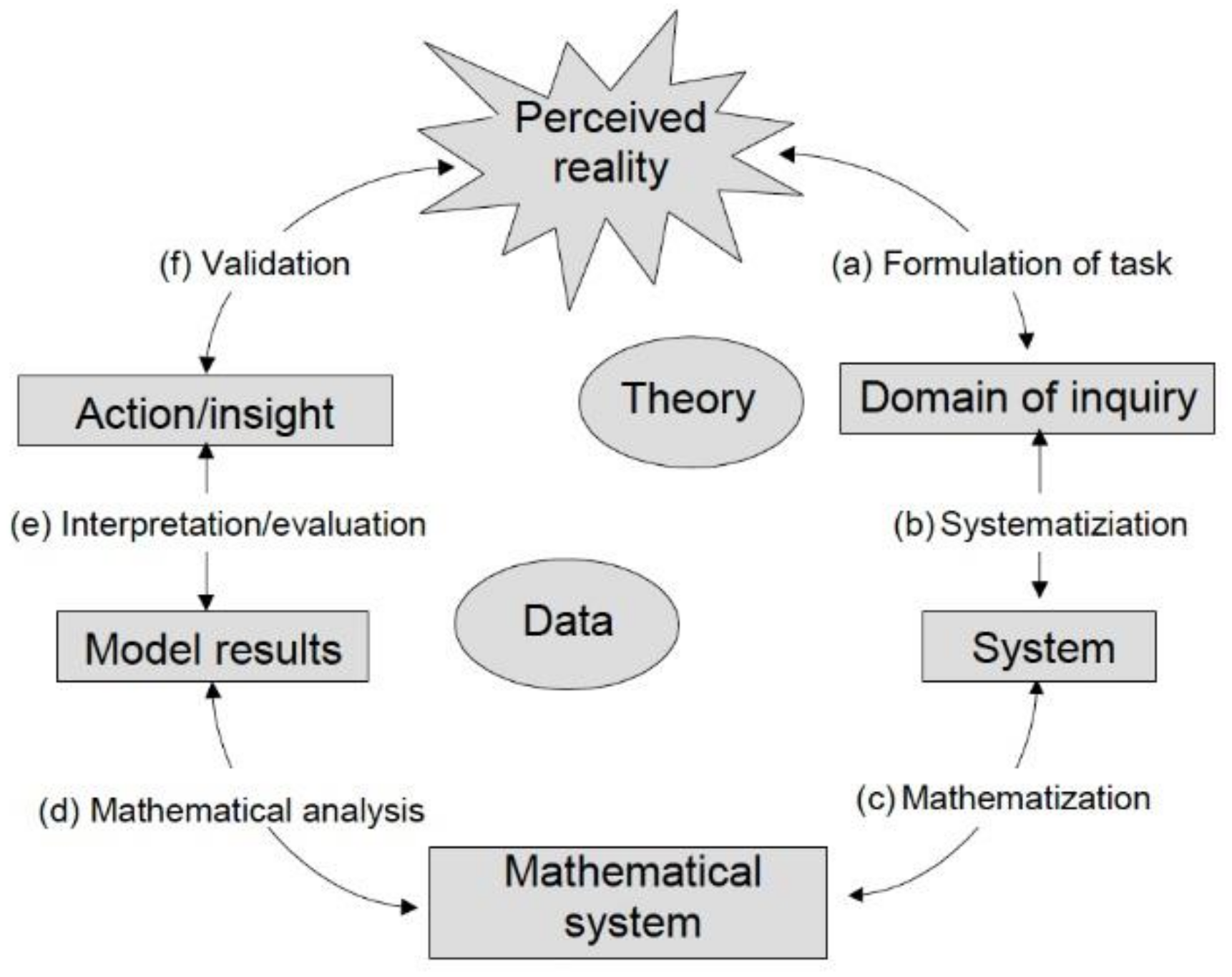
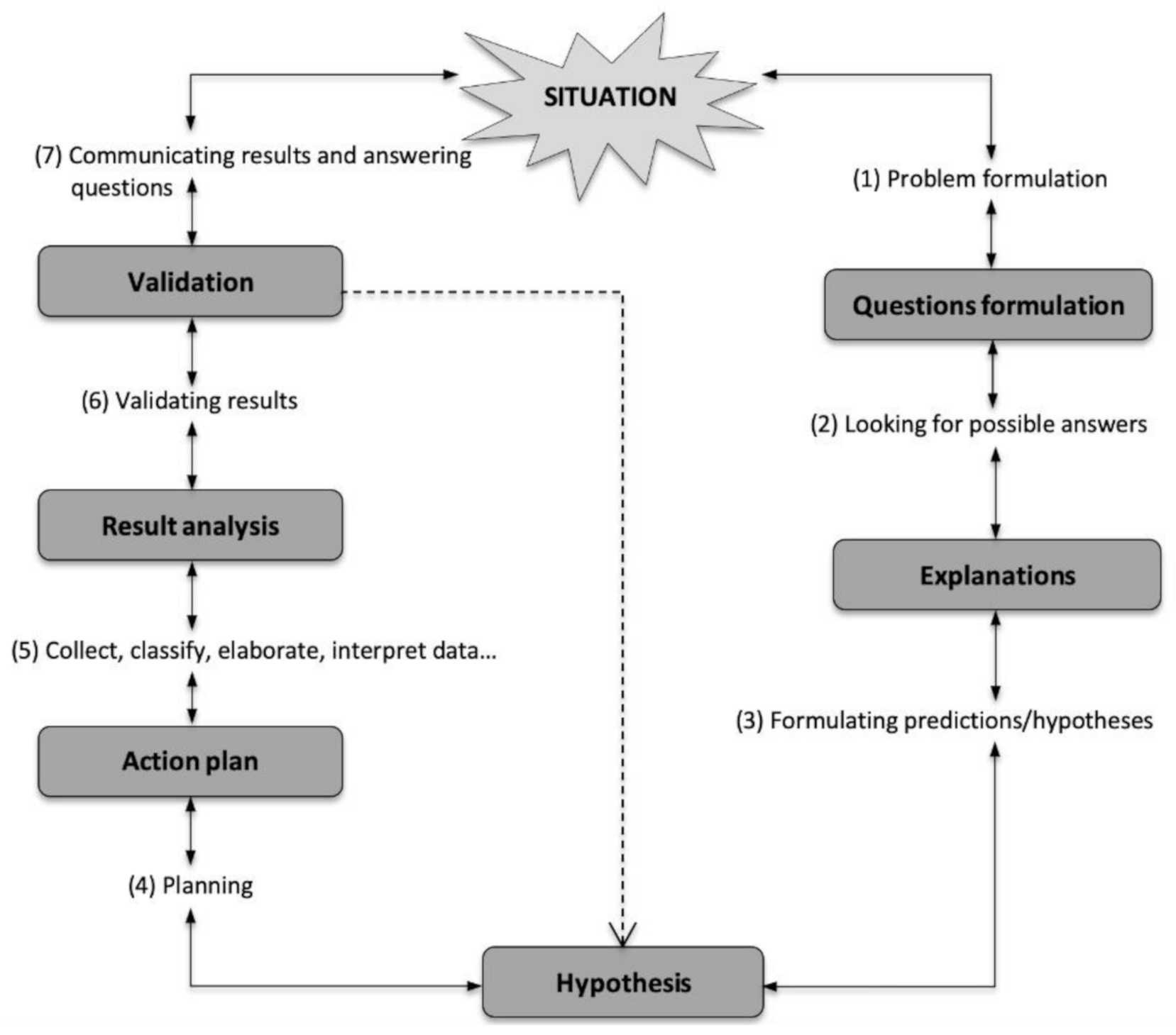
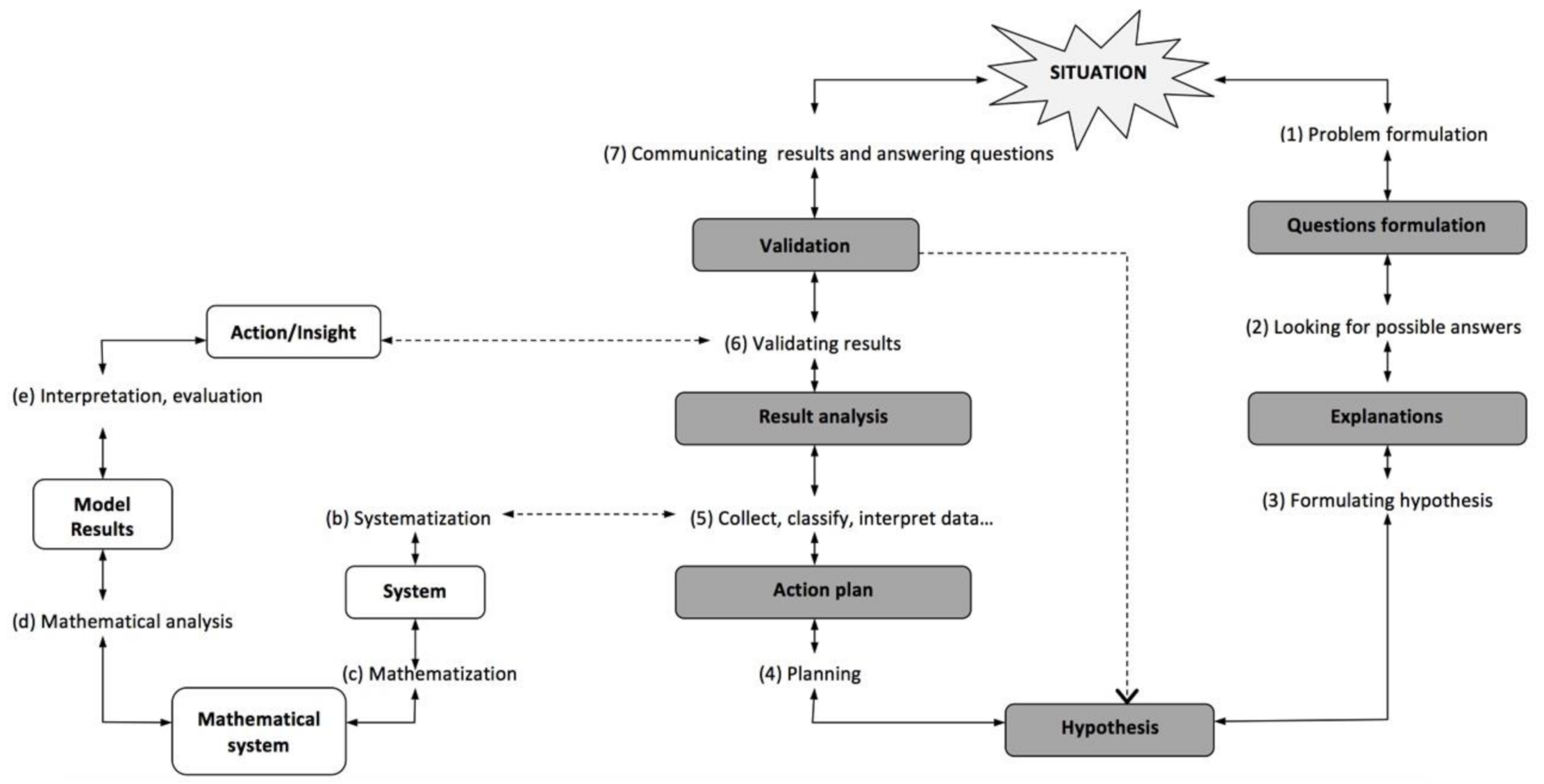
Based on this analysis, we obtained the relationships between the two processes shown in
Figure 5. These relationships led us to propose a model (
Figure 6) that integrates both processes here considered. The sub-processes corresponding to an inquiry cycle, in accordance with the model used by Sala Sebastià [
28], are represented on the right in
Figure 6. In the analysis of the teaching sequence, we observed that both processes begin with the
problematization ([Ma] and [I1]) of a real-life situation, as we have seen in the implementation analyzed. After the emergence of some derived questions [I2], a process is initiated to look for answer to them—which could correspond to the so-called
domain of inquiry in the Blomhøj [
20] diagram (
Figure 1). We consider that, at this point, both cycles could be connected.
Different
hypotheses can be considered (sub-process 3 in
Figure 3 and
Figure 6) and, in order to validate them—or reject them—, an action plan is drawn up (sub-process 4 in
Figure 3 and
Figure 6) to
collect data and
select relevant data in order to
classify, organize and interpret them (sub-process 5 in
Figure 3 and
Figure 6). Modeling can come into play at this stage when looking for the validation of the hypotheses under consideration. The inquiry cycle could again be connected with a modeling cycle (on the left in
Figure 6) in the 5 sub-processes, when the students carried out the inquiry and had to mathematize the data collected—as we have seen in the implementation analysis—. This connection is shown in
Figure 6 by a horizontal dotted arrow. The left part of
Figure 6 displays the cycle of modeling, adapted from the original model of Blomhøj [
20].
The proposed integrative model (
Figure 6) shows how the modeling cycle is initiated after the sub-process (5)—sub-process (b) on the left part in
Figure 6 corresponding to the
systematization of the data for its subsequent
mathematization (sub-process c). Next come the sub-processes including the
mathematical analysis (sub-process d), and the
interpretation and/or
evaluation of the resulting model. This sub-process is another shared characteristic (shown by another horizontal dotted arrow) between the two cycles.
Validation is a common sub-process in the two cycles: it is sub-process f of the modeling (in
Figure 1) and sub-process 6 of the inquiry (in
Figure 3). In both processes, as observed in the analysis of the implementation, this step consists in validating the constructed model. Its validity is evaluated taking into account the inquiry context, data and/or theoretical knowledge and personal or shared experience. When the model is not validated and it needs to be either improved or rejected, or a different model needs to be built, the modeling cycle can start again from sub-process 5 based on the
collection of new data or a previous sub-process (see the vertical dotted arrow inside the cycle of inquiry in
Figure 6), with the
formulation of new hypotheses. Once the validation stage of the model(s) is completed, the sub-process consisting in
communicating results begins (sub-process 7 in
Figure 6) during which questions from the initial problem are answered. At this stage, at the end of the cycle of inquiry, it is likely–and desirable–that new
questions be generated in relation to the initial problem thus launching new cycles of inquiry.
We consider the integrative model presented in this section useful to analyze other teaching proposals originated in other kinds of interdisciplinary contexts for inquiry. It can also be used as a descriptive and analytical tool, and as a design-oriented tool to help provide a blended view of inquiry and mathematical modeling. In these terms, this work could constitute a significant contribution to the field.