2.1. Time Cycle Theory and Division of Time
Definition 1. Price (point) of a stock (index).Let the price of a stock per daybe a function of date.
P.S. Based on the fact that we only focused on indices in this paper, we did not distinguish between the price and the point, the stock and the stock index.
Definition 2. Extreme point of range. Extreme point of rangeis an extreme point over n days before and after, t is a date. We call it an n-day extreme point, where n is an integer, i.e.,
If:
, is a high n-day extreme point;
, is a low n-day extreme point.
Usually, we call them both n-day extreme points in brief.
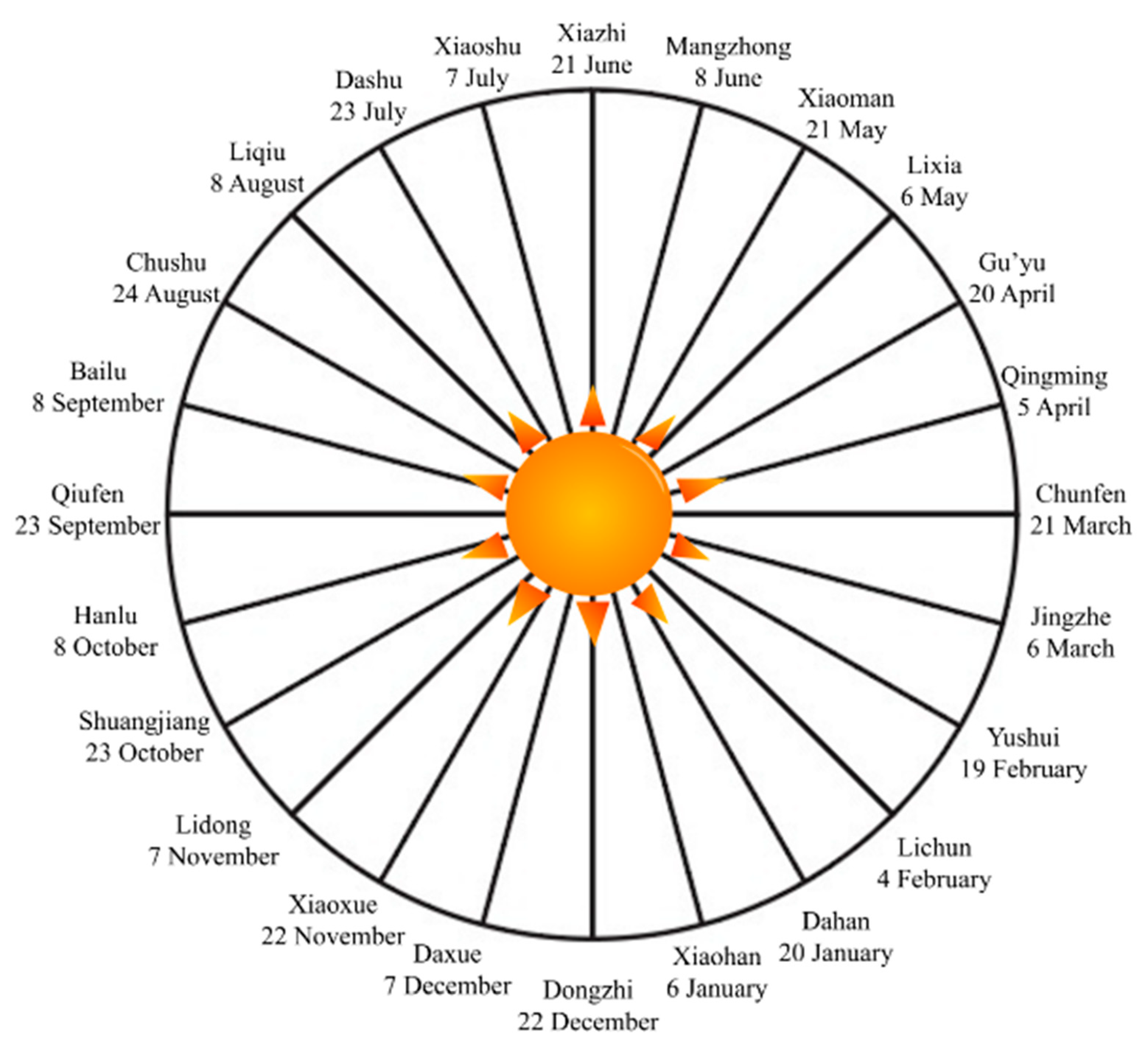
The names of these 24 solar terms are only shown in pinyin and the readers can easily find the explanations online (
Table 1). Every solar term has its significant and irreplaceable meaning in the Chinese culture.
What is more, the names of solar terms in the table are ordered according to the Chinese lunar calendar, where Lichun is the first term in a lunar year, Yushui is the second term and Dahan is the last term. However, for convenience, the numbering of solar terms is according to the international solar calendar, in which Xiaohan is the first, happening around 5 January each year while Dongzhi is the last, taking place near 22 December each year. The order above is just for convenience in later mathematical equations.
Definition 3. Strong turning point. When n = 20, we call an n-day extreme point a strong turning point
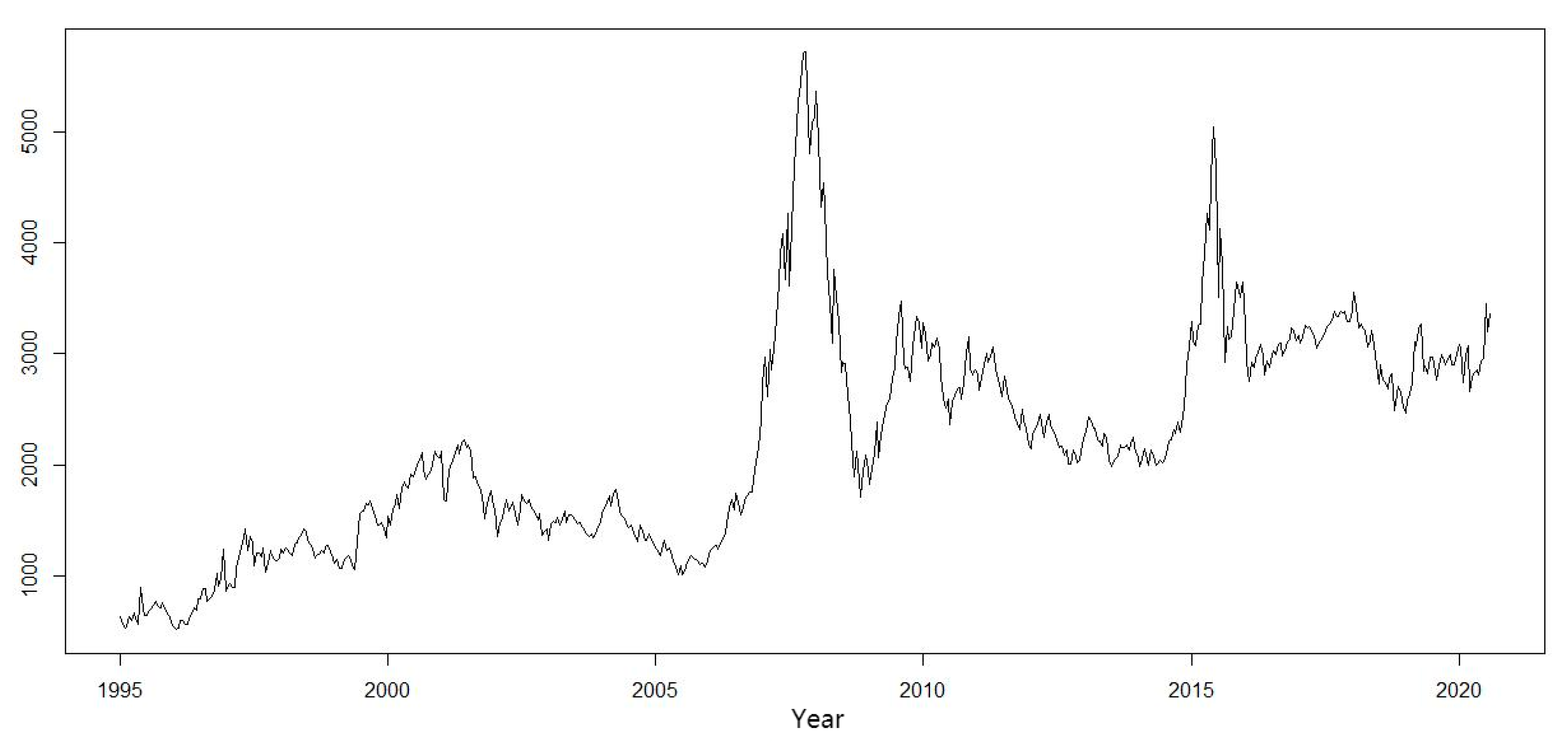
We finally screened out 174 strong turning points. The sequence of strong turning points is , k = 1, 2, 3…, 174; 6436 daily closing prices of the Shanghai Index were taken from 3 January 1995 to 14 August 2020 (the day this study began); the sequence is , n = 1, 2, 3…, 6436, representing the order of market trading days.
We then fitted the daily price based on the interpolation of these 174 strong turning points:
For the adjacent solar points
, we set up a linear polynomial:
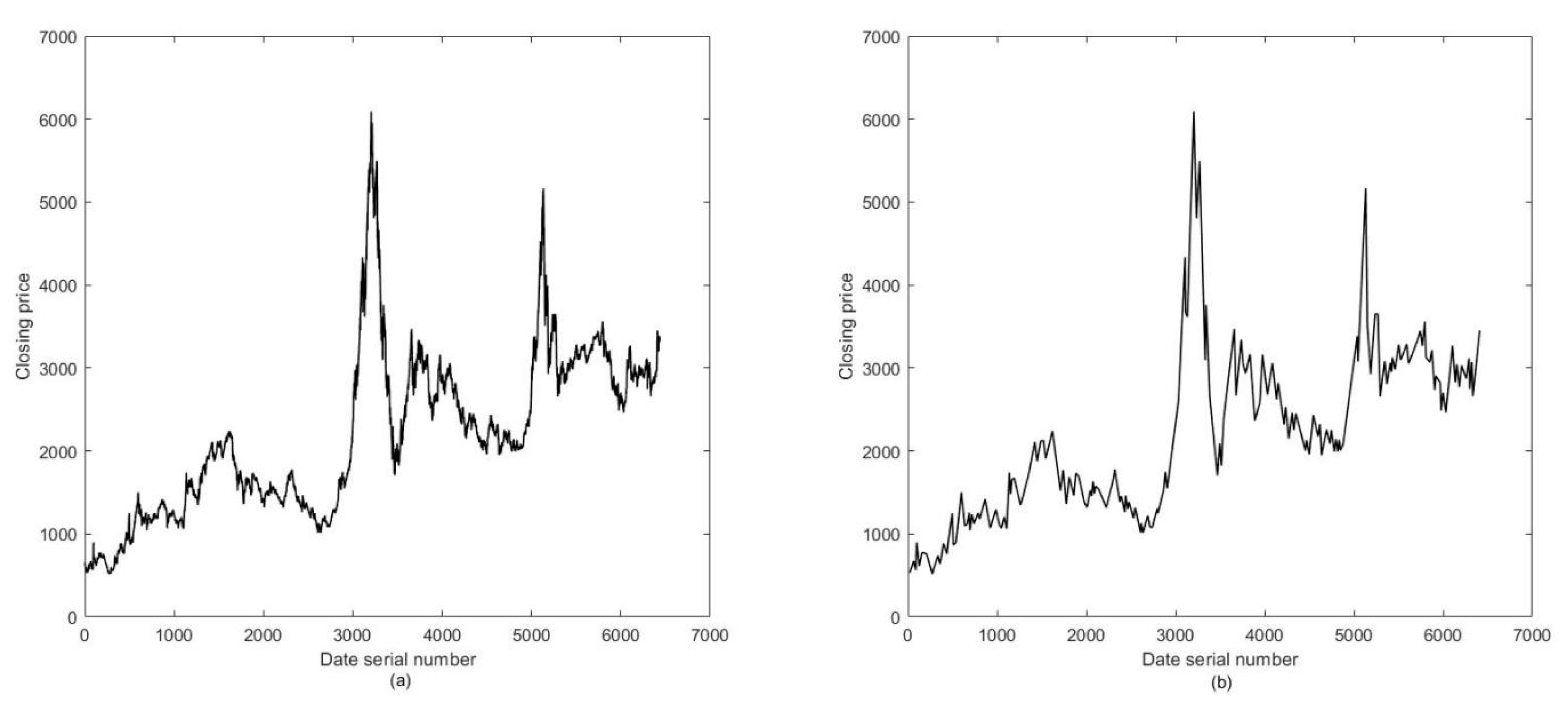
Altogether, from all , we eventually obtained 6436 interpolated price data (including 174 strong turning points themselves).
We obtained the correlation coefficient
0.9878
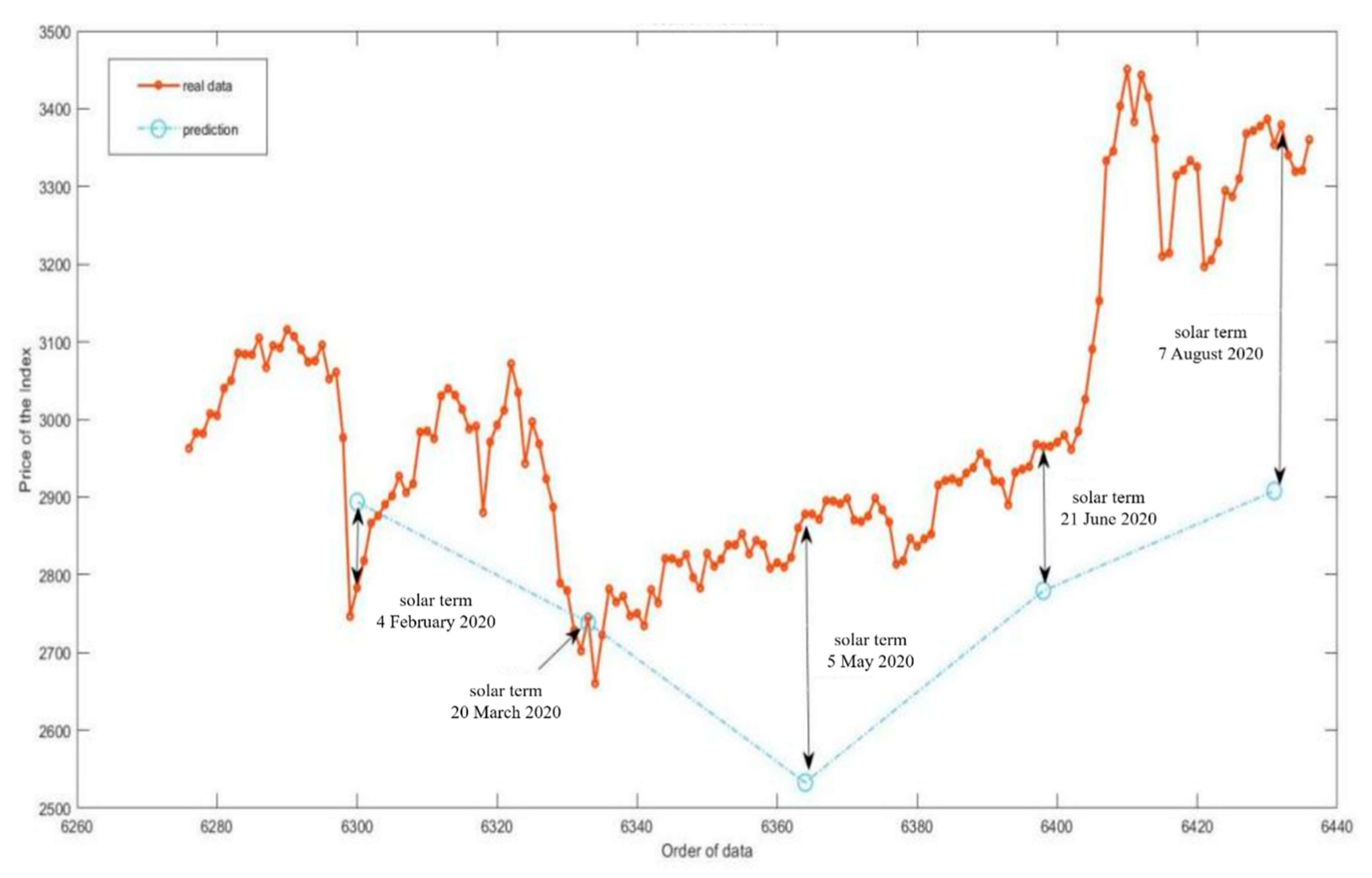
We refined 174 strong turning points to replace 6436 daily price data, which seems to lose a great portion of information; however, it appeared that the 174 strong turning points could still fit the trend of the index in the previous 25 years well. That was because most of the daily price data simply belonged to the link between two adjacent extreme points (may have been strong turning points) and did not have extra information (i.e., every trend had already been presented by two extreme points). Instead, more meaningless price data only bring in more instability, volatility and error that may interfere with the investors’ observations (
Figure 3).
That provides a reference for long-term investors: when the price does not reach the extent of a strong turning point (in fact, we often choose n = 10 or 15 for different terms of investment), the index would not have a strong reversal, and the investor can keep holding their stock. When the index goes over or falls below this extent, one would better not expect it to restore soon and it is a time to buy or to sell.
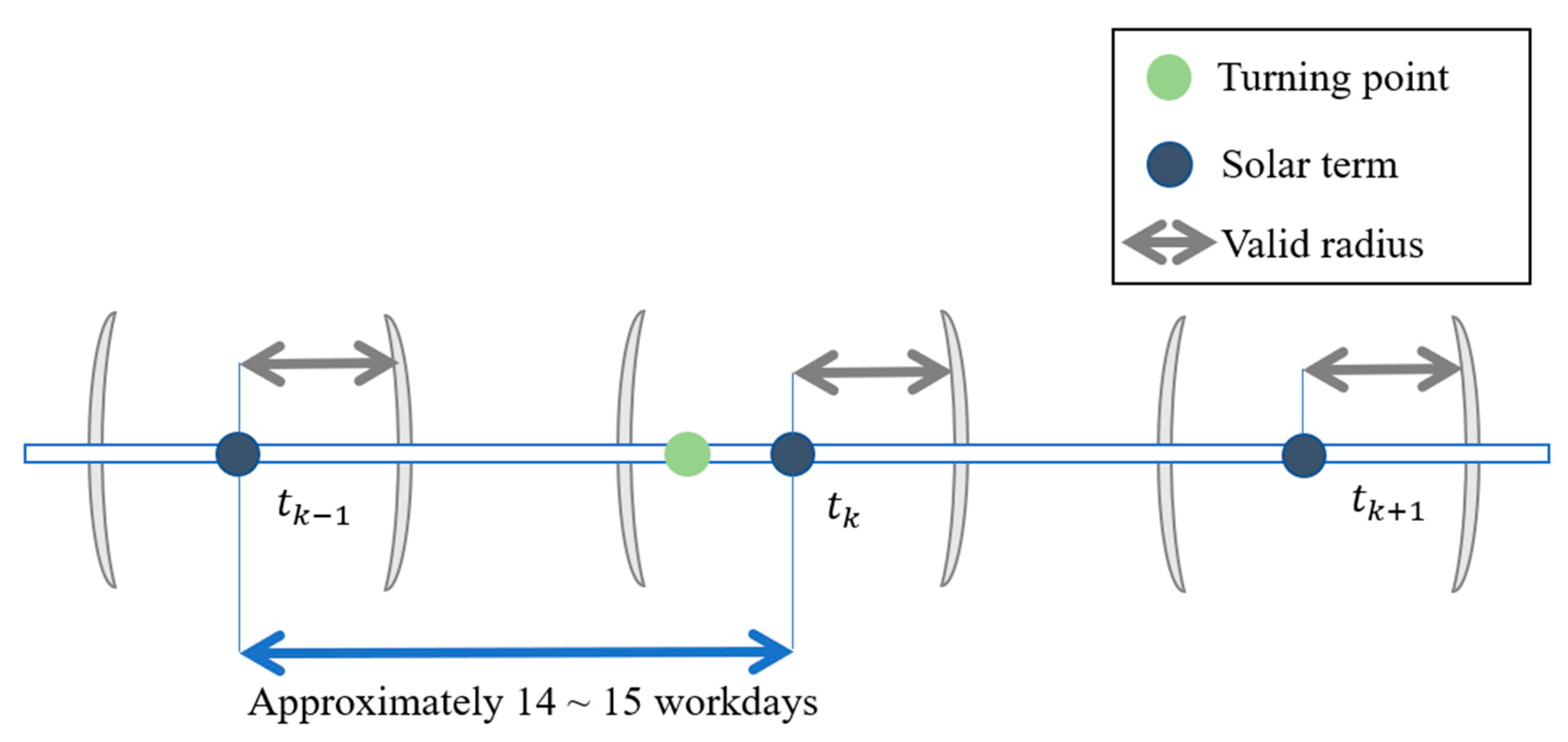
Definition 4. Valid time radius: m-day valid time radius: when an n-day extreme point is close to the nearest solar term point within m days (before or after), we believe that this n-day extreme point is related to that solar term point and the solar term is valid (Figure 4). 2.2. Valid Extreme Point
TQ refers to the total quantity of n-day extreme points of a stock index while VQ stands for the valid extreme points among those total n-day extreme points. We then used the proportion to estimate the probability of validity (p = proportion = VQ/TQ) which means the probability of p that a solar term causes the reversal of the trend of the stock index.
The result of the China Second Board Index was similar to the Shanghai index, and that showed the applicability to Chinese stock indices.
In the medium-term and long-term stock investment, the radius conditions of three days and four days were enough to provide a strong reference for investment strategy. The n-day extreme points of different n values often occurred near the solar term point, and investors should pay more attention to the three or four days before and after the solar term. If the price is too high (too low), then we need to be alert. After several verifications with different n, the proportions were similar where the probability was over 80% with the 4-day valid time radius while it only occupies a half of the days between two solar terms (i.e., 4 days before and after occupy 8 days in 15 workdays between adjacent solar terms).
In this way, we supposed that solar terms have an impact on the stock trend and it is like damping, forcing the stock trend to turn or at least hinder its present trend status. With a solar term every 15 days, the stock trend was suggested to have a major change, forming what we saw, ups and downs in serrated fluctuations.
In this section, we verified that a turn or a reversal (i.e., an n-day extreme point, n ≥ 5) always occurred near solar terms.
2.3. Alert Period
In this chapter, we show a practical example of how to react and make actual stock index investment decisions. As we confirmed before, predicting a certain price is almost impossible; thus, we estimated a relative index. Furthermore, we needed to be dynamic, which meant that every movement and change was possible, and we did not set up a goal that it will rise or fall by a specific time; the philosophy is that we judge by the present status, as well as welcome the use of news and other message for assistance.
Based on the efficient markets theory (Eugene Fama, 1970), we were not able to predict the absolute price, but with the statistics above, we were able to provide a relative trend-turning strategy, in which we assess the n value in every daily closing price in the recent days to make dynamic qualitative analysis of the probability of reversal of the coming solar term.
As time goes forward, when it comes to 4 days before a coming solar term, we are in the alert period and when we are 4 days after this solar term, we are out of the alert period.
The period at most lasts for 8 to 9 days but may end earlier if there’s already a significant reversal (or turning point) taking place during the period. As time moves ahead, combine the biggest n value so far in the present alert period and the quantity of the remaining days in the present period; the probability of forecasting whether there is a reversal of the present trend in the period (or turning point) converges to 100%.
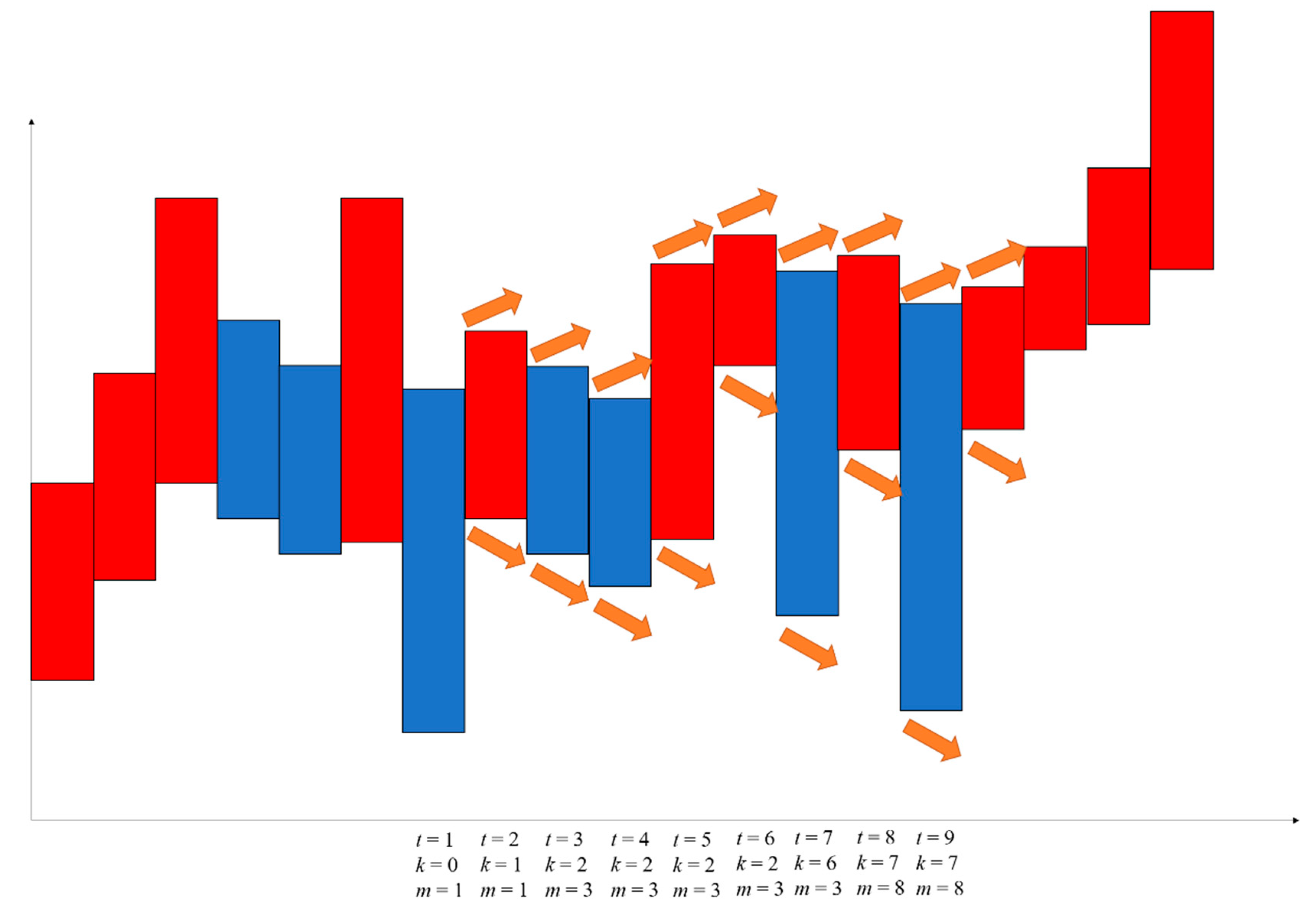
Event stands for the predictability of the existence of n-day extreme points in one alert period of a solar term. Right now is No.t day of the present alert period.
Event stands for no significant reversal of the trend in the first k days in the alert period.
Event stands for the biggest n value of the n-day extreme point in the present alert period which we call m for clarity (if the stock index enters an alert period after rising, then we only focus on the low n-day extreme point to be m, and vice versa.)
P.S. only means the possibility to make a right judgement or forecast of the trend reversal (i.e., there are n-day extreme points or not) rather than to predict the existence of n-day extreme points. The word “predictability” makes a big difference in the definition. The n value is chosen by investors according to their investment term.
For long-term investment, we suggest it to be over 15, for medium-term investment, it should be around 10, and for short-term investors,
n can be around 5.
Generally, the alert period of each solar term is no more than 9 days (i.e., 4 days after, 4 days before plus the solar term itself)
In fact, when we use the concept of conditional expectations above, the real probability in the statistics
Table 2 and
Table 3 is much higher.
The equation provides a dynamic qualitative analysis as we are never sure about the real P(A) under and which appears not to contradict the efficient markets theory. The stock market contains both relative rules and absolute irregularity at the same time. The best for investor is to use the relative rules as much as possible.
The orange arrows mean the probability to rise or fall and the longer an arrow is, the higher the probability it stands for.
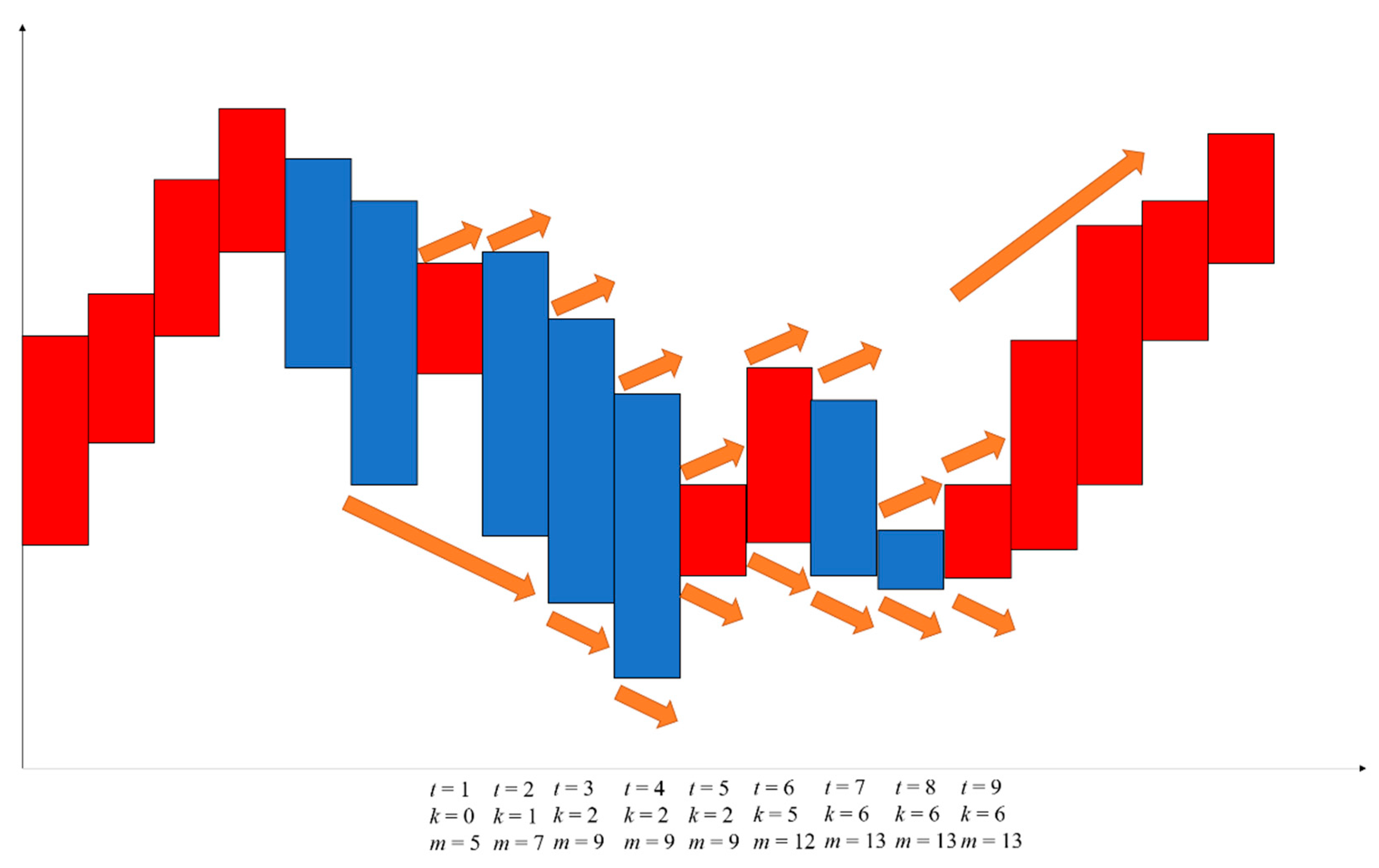
This is a virtual case; we made it to better explain our strategy and vividly show how our method works in real trade (
Figure 5 and
Figure 6).
In that case, we found that the actual reversal point (actually, it was a 13-day extreme point) reached the m value of 13 where the price was much lower than that outside the alert period; it also had a very long time to another similar low price.
As the m value becomes bigger and the time is closing to the solar term, we suppose that the possibility of reversal is higher. There may be several signals to show the potential turns and reversal such as t = 5 (goes high after a very low price with a large m value) and t = 9 (the actual turning point). Therefore, the decision should be made dynamically, according to the m and k values in the past. Significant reversals in the alert period are always the real reversal points in stock indices.
Figure 6 shows a very frequent case where the index does not have a reversal near the solar term; although there are high price and low price when
t = 3 or
t = 7, it is not low enough compared with a recent extreme point (e.g., the day before
t = 1 and 5 days before
t = 1). Despite the fact that
t = 3 or
t = 7 correspond to the two lowest prices in the alert period, there are other lower prices outside the period very close to them, so they do not work.
The case contradicts the common sense, that is, buying on the low and selling on the high; the case proved it only in the alert period, and it is necessary to assess it not according to how many days the stock has been falling in total, but combine the m value it creates with the distance to the solar term.
In other words, while getting closer to the solar term, there is a higher possibility to have a reversal of the trend, but if the biggest n is not so big so far, the probability is always low no matter how close to or far from the solar term it is. The conclusion turns out to be a turbulence but not a reversal or turning point and, in this way, investors can hold their stock at least until the next alert period and the stock index will keep its trend like before the alert period.