Abstract
Graph theory is a powerful representation and problem-solving tool, but it is not included in present curriculum at school levels. In this study we perform a didactic proposal based in graph theory, to provide students useful and motivational tools for problem solving. The participants, who were highly skilled in mathematics, worked on map coloring, Eulerian cycles, star polygons and other related topics. The program included six sessions in a workshop format and four creative sessions where participants invented their own mathematical challenges. Throughout the experience they applied a wide range of strategies to solve problems, such as look for a pattern, counting strategies or draw the associated graph, among others. In addition, they created as challenges the same type of problems posed in workshops. We conclude that graph theory successfully increases motivation of participants towards mathematics and allows the appearance and enforcement of problem-solving strategies.
1. Introduction
In this paper we show the results of the implementation of the didactic proposal developed in [1] with minor changes. We state main previous results and briefly sketch the structure of the proposal. All details can be found in [1]. In this proposal we introduce graph theory [2] for gifted primary school students as a motivational tool of representation and problem solving. This could be a first step to finally include graph theory at school levels.
A graph is a set of vertices (points) with some of them connected by edges (lines). Graph theory is not included in current school curriculum in Spain, neither in primary nor secondary education [3,4]. In other countries, discrete mathematics is proposed to be included in school levels [5] and highly recommended for students aged between 5 and 18 years old [6,7].
Several authors suggest the inclusion of graph theory at school and highlight its importance as a tool to model real-life situations, learn mathematical styles of thinking and solve problems [8,9,10]. In this line, some experimental studies have been carried out, especially with secondary education students, but there are hardly any experiences with primary education or gifted students. We mention here previous work with primary education students.
Starting from map coloring [8], an experience with students aged between 5 and 14 years old is presented in [11]. They propose that map coloring activities for this age range should be ordered by level of difficulty but neither their methodology nor results are clearly presented. They conclude students can translate a map into a graph from 7 years old, and when over 9 years old they can construct the graph corresponding to a map and color it.
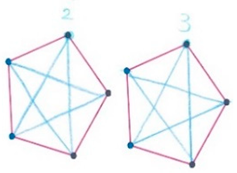
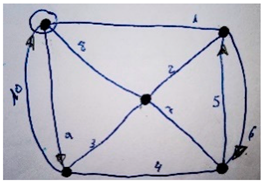
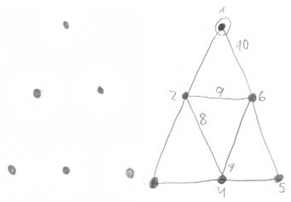
In Italy, some teaching experiments have been performed. About fifty 8–9 year old students participated in 12 sessions, one weekly meeting along 3 months, involving Eulerian and semi-Eulerian graphs, Hamiltonian graphs, planar graphs and graph coloring [12]. Using the laboratorian methodology, the authors propose activities such as problems to be solved with the help of paper and pencil, and online games such as YED Graph Editor. They claim that most students were able to solve the activities, increased their logical skills and active participation in class, and moreover, after this experience, they understood mathematics as a game. Following this line of work, in [13] they present an approach to mathematics and connections of mathematics with real life by means of Eulerian graphs. Contents treated with primary education students include definition of graph, planar graph, vertex coloring, Eulerian graph, and Hamiltonian graph. A planar graph is a graph that can be drawn with no crossing edges. A Eulerian graph is a graph having a Eulerian cycle, that is a closed path (starting and finishing in the same vertex) passing only once for every edge, although it is allowed to pass more than one time for the vertices. A Hamiltonian graph is a graph having a Hamiltonian cycle, that is, a closed path passing only once for every vertex. Figure 1 shows several examples of these types of graphs. At the end of the experience, students were able to recognize main parts of a graph, draw and represent a graph, solve problems using graphs, and they found graphs were fun and motivating.

Figure 1.
Basic graphs. Examples of (a) graph; (b) planar graph; (c) nonplanar graph; (d) Eulerian graph; (e) non-Eulerian graph; (f) Eulerian graph, but non-Hamiltonian graph; (g) Hamiltonian graph, non-Eulerian graph.
A learning trajectory to teach Eulerian paths is developed in [14]. An outdoor didactical approach is used to give the participants a realistic point of view of the mathematics involved in the classical Köningsberg bridges problem [8], that it is used to motivate and introduce graphs. They use a combination of maps and paper and pencil activities to lead the students to a better understanding of the existence or not of a Eulerian path (a path passing only once for every edge) inside a graph. Along the experience they notice an improvement of collaborative problem-solving skills in the students.
Graph theory [2] can be introduced in different ways, such as map coloring or Eulerian paths, among others. Our proposal aligns with this classical approach, it begins with map coloring, posed as a challenge to solve, and carries on with Eulerian cycles, we further relate graphs with classical handshake problem [15] and other applications of graphs.
The original proposal developed in [1] is structured in four stages according to the teaching–learning methodology of Dienes [16]. The first activity is presented as a challenge (Adaptation), followed by some activities to practice the new concept with concrete examples (Structuring); then the student should be able to abstract the underlying mathematical concepts (Abstraction), and finally he/she reasons about what has been learned, discovering connections to other mathematical concepts (Reasoning). Table 1 summarizes activities and sessions proposed at each stage.

Table 1.
Sessions, topics and activities in the original proposal.
This proposal aims to work individually with each participant, using a methodology based on the Pólya problem-solving model [17], posing questions that guide the participant in solving the problem. All the detailed questions that can be used throughout the experience can be found in [1]. This proposal [1] is designed for students 8 years and older.
Here, we briefly describe proposed activities. We started with map coloring, asking the participant if he/she could color the map of Spain with as few colors as possible, such that neighboring regions do not have the same color. This motivates the appearance of the associated graph to the map; we suggested setting a point in every region and joining points in neighboring regions with a line. In the second session, we presented the Köningsberg bridges problem and suggested the use of graphs after a few unsuccessful attempts. In the third session, we presented Eulerian cycles by giving the participant some examples to check and then proposing him/her to create more Eulerian and non-Eulerian cycles. In the fourth session, we posed the handshake problem (see Appendix A), and in the last session we worked on drawing star polygons and related this topic to the previous one by counting the edges of the star polygons.
Two gifted students of 8 and 9 years old participated in the exploratory phase of the study. They correctly carried out the proposed tasks, showing great interest in them, but having some difficulties in some parts. This led us to make some changes to the original didactic proposal. The results of this exploratory study were presented in [18].
Our main goal is to encourage the use of graphs as a tool for representation and problem solving in primary education classrooms from a playful perspective. As a first step, we implemented this proposal with primary education students having high skills in mathematics, as part of an enrichment program. This experience provided students with suitable mathematical contents to improve the development of their problem-solving skills.
2. Materials and Methods
2.1. Description of the Settings
The experience was developed inside an enrichment program during the 2018/2019 academic year. Weekly sessions of 45 min in format of workshops were performed with 7 participants, within school hours, outside the normal classroom. The program included graph theory, classical problems of combinatory, logic, probability and geometry using a wide range of manipulative resources to motivate participants. Results obtained with manipulatives can be found in [19].
The original proposal [1] was intended to be developed individually with each participant, so we adapted the work situation to make it suitable for 7 participants working at the same time. When a question is settled, participants start attacking the problem individually, and after a while, they work in collaborative groups. We distributed participants in 3 groups using age criteria. Participants with the same age (or very close) were assigned to the same group. Youngest participants worked mainly in a group (G1 group). Workshops alternated with sessions where participants invented their own mathematical challenges. Working in groups, they had to propose a challenge and a suitable solution two weeks later, uploading the problem and its solution to a web page available for all students at their school.
Our proposal is structured following the teaching stages of the Dienes teaching–learning methodology [16].
- Initial challenge (Adaptation): Activity posed as a challenge aimed to create curiosity in the students so that they want to learn about the subject.
- Practice of the new concept (Structuring): We use graphs to represent routes or pathways under certain conditions.
- Abstraction (Abstraction): Graphs are used to solve a problem of greater difficulty than previous ones, where more abstract mathematical processes appear, in this case induction and generalization.
- Closing activities (Reasoning): The objective is to relate the graphs that were studied with other mathematical concepts.
The methodology employed in every workshop is inspired by the Pólya problem-solving model [17]. We pose a question as a challenge and let the participants try to solve it freely, then, we go on by giving some hint, and we continue asking them new questions. We avoid theoretical explanations and formal definitions; the students build the concepts involved and their own knowledge in a guided learning process.
The sessions and topics treated are summarized in Table 2, together with activities proposed to participants. We have modified the order of some activities with respect to the original proposal explained in [1] (suitable for students aged 8 and over) to make it accessible for younger participants, simplifying the structuring stage and extending the reasoning phase. We decided to vary the order of the activities according to their degree of difficulty, moving the Köningsberg bridges problem to the last stage. We also lowered the degree of difficulty of some activities. A description of activities proposed and basic definitions can be found in Appendix A.

Table 2.
Sessions, topics and activities.
2.2. Description of the Participants
The participants belong to a public school, located in Toledo (Castilla-La Mancha, Spain), and were selected by faculty because of their high academic performance in mathematics. Participants do not have a formal diagnosis of giftedness, but both their teachers and their families agree that they have great creativity, learn faster than mates, like to investigate tasks that interest them, and go beyond what is proposed in the classroom. Therefore, they meet characteristics appropriate of gifted people [20,21]. Table 3 shows data for the participants. Following age criteria, the participants were organized into 3 groups (Table 3).

Table 3.
Participants.
3. Results
In the following sections, we describe the results obtained during the experience.
3.1. Map Coloring
The first session was devoted to map coloring. Figure 2 and Figure 3 show the first attempt of coloring the map of Spain [22] with as few colors as possible, such that neighboring regions do not have the same color. Participants A3 and A6 use five colors and participant A4 uses four colors, but two neighboring regions have the same color. Students A3 and A4 make several efforts to complete the map with four colors.

Figure 2.
First attempt of coloring the map of Spain. Drawing made by participant: (a) A3; (b) A6; (c) A4.
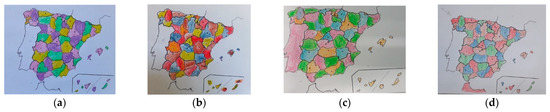
Figure 3.
First attempt of coloring the map of Spain. Drawing made by participant: (a) A1; (b) A2 (orange is yellow); (c) A5; (d) A7.
The other participants color the map with four colors starting from left to right, from top to bottom or using the same color and jumping from one region to another.
Then, they are asked to draw a continuous line joining all regions such that regions with same color are not directly joined. They use the previous map and try to join the points without lifting the pencil from the paper. Participants A1, A4 and A6 do not get a cycle, as seen in Figure 4. Participant A4 even forgets some regions.
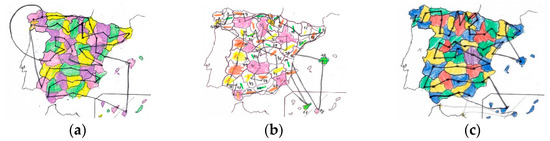
Figure 4.
Failed attempt of Eulerian cycle. Drawing made by participant: (a) A1; (b) A4; (c) A6.
However, all participants understood the problem, they do not draw a cycle because the first and last region of the path both have the same color (pink in A1 drawing, red in A4 drawing, blue in A6 drawing). The other participants draw a Eulerian cycle, as seen in Figure 5.
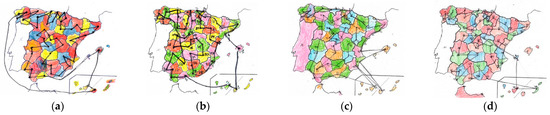
Figure 5.
Example of Eulerian cycle. Drawing made by participant: (a) A2; (b) A3; (c) A5; (d) A7.
We can observe several strategies to draw the cycle. Some participants labeled the vertices (A3, A4, A5 and A7); they go from left to right, going up and down; going from exterior regions to interior regions (A4 and A5). The cycle made by participant A2 is the only one that follows an ordered pattern with no crossing edges (planar graph). All participants looked for patterns as a problem-solving strategy.
3.2. Star Polygons
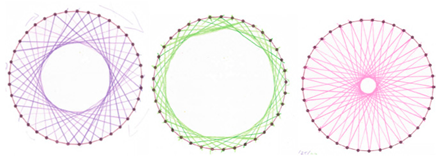
Using a template with regular polygons of 4, 5, 9, 17 and 37 edges, we ask participants to draw star polygons by jumping a certain number of vertices without lifting the pencil from the paper. They choose jumps randomly, even larger than the number of vertices of the polygon. Figure 6 shows several examples. Participants A1, A2 and A3 only work with a pentagon and enneagon. All participants draw the star polygon 5/2 inside the pentagon, but only A1, A2, A3 and A7 find 9/2 and 9/4 inside the enneagon.
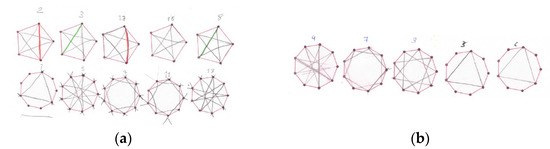
Figure 6.
Star polygons. Drawing made by participant: (a) A2 (similar to the one made by A1); (b) A3.
In the case of 17 and 37 edges, participants A4, A5, A6 and A7 obtain some star polygons, the findings of A6 and A7 being more elaborated, as shown in Figure 7.

Figure 7.
Star polygons. Drawing made by participant: (a) A4; (b) A5; (c) A6; (d) A7.
Now we ask participants (except A1 and A2) why they think we get the same star polygons with different jump numbers. They try several wrong arguments: because the jump is a prime number, the jump is a multiple of a certain number, some jumps are even numbers and others are odd numbers, etc. Only A3 reaches the correct answer arguing over the enneagon, concluding that a jump of 2 vertices gives the same star polygon as a jump of 7 vertices because 7 + 2 = 9 (and repeats the same argument for 4 + 5 = 9; 3 + 6 = 9).
Participants used the trial and error method as a problem-solving strategy; however, they fail to generalize their conclusions. Only one participant, A3, found the correct answer in the particular case of the enneagon, although he does not verify this result with the other regular polygons.
3.3. Give Me Five
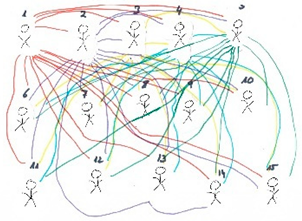
We reformulate the handshake problem, giving to the students a list of questions to solve (see Appendix A), including how many times 2, 3, 4, 5, 9, 17 and 27 people high-five when they meet. In the last question, they were asked to explain the process followed to get the results.
All participants use a drawing to support a counting strategy, but not all of them discover a correct counting pattern. Figure 8 shows drawings made by participants that reach best performance.

Figure 8.
Counting strategies. Drawing made by participant: (a) A6; (b) A1.
As shown in Figure 8, participants A6 and A1 use graphs to count the number of high fives, counting the edges between points in cases where the number of people is small. When they realize that every person greets the number of people minus one (participant A1 even writes it) they employ an inductive counting strategy. Participant A1 needs some help to perform the computations and finally uses a calculator.
Participant A5 uses induction but finds a wrong pattern, adding all the numbers from the given number of people until 1. The other participants give some correct answers, but they do not reach the use of induction. Figure 9 shows their performance from highest (Figure 9a, participant A5) to lowest (Figure 9e, participant A4).
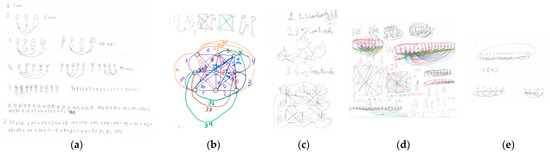
Figure 9.
Counting strategies. Drawing made by participant: (a) A5; (b) A2; (c) A3; (d) A7; (e) A4.
3.4. Path Tracing/Eulerian Cycles
We explain to them the meaning of Eulerian cycle (see Appendix A). Next, we ask them to draw a graph with a Eulerian cycle stating the number of edges left out or arriving to each vertex, in a set of six vertices. Figure 10 summarizes the answers given by the participants. They surround the starting vertex with a circle, except participant A7.
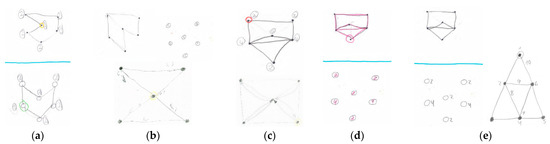
Figure 10.
Tracing Eulerian cycles. Drawing made by participant: (a) A3; (b) A5; (c) A4; (d) A6; (e) A7.
Afterward, we gather their work in common, and every participant shows and explains his/her graphs to the others. We then encourage them to create more graphs with Eulerian cycles and other graphs with no Eulerian cycles. We show some of the created graphs in Figure 10.
We give to the participants a template with nine points (see Appendix A) and ask them to join all the points using only four straight lines, without lifting the pencil from the paper and crossing only once through each edge. All participants solve the puzzle correctly, except participants A1 and A2 who do it with help of the researcher.
Participants use the trial and error method again, together with use of symmetry.
In this session and the following ones, participants A1 and A2 solve all the activities with the help of the researcher; therefore, we do not include the rest of their performance.
3.5. Seven Bridges of Köningsberg
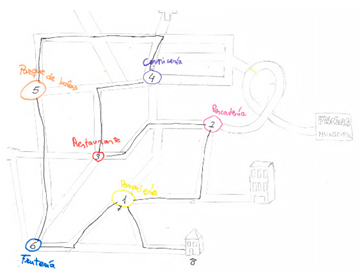
After telling the story of the Seven Bridges of Köningsberg, we give the participants an image [23] with the representation of the city and pose some questions (see Appendix A). Figure 11 shows the participants’ attempts to find a closed walking path through the four areas of the city, crossing each bridge only once (Eulerian cycle).

Figure 11.
Köningsberg bridges. Drawing made by participant: (a) A7; (b) A6; (c) A5; (d) A3; (e) A4.
Only participants A7 and A6 set a dot in every region and draw the associated graph to the city map. The other participants forget to connect some points or they focus directly on the bridges and do not consider points to mark each region. However, all participants affirm that is not possible to cross the city in that way. They apply the associated graph to the problem, and use the guess-and-check method and direct reasoning as problem-solving strategies.
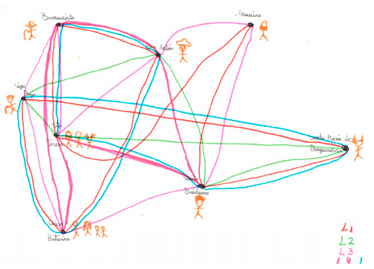
When we ask if they observe any differences between their first/last vertex chosen and other vertices, all of them say yes. We ask them to count the number of edges that leave out or reach to each vertex (degree of a vertex) and what should be the number of edges passing though each vertex for such path to be possible. That is, how many times would it be necessary to cross every bridge to complete a closed path across all the bridges (at least once). Figure 12 summarizes answers given by students, where they drew the associated graph indicating the paths. All of them conclude that the number of edges must be an even number.

Figure 12.
Graphs associated with Köningsberg bridges. Drawing made by participant: (a) A6; (b) A7; (c) A5; (d) A3; (e) A4.
3.6. Chess Routes
We motivate the activity by showing a chess set, reminding the rules for moving each chess piece. Then, we let the participants practice the different movements on the chessboard. Later, we give a drawn chessboard [24] to the participants and ask if the knight can go through all the squares, passing only once through each one. That is, we are asking the participants to find a Hamiltonian graph. Answers given by participants are collected in Figure 13 and ordered by achievement; none of them manages to complete the tour.
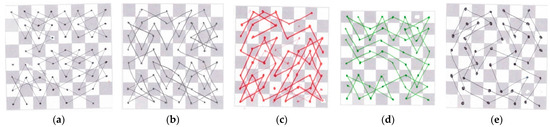
Figure 13.
Chess routes with a knight. Drawing made by participant: (a) A5; (b) A7; (c) A3; (d) A4; (e) A6.
In Figure 13, we can observe that the best performance is reached by participant A5. Repeating some patterns, A5 is able to pass through almost all squares. Participant A7 is also able to pass through all squares around a chosen one, but forgets to go through that one, although at the end gets a connected graph. A5 and A6 get a graph with two nonconnected components, and A3 and A4 get more than two components. All of them except A6 follow some patterns and repeat them along the chessboard. A6 makes some mistakes joining the vertices, following a wrong knight movement.
After the knight, we let them choose another chess piece and try again, and in this case, some of them are able to complete the path. Results can be seen in Figure 14, ordered by achievement. We observe that participants A5, A3 and A7 choose a pattern to complete the path along the chessboard. Participants A4 and A6, however, do not choose a pattern and therefore cannot complete the path, missing some squares or passing twice through some of them.
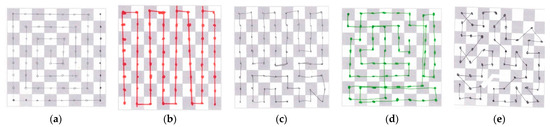
Figure 14.
Chess routes. Drawing made by participant: (a) A5 using a rook; (b) A3 using a rook; (c) A7 using the queen; (d) A4 using a rook; (e) A6 using the king.
Participants show good performance looking for patterns and apply them to solve the problem. Some of them also use symmetry as a problem-solving strategy.
3.7. Mathematical Challenges
Challenges were created by participants working in groups. They start by brainstorming and then choose an idea as a challenge; they write it, solve it and finally they record a video with the question and another one with the answer. Proposals involving graph theory are collected in Table 4.

Table 4.
Challenges posed by participants.
As observed in Table 4, participants create similar activities to that ones already solved during the experience, using analogy, simplification and variation of the original problems.
All groups pose challenges consisting of drawing star polygons; G2 and G3 do it in two of the challenges. All groups use routes and cycles or Eulerian cycles, or problems joining points, but only G1 creates a challenge similar to the handshake problem (challenge number 3).
These activities created by participants prove that they are able to apply the learned knowledge to similar situations as the ones already solved.
4. Discussion
In the first activity, all participants except A6 color the map with four colors. This matches with results of [11], where all participants color correctly between three and six different maps after several attempts. To perform the activities, they start looking for a pattern to successfully color the map with four colors. To highlight the patterns followed, we ask them to draw a Eulerian cycle. All of them understand the problem and use patterns to carry out the activity.
The next two sessions offer an original approach which differs from those found in previous work [11,12,13,14]. In the second session, we use star polygons to practice Eulerian cycles. Only one participant generalizes his results, but all participants understand the notion of star polygon. In the third session, we apply graphs to solve the handshake problem. Participants develop graph-supported counting strategies and some of them successfully use induction. The results of both sessions show that graphs can be used to develop and support other thinking strategies such as generalization and induction.
The reasoning stage is mainly devoted to deepening the understanding of Eulerian paths and cycles; Hamiltonian graphs appear briefly in the last session. We finally explain the definition of Eulerian cycle and propose to the participants some activities to distinguish Eulerian and non-Eulerian cycles before presenting the Köningsberg bridges problem, which is frequently used in the literature to introduce graphs [12,13,14].
In [12], the author introduces the notion of a graph with this problem and guides the students to solve it using graphs as a mathematical model. Keeping the problem unsolved during some lessons motivates the curiosity of participants, but when the author explains the concept of Eulerian cycle, some participants get confused and think that all the graphs fulfill the condition.
Our approach avoids this confusion; all participants understand the notion of degree of a vertex and draw different examples of Eulerian graphs before tackling the Köningsberg bridges problem. All the participants affirm that it is impossible to find such a path, and some of them use the associated graph with the problem by themselves.
Therefore, our findings are in line with the previous results obtained by other authors, who state that graphs increased the logical abilities of the participants [12]; they were able to draw and represent graphs and to solve problems using graphs [13].
Moreover, our results prove that graphs have also brought out other problem-solving strategies, which have not been described in previous studies.
The involvement of the participants in the challenges shows that they have enjoyed the experience, so we have fulfilled the objective of motivating them through graph theory, as was also shown in previous research [12,13].
5. Conclusions
As we have seen throughout the activities performed by the participants, they have applied several strategies for problem solving, such as look for a pattern, trial and error method, counting strategies, induction, use symmetry, associated graph, guess and check method and direct reasoning.
Introducing the concept of graphs and some basic results of graph theory allowed participants to graphically represent abstract situations and develop several problem-solving strategies.
They also created their own problems by analogy, using a simpler problem, related problem or variation of the problem. This is also evidence of learning by imitation. Participants propose similar activities to those worked during workshops, simplifying them when they found it difficult to solve them.
Challenge 3 also shows that participants applied graph theory to real-life problems, making mathematical connections through graphs, relating mathematics to everyday life situations.
Graphs are shown to be a useful and powerful tool for increasing participants’ problem-solving skills and their motivation towards mathematics.
It would be necessary to review the reasoning phase to adapt it to participants less than 8 years of age. Futures lines of research include the implementation of the didactic proposal inside an ordinary classroom, in order to check if similar problem-solving strategies arise.
Author Contributions
Conceptualization, R.B.; methodology, R.B. and M.G.-M.; validation, R.B. and M.G.-M.; formal analysis, R.B. and M.G.-M.; investigation, M.G.-M.; resources, M.G.-M.; data curation, M.G.-M.; writing—original draft preparation, R.B.; writing—review and editing, R.B. and M.G.-M.; visualization, R.B. and M.G.-M.; supervision, R.B.; project administration, R.B.; funding acquisition, R.B. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by Ministerio de Ciencia e Innovación (PID2019-105677RB-100/AEI/10.13039/501100011033); Departamento de Matemáticas, Universidad de Castilla-La Mancha; UCLM, grant number 2019-GRIN-27026 and 2020-GRIN-28809. M.G.-M. was partially funded by Junta de Comunidades de Castilla-La Mancha (PREJCCM2019/7).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
Authors thank the collaborating public school, participants and their families for their invaluable help in carrying out this research.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this section, we briefly explain activities proposed to participants and sketch some basic definitions; more details about graph theory can be found, for example, in [2] or [8].
Four color theorem states that it is possible to color any geographical map with four colors, such that neighboring regions do not have the same color. In session 1, we ask participants if they can color the map of Spain with as few colors as possible. The map of Spain that we have used can be found in [22]. Next, we introduce the idea of graph and cycle asking them to draw a continuous line joining all regions such that regions with the same color are not directly joined. This implies looking for a path that jumps from one region to another, and they use dots that are already marked on the map to complete the path without forgetting any region.
Graphs can be walkable, describing paths that go from one vertex to another. A path is, therefore, a set of vertices connected by edges. The idea of cycle and Eulerian cycle also appear here. A cycle is a closed path, starting and finishing in the same vertex; and a Eulerian cycle is a closed path passing only once for every edge, although it is allowed to pass more than one time for the vertices. Graphs which can be drawn with no crossing edges are planar graphs.
A star polygon is a polygon obtained by joining nonconsecutive vertices in a regular polygon, that is, jumping 2 by 2, 3 by 3, … and going through all vertices, such that we can draw it without lifting the pencil from the paper. This jump is called polygon density and the usual notation is n/q, where n is the number of vertices of the regular polygon and q is the polygon density. For example, 5/2 is a five-pointed star inside a pentagon. Star polygons can be seen as graphs, and in fact, as Eulerian cycles. The star polygon n/(n − q) is the same as n/q because orientation does not matter when we draw star polygons.
Star polygons have a wide collection of interesting properties; some examples with hexagon and octagon can be seen in [26].
Handshake problem or Party problem [15] (p. 60) is a classical combinatorial problem saying that if there are n people in a room and they all shake hands, how many handshakes are there? We adapt the problem to school context by changing handshakes to high fives. In session 3, we give the following list of questions to the participants:
- How many times 2 people high-five when they meet?
- How many times 3 people high-five when they meet?
- How many times 4 people high-five when they meet?
- How many times 5 people high-five when they meet?
- How many times 9 people high-five when they meet?
- How many times 17 people high-five when they meet?
- How many times 27 people high-five when they meet?
- How did you get the answers?
We expected participants to use graphs to represent the problem and cause the use of induction. The computation of this number using induction gives us the sum of 1 + 2 + 3 + 4 + … + (n − 1) high fives, counting for 2 people (1 high five), 3 people (1 + 2) and so on.
Complete graphs [2] also appear here. A complete graph is one where every pair of vertices is connected by an edge. A complete graph of n vertices has n(n − 1)/2 edges because each vertex is connected with all the others, that is, (n − 1), so we have n(n − 1) edges, but we need to divide by 2 to avoid counting them twice. If we draw the associated graph representing the high five problem, we get a complete graph, so it is possible to compute the number of high fives using the previous formula. Both formulas coincide.
In session 4, we introduce the definition of Eulerian cycle and let the notion of degree of a vertex arise. The degree of a vertex is the number of edges leaving out or entering that vertex. This notion becomes necessary for the next session.
Session 5 is devoted to the Seven Bridges of Köningsberg problem [2,8] solved by Leonhard Euler, in what gave birth to graph theory. Köningsberg city (Kaliningrad currently) has a river called Pregel that divides the city in 4 zones joined by 7 bridges. The problem is to find a closed path walking through the 4 areas of the city, crossing each bridge only once. Euler proved that this is impossible by drawing a graph representing the problem and concluding that the problem has no solution because all vertices have odd degree. Such a path is called a Eulerian cycle in his honor.
We start the session with the story of the Seven Bridges of Köningsberg and give one illustration [23] to students. Then, we pose some questions:
- Can you find a way walking through the 4 areas of the city, crossing each bridge only once and going back to the starting point?
- Can you see any difference between the starting point and the other ones?
- Count the number of edges leaving out or arriving at each vertex.
- How many times would it be necessary to cross every bridge to complete a closed path going through all the bridges (at least once).
In session 6, we pose a problem involving chess routes [8] (p. 108). After introducing the activity, we give to the participants an image with a chessboard [24] and ask them:
- Can the knight go through all the squares, passing only once through each one? Can you prove it?
- Now choose the chess piece you prefer and try again.
- These ways described by chess pieces are Hamiltonian paths. A Hamiltonian path is a path (nonclosed path) passing only once for every vertex.
References
- Blanco, R.; García-Moya, M. Actividades con grafos para estudiantes con AACC. Edma 0-6 2019, 8, 92–108. [Google Scholar]
- Wilson, R.J. Introduction to Graph Theory; Longman Group Ltd.: Essex, UK, 1996. [Google Scholar]
- BOE (03/01/2014). Real Decreto 126/2014, del 28 de Febrero, por el que se Establece el Currículo Básico de la Educación Primaria. Available online: https://www.boe.es/eli/es/rd/2014/02/28/126/con (accessed on 2 July 2021).
- BOE (03/01/2015). Real Decreto 1105/2014, de 26 de Diciembre, por el que se Establece el Currículo Básico de la Educación Secundaria Obligatoria y del Bachillerato. Available online: https://www.boe.es/eli/es/rd/2014/12/26/1105/con (accessed on 2 July 2021).
- Rosentein, J.; Franzblau, D.; Roberts, F. (Eds). Discrete Mathematics in the Schools; DIMACS Series in Discrete Mathematics Computer Science; American Mathematical Society (AMS): Providence, RI, USA, 1997; Volume 36. [Google Scholar]
- National Council of Teachers of Mathematics. Curriculum and Evaluation Standards for School Mathematics; The Council: Reston, VA, USA, 1989; Available online: http://www.standards.nctm.org/index.htm (accessed on 1 April 2021).
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics; The Council: Reston, VA, USA, 2000; Available online: http://www.standards.nctm.org/index.htm (accessed on 1 April 2021).
- Alsina, C. Mapas del Metro y Redes Neuronales: La Teoría de Grafos; RBA Coleccionables, S.A.: Barcelona, Spain, 2010. [Google Scholar]
- Coriat, M.; Sancho, J.; Marín, A.; Gonzalvo, P. Nudos y Nexos. Redes en la Escuela; Síntesis: Madrid, Spain, 1989. [Google Scholar]
- Niman, J. Graph Theory in the Elementary School. Educ. Stud. Math. 1975, 6, 351–373. [Google Scholar] [CrossRef]
- Braicovich, T.; Cognigni, R. Coloreando la geografía desde el plano al toroide. Números 2011, 76, 135–148. [Google Scholar]
- Ferrarello, D. Graphs in primary school: Playing with technology. In Mathematics and technology, Advances in Mathematics Education; Aldon, G., Hitt, F., Bazzini, L., Gellert, U., Eds.; Springer: Cham, Switzerland, 2017; pp. 143–169. [Google Scholar] [CrossRef]
- Ferrarello, D.; Mammana, M.F. Graph Theory in Primary, Middle, and High School. In Teaching and Learning Discrete Mathematics Worldwide: Curriculum and Research; Hart, E., Sandefur, J., Eds.; ICME-13 Monographs; Springer: Cham, Switzerland, 2018; pp. 183–200. [Google Scholar] [CrossRef]
- Gaio, A.; Branchetti, L.; Capone, R. Learning Math Outdoors: Graph Theory using Maps. In Research on Outdoor STEM Education in the Digital Age, Proceedings of the ROSETA Online Conference in June 2020; Ludwig, M., Jablonski, S., Caldeira, A., Moura, A., Eds.; Ludwig, M., Jablonski, S., Caldeira, A., Moura, A., Eds.; WTM: Münster, Germany, 2020; pp. 95–102. [Google Scholar] [CrossRef]
- D’Angelo, J.P.; West, D.B. Mathematical Thinking: Problem-Solving and Proofs; Prentice-Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Dienes, Z.P. Las Seis Etapas del Aprendizaje de Matemáticas; Teide: Barcelona, Spain, 1977. [Google Scholar]
- Pólya, G. How to Solve It: A New Aspect of Mathematical Method; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Blanco, R.; García-Moya, M. Propuesta didáctica para introducir la teoría de grafos en educación primaria. In Proceedings of the 8th International Congress of Educational Sciences and Development, Pontevedra, Spain, 28–30 October 2020; Bermúdez, M.P., Ed.; Asociación Española de Psicología Conductual (AEPC): Granada, Spain; p. 58. ISBN 978-84-09-19786-6.
- García-Moya, M.; Blanco, R.; Fernández-Cézar, R. Matemáticas manipulativas y alto rendimiento. In Inclusión, Tecnología y Sociedad: Investigación e Innovación en Educación; Marín Marín, J.A., Gómez García, G., Ramos Navas-Parejo, M., Campos Soto, M.N., Eds.; Editorial Dykinson: Madrid, Spain, 2019; pp. 2264–2277. ISBN 978-84-1324-491-4. [Google Scholar]
- Martínez Torres, M. Características del alumnado con altas capacidades. In Altas Capacidades Intelectuales. Pautas de Actuación, Orientación, Intervención y Evaluación en El Periodo Escolar; Torres Martínez, M., Guirado, Á., Eds.; Graó: Barcelona, Spain, 2012; pp. 71–118. [Google Scholar]
- Renzulli, J.S. El concepto de los tres anillos de la superdotación: Un modelo de desarrollo para una productividad creativa. In Intervención e Investigación Psicoeducativa en Alumnos Superdotados; Benito, Y., Ed.; Amarú Ediciones: Salamanca, Spain, 1994; pp. 41–78. [Google Scholar]
- Pinterest. Available online: https://www.pinterest.es/pin/785737466221794150/ (accessed on 22 May 2021).
- Grupo Alquerque. Available online: http://www.grupoalquerque.es/ferias/2016/archivos/puentes/puentes_h1.pdf (accessed on 22 May 2021).
- FreePrintable. Available online: https://www.freeprintable.com/free-printables/blank-chess-board (accessed on 22 May 2021).
- Dibujos. Available online: https://geografia-espanola.dibujos.net/castilla-la-mancha.html (accessed on 22 May 2021).
- Fernández, I.; Reyes, E. Geometría con El Hexágono y El Octógono: Papiroflexia, Proporciones, Disecciones, Cuadraturas, Mosaicos, Geometría Sagrada; Proyecto Sur, D.L.: Armilla, Spain, 2003. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).