In this section, the proposed algorithm is used to solve classification and image restoration problems. The performance of Algorithm 9 is evaluated and compared with Algorithms 3, 5, and 6.
4.1. Data Classification
Data classification is a major branch of problems in machine learning, which is an application of artificial intelligence (AI) possessing the ability to learn and improve from experience without being programmed. In this work, we focused on one particular learning technique called
extreme learning machine (ELM) introduced by Huang et al. [
29]. It is defined as follows.
Let
be a training set of
N samples, where
is an
input and
is a
target. The output of ELM with
M hidden nodes and activation function
G is defined by:
where
is the weight vector connecting the
i-th hidden node and the input node,
is the weight vector connecting the
i-th hidden node and the output node, and
is the bias. The hidden layer output matrix
is formulated as:
The main goal of ELM is to find an optimal weight such that where is the training set. If the Moore–Penrose generalized inverse of exists, then is the desired solution. However, in general cases, may not exist or be challenging to find. Hence, to avoid such difficulties, we applied the concept of convex minimization to find without relying on .
To prevent overfitting, we used the
least absolute shrinkage and selection operator (LASSO) [
30], formulated as follows:
where
is a regularization parameter. In the setting of convex minimization, we set
and
.
Iris dataset [
31]: Each sample in this dataset has four attributes, and the set contains three classes with fifty samples for each type.
Heart disease dataset [
32]: This dataset contains 303 samples, each of which has 13 attributes. In this dataset, we classified two classes of data.
Wine dataset [
33]: In this dataset, we classified three classes of one-hundred seventy-eight samples. Each sample contained 13 attributes.
In all experiments, we used the sigmoid as the activation function with the number of hidden nodes
The accuracy of the output is calculated by:
We also utilized 10-fold cross-validation to evaluate the performance of each algorithm and used the
average accuracy as the evaluation tool. It is defined as follows:
where
N is the number of sets considered during cross-validation (
),
is the number of correctly predicted data at fold
i, and
is the number of all data at fold
i.
We used 10-fold cross-validation to split the data into training sets and testing sets; more information can be seen in
Table 1.
All parameters of Algorithms 3, 5, 6 and 9 were chosen as in
Table 2.
The inertial parameters
of Algorithm 9 may vary depending on the dataset, since some
work well on specific datasets. We used the following two choices of
in our experiments.
The regularization parameters for each dataset and algorithm were chosen to prevent overfitting, i.e., a model obtained from the algorithm achieves high accuracy on the training set, but low accuracy on the testing set in comparison, so it cannot be used to predict the unknown data. It is known that when is too large, the model tends to underfit, i.e., low accuracy on the training set, and cannot be used to predict the future data. On the other hand, if is too small, then it may not be enough to prevent a model from overfitting. In our experiment, for each algorithm, we chose a set of that satisfies , where and are the average accuracy of the training set and testing set, respectively. Under this criterion, we can prevent the studied models from overfitting. Then, from these candidates, we chose , which yields high for each algorithm. Therefore, the models obtained from Algorithms 3, 5, 6 and 9 can be effectively used to predict the unknown data.
By this process, the regularization parameters
for Algorithms 5, 6, and 9 were as in
Table 3.
We assessed the performance of each algorithm at the 300th iteration with the average accuracy. The results can be seen in
Table 4.
As we see from
Table 4, from the choice of
, all models obtained from Algorithms 3, 5, 6 and 9 had reasonably high average accuracy on both the training and testing sets for all datasets. Moreover, we observed that a model from Algorithm 9 performed better than the models from other algorithms in terms of the accuracy in all experiments conducted.
4.2. Image Restoration
We first recall that an image restoration problem can be formulated as a simple mathematical model as follows:
where
is the original image,
is a blurring matrix,
b is an observed image, and
w is noise. The main objective of image restoration is to find
x from given image
blurring matrix
A, and noise
w.
In order to solve (
16), one could implement LASSO [
30] and reformulate the problem in the following form.
where
is a regularization parameter. Hence, it can be viewed as a convex minimization problem. Therefore, Algorithms 3, 5, 6 and 9 can be used to solve an image restoration problem.
In our experiment, we used the
color image as the original image. We used Gaussian blur of size
and standard deviation four on the original image and obtained the blurred image. In order to assess the performance of each algorithm, we implemented the
peak-signal-to-noise ratio (PSNR) [
34] defined by:
For any original image x and deblurred image , the mean squared error (MSE) is calculated by where M is the number of pixels of x. We also need to mention that an algorithm with a higher PSNR performs better than one with a lower PSNR.
The control parameters of each algorithm were chosen as
. As the inertial parameter
of Algorithm 9, we used the following:
As for the regularization parameter
, we experimented on
varying from zero to one for each algorithm. In
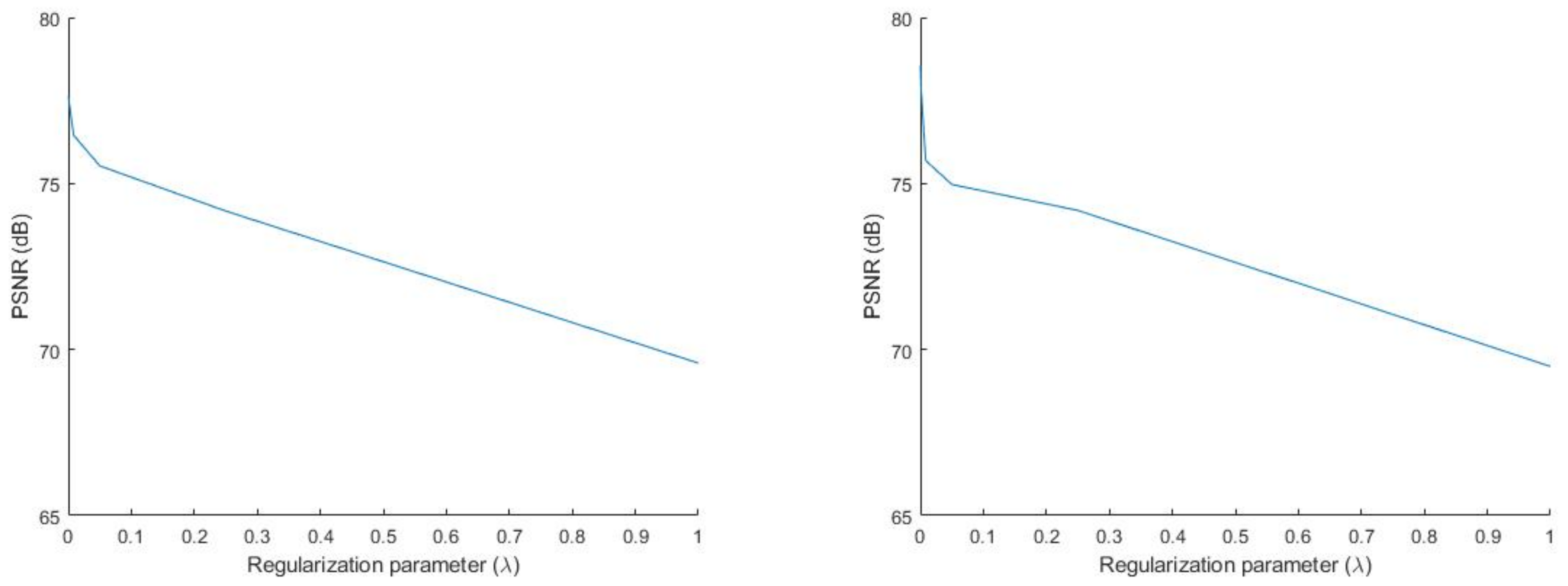
Figure 1, we show the PSNR of Algorithms 3 and 5 with respect to
at the 200th iteration. In
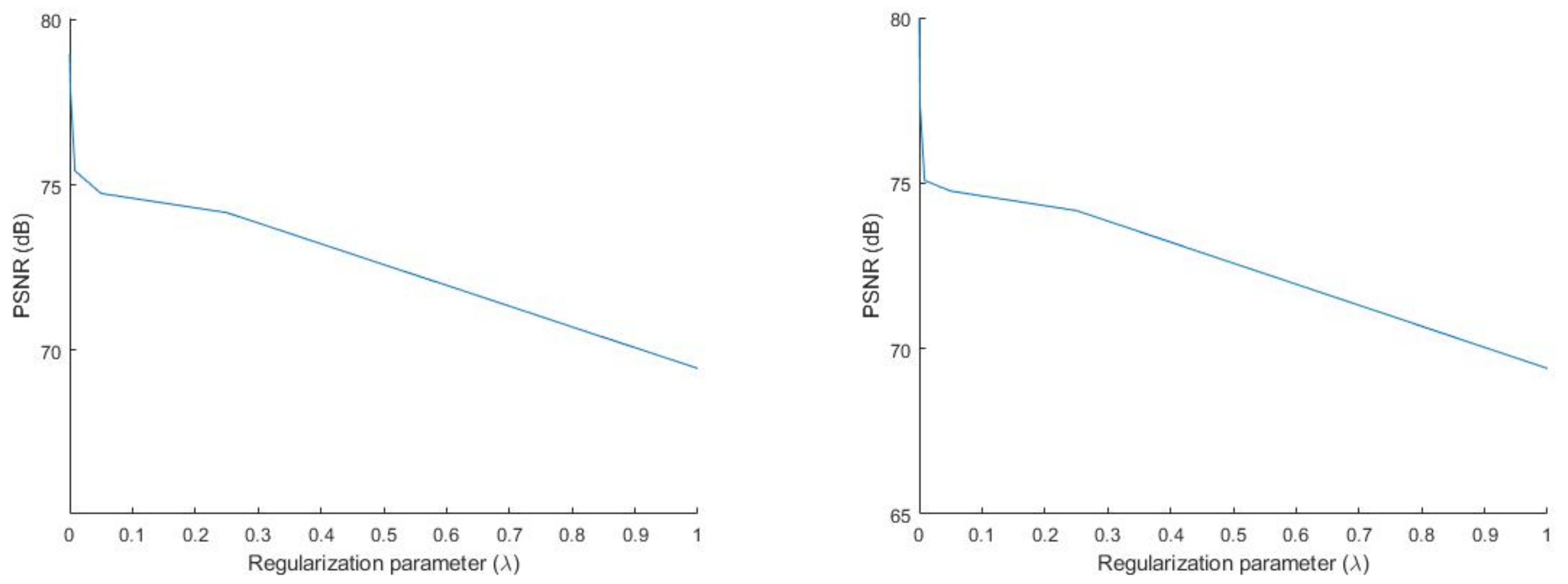
Figure 2, we show the PSNR of Algorithms 6 and 9 with respect to
at the 200th iteration.
We observe from
Figure 1 and
Figure 2 that the PSNRs of Algorithms 3, 5, 6 and 9 increased as
became smaller. Based on this, for the next two experiments, we chose
to be small to obtain a high PSNR for all algorithms. Next, we observed the PSNR of each algorithm when
was small (
). In
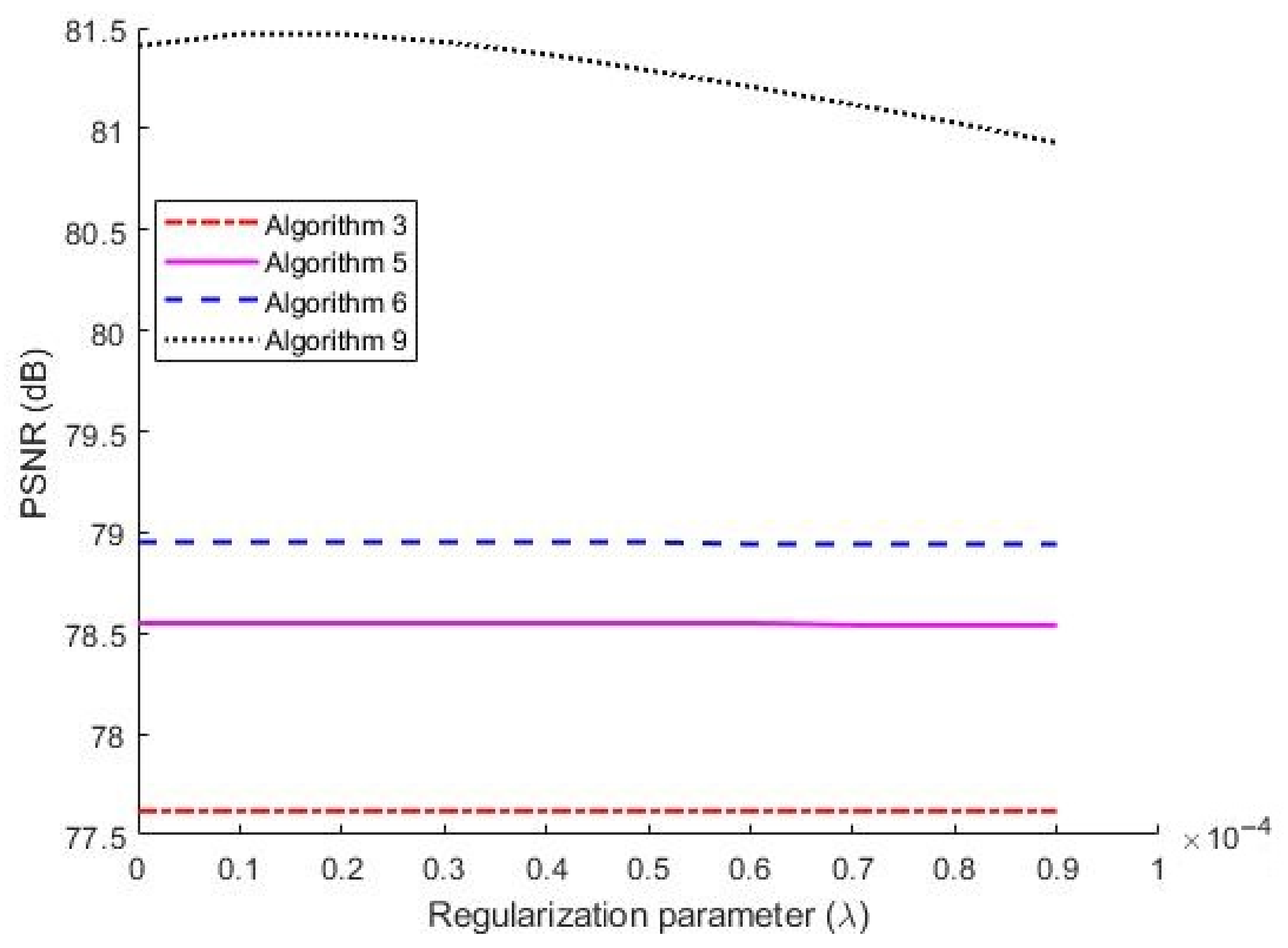
Figure 3, we show the PSNR of each algorithm with respect to
at the 200th iteration.
We see from
Figure 3 that Algorithm 9 offered a higher PSNR than the other algorithms.
In the next experiment, we chose
for each algorithm and evaluated the performance of each algorithm at the 200th iteration; see
Table 5 for the results.
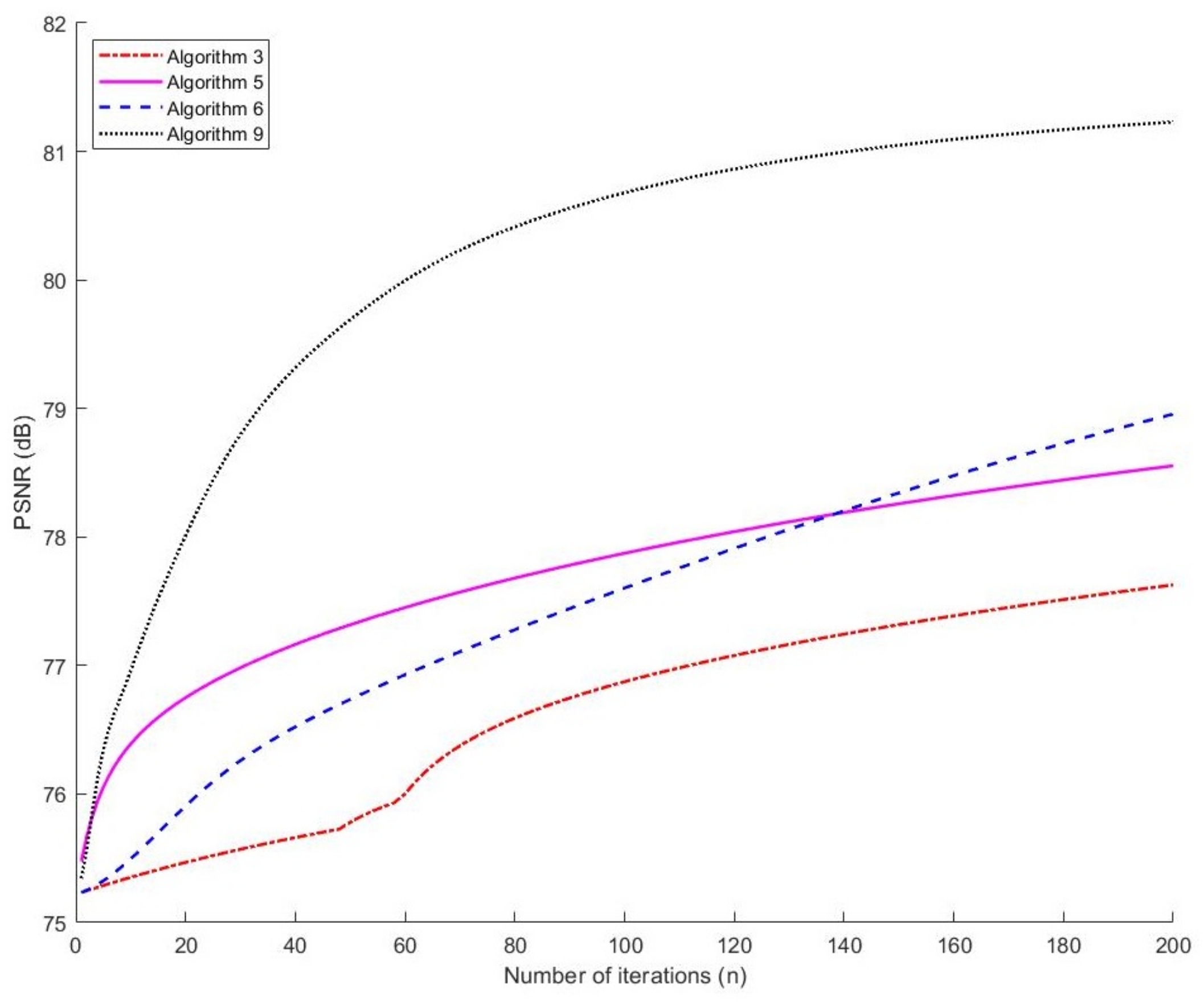
In
Figure 4, we show the PSNR of each algorithm at each step of iteration.
In
Figure 5, we show the original test image, blurred image and deblurred images obtained from Algorithms 3, 5, 6 and 9. As we see from
Table 5 and
Figure 4, Algorithm 9 achieved the highest PSNR.