Abstract
For this paper, we are interested in network formation of endothelial cells. Randomly distributed endothelial cells converge together to create a vascular system. To develop a mathematical model, we make assumptions on individual cell movement, leading to a velocity jump model with chemotaxis. We use scaling arguments to derive an anisotropic chemotaxis model on the population level. For this macroscopic model, we develop a new numerical solver and investigate network-type pattern formation. Our model is able to reproduce experiments on network formation by Serini et al. Moreover, to our surprise, we found new spatial criss-cross patterns due to competing cues, one direction given by tissue anisotropy versus a different direction due to chemotaxis. A full analysis of these new patterns is left for future work.
MSC:
92C17
1. Introduction
Network formation is an important process in many biological tissues. For example, in angiogenesis, blood vessels sprout and grow to form functioning vascular networks [1], or lung tissue, which forms a complex network of bronchioli. Another example is the developing brain, where glial cells grow cellular protrusions, which eventually mature into a synaptic neuronal network [2]. In addition, on the pathological side, we see network formation, for example, in brain cancer growth [3,4]. Thus, a good understanding of network formation can help to identify healthy and pathological processes and provide information for control through treatments. Mathematical modeling has played an important role in physiological processes for many years, and the modeling of network formation is no different. The mathematical approaches are manifold, involving agent-based models, stochastic processes, and continuum models [3,5]. In most of these models, a leader cell (or tip cell) invades new areas, leaving a trail behind, which follower cells can identify and follow. Eventually, the trail forms connections and matures into a network.
A different mechanism for network formation acts in vasculogenesis [6,7,8]. The spatial interaction of moving endothelial cells leads to a spontaneous network formation, in a process that is not based on a trail following mechanism but rather arises as macroscopic pattern formation in a chemotaxis system. Serini et al. [6,7] performed experiments and developed a mathematical chemotaxis model to describe this process. Serini’s et al. model is based on a macroscopic population-level description, which we discuss in a bit more detail in Section 2. Here, in this paper, we generalize Serini’s et al. approach and consider a chemotaxis-transport equation model, which is based on detailed microscopic cell movement patterns often referred to as “run and tumble” [9,10,11,12,13].
There are several ways to include chemotaxis, the active orientation of individuals along chemical gradients, into continuum models [14]. In the case of transport equations of diffusion type, chemotaxis was included by Alt [10] and analyzed in detail by Hillen and Othmer [12,13]. Chalub et al. [15], and Bellomo and Winkler [16] used the kinetic theory for active particles [17] to derive chemotaxis models. Chalub et al. [15] develop a complete existence and solution theory for these models, and their methods can be applied to our model below with minimal modifications. The details of the existence results have been worked out in great detail in Thiessen [18]. Here, we follow the idea of Kumar and Surulescu [19], where we derive a fully anisotropic chemotaxis model from an anisotropic transport equation framework. The chemotaxis-transport approach has been recently applied by Kumar et al. [19,20] to describe tumor-palisades. Tumor palisades arise as microscopic patterns in certain brain cancers, where cancer cells arrange themselves in a ring-like structure. In Kumar et al. [19], it is shown through mathematical modeling that these structures are likely a result of increased acidity in the tumor center.
In the general chemotaxis-transport framework, we repeat a similar process to Kumar et al. and once again retrieve anisotropic diffusion. Using parabolic scaling methods, we find an anisotropic chemotaxis model, which shows network forming properties, but not only that. The anisotropic chemotaxis model balances two causes of anisotropy, the directionality of the underlying tissue and the orientation of the chemotactic gradient. These two effects compete, leading to interesting criss-cross patterns, which have never been observed before in a mathematical model. Accurate numerical simulation of the anisotropic chemotaxis model is a challenge, and we develop an efficient finite volume finite difference solver (FVFD). The numerical solver was inspired by the work of Chertock et al. [21], where a second-order finite volume finite difference solver for a closely related Keller-Segel system was developed.
Our results give new insights into the interplay of two-directional cues on moving populations. The directional effects do not arise as a naive linear combination of each individual effect; rather, the anisotropy and chemotaxis sensing can interact in complicated ways. Further analysis of mutliple directional cues in a transport equation framework is currently been investigated by Conte and Loy [22].
The paper is organized as follows. In Section 2, we revisit the model of Serini et al. [6] and we give some background material on transport equations in biology. In Section 3, we develop the transport-chemotaxis model, and we perform the parabolic scaling to derive the anisotropic chemotaxis model (34). In Section 5, we develop an efficient numerical solver, and we apply it to some relevant examples. Here, we show the occurrence of the new criss-cross patterns. We close with a Discussion Section 6.
2. Background
2.1. The Network Model of Serini et al.
In 2003, Serini et al. [6] performed experiments on vascular endothelial cells and developed a continuum model to explain vascularization. Endothelial cells were cultured on a matrigel surface, and over time network forming patterns were observed. These patterns are controlled by the total cell density and by the strength of their chemotactic response. Small cell densities lead to local cell alignment, intermediate cell densities lead to cell network formation, while large cell densities lead to broadly aligned “highway” networks.
From the experiments in Serini et al. [6], we can identify time and space scales, which will inform the parabolic scaling, which we do later. From the videos and images provided, we find a microscopic time scale of 1 min, where cells change direction about once every 4 min. During an observation of 1 min, they travel a distance of maximal 0.05 mm. The macroscopic scale of observation is about 5–9 h on a domain of about 1 mm. If we introduce a small parameter , then we find the ratios
The mathematical model of Serini et al. [6] is a system of three partial differential equations for the balance of cell density, macroscopic cell population momentum and the chemoattractant. The cell population is described by a continuous density and population movement is described by a macroscopic velocity . Gradients of a chemoattractant act as accelerating force on the population velocity, while the chemoattractant S is released by cells, diffuses through the environment and degrades over time. The resulting equations are
where is a constant denoting the strength of chemoattractant sensing, D is the diffusion constant of the signal, is the rate of chemoattractant production, and is the decay rate of the chemoattractant. Finally, the term p denotes a pressure term, which is used to regularize the solutions and avoid unrealistic density blow-up. The model reproduces the observed network patterns very well, confirming that network patterns only formed with a cell density of at least 100 cells/mm.
Here, we extend the Serini et al. [6] model (2) in two ways. Firstly, instead of using a macroscopic population-level description for mass and momentum balance, we go back to the behavior of individual cells. We develop a transport equation model that includes movement characteristics, such as cell velocity, turning frequency, and choice of preferred directions. Secondly, our formulation allows for a very natural inclusion of tissue anisotropies that arise from aligned tissue structures, such as collagen fibers, nerve fiber bundles, etc. Coupled with chemotaxis, we obtain an exciting interaction between cell movement, tissue anisotropy, and chemotaxis. The main focus of our paper is to better understand this interaction.
2.2. Transport Equations
Transport equations have become a powerful tool for spatial modeling in biology. They are particularly useful in cases where individual particles, such as cells or animals, can be followed and characteristics about their path, such as speed, direction, and turning rate, can be measured. In the context of this paper, we are concerned about two forms of cell alignment. On the one hand, cells align with linear features of the underlying tissue, such as blood vessels or nerve fibers or collagen fibers. In addition, cells react to a chemoattractant and orient themselves in the direction of increased concentration. A transport equation framework is an ideal environment to develop models for oriented movement.
Transport equations describe the time evolution of a particle density at time , location and velocity . We consider a periodic bounded domain , or the whole space . We introduce a set V to denote the possible velocities of the particles and we usually take , with . The time evolution of is described by the transport equation
where the index t denotes the partial time derivative, and is the turning operator, which describes the specific directional changes of the particles [9,10,12,23]. describes how particles chose a new direction, how strongly they are influenced by the underlying directional information, and how persistent their movement is. Typically, is defined via an integral operator representation:
where the first term on the right-hand side gives the rate at which particles switch away from velocity v, and the second term denotes the switching into velocity v from all other velocities . The spatially dependent parameter is the turning rate, while is the mean run time at location x. The traditional literature has focused on the case of constant turning rate [12,23], while direction-dependent turning rates have recently been studied in Reference [24]. The kernel denotes the probability density of switching velocity from to v, given that a turn occurs at location x. The properties of the turning kernel T are the key to the following analysis, and many different choices are possible. Roughly, we can classify the most important cases into three categories, where we will focus on the last one in this manuscript.
- Boltzmann equations: Transport equations, such as (3), have a long history in thermodynamics and physics [25]. In that case, the turning kernel is a non-linear collision kernel between gas particles (or other particles) and the set of velocities V is unbounded. On the other hand, a linear kernel, such as (4), arises as linearization on a so-called Maxwellian distribution [25]. We see later that an important difference to biological applications is the fact that the Boltzmann equation conserves mass, momentum, and energy, i.e., the kernel (null space) of the interaction operator is five-dimensional. In our applications, we have only one conserved quantity: mass, and only in cases where there is no particle birth or death.
- Diffusive transport equations: The diffusive transport equation is characterized by a turning operator , whose kernel consists of functions that are constant in velocity. This means, in equilibrium, there are no preferred directions, and on a long time scale, the dynamic becomes diffusion-like. In References [12,13], we developed a complete theory of diffusive transport equations, and we have shown how chemotaxis models can arise within this theory.
- Anisotropic transport equations: In this case, particles have strong orientational guidance. This guidance arises either through a preferred equilibrium distribution, called the Maxwellian, or it arises from external directional cues. The models in this class fall within the kinetic theory for active particles (KTAP) [16,17]. Mathematically, this case is characterized via a non-trivial one-dimensional kernel of the turning operator . The case of an external directional guidance is of interest here, and a whole theory for external directional cues was developed in References [26,27,28]. We present this case in more detail.
In the anisotropic case, it is assumed that the turning operator does not depend on the incoming velocity , i.e.,
where q satisfies . This assumption seems restrictive since many species would show some form of persistence in the movement direction, and it is entirely possible to include such a dependence into an anisotropic movement, as well. However, it has been shown in many applications that the simplifying assumption (5) is extremely useful in the modeling process, and it can be justified in many cases (certainly for cancer invasions [29] and for sea turtle navigation [30]).
The anisotropic framework was developed in Reference [26] and extended in Reference [27]. We consider a given environment, where at each location in space a distribution of preferred directions is given, where is a unit vector. We assume
We assume that particles that are changing direction do so by using the underlying network structure, i.e., we assume that , where denotes the corresponding unit vector. Since is a probability distribution on , and q a probability distribution on the set of velocities V, we need to normalize appropriately:
with
This definition motivates us to abuse notation and call q the directional distribution of the underlying environment. In doing so, we need to remember that q is a rescaled version of , which is really the directional distribution of the underlying environment.
To summarize, the anisotropic transport equation has the form
For the following analysis, it is useful to consider two statistical quantities of q, the expectation and the variance-covariance matrix of on V:
Let us discuss a few examples of directional distributions q. For these examples, we assume that the particle speed is constant s, i.e., . The extension to is straightforward, but it introduces some extra parameters that need to be carried through the integrals.
- Uniform distribution: The simplest case arises if there is no directional cue at all. In this case,This uniform case is also included in the class of diffusive transport equations mentioned above. In this case,where denotes the identity matrix.
- Strictly-aligned tissue: If all fibers are pointing in the same direction , thenIn this case,
- von-Mises distribution: The von-Mises distribution is the analog of the normal distribution on the unit sphere . Strictly speaking, it is called von-Mises distribution only on . In higher dimensions, it is called the Fisher distribution. However, the functional form is the same as in 2-D [31]. In 2-D, the von-Mises distribution iswhere is the parameter of concentration, are given preferred directions, and is the modified Bessel function of first kind of order 0. As , the von-Mises distribution becomes uniform (case 1), and, for , the von-Mises distribution becomes singular (case 2). The expectation and variance of the two-dimensional von-Mises distribution are [31]where denote the modified Bessel functions of the first kind of order 1, 2, and 3, respectively.
- Bimodal distributions: In many cases, q is symmetric, and guidance up a fiber or down a fiber has the same probability, . For example, the bimodal von Mises distribution iswith expectation and variance [31]
Note that, instead of using a dyadic product , some authors prefer to use a tensor product . We have no preference, but we chose to use only one of these notations.
3. Chemotaxis-Transport Equations
As discussed in the Introduction, chemotaxis effects have been included into the kinetic framework by several authors [10,12,13,15,16,17,18,19]. We now extend the model (6) to include the effect of chemotaxis. For simplicity, we are considering the spatial domain to be the torus, which we will denote as . The turning operator only involves cells changing velocity and, therefore, should not affect the number of cells. Assuming that the number of cells remains the same, we gain the constraint on the turning operators
The corresponding conservation law can be obtained by integrating (3) over the velocity domain
where we use the density of cells and the first moment as
Remark 1
([23]). For positive solutions of the kinetic equation, we have , thanks to conservation of mass.
To include chemotaxis into the transport equation framework, we assume that the turning kernel T depends on the cell density and the gradient of the chemotactic signal S. . The movement of the chemical signal is traditionally defined as a diffusion equation. However, depending on the time scale at which the chemoattractant diffuses, one can consider that chemoattractant is at equilibrium, then the resulting concentration is given by a Poisson type equation. Under this fast diffusion assumption, powerful results on existence and uniqueness have been obtained [32]. We take the traditional route and describe the motion as a diffusion equation, where the chemoattractant production is proportional to the cell density, and the chemoattractant degrades over time. These assumptions give us the diffusion equation
Here, is the concentration of the chemoattractant, is the diffusion constant associated with how the chemoattractant moves through the environment, is the rate of production of the chemoattractant by the cells, and is the rate of degradation of the chemoattractant.
For our purposes, we specify the turning operator further. Inspired by Reference [13], we split the two guiding effects into the environmental contribution q and chemotactic effects as
Here, we allow the environmental cues to depend on the cell density . The rate describes the chemotactic strength, based on the concentration of the signal S. In most examples, b is a constant. The factor is a volume filling term, and it allows chemotactic movement only into areas where there is space available. The variable v denotes the outgoing velocity, and is the gradient of S. To ensure that T is a probability distribution, we need , which we generalize into the following assumptions:
The examples we will be looking at is the von-Mises distributions (8) or (11) for q and
where is the general sensing strength, and is a matrix that describes the directional dependence on sensing the chemoattractant. Note that the above form of is a general second order expansion of a function of v with vanishing odd moments.
We can take advantage of the structure we have provided, and the turning operator (3) becomes
Inputting this turning operator into (3), we obtain the main chemotaxis-transport system of this paper:
We now have a mesoscopic set of equations; in the coming chapters, we will take the parabolic scaling of these equations to get a macroscopic system and explore numerics to get insight into pattern formation.
4. Parabolic Scaling
We have seen above that the transport Equation (20) acts on microscopic scales. For example, in the case of Serini’s experiments [6], we have a microscopic time scale of minutes and a microscopic length scale of about 0.05 mm, while the macroscopic scales are several hours and millimeter. This situation allows us to use parabolic scaling to derive a model that lives on the macroscopic scale. The parabolic scaling of transport equations is a well-documented method, and explorations can be found in References [10,12,15,16,19,23], for example. Similar to the scaling (1), we assume there is a small parameter such that space and time are scaled as
Then, the above transport Equation (20) becomes
To analyze the scaled Equation (22), we take the scaled coordinates and make a regular expansion in , called a Hilbert expansion [33]:
A further assumption is that all of the mass is contained in the first order
Substituting the Hilbert expansions into the rescaled transport Equation (22) and comparing terms of equal order yields a countable number of equations at different orders that all must vanish independently. The zeroth-order equation is given by
The next order of gives
Solving this equation in terms of leads to
To get a closed system for the first term in the Hilbert expansion , we look at the terms
Integrating over V, the right-hand side vanishes, and substituting from (27) and from (25) yields an equation in terms of
To simplify this equation, we temporarily use index notation, where, according to Einsteins summation convention, we sum over repeated indices.
Using the previously defined expectation and variance (7), we can write the above equation in a more compact form with the identity
We use the same definition of expectation and variance for other functions; for example, for we have
Combined with the above chemotaxis Equation (21), we obtain the macroscopic anisotropic chemotaxis system
where , and . In other words, on the microscopic scale, the rates and are small, and, on the macroscopic scale, they are of order one. Since we are solving the chemotaxis model only on the macroscopic scale, we remove the overline-tilde’s and simply keep and .
The system (34) is a generalization of the typical Keller-Segel equations [34] in the sense that we include anisotropic diffusion , and anisotropic chemotaxis . The effect of the and terms are nonuniform diffusion and mixing of the into other directions (chemotactic mixing). Of course, the above scenarios are dependent on the given distributions and . For instance, if q and b are uniform distributions in v, then the above model is the fully isotropic Keller-Segel system [14].
Examples
To explore the effects of anisotropy, we consider the examples that we mentioned above. We use a bimodal von-Mises distribution for q as in (11) and a second-order expansion for b from (18). The moments of the bimodal von Mises distribution are given in (12). For example, when the fiber direction is in the top-right diagonal direction , then
The first term is isotropic diffusion while the second term causes diffusion to be increased along the directions and . The strength of the anisotropy is based on the concentration parameter k, where limiting cases are as , making the diffusion tensor isotropic, and the case as , making the diffusion tensor to be maximally anisotropic.
To compute the second moment for b from (18), we use index notation and summation convention, and we ignore the explicit x dependence:
We move the constants out of the integrals and define a general mean velocity tensor to be
Then, we can rewrite
and, using the Lemma 2.2 from Hillen [35], we explicitly compute the ’s from (36) as
where the set of pairs of indices out of is defined as
We compute the sum explicitly since there is only 12 combinations, and, due to the symmetry of the Kronecker delta, there are only 3 unique terms:
Using the properties of the Kronecker delta, we can convert back to matrix notation
As a result, we have anisotropic components caused by the off-diagonal pieces of A. If A has nonzero off-diagonal components, then has a mixing effect on the chemotactic velocity
To illustrate the chemotactic mixing in two dimensions, we consider
the velocity in the x direction is dependent on the chemotactic gradient in the y direction, and vice versa. In summary, the new terms create non-uniform diffusion and mixing of influence of the chemotactic gradient. The effect of the chemotactic mixing will be shown through numerics in the next section.
5. Numerics
In this section, we numerically explore the effect of anisotropy on chemotaxis. For this exploration, we return to the example of the endothelial cells randomly distributed to form a vascular network. We describe this motion using the parabolic limit (34). For the domain, we consider the two-dimensional square with a periodic boundary condition. We discretize this square into smaller squares with side lengths of h and index these squares by the indices , representing the x-coordinate and y-coordinate, respectively. Both indices run from , where .
5.1. Hybrid FVFD Scheme
For the numerical scheme, we will closely follow the method proposed by Chertock et al. [21]. Chertock et al. derived a second-order hybrid finite volume finite difference (FVFD) scheme for the classical Keller Segel model
They were able to show positivity preservation for this scheme based on reasonable CFL conditions, making it ideal for our problem. The numerical scheme is based on the Godunov scheme for conservation laws [36] to ensure the conservation of particle mass. Since our system has added complexities through the anisotropic diffusion terms, we need to take special care identifying the appropriate upwind terms in the numerical flux. For this reason, we will go through the scheme in detail to exhibit these differences. To begin, we have to write (34) in the form of fluxes along the axes; for this purpose, we write (34) in two dimensions:
On the above mesh, the goal is to write the system as a semi-discrete hybrid FVFD scheme, which takes the form of
where the averaged cell density is , and is the point value of the chemoattractant. are the numerical fluxes in the x and y directions, and is the discrete Laplacian.
We discretize the equations with a finite volume method since finite volume methods are conservative. The conservative property of this scheme can be seen by looking at the conservation law
where u is the state of the solution, and is the corresponding flux vector. Now, we divide the domain of this problem into finite volumes , and integrating over one such cell yields
On integrating the first term to get the volume average (like the approximation ) and applying the divergence theorem to the second yields
where is the surface of the volume of , and is the outward normal. Now, since the change of cell averages is determined by the edge fluxes, any gain of one cell is a loss for another. Dividing by yields
In the case of two dimensions, we just need to keep track of the fluxes at the four edges surrounding a point. In our case, we subdivide our domain into squares with side length h centered at each grid point, and then the change in state cell average is
where , , , and represent point values on the dual grid of spacing (see Figure 1).
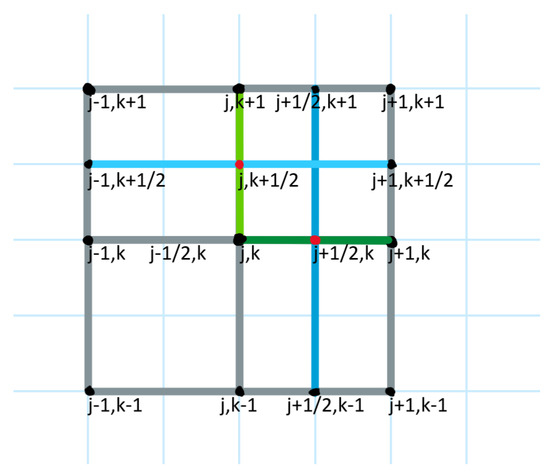
Figure 1.
Stencil for the numerical flux for , and . The green lines represent the derivatives in the upwind directions, and the blue lines represent the derivatives in the perpendicular directions. Note that the upwind direction can be any of N, S, E, W, and, here, we only show the N and E cases.
Based on Chertock et al.’s method [21], we write the numerical fluxes as follows:
where u and v are the chemotactic velocities,
and the point values and are computed in a upwind manner as
The one-sided point values, at the interfaces , , , and , are computed using the second order piecewise linear reconstruction
To ensure that the above point values are second-order and non-negative, slopes are computed adaptively:
with the flux limiter minmod
The positivity of the reconstructed cell density point values is guaranteed by the positivity preserving generalized minmod limiter [37,38,39,40], with the assumption that the underlying cell averages are positive. Now, the scaled cell density derivatives are computed via central differences
Note that, in addition to Chertock’s scheme [21], here, we have anisotropic flux terms
which need special attention. We compute those as a finite difference over a double-spaced interval since this allows us to use point values on grid points that are already computed (see Figure 1). Note that, in this formulation, we do not need values on diagonal points of the form , making the scheme a bit easier.
The chemotactic derivatives , ,, and are computed similarly.
For the discrete Laplacian, we use the standard five-point stencil [41] to obtain a second-order approximation
To evolve this semi discrete scheme through time, we chose to use a second order adaptive Runge-Kutta scheme [42].
5.2. Parameters
The system has a couple of parameters we have to determine namely, the production rate of the chemoattractant, the degradation rate, the turning rate, the diffusion rate of the chemoattractant, and the forms of the distributions , , and . With the purpose of looking at vascular assembly, we can find the constant parameters, = 3600 s, from Reference [6], = 10 cm/s from Reference [43], and = 1785.71/s from Reference [44]. We take the initial condition to be a linear combination of Gaussian’s
where is a sequence of random numbers drawn from the uniform distribution on . This initial condition represents a random distribution of cells on a petri dish, which have a radius of . From available data of molecular radii [45,46], we can estimate the radius of a cell to be = 0.003 cm. With the general parameters defined, we can move onto the numerical experiments.
5.3. Scheme Test
In this numerical experiment, we attempt to show that our scheme’s significant features are present for varying grid sizes. To show the invariance with respect to grid sizes, we take a single Gaussian in the center as the initial condition. As for the fiber and sensing directions, we use the von Mises distribution for q (11) and the quadratic form for b (18), as discussed earlier.
with diagonal anisotropy
Calculating the variances (35) and (40), we find
where the max velocity , and the concentration parameter is .
In Figure 2, we show the initial condition in Figure 2a and two simulations at time with different grid sizes. The grid size in Figure 2b is , and, in Figure 2c, it is . The two computations are qualitatively identical. These computations show the two main properties of our system. First, the cell density diffuses anisotropically along the main diagonal direction, which results from our choice of . Secondly, the peak splits into two aggregations near the center, which results from the chemotactic mixing at highly dense regions. In the following numerical experiments, we will further explore these aspects of the system and show that they lead to network formation.
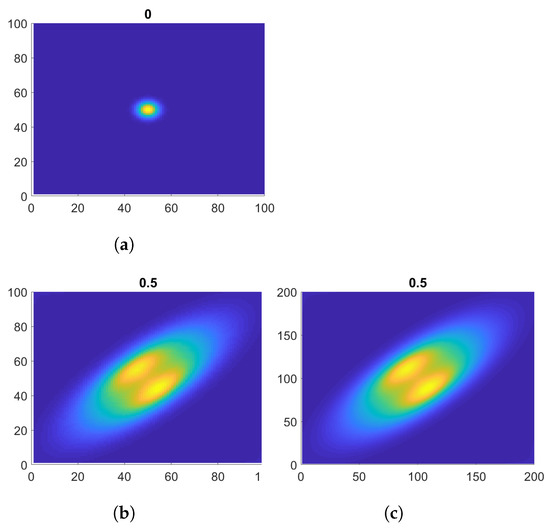
Figure 2.
Numerical test. (a) Initial condition as a Gaussian centered in the domain. (b) Grid size of , numerical result at time . (c) Grid size of , numerical result at .
5.4. Vascular Network Formation
In this numerical experiment, we are interested in replicating previous models’ results in looking at vascular network formation as considered in Serini et al. [6,7]. In their experiments, they took the randomly distributed cells, with b being constant. For the distribution q, the choice is a little more complicated. In Serini et al. [6,47], they propose a pressure term to deal with cell compression. They derived their models through the moment closure taking the form
where is the first moment of the pressure p. We match the pressure term with the strength of our anisotropic diffusion by setting . One of the critical findings of References [6,47] was that the formation of networks arises only for cell densities larger or equal to a critical value. For the above parameters, this value is 100 cells/mm.
To try to recreate the experiment in Reference [6], we evolve the Equation (34) from the initial condition (51) with the parameters
in addition, we take
In Figure 3, we show simulations of network formation for increasing total cell density. The top row shows the random initial condition, while the second row shows a snap-shot at time . In all three cases, localized structures are forming. For cell densities of 100 cells/ mm, the patterns still appear as local aggregates; however, for larger cell densities of 200 and 400, larger-scale structures arise that resemble networks. Notably, we were able to obtain qualitatively similar results to those in References [6,47], despite using a different class of equations. One explanation lies in a moment closure approach that can be performed in the model of (53) and (54). Doing the moment closure in their model will lead to our macroscopic Equation (34) in the isotropic case (i.e., q and b are uniform in v). Details on moment closure methods are discussed elsewhere and are not part of our study here (see References [28,47]).
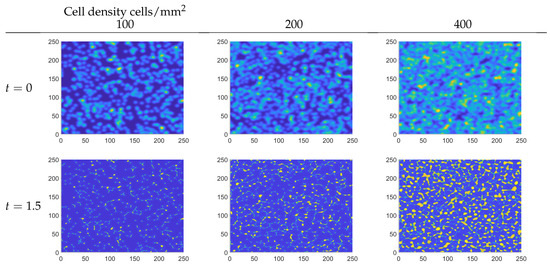
Figure 3.
Formation of networks: The first row shows random initial conditions with cell densities of 100, 200, 400 cells/mm. The second row shows the solution at time s for cell density of 100, 200, 400 cells/mm, respectively.
5.5. Anisotropic Diffusion
For this numerical experiment, we are interested in looking at the effects of anisotropic diffusion. We evolve the Equation (34) from the initial condition (51) with the parameters (55), and to explore anisotropic diffusion, we take
with dominant direction along the main diagonal, i.e., , which means that the variance matrices (35) and (40) take the form
From Figure 4, we can see that inclusion of anisotropy in direction of severely changes the system dynamics. There is still network formation, but now it is biased into the direction of anisotropy. As we increase the concentration parameter k, there is a tighter and tighter spread along the diagonal. We can also localize anisotropic effects to certain regions of the domain by taking the concentration parameter to be a function of x. For example, in the third column in Figure 4, we keep anisotropy in the center of the domain while removing it towards the boundary, i.e.,
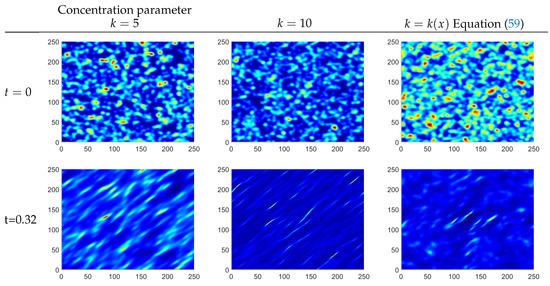
Figure 4.
Inclusion of anisotropy for different values of the concentration parameter k. Cell densities are shown at time (first row) and time (second row), where the total cell density is 200 cells/mm in each of the plots.
We clearly see the effect of anisotropy in the domain center, while the regions near the boundaries behave isotropic.
5.6. Chemotactic Mixing
In this numerical experiment, we evolve the Equation (34) from the initial condition (51) with the parameters (55), and we are going to explore mixing of the chemotactic velocities through an anisotropy term in b. As seen at the end of Section 4, chemotactic mixing is where the chemotactic gradient in one direction affects the movement in all directions. For this effect to occur, we require non-zero off-diagonal components to ; therefore, we take
with variance given in (40), with the choice of
yielding the variance
From Figure 5, we can see that the effect of the chemotaxis mixing is comparable to the effect of non-uniform diffusion as we have seen in the previous numerical experiment. The difference is that the chemotactic mixing seems to affect the diffusion along the diagonal , but the chemotaxis term usually acts as a deterrent, reducing movement away from high-density regions. Therefore, we hypothesize that the chemotaxis term is not promoting movement along the direction, but discouraging diffusion along , while leaving diffusion along unimpeded, giving the structures in Figure 5.

Figure 5.
Velocity mixing. (a) Initial condition with cell density of 200 cells/mm. (b) Solution at 0.32 s.
5.7. Anisotropic Diffusion vs. Chemotactic Mixing
Now, we wish to examine the interaction between the fiber distributions q and the chemotactic velocity mixing. For this, we consider the q in (57) with the concentration parameter , and b in (18). According to the previous numerical experiments, these choices of distributions should act in opposition to each other, q along , and b along . We take the same initial condition as in previous numerical experiments.
From the time series in Figure 6, we can see two regimes. The first regime is where the anisotropic diffusion dominates, and we see the orientation of the cells along the positive diagonal. The second regime occurs at the end of the simulation, where the higher density regions are pulled towards the diagonal, and the lower density regions continue on their path. The split in dominance occurs because the chemotaxis terms’ strength is dependent on the density and time. Since the chemoattractant concentration starts at zero, the anisotropic diffusion initially takes control. This state of affairs continues until the anisotropic diffusion squeezes the solution enough to reach a cell density critical point. The chemotaxis terms dominate for intermediate cell densities inducing movement along the orthogonal diagonal. The result is this crisscrossing knitting pattern. To investigate this effect further, we look at the magnitude of the chemotactic and anisotropic fluxes, given by
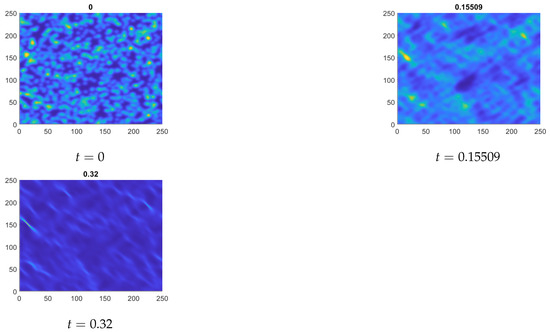
Figure 6.
Anisotropic diffusion and anisotropic chemotaxis at different times. The cell density is 200 cells/mm.
The chemotactic flux is proportional to ; hence, it is maximal for . It is also proportional to the chemotactic gradient . The anisotropic flux has no dependence in the amplitude, but a dependence inside the divergence term. We plot and for three time points in Figure 7 for the same parameter values as in Figure 6.
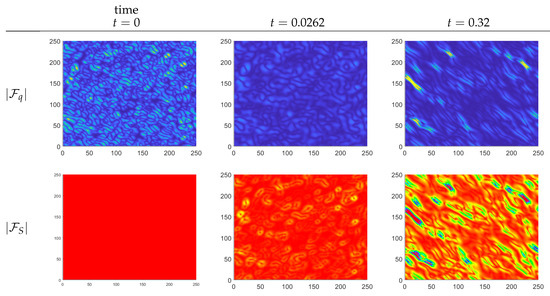
Figure 7.
Time series of the magnitude of the fluxes (top row) and , (bottom row) in the criss-cross regime. Here, we use the same parameter values as in Figure 6.
Initially (at ), we see the initial condition for the anisotropy q in the first row, and since there is no chemical concentration S yet, . Note that the first row in Figure 7 only shows the magnitude of . The dominant direction is always the diagonal . At the time , we are in the regime where continues to diffuse in mainly the (1, 1) direction, whereas has just appeared. We see already torus-like structures, which indicate that the chemotactic flux is maximal for an intermediate cell density and declines again as . As we continue to time , the amplitude of the two fluxes are essentially the same. However, the anisotropic flux is still in the dominant direction , while the chemotactic flux is in direction . Hence, we see the competition in those two directions.
We see numerically fascinating patterns that have, to our knowledge, never been reported in a chemotaxis system. The effects of anisotropy and chemotaxis interact in complicated ways.
5.8. Entrapment by Fibres
For this numerical simulation, we are interested if we can trap a group of cells behind a fiber wall, with some food on the other side to incentivize attempts to escape. We take a horizontally aligned fiber wall as
with
We consider a domain of and assume the linear feature is concentrated at with concentration parameter
This choice of causes anisotropy on the line centered at along the x-axis and isotropic in other directions. For initial conditions, we take the same Gaussian bumps as before but only place them above the fiber (Figure 8a), and we place a large concentration of the chemoattractant below the fiber wall (Figure 8b). We want to see the cells can transfer through this barrier and find the chemotactic signal.
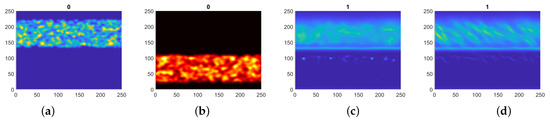
Figure 8.
(a) The initial condition of cells above the fiber wall at y = 125, (b) the initial condition of the chemoattractant, (c) the final state without anisotropy, and (d) the final state with anisotropy.
From Figure 8c, we can see that most of the cells continue their normal development as seen in the other simulations, and only a small portion of the cells gets attracted to the fiber wall. They start moving along the fiber wall while a fraction () manages to cross and aggregate below the fiber wall. If we increase the amount of chemoattractant, we see more escape, and if we decrease the amount, fewer cells cross the fiber wall. In Figure 8d, we included chemotactic mixing of gradient and anisotropy. For the chemotactic mixing case, we took (18) with the same matrix A, and with . In that case, the cell movement is aligned in the diagonal direction, and the crossing appears more effective, as of the population can cross.
6. Discussion
In this paper, we analyzed two effects that can lead to directional orientation of moving particles: chemotaxis and anisotropy. The influence of chemotaxis on particle movement, particle aggregations, pattern formation and blow-up has been studied extensively over the past decades. Comprehensive reviews can be found in Horstmann 2003 [48,49], Hillen and Painter 2009 [14], and Bellomo et al. 2015 [16]. If chemotaxis is combined with tissue anisotropy, then new effects arise. For example, Kumar et al. [19] show that the combination of repulsive Ph-taxis and tissue anisotropy can lead to palisade formation, as found in glioma histologies. We show here that anisotropic chemotaxis can explain vasculogenesis as in experiments of Serini et al. [6], that it produces new types of criss-cross patterns, and that it can be used to study the effect of trapping of chemotactic populations through linear features of the tissue.
The anisotropic chemotaxis model (34) was derived from a mesoscopic description using kinetic transport equations. This framework includes cell-specific characteristics, such as cell velocity, turning rates, tissue anisotropy, and chemotactic mixing. All these terms are informed from individual particle tracking. Finally, through a parabolic scaling technique, the macroscopic anisotropic chemotaxis model (34) is derived. The numerical solution of the anisotropic chemotaxis model shows new challenges through the presence of the anisotropic terms. To address this challenge, we use a powerful reaction-advection-diffusion solver of Chertock et al. [21] and modify it to include anisotropy. We can do this without the inclusion of additional diagonal grid points (as done in Kumar [19], for example), rather, using a smart averaging over grid points that are already defined (see the details in Section 5). Using this numerical scheme, we went through numerous simulations; the first numerical experiment we did was to recreate the vascular network assembly results in Serini et al. [6]. We were able to match our solutions to theirs qualitatively; our ability to do this suggests that the flux rapidly relaxes to the equilibrium in their hyperbolic model (2). For the other numerical experiments, we explored the effects of anisotropic diffusion and chemotactic velocity mixing. For the anisotropic diffusion, the effect is essentially smearing the cells along the fiber direction since movement along those directions is favored. The chemotactic velocity had the opposite effect. The mixing dissuaded movement along those directions, but unaffected diffusion along its complement, retrieving similar results as the anisotropic diffusion. Subsequently, we experimented numerically on the inclusion of both the anisotropic diffusion and the chemotactic mixing, which lead to a mixed regime setup. In regions with low cell density, the anisotropic diffusion would dominate, but the chemotactic velocity would govern the motion in high-density regions. Finally, we were interested if chemotactic mixing would help cells move past a fiber wall. We found that the population gets partially trapped by linear tissue features.
The following steps ask for a complete analysis of the observed pattern formation mechanism. It is unknown what type of bifurcation would lead to network patterns and/or criss-cross patterns. It is our plan for future research to investigate the underlying instabilities.
Overall, we show that tissue anisotropy can profoundly affect chemotactic orientation, explaining new biological phenomena.
Author Contributions
Supervision, T.H.; Writing—original draft, R.T.; Writing—review & editing, T.H. All authors have read and agreed to the published version of the manuscript.
Funding
R.T. acknowledges support from a Canadian Graduate Scholarship of the Natural Sciences and Engineering Research Council of Canada (NSERC) and a Queen Elizabeth II Graduate Scholarship. T.H. is grateful for support through an NSERC Discovery Grant RGPIN-2017-04158.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank two anonymous referees for their comments to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Folkman, J. Angiogenesis. In Biology of Endothelial Cells; Jaffe, E.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Stiles, J. The Fundamentals of Brain Development: Integrating Nature and Nurture; Harvard University Press: Boston, MA, USA, 2008. [Google Scholar]
- Flegg, J.; Menon, S.; Byrne, H.; McElwain, D. A Current Perspective on wound Healing and Tumor-Induced Angiogenesis. Bull. Math. Biol. 2020, 82, 23–45. [Google Scholar] [CrossRef] [PubMed]
- Osswald, M.; Jung, E.; Sahm, F.; Solecki, G.; Venkataramani, V.; Blaes, J.; Weil, S.; Horstmann, H.; Wiestler, B.; Syed, M.; et al. Brain tumour cells interconnect to a functional and resistant network. Nature 2015, 528, 93–98. [Google Scholar] [CrossRef]
- Balding, D.; McElwain, D. A Mathematical Model of Tumor-Induced Capillary Growth. J. Theor. Biol. 1985, 114, 53–73. [Google Scholar] [CrossRef]
- Serini, G.; Ambrosi, D.; Giraudo, E.; Gamba, A.; Preziosi, L.; Bussolino, F. Modeling the early stages of vascular network assembly. EMBO J. 2003, 22, 1771–1779. [Google Scholar] [CrossRef]
- Ambrosi, D.; Gamba, A.; Serini, G. Cell directional and chemotaxis in vascular morphogenesis. Bull. Math. Biol. 2004, 66, 1851–1873. [Google Scholar] [CrossRef] [PubMed]
- Coffin, J.; Poole, T. Endothelial cell origin and migration in embryonic heart and cranial blood vessel development. Anat. Rec. 1991, 231, 383–395. [Google Scholar] [PubMed]
- Stroock, D. Some stochastic processes which arise from a model of the motion of a bacterium. Probab. Theory Rel. Fields 1974, 28, 305–315. [Google Scholar] [CrossRef]
- Alt, W. Biased Random Walk Model for Chemotaxis and Related Diffusion Approximation. J. Math. Biol. 1980, 9, 147–177. [Google Scholar] [CrossRef] [PubMed]
- Othmer, H.; Dunbar, S.; Alt, W. Models of dispersal in biological systems. J. Math. Biol. 1988, 26, 263–298. [Google Scholar] [CrossRef]
- Hillen, T.; Othmer, H. The diffusion limit of transport equations derived from velocity jump processes. SIAM J. Appl. Math. 2000, 61, 751–775. [Google Scholar]
- Othmer, H.; Hillen, T. The diffusion limit of transport equations II: Chemotaxis equations. SIAM J. Appl. Math. 2002, 62, 1222–1250. [Google Scholar] [CrossRef]
- Hillen, T.; Painter, K. A User’s Guide to PDE Models for Chemotaxis. J. Math. Biol. 2009, 58, 183–217. [Google Scholar] [CrossRef] [PubMed]
- Chalub, F.A.; Markowich, P.A.; Perthame, B.; Schmeiser, C. Kinetic models for chemotaxis and their drift-diffusion limits. In Nonlinear Differential Equation Models; Springer: Berlin/Heidelberg, Germany, 2004; pp. 123–141. [Google Scholar]
- Bellomo, N.; Belloquid, A.; Tao, Y.; Winkler, M. Toward a mathematical theory of Keller–Segel models of pattern formation in biological tissues. Math. Model. Methods Appl. Sci. 2015, 25, 1663–1763. [Google Scholar] [CrossRef]
- Bellomo, N. Modeling Complex Living Systems—Kinetic Theory and Stochastic Game Approach; Birkhauser: Boston, MA, USA, 2008. [Google Scholar]
- Thiessen, R. Analysis of Scaling Limits of the Kinetic Chemotaxis Equations. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2020. [Google Scholar]
- Kumar, P.; Li, J.; Surulescu, C. Multiscale modeling of glioma pseudopalisades: Contributions from the tumor microenvironment. J. Math. Biol. 2021, 82, 1–45. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Surulescu, C. A flux-limited model for glioma patterning with hypoxia-induced angiogenesis. Symmetry 2020, 12, 1870. [Google Scholar] [CrossRef]
- Chertock, A.; Epshteyn, Y.; Hu, H.; Kurganov, A. High-order positivity-preserving hybrid finite-volume-finite-difference methods for chemotaxis systems. Adv. Comput. Math. 2018, 44, 327–350. [Google Scholar] [CrossRef]
- Conte, M.; Loy, N. Multi-cue kinetic model with non-local sensing for cell migration on a fibers network with chemotaxis. arXiv 2021, arXiv:2006.09707. [Google Scholar]
- Perthame, B. Transport Equations in Biology; Birkhäuser: Boston, MA, USA, 2007. [Google Scholar]
- Loy, N.; Hillen, T.; Painter, K. Direction-Dependent Turning Leads to Anisotropic Diffusion and Persistence. Eur. J. Appl. Math. 2021. to appear. [Google Scholar] [CrossRef]
- Cercignani, C.; Illner, R.; Pulvirenti, M. The Mathematical Theory of Diluted Gases; Springer: New York, NY, USA, 1994. [Google Scholar]
- Hillen, T. M5 Mesoscopic and Macroscopic Models for Mesenchymal Motion. J. Math. Biol. 2006, 53, 585–616. [Google Scholar] [CrossRef]
- Painter, K. Modelling migration strategies in the extracellular matrix. J. Math. Biol. 2009, 58, 511–543. [Google Scholar] [CrossRef]
- Hillen, T.; Painter, K. Transport and Anisotropic Diffusion Models for Movement in Oriented Habitats. In Dispersal, Individual Movement and Spatial Ecology: A Mathematical Perspective; Lewis, M., Maini, P., Petrovskii, S., Eds.; Springer: Heidelberg, Germany, 2013; pp. 177–222. [Google Scholar]
- Swan, A.; Hillen, T.; Bowman, J.; Murtha, A. An Anisotropic Model for Glioma Spread. Bull. Math. Biol. 2017, 80, 1259–1291. [Google Scholar] [CrossRef]
- Painter, K.; Hillen, T. Navigating the Flow: Individual and continuum models for homing in flowing environments. R. Soc. Interface 2015, 12, 20150647. [Google Scholar] [CrossRef] [PubMed]
- Hillen, T.; Painter, K.; Swan, A.; Murtha, A. Moments of von Mises and Fisher Distributions and Applications. Math. Biosci. Eng. 2017, 14, 673. [Google Scholar] [CrossRef] [PubMed]
- Corrias, L.; Perthame, B.; Zaag, H. Global solutions of some chemotaxis and angiogenesis systems in high space dimensions. Milan J. Math. 2004, 72, 1–28. [Google Scholar] [CrossRef]
- Chauviere, A.; Hillen, T.; Preziosi, L. Modeling cell movement in anisotropic and heterogeneous network tissues. Netw. Heterog. Media 2007, 2, 333. [Google Scholar] [CrossRef]
- Keller, E.F.; Segel, L.A. Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 1970, 26, 399–415. [Google Scholar] [CrossRef]
- Hillen, T. On the L2-moment closure of transport equations: The general case. Discret. Contin. Dyn. Syst. B 2005, 5, 299. [Google Scholar] [CrossRef]
- LeVeque, R. Numerical Methods for Conservation Laws; Springer: Basel, Switzerland, 1992. [Google Scholar]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Lie, K.A.; Noelle, S. On the artificial compression method for second-order nonoscillatory central difference schemes for systems of conservation laws. SIAM J. Sci. Comput. 2003, 24, 1157–1174. [Google Scholar] [CrossRef]
- Nessyahu, H.; Tadmor, E. Non-oscillatory central differencing for hyperbolic conservation laws. J. Comput. Phys. 1990, 87, 408–463. [Google Scholar] [CrossRef]
- Sweby, P.K. High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Anal. 1984, 21, 995–1011. [Google Scholar] [CrossRef]
- Haberman, R. Elementary Applied Partial Differential Equations; Prentice Hall: Englewood Cliffs, NJ, USA, 1983; Volume 987. [Google Scholar]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef]
- Pluen, A.; Netti, P.A.; Jain, R.K.; Berk, D.A. Diffusion of macromolecules in agarose gels: Comparison of linear and globular configurations. Biophys. J. 1999, 77, 542–552. [Google Scholar] [CrossRef]
- Stokes, C.L.; Lauffenburger, D.A.; Williams, S.K. Migration of individual microvessel endothelial cells: Stochastic model and parameter measurement. J. Cell Sci. 1991, 99, 419–430. [Google Scholar] [CrossRef]
- Walter, M.R.; Cook, W.J.; Ealick, S.E.; Nagabhushan, T.L.; Trotta, P.P.; Bugg, C.E. Three-dimensional structure of recombinant human granulocyte-macrophage colony-stimulating factor. J. Mol. Biol. 1992, 224, 1075–1085. [Google Scholar] [CrossRef]
- Muller, Y.A.; Christinger, H.W.; Keyt, B.A.; de Vos, A.M. The crystal structure of vascular endothelial growth factor (VEGF) refined to 1.93 Å resolution: Multiple copy flexibility and receptor binding. Structure 1997, 5, 1325–1338. [Google Scholar] [CrossRef]
- Filbet, F.; Laurençot, P.; Perthame, B. Derivation of hyperbolic models for chemosensitive movement. J. Math. Biol. 2005, 50, 189–207. [Google Scholar] [CrossRef]
- Horstmann, D. From 1970 until present: The Keller-Segel model in chemotaxis and its consequences I. Jahresberichte der DMV 2003, 105, 103–165. [Google Scholar]
- Horstmann, D. From 1970 until present: The Keller-Segel model in chemotaxis and its consequences II. Jahresberichte der DMV 2003, 106, 51–69. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).