A Two-Dimensional Thermoelasticity Solution for Bimodular Material Beams under the Combination Action of Thermal and Mechanical Loads

Abstract

A typical characteristic of bimodular material beams is that when bending, the neutral layer of the beam does not coincide with its geometric middle surface since the mechanical properties of materials in tension and compression are different. In the classical theory of elasticity, however, this characteristic has not been considered. In this study, a bimodular simply-supported beam under the combination action of thermal and mechanical loads is theoretically analyzed. First, a simplified mechanical model concerning the neutral layer is established. Based on this mechanical model, Duhamel’s theorem is used to transform the thermoelastical problem into a pure elasticity problem with imaginary body force and surface force. In solving the governing equation expressed in terms of displacement, a special solution of the displacement equation is found first, and then by utilizing the stress function method based on subarea in tension and compression, a supplement solution for the displacement governing equation without the thermal effect is derived. Lastly, the special solution and supplement solution are superimposed to satisfy boundary conditions, thus obtaining a two-dimensional thermoelasticity solution. In addition, the bimodular effect and temperature effect on the thermoelasticity solution are illustrated by computational examples.

1. Introduction

In the classical theory of elasticity [1], it is generally assumed that materials exhibit the same elastic properties in tension and compression, but this is only a simplified result and does not account for the nonlinear characteristics of materials. Many studies have indicated that most materials [2,3], including concrete, ceramics, graphite, rubber and some biomedical materials, exhibit different tensile and compressive strains when they are subjected to tensile and compressive stresses with the same magnitude. Thus, these materials exhibit different elastic moduli in tension and compression, and are called bimodular materials [4]. Generally, there are two basic material models widely used in theoretical analysis within the engineering profession. One is the criterion of positive–negative signs in the longitudinal strain of fibers proposed by Bert [5]. This model is mainly applicable to orthotropic materials and is therefore widely used in the analysis of laminated composites [6,7,8,9]. Another model is the criterion of positive–negative signs of principal stress proposed by Ambartsumyan [10], which is mainly applicable to isotropic materials. In structural analysis, this model is of particular significance, since it is this factor that determines whether the point is in tension or in compression. This paper will focus on the study of the latter model based on principal direction.

Ambartsumyan [10] linearized the bimodular materials model by two straight lines whose tangents at the origin are discontinuous, as shown in Figure 1, in which $\sigma$ is the principal stress and $\epsilon$ is the principal strain. The basic assumptions of this model are as follows: (1) The studied body is continuous, elastic, homogeneous, and isotropic; (2) Small deformation is satisfied; (3)Young’s modulus of elasticity and Poisson’s ratio of materials are $E^{+}$ and ${\mu }^{+}$ when the materials are in tension along a certain principal direction; and they are $E^{-}$ and ${\mu }^{-}$ when the materials are in compression; (4) When the three principal stresses are uniformly positive or uniformly negative, the three basic equations are essentially the same as those of the classical theory of elasticity; when the signs of the three principal stresses are different, the differential equations of equilibrium and the geometrical equations are the same as those of the classical theory of elasticity, with the exception of the physical equations; (5) ${\mu }^{+}/E^{+}={\mu }^{-}/E^{-}$ is introduced and this will ensure symmetry of the flexibility matrix.

Due to the fact that this bimodular theory defines its constitutive model based on principal directions, the principal stress is generally obtained as a final result but not as a known condition before solving; this inevitably incurs difficulties of description of the stress state of a point. In addition, this model lacks the ability to describe experimental results of elastic coefficients in the complex states of stress. Analytical solutions are available in a few simple cases, although they only concern beams and plates [11,12,13,14]. In some complex problems, it is necessary to resort to the finite element method (FEM) based on an iterative technique [15,16,17,18,19]. According to our literature collection, there are only a few works on the application of a bimodular materials model in the analysis of thermal stress, and even if there are several studies, most of them are based on the Bert model, not on the Ambartsumyan model.

In the theory of thermoelasticity [20], the influence of temperature field in the governing equations is presented through the constitutive law, in which the modulus of elasticity of materials is an important constant. The theory of linear thermoelasticity is established on linear supplement of thermal strains to mechanical strains. Generally, problems of thermoelasticity have been solved by finding solutions of the Lamé displacement equations when a body is acted upon by arbitrary mass forces. Thus, many basic thermoelasticity problems have been considered within the classical theory of elasticity. This is the classical body force analogy, which may date back to Duhamel, who made great contribution to this field in history.

With the development of the theory of thermoelasticity, some generalized thermoelastic models have been proposed for transient responses in many applications (for example, ultra-fast lasers heating and low temperatures) where the classical theory of thermoelasticity fails. Some representative theories in this regard can be found in [21,22,23,24]. It should be emphasized that Green and Lindsay’s theory has been addressed for many types of media, in which Marin et al. [25] used this theory in the context of the dipolar thermoelastic bodies. On the other hand, besides the development of the theory itself, it is also very important to apply the theory to the analysis of the engineering components, or more specially, it is equally important to analyze the thermoelastic behavior of engineering structures, for example, the thermoelasticity behaviors of nanobeams [26], microbeams [27], composite beams [28], and laminated beams [29]. Of course, the bimodular material beams should also be included in the thermoelastical analysis of structures.

At present, the bimodular problem is mostly not considered in the theory of thermoelasticity. Once the bimodular problem is introduced into the theory of thermoelasticity, it is predictable that there will be changes in the governing equation used for the solution of the bimodular thermal problem and in the solving method, and what are the corresponding changes? This study will focus on the establishment of the displacement governing equation and the corresponding solving process, with the emphasis on the differences introduced by bimodular characteristics of materials.

This study is devoted to obtaining a two-dimensional thermoelasticity solution for the bimodular beam under the combination action of thermal and mechanical loads. For this purpose, this paper is organized as follows. First, the mechanical model based on the neutral layer is established in Section 2, thus realizing the regional segmentation of tension and compression. The governing equation expressed in terms of displacement components is given in Section 3, and the composition of the solution is presented in Section 4. Aiming at the governing equation, the special solution and corresponding supplement solution are derived in Section 5, in which the supplement solution is obtained by applying the stress function method as well as the de Saint-Venant’s Principle. In Section 6, some typical computational examples are given, in which the bimodular effect and temperature effect on the thermoelasticity solution are discussed. Section 7 is the conclusions.

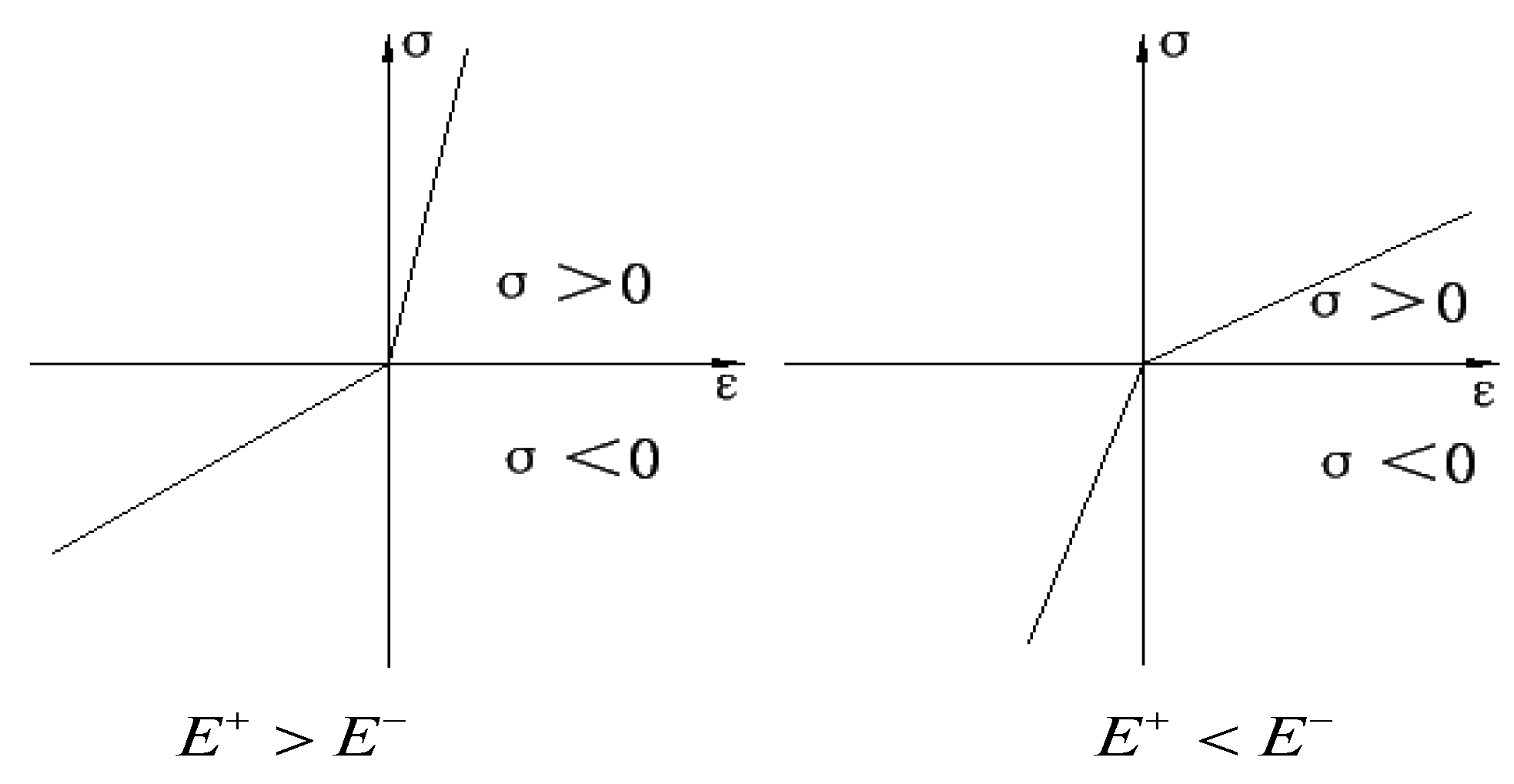
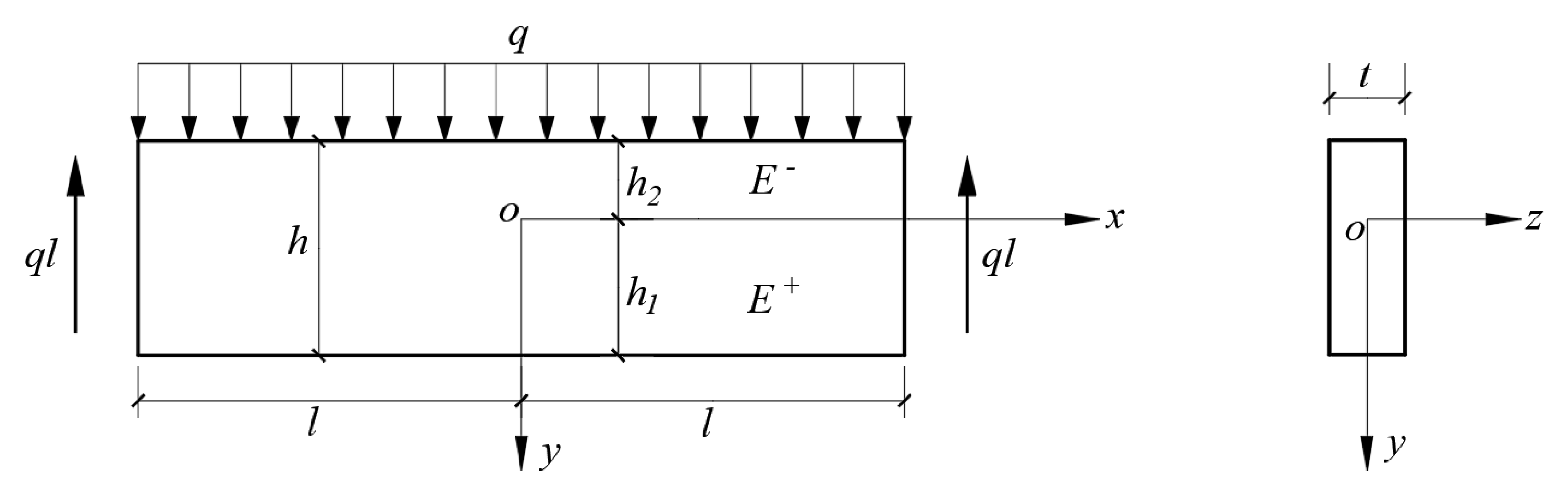
2. Mechanical Model Based on Neutral Layer

A rectangular section beam with the height h and thickness t is subjected to the bending moment M at its two ends, and we isolated a part from the whole beam as our studied object, as shown in Figure 2. Obviously, the beam will deflect downward to resist the external bending moment, thus resulting in tension in the lower part of the beam and compression in the upper part. For convenience, we established the x-axis of the coordinate system (xoy) on the unknown neutral axis, which may be determined thereafter. The height of the tensile part of the beam is $h_1$ and the corresponding modulus in this part is $E^{+}$; while at the same time, the compressive height and the modulus in the compressive part is $h_2$ and $E^{-}$, as shown in Figure 2, in which $y_0$ is the offset distance between the neutral axis and the geometrical middle layer.

According to the plane section assumption, the curvature $\rho$ of the neutral axis may be expressed as

$$\frac{1}{\rho }=\frac{d\theta }{dx},$$

(1)

in which, $dx$ and $d\theta$ denote the length and rotation angle of a segment on the neutral axis, respectively, as shown in Figure 2. The relative elongation of the segment AB with distance y from the neutral axis, ${\epsilon }_x$, is equal to

$${\epsilon }_x=\frac{(y+\rho )d\theta -\rho d\theta }{dx}=y\frac{d\theta }{dx}=\frac{y}{\rho }.$$

(2)

Thus the tensile normal stress and compressive normal one may be expressed as follows

$${\sigma }_x^{+}=E^{+}\frac{y}{\rho }, 0\le y\le h_1; {\sigma }_x^{-}=E^{-}\frac{y}{\rho }, -h_2\le y\le 0.$$

(3)

The condition of equilibrium gives

$${\displaystyle {\int }_0^{h_1}{\sigma }_x^{+}tdy}+{\displaystyle {\int }_{-h_2}^0{\sigma }_x^{-}tdy}=0,$$

(4)

and

$${\displaystyle {\int }_0^{h_1}{\sigma }_x^{+}ytdy}+{\displaystyle {\int }_{-h_2}^0{\sigma }_x^{-}ytdy}=M.$$

(5)

Combining Equations (3) and (4) yields

$$E^{+}{h}_1^2=E^{-}{h}_2^2.$$

(6)

After considering $h_1+h_2=h$, we have

$$h_1=\frac{\sqrt{E^{-}}}{\sqrt{E^{+}}+\sqrt{E^{-}}}h,h_2=\frac{\sqrt{E^{+}}}{\sqrt{E^{+}}+\sqrt{E^{-}}}h$$

(7)

which determines the location of the unknown neutral axis. Similarly, combining Equations (3) and (5) yields

$$\frac{1}{\rho }\left(\frac{E^{+}t{h}_1^3}{3}+\frac{E^{-}t{h}_2^3}{3}\right)=M.$$

(8)

If D is defined as the bending stiffness of the bimodular problem, that is,

$$D=\frac{t}{3}(E^{+}{h}_1^3+E^{-}{h}_2^3).$$

(9)

Equation (8) will return to a familiar form

$$\frac{1}{\rho }=\frac{M}{D}.$$

(10)

When $E^{+}=E^{-}=E$, we have $h_1=h_2=h/2$, the above expressions may be reduced to the classical forms, in which $D=Et{h}^3/12$. Thus, we establish the so-called mechanical model on subarea in tension and compression under mechanical loads. Next, based on this model, we will analyze the thermal stress of a bimodular beam under the combination action of mechanical and thermal loads.

It should be noted here that if the bimodular materials beam is subjected to uniformly distributed loads, not only the bending moment but also the shearing forces will develop in the beam, that is to say, the beam is under lateral bending but under pure bending. In this case, the mechanical model based on the neutral layer is still applicable since the shearing stress has no influence on the determination of the neutral axis, which depends only on the bending stress. This conclusion was demonstrated by Yao and Ye [11].

3. Displacement Governing Equation

The problem we consider here is a typical plane stress problem concerning thermal effect. If we let ${\epsilon }_x,{\epsilon }_y$ and ${\gamma }_{xy}$ be the strain components of a plane stress problem and ${\sigma }_x,{\sigma }_y$ and ${\tau }_{xy}$ be the corresponding stress components, $\alpha$ represents the linear thermal expansion coefficient and T represents the temperature variation, the physical equation of the two-dimensional theory of thermoelasticity may be given as follows

$$\{\begin{array}{l}{\epsilon }_x=\frac{1}{E^{+/-}}\left({\sigma }_x-\mu {\sigma }_y\right)+\alpha T\\ {\epsilon }_y=\frac{1}{E^{+/-}}\left({\sigma }_y-\mu {\sigma }_x\right)+\alpha T\\ {\gamma }_{xy}=\frac{2(1+\mu )}{E^{+/-}}{\tau }_{xy}\end{array},$$

(11)

in which the tensile-compressive Young’s modulus is denoted by $E^{+/-}$. In our study, however, there is no way to specify that, from the very beginning, the stress state of any point is tensile or compressive, thus we have to express the modulus in the form of $E^{+/-}$. Once the final result is obtained, with the stress state becoming clear, we can differentiate the tension from the compression. This fact is quite different from the case that is only under mechanical load shown in Section 2, in which the so-called subarea in tension and compression, that is, the neutral axis, is obvious from the beginning and may also be determined later. However, under the combination action of mechanical and thermal loads, not only the bending from the mechanical load, but also the axial tension or compression from the temperature rise, may have influences on the final stress results, thus the so-called neutral layer becomes obscure at present. Therefore, the form $E^{+/-}$ has to be adopted to express the physical equation for the time being.

For the physical equation, we may have another form as follows,

$$\{\begin{array}{l}{\sigma }_x=\frac{E^{+/-}}{1-{\mu }^2}({\epsilon }_x+\mu {\epsilon }_y)-\frac{\alpha T{E}^{+/-}}{1-\mu }\\ {\sigma }_y=\frac{E^{+/-}}{1-{\mu }^2}({\epsilon }_y+\mu {\epsilon }_x)-\frac{\alpha T{E}^{+/-}}{1-\mu }\\ {\tau }_{xy}=\frac{E^{+/-}}{2(1+\mu )}{\gamma }_{xy}\end{array}.$$

(12)

If we let u and v be the displacement along x and y direction, respectively, the geometrical equation of the plane problem gives [1]

$${\epsilon }_x=\frac{\partial u}{\partial x},{\epsilon }_y=\frac{\partial v}{\partial y},{\gamma }_{xy}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}.$$

(13)

Substituting Equation (13) into Equation (12), we may obtain the stress components expressed in terms of the displacement u and v and the temperature variation T as

$$\{\begin{array}{l}{\sigma }_x=\frac{E^{+/-}}{1-{\mu }^2}(\frac{\partial u}{\partial x}+\mu \frac{\partial v}{\partial y})-\frac{\alpha T{E}^{+/-}}{1-\mu }\\ {\sigma }_y=\frac{E^{+/-}}{1-{\mu }^2}(\frac{\partial v}{\partial y}+\mu \frac{\partial u}{\partial x})-\frac{\alpha T{E}^{+/-}}{1-\mu }\\ {\tau }_{xy}=\frac{E^{+/-}}{2(1+\mu )}\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)\end{array}.$$

(14)

Substituting Equation (14) into the equation of equilibrium of the plane problem

$$\{\begin{array}{l}\frac{\partial {\sigma }_x}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+X=0\\ \frac{\partial {\sigma }_y}{\partial y}+\frac{\partial {\tau }_{xy}}{\partial x}+Y=0\end{array},$$

(15)

in which $X$ and $Y$ are the body forces along x and y directions, respectively, we will have the Lamé equation, which may be used in the displacement method (noting $X=Y=0$).

$$\{\begin{array}{l}\frac{{\partial }^{2}u}{\partial x^2}+\frac{1-\mu }{2}\frac{{\partial }^{2}u}{\partial y^2}+\frac{1+\mu }{2}\frac{{\partial }^{2}v}{\partial x\partial y}-\left(1+\mu \right)\alpha \frac{\partial T}{\partial x}=0\\ \frac{{\partial }^{2}v}{\partial y^2}+\frac{1-\mu }{2}\frac{{\partial }^{2}v}{\partial x^2}+\frac{1+\mu }{2}\frac{{\partial }^{2}u}{\partial x\partial y}-\left(1+\mu \right)\alpha \frac{\partial T}{\partial y}=0\end{array}.$$

(16)

In addition, substituting Equation (14) into the following stress boundary condition of the plane problem

$$\{\begin{array}{l}l{({\sigma }_x)}_s+m{({\tau }_{xy})}_s=\overline{X}\\ m{({\sigma }_y)}_s+l{({\tau }_{xy})}_s=\overline{Y}\end{array},$$

(17)

in which, l and m are direction cosines, and $\overline{X}$ and $\overline{Y}$ are the surfaces forces, we will have the stress boundary condition used in the displacement method (noting $\overline{X}=\overline{Y}=0$).

$$\{\begin{array}{l}l{\left(\frac{\partial u}{\partial x}+\mu \frac{\partial v}{\partial y}\right)}_s+m\frac{1-\mu }{2}{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}_s=l(1+\mu )\alpha T\\ m{\left(\frac{\partial v}{\partial y}+\mu \frac{\partial u}{\partial x}\right)}_s+l\frac{1-\mu }{2}{\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)}_s=m(1+\mu )\alpha T\end{array}.$$

(18)

Therefore, the Lamé equation and corresponding boundary conditions of a two-dimensional thermoelasticity problem are established, as shown in Equations (16) and (18), also including displacement boundary condition not listed here.

Comparing Equations (16) and (18) with the counterparts in the plane stress problem without thermal effect, it is found that the original $X$ and $Y$ are now replaced by $-\alpha E^{+/-}(\partial T/\partial x)/(1-\mu )$ and $-\alpha E^{+/-}(\partial T/\partial y)/(1-\mu )$, respectively, and the original $\overline{X}$ and $\overline{Y}$ are now replaced by $l\alpha T{E}^{+/-}/(1-\mu )$ and $m\alpha T{E}^{+/-}/(1-\mu )$, respectively. This fact suggests to us that under certain displacement boundary conditions, the displacement due to temperature variation T is equal to the displacement of the elastic body without temperature variation, which is subjected to the imaginary body forces, $-\alpha E^{+/-}(\partial T/\partial x)/(1-\mu )$ and $-\alpha E^{+/-}(\partial T/\partial y)/(1-\mu )$, and the imaginary surface forces, $l\alpha T{E}^{+/-}/(1-\mu )$ and $m\alpha T{E}^{+/-}/(1-\mu )$. Therefore, the thermoelasticity plane stress problem is transformed into a pure elasticity problem under the action of the known body forces and known surface forces; this is Duhamel’s theorem that we are familiar with.

It should be noted here that there exists no term of modulus of elasticity in Equations (16) and (18) since this term is eliminated during the derivation of the two equations. For the classical thermoelasticity problem with singular modulus, this conclusion is true, which may be easily found in many textbooks. However, once the bimodular effect is introduced, will the form of the equations change? From Equations (14) and (15), we may see that whether the tensile modulus or the compressive modulus may be eliminated will depend on the fact that ${\sigma }_x$ and ${\tau }_{xy}$ have the same positive or negative sign, or ${\sigma }_y$ and ${\tau }_{xy}$ have the same sign. First, ${\sigma }_x$ and ${\sigma }_y$ are two normal stresses along the directions of x and y, respectively, and they may be positive or negative; in this case, the positive or negative sign of ${\tau }_{xy}$ is a relatively key factor, that is to say, whether the sign of ${\tau }_{xy}$ may change as the sign of the corresponding ${\sigma }_x$ and ${\sigma }_y$ during the derivation. In the bimodular theory proposed by Ambartsumyan, there is a basic assumption that ${\mu }^{+}/E^{+}={\mu }^{-}/E^{-}$, which ensures the symmetry of the flexibility matrix. In this study, we ignore the difference of ${\mu }^{+}$ and ${\mu }^{-}$, regarding them as a constant $\mu$, thus when only ${\tau }_{xy}$ is considered, according to ${\mu }^{+}/E^{+}={\mu }^{-}/E^{-}$, we may have $E^{+}=E^{-}$ only in this case. That is to say, the positive of negative sign of ${\tau }_{xy}$ may change as the positive of negative sign of ${\sigma }_x$ and ${\sigma }_y$. Therefore, even if the bimodular effect is introduced, the basic forms of Equations (16) and (18) remain unchanged.

4. Composition of Solution

Generally speaking, under the stress boundary condition (18) and displacement boundary condition, it is hard to obtain the analytical solution of the governing Equation (16). In an actual solving process, it is a common practice to follow the next two steps. First, any special solution of Equation (16) is found that does not necessarily satisfy the boundary conditions. Second, another supplement solution is found, not considering temperature changes, and then by superimposing the supplement solution and the previous special solution, the total stress is obtained to satisfy the boundary conditions.

To find the special solution of Equation (16), a potential function of displacement, $\psi (x,y)$, is introduced and the special solution of displacement may be taken as

$$u^{\prime }=\frac{\partial \psi }{\partial x},v^{\prime }=\frac{\partial \psi }{\partial y}.$$

(19)

Regarding the $u^{\prime }$ and $v^{\prime }$ as u and v, respectively, and substituting them into Equation (16), we have

$$\{\begin{array}{l}\frac{\partial }{\partial x}{\nabla }^2\psi =(1+\mu )\alpha \frac{\partial T}{\partial x}\\ \frac{\partial }{\partial y}{\nabla }^2\psi =(1+\mu )\alpha \frac{\partial T}{\partial y}\end{array}.$$

(20)

Note that $\mu$ and $\alpha$ are both constants in this problem, this shows if the function $\psi (x,y)$ can satisfy the following differential equation

$${\nabla }^2\psi =(1+\mu )\alpha T,$$

(21)

then the $\psi (x,y)$ can satisfy Equation (20), thus also satisfying Equation (16). Finally, the $u^{\prime }$ and $v^{\prime }$ in Equation (19) may be selected as a special solution of displacement. Substituting Equations (19) and (21) into Equation (14), the stress component corresponding to the special solution of displacement may be obtained as

$$\{\begin{array}{l}{{\sigma }_x}^{\prime }=-\frac{E^{+/-}}{1+\mu }\frac{{\partial }^2\psi }{\partial y^2}\\ {{\sigma }_y}^{\prime }=-\frac{E^{+/-}}{1+\mu }\frac{{\partial }^2\psi }{\partial x^2}\\ {{\tau }_{xy}}^{\prime }=\frac{E^{+/-}}{1+\mu }\frac{{\partial }^2\psi }{\partial x\partial y}\end{array}.$$

(22)

On the other hand, the supplement solution of displacement, $u^{″}$ and $v^{″}$, need to satisfy the homogeneous form of Equation (16), this gives

$$\{\begin{array}{l}\frac{{\partial }^2{u}^{″}}{\partial x^2}+\frac{1-\mu }{2}\frac{{\partial }^2{u}^{″}}{\partial y^2}+\frac{1+\mu }{2}\frac{{\partial }^2{v}^{″}}{\partial x\partial y}=0\\ \frac{{\partial }^2{v}^{″}}{\partial y^2}+\frac{1-\mu }{2}\frac{{\partial }^2{v}^{″}}{\partial x^2}+\frac{1+\mu }{2}\frac{{\partial }^2{u}^{″}}{\partial x\partial y}=0\end{array}.$$

(23)

By using Equation (14) and also letting $T=0$, we have the stress components corresponding to the supplement solution of displacement,

$$\{\begin{array}{l}{{\sigma }_x}^{″}=\frac{E^{+/-}}{1-{\mu }^2}(\frac{\partial u^{″}}{\partial x}+\mu \frac{\partial v^{″}}{\partial y})\\ {{\sigma }_y}^{″}=\frac{E^{+/-}}{1-{\mu }^2}(\frac{\partial v^{″}}{\partial y}+\mu \frac{\partial u^{″}}{\partial x})\\ {{\tau }_{xy}}^{″}=\frac{E^{+/-}}{2(1+\mu )}\left(\frac{\partial v^{″}}{\partial x}+\frac{\partial u^{″}}{\partial y}\right)\end{array}.$$

(24)

Lastly, the total displacement is

$$u=u^{\prime }+u^{″},v=v^{\prime }+v^{″},$$

(25)

which needs to satisfy displacement boundary conditions. In addition, the total stress is

$${\sigma }_x={{\sigma }_x}^{\prime }+{{\sigma }_x}^{″},{\sigma }_y={{\sigma }_y}^{\prime }+{{\sigma }_y}^{″},{\tau }_{xy}={{\tau }_{xy}}^{\prime }+{{\tau }_{xy}}^{″} ,$$

(26)

which needs to satisfy stress boundary conditions.

5. Obtainment of Solution

5.1. Special Solution

If the temperature variation is always a function of y, that is, $T=T(y)$, it is easy to obtain the special solution according to the description above. Substituting Equation (21) into Equation (22), the following stress components may be obtained

$$\{\begin{array}{l}{{\sigma }_x}^{\prime }=-E^{+/-}\alpha T(y)=-E^{-}\alpha T(y)\\ {{\sigma }_y}^{\prime }=0\\ {{\tau }_{xy}}^{\prime }=0\end{array},$$

(27)

which corresponds to the special solution of displacement. Note that the ${{\sigma }_x}^{\prime }$ in the special solution always corresponds to the compressive stress since the linear thermal expansion coefficient $\alpha$ is positive and $T(y)$ also represents the temperature rise. Therefore, the $E^{+/-}$ in the term ${{\sigma }_x}^{\prime }$ should be modified as $E^{-}$, according to the bimodular characteristics of tension and compression described above.

5.2. Supplement Solution and Superposition with Special Solution

In an elasticity problem only with stress boundary conditions, it is hard to find the supplement solution of displacement. To overcome the difficulties, it is a common practice to adopt the stress function method, that is, introduce a stress function, $\phi (x,y)$, and then express the stress components corresponding to the supplement solution of displacement as follows

$${{\sigma }_x}^{″}=\frac{{\partial }^2\phi }{\partial x^2},{{\sigma }_y}^{″}=\frac{{\partial }^2\phi }{\partial y^2},{{\tau }_{xy}}^{″}=-\frac{{\partial }^2\phi }{\partial x\partial y} ,$$

(28)

in which the selection for $\phi (x,y)$ may be carried out according to the specific stress boundary conditions, which has been demonstrated in many real examples.

As shown in Figure 3, a simply-supported beam in a thermal environment is subjected to the uniformly distributed loads, in which the beam consists of certain bimodular materials, and it will deflect downward to resist the external loads, thus resulting in tension in the lower part of the beam and compression in the upper part. In Figure 3, the span length of the beam is 2l, the height is h and the thickness is t and is taken as unit 1; q is the magnitude of the uniformly distributed loads and ql denotes the reaction of two supports of the beam. Note that in such a bimodular beam, the tensile height of the beam is $h_1$, the compressive height $h_2$; accordingly, the tensile modulus is $E^{+}$ in the tensile part and the compressive modulus is $E^{-}$ in the compressive part. For convenience, we establish the x-axis of the coordinate system (xyz) on the known neutral axis, which was determined in Section 2.

If the two plane dimensions of the beam, 2l and h, are in the same order of magnitude, it is hard to obtain the analytical solution of this problem. However, if $2l>>h$, the left and right sides of the beam become second boundary, thus making the application of the de Saint-Venant’s Principle rational. For this purpose, the following stress function is adopted

$$\phi (x,y)=\frac{x^2}{2}f(y)+x{f}_1(y)+f_2(y),$$

(29)

in which, $f(y)$, $f_1(y)$ and $f_2(y)$ are three unknown function of y. The obtainment of this stress function is based on the so-called semi-inverse method, which may be simply described as follows. First, according to the real stress condition, the beam is subjected to the uniformly distributed loads along the direction of span length, and it is assumed that the stress component along y direction does not change with x, thus beginning with ${\sigma }_y=f(y)$. Using ${\sigma }_y={\partial }^2\phi /{\partial }^{2}x$ and integrating twice with respect to x, Equation (29) may be derived. By satisfying the consistency equation ${\nabla }^4\phi (x,y)=0$, in which ${\nabla }^4$ denotes the dual Laplace operator, as well as after considering the symmetry of this problem, that is, $f_1(y)=0$, lastly the stress function expressed in terms of unknown constants may be obtained,

$$\phi (x,y)=\frac{x^2}{2}(A{y}^3+B{y}^2+Cy+D)-\frac{A}{10}{y}^5-\frac{B}{6}{y}^4+H{y}^3+K{y}^2,$$

(30)

in which, A, B, C, D, H and K are six unknown constants that may be determind by boundary conditions. Note that the mechanical model on subarea in tension and compression is adopted here, the stress components are given in the tensile part and the compressive one, respectively. Substituting Equation (30) into Equation (28), we have the stress components expressed in terms of unknown constants, for the tensile part, $0\le y\le h_1$

$$\{\begin{array}{l}{{\sigma }_x^{+}}^{″}=\frac{x^2}{2}(6A^{+}y+2B^{+})-2A^{+}{y}^3-2B^{+}{y}^2+6H^{+}y+2K^{+}\\ {{\sigma }_y^{+}}^{″}=A^{+}{y}^3+B^{+}{y}^2+C^{+}y+D^{+}\\ {{\tau }_{xy}^{+}}^{″}=-x(3A^{+}{y}^2+2B^{+}y+C^{+})\end{array},$$

(31)

and for the compressive part, $-h_2\le y\le 0$,

$$\{\begin{array}{l}{{\sigma }_x^{-}}^{″}=\frac{x^2}{2}(6A^{-}y+2B^{-})-2A^{-}{y}^3-2B^{-}{y}^2+6H^{-}y+2K^{-}\\ {{\sigma }_y^{-}}^{″}=A^{-}{y}^3+B^{-}{y}^2+C^{-}y+D^{-}\\ {{\tau }_{xy}^{-}}^{″}=-x(3A^{-}{y}^2+2B^{-}y+C^{-})\end{array}.$$

(32)

Now, superposing with the special solution (27), we have, for $0\le y\le h_1$,

$$\{\begin{array}{l}{\sigma }_x^{+}=-\alpha E^{-}T(y)+\frac{x^2}{2}(6A^{+}y+2B^{+})-2A^{+}{y}^3-2B^{+}{y}^2+6H^{+}y+2K^{+}\\ {\sigma }_y^{+}=A^{+}{y}^3+B^{+}{y}^2+C^{+}y+D^{+}\\ {\tau }_{xy}^{+}=-x(3A^{+}{y}^2+2B^{+}y+C^{+})\end{array},$$

(33)

and for $-h_2\le y\le 0$,

$$\{\begin{array}{l}{\sigma }_x^{-}=-\alpha E^{-}T(y)+\frac{x^2}{2}(6A^{-}y+2B^{-})-2A^{-}{y}^3-2B^{-}{y}^2+6H^{-}y+2K^{-}\\ {\sigma }_y^{-}=A^{-}{y}^3+B^{-}{y}^2+C^{-}y+D^{-}\\ {\tau }_{xy}^{-}=-x(3A^{-}{y}^2+2B^{-}y+C^{-})\end{array},$$

(34)

in which the quantities with superscript ‘+’ denote the quantities relating to tension and the quantities with superscript ‘−’ denote the quantities relating to compression. Note that after the subarea in tension and compression, the number of undetermined constants is double, from the original six to twelve. Obviously, not only stress boundary conditions but also certain continuity conditions need to be combined to determine these unknown constants.

These total stresses should satisfy the following boundary conditions: first, at the bottom of the beam,

$${\sigma }_y^{+}=0 {\tau }_{xy}^{+}=0 \mathrm{at} y=h_1,$$

(35)

and at the top of the beam,

$${\sigma }_y^{-}=-q {\tau }_{xy}^{-}=0 \mathrm{at} y=-h_2.$$

(36)

Due to $2l>>h$ indicated above, the left and right sides become the secondary conditions, thus the de Saint-Venant’s Principle may be used to formulate the boundary conditions at two ends of the beam. At $x=\pm l$, three boundary conditions with integrals are as follows

$${\displaystyle {\int }_{-h_2}^0{\sigma }_x^{-}tdy+{\displaystyle {\int }_0^{h_1}{\sigma }_x^{+}tdy=0}},$$

(37)

$${\displaystyle {\int }_{-h_2}^0{\sigma }_x^{-}tydy+{\displaystyle {\int }_0^{h_1}{\sigma }_x^{+}tydy=0}},$$

(38)

$${\displaystyle {\int }_{-h_2}^0{\tau }_{xy}^{-}tdy+{\displaystyle {\int }_0^{h_1}{\tau }_{xy}^{+}tdy=-ql}}.$$

(39)

Obviously, the above boundary conditions are insufficient for solving the twelve unknown constants. Therefore, the continuity conditions at the neutral axis must be used, which gives

$${\sigma }_y^{+}={\sigma }_y^{-} {\tau }_{xy}^{+}={\tau }_{xy}^{-} \mathrm{at} y=0,$$

(40)

and the normal stress along x direction should be zero, that is,

$${\sigma }_x^{+}={\sigma }_x^{-}=0 \mathrm{at} y=0.$$

(41)

Eventually, the twelve unknown constants may be determined by the boundary conditions (35)–(39), in combination with the continuity conditions (40) and (41).

Now, let us begin with the application of continuity conditions. First, substituting the last two expressions of Equations (33) and (34) into Equation (40), we have

$$C^{+}=C^{-}, D^{+}=D^{-}.$$

(42)

Substituting the first expression of Equations (33) and (34) into Equation (41), we have

$${\sigma }_x^{+}=B^{+}{x}^2+2K^{+}=0, {\sigma }_x^{-}=B^{-}{x}^2+2K^{-}=0.$$

(43)

It should be noted here that the neutral axis of the beam is determined only under the action of mechanical load, which has nothing to do with the thermal load, thus the term $-\alpha E^{-}T(y)$ in ${\sigma }_x^{+}$ and ${\sigma }_x^{-}$ should not be included here. Thus, to satisfy (43) for all x, we obtain

$$B^{+}=B^{-}=K^{+}=K^{-}=0.$$

(44)

It is found that after the application of all continuity conditions, we obtain six relations concerning the twelve unknown constants, as shown in Equations (42) and (44).

Substituting the last two expressions of Equations (33) and (34) into Equations (35) and (36), we have

$$A^{+}{h}_1^3+B^{+}{h}_1^2+C^{+}{h}_1+D^{+}=0,$$

(45)

$$3A^{+}{h}_1^2+2B^{+}{h}_1+C^{+}=0,$$

(46)

$$-A^{-}{h}_2^3+B^{-}{h}_2^2-C^{-}{h}_2+D^{-}=-q,$$

(47)

and

$$3A^{-}{h}_2^2-2B^{-}{h}_2+C^{-}=0.$$

(48)

Substituting the last two expressions of Equations (33) and (34) into Equations (37) and (38), we have

$$\begin{array}{l}{\displaystyle {\int }_{-h_2}^0[-\alpha E^{-}T(y)+\frac{l^2}{2}(6A^{-}y+2B^{-})-2A^{-}{y}^3-2B^{-}{y}^2+6H^{-}y+2K^{-}]}dy\\ +{\displaystyle {\int }_0^{h_1}[-\alpha E^{-}T(y)+\frac{l^2}{2}(6A^{+}y+2B^{+})-2A^{+}{y}^3-2B^{+}{y}^2+6H^{+}y+2K^{+}]}dy=0\end{array},$$

(49)

and

$$\begin{array}{l}{\displaystyle {\int }_{-h_2}^0[-\alpha E^{-}T(y)+\frac{l^2}{2}(6A^{-}y+2B^{-})-2A^{-}{y}^3-2B^{-}{y}^2+6H^{-}y+2K^{-}]}ydy\\ +{\displaystyle {\int }_0^{h_1}[-\alpha E^{-}T(y)+\frac{l^2}{2}(6A^{+}y+2B^{+})-2A^{+}{y}^3-2B^{+}{y}^2+6H^{+}y+2K^{+}]}ydy=0\end{array}.$$

(50)

Using Equations (45)–(50) in combination of Equations (42) and (44), we obtain

$$\begin{array}{l}{A}^{+}=-\frac{q}{2h{h}_1^2},A^{-}=-\frac{q}{2h{h}_2^2},B^{+}=B^{-}=0,C^{+}=C^{-}=\frac{3q}{2h},D^{+}=D^{-}=-\frac{q{h}_1}{h},\\ H^{+}=\frac{J_1{h}_2}{3h{h}_1^2}+\frac{J_2}{2h{h}_1^2}+\frac{q{l}^2}{4h{h}_1^2}-\frac{q{N}_1}{10h},H^{-}=\frac{J_1{h}_1}{3h{h}_2^2}+\frac{J_1}{2h{h}_2^2}+\frac{q{l}^2}{4h{h}_2^2}-\frac{q{N}_2}{10h},\\ K^{+}=K^{-}=0\end{array},$$

(51)

in which, $J_1$ and $J_2$ are two integral terms about $T(y)$, $N_1$ and $N_2$ are two known constants, they are, respectively,

$$\begin{array}{l}{J}_1={\displaystyle {\int }_{-h_2}^0[-\alpha E^{-}T(y)]}dy+{\displaystyle {\int }_0^{h_1}[-\alpha E^{-}T(y)]}dy\\ J_2={\displaystyle {\int }_{-h_2}^0[-\alpha E^{-}T(y)]}ydy+{\displaystyle {\int }_0^{h_1}[-\alpha E^{-}T(y)]}ydy\end{array},$$

(52)

and

$$N_1=1-\frac{1}{6}\frac{h_2}{h_1}+\frac{1}{6}{\left(\frac{h_2}{h_1}\right)}^2,N_2=1-\frac{1}{6}\frac{h_1}{h_2}+\frac{1}{6}{\left(\frac{h_1}{h_2}\right)}^2.$$

(53)

Up to now, Equation (39) has not been used. Substituting the known solution into Equation (39), it is found that it is naturally satisfied. Lastly, substituting the known constants into Equations (33) and (34), we have the final stress for the tensile part $0\le y\le h_1$,

$$\{\begin{array}{l}{\sigma }_x^{+}=-\alpha E^{-}T(y)+\frac{3q}{2h{h}_1^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_1^2}-\frac{3}{5}{N}_1\right)+\left(\frac{2J_1{h}_2}{h{h}_1^2}+\frac{3J_2}{h{h}_1^2}\right)y\\ {\sigma }_y^{+}=-\frac{q}{2h{h}_1^2}{y}^3+\frac{3q}{2h}y-\frac{q{h}_1}{h}\\ {\tau }_{xy}^{+}=\frac{3q}{2h{h}_1^2}x{y}^2-\frac{3q}{2h}x\end{array}$$

(54)

and for the compressive part $-h_2\le y\le 0$,

$$\{\begin{array}{l}{\sigma }_x^{-}=-\alpha E^{-}T(y)+\frac{3q}{2h{h}_2^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_2^2}-\frac{3}{5}{N}_2\right)+\left(\frac{2J_1{h}_1}{h{h}_2^2}+\frac{3J_2}{h{h}_2^2}\right)y\\ {\sigma }_y^{-}=-\frac{q}{2h{h}_2^2}{y}^3+\frac{3q}{2h}y-\frac{q{h}_1}{h}\\ {\tau }_{xy}^{-}=\frac{3q}{2h{h}_2^2}x{y}^2-\frac{3q}{2h}x\end{array}$$

(55)

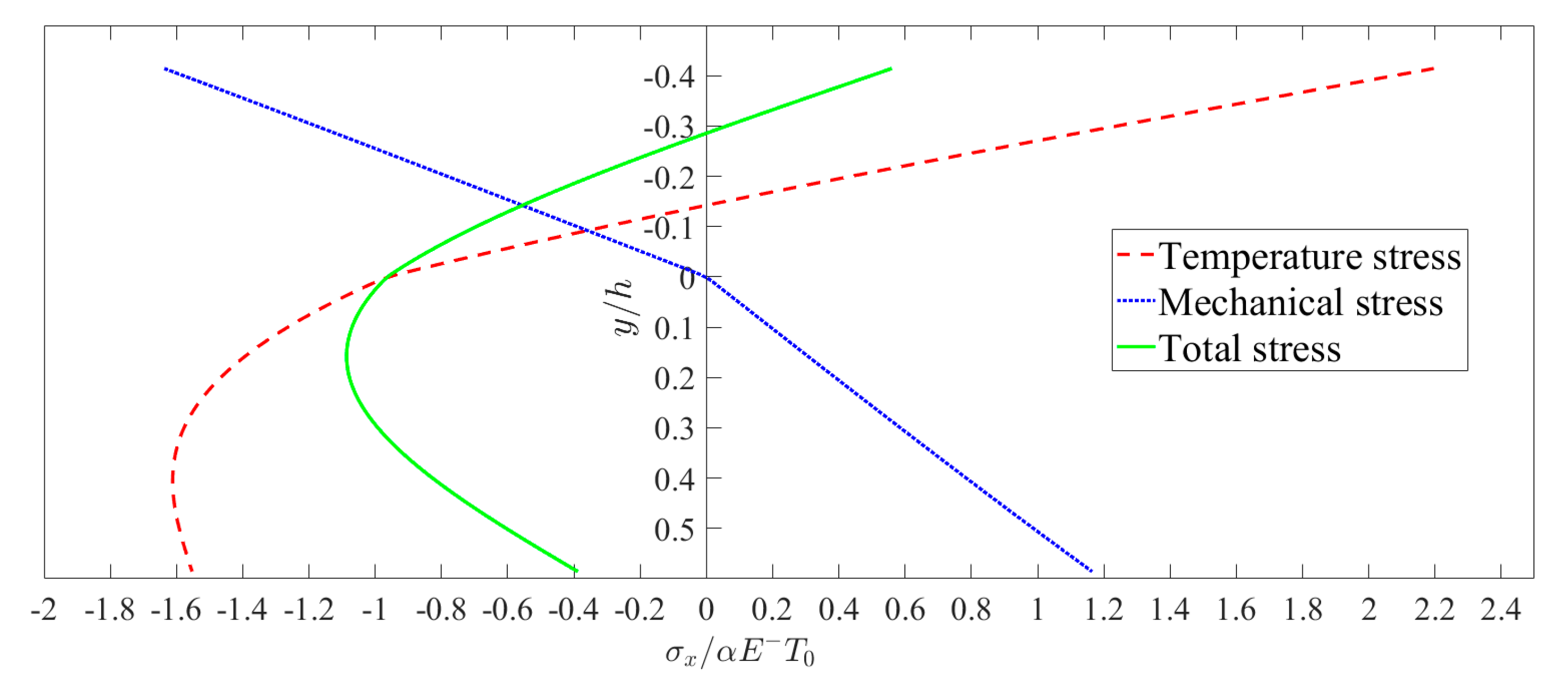
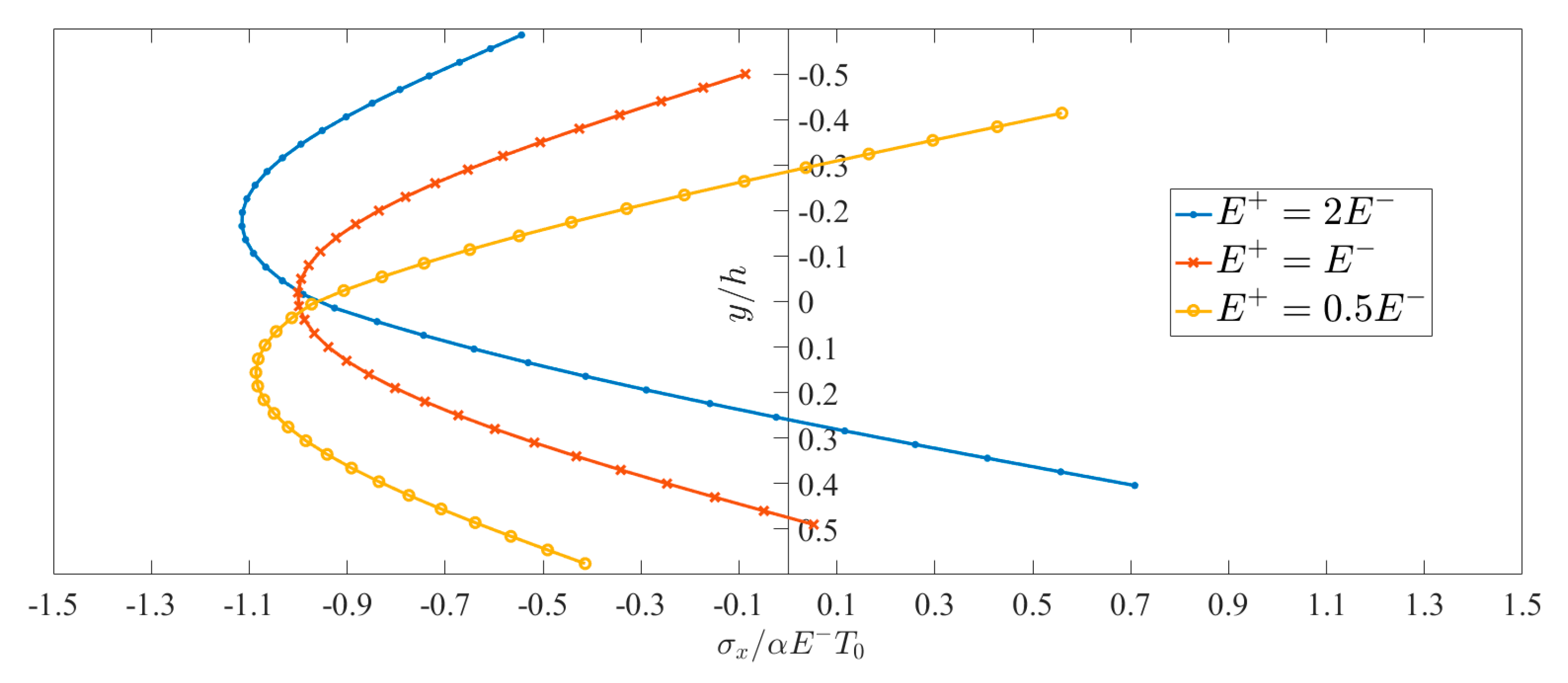
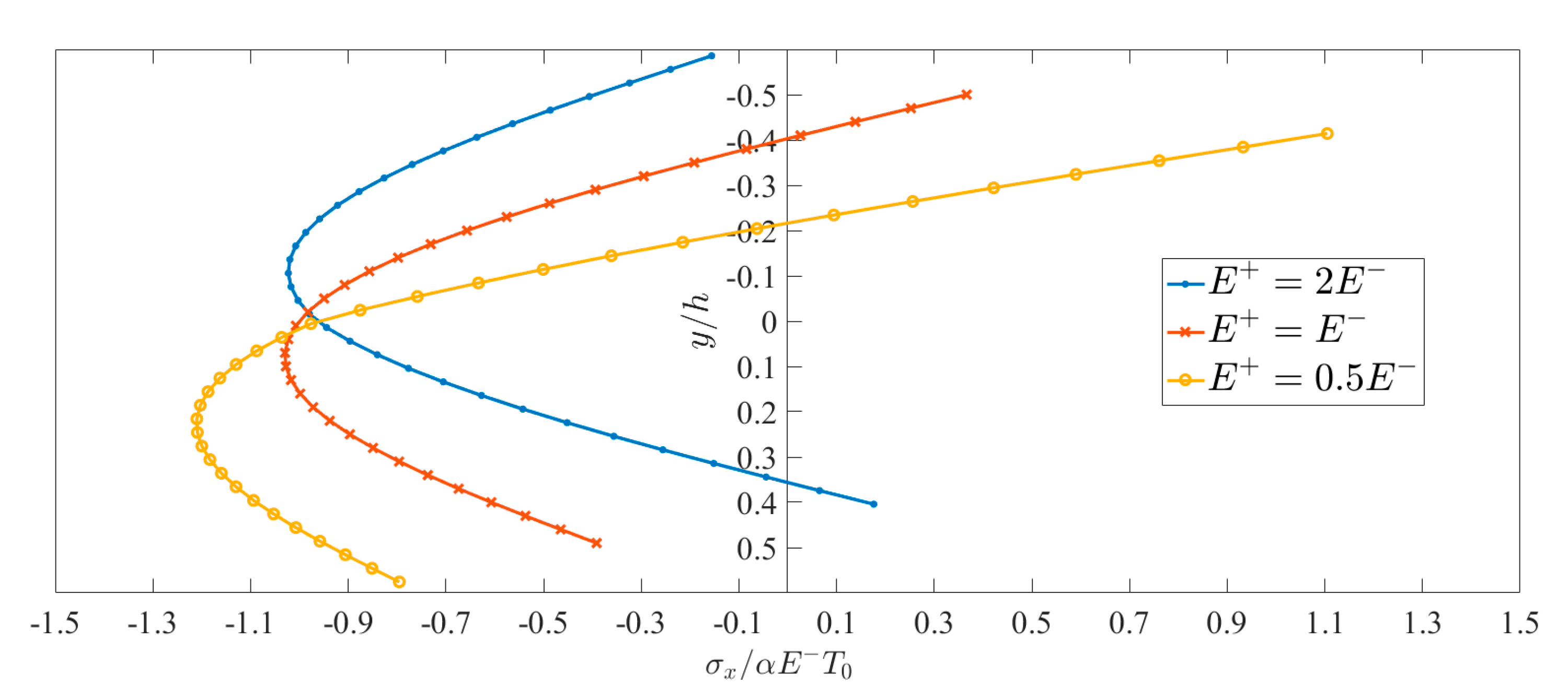
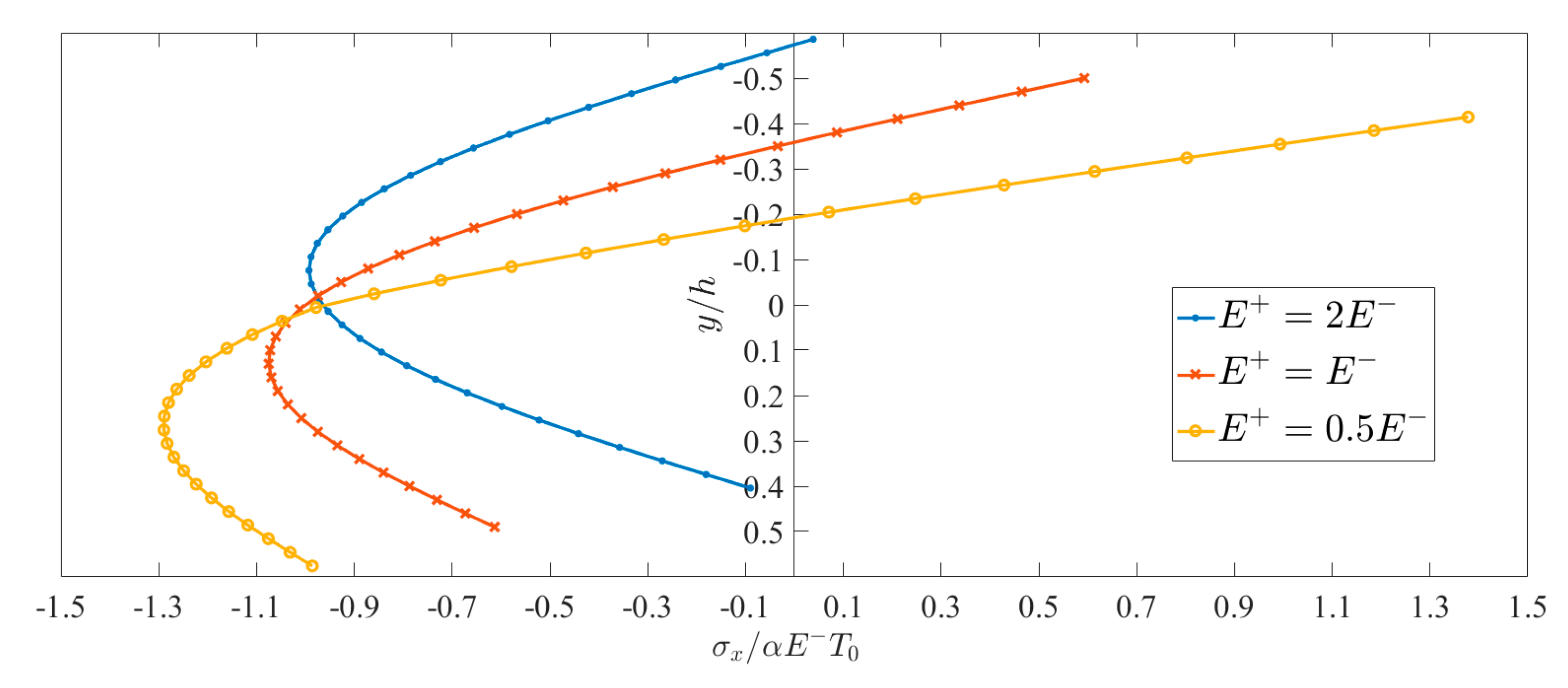
6. Results and Discussions

6.1. A Computational Example

If the function of the temperature rise is known, for example, we assume the highest temperature rise takes place at the middle of the beam and the lowest temperature rise at the up and down edges, this temperature rise may be simulated with a function as

$$T(y)=T_0\cos \frac{y-y_0}{h}\pi ,$$

(56)

in which $T_0$ is the temperature at the center and $y_0$ is the distance of the geometric center of the beam from the neutral axis, see Figure 2. Via Equation (7) and $h/2+y_0=h_1$ (or $h/2-y_0=h_2$), the magnitude of $y_0$ may be determined as

$$y_0=\frac{\sqrt{E^{-}}-\sqrt{E^{+}}}{\sqrt{E^{-}}+\sqrt{E^{+}}}\frac{h}{2}.$$

(57)

Substituting the known $T(y)$ into Equation (52), the two integrals may be computed as

$$\begin{array}{l}{J}_1=\frac{-\alpha E^{-}{T}_{0}h}{\pi }\left(\sin \frac{h_2+y_0}{h}\pi +\sin \frac{h_1-y_0}{h}\pi \right)\\ J_2=\frac{\alpha E^{-}{T}_{0}h}{{\pi }^2}\left(\pi h_2\sin \frac{h_2+y_0}{h}\pi -\pi h_1\sin \frac{h_1-y_0}{h}\pi +h\cos \frac{h_2+y_0}{h}\pi -h\cos \frac{h_1-y_0}{h}\pi \right)\end{array}.$$

(58)

Thus, the normal stress along x direction is, for $0\le y\le h_1$,

$$\begin{array}{l}{\sigma }_x^{+}=-\alpha E^{-}{T}_0\cos \frac{y-y_0}{h}\pi +\frac{3q}{2h{h}_1^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_1^2}-\frac{3}{5}{N}_1\right)\\ +\alpha E^{-}{T}_0\left[\begin{array}{l}-\frac{2h_2}{\pi h_1^2}\left(\sin \frac{h_2+y_0}{h}\pi +\sin \frac{h_1-y_0}{h}\pi \right)\\ +\frac{3}{{\pi }^2{h}_1^2}\left(\pi h_2\sin \frac{h_2+y_0}{h}\pi -\pi h_1\sin \frac{h_1-y_0}{h}\pi +h\cos \frac{h_2+y_0}{h}\pi -h\cos \frac{h_1-y_0}{h}\pi \right)\end{array}\right]y\end{array}.$$

(59)

and for $-h_2\le y\le 0$,

$$\begin{array}{l}{\sigma }_x^{-}=-\alpha E^{-}{T}_0\cos \frac{y-y_0}{h}\pi +\frac{3q}{2h{h}_2^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_2^2}-\frac{3}{5}{N}_2\right)\\ +\alpha E^{-}{T}_0\left[\begin{array}{l}-\frac{2h_1}{\pi h_2^2}\left(\sin \frac{h_2+y_0}{h}\pi +\sin \frac{h_1-y_0}{h}\pi \right)\\ +\frac{3}{{\pi }^2{h}_2^2}\left(\pi h_2\sin \frac{h_2+y_0}{h}\pi -\pi h_1\sin \frac{h_1-y_0}{h}\pi +h\cos \frac{h_2+y_0}{h}\pi -h\cos \frac{h_1-y_0}{h}\pi \right)\end{array}\right]y\end{array}.$$

(60)

Note that there are four terms in the above stress expression, in which the first and the fourth are from the temperature stress, and the second and the third are from mechanical stress. In the mechanical stress, the second stands for the stress from the bending moment in a one-dimensional solution, while the third stands for the rectified term from a two-dimensional elasticity solution.

When $E^{+}=E^{-}=E$, we have $h_1=h_2=h/2$, $y_0=0$, $J_1=-2E\alpha T_{0}h/\pi$,$J_2=0$ and $N_1=N_2=1$. Substituting them into Equations (59) and (60), the stress expression without bimodular effect is obtained as follows

$${\sigma }_x=-\alpha E{T}_0\left(\frac{8}{\pi }\frac{y}{h}+\cos \frac{y}{h}\pi \right)+\frac{6q}{h^3}(l^2-x^2)y+q\frac{y}{h}\left(4\frac{y^2}{h^2}-\frac{3}{5}\right).$$

(61)

Thus, the regression of the solution is satisfied, which also verifies the correctness of the derivation from the side.

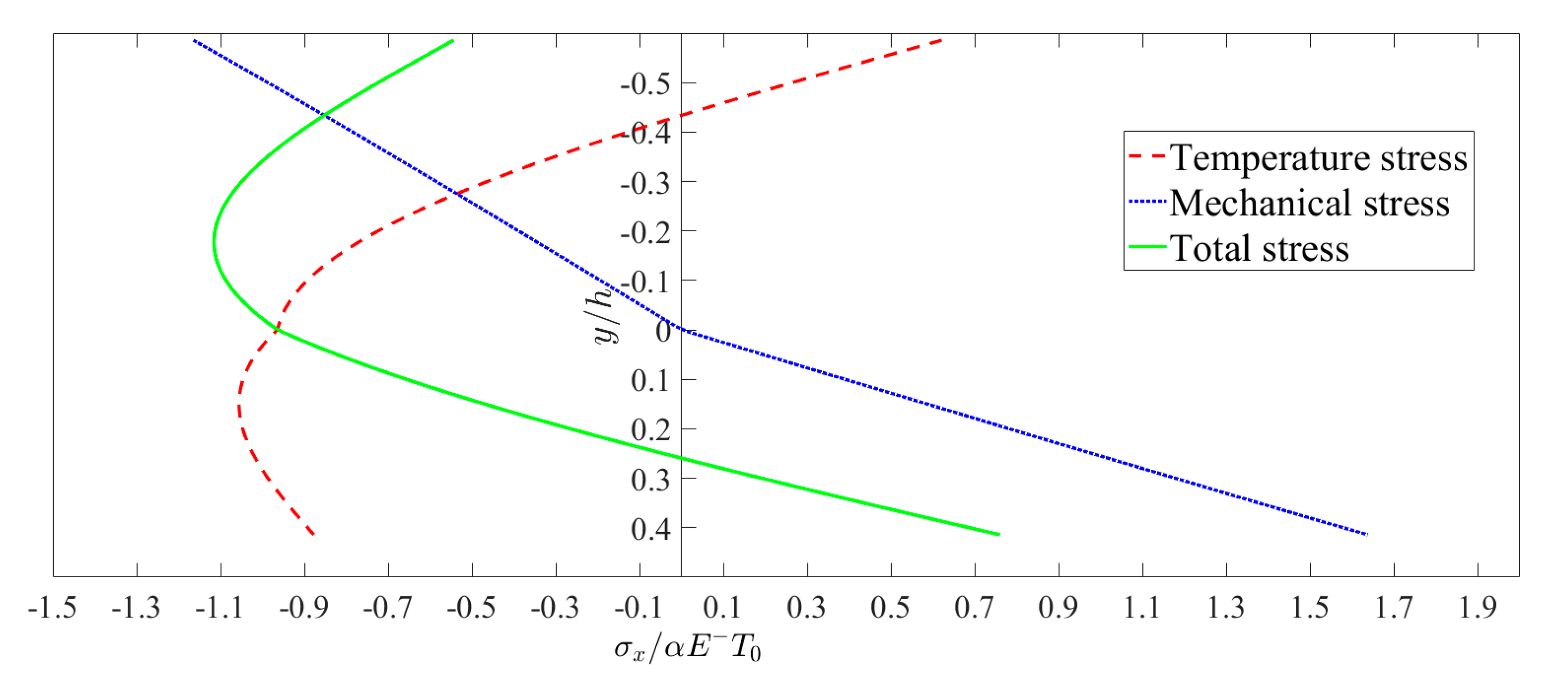
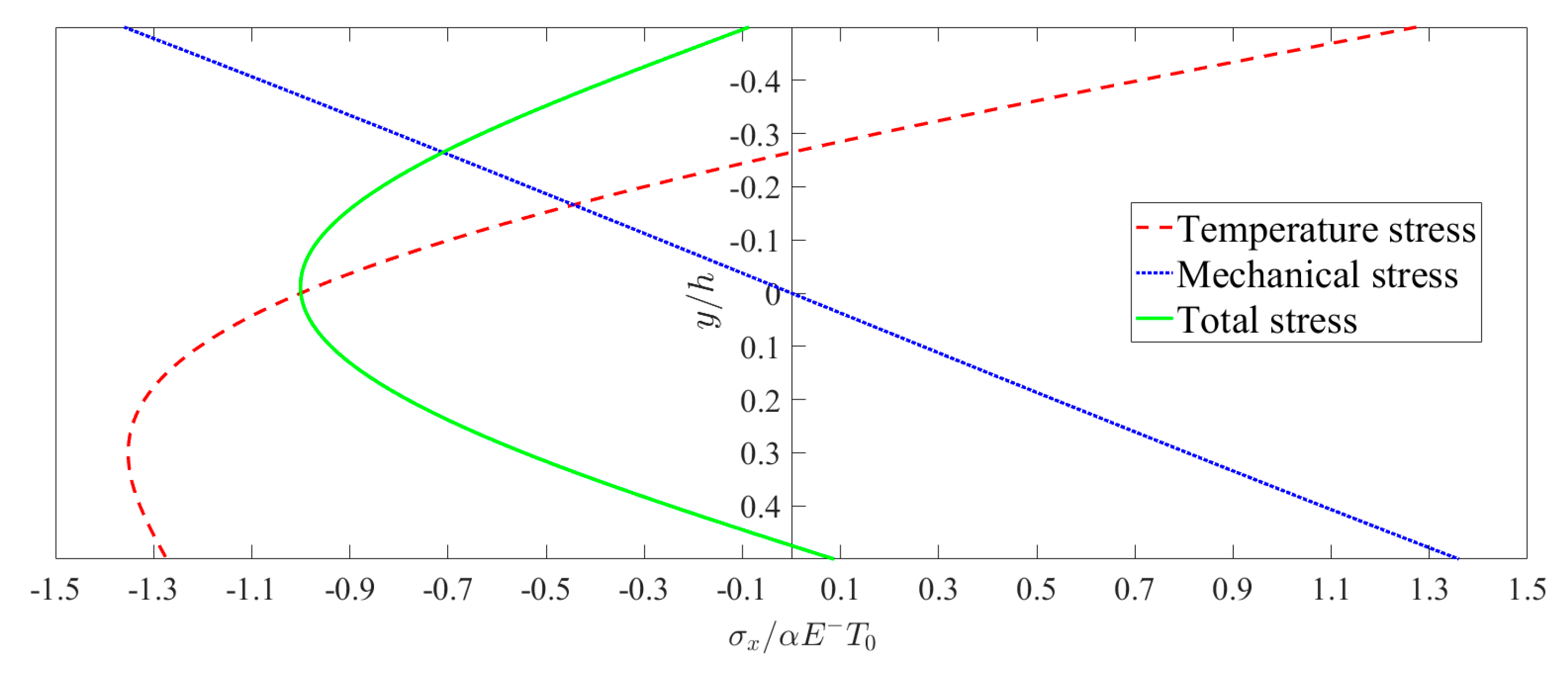
6.2. Bimodular Effect on Thermoelasticity Solution

For analyzing the bimodular effect on the final stress ${\sigma }_x$, the following three typical cases relating to modulus are adopted: (1) $E^{+}=2E^{-}$, (2) $E^{+}=E^{-}$ and (3) $E^{+}=0.5E^{-}$, which correspond to, respectively, the tensile modulus is greater than, equal to and less than the compressive modulus. Thus, the tensile modulus and the compressive one, as well as the tensile section height, the compressive one and the distance between the geometrical middle surface and the neutral layer, are given in

Table 1. Values for three bimodular cases.

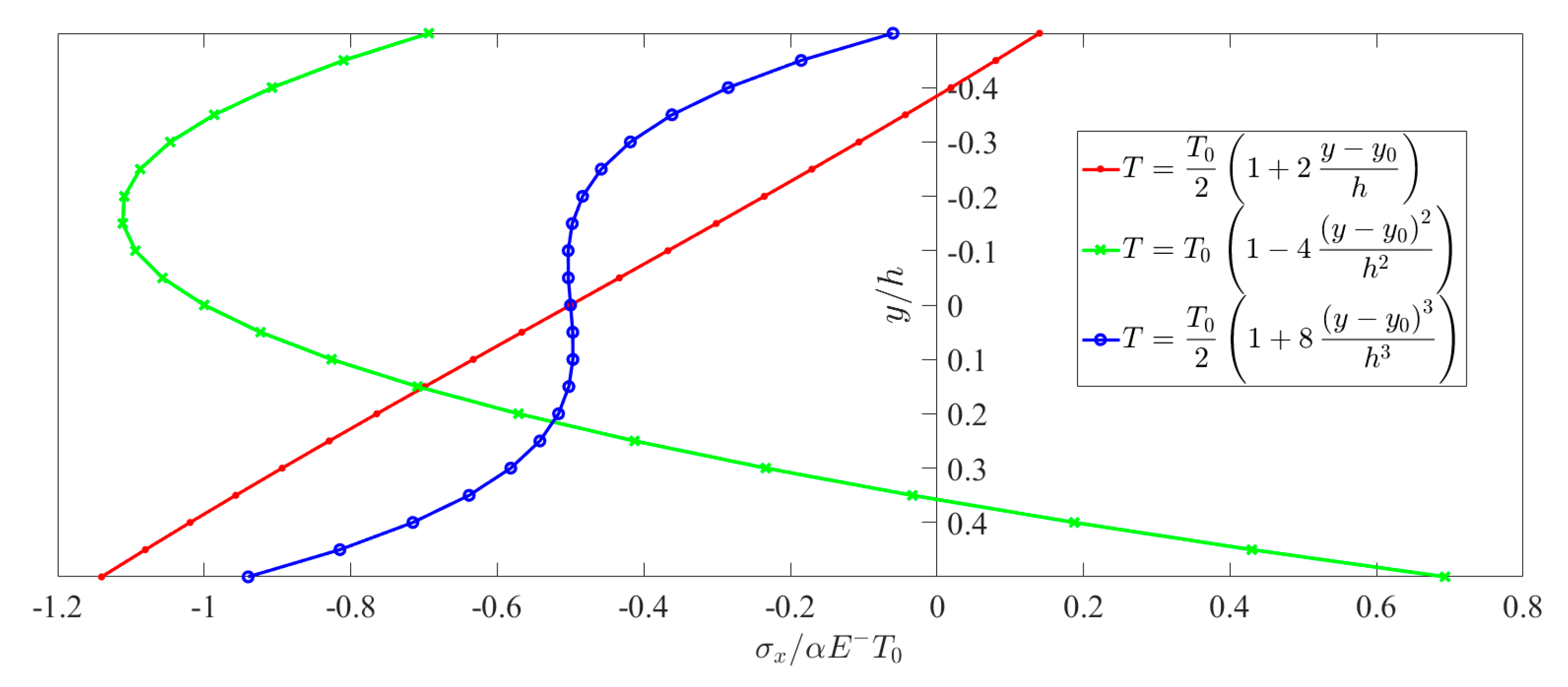
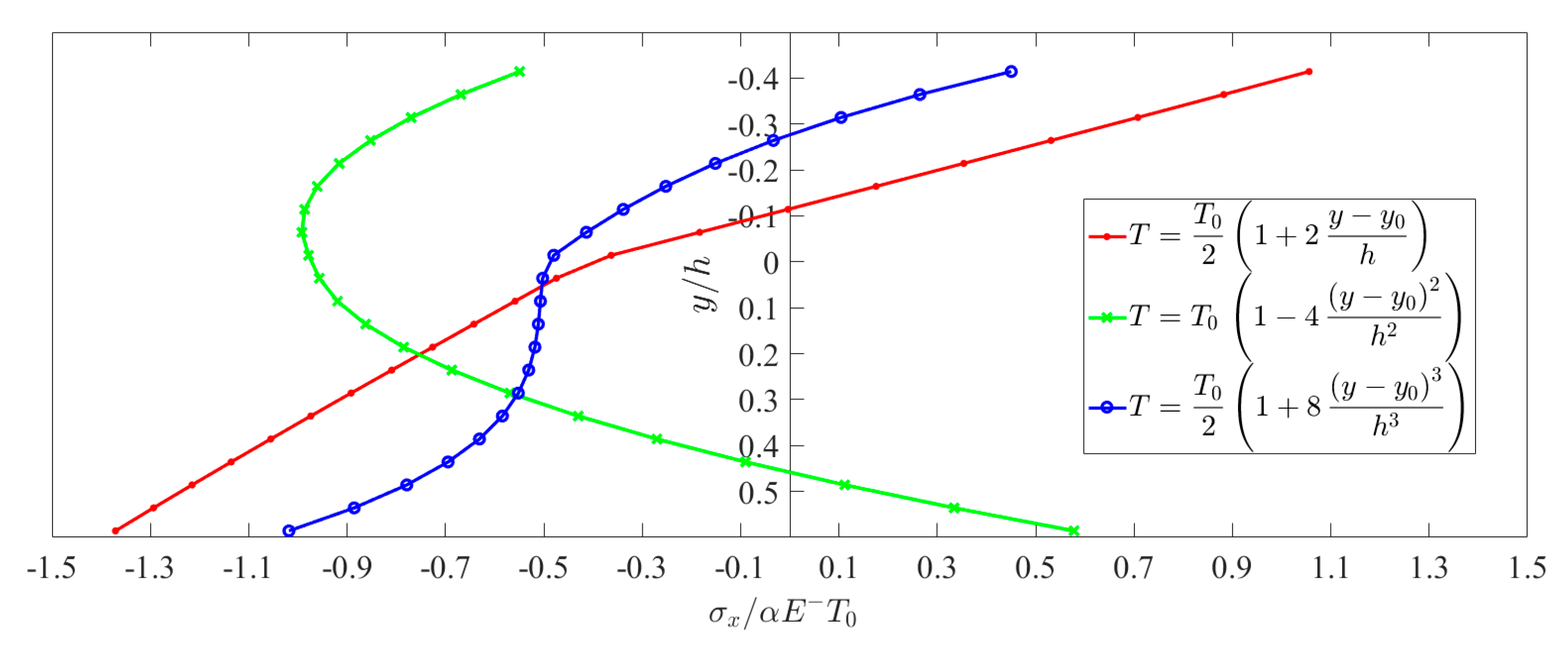
Bimodular Cases	Tensile Modulus	Compressive Modulus	${\mathit{h}}_1/\mathit{h}$	${\mathit{h}}_2/\mathit{h}$	${\mathit{y}}_0/\mathit{h}$
$E^{+}>E^{-}$	$2E^{-}$	$E^{-}$	0.4142	0.5858	−0.0858
$E^{+}=E^{-}$	$E^{-}$	$E^{-}$	0.5	0.5	0
$E^{+}<E^{-}$	$0.5E^{-}$	$E^{-}$	0.5858	0.4142	0.0858

in dimensionless form.

For a better understanding of the effects of the parameters on the stress, all figures in this section are plotted in dimensionless form, in which the x-axis stands for the dimensionless stress ${\sigma }_x/\alpha E^{-}{T}_0$ and the y-axis for the dimensionless section height $y/h$. On the cross section of the beam midspan, the bending moment achieves the most, thus we take this section $x=0$ as our analysis object. In addition, it is also necessary to give the relative magnitudes between $\alpha E^{-}{T}_0$ and the intensity q of the uniformly distributed loads, thus after considering the real case, we take the following three ratios: (1) $\alpha E^{-}{T}_0/q=20$, (2) $\alpha E^{-}{T}_0/q=30$ and (3) $\alpha E^{-}{T}_0/q=40$. At the same time, the ratio of beam span to beam height is assumed to be 6, that is, $2l/h=6$, to agree with the geometrical characteristic of a two-dimensional deep beam.

Figure 4, Figure 5 and Figure 6 show the stress composition from the temperature stress, the mechanical stress, and total stress under three bimodular cases, in which only the curves when $\alpha E^{-}{T}_0/q=20$ are given here, and the other two cases, that is, $\alpha E^{-}{T}_0/q=30$ and $\alpha E^{-}{T}_0/q=40$, are not presented here since they are basically the same as Figure 4, Figure 5 and Figure 6.

From Figure 4, Figure 5 and Figure 6, it is easy to see that

(i) Under three cases of different moduli, the mechanical stresses all present as obviously linear, although the stress ${\sigma }_x$ is the cubic relation with respect to y; this indicates that the second term in the stress expressions is dominant, compared to the third, whose influence on the mechanical stress is relatively small.

(ii) When $E^{+}=E^{-}$, the slopes of the straight line are consistent in the tensile and compressive parts since the stress growth ratio is constant with the strain (which is proportional to the distance along the y-axis); when $E^{+}=2E^{-}$, the slope of the straight line in the compressive part is greater than that in the tensile part, showing that when $E^{+}>E^{-}$, the stress growth has slowed down; when $E^{+}=0.5E^{-}$, the slope of the straight line in the compressive part is smaller than that in the tensile part, showing that when $E^{+}<E^{-}$, the stress growth has accelerated.

(iii) The temperature stress curves basically present the shape of a cosine function, having no up and down symmetry. After superposition with the mechanical stress curves, which are linear, the total stress curves still present the shape of a cosine function, only having their vertices somewhat offset.

Figure 7, Figure 8 and Figure 9 show that the total stress when $\alpha E^{-}{T}_0/q=20$, $\alpha E^{-}{T}_0/q=30$ and $\alpha E^{-}{T}_0/q=40$ varies with the section height direction, in which three bimodular cases are given.

From Figure 7, Figure 8 and Figure 9, it is easy to see that

(i) Under three cases of different moduli, and also for $\alpha E^{-}{T}_0/q=20$, $\alpha E^{-}{T}_0/q=30$ and $\alpha E^{-}{T}_0/q=40$, the total stress curves all present the shape of a cosine function, having no up and down symmetry, and their vertices are at different places.

(ii) With the decrease of q, or alternatively, with the increase of $\alpha E^{-}{T}_0$, that is, from Figure 7, Figure 8 and Figure 9, we may find that when $\alpha E^{-}{T}_0/q=20$, there are some tensile stresses in the lower part of the beam (see Figure 7), when $\alpha E^{-}{T}_0/q=30$, there are only small quantities of tensile stresses remaining (see Figure 8), and when $\alpha E^{-}{T}_0/q=40$, there are no any tensile stresses in the lower part (see Figure 9). The tensile stress situation in the upper part of the beam is just the opposite.

(iii) Under three cases of different moduli, and also for $\alpha E^{-}{T}_0/q=20$, $\alpha E^{-}{T}_0/q=30$ and $\alpha E^{-}{T}_0/q=40$, most of the total stresses are in compression, this reveals that after the introduction of the temperature stress, the original stress state with tension in the lower part and compression in the upper part, now gradually transits to the status almost in compression. This phenomenon is especially obvious for the case $E^{+}=2E^{-}$.

6.3. Temperature Effect on Thermoelasticity Solution

For analyzing the temperature effect on the thermoelasticity solution, the three modes of temperature rise, including linear, square, and cubic relations, are taken to discuss the different modes of temperature rise on the thermal stress, in which the maximum temperature rise keeps $T_0$ in the three modes. First, for the linear temperature rise, we have

$$T(y)=\frac{T_0}{2}\left[1+\frac{2\left(y-y_0\right)}{h}\right].$$

(62)

Substituting the known $T(y)$ into Equation (52), the two integrals give

$$\begin{array}{l}{J}_1=\frac{-\alpha E^{-}{T}_0}{2}(\frac{h_1-h_2}{2}+h-2y_0)\\ J_2=\frac{-\alpha E^{-}{T}_0}{2}\left[\frac{2(h_1^3+h_2^3)}{3h}+\frac{h_1^2-h_2^2}{2}(1-\frac{2y_0}{h})\right]\end{array}.$$

(63)

Thus, the normal stress along x direction is, for $0\le y\le h_1$

$$\begin{array}{l}{\sigma }_x^{+}=-\alpha E^{-}\frac{T_0}{2}[1+\frac{2(y-y_0)}{h}]+\frac{3q}{2h{h}_1^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_1^2}-\frac{3}{5}{N}_1\right)\\ -\frac{\alpha E^{-}{T}_0}{2}\left\{\begin{array}{l}\frac{2h_2}{h{h}_1^2}\left(\frac{h_1-h_2}{2}+h-2y_0\right)\\ +\frac{3}{h{h}_1^2}\left[\frac{2(h_1^3+h_2^3)}{3h}+\frac{h_1^2-h_2^2}{2}(1-\frac{2y_0}{h})\right]\end{array}\right\}y\end{array},$$

(64)

and for $-h_2\le y\le 0$

$$\begin{array}{l}{\sigma }_x^{-}=-\alpha E^{-}\frac{T_0}{2}[1+\frac{2(y-y_0)}{h}]+\frac{3q}{2h{h}_2^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_2^2}-\frac{3}{5}{N}_2\right)\\ -\frac{\alpha E^{-}{T}_0}{2}\left\{\begin{array}{l}\frac{2h_1}{h{h}_2^2}\left(\frac{h_1-h_2}{2}+h-2y_0\right)\\ +\frac{3}{h{h}_2^2}\left[\frac{2(h_1^3+h_2^3)}{3h}+\frac{h_1^2-h_2^2}{2}(1-\frac{2y_0}{h})\right]\end{array}\right\}y\end{array}.$$

(65)

Similarly, for the square temperature rise, we have

$$T(y)=T_0\left[1-\frac{4{\left(y-y_0\right)}^2}{h^2}\right],$$

(66)

$$\begin{array}{l}{J}_1=-\alpha E^{-}{T}_0[-\frac{4\left(h_1^2+h_2^3\right)}{3h^2}+\frac{y_0(h_1-h_2)}{h}+h-\frac{4y_0^2}{h}]\\ J_2=-\alpha E^{-}{T}_0\left[-\frac{h_1^4-h_2^4}{h^2}+\frac{8y_0(h_1^3+h_2^3)}{3h^2}+\frac{h_1^2-h_2^2}{2}(1-\frac{4y_0^2}{h^2})\right]\end{array}.$$

(67)

Thus, the normal stress along x direction is, for $0\le y\le h_1$

$$\begin{array}{l}{\sigma }_x^{+}=-\alpha E^{-}{T}_0[1-\frac{4{(y-y_0)}^2}{h^2}]+\frac{3q}{2h{h}_1^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_1^2}-\frac{3}{5}{N}_1\right)\\ -\alpha E^{-}{T}_0\left\{\begin{array}{l}\frac{2h_2}{h{h}_1^2}\left[-\frac{4(h_1^3+h_2^3)}{3h^2}+\frac{y_0(h_1-h_2)}{h}+h-\frac{4y_0^2}{h}\right]\\ +\frac{3}{h{h}_1^2}[-\frac{h_1^4-h_2^4}{h^2}+\frac{8y_0(h_1^3+h_2^3)}{3h^2}+\frac{h_1^2-h_2^2}{2}(1-\frac{4y_0^2}{h^2})]\end{array}\right\}y\end{array},$$

(68)

and for $-h_2\le y\le 0$,

$$\begin{array}{l}{\sigma }_x^{-}=-\alpha E^{-}{T}_0[1-\frac{4{(y-y_0)}^2}{h^2}]+\frac{3q}{2h{h}_2^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_2^2}-\frac{3}{5}{N}_2\right)\\ -\alpha E^{-}{T}_0\left\{\begin{array}{l}\frac{2h_1}{h{h}_2^2}\left[-\frac{4(h_1^3+h_2^3)}{3h^2}+\frac{y_0(h_1-h_2)}{h}+h-\frac{4y_0^2}{h}\right]\\ +\frac{3}{h{h}_2^2}[-\frac{h_1^4-h_2^4}{h^2}+\frac{8y_0(h_1^3+h_2^3)}{3h^2}+\frac{h_1^2-h_2^2}{2}(1-\frac{4y_0^2}{h^2})]\end{array}\right\}y\end{array}.$$

(69)

For the cubic temperature rise, we have

$$T(y)=\frac{T_0}{2}\left[1+\frac{8{\left(y-y_0\right)}^3}{h^3}\right],$$

(70)

$$\begin{array}{l}{J}_1=\frac{-\alpha E^{-}{T}_0}{2}\left[\frac{2(h_1^4-h_2^4)}{h^3}-\frac{8y_0(h_1^3+h_2^3)}{h^3}+\frac{12y_0^2(h_1-h_2)}{h^2}+h-\frac{8y_0^3}{h^2}\right],\\ J_2=\frac{-\alpha E^{-}{T}_0}{2}\left[\frac{8(h_1^5+h_2^5)}{5h^3}-\frac{6y_0(h_1^4-h_2^4)}{h^3}+\frac{8y_0^2(h_1^3+h_2^3)}{h^3}+\frac{h_1^2-h_2^2}{2}(1-\frac{8y_0^3}{h^3})\right]\end{array},$$

(71)

Thus, the normal stress along x direction is, for $0\le y\le h_1$,

$$\begin{array}{l}{\sigma }_x^{+}=-\alpha E^{-}\frac{T_0}{2}[1+\frac{8{(y-y_0)}^3}{h^3}]+\frac{3q}{2h{h}_1^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_1^2}-\frac{3}{5}{N}_1\right)\\ -\frac{\alpha E^{-}{T}_0}{2}\left\{\begin{array}{l}\frac{2h_2}{h{h}_1^2}\left[\frac{2(h_1^4-h_2^4)}{h^3}-\frac{8y_0(h_1^3+h_2^3)}{h^3}+\frac{12y_0^2(h_1-h_2)}{h^2}+h-\frac{8y_0^3}{h^2}\right]\\ +\frac{3}{h{h}_1^2}\left[\frac{8(h_1^5+h_2^5)}{5h^3}-\frac{6y^0(h_1^4-h_2^4)}{h^3}+\frac{8y_0^2(h_1^3+h_2^3)}{h^3}+\frac{h_1^2-h_2^2}{2}(1-\frac{8y_0^3}{h^3})\right]\end{array}\right\}y\end{array}$$

(72)

and for $-h_2\le y\le 0$

$$\begin{array}{l}{\sigma }_x^{-}=-\alpha E^{-}\frac{T_0}{2}[1+\frac{8{(y-y_0)}^3}{h^3}]+\frac{3q}{2h{h}_2^2}(l^2-x^2)y+\frac{q}{h}y\left(\frac{y^2}{h_2^2}-\frac{3}{5}{N}_2\right)\\ -\frac{\alpha E^{-}{T}_0}{2}\left\{\begin{array}{l}\frac{2h_1}{h{h}_2^2}\left[\frac{2(h_1^4-h_2^4)}{h^3}-\frac{8y_0(h_1^3+h_2^3)}{h^3}+\frac{12y_0^2(h_1-h_2)}{h^2}+h-\frac{8y_0^3}{h^2}\right]\\ +\frac{3}{h{h}_2^2}[\frac{8(h_1^5+h_2^5)}{5h^3}-\frac{6y_0(h_1^4-h_2^4)}{h^3}+\frac{8y_0^2(h_1^3+h_2^3)}{h^3}+\frac{h_1^2-h_2^2}{2}(1-\frac{8y_0^3}{h^3})]\end{array}\right\}y\end{array}.$$

(73)

Taking the case $\alpha E^{-}{T}_0/q=20$ as an example, the total thermal stress curves are plotted under the three modes of temperature rise, as shown in Figure 10, Figure 11 and Figure 12, which correspond to the three modulus cases, $E^{+}=2E^{-}$, $E^{+}=E^{-}$ and $E^{+}=0.5E^{-}$, respectively. Figure 10, Figure 11 and Figure 12 show that the variation trends of the three thermal stress curves are basically the same as those from the three modes of temperature rise, in which the curve from the square relation is basically consistent with the curve from the cosine relation, with a vertex but no up and down symmetry.

Table 2. Dimensionless thermal stresses and amplitude values.

Bimodular Cases	Linear			Square			Cubic
	Top Stress	Bottom Stress	Amplit. Value 1	Max Tens. Stress	Max Compr. Stress	Amplit. Value	Top Stress	Bottom Stress	Amplit. Value
$E^{+}=2E^{-}$	−0.43	−0.71	0.28	0.96	−1.25	2.21	−0.42	−0.83	0.41
$E^{+}=E^{-}$	0.14	−1.14	1.28	0.69	−1.11	1.80	−0.06	−0.94	0.88
$E^{+}=0.5E^{-}$	1.06	−1.37	2.43	0.58	−1.00	1.58	0.45	−1.02	1.47

¹ If two stresses are the same positive–negative sign, take the absolute value after their subtraction; if they are the contrary sign, take the sum of the two abstract values of two stresses.

lists dimensionless thermal stresses for the linear, square, and cubic rise modes as well as the variations of amplitude value throughout the beam. The computation of amplitude value is, for the linear and cubic relation, from the top to bottom of the beam; and for the square relation, is from the maximum tensile stress to maximum compressive one. It is easy to see from Table 2 that, under the temperature rise mode of square relation, the amplitude is 2.21 for $E^{+}=2E^{-}$, versus 1.80 for $E^{+}=E^{-}$, and decreases to 1.58 for $E^{+}=0.5E^{-}$; under the temperature rise mode of linear and cubic relations, the case is just the opposite. Under the linear rise, the amplitude is 0.28 for $E^{+}=2E^{-}$, versus 1.28 for $E^{+}=E^{-}$, and increases to 2.43 for $E^{+}=0.5E^{-}$; and under the cubic rise, the amplitude is 0.41 for $E^{+}=2E^{-}$, versus 0.88 for $E^{+}=E^{-}$, and increases to 1.47 for $E^{+}=0.5E^{-}$. This indicates that if the highest temperature rise takes place in the middle of the beam, like the square relation, more attention should be given when $E^{+}>E^{-}$, and if the highest temperature rise takes place at the bottom of the beam, like the linear and cubic relations, more attention should be given when $E^{+}<E^{-}$.

7. Concluding Remarks

In this study, based on the simplified mechanical model on regional segmentation of tension and compression, we obtained a two-dimensional thermoelasticity solution of a bimodular rectangular section beam under the combination action of thermal and mechanical loads. The following conclusions can be drawn.

(i) After the introduction of the bimodular effect, there is no essential change in the form of displacement governing the equation and the composition of the solution since the modulus of elasticity is not included in Lamé’s displacement equation.

(ii) The stress superposition of special solution and supplement solution shows clearly the stress composition contributed by the thermal load and mechanical load, respectively. Which one is dominant will depend on the relative magnitude between the external load q and the thermal stress term $\alpha E^{-}{T}_0$.

(iii) Different temperature rise modes will influence the distribution of thermal stresses. The analysis of the amplitude values of thermal stresses indicates that if the highest temperature rise takes place in the middle of the beam, the amplitude varies from 2.21 ($E^{+}=2E^{-}$) to 1.58 ($E^{+}=0.5E^{-}$); while if the highest temperature rise takes place at the bottom of the beam, the case is just the opposite. Specifically, the amplitude varies from 0.28 to 2.43 for the linear rise and from 0.41 to 1.47 for the cubic rise.

(iv) The introduction of bimodular characteristics will bring great change in the total stress. More specifically, when the tensile modulus is greater than the compressive one, most of the total stresses are in compression, which should be give more consideration in the analysis and design of bimodular material beams.

In addition, this study may be further extended into the field of functionally graded materials. In this case, however, the obtained solution of the Lamé displacement equation will be somewhat challenging, due to the fact that not only the modulus of elasticity but also some redundant strain terms will appear in this equation. The changes of the governing equation and the investigation into the corresponding solving methods (for example, the application of the multi-parameter perturbation method [30]) will present us with huge challenges. At the same time, in a thermal environment, the investigation into bimodular functionally graded piezoelectric beams [31] as well as into carbon nanotube-reinforced composite curved sandwich nanobeams [32] points out our future research direction. The relevant work is in progress.