Abstract
Many infectious diseases are deadly to humans. The Aedes aegypi mosquito is the principal vector of infectious diseases that include chikungunya, dengue, yellow fever, and zika. Some factors such as survival time and aging are vital in its development and capacity to transmit the pathogens, which in turn are affected by environmental factors such as temperature. In this paper, we consider aging as the biological wear and tear presented in some mosquito populations over time, whereas survival is considered as the maximum time that a mosquito lives. We propose statistical methods that are commonly used in engineering for reliability analysis to compare transmission riskiness among different mosquitoes. We conducted a case study in three Colombian cities: Bello, Riohacha, and Villavicencio. In this study, we detected that the Aedes aegypi female mosquitoes in Bello live longer than in Riohacha and Villavicencio, and the females in Riohacha live longer than those in Villavicencio. Regarding aging, the females from Riohacha age slower than in Villavicencio and the latter age slower than in Bello. Mosquito populations that age slower are considered young and the other ones are old. In addition, we detected that the females from Bello in the temperature range of 27 C–28 C age slower than those in Bello at higher temperatures. In general, a young female has a higher risk of transmitting a disease to humans than an old female, regardless of its survival time. These findings have not been previously reported in studies of this type of infectious diseases and contributed to new knowledge in biomedicine.
1. Introduction, Case Study, and Description
1.1. Introduction
Many infectious diseases have been very important for epidemiology, prevention, and virology. The Aedes aegypti is a cosmopolitan mosquito and the principal vector of infectious diseases such as chikungunya, dengue, yellow fever, and zika [1,2,3,4]. The female mosquitoes transmit these diseases by biting infectious hosts, spreading over greater distances, and surviving until they become infectious vectors and biting other susceptible humans [5]. This phenomenon, which describes the ability of a mosquito population to spread a disease [6,7], is a risk to the human population. Some factors that affect this ability are aging and survival time [8,9,10,11].
In the present study, we considered: (i) the term aging as the biological wear and tear presented in a mosquito population over time; and (ii) the term survival as the maximum time that a mosquito lives. Therefore, a mosquito population might long-lived but faster aging over time. We call this a long-lived but old population. The opposite case occurs when a mosquito population has less longevity but slower aging over time. In such a case, we call this a short-lived but young population. Additionally, other cases could occur, that is, short-lived populations that are old or remain young. Thus, survival and aging could vary across populations and locations because they may be sensitive to climate such as temperature [12,13].
Temperature is an important factor that affects mosquitoes’ survival due to their poikilothermic nature [5,12,14]. This means that their internal temperature varies as the environmental temperature changes, which affects their development and survival [5,15]. Their aging has been experimentally evidenced for male and female mosquitoes [7,16,17,18]. This is considered as a relevant factor in transmission risk because the females are more likely to transmit pathogens if they bite an infected host when they have higher fitness [18,19]. Furthermore, aging decreases Aedes aegypti fecundity, vectorial capacity, and consequently transmission intensity [18].
A number of authors have modeled the survival of Aedes mosquitoes with the exponential [20,21,22,23], Gompertz and logistic [15,16,24], and Weibull [15,25,26] statistical distributions, where the best-fit model was provided by the Weibull distribution [16]. The survival function of Aedes females considering populations of Aedes aegypti and Aedes albopictus was modeled in [5]. The advantages of using parametric models to describe the survival function include their theoretical properties and the aging comparison via stochastic order.
We considered aging from two view points: (i) by assuming that the hazard rate (HR) increases with age [16]; and (ii) in terms of the convex transform (CT) order. This order is a mathematical formalization to compare the aging velocity of two populations via an increasing HR [19]. The age-dependent mortality of Aedes aegypti based on the HR function was studied in [16,27]. However, to the best of our knowledge, no studies that simultaneously consider aging and survival phenomena have been reported to date.
1.2. Definition of the Case Study
Next, we describe the characteristics of the case study and indicate the zones where the data were collected. The Aedes aegypti mosquito is distributed in tropical and subtropical areas [28] and affects many countries including Colombia, where the extrinsic conditions favor its reproduction and survival [29]. In Colombia, the proliferation of this vector is a public health problem for different cities because it transmits diseases including chikungunya, dengue, yellow fever, and zika. Hence, it is important to obtain information about vector populations to design control strategies. In this paper, we studied the mosquito’s risk over human population by analyzing vector aging and survival in three endemic cities in Colombia: Bello, Riohacha, and Villavicencio, whose geographical locations are presented in Figure 1.
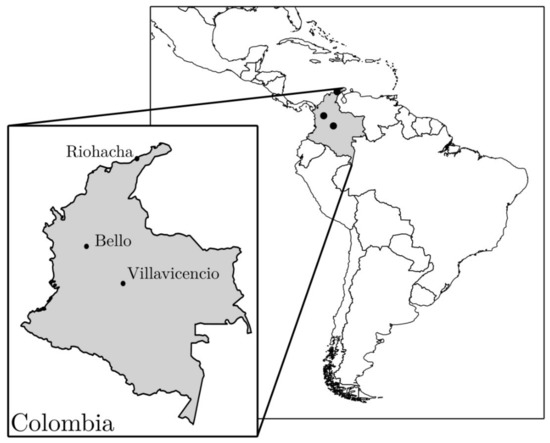
Figure 1.
Map of the Colombian urban areas considered in this study.
For each city studied, we describe the following climatic and geographical conditions:
- (i)
- Bello city is located in the Andean Mountains (1310 m above mean sea level (m.a.s.l.)), with an average rainfall of 1542 mm and average minimum/maximum temperatures of 17 C/28 C, respectively.
- (ii)
- Riohacha is a city close to the Caribbean Sea (5 m.a.s.l.) and the Riohacha river, with an average rainfall of 546 mm and average minimum/maximum temperatures of 24 C/33 C, respectively.
- (iii)
- Villavicencio city is located in the Eastern Plains at 467 m.a.s.l., with an average rainfall of 4537 mm and average minimum/maximum temperatures of 21 C/30 C, respectively.
- (iv)
- For these three cities, the average humidities are very similar with a value of approximately 77%. In addition, Figure 1 indicates that each study zone is far from the other two zones and all of them present different geographic conditions.
The data of Aedes aegypti females were collected from a laboratory. We considered mosquitoes at immature stages from natural breeding sites in Bello, Riohacha, and Villavicencio. Then, we reared them under laboratory conditions, that is, humidity at 80%, day length of 12 h, and a constant temperature depending on the assay. For Bello, Riohacha, and Villavicencio, we reared mosquitoes at 23 C and 27 C, where the sample size for each temperature and the descriptive statistics for the total count of data are shown in Table 1, while the boxplot is displayed in Figure 2.

Table 1.
Descriptive statistics of Colombian mosquito lifetime data (in days) for each indicated city.
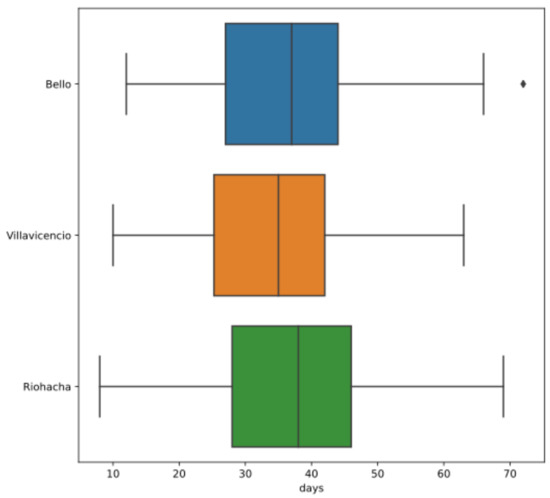
Figure 2.
Boxplot for each indicated city with Colombian mosquito lifetime data (in days), where the dot symbol to the right in Bello is an outlier.
Observe that only for the city of Bello were different temperatures observed, such as 28 C, 30 C, and 32 C, with sample sizes 42, 55, and 65, respectively. Therefore, a spline interpolation analysis to estimate survival functions at different temperatures was only performed for Bello. Note that each experimental assay has an error of C. Thus, we submerged the eggs from the fifth-generation in dechlorinated water and counted the larvae that emerged. The adult mosquitoes were fed with a solution of 10% sugar and 90% water. After six days of emerging, the females were fed with chicken blood two times per week. We counted the number of deaths per day and reported that none of the mosquito populations were infected with the virus.
Note that the count of data used in the application is a consequence of what was observed in the laboratory. For example, in [5], the authors performed interpolation with a lesser count of temperatures due to the cost and complexity of obtaining laboratory data.
To determine the aging and survival factors of Aedes aegypti mosquitoes through statistical methods, we fit them using the number of female mosquito deaths from life tables for each study city and built such tables using the methodology for the experimental assay proposed in [30]. All experimental assays performed in this study were approved by Ethics Committee for Animal Experiments (in Spanish, CEEA), Colombia.
Table 1 reports the main descriptive statistics of the lifetime data (in days) considered in this study. From this table, note that there is not much difference in the statistics of lifetimes of females from the three Colombian cities, and the same conclusion can be drawn from the boxplot in Figure 2. The Mann–Whitney test [31] may be applied to contrast whether these data sets come from the same population. In addition, we might compare the empirical distribution functions of these sets of lifetimes to assess whether any city has mosquitoes with longer lifetimes. This comparison is addressed in Section 3 by using reliability theory. As mentioned previously, we observed that the size of the data set utilized here was in agreement with what was employed in the laboratory [5].
1.3. Objective and Description of the Paper
The main objective of this study was to perform a match between the aging and survival phenomena with the mosquito risk to transmit the pathogen. Here, we analyzed that a long-lived and younger population may present a higher risk because the wear and tear are less over time. This gives the mosquitoes the possibility to breed, feed, and transmit a disease for a longer time than an older population. Therefore, in this paper, we analyzed the relationship among aging, risk, survival, and temperature in Aedes aegypi mosquito populations from three cities in Colombia, a region strongly affected by the vector-borne diseases. We incorporated some effects of age-dependent mortality into the models used in the literature [5,7,32]. In addition, we present a statistical method to compare the aging among the mosquito populations from three Colombian cities which allowed us to contrast their risk of contagious. The findings reported in this investigation have not been presented previously and have contributed to the development of knowledge in biomedicine. We employed the MATLAB software [33] to implement our methodology.
The remainder of the paper is organized as follows. In Section 2, the statistical methods to compare survival and aging among populations are introduced. Section 3 applies the statistical methods and models described in Section 2 to analyze the data collected. In Section 4, we discuss the results of the study based on the analysis of the model comparisons and address the conclusions of this study.
2. Statistical Methods
In this section, we present elements of reliability analysis, non-parametric/parametric fitting of the survival function, some ideas on general and robust regression, and a non-parametric test to compare statistical distributions.
2.1. Elements of Reliability Analysis
Let T be a random variable that corresponds in our case study to the lifetime of Aedes aegypti females, where f is its corresponding probability density function, and F is the associated cumulative distribution function. Then, we defined the survival function as , indicating the probability of surviving at time t. The HR function is established by , meaning the propensity to die at time t. The reversed hazard (RH) rate is stated as , expressing the intensity of having died before time t, given a death at time t. We consider the function . Note that is the mean residual life at time t. The previous functions allow us to define some useful stochastic orders to obtain the main results of this study.
Let and be two random variables that, in our case, represent the lifetimes of two individual populations (for example, the Aedes aegypi mosquito populations from Bello and Riohacha), with the cumulative distribution functions F and G, and density functions f and g, respectively. Consider the following for and :
- (i)
- The survival function leads to the concept of usual stochastic (ST) order in which the random variable is less than the random variable , denoted by , if only if the survival function of is everywhere less than the survival function of .
- (ii)
- The HR function, also named failure rate function, leads to the concept of HR order in which is less than , denoted by , if and only if the HR function of is everywhere less than the HR function of .
- (iii)
- The RH rate function permits us to obtain the concept of RH order in which the random variable is less than the random variable , denoted by , if only if the RH rate function of is everywhere less than the RH rate function of .
- (iv)
- The function above defined leads to the concept of convex (CX) order in which is less than , denoted by , if and only if the function of is everywhere less than the function of and . Since is the mean residual life at time t, then implies that the mean residual life of is less than the mean residual life of .
For a deeper discussion of stochastic order to compare lifetimes and aging classes, we refer the reader to [34]. We recall that the HR function means the propensity to die in the instant immediately after t. Therefore, an increasing HR means that, in our framework, the mosquito is aging. Note that the exponential distribution has a constant HR, which indicates that, for example, the mosquito does not age since this distribution has the Markov property, also named memoryless property. However, aging can be analyzed by the CT order.
The CT order was studied in [19] to analyze aging for parallel systems. Note that a population of Aedes aegypti females, stated in terms of a lifetime , ages faster than another population with lifetime , denoted by , if and only if is convex in t on the support of . The convexity of means that the function is increasing in Observe that the CT order is an important concept to compare aging between individuals (mosquitoes in our case) [19], since it reflects one distribution with an HR that increases more quickly than another individual, that is, one of them ages faster than the another one. Based on the CT order, this study compares the aging speed of the Aedes aegypti females in the three Colombian cities considered.
2.2. Non-Parametric and Parametric Survival Analysis
The empirical distribution function of T, denoted by , is the cumulative distribution function that assigns a mass of at each observed point , with , where n is the sample size; for more details of the empirical distribution function, see p. 13 in [35]. Note that, in this study, is an observed value of the Aedes aegypti female lifetime i. Formally, the empirical distribution function is defined as
where I is the indicator function given by
In order to parametrically fit the survival function, we considered the exponential, Gompertz, log-logistic, and Weibull distributions. As mentioned, the Gompertz and log-logistic distributions are commonly used as parametric models in human mortality, whereas the exponential and Weibull distributions are often employed to parametrically model survival times [36,37]. The Weibull distribution has been used for modeling the Aedes aegypti mortality [16]. We fit parametric models using two MATLAB functions named distributionFitter and lifetablefit by means of https://www.mathworks.com/help/stats/distributionfitter.html (accessed on 22 June 2021) and https://www.mathworks.com/help/finance/lifetablefit.html (accessed on 22 June 2021).
The Weibull cumulative distribution function for a lifetime T is established as
By applying the logarithm in the expression stated in (2), we have that
Based on defined as in (1), we get from (3) that , where can be obtained as , with being the ith ordered value (observed order statistic) of , that is, we have the lifetime data and their corresponding ordered values . In addition, also from (3), observe that , , and , for . Note that the dependent variable is stated in terms of the empirical distribution function of the data corresponding to the Aedes aegypti female lifetimes and the independent variable is in terms of these lifetimes.
2.3. Regression Analysis
According to (3) and by defining , , and , with and , the estimation of regression coefficients by the ordinary least squares method is established as
It is known that the estimator associated with (4) is unbiased and consistent under the normality, homoscedasticity, and independence assumptions.
An alternative to the linear relationship among the dependent and independent variables is to relax the assumptions of the general linear regression to do the robust modeling, decreasing the influence of outliers. Some common techniques of robust statistics that are described in [38], and more recently in [39], can be considered.
In this paper, we used the iterative reweighed least squares (IRLS) technique [40] to estimate the regression parameters . At the first iteration, IRLS utilizes the classic general linear regression and then incorporates a matrix () that depends on a weighting function . The estimation of regression coefficients , where and are defined in (4), whereas at the first iteration is an n-dimensional identity matrix. The IRLS technique is an important extension of the weighted least squares that search, iteratively, to decrease the influence of outliers by assigning weights to cases in each step. Note that the function down-weights cases that are further off the regression line in the last iteration. We use a MATLAB implementation for robust regression available in the toolbox statistics. Observe that this MATLAB implementation strictly follows the bi-square weight function. This robust regression method is employed to find the statistical distribution that best fits the data. In this case, we use the MATLAB implementation of the IRLS technique and the Weibull distribution linearization shown in (3). In general, through transformations, a supposed theoretical distribution is linearized, and with the robust regression technique, we identify which distribution best fits the data.
2.4. Non-Parametric Test
The Mann–Whitney test is a non-parametric approach which allows us to compare two distributions. This test also enables us to compare the probability that an observation from a population exceeds an observation from another population , which is equivalent to stating as an alternative hypothesis that the distributions of and are not the same. The Mann–Whitney test is formulated as follows.
Let and be two random variables (for example, the lifetimes of two mosquito populations in Bello and Riohacha). Then, the hypotheses to be tested for comparing the probability that an observation from the population exceeds an observation from the population are stated as
versus
Using a parametric fitting, we can test the above hypotheses to compare the survival functions from two samples of each population. When the random variables are assumed to be continuous, we utilize use the Mann–Whitney test to show a difference in medians. However, one might explore their descriptive statistics presented in Table 1, and the boxplot displayed in Figure 2, from where there is not much difference in the lifetime medians of Aedes aegypti females in the three Colombian cities. Note that these medians are only point estimates. However, with the Mann–Whitney test, the same conclusion is reached when all data, not classified by temperature, are considered. In Section 3, we discuss that the temperature is an important factor that affects mosquito lifetimes. Hence, the Mann–Whitney test is again applied to establish whether the lifetimes at different temperatures have different distributions.
3. Statistical Analysis of the Case Study
In this section, we provided the three main results of our investigation. The first one is a comparison of the survival among Aedes aegypti populations of the three Colombian cities studied. The second one compares the aging speed of Aedes aegypti females for these three cities. Then, we analyzed both survival and aging through different temperatures only for the Bello population.
3.1. Survival Analysis of Aedes aegypti Females
In the regression models utilized for each city, the total count of data reported in Table 1 are considered. In Figure 3, we show the exponential, Gompertz, log-logistic, and Weibull fittings for the survival function of the samples from Bello, Riohacha, and Villavicencio. Note that the exponential model does not fit as well as the other analyzed models because it does not consider the age-dependent mortality. The exponential distribution assumes that the mortality is constant across time [41], which was also mentioned in [25] for the Bello population. Consequently, the exponential model does not the catch aging phenomenon and does not fit well with our real data.
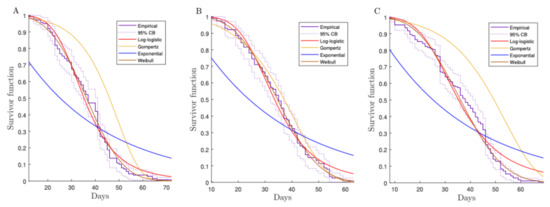
Figure 3.
Survival curves for the indicated model with Colombian mosquito lifetime data (in days) from Bello (A), Villavicencio (B), and Riohacha (C).
The best fitting is provided by the Weibull model, which can represent lifetimes with decreasing and increasing HRs through the shape parameter when it is less or greater than one, respectively. This means that the mortality rate is decreasing or increasing over time, respectively. When , there is no change in the mortality rate, since it is the exponential case [42]. The estimates of for this study are reported in Table 2.

Table 2.
Adjusted and estimated parameters by 95% CI of the linearized Weibull distribution function with Colombian mosquito lifetime data for the indicated city.
The log-logistic model could represent both monotonic and non-monotonic aging based on its scale parameter. Hence, this model could also fit our data [43,44].
The Gompertz distribution does not fit as well as the Weibull and log-logistic distributions for the Bello and Riohacha populations. However, it follows the tendency of real data because it also represents the change in the mortality rate as an exponential model with aging [43,44].
The linearization of the Weibull cumulative distribution function with estimated parameters is shown in Figure 4. The real data are plotted after applying a Weibull transformation and these follow a linear tendency with the presence of some outliers. To decrease the influence of the outliers, the Weibull parameters were estimated by using IRLS robust regression. The estimation of parameters is reported in Table 2, where confidence intervals (CIs) for the parameters were obtained by using 1000 bootstrap samples, each of the size of the original data set. From the Weibull defined in (2), the HR function may be obtained as , for , which indicates, as mentioned, the propensity to die at time t. Note that is a shape parameter; see p. 231 in [34]. If , the HR is decreasing over time, which means that as the mosquito survives longer, its probability of death is lower, indicating that the individual populations rejuvenates. If , then this indicates that the HR is increasing over time, meaning that there is an aging process, and the mosquitoes are more likely to die as time progresses. If , we have the exponential distribution that has a constant HR, that is, no aging nor rejuvenation exists.
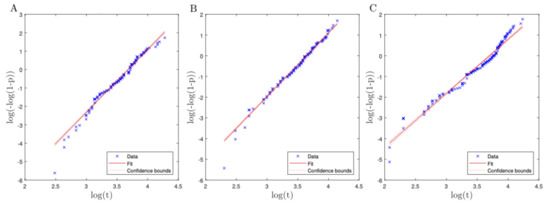
Figure 4.
Fitted Weilbull linearization with Colombian mosquito lifetime data from Bello (A), Villavicencio (B), and Riohacha (C).
From Table 2, we observe that the point estimate of for the three cities is greater than one. Furthermore, the CI in both limits is also greater than one. Thus, there is sufficient statistical evidence in the sample to conclude that the lifetimes of Aedes aegypti females in the three cities have increasing HR, which is visually supported by the graphical plots of these HR functions in Figure 5A. The adjusted is also shown in Table 2, where the fitted linearized model exceeds in all cases, meaning that the Weibull distribution is appropriate to explain these data. It is well known that the median of the Weibull distribution is given by . Then, from the results reported in Table 2, we can obtain that the median lifetimes in the cities considered are 35.55, 35.037, and 33.847 days, for Bello, Riohacha, and Villavicencio, respectively. Observe that these median values are similar to those values obtained in the descriptive analysis reported in Table 1.
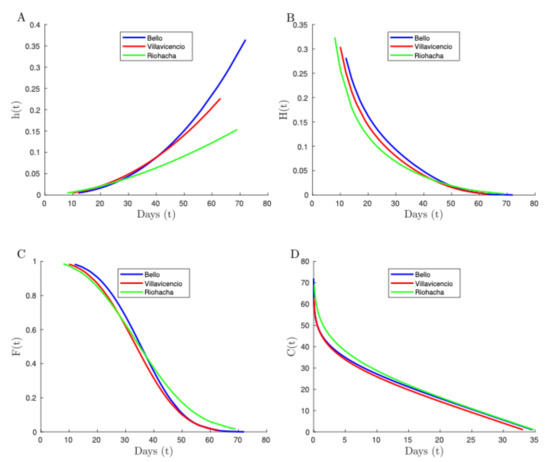
Figure 5.
Plots of the HR (A), RH rate (B), survival function (C), and convex order (D), with Colombian mosquito lifetime data in each indicated city.
We used the two-tailed Kolmogorov–Smirnov (KS) test to choose the best model and report all KS test results in Table 3. From this table, note that the Weibull fitting is the best one for all cities because its p-value is the highest, followed by the log-logistic, Gompertz, and exponential fittings. The p-value comparison indicates that the empirical distribution function for each sample is closer to the Weibull distribution. Hence, we modeled the survival function for the data sets from these three cities with the Weibull distribution. Therefore, hereafter, we make the survival analysis and stochastic comparison by using the Weibull fitting.

Table 3.
p-value of the KS test for the indicated model and city with Colombian mosquito lifetime data.
The comparison of Aedes aegypti females’ lifetimes from Bello, Riohacha, and Villavicencio is shown in Figure 5, where the HR (A) is not a good criterion to compare these cities because pairs of HRs overlap with one another. Thus, according to the orders established in Section 2.1, they are not comparable under the HR criterion. However, the RH rate (B) and survival function (C) allow us to identify that females Aedes aegypti from Bello live longer than females from Villavicencio due to the Bello curve being above the Villavicencio curve. Females from Riohacha cannot be easily compared with the other two cities based on the HR (B) and survival function (C) criteria because the Riohacha curves overlap with the other two curves. Therefore, other weaker comparison criteria must be considered, for example, the convex order (D) which shows that Aedes aegypti females from Riohacha have a greater mean residual life than females from Bello and Villavicencio. We checked the difference among the respective fitted Weibull distributions by using the Mann–Whitney test and report the results in Table 4. In this table, the Mann–Whitney statistic and its p-value indicate the equality of any two pairs of distributions that should not be rejected at a 5% significance.

Table 4.
Mann–Whitney values when comparing each indicated cities with mosquito lifetime data.
According to the results presented in Figure 5, we compared and deduced a survival order relationship among the populations of the studied cities as follows. Let , and be Aedes aegypti female lifetimes of Bello, Riohacha, and Villavicencio, respectively. Then, we concluded from Figure 5C that . The aforementioned stochastic order means that Bello females live longer than Villavicencio females, but Bello and Riohacha are not comparable in this stochastic order. However, from Figure 5D, and . Hence, both and are comparable in the convex order, which means that the mean residual life in Riohacha seems to be greater than in the other two cities. Note that this conclusion seems to indicate that the female mosquitoes from Bello are riskier to humans due to the fact that they live longer and then they can transmit the disease for more time. Nevertheless, there are more factors that could define the risk of transmission, for example, aging, since a young population could reproduce more and improve vectorial capacity. Therefore, a combination of long lifetime and slow aging may be the characteristic of a high-risk mosquitoes population. Thus, in the following subsection, we performed an analysis relating both phenomena (aging and survival) to determine the riskier mosquito population to humans.
3.2. Aging Speed Analysis of Aedes aegypti Females
Let F, G, and H be the cumulative distribution function of Aedes aegypti females lifetimes for Bello, Villavicencio, and Riohacha, respectively. We introduced an analytic comparison of aging among the different populations using the CT order comparison. Computing the CT order comparison for each pair of cities, we obtained that . From Figure 6, note that females from Bello age faster than females from Riohacha and Villavicencio. Moreover, the females from Villavicencio age faster than females from Riohacha.
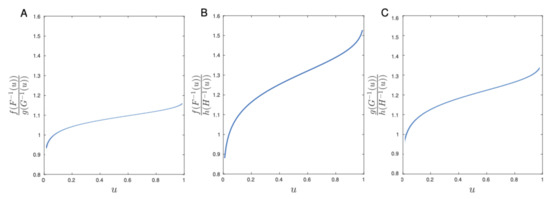
Figure 6.
Aging curves via the CT order with Colombian mosquito lifetime data from Bello versus Riohacha (A), Bello versus Villavicencio (B), and Riohacha versus Villavicencio (C).
From the comparison among the populations of the three cities of the case study, we concluded that Aedes aegypti females from Bello live longer than females from Villavicencio. In contrast, females from Riohacha have a mean residual life greater than both Bello and Villavicencio. Furthermore, we reported that females from Bello age faster than females from Riohacha and Villavicencio, while the females from Villavicencio age faster than females from Riohacha. Therefore, females from Riohacha are more dangerous than females from Villavicencio, and then the latter are more dangerous than females from Bello. This is because younger populations have a greater vectorial capacity to reproduce and quickly infect the human population. Thus, in general, Aedes aegypti females from Riohacha are the most dangerous because they age slower and have a longer mean residual life than other cities.
3.3. Survival and Aging Analysis of Aedes aegypti Females
We performed an analysis to determine how the aging and survival of Aedes aegypti from Bello are simultaneously affected by different temperatures. As mentioned in the introduction, the temperature is an important factor that affects mosquitoes’ survival due to their poikilothermic nature. This means that their internal temperature varies as the environmental temperature changes, affecting their development and survival. As discussed in [5], although there are other important factors such as humidity and photoperiod, the effects of temperature were rigorously quantified and frequently identified as the most relevant factor for the survival of Aedes aegypti females. However, the relationship between aging, speed, and temperature has not been studied in detail. Therefore, we focused on the analysis of the relationship temperature-survival and temperature-aging.
We used Bello data to interpolate the lifetimes and determine a temperature range where aging is the slowest one. Then, we analyzed survival and aging across a range of temperatures. Since just five temperatures were observed in Bello city, an interpolation of the survival function has been considered at intermediate unobserved temperatures. We interpolate the survival functions for each of the five temperatures observed in Bello. Hence, a cubic spline methodology is implemented to estimate the survival surface. Figure 7A shows the interpolated survival function in the temperature range from 27 C to 32 C, where Figure 7B is a two-dimensional representation of Figure 7A. Note that the x-axis is the time in days, the y-axis is the temperature in Celsius degrees, and the z-axis represents the proportion surviving according to the color bar scale. Following the trend of the 50th percentile represented by the first dashed line, observe that the temperatures where the color of the light is more durable, ideal temperatures are detected for the survival of Aedes aegypti females of Bello, assuming that the temperature is constant over time.
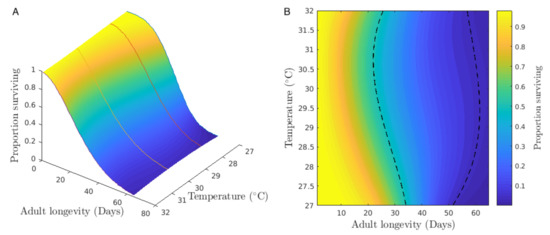
Figure 7.
Plots of proportion surviving by time and temperature (A) and its 2D representation (B) for Aedes aegypti females from Bello across a range of temperatures with Colombian mosquito lifetime data. Colors from light to dark show survival from 100 to 0% of the population remaining. Dark color indicates that <1% of the population remains. Dashed black lines show the 50th and 95th percentiles of the original population remaining.
An analysis for the dangerousness of the Aedes aegypti female population from Bello is provided in Figure 8 in terms of the temperature, ranging 27 C to 32 C by 2.5 C, where the interpolated survival functions (Figure 7) are compared by pairs of temperatures in terms of survival and aging. Figure 8A shows the aging analysis for all possible temperatures, with the light color indicating that an Aedes aegypti female population at the temperature of the x-axis ages faster than an Aedes aegypti female population at the temperature of the y-axis. In the same sense, for the dark color, an Aedes aegypti female population at the temperature of the x-axis ages slower than an Aedes aegypti female population at a temperature of the y-axis. In Figure 8B, the dark color indicates that an Aedes aegypti female population at the temperature of the y-axis lives longer than an Aedes aegypti female population at the temperature of the x-axis. By using the Mann–Whitney test, in Figure 8C, the light color indicates that an Aedes aegypti female population at the temperature of the x-axis has another distribution function than an Aedes aegypti female population at the temperature of the y-axis. Therefore, based on the interpolation, the survival functions for all possible different temperatures in the range seem to be different.
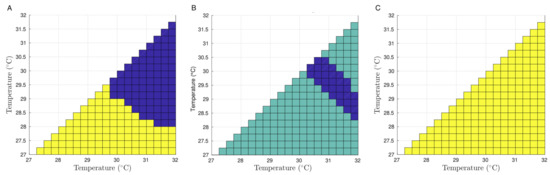
Figure 8.
Dangerousness of Aedes aegypti females from Bello at temperatures between 27 C and 32 C using the convex order (A), survival function (B), and Mann–Whitney test (C).
4. Results, Discussion and Conclusions
In this investigation, lifetimes data of Aedes aegypti female mosquitoes collected from three Colombian cities were analyzed and compared using the survival function, hazard rate, and reversed hazard rate. In addition, we introduced the convex order function to the survival analysis. Note that the convex order comparison criterion is weaker than the other criteria, but it is stronger than the two-sample t-test for differences in means. Therefore, it is useful for the comparison between two samples when some criteria are not determinant.
We determined that the convex transform order is a statistical method that allowed us to compare the speed of aging between two different populations, using data from the Bello, Riohacha, and Villavicencio cities. Comparative analysis of the aging of potentially infectious populations, together with its survival analysis, enabled us to rank the danger of different vector populations. Furthermore, an analysis of the aging and survival of Aedes aegypti females permitted us to determine the temperatures, within a range, where the dangerousness of the population, in terms of the ability to transmit pathogens, is the highest one.
We conclude from the results obtained that females from Bello, at temperatures of 27–32 C, aged slower than the Aedes aegypti females at higher temperatures. That is, females from Bello at temperatures of 27–28 C are more dangerous than females at temperatures of 31–32 C, under laboratory conditions. In addition, temperature variation is important for both survival and dengue transmission, because of studies such as [45] which reported that, at temperatures near 28 C, the rates of infection, dissemination, and transmission of disease are higher than at low temperatures. This increases the riskiness of populations that survive better at temperatures near 28 C as in Bello. Even more, it is important to perform this kind of study for other vector populations to determine their transmission risk potential, and therefore, develop control strategies, prioritizing the affected human populations.
We argue that the survival of Aedes aegypti females is not the most critical component of their ability to transmit pathogens. According to our definition of risk population, we determined that a young population is riskier than an old population, even if the last one lives longer. Hence, the analyses performed for Colombian mosquito populations showed that the most critical one is Riohacha due to their slowest aging, as even Riohacha mosquitoes live less than other populations. Our most relevant finding is that, if population B lives longer than population A, and B ages faster than A, then A is more dangerous than B.
For future studies, we suggest performing analyses related to mosquito mortality in the field which would provide more realistic data with regard to the Aedes population. As indicated in [44], aging is mostly appreciated in long-living or low-mortality mosquito populations, that is, those raised under laboratory conditions. Furthermore, we propose as future work to perform this study with Aedes aegypti females in the field and other populations, which would allow us to conclude which population is riskier than others and what advice about control strategies can be provided. It is important to note that we used data from mosquitoes that were not infected. Hence, for future studies, we also suggest implementing the proposed models to identify the survival time, the aging, and risk for the different mosquito populations infected with chikungunya, dengue, yellow fever, and zika. Moreover, it is of interest to determine how the infection could affect the fitness and vectorial capacity of the infected mosquito through the change in survival time and aging process. A direct competitor of the Weibull distribution is the Birnbaum–Saunders model, so its use could be explored to improve the Weibull fitting in the context of the present study [46,47,48].
Author Contributions
Data curation, H.V., H.L.; formal analysis, H.V., H.L., M.T., A.C.-L., V.L.; investigation, H.V., H.L., M.T., A.C.-L.; methodology, H.V., H.L., M.T., A.C.-L., V.L., Y.L.; writing—original draft, H.V., H.L., M.T., A.C.-L.; writing—review and editing, V.L., Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
Research of H.V., H.L., M.T., and A.C.-L. was supported by COLCIENCIAS, grant number 111572553478, from the Colombian Administrative Department of Science, Technology and Innovation. Research of V.L. was partially supported by FONDECYT, grant number 1200525, from the National Agency for Research and Development (ANID) of the Chilean government under the Ministry of Science, Technology, Knowledge and Innovation.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data analyzed in this paper are available from the authors under request and authorization of the Biology and Infectious Disease Control Laboratory from the Universidad de Antioquia, Colombia.
Acknowledgments
The authors would also like to thank the editor and three reviewers for their constructive comments which led to improving the presentation of the manuscript. The authors thank to the Biology and Infectious Disease Control Laboratory from the Universidad de Antioquia, Colombia, who provided the mosquito data analyzed in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zafar, Z.U.A.; Ali, N.; Shah, Z.; Zaman, G.; Roy, P.; Deebani, W. Hopf bifurcation and global dynamics of time delayed dengue model. Comput. Methods Programs Biomed. 2020, 195, 105530. [Google Scholar] [CrossRef] [PubMed]
- Brady, O.J.; Gething, P.W.; Bhatt, S.; Messina, J.P.; Brownstein, J.S.; Hoen, A.G.; Hay, S.I. Refining the global spatial limits of dengue virus transmission by evidence-based consensus. PLoS Negl. Trop. Dis. 2012, 6, e1760. [Google Scholar] [CrossRef] [PubMed]
- Jentes, E.S.; Poumerol, G.; Gershman, M.D.; Hill, D.R.; Lemarch, J.; Lewis, R.F.; Monath, T.P. The revised global yellow fever risk map and recommendations for vaccination, 2010: Consensus of the informal who working group on geographic risk for yellow fever. Lancet Infect. Dis. 2011, 11, 622–632. [Google Scholar] [CrossRef]
- Otero, M.; Solari, H.G.; Schweigmann, N. A stochastic population dynamics model for Aedes Aegypti: Formulation and application to a city with temperate climate. Bull. Math. Biol. 2006, 68, 1945–1974. [Google Scholar] [CrossRef]
- Brady, O.J.; Johansson, M.A.; Guerra, C.A.; Bhatt, S.; Golding, N.; Pigott, D.M.; Hay, S.I. Modelling adult Aedes aegypti and Aedes albopictus survival at different temperatures in laboratory and field settings. Parasites Vectors 2013, 6, 351. [Google Scholar] [CrossRef] [Green Version]
- Garrett-Jones, C.; Shidrawi, G. Malaria vectorial capacity of a population of Anopheles Gambiae: An exercise in epidemiological entomology. Bull. World Health Organ. 1969, 40, 531. [Google Scholar]
- Styer, L.M.; Carey, J.R.; Wang, J.L.; Scott, T.W. Mosquitoes do senesce: Departure from the paradigm of constant mortality. Am. J. Trop. Med. Hyg. 2007, 76, 111–117. [Google Scholar] [CrossRef]
- Lunde, T.M.; Bayoh, M.N.; Lindtjørn, B. How malaria models relate temperature to malaria transmission. Parasites Vectors 2013, 6, 20. [Google Scholar] [CrossRef] [Green Version]
- Macdonald, G. Epidemiological basis of malaria control. Bull. World Health Organ. 1956, 15, 613. [Google Scholar]
- Reisen, W.K.; Mahmood, F.; Parveen, T. Anopheles culicifacies giles: A release-recapture experiment with cohorts of known age with implications for malaria epidemiology and genetical control in Pakistan. Trans. R. Soc. Trop. Med. Hyg. 1980, 74, 307–317. [Google Scholar] [CrossRef]
- Smith, D.L.; Battle, K.E.; Hay, S.I.; Barker, C.M.; Scott, T.W.; McKenzie, F.E. Ross, MacDonald, and a theory for the dynamics and control of mosquito-transmitted pathogens. PLoS Pathog. 2012, 8, e1002588. [Google Scholar] [CrossRef] [Green Version]
- Alto, B.W.; Bettinardi, D. Temperature and dengue virus infection in mosquitoes: Independent effects on the immature and adult stages. Am. J. Trop. Med. Hyg. 2013, 88, 497–505. [Google Scholar] [CrossRef]
- Huang, Y.J.S.; Higgs, S.; Vanlandingham, D.L. Arbovirus-mosquito vector-host interactions and the impact on transmission and disease pathogenesis of arboviruses. Front. Microbiol. 2019, 10, 22. [Google Scholar] [CrossRef]
- Yang, H.; Macoris, M.; Galvani, K.; Andrighetti, M.; Wanderley, D. Assessing the effects of temperature on the population of Aedes aegypti, the vector of dengue. Epidemiol. Infect. 2009, 137, 1188–1202. [Google Scholar] [CrossRef] [Green Version]
- Delatte, H.; Gimonneau, G.; Triboire, A.; Fontenille, D. Influence of temperature on immature development, survival, longevity, fecundity, and gonotrophic cycles of Aedes albopictus, vector of chikungunya and dengue in the Indian ocean. J. Med Entomol. 2009, 46, 33–41. [Google Scholar] [CrossRef]
- Degallier, N.; Servain, J.; Lucio, P.S.; Hannart, A.; Dur, B.; de Souza, R.N.; Mota, R.Z. The influence of local environment on the aging and mortality of Aedes aegypti: Case study in Fortaleza-CE, Brazil. J. Vector Ecol. 2012, 37, 428–441. [Google Scholar] [CrossRef]
- Harrington, L.C.; Jones, J.J.; Kitthawee, S.; Sithiprasasna, R.; Edman, J.D.; Scott, T.W. Age-dependent survival of the dengue vector Aedes aegypti (diptera: Culicidae) demonstrated by simultaneous release–recapture of different age cohorts. J. Med. Entomol. 2008, 45, 307–313. [Google Scholar]
- Maciel-de-Freitas, R.; Koella, J.C.; Lourenço-de-Oliveira, R. Lower survival rate, longevity and fecundity of Aedes aegypti (diptera: Culicidae) females orally challenged with dengue virus serotype 2. R. Soc. Trop. Med. Hyg. 2011, 105, 452–458. [Google Scholar] [CrossRef]
- Kochar, S.; Xu, M. Comparisons of parallel systems according to the convex transform order. J. Appl. Probab. 2009, 46, 342–352. [Google Scholar] [CrossRef] [Green Version]
- Harrington, L.C.; Buonaccorsi, J.P.; Edman, J.D.; Costero, A.; Kittayapong, P.; Clark, G.G.; Scott, T.W. Analysis of survival of young and old Aedes aegypti (diptera: Culicidae) from Puerto Rico and Thailand. J. Med. Entomol. 2001, 38, 537–547. [Google Scholar] [CrossRef] [Green Version]
- Muir, L.E.; Kay, B.H. Aedes aegypti survival and dispersal estimated by mark-release-recapture in northern Australia. Am. J. Trop. Med. Hyg. 1998, 58, 277–282. [Google Scholar] [CrossRef] [Green Version]
- David, M.R.; Lourenço-de-Oliveira, R.; Freitas, R.M.D. Container productivity, daily survival rates and dispersal of Aedes aegypti mosquitoes in a high income dengue epidemic neighbourhood of Rio de Janeiro: Presumed influence of differential urban structure on mosquito biology. Memórias Do Inst. Oswaldo Cruz 2009, 104, 927–932. [Google Scholar] [CrossRef] [Green Version]
- Tsuda, Y.; Takagi, M.; Wang, S.; Wang, Z.; Tang, L. Movement of Aedes aegypti (diptera: Culicidae) released in a small isolated village on Hainan Island, China. J. Med Entomol. 2001, 38, 93–98. [Google Scholar] [CrossRef]
- Lee, E.; Go, O. Survival analysis in public health research. Annu. Rev. Public Health 1997, 18, 105–134. [Google Scholar] [CrossRef] [Green Version]
- Catano-Lopez, A.; Rojas-Diaz, D.; Laniado, H.; Arboleda-Sánchez, S.; Puerta-Yepes, M.E.; Lizarralde-Bejarano, D.P. An alternative model to explain the vectorial capacity using as example Aedes aegypti case in dengue transmission. Heliyon 2019, 5, e02577. [Google Scholar] [CrossRef] [Green Version]
- Wilson, D.L. The analysis of survival (mortality) data: Fitting Gompertz, Weibull, and logistic functions. Mech. Aging Dev. 1994, 74, 15–33. [Google Scholar] [CrossRef]
- Styer, L.M.; Minnick, S.L.; Sun, A.K.; Scott, T.W. Mortality and reproductive dynamics of Aedes aegypti (diptera: Culicidae) fed human blood. Vector-Borne Zoonotic Dis. 2007, 7, 86–98. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.M.; Macoris, M.; Galvani, K.C.; Andrighetti, M. Follow up estimation of Aedes aegypti entomological parameters and mathematical modelling. BioSystems 2011, 103, 360–371. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, L.T.; Maidana, N.A.; Ferreira, W.C.; Pulino, P.; Yang, H.M. Mathematical models for the Aedes aegypti dispersal dynamics: Travelling waves by wing and wind. Bull. Math. Biol. 2005, 67, 509–528. [Google Scholar] [CrossRef] [PubMed]
- Lizarralde-Bejarano, D.P.; Arboleda-Sanchez, S.; Puerta-Yepes, M.E. Understanding epidemics from mathematical models: Details of the 2010 dengue epidemic in Bello (Antioquia, Colombia). Appl. Math. Model. 2017, 43, 566–578. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Clements, A.; Paterson, G. The analysis of mortality and survival rates in wild populations of mosquitoes. J. Appl. Ecol. 1981, 18, 373–399. [Google Scholar] [CrossRef]
- Xue, D. MATLAB Programming: Mathematical Problem Solutions; de Gruyter: New York, NY, USA, 2020. [Google Scholar]
- Marshall, A.W.; Olkin, I. Life Distributions; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wasserman, L. All of Nonparametric Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Lambert, P.C.; Thompson, J.R.; Weston, C.L.; Dickman, P.W. Estimating and modeling the cure fraction in population-based cancer survival analysis. Biostatistics 2006, 8, 576–594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sparling, Y.H.; Younes, N.; Lachin, J.M.; Bautista, O.M. Parametric survival models for interval-censored data with time-dependent covariates. Biostatistics 2006, 7, 599–614. [Google Scholar] [CrossRef]
- Wager, T.D.; Keller, M.C.; Lacey, S.C.; Jonides, J. Increased sensitivity in neuroimaging analyses using robust regression. Neuroimage 2005, 26, 99–113. [Google Scholar] [CrossRef]
- Velasco, H.; Laniado, H.; Toro, M.; Leiva, V.; Lio, Y. Robust three-step regression based on comedian and its performance in cell-wise and case-wise outliers. Mathematics 2020, 8, 1259. [Google Scholar] [CrossRef]
- Fritsch, V.; DaMota, B.; Varoquaux, G.; Frouin, V.; Loth, E.; Poline, J.B.; Thirion, B. Robust group-level inference in neuroimaging genetic studies. In Proceedings of the 2013 International Workshop on Pattern Recognition in Neuroimaging, Philadelphia, PA, USA, 22–24 June 2013; pp. 21–24. [Google Scholar]
- Hugo, L.E.; Jeffery, J.A.L.; Trewin, B.J.; Wockner, L.F.; Yen, N.T.; Le, N.H.; Nghia, L.T.; Hine, E.; Ryan, P.A.; Kay, B.H. Adult survival of the dengue mosquito Aedes aegypti varies seasonally in central Vietnam. PLoS Negl. Trop. Dis. 2014, 8, e2669. [Google Scholar] [CrossRef]
- Galar, D.; Kumar, U. Prognosis. In eMaintenance; Elsevier: Amsterdam, The Netherlands, 2017; pp. 311–370. [Google Scholar]
- Farewell, V.T. Mixture models in survival analysis: Are they worth the risk? Can. J. Stat. 1986, 14, 257–262. [Google Scholar] [CrossRef]
- Ryan, S.J.; Ben-Horin, T.; Johnson, L.R. Malaria control and senescence: The importance of accounting for the pace and shape of aging in wild mosquitoes. Ecosphere 2015, 6, art170. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Lai, Z.; Zhou, T.; Jia, Z.; Gu, J.; Wu, K.; Chen, X.G. Temperature increase enhances Aedes albopictus competence to transmit dengue virus. Front. Microbiol. 2017, 8, 2337. [Google Scholar] [CrossRef] [Green Version]
- Leiva, V.; Ruggeri, F.; Saulo, H.; Vivanco, J.F. A methodology based on the Birnbaum-Saunders distribution for reliability analysis applied to nano-materials. Reliab. Eng. Syst. Saf. 2017, 157, 192–201. [Google Scholar] [CrossRef]
- Athayde, E.; Azevedo, A.; Barros, M.; Leiva, V. Failure rate of Birnbaum-Saunders distributions: Shape, change-point, estimation and robustness. Braz. J. Probab. Stat. 2019, 33, 301–328. [Google Scholar] [CrossRef] [Green Version]
- Costa, E.; Santos-Neto, M.; Leiva, V. Optimal sample size for the Birnbaum-Saunders distribution under decision theory with symmetric and asymmetric loss functions. Symmetry 2021, 13, 926. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).