A Multispecies Cross-Diffusion Model for Territorial Development
Abstract
1. Introduction
1.1. Discrete Model
1.2. Phases and an Order Parameter
1.2.1. Expected Agent Density
1.2.2. An Order Parameter
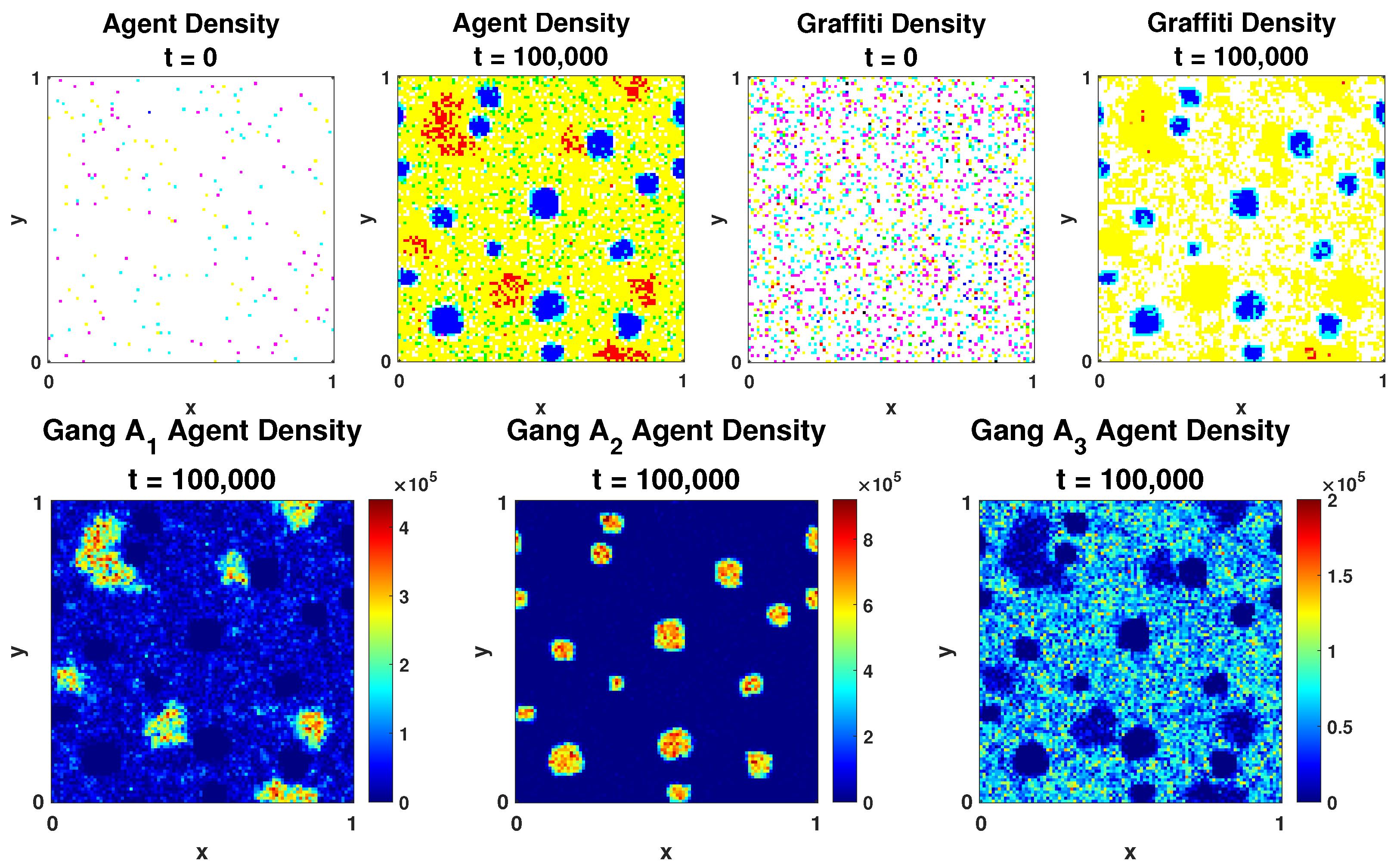
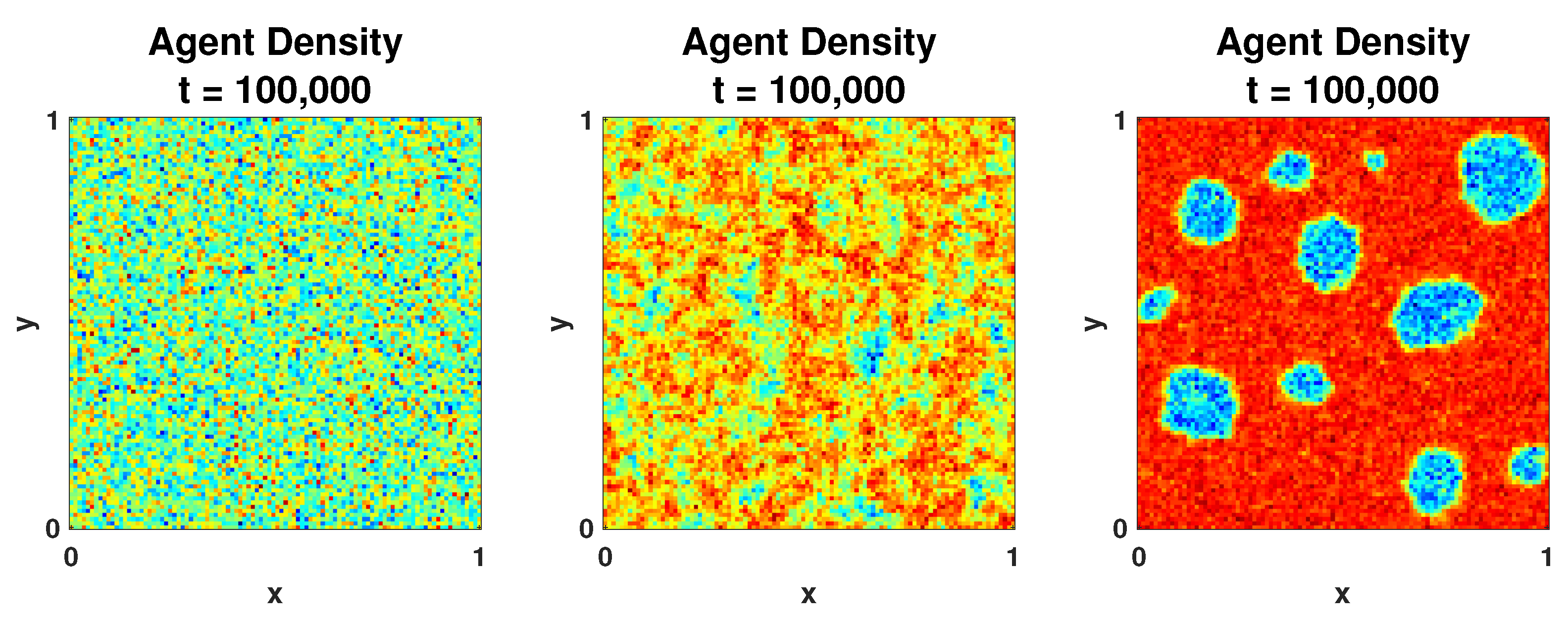
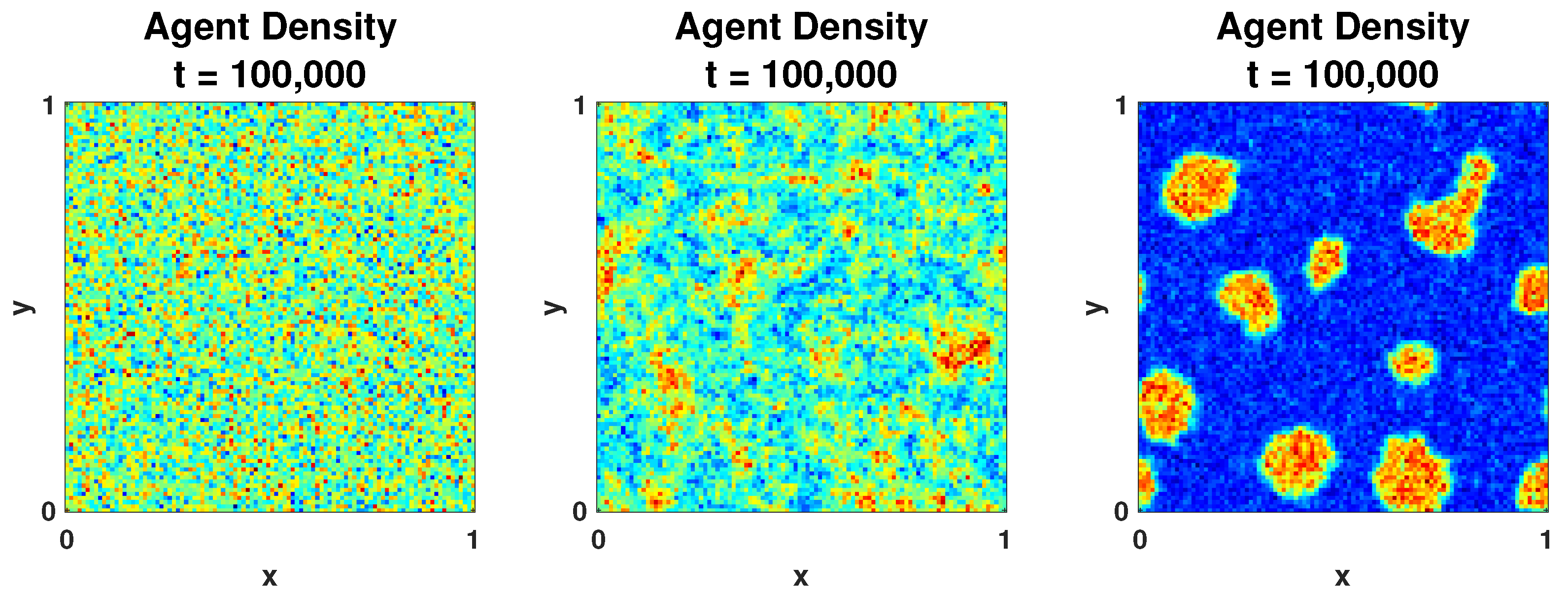
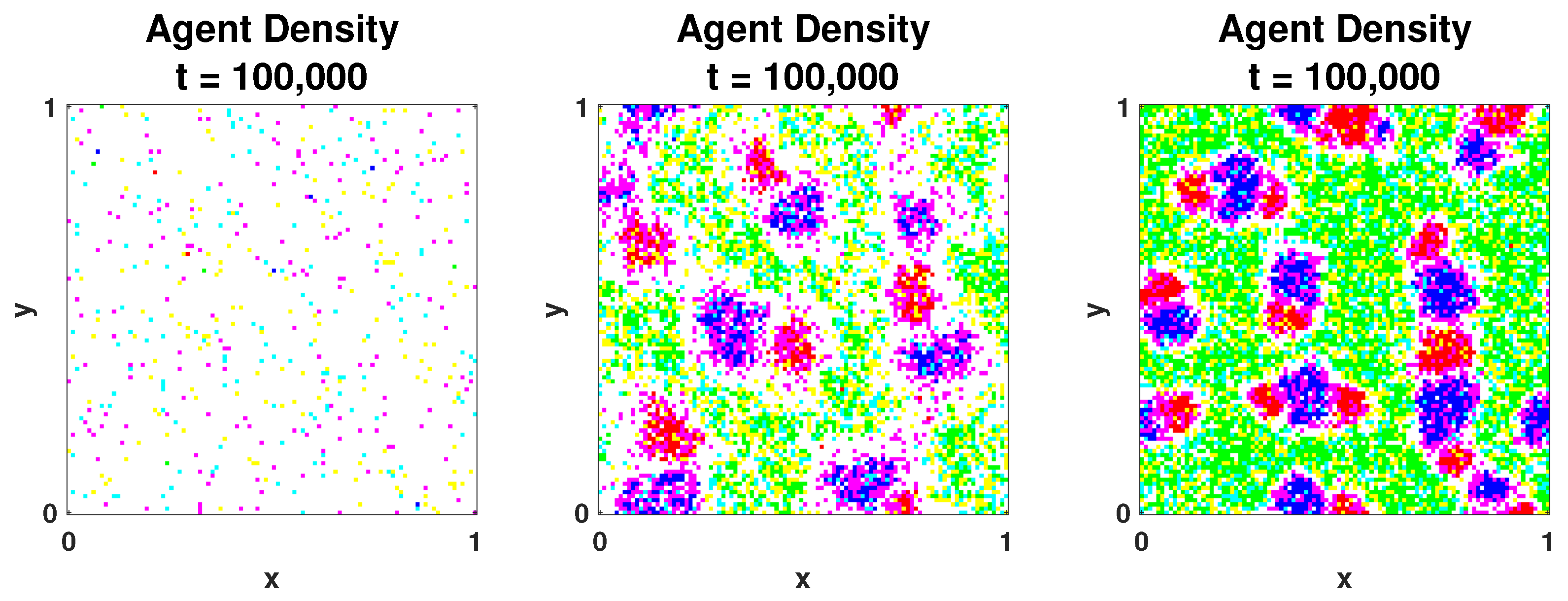
2. Simulations of the Discrete Model
2.1. Well-Mixed State
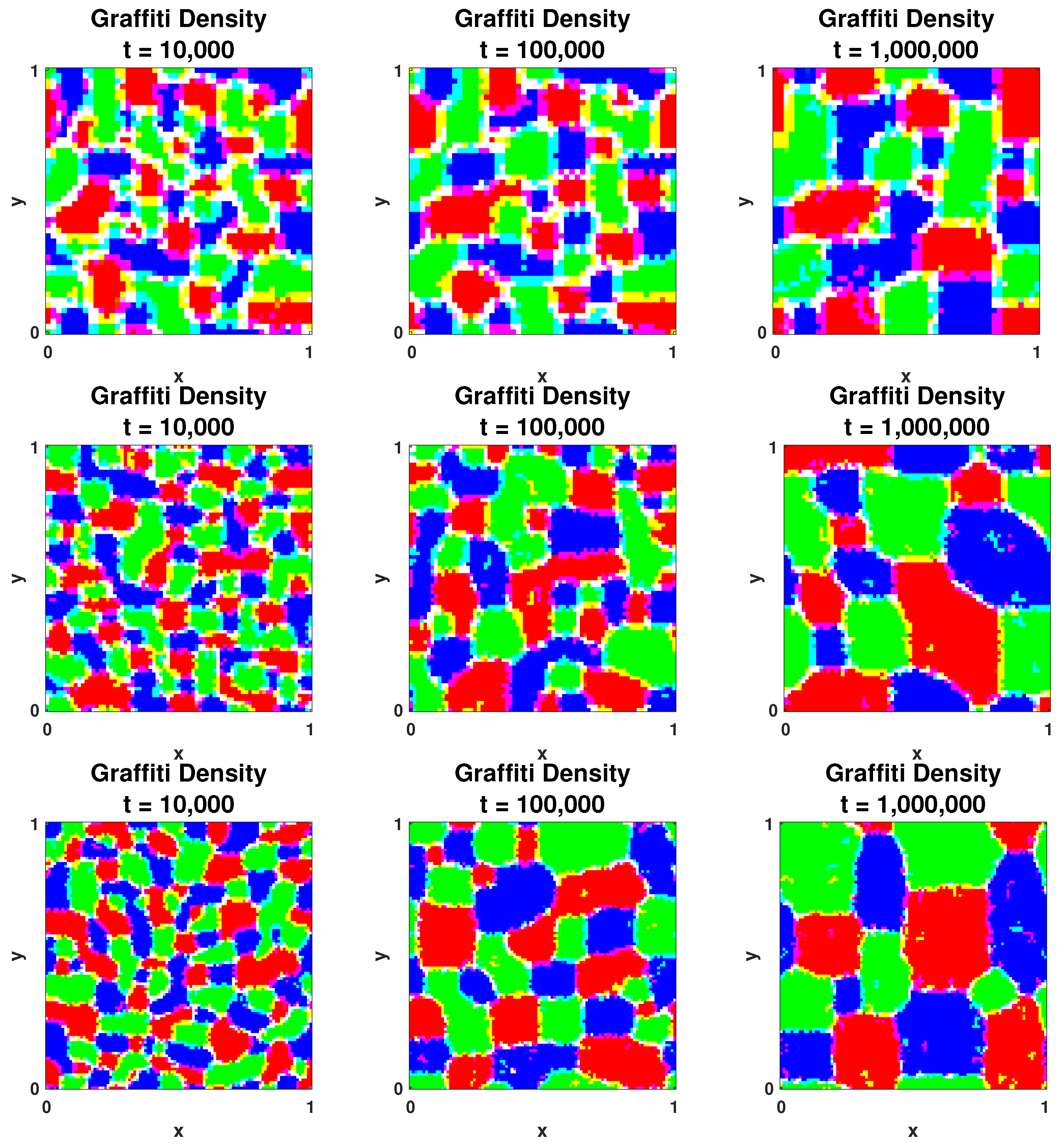
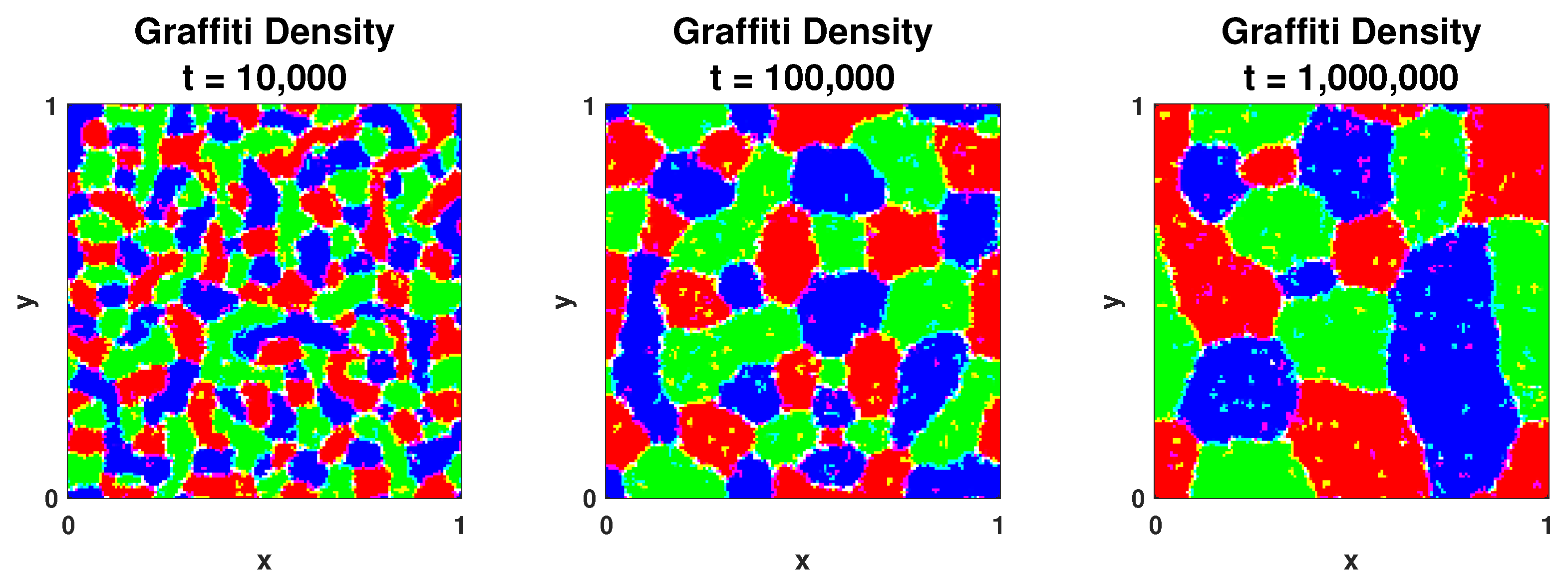
2.2. Segregated State
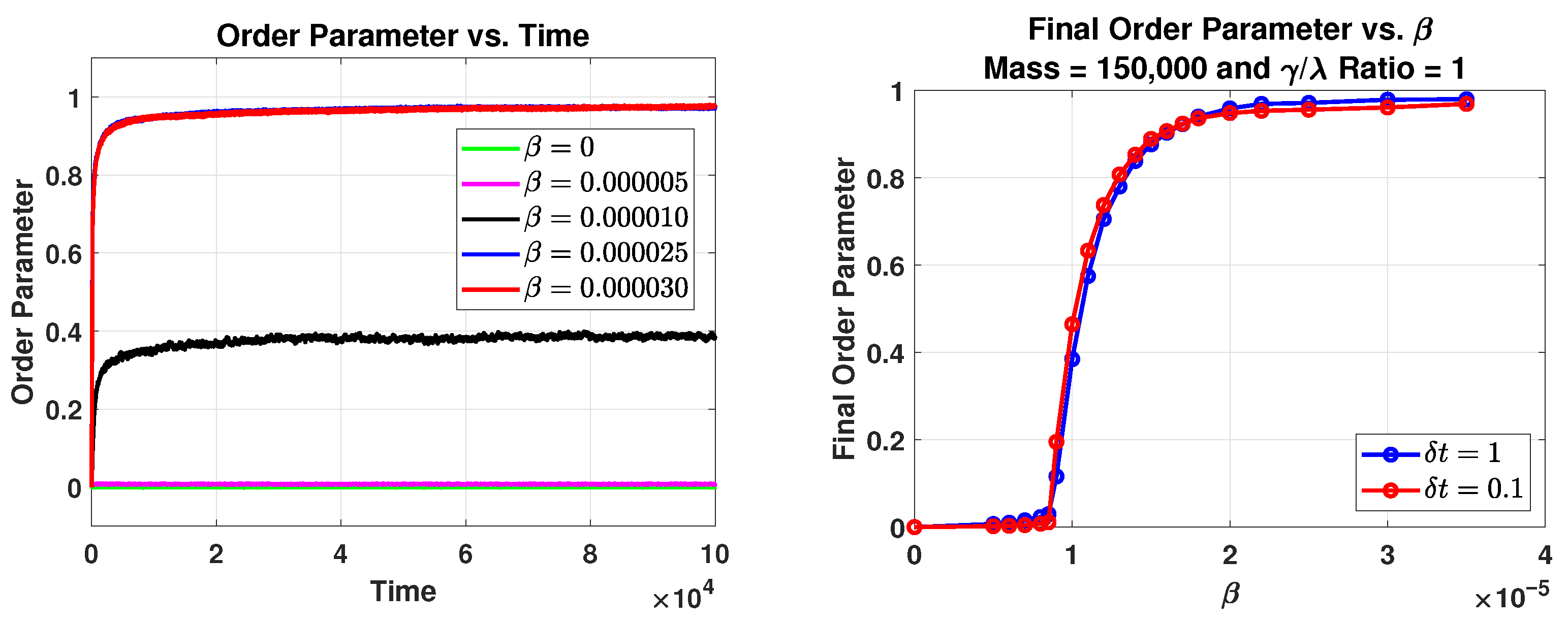
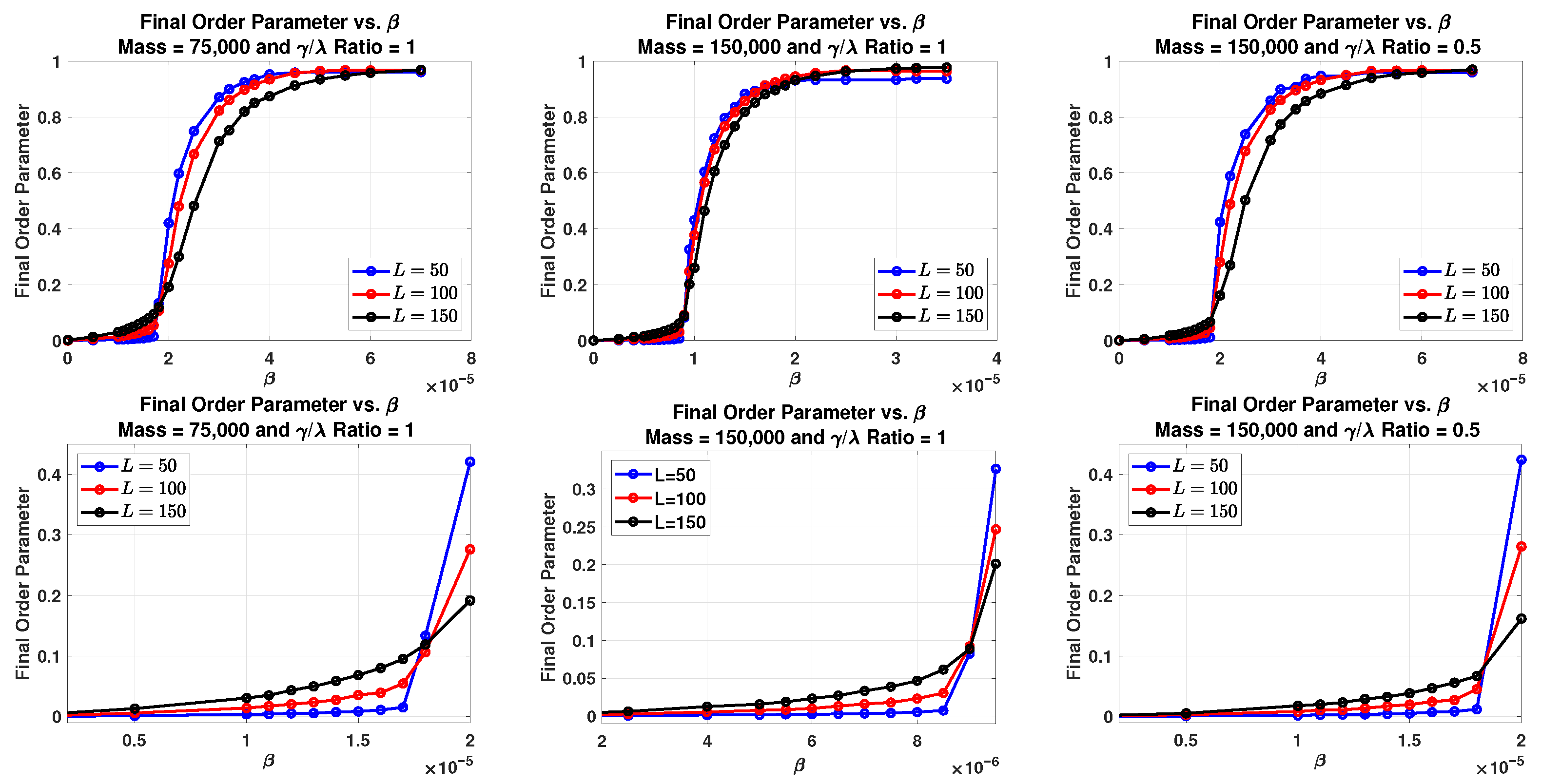
2.3. System Parameters and the Discrete Phase Transition
2.3.1. Effects of
2.3.2. Effects of Other Parameters
3. Deriving the Convection-Diffusion System
3.1. Continuum Graffiti Density
3.2. Continuum Agent Density
3.2.1. Tools for the Derivation
3.2.2. The Derivation
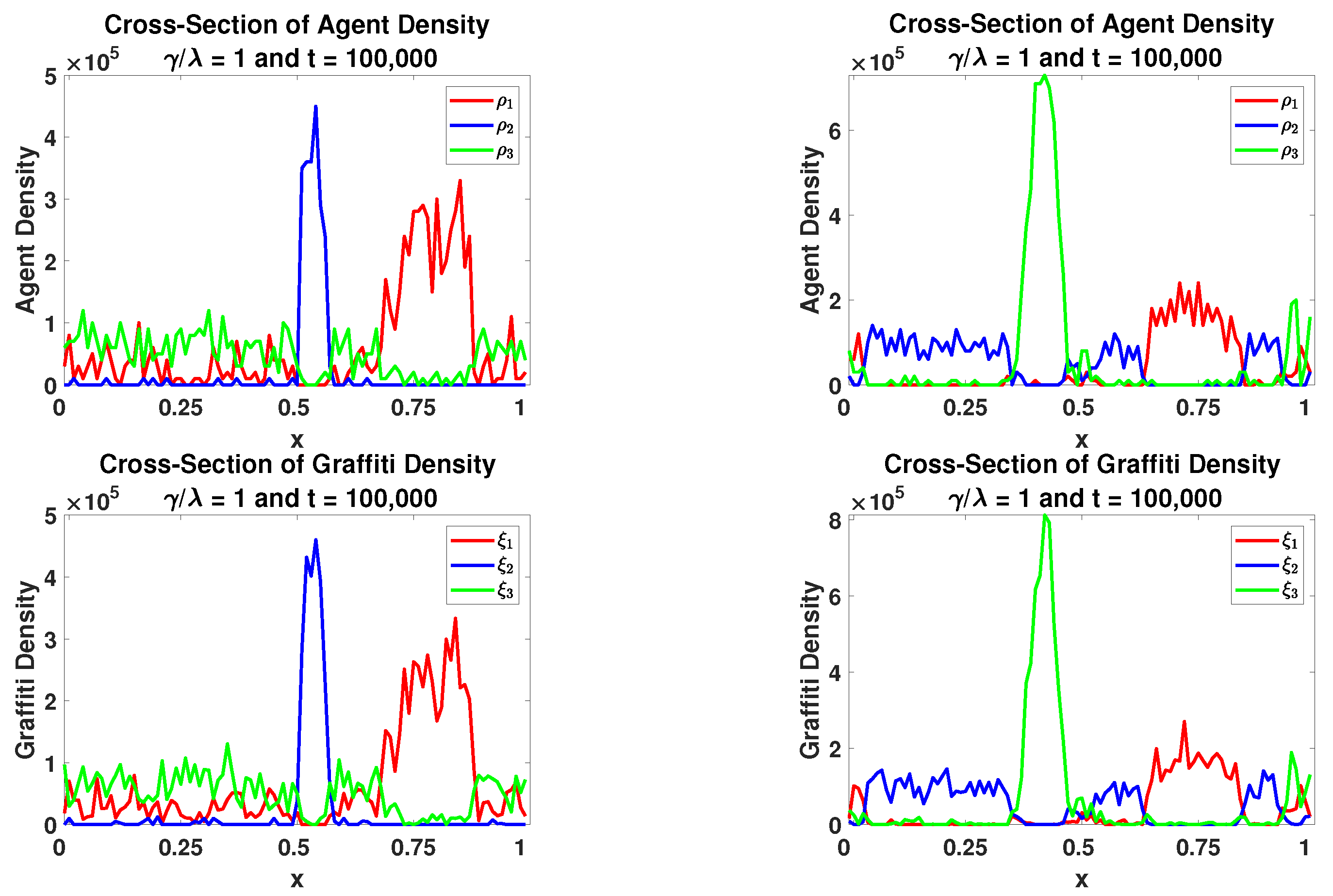
3.3. Steady-State Solutions
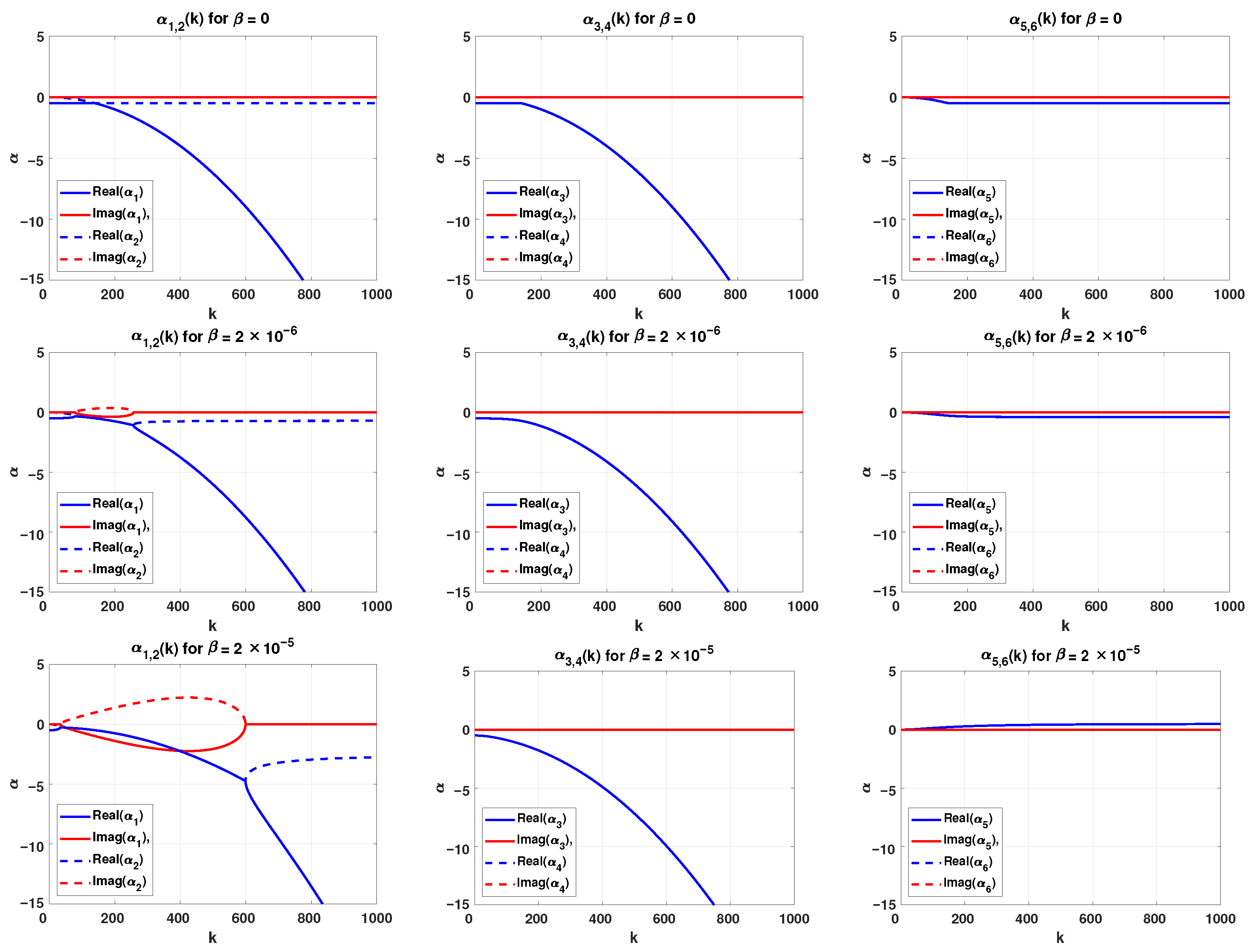
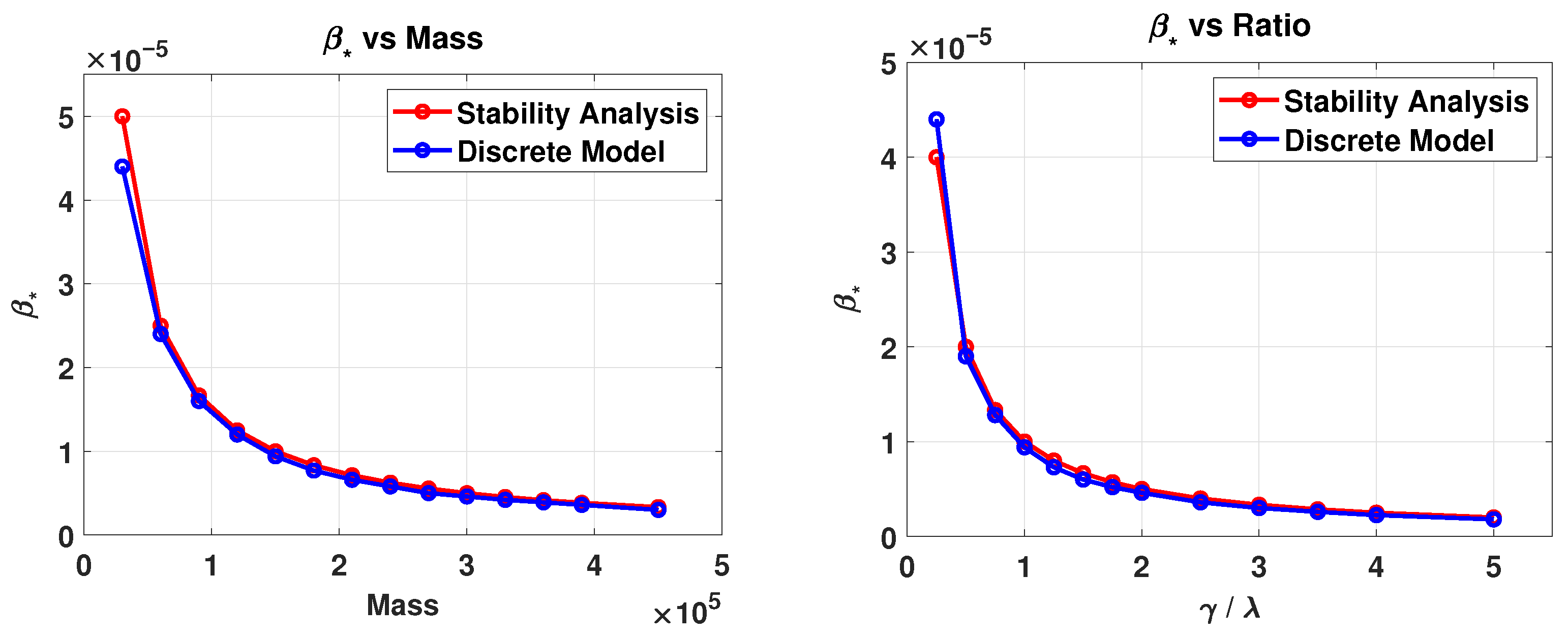
4. Linear Stability Analysis
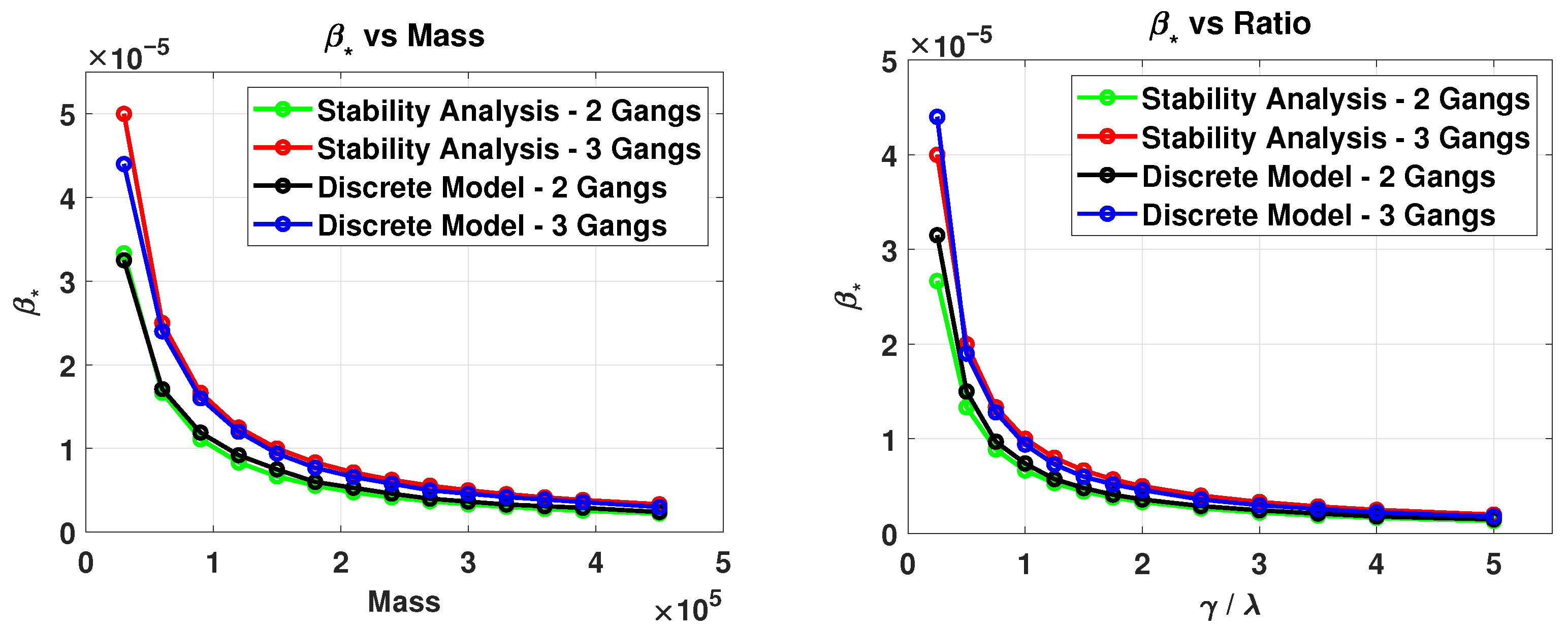
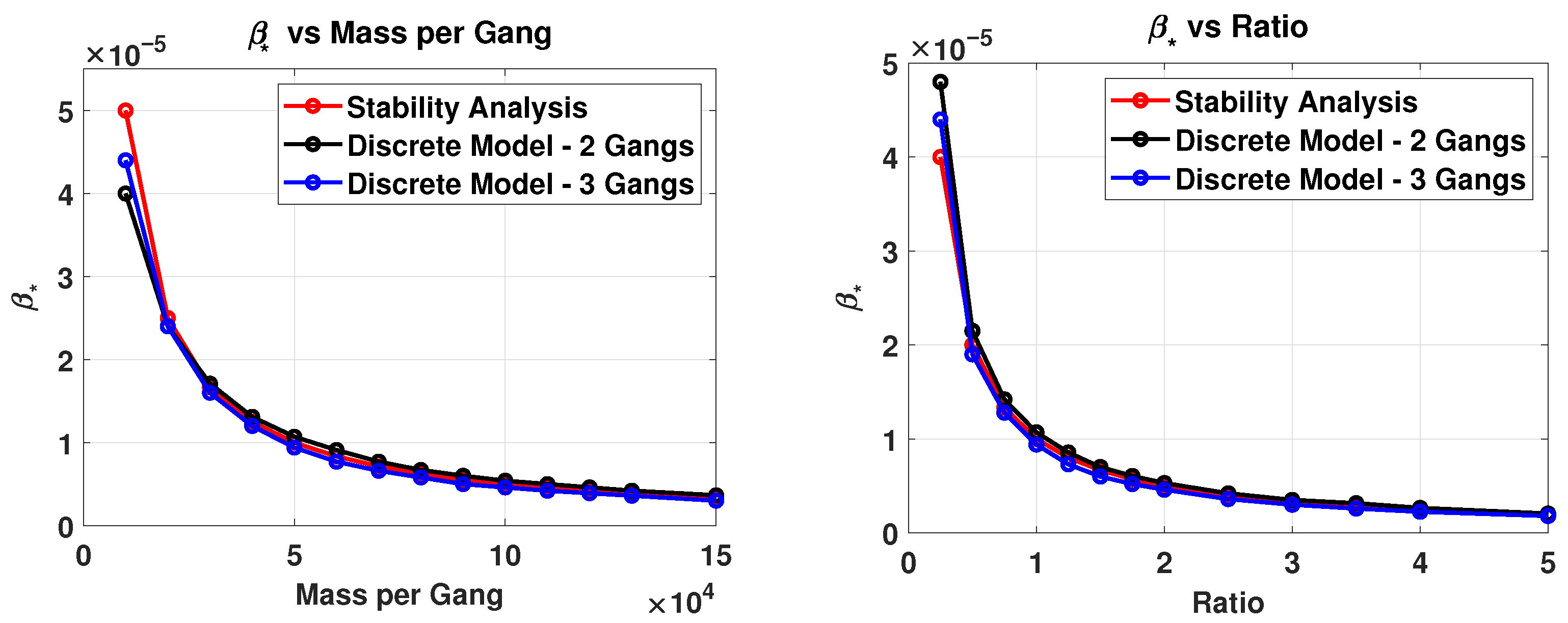
5. Variations of the Model: Varying by Gang
5.1. Timidity Model (Variation 1)
5.2. Threat Level Model (Variation 2)
5.3. Finding Critical for the Variations: Linear Stability Analysis
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Temeles, E.J. The role of neighbours in territorial systems: When are they ‘dear enemies’? Anim. Behav. 1994, 47, 339–350. [Google Scholar] [CrossRef]
- Sack, R.D. Human Territoriality: Its Theory and History; Cambridge University Press: Cambridge, UK, 1986; Volume 7. [Google Scholar]
- Schenk, H.J.; Callaway, R.M.; Mahall, B. Spatial root segregation: Are plants territorial? Adv. Ecol. Res. 1999, 28, 145–180. [Google Scholar]
- May, F.; Ash, J. An assessment of the allelopathic potential of Eucalyptus. Aust. J. Bot. 1990, 38, 245–254. [Google Scholar] [CrossRef]
- Moorcroft, P.R.; Lewis, M.A.; Crabtree, R.L. Home Range Analysis Using A Mechanistic Home Range Model. Ecology 1999, 80, 1656–1665. [Google Scholar] [CrossRef]
- Moorcroft, P.R.; Lewis, M.A.; Crabtree, R.L. Mechanistic Home Range Models Capture Spatial Patterns and Dynamics of Coyote Territories in Yellowstone. Proc. R. Soc. B 2006, 273, 1651–1659. [Google Scholar] [CrossRef]
- Peters, R.P.; Mech, L.D. Scent marking in wolves. Am. Sci. 1975, 63, 628–637. [Google Scholar] [PubMed]
- Lewis, M.; White, K.; Murray, J. Analysis of a Model for Wolf Territories. J. Math. Biol. 1997, 35, 749–774. [Google Scholar] [CrossRef]
- Potts, J.R.; Lewis, M.A. Spatial memory and taxis-driven pattern formation in model ecosystems. Bull. Math. Biol. 2019, 81, 2725–2747. [Google Scholar] [CrossRef]
- Alsenafi, A.; Barbaro, A.B. A convection—Diffusion model for gang territoriality. Phys. A Stat. Mech. Its Appl. 2018, 510, 765–786. [Google Scholar] [CrossRef]
- Krause, A.L.; Van Gorder, R.A. A non-local cross-diffusion model of population dynamics II: Exact, approximate, and numerical traveling waves in single-and multi-species populations. Bull. Math. Biol. 2020, 82, 113. [Google Scholar] [CrossRef]
- Taylor, N.P.; Kim, H.; Krause, A.L.; Van Gorder, R.A. A non-local cross-diffusion model of population dynamics I: Emergent spatial and spatiotemporal patterns. Bull. Math. Biol. 2020, 82, 112. [Google Scholar] [CrossRef] [PubMed]
- Brown, W.K. Graffiti, identity and the delinquent gang. Intern. J. Offender Comp. Criminol. 1978, 22, 46–48. [Google Scholar] [CrossRef]
- De Genova, N. America Abjection Chicanos, Gangs and Mexican/Migrant Transnationality in Chicago. Aztlán J. Chicano Stud. 2008, 34, 141–174. [Google Scholar]
- Adams, K.; Winter, A. Gang Graffiti as a Discourse Genre. J. Socioling. 1997, 1, 337–360. [Google Scholar] [CrossRef]
- Ley, D.; Cybriwsky, R. Urban graffiti as territorial markers. Ann. Assoc. Am. Geogr. 1974, 64, 491–505. [Google Scholar] [CrossRef]
- Smith, L.M.; Bertozzi, A.L.; Brantingham, P.J.; Tita, G.E.; Valasik, M. Adaptation of an Ecological Territiorial Model to Street Gang Spatial Patterns in Los Angeles. Discret. Contin. Dyn. Syst. 2012, 32, 3223–3244. [Google Scholar] [CrossRef]
- Hegemann, R.A.; Smith, L.M.; Barbaro, A.B.; Bertozzi, A.L.; Reid, S.E.; Tita, G.E. Geographical influences of an emerging network of gang rivalries. Phys. A Stat. Mech. Its Appl. 2011, 390, 3894–3914. [Google Scholar] [CrossRef]
- Barbaro, A.B.; Chayes, L.; D’Orsogna, M.R. Territorial developments based on graffiti: A statistical mechanics approach. Physica A 2013, 392, 252–270. [Google Scholar] [CrossRef]
- Ising, E. Beitrag zur theorie des ferromagnetismus. Z. Phys. Hadron. Nucl. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Van Gennip, Y.; Hunter, B.; Ahn, R.; Elliott, P.; Luh, K.; Halvorson, M.; Reid, S.; Valasik, M.; Wo, J.; Tita, G.E.; et al. Community detection using spectral clustering on sparse geosocial data. SIAM J. Appl. Math. 2013, 73, 67–83. [Google Scholar] [CrossRef]
- Short, M.B.; D’Orsogna, M.R.; Pasour, V.B.; Tita, G.E.; Brantingham, P.; Bertozzi, A.L.; Chayes, L.B. A Statistical Model of Criminal Behavior. Math. Model. Methods Appl. Sci. 2008, 18, 1249–1267. [Google Scholar] [CrossRef]
- Rodríguez, N. On the global well-posedness theory for a class of PDE models for criminal activity. Phys. D Nonlinear Phenom. 2013, 260, 191–200. [Google Scholar] [CrossRef]
- Rodriguez, N.; Bertozzi, A. Local existence and uniqueness of solutions to a PDE model for criminal behavior. Math. Model. Methods Appl. Sci. 2010, 20, 1425–1457. [Google Scholar] [CrossRef]
- Berestycki, H.; Rodriguez, N.; Ryzhik, L. Traveling wave solutions in a reaction-diffusion model for criminal activity. Multiscale Model. Simul. 2013, 11, 1097–1126. [Google Scholar] [CrossRef]
- Jones, P.A.; Brantingham, P.J.; Chayes, L.R. Statistical Models of Criminal Behavior: The Effects of Law Enforcement Actions. Math. Model. Methods Appl. Sci. 2010, 20, 1397–1423. [Google Scholar] [CrossRef]
- Zipkin, J.R.; Short, M.B.; Bertozzi, A.L. Cops on the dots in a mathematical model of urban crime and police response. Discret. Contin. Dyn. Syst. Ser. B 2014, 19, 1479–1506. [Google Scholar] [CrossRef]
- Mei, L.; Wei, J. The existence and stability of spike solutions for a chemotax is system modeling crime pattern formation. Math. Model. Methods Appl. Sci. 2020, 30, 1727–1764. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Bertozzi, A.L.; Short, M.B. A stochastic-statistical residential burglary model with independent Poisson clocks. Eur. J. Appl. Math. 2021, 32, 35–38. [Google Scholar] [CrossRef]
- Berestyki, H.; Rodríguez, N. Analysis of a heterogeneous model for riot dynamics: The effect of censorship of information. Eur. J. Appl. Math. 2016, 27, 554. [Google Scholar] [CrossRef]
- Rodríguez, N.; Ryzhik, L. Exploring the effects of social preference, economic disparity, and heterogeneous environments on segregation. Commun. Math. Sci. 2016, 14, 363–387. [Google Scholar] [CrossRef]
- D’Orsogna, M.R.; Perc, M. Statistical physics of crime: A review. Phys. Life Rev. 2015, 12, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Barbaro, A.B.; Rodriguez, N.; Yoldaş, H.; Zamponi, N. Analysis of a cross-diffusion model for rival gangs interaction in a city. arXiv 2020, arXiv:2009.04189. [Google Scholar]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Courier Corporation: Gloucester, MA, USA, 2007. [Google Scholar]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Dolak, Y.; Schmeiser, C. Kinetic models for chemotaxis: Hydrodynamic limits and spatio-temporal mechanisms. J. Math. Biol. 2005, 51, 595–615. [Google Scholar] [CrossRef] [PubMed]
- Short, M.B.; Bertozzi, A.L.; Brantingham, P.J. Nonlinear Patterns in Urban Crime: Hotspots, Bifurcations, and Suppression. SIAM J. Appl. Dyn. Syst. 2010, 9, 462–483. [Google Scholar] [CrossRef]
- Briscoe, B.K.; Lewis, M.A.; Parrish, S.E. Home Range Formation in Wolves Due to Scent Making. Bull. Math. Biol. 2002, 64, 261–284. [Google Scholar] [CrossRef]
- White, K.; Lewis, M.; Murray, J. A Model for Wolf-Pack Territory Formation and Maintenance. J. Theor. Biol. 1996, 178, 29–43. [Google Scholar] [CrossRef]
- Patlak, C.S. Random walk with persistence and external bias. Bull. Math. Biophys. 1953, 15, 311–338. [Google Scholar] [CrossRef]
- Keller, E.F.; Segel, L.A. Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 1970, 26, 399–415. [Google Scholar] [CrossRef]
- Morisita, M. Population density and dispersal of a water strider. Gerris lacustris: Observations and considerations on animal aggregations. Contrib. Physiol. Ecol. Kyoto Univ. 1950, 65, 1–149. [Google Scholar]
- Morisita, M. Habitat preference and evaluation of environment of an animal. Experimental studies on the population density of an antlion, Glenuroides japonicus M’L. [= correctly Hagenomyia micans]. I. Physiol. Ecol. 1952, 5, 1–16. [Google Scholar]
- Gurtin, M.E.; Pipkin, A. A note on interacting populations that disperse to avoid crowding. Q. Appl. Math. 1984, 42, 87–94. [Google Scholar] [CrossRef]
- Vanag, V.K.; Epstein, I.R. Cross-diffusion and pattern formation in reaction—Diffusion systems. Phys. Chem. Chem. Phys. 2009, 11, 897–912. [Google Scholar] [CrossRef]
- Burger, M.; Carrillo, J.A.; Pietschmann, J.F.; Schmidtchen, M. Segregation effects and gap formation in cross-diffusion models. Interfaces Free. Boundaries 2020, 22, 175–203. [Google Scholar] [CrossRef]
- Di Francesco, M.; Esposito, A.; Fagioli, S. Nonlinear degenerate cross-diffusion systems with nonlocal interaction. Nonlinear Anal. 2018, 169, 94–117. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Huang, Y.; Schmidtchen, M. Zoology of a nonlocal cross-diffusion model for two species. SIAM J. Appl. Math. 2018, 78, 1078–1104. [Google Scholar] [CrossRef]
- Bruna, M.; Burger, M.; Ranetbauer, H.; Wolfram, M.T. Cross-diffusion systems with excluded-volume effects and asymptotic gradient flow structures. J. Nonlinear Sci. 2017, 27, 687–719. [Google Scholar] [CrossRef]







| Parameter Set | Gang | Value of | % Territory, Model 1 | % Territory, Model 2 |
|---|---|---|---|---|
| Set 1 | Gang 1 | % | % | |
| Gang 2 | % | % | ||
| Gang 3 | % | % | ||
| Set 2 | Gang 1 | % | % | |
| Gang 2 | % | % | ||
| Gang 3 | % | % | ||
| Set 3 | Gang 1 | % | % | |
| Gang 2 | % | % | ||
| Gang 3 | % | % | ||
| Set 4 | Gang 1 | % | % | |
| Gang 2 | % | % | ||
| Gang 3 | % | % | ||
| Set 5 | Gang 1 | % | % | |
| Gang 2 | % | % | ||
| Gang 3 | % | % | ||
| Set 6 | Gang 1 | % | % | |
| Gang 2 | % | % | ||
| Gang 3 | % | % |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsenafi, A.; Barbaro, A.B.T. A Multispecies Cross-Diffusion Model for Territorial Development. Mathematics 2021, 9, 1428. https://doi.org/10.3390/math9121428
Alsenafi A, Barbaro ABT. A Multispecies Cross-Diffusion Model for Territorial Development. Mathematics. 2021; 9(12):1428. https://doi.org/10.3390/math9121428
Chicago/Turabian StyleAlsenafi, Abdulaziz, and Alethea B. T. Barbaro. 2021. "A Multispecies Cross-Diffusion Model for Territorial Development" Mathematics 9, no. 12: 1428. https://doi.org/10.3390/math9121428
APA StyleAlsenafi, A., & Barbaro, A. B. T. (2021). A Multispecies Cross-Diffusion Model for Territorial Development. Mathematics, 9(12), 1428. https://doi.org/10.3390/math9121428






