Dynamics under Uncertainty: Modeling Simulation and Complexity
Author Contributions
Funding
Conflicts of Interest
References
- Stanković, M.; Stević, Ž.; Das, D.; Subotić, M.; Pamučar, D. A New Fuzzy MARCOS Method for Road Traffic Risk Analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef]
- Fu, C.; Feng, G.; Ma, J.; Lu, K.; Yang, Y.; Gu, F. Predicting the Dynamic Response of Dual-Rotor System Subject to Interval Parametric Uncertainties Based on the Non-Intrusive Metamodel. Mathematics 2020, 8, 736. [Google Scholar] [CrossRef]
- Žižović, M.; Pamučar, D.; Ćirović, G.; Žižović, M.; Miljković, B. A Model for Determining Weight Coefficients by Forming a Non-Decreasing Series at Criteria Significance Levels (NDSL). Mathematics 2020, 8, 745. [Google Scholar] [CrossRef]
- Li, L.; Liao, F. Preview Control for MIMO Discrete-Time System with Parameter Uncertainty. Mathematics 2020, 8, 756. [Google Scholar] [CrossRef]
- Pribićević, I.; Doljanica, S.; Momčilović, O.; Das, D.; Pamučar, D.; Stević, Ž. Novel Extension of DEMATEL Method by Trapezoidal Fuzzy Numbers and D Numbers for Management of Decision-Making Processes. Mathematics 2020, 8, 812. [Google Scholar] [CrossRef]
- Žižović, M.; Pamučar, D.; Albijanić, M.; Chatterjee, P.; Pribićević, I. Eliminating Rank Reversal Problem Using a New Multi-Attribute Model—The RAFSI Method. Mathematics 2020, 8, 1015. [Google Scholar] [CrossRef]
- Hamzenejad, A.; Jafarzadeh Ghoushchi, S.; Baradaran, V.; Mardani, A. A Robust Algorithm for Classification and Diagnosis of Brain Disease Using Local Linear Approximation and Generalized Autoregressive Conditional Heteroscedasticity Model. Mathematics 2020, 8, 1268. [Google Scholar] [CrossRef]
- Pamučar, D.; Ecer, F.; Cirovic, G.; Arlasheedi, M. Application of Improved Best Worst Method (BWM) in Real-World Problems. Mathematics 2020, 8, 1342. [Google Scholar] [CrossRef]
- Ulutaş, A.; Karabasevic, D.; Popovic, G.; Stanujkic, D.; Nguyen, P.; Karaköy, Ç. Development of a Novel Integrated CCSD-ITARA-MARCOS Decision-Making Approach for Stackers Selection in a Logistics System. Mathematics 2020, 8, 1672. [Google Scholar] [CrossRef]
- Aleksić, A.; Nedeljković, S.; Jovanović, M.; Ranđelović, M.; Vuković, M.; Stojanović, V.; Radovanović, R.; Ranđelović, M.; Ranđelović, D. Prediction of Important Factors for Bleeding in Liver Cirrhosis Disease Using Ensemble Data Mining Approach. Mathematics 2020, 8, 1887. [Google Scholar] [CrossRef]
- Salmeron, J.; Ruiz-Celma, A. Synthetic Emotions for Empathic Building. Mathematics 2021, 9, 701. [Google Scholar] [CrossRef]
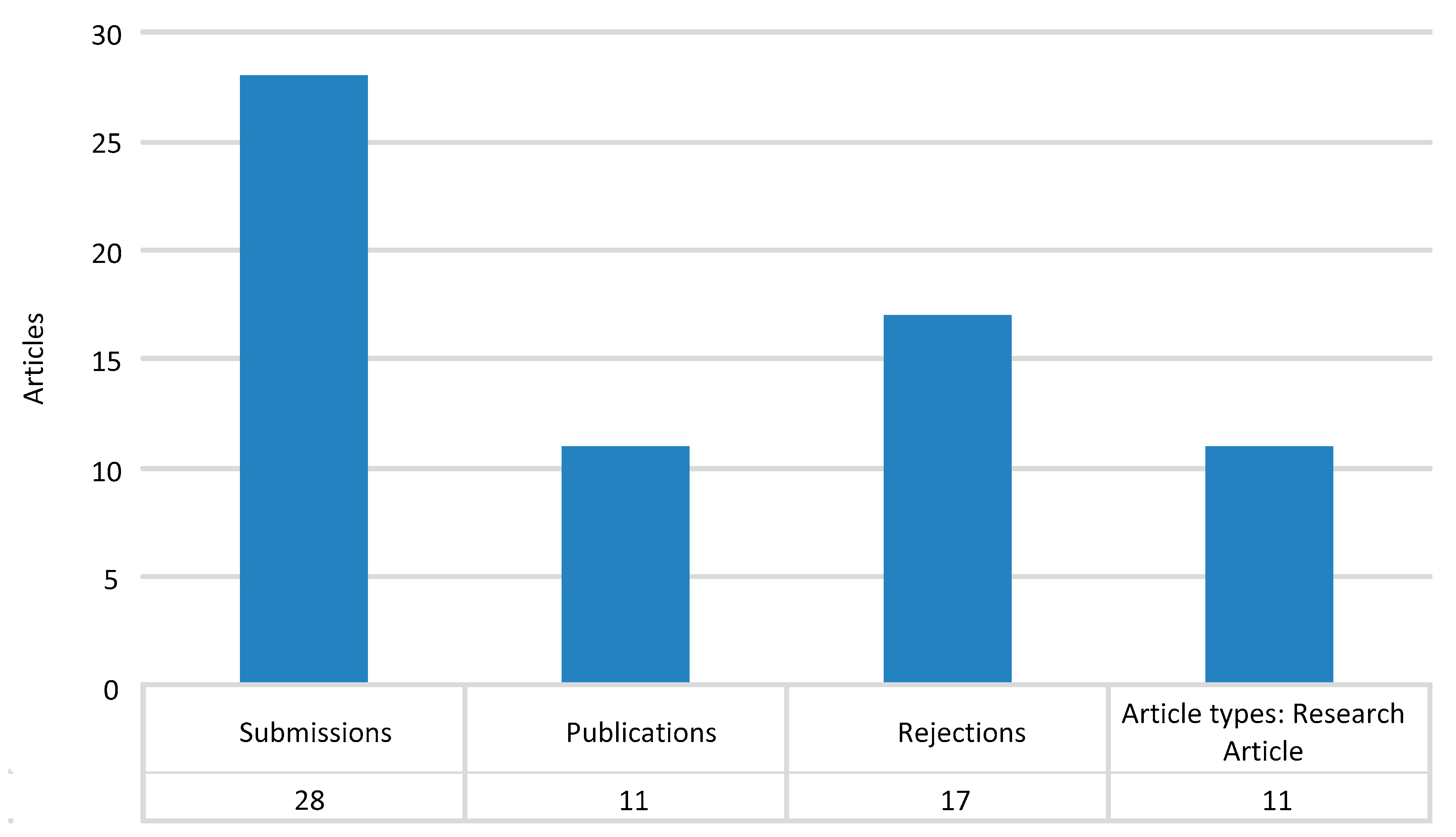
| Countries | Countries |
|---|---|
| Serbia | 7 |
| Bosnia and Herzegovina | 2 |
| China | 2 |
| South Africa | 2 |
| Turkey | 2 |
| Vietnam | 2 |
| Chile | 1 |
| India | 1 |
| Saudi Arabia | 1 |
| Spain | 1 |
| Iran | 1 |
| UK | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pamučar, D.; Marinković, D.; Kar, S. Dynamics under Uncertainty: Modeling Simulation and Complexity. Mathematics 2021, 9, 1416. https://doi.org/10.3390/math9121416
Pamučar D, Marinković D, Kar S. Dynamics under Uncertainty: Modeling Simulation and Complexity. Mathematics. 2021; 9(12):1416. https://doi.org/10.3390/math9121416
Chicago/Turabian StylePamučar, Dragan, Dragan Marinković, and Samarjit Kar. 2021. "Dynamics under Uncertainty: Modeling Simulation and Complexity" Mathematics 9, no. 12: 1416. https://doi.org/10.3390/math9121416
APA StylePamučar, D., Marinković, D., & Kar, S. (2021). Dynamics under Uncertainty: Modeling Simulation and Complexity. Mathematics, 9(12), 1416. https://doi.org/10.3390/math9121416






