Synthetic Emotions for Empathic Building
Abstract
1. Introduction
2. Theoretical Background
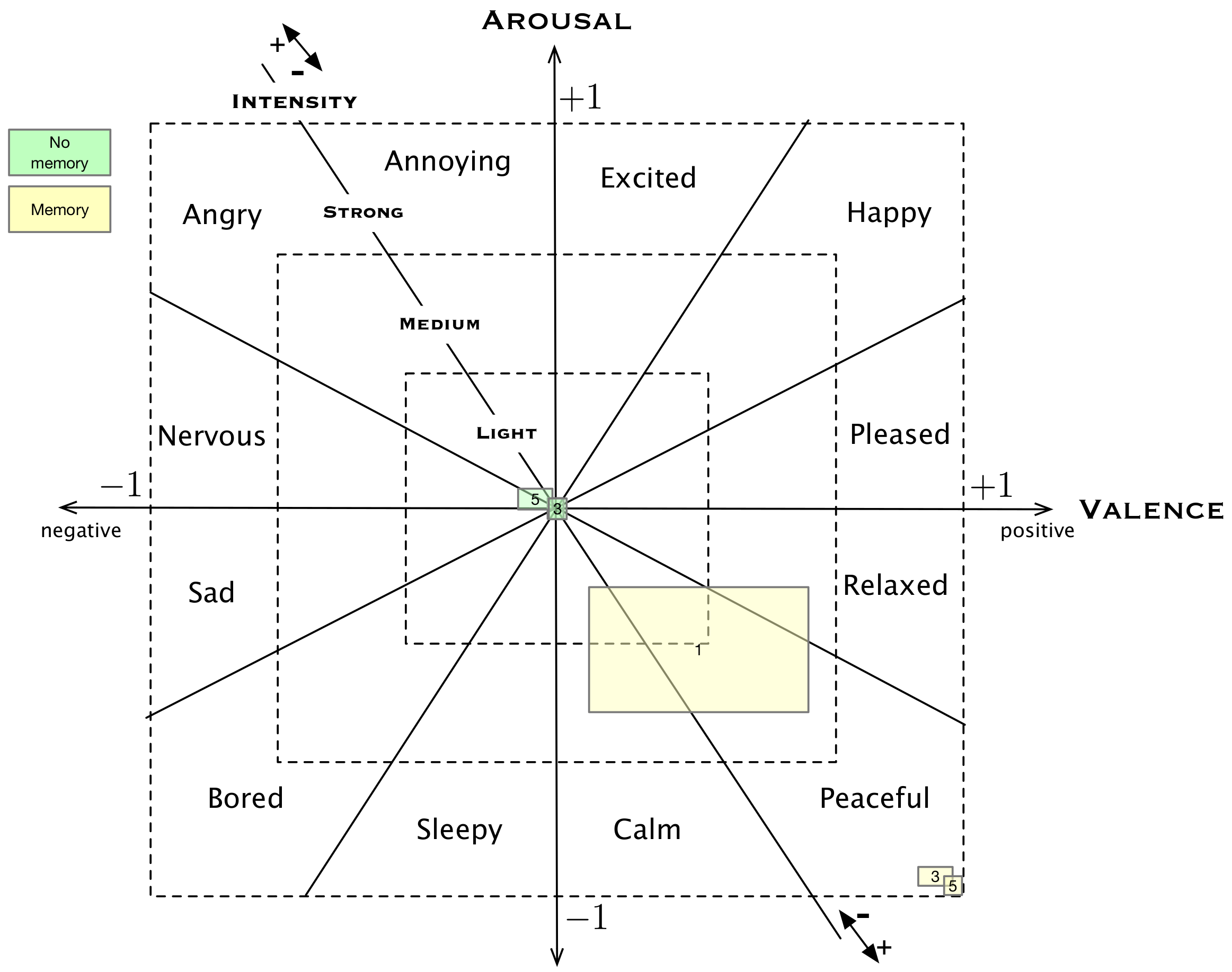
2.1. Thayer’s Emotion Model
2.2. Emotional-Based AI Systems
3. Fuzzy Grey Cognitive Maps
3.1. Fundamentals
- If the stability is reached, the FGCM inference process stop. It achieves a steady pattern of nodes’ states, the so-called grey fixed-point attractor, or grey hidden pattern. This steady grey vector state shows the impact of the initial grey vector state on the final state of each FGCM grey node.
- In addition, the grey vector state could keep cycling between some fixed states. This situation is known as the limit grey cycle.
- A third possible state with a continuous activation function would be a grey chaotic attractor. It is when, instead of a steady-state, the FGCMs keep generating different grey vector states for each iteration.
3.2. FGCM Advantages over FCM
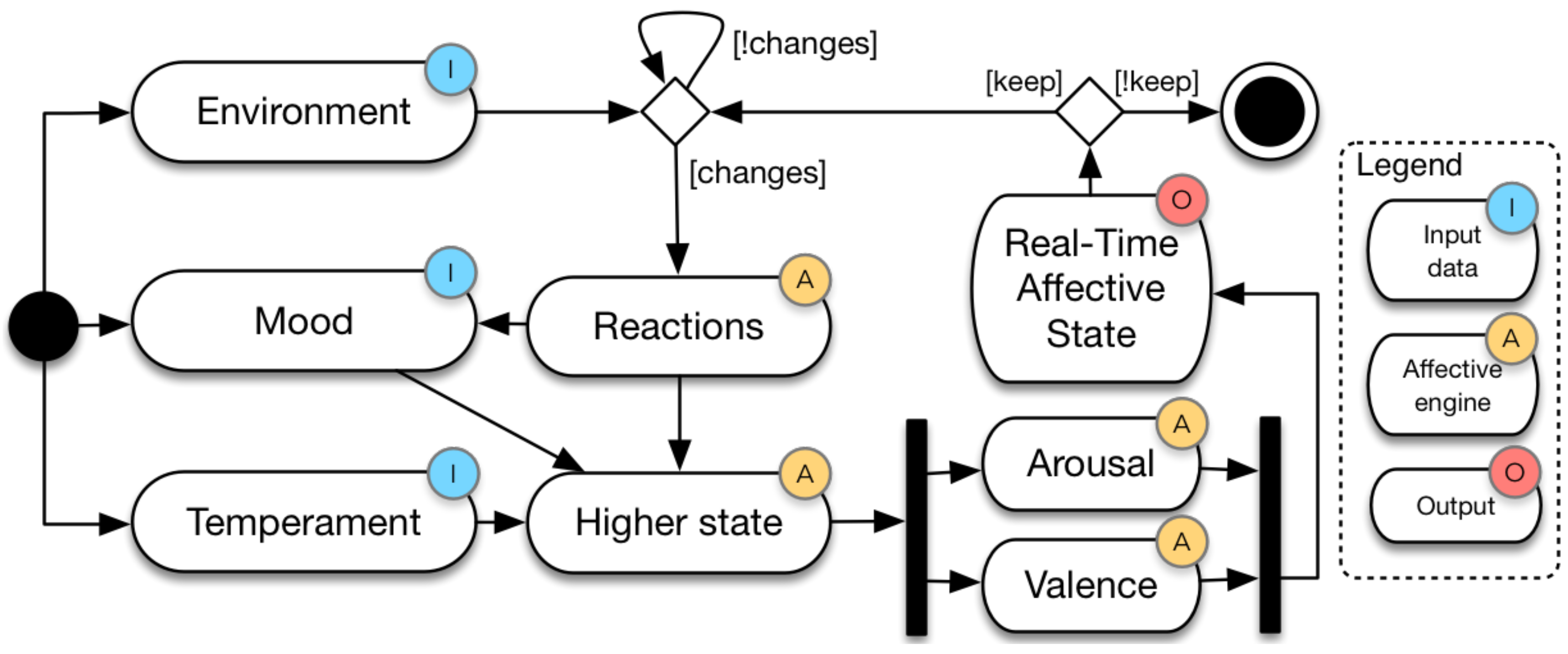
4. Proposal
Methodology
5. Experiments and Discussion
5.1. Experiment 1
5.2. Experiment 2
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brun, Y.; Serugendo, G.D.M.; Gacek, C.; Giese, H.; Kienle, H.; Litoiu, M.; Muller, H.; Pezze, M.; Shaw, M. Engineering Self-Adaptive Systems through Feedback Loops. In Software Engineering for Self-Adaptive Systems. Lecture Notes in Computer Science; Cheng, B.H.C., de Lemos, R., Giese, H., Inverardi, P., Magee, J., Eds.; Springer: Heidelberg/Berlin, Germany, 2009; pp. 48–70. [Google Scholar]
- Precup, R.-E.; Preitl, S.; Petriu, E.; Bojan-Dragos, C.-A.; Szedlak-Stinean, A.-I.; Roman, R.-C.; Hedrea, E.-L. Model-Based Fuzzy Control Results for Networked Control Systems. Rep. Mech. Eng. 2020, 1, 10–25. [Google Scholar] [CrossRef]
- Ghosh, I.; Datta Chaudhuri, T. FEB-Stacking and FEB-DNN Models for Stock Trend Prediction: A Performance Analysis for Pre and Post Covid-19 Periods. Decis. Mak. Appl. Manag. Eng. 2021, 4, 51–84. [Google Scholar] [CrossRef]
- Tziallas, G.; Theodoulidis, B. A controller synthesis algorithm for building self-adaptive software. Inf. Softw. Technol. 2004, 46, 719–727. [Google Scholar] [CrossRef]
- Khakpour, N.; Jalili, S.; Talcott, C.; Sirjani, M.; Mousavi, M.R. PobSAM: Policy-based Managing of Actors in Self-Adaptive Systems. Electron. Notes Theor. Comput. Sci. 2010, 263, 129–143. [Google Scholar] [CrossRef]
- Lee-Johnson, C.P.; Carnegie, D.A. Mobile Robot Navigation Modulated by Artificial Emotions. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2010, 40, 469–480. [Google Scholar] [CrossRef] [PubMed]
- Shurong, N.; Jie, P.; Guangmei, X.; Guangping, Z.; Xuyan, T. Study on Artificial Emotion Model. In Proceedings of the ICNN&B ’05. International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2005; Volume 3, pp. 1420–1424. [Google Scholar]
- Hoerger, M.; Quirk, S.W. Affective forecasting and the Big Five. Personal. Individ. Differ. 2010, 49, 972–976. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tao, J.; Tan, T.; Picard, R.W. Affective Computing and Intelligent Interaction; Springer: Berlin, Germany, 2005. [Google Scholar]
- Guojiang, W.; Xiaoxiao, W.; Kechang, F. Behaviour decision model of intelligent agent based on artificial emotion. In Proceedings of the 2nd International Conference on Advanced Computer Control (ICACC), Shenyang, China, 29–31 January 2010; pp. 185–189. [Google Scholar]
- Albornoz, E.M.; Milone, D.H.; Rufiner, H.L. Spoken emotion recognition using hierarchical classifiers. Comput. Speech Lang. 2011, 25, 556–570. [Google Scholar] [CrossRef]
- Clavel, C.; Vasilescu, I.; Devillers, L.; Richard, G.; Ehrette, T. Fear-type emotion recognition for future audio-based surveillance systems. Speech Commun. 2008, 50, 487–503. [Google Scholar] [CrossRef]
- Devillers, L.; Vidrascu, L. Speaker Classification II: Selected Projects. In Lecture Notes in Computer Science; Chapter: Real-Life Emotion Recognition in Speech; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4441/2007, pp. 34–42. [Google Scholar]
- Tacconi, D.; Mayora, O.; Lukowicz, P.; Arnrich, B.; Setz, C.; Trster, G.; Haring, C. Activity and emotion recognition to support early diagnosis of psychiatric diseases. In Proceedings of the 2nd International Conference on Pervasive Computing Technologies for Healthcare’08 Tampere, Tampere, Finland, 30 January–1 February 2008; pp. 100–102. [Google Scholar]
- Yildirim, S.; Narayanan, S.; Potamianos, A. Detecting emotional state of a child in a conversational computer game. Comput. Speech Lang. 2011, 25, 29–44. [Google Scholar] [CrossRef]
- Murray, I.R.; Arnott, J.L. Applying an analysis of acted vocal emotions to improve the simulation of synthetic speech. Comput. Speech Lang. 2008, 22, 107–129. [Google Scholar] [CrossRef]
- Schindler, K.; Van Gool, L.; de Gelder, B. Recognizing emotions expressed by body pose: A biologically inspired neural model. Neural Netw. 2008, 21, 1238–1246. [Google Scholar] [CrossRef]
- Vinhas, V.; Reis, L.P.; Oliveira, E. Dynamic multimedia content delivery based on real-time user emotions. Multichannel online biosignals towards adaptative GUI and content delivery. In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing & Biosignals, Porto, Portugal, 14–17 January 2009; pp. 299–304. [Google Scholar]
- Ortony, A.; Clore, G.; Collins, A. The Cognitive Structure of Emotions; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Marreiros, G.; Santos, R.; Ramos, C.; Neves, J.; Novais, P.; Machado, J.; Bulas-Cruz, J. Ambient Intelligence in Emotion Based Ubiquitous Decision Making. In Proceedings of the Artificial Intelligence Techniques for Ambient Intelligence, IJCAI’07—Twentieth International Joint Conference on Artificial Intelligence, Hyderabad, India, 6–12 January 2007. [Google Scholar]
- Thayer, R.E. The Biopsychology of Mood and Arousal; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Acampora, G.; Loia, V.; Vitiello, A. Distributing Emotional Services in Ambient Intelligence through Cognitive Agents. Serv. Oriented Comput. Appl. 2011, 5, 17–35. [Google Scholar] [CrossRef]
- Yang, Y.-H.; Lin, Y.-C.; Su, Y.-F.; Chen, H.H. Music emotion classification: A regression approach. In Proceedings of the IEEE International Conference Multimedia & Expo, Beijing, China, 2–5 July 2007; pp. 208–211. [Google Scholar]
- Zhou, J.; Yu, C.; Riekki, J.; Karkkainen, E. AmE framework: A model for emotion-aware ambient intelligence. In Proceedings of the The Second International Conference on Affective Computing and Intelligent Interaction (ACII2007), Lisbon, Portugal, 12–14 September 2007. [Google Scholar]
- Sharada, G.; Ramanaiah, O.B.V. An Artificial Intelligence Based Neuro-Fuzzy System Emotional Intelligence. Int. J. Comput. Appl. 2010, 1, 74–79. [Google Scholar] [CrossRef]
- Setiono, D.; Saputra, D.; Putra, K.; Moniaga, J.V.; Chowandaa, A. Enhancing Player Experience in Game With Affective Computing. Procedia Comput. Sci. 2021, 179, 781–788. [Google Scholar] [CrossRef]
- Han, J.; Zhang, Z.; Pantic, M.; Schuller, B. Internet of emotional people: Towards continual affective computing cross cultures via audiovisual signals. Future Gener. Comput. Syst. 2021, 114, 294–306. [Google Scholar] [CrossRef]
- Kratzwald, B.; Ilić, S.; Kraus, M.; Feuerriegel, S.; Prendinger, H. Deep learning for affective computing: Text-based emotion recognition in decision support. Decis. Support Syst. 2018, 115, 24–35. [Google Scholar] [CrossRef]
- Salmeron, J.L. Augmented fuzzy cognitive maps for modelling LMS critical success factors. Knowl. Based Syst. 2009, 22, 275–278. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Lopez, C. Forecasting Risk Impact on ERP Maintenance with Augmented Fuzzy Cognitive Maps. IEEE Trans. Softw. Eng. 2011, 38, 439–452. [Google Scholar] [CrossRef]
- Salmeron, J.L. Fuzzy cognitive maps for artificial emotions forecasting. Appl. Soft Comput. 2012, 12, 3704–3710. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Rahimi, S.A.; Navalie, A.M.; Sadeghpour, A. Medical Diagnosis of Rheumatoid Arthritis using Data driven PSO-FCM. Neurocomputing 2017, 232, 104–112. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Ruiz-Celma, A.; Mena, A. Learning FCMs with multi-local and balanced memetic algorithms for forecasting drying processes. Neurocomputing 2017, 232, 52–57. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Vidal, R.; Mena, A. Ranking Fuzzy Cognitive Maps based scenarios with TOPSIS. Expert Syst. Appl. 2012, 39, 2443–2450. [Google Scholar] [CrossRef]
- Vanhoenshoven, F.; Napoles, G.; Froelich, W.; Salmeron, J.L.; Vanhoof, K. Pseudoinverse Learning of Fuzzy Cognitive Maps for Multivariate Time Series Forecasting. Appl. Soft Comput. 2020, 95, 106461. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Papageorgiou, E.I. A Fuzzy Grey Cognitive Maps-based Decision Support System for Radiotherapy Treatment Planning. Knowl. Based Syst. 2012, 30, 151–160. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Salmeron, J.L. Modelling grey uncertainty with Fuzzy Grey Cognitive Maps. Expert Syst. Appl. 2010, 37, 7581–7588. [Google Scholar] [CrossRef]
- Froelich, W.; Salmeron, J.L. Evolutionary Learning of Fuzzy Grey Cognitive Maps for the Forecasting of Multivariate, Interval-Valued Time Series. Int. J. Approx. Reason. 2014, 55, 1319–1335. [Google Scholar] [CrossRef]
- Rodriguez-Repiso, L.; Setchi, R.; Salmeron, J.L. Modelling IT Projects success with Fuzzy Cognitive Maps. Expert Syst. Appl. 2007, 32, 543–559. [Google Scholar] [CrossRef]
- Salmeron, J.L. An Autonomous FGCM-based System for Surveillance Assets Coordination. J. Grey Syst. 2016, 28, 27–35. [Google Scholar]
- Salmeron, J.L.; Gutierrez, E. Fuzzy Grey Cognitive Maps in Reliability Engineering. Appl. Soft Comput. 2012, 12, 3818–3824. [Google Scholar] [CrossRef]
- Xirogiannis, G.; Glykas, M. Fuzzy cognitive maps in business analysis and performance-driven change. IEEE Trans. Eng. Manag. 2004, 51, 334–351. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Salmeron, J.L. Learning Fuzzy Grey Cognitive Maps using Nonlinear Hebbian-based approach. Int. J. Approx. Reason. 2012, 53, 54–65. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Papageorgiou, E.I. Fuzzy Grey Cognitive Maps and Nonlinear Hebbian Learning in process control. Appl. Intell. 2014, 41, 223–234. [Google Scholar] [CrossRef]
- Napoles, G.; Salmeron, J.L.; Vanhoof, K. Construction and Supervised Learning of Long-Term Grey Cognitive Networks. IEEE Trans. Cybern. 2021, 51, 686–695. [Google Scholar] [CrossRef] [PubMed]
- Salmeron, J.L.; Palos, P. Uncertainty propagation in Fuzzy Grey Cognitive Maps with Hebbian-like learning algorithms. IEEE Trans. Cybern. 2019, 49, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Bueno, S.; Salmeron, J.L. Benchmarking main activation functions in fuzzy cognitive maps. Expert Syst. Appl. 2009, 36 Pt 1, 5221–5229. [Google Scholar] [CrossRef]

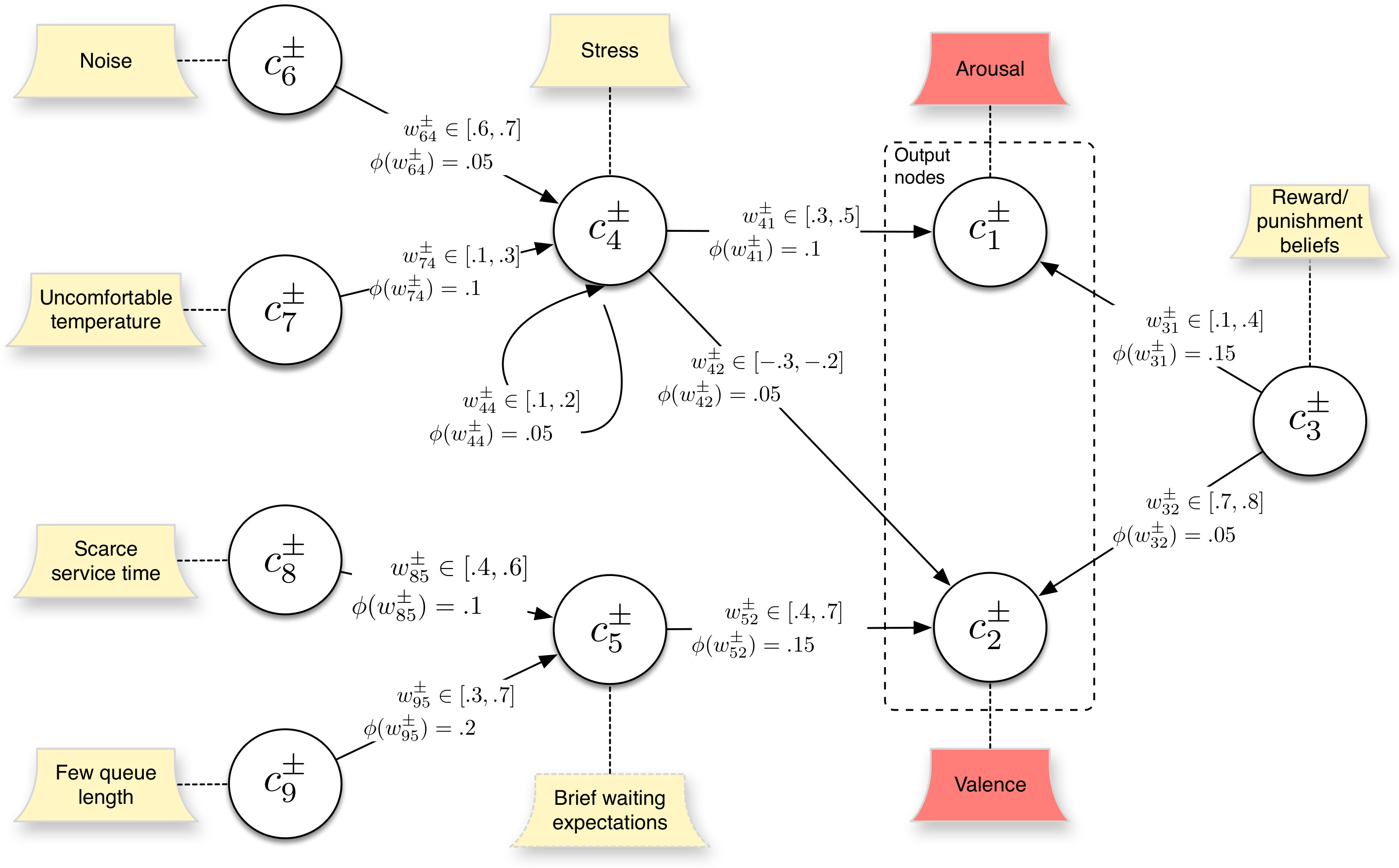

| Node () | Label | Description |
|---|---|---|
| Arousal | State of being awake or reactive to stimuli | |
| Valence | The intrinsic attractiveness (positive valence) or aversiveness (negative valence) of an emotion | |
| Reward/Punishment | Reward is related with the queue’s purpose | |
| Stress | A person’s response to a stressor such as noise or uncomfortable temperature | |
| Waiting expectations | Waiting time | |
| Noise | Environmental noise | |
| Uncomfortable | Temperature higher or lower than comfortable | |
| Scarce service time | Waiting time for each person | |
| Few queue length | People in the queue |
| Steady State | Greyness | ||||||
|---|---|---|---|---|---|---|---|
| Slope | c1 | c2 | Emotion | c1 | c2 | ||
| F | tanh | 1 | [0.0, ] | [, 0.0] | neutral | ||
| F | tanh | 3 | [0.0, ] | [, 0.0] | neutral | ||
| F | tanh | 5 | [0.0, 0.1360] | [−0.0819, −0.0] | ligth nervous | ||
| T | tanh | 1 | [0.0380, 0.1766] | [0.1308, 0.4200] | ligth pleased | ||
| T | tanh | 3 | [0.3275, 0.9073] | [0.8188, 0.9958] | med-strong happy | ||
| T | tanh | 5 | [0.7331, 0.9990] | [0.9953, 0.9999] | strongly happy | ||
| Steady State | Greyness | ||||||
|---|---|---|---|---|---|---|---|
| Slope | c1 | c2 | Emotion | c1 | c2 | ||
| F | tanh | 1.0 | [, 0.0] | [0.0, ] | neutral | ||
| F | tanh | 3.0 | [, 0.0] | [0.0, ] | neutral | ||
| F | tanh | 5.0 | [−0.1360, 0.0] | [0.0, 0.0820] | almost neutral | ||
| T | tanh | 1.0 | [−0.4135, −0.1936] | [0.1794, 0.6163] | medium peaceful | ||
| T | tanh | 3.0 | [−0.9966, −0.9274] | [0.8990, 0.9999] | strongly peaceful | ||
| T | tanh | 5.0 | [−1.0, −0.9993] | [0.9978, 1.0] | strongly peaceful | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salmeron, J.L.; Ruiz-Celma, A. Synthetic Emotions for Empathic Building. Mathematics 2021, 9, 701. https://doi.org/10.3390/math9070701
Salmeron JL, Ruiz-Celma A. Synthetic Emotions for Empathic Building. Mathematics. 2021; 9(7):701. https://doi.org/10.3390/math9070701
Chicago/Turabian StyleSalmeron, Jose L., and Antonio Ruiz-Celma. 2021. "Synthetic Emotions for Empathic Building" Mathematics 9, no. 7: 701. https://doi.org/10.3390/math9070701
APA StyleSalmeron, J. L., & Ruiz-Celma, A. (2021). Synthetic Emotions for Empathic Building. Mathematics, 9(7), 701. https://doi.org/10.3390/math9070701







