Modeling Interactions among Migration, Growth and Pressure in Tumor Dynamics
Abstract
1. Introduction
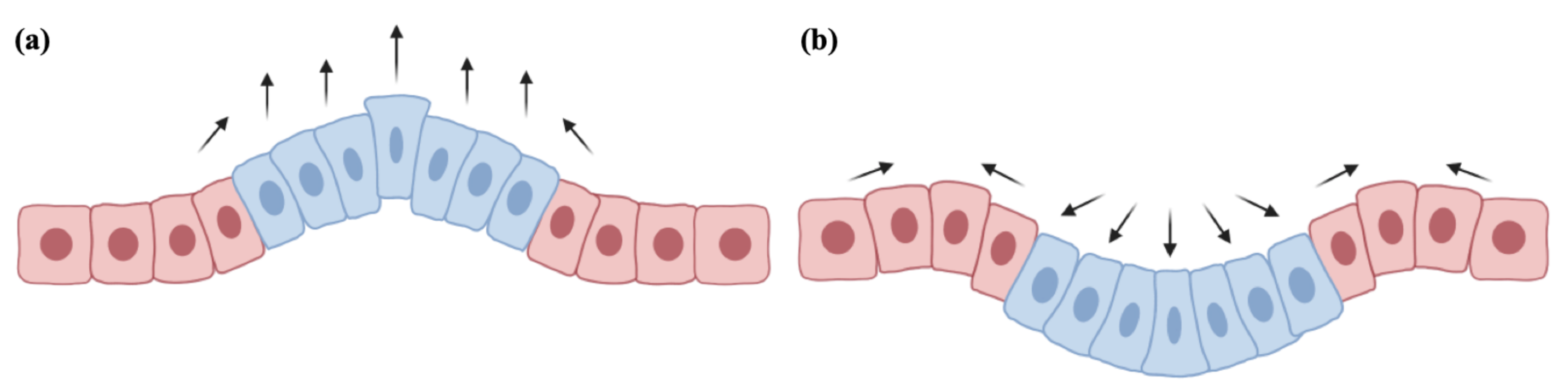
2. Biomechanical Mathematical Modeling
2.1. Internal Pressure and Growth
2.2. Some Mathematical Properties of the Growth Model with Internal Pressure
- , for some . Then, , for every ,
- , for some . Then, , for every ,
2.3. Cell Density Evolution
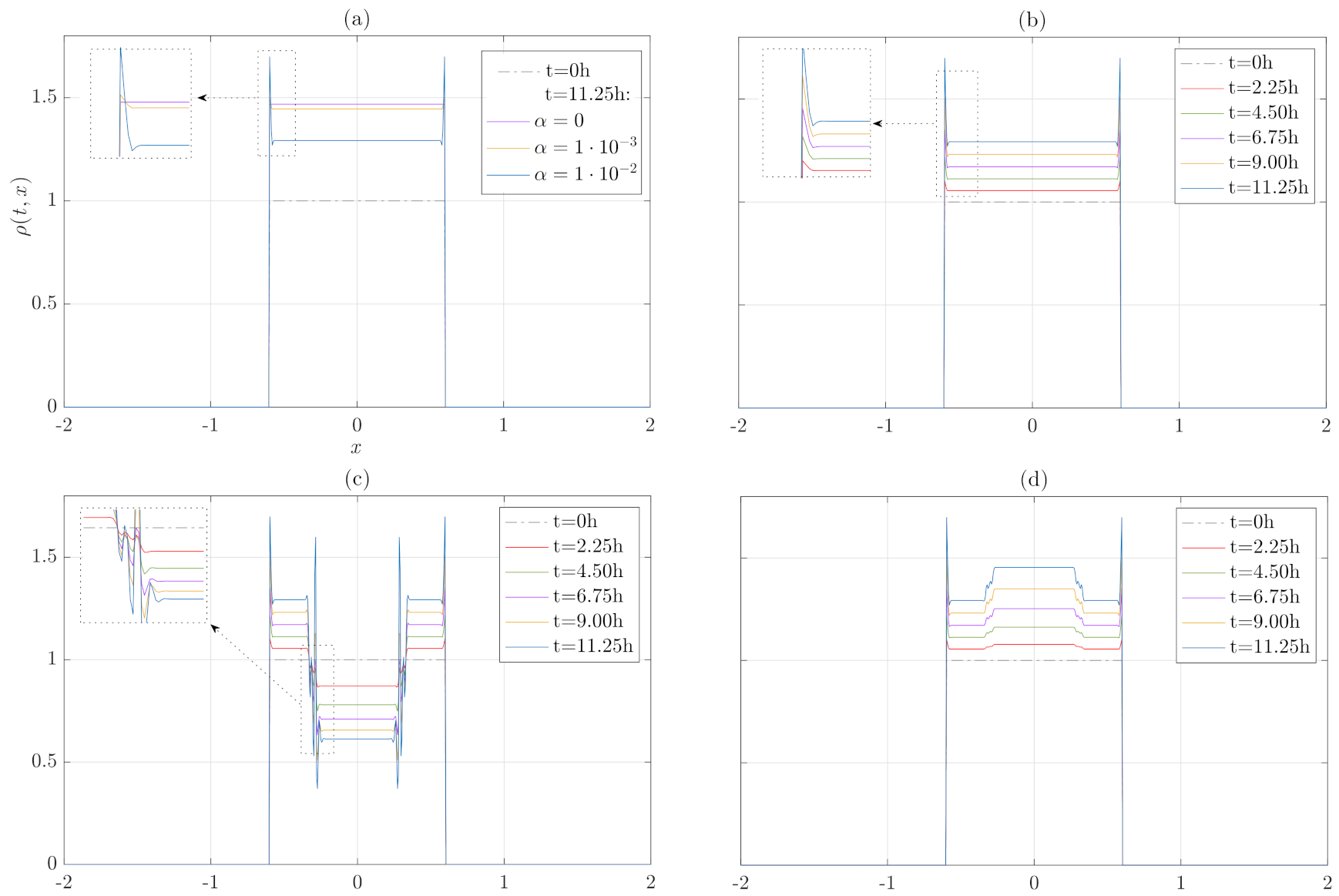
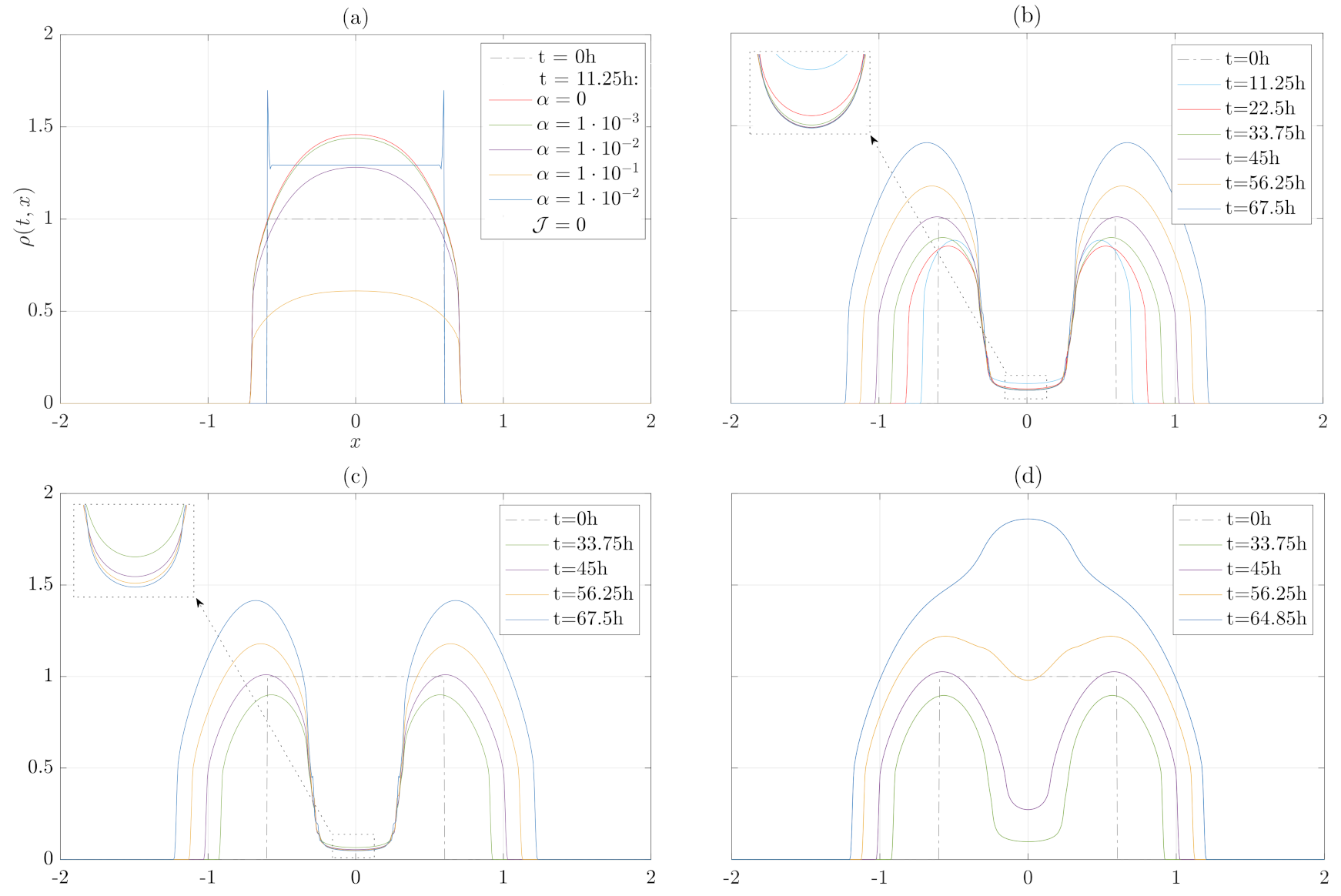
3. Numerical Results
3.1. Numerical Treatment of the Model
3.2. Growth and Internal Pressure Dependence without Migration
3.3. Migration, Growth and Pressure Interactions
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Roose, T.; Chapman, S.J.; Maini, P.K. Mathematical models of avascular tumor growth. SIAM Rev. 2007, 49, 179–208. [Google Scholar] [CrossRef]
- Bellomo, N.; Li, N.; Maini, P.K. On the foundations of cancer modelling: Selected topics, speculations, and perspectives. Math. Model. Methods Appl. Sci. 2008, 18, 593–646. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- Alarcón, T.; Byrne, H.M.; Maini, P.K. A multiple scale model for tumor growth. Multiscale Model. Simul. 2005, 3, 440–475. [Google Scholar] [CrossRef]
- Corbin, G.; Engwer, C.; Klar, A.; Nieto, J.; Soler, J.; Surulescu, C.; Wenske, M. Modeling glioma invasion with anisotropy-and hypoxia-triggered motility enhancement: From subcellular dynamics to macroscopic pdes with multiple taxis. arXiv 2020, arXiv:2006.12322. [Google Scholar] [CrossRef]
- Camphausen, K.; Purow, B.; Sproull, M.; Scott, T.; Ozawa, T.; Deen, D.F.; Tofilon, P.J. Influence of in vivo growth on human glioma cell line gene expression: Convergent profiles under orthotopic conditions. Proc. Natl. Acad. Sci. USA 2005, 102, 8287–8292. [Google Scholar] [CrossRef]
- Kalluri, R.; Weinberg, R.A. The basics of epithelial-mesenchymal transition. J. Clin. Investig. 2009, 119, 1420–1428. [Google Scholar] [CrossRef]
- Helmlinger, G.; Netti, P.A.; Lichtenbeld, H.C.; Melder, R.J.; Jain, R.K. Solid stress inhibits the growth of multicellular tumor spheroids. Nat. Biotechnol. 1997, 15, 778. [Google Scholar] [CrossRef]
- Roca-Cusachs, P.; Conte, V.; Trepat, X. Quantifying forces in cell biology. Nat. Cell Biol. 2017, 19, 742–751. [Google Scholar] [CrossRef]
- Jain, R.K.; Martin, J.D.; Stylianopoulos, T. The role of mechanical forces in tumor growth and therapy. Annu. Rev. Biomed. Eng. 2014, 16, 321–346. [Google Scholar] [CrossRef]
- Cheng, G.; Tse, J.; Jain, R.K.; Munn, L.L. Micro-environmental mechanical stress controls tumor spheroid size and morphology by suppressing proliferation and inducing apoptosis in cancer cells. PLoS ONE 2009, 4, e4632. [Google Scholar] [CrossRef]
- Cheung, T.H.; Rando, T.A. Molecular regulation of stem cell quiescence. Nat. Rev. Mol. Cell Biol. 2013, 14, 329–340. [Google Scholar] [CrossRef]
- Broders-Bondon, F.; Ho-Bouldoires, T.H.N.; Fernandez-Sanchez, M.E.; Farge, E. Mechanotransduction in tumor progression: The dark side of the force. J. Cell Biol. 2018, 217, 1571–1587. [Google Scholar] [CrossRef]
- Rodriguez, E.K.; Hoger, A.; McCulloch, A.D. Stress-dependent finite growth in soft elastic tissues. J. Biomech. 1994, 27, 455–467. [Google Scholar] [CrossRef]
- Taber, L.A. Biomechanics of Growth, Remodeling, and Morphogenesis. Appl. Mech. Rev. 1995, 48, 487. [Google Scholar] [CrossRef]
- Ambrosi, D.; Preziosi, L. On the closure of mass balance models for tumor growth. Math. Model. Methods Appl. Sci. 2002, 12, 737–754. [Google Scholar] [CrossRef]
- Weis, J.A.; Miga, M.I.; Arlinghaus, L.R.; Li, X.; Abramson, V.; Chakravarthy, A.B.; Pendyala, P.; Yankeelov, T.E. Predicting the response of breast cancer to neoadjuvant therapy using a mechanically coupled reaction–diffusion model. Cancer Res. 2015, 75, 4697–4707. [Google Scholar] [CrossRef]
- Hormuth, D.A.; Weis, J.A.; Barnes, S.L.; Miga, M.I.; Rericha, E.C.; Quaranta, V.; Yankeelov, T.E. A mechanically coupled reaction–diffusion model that incorporates intra-tumoural heterogeneity to predict in vivo glioma growth. J. R. Soc. Interface 2017, 14, 20161010. [Google Scholar] [CrossRef]
- Lorenzo, G.; Hughes, T.J.; Dominguez-Frojan, P.; Reali, A.; Gomez, H. Computer simulations suggest that prostate enlargement due to benign prostatic hyperplasia mechanically impedes prostate cancer growth. Proc. Natl. Acad. Sci. USA 2019, 116, 1152–1161. [Google Scholar] [CrossRef]
- Chen, C.; Byrne, H.; King, J. The influence of growth-induced stress from the surrounding medium on the development of multicell spheroids. J. Math. Biol. 2001, 43, 191–220. [Google Scholar] [CrossRef]
- Humphrey, J.; Rajagopal, K. A constrained mixture model for growth and remodeling of soft tissues. Math. Model. Methods Appl. Sci. 2002, 12, 407–430. [Google Scholar] [CrossRef]
- Roose, T.; Netti, P.A.; Munn, L.L.; Boucher, Y.; Jain, R.K. Solid stress generated by spheroid growth estimated using a linear poroelasticity model. Microvasc. Res. 2003, 66, 204–212. [Google Scholar] [CrossRef]
- Bevilacqua, G.; Perthame, B.; Schmidtchen, M. The Aronson-Bénilan Estimate in Lebesgue Spaces. arXiv 2020, arXiv:2007.15267. [Google Scholar]
- Perthame, B.; Quirós, F.; Vázquez, J.L. The Hele–Shaw asymptotics for mechanical models of tumor growth. Arch. Ration. Mech. Anal. 2014, 212, 93–127. [Google Scholar] [CrossRef]
- Perthame, B.; Tang, M.; Vauchelet, N. Traveling wave solution of the Hele–Shaw model of tumor growth with nutrient. Math. Model. Methods Appl. Sci. 2014, 24, 2601–2626. [Google Scholar] [CrossRef]
- Perthame, B.; Quirós, F.; Tang, M.; Vauchelet, N. Derivation of a Hele-Shaw type system from a cell model with active motion. Interfaces Free. Boundaries 2014, 16, 489–508. [Google Scholar] [CrossRef]
- Shraiman, B.I. Mechanical feedback as a possible regulator of tissue growth. Proc. Natl. Acad. Sci. USA 2005, 102, 3318–3323. [Google Scholar] [CrossRef]
- Lubarda, V.A.; Hoger, A. On the mechanics of solids with a growing mass. Int. J. Solids Struct. 2002, 39, 4627–4664. [Google Scholar] [CrossRef]
- Trepat, X.; Wasserman, M.R.; Angelini, T.E.; Millet, E.; Weitz, D.A.; Butler, J.P.; Fredberg, J.J. Physical forces during collective cell migration. Nat. Phys. 2009, 5, 426–430. [Google Scholar] [CrossRef]
- Conte, M.; Casas-Tinto, S.; Soler, J. Modeling invasion patterns in the glioblastoma battlefield. PLoS Comput. Biol. 2021, 17, e1008632. [Google Scholar] [CrossRef]
- Calvo, J.; Campos, J.; Caselles, V.; Sánchez, Ó.; Soler, J. Flux-saturated porous media equations and applications. EMS Surv. Math. Sci. 2015, 2, 131–218. [Google Scholar] [CrossRef]
- Dębiec, T.; Perthame, B.; Schmidtchen, M.; Vauchelet, N. Incompressible limit for a two-species model with coupling through Brinkman’s law in any dimension. J. Mathé. Pures Appl. 2021, 145, 204–239. [Google Scholar] [CrossRef]
- Ambrosi, D.; Mollica, F. On the mechanics of a growing tumor. Int. J. Eng. Sci. 2002, 40, 1297–1316. [Google Scholar] [CrossRef]
- Voutouri, C.; Mpekris, F.; Papageorgis, P.; Odysseos, A.D.; Stylianopoulos, T. Role of constitutive behavior and tumor-host mechanical interactions in the state of stress and growth of solid tumors. PLoS ONE 2014, 9, e104717. [Google Scholar]
- Ambrosi, D.; Ben Amar, M.; Cyron, C.J.; DeSimone, A.; Goriely, A.; Humphrey, J.D.; Kuhl, E. Growth and remodelling of living tissues: Perspectives, challenges and opportunities. J. R. Soc. Interface 2019, 16, 20190233. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M.; Berestetskii, V.; Pitaevskii, L. Course of Theoretical Physics: Theory of Elasticity; Butterworth-Heinemann: Oxford, UK, 1995. [Google Scholar]
- Epstein, M. Mathematical characterization and identification of remodeling, growth, aging and morphogenesis. J. Mech. Phys. Solids 2015, 84, 72–84. [Google Scholar] [CrossRef]
- Hetnarski, R.B.; Eslami, M.R.; Gladwell, G. Thermal Stresses: Advanced Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2009; Volume 41. [Google Scholar]
- Ramírez-Weber, F.A.; Kornberg, T.B. Cytonemes: Cellular processes that project to the principal signaling center in Drosophila imaginal discs. Cell 1999, 97, 599–607. [Google Scholar] [CrossRef]
- Cardozo, M.J.; Sánchez-Arrones, L.; Sandonis, A.; Sánchez-Camacho, C.; Gestri, G.; Wilson, S.W.; Guerrero, I.; Bovolenta, P. Cdon acts as a Hedgehog decoy receptor during proximal-distal patterning of the optic vesicle. Nat. Commun. 2014, 5, 1–13. [Google Scholar] [CrossRef]
- Kornberg, T.B.; Gilboa, L. Nanotubes in the niche. Nature 2015, 523, 292–293. [Google Scholar] [CrossRef]
- Huang, H.; Liu, S.; Kornberg, T.B. Glutamate signaling at cytoneme synapses. Science 2019, 363, 948–955. [Google Scholar] [CrossRef]
- González-Méndez, L.; Seijo-Barandiarán, I.; Guerrero, I. Cytoneme-mediated cell–cell contacts for Hedgehog reception. Elife 2017, 6, e24045. [Google Scholar] [CrossRef]
- Verbeni, M.; Sánchez, O.; Mollica, E.; Siegl-Cachedenier, I.; Carleton, A.; Guerrero, I.; i Altaba, A.R.; Soler, J. Morphogenetic action through flux-limited spreading. Phys. Life Rev. 2013, 10, 457–475. [Google Scholar] [CrossRef]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-HillBook Company: New York, NY, USA, 1955. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Casas-Vázquez, J.; Jou, D. Nonequilibrium temperature versus local-equilibrium temperature. Phys. Rev. E 1994, 49, 1040. [Google Scholar] [CrossRef]
- Rubin, M. Hyperbolic heat conduction and the second law. Int. J. Eng. Sci. 1992, 30, 1665–1676. [Google Scholar] [CrossRef]
- Calvo, J.; Campos, J.; Caselles, V.; Sánchez, O.; Soler, J. Pattern formation in a flux limited reaction–diffusion equation of porous media type. Invent. Math. 2016, 206, 57–108. [Google Scholar] [CrossRef]
- Calvo, J.; Campos, J.; Caselles, V.; Sánchez, Ó.; Soler, J. Qualitative behavior for flux-saturated mechanisms: Traveling waves, waiting time and smoothing effects. J. Eur. Math. Soc. 2017, 19, 441–472. [Google Scholar] [CrossRef]
- Campos, J.; Soler, J. Qualitative behavior and traveling waves for flux-saturated porous media equations arising in optimal mass transportation. Nonlinear Anal. 2016, 137, 266–290. [Google Scholar] [CrossRef]
- Campos, J.; Guerrero, P.; Sánchez, Ó.; Soler, J. On the analysis of traveling waves to a nonlinear flux limited reaction–diffusion equation. Annales de l’IHP Analyse non Linéaire 2013, 30, 141–155. [Google Scholar] [CrossRef]
- Andreu, F.; Calvo, J.; Mazón, J.M.; Soler, J. On a nonlinear flux-limited equation arising in the transport of morphogens. J. Differ. Equ. 2012, 252, 5763–5813. [Google Scholar] [CrossRef]
- Arias, M.; Campos, J.; Soler, J. Cross-diffusion and traveling waves in porous-media flux-saturated Keller–Segel models. Math. Model. Methods Appl. Sci. 2018, 28, 2103–2129. [Google Scholar] [CrossRef]
- Campos, J.; García, C.; Soler, J. Kinks and solitons in linear and nonlinear-diffusion Keller-Segel type models with logarithmic sensitivity. arXiv 2021, arXiv:2102.13480. [Google Scholar]
- Shu, C.W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations; Springer: Berlin/Heidelberg, Germany, 1998; pp. 325–432. [Google Scholar]
- Diaz, M.A. Weighted Essentially Non-Oscillatory (WENO) Scheme. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/44639-weighted-essentially-non-oscillatory-weno-scheme (accessed on 10 March 2020).
- Park, K.; Millet, L.J.; Kim, N.; Li, H.; Jin, X.; Popescu, G.; Aluru, N.; Hsia, K.J.; Bashir, R. Measurement of adherent cell mass and growth. Proc. Natl. Acad. Sci. USA 2010, 107, 20691–20696. [Google Scholar] [CrossRef]
- Pogoda, K.; Chin, L.; Georges, P.C.; Byfield, F.J.; Bucki, R.; Kim, R.; Weaver, M.; Wells, R.G.; Marcinkiewicz, C.; Janmey, P.A. Compression stiffening of brain and its effect on mechanosensing by glioma cells. New J. Phys. 2014, 16, 075002. [Google Scholar] [CrossRef]
- Stylianopoulos, T.; Munn, L.L.; Jain, R.K. Reengineering the physical microenvironment of tumors to improve drug delivery and efficacy: From mathematical modeling to bench to bedside. Trends Cancer 2018, 4, 292–319. [Google Scholar] [CrossRef]
- Heyden, S.; Ortiz, M. Oncotripsy: Targeting cancer cells selectively via resonant harmonic excitation. J. Mech. Phys. Solids 2016, 92, 164–175. [Google Scholar] [CrossRef]


| Parameter | Description | Value [Unit] | Source |
|---|---|---|---|
| Tumor viscosity | 0.348 | [31] | |
| Tumor velocity | 0.87 | [31] | |
| Net proliferation rate | 3.45 | [31] | |
| K | Carrying capacity | [31] | |
| Growth area rate | See description | ||
| Bulk modulus | ≈3.33 [KPa] | See description | |
| Shear modulus | ≈0.34 [KPa] | See description | |
| Cytonemes | 60 [m] | See description |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanco, B.; Campos, J.; Melchor, J.; Soler, J. Modeling Interactions among Migration, Growth and Pressure in Tumor Dynamics. Mathematics 2021, 9, 1376. https://doi.org/10.3390/math9121376
Blanco B, Campos J, Melchor J, Soler J. Modeling Interactions among Migration, Growth and Pressure in Tumor Dynamics. Mathematics. 2021; 9(12):1376. https://doi.org/10.3390/math9121376
Chicago/Turabian StyleBlanco, Beatriz, Juan Campos, Juan Melchor, and Juan Soler. 2021. "Modeling Interactions among Migration, Growth and Pressure in Tumor Dynamics" Mathematics 9, no. 12: 1376. https://doi.org/10.3390/math9121376
APA StyleBlanco, B., Campos, J., Melchor, J., & Soler, J. (2021). Modeling Interactions among Migration, Growth and Pressure in Tumor Dynamics. Mathematics, 9(12), 1376. https://doi.org/10.3390/math9121376







