Distributed State Estimation Based Distributed Model Predictive Control
Abstract
1. Introduction
2. Preliminaries
2.1. Notation and Definitions
2.2. System Description
2.3. Stabilizability Assumptions
2.4. Observability Assumptions
3. Distributed LMPC Based on Distributed State Estimation
3.1. Implementation Algorithm
- 1.
- At , the augmented nonlinear observer based on of each subsystem is initialized with the subsystem output measurement and the initial subsystem state guess , .
- 2.
- At , if , go to Step 2.1; otherwise, go to Step 2.2.
- 2.1
- The subsystem state estimate , , , is calculated continuously by the corresponding augmented nonlinear observer based on the output measurements of subsystem i, the output measurements and state estimates of its related subsystems l, , received by subsystem i via communication network. The estimate result is sent to the corresponding of subsystem i and go to Step 3.
- 2.2
- The local of subsystem i estimates the current optimal subsystem state estimate , , , based on current and previous output measurement of subsystem i with , the previous output measurements and subsystem state estimates and from subsystems l, , with , are sent to subsystem i via communication network, where is the horizon of the . The estimate , , is sent to the corresponding subsystem and go to Step 3.
- 3.
- Based on or , , the of subsystem i calculates the future input trajectory for , where denotes the prediction horizon of . The first value of the input trajectory , , is applied to the system.
- 4.
- Go to Step 2. ().
3.2. Subsystem Observer Design
3.3. Subsystem Observer-Enhanced MHE
3.4. Subsystem Lyapunov MPC
4. A Brief Stability Analysis
5. The Simulation Application
5.1. Chemical Process
5.2. Observer and Controller Designs
5.3. MHE and LMPC Designs
5.4. Simulation Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Scattolini, R. Architectures for distributed and hierarchical model predictive control—A review. J. Process Control 2009, 19, 723–731. [Google Scholar] [CrossRef]
- Christofides, P.D.; Scattolini, R.; de la Peña, D.M.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Rocha, R.R.; Oliveira-Lopes, L.C.; Christofides, P.D. Partitioning for distributed model predictive control of nonlinear processes. Chem. Eng. Res. Des. 2018, 139, 116–135. [Google Scholar] [CrossRef]
- Zhang, A.; Yin, X.; Liu, J. Distributed economic model predictive control of wastewater treatment plants. Chem. Eng. Res. Des. 2019, 141, 144–155. [Google Scholar] [CrossRef]
- Hassanzadeh, B.; Liu, J.; Forbes, J.F. A bi-level optimization approach to coordination of distributed model predictive control systems. Ind. Eng. Chem. Res. 2017, 57, 1516–1530. [Google Scholar] [CrossRef]
- Hassanzadeh, B.; Hallas, P.; Liu, J.; Forbes, J.F. Distributed model predictive control of nonlinear systems based on price-driven coordination. Ind. Eng. Chem. Res. 2016, 55, 9711–9724. [Google Scholar] [CrossRef]
- Rashedi, M.; Liu, J.; Huang, B. Triggered communication in distributed adaptive high-gain EKF. IEEE Trans. Ind. Inform. 2018, 14, 58–68. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, J.; Zou, T.; Yuan, D. Distributed extended Kalman filtering for wastewater treatment processes. Ind. Eng. Chem. Res. 2016, 55, 7720–7729. [Google Scholar] [CrossRef]
- Wilson, D.; Agarwal, M.; Rippin, D. Experiences implementing the extended Kalman filter on an industrial batch reactor. Comput. Chem. Eng. 1998, 22, 1653–1672. [Google Scholar] [CrossRef]
- Farina, M.; Ferrari-Trecate, G.; Scattolini, R. Distributed moving horizon estimation for linear constrained systems. IEEE Trans. Autom. Control 2010, 55, 2462–2475. [Google Scholar] [CrossRef]
- Farina, M.; Ferrari-Trecate, G.; Scattolini, R. Distributed moving horizon estimation for nonlinear constrained systems. Int. J. Robust Nonlinear Control 2012, 22, 123–143. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J. Distributed moving horizon estimation for nonlinear systems with bounded uncertainties. J. Process Control 2013, 23, 1281–1295. [Google Scholar] [CrossRef]
- Liu, J. Moving horizon state estimation for nonlinear systems with bounded uncertainties. Chem. Eng. Sci. 2013, 93, 376–386. [Google Scholar] [CrossRef]
- Yin, X.; Arulmaran, K.; Liu, J.; Zeng, J. Subsystem decomposition and configuration for distributed state estimation. AIChE J. 2016, 62, 1995–2003. [Google Scholar] [CrossRef]
- Yin, X.; Liu, J. Distributed moving horizon state estimation of two-time-scale nonlinear systems. Automatica 2017, 79, 152–161. [Google Scholar] [CrossRef]
- Yin, X.; Decardi-Nelson, B.; Liu, J. Subsystem decomposition and distributed moving horizon estimation of wastewater treatment plants. Chem. Eng. Res. Des. 2018, 134, 405–419. [Google Scholar] [CrossRef]
- Yin, X.; Zeng, J.; Liu, J. Forming distributed state estimation network from decentralized estimators. IEEE Trans. Control Syst. Technol. 2019, 27, 2430–2443. [Google Scholar] [CrossRef]
- Yin, X.; Liu, J. Subsystem decomposition of process networks for simultaneous distributed state estimation and control. AIChE J. 2019, 65, 904–914. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J. Lyapunov-Based MPC with Robust Moving Horizon Estimation and its Triggered Implementation. AIChE J. 2013, 59, 4273–4286. [Google Scholar] [CrossRef]
- Ellis, M.; Zhang, J.; Liu, J.; Christofides, P. Robust moving horizon estimation based output feedback economic model predictive control. Syst. Control Lett. 2014, 68, 101–109. [Google Scholar] [CrossRef]
- Christofides, P.D.; Davis, J.F.; El-Farra, N.H.; Clark, D.; Harris, K.R.D.; Gipson, J.N. Smart plant operations: Vision, progress and challenges. AIChE J. 2007, 53, 2734–2741. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Christofides, P.D. A distributed control framework for smart grid development: Energy/water system optimal operation and electric grid integration. J. Process Control 2011, 21, 1504–1516. [Google Scholar] [CrossRef]
- Ahrens, J.H.; Khalil, H.K. High-gain observers in the presence of measurement noise: A switched-gain approach. Automatica 2009, 45, 936–943. [Google Scholar] [CrossRef]
- Liu, S.; Liu, J. Distributed Lyapunov-based model predictive control with neighbor-to-neighbor communication. AIChE J. 2014, 60, 4124–4133. [Google Scholar] [CrossRef]
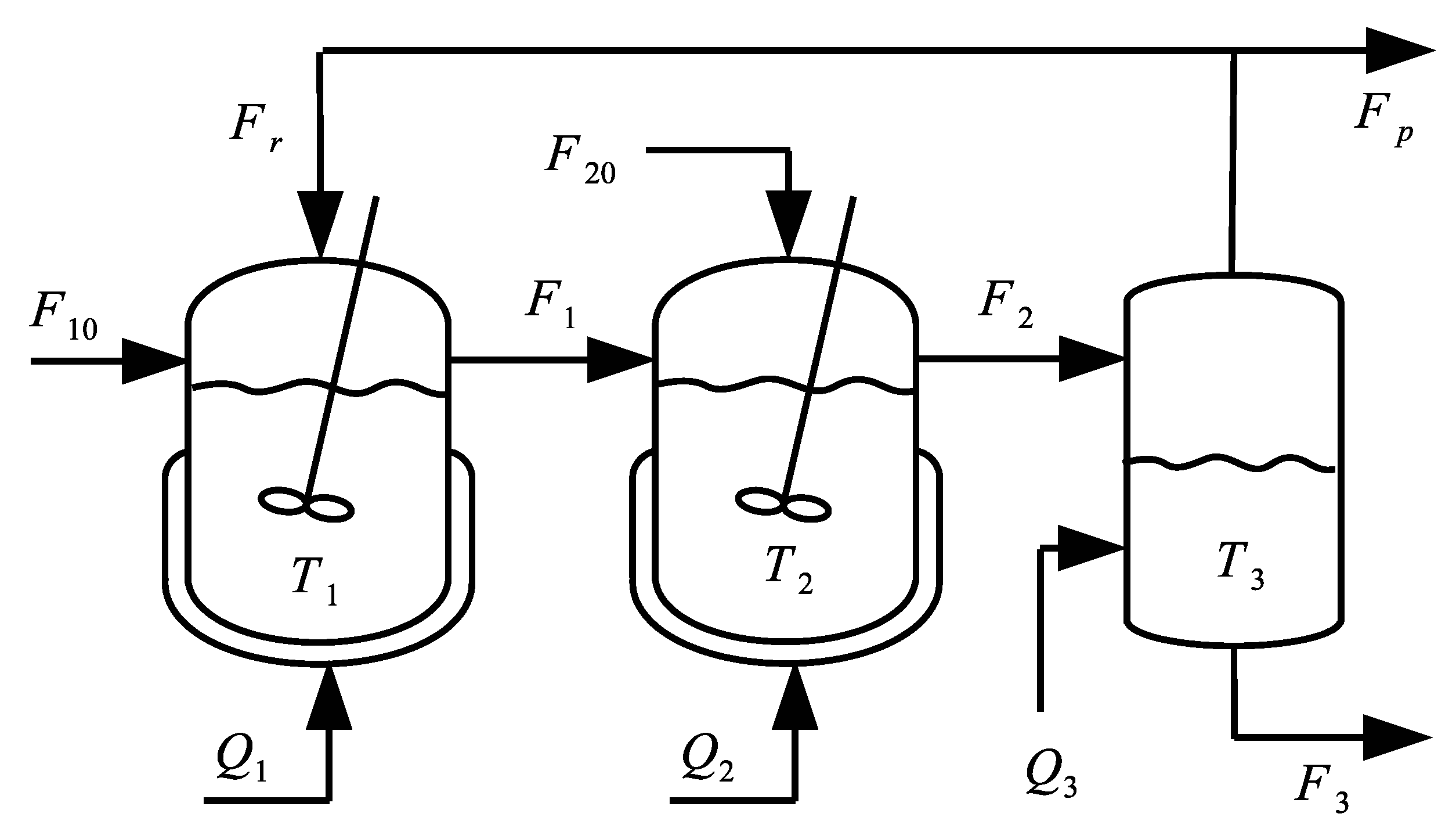
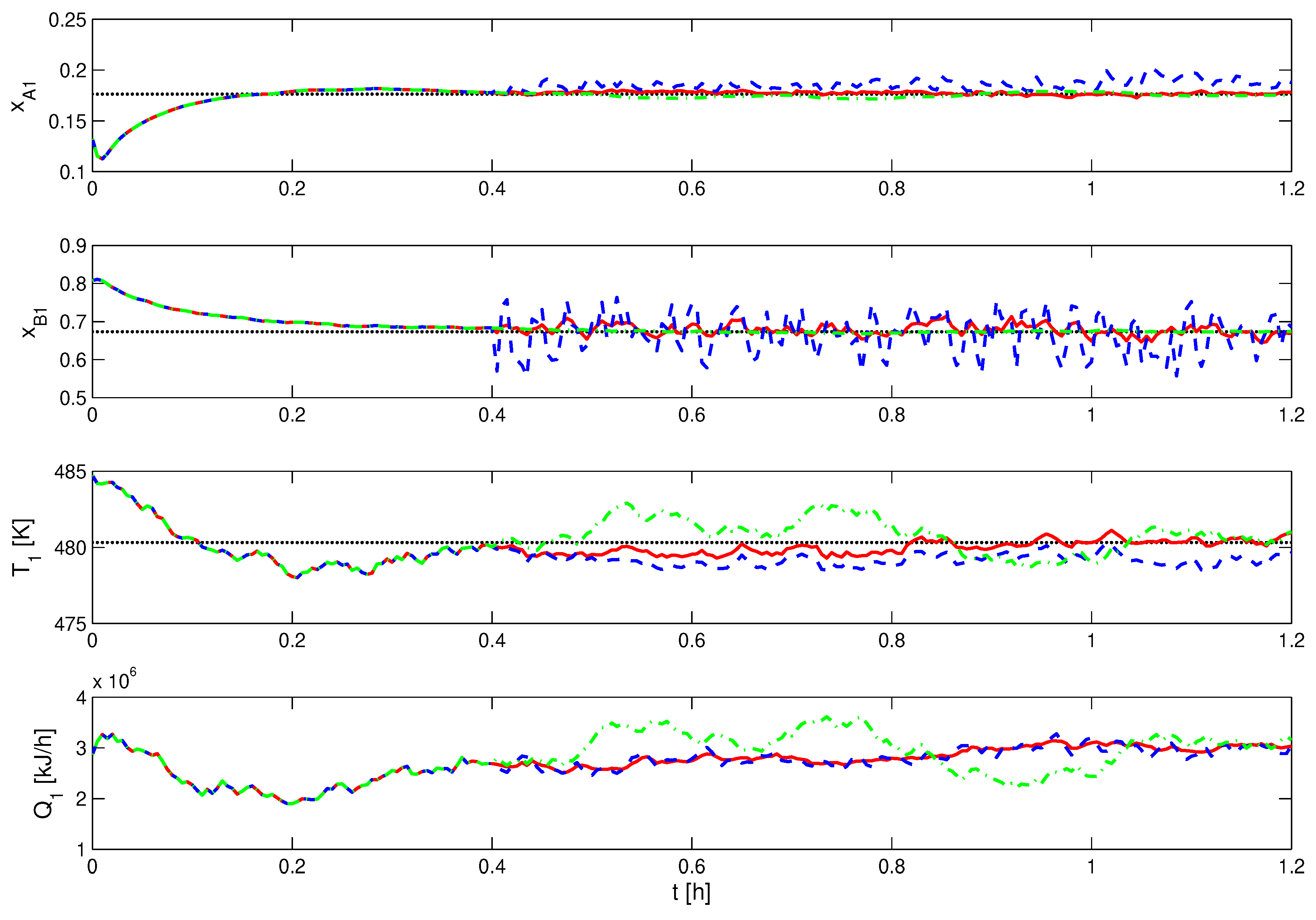

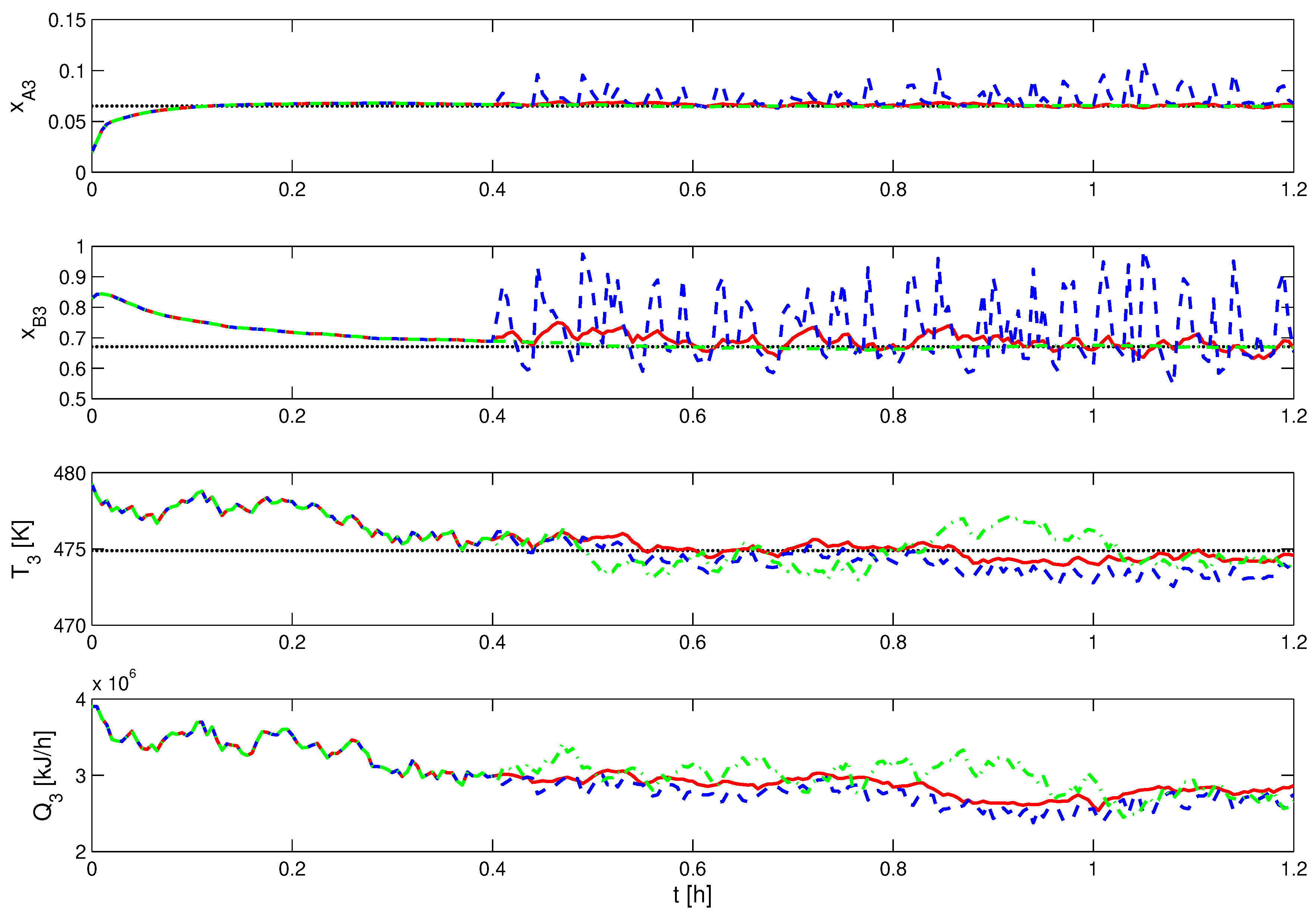

| Variable | Steady State Value | Variable | Steady State Value |
|---|---|---|---|
| [K] | |||
| [K] | |||
| [K] | |||
| [KJ/h] | |||
| [KJ/h] | |||
| [KJ/h] |
| Run | Scheme I | Scheme II | Scheme III |
|---|---|---|---|
| 1 | 6522.4 () | 7470.6 | 8244.6 () |
| 2 | 9338.0 () | 9972.1 | 15,760.0 () |
| 3 | 4898.0 () | 5084.9 | 6442.7 () |
| 4 | 4913.3 () | 5087.1 | 5711.2 () |
| 5 | 6476.6 () | 6971.0 | 8710.7 () |
| 6 | 5874.9 () | 6355.3 | 8789.3 () |
| 7 | 7102.8 () | 8158.9 | 9872.5 () |
| 8 | 4005.1 () | 4325.2 | 5986.3 () |
| 9 | 5120.1 () | 5483.0 | 6011.1 () |
| 10 | 6813.5 () | 7592.6 | 11,156.2 () |
| 11 | 6263.8 () | 6717.0 | 9571.7 () |
| 12 | 6169.7 () | 6717.0 | 7052.0 () |
| 13 | 6126.9 () | 6717.0 | 6455.5 () |
| 14 | 6101.1 () | 6717.0 | 6209.4 () |
| 15 | 6073.4 () | 6717.0 | 6079.9 () |
| Horizon | Sub-System | Scheme II (s) | Scheme II (s) | Scheme III (s) |
|---|---|---|---|---|
| 2.3280 | 0.0023 | 1.6878 | ||
| 1.7162 | 0.0022 | 1.6660 | ||
| 2.2600 | 0.0022 | 1.6625 | ||
| 29.9427 | 0.0025 | 26.7433 | ||
| 25.3235 | 0.0027 | 22.6616 | ||
| 28.7194 | 0.0027 | 26.0822 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, J.; Liu, J. Distributed State Estimation Based Distributed Model Predictive Control. Mathematics 2021, 9, 1327. https://doi.org/10.3390/math9121327
Zeng J, Liu J. Distributed State Estimation Based Distributed Model Predictive Control. Mathematics. 2021; 9(12):1327. https://doi.org/10.3390/math9121327
Chicago/Turabian StyleZeng, Jing, and Jinfeng Liu. 2021. "Distributed State Estimation Based Distributed Model Predictive Control" Mathematics 9, no. 12: 1327. https://doi.org/10.3390/math9121327
APA StyleZeng, J., & Liu, J. (2021). Distributed State Estimation Based Distributed Model Predictive Control. Mathematics, 9(12), 1327. https://doi.org/10.3390/math9121327







