Analysis of Stochastic Generation and Shifts of Phantom Attractors in a Climate–Vegetation Dynamical Model
Abstract
1. Introduction
2. Deterministic Model
3. Stochastic Model
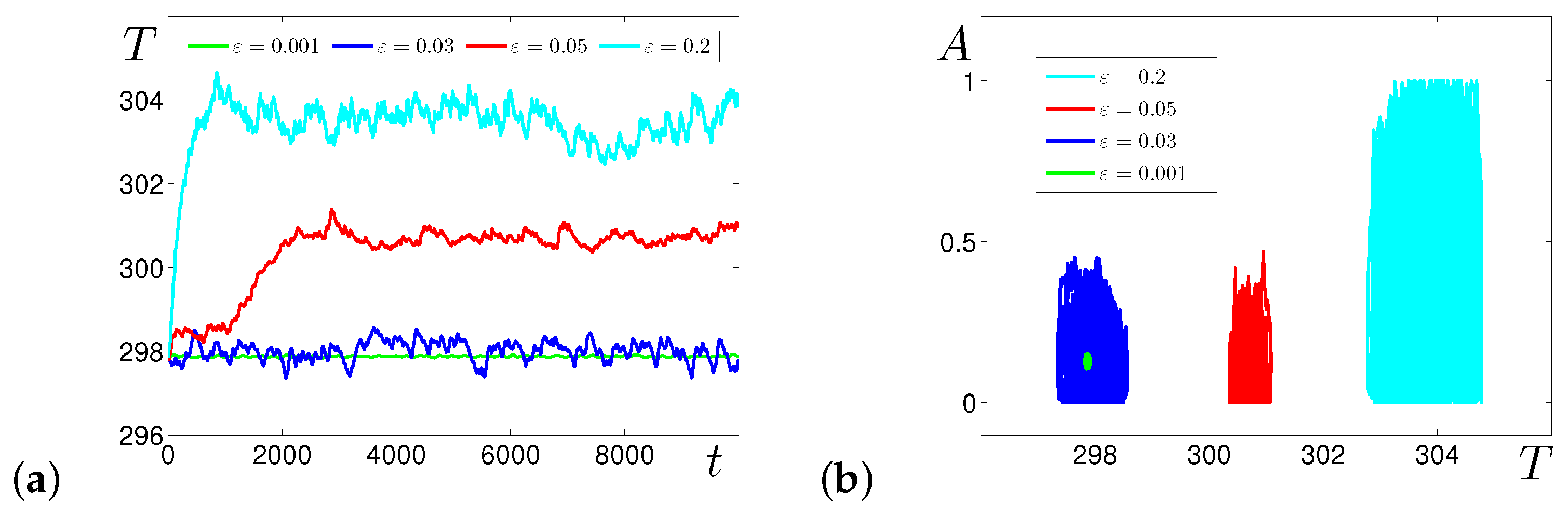
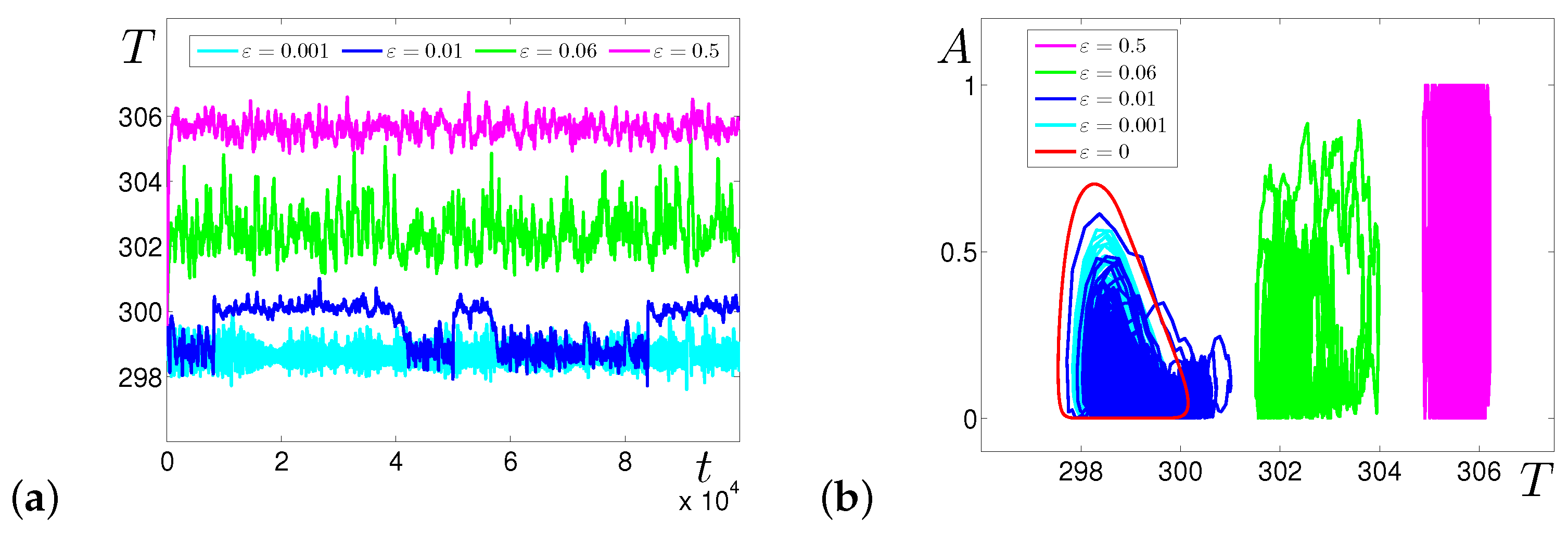
3.1. Effects of Additive Noise
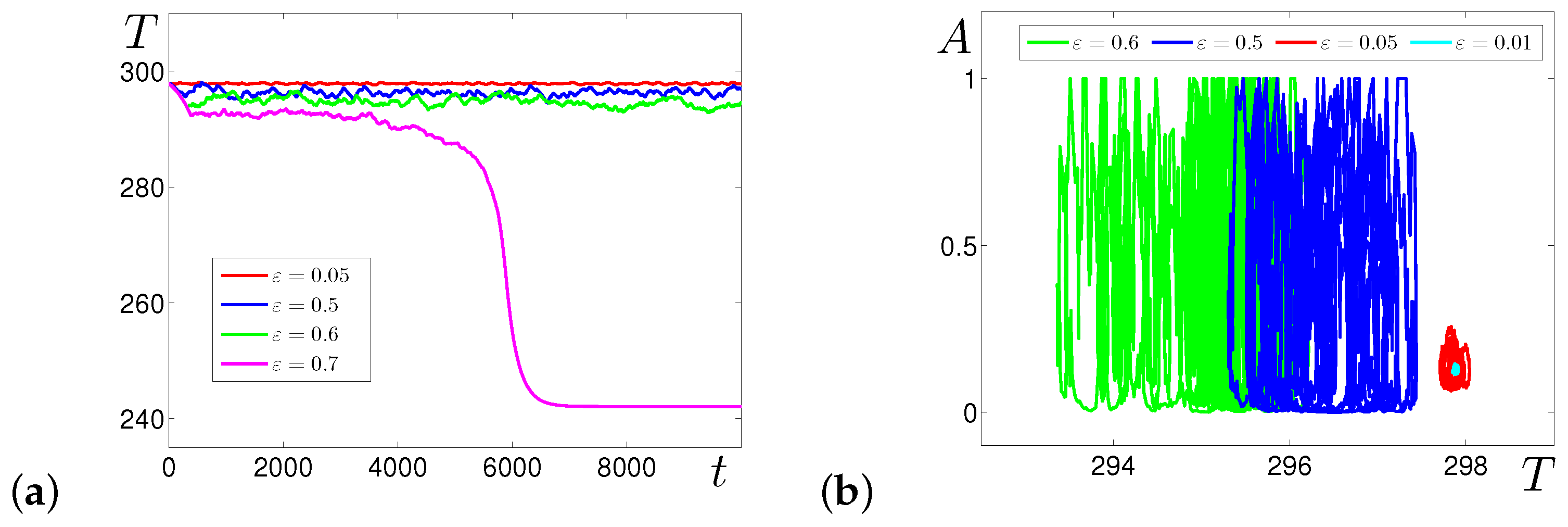
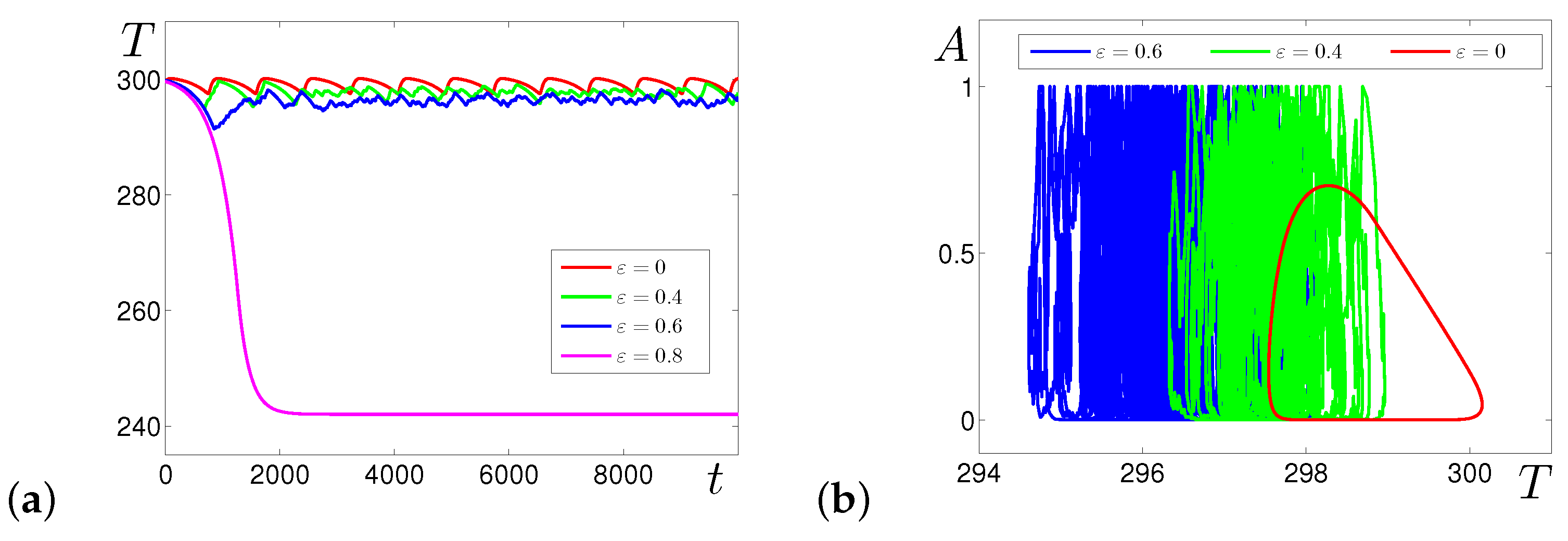
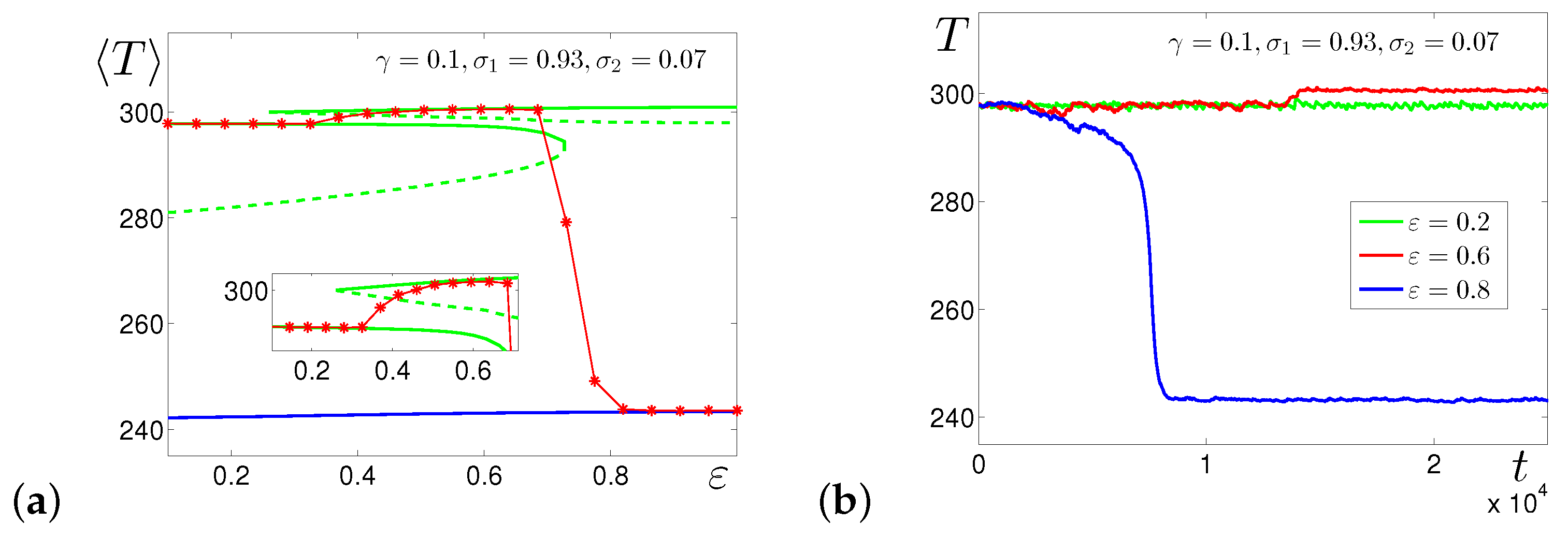
3.2. Effects of Multiplicative Noise
4. Method “Freeze and Average” in the Analysis of “Phantom” Attractors
4.1. Additive Noise
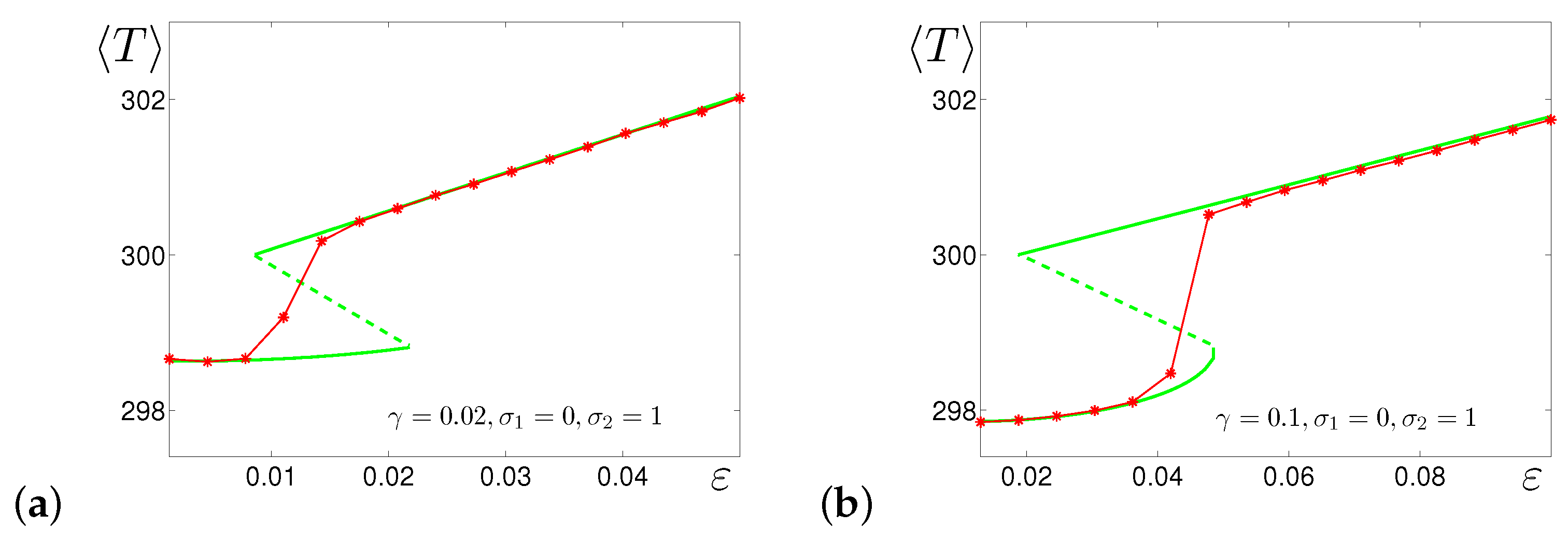
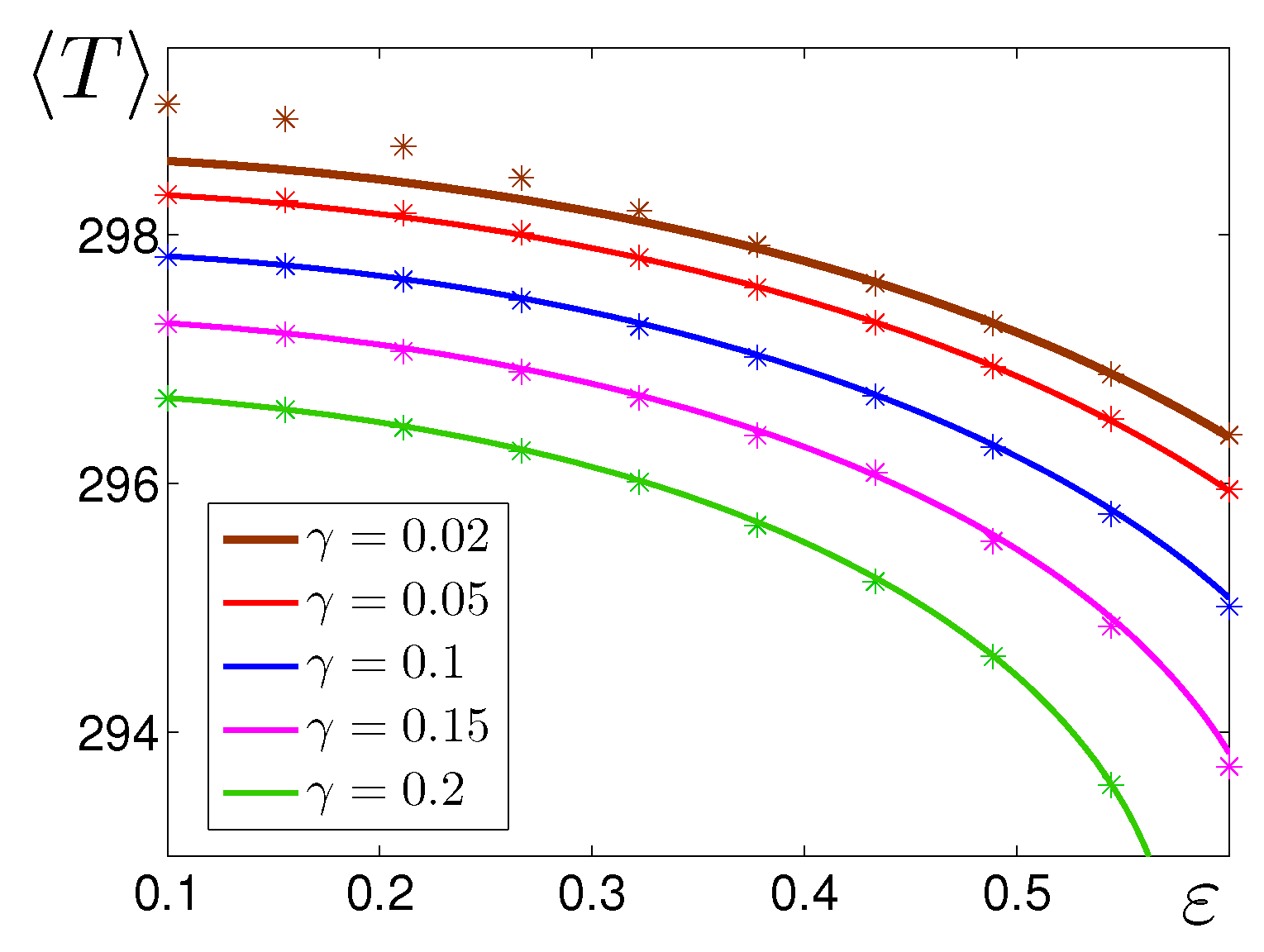
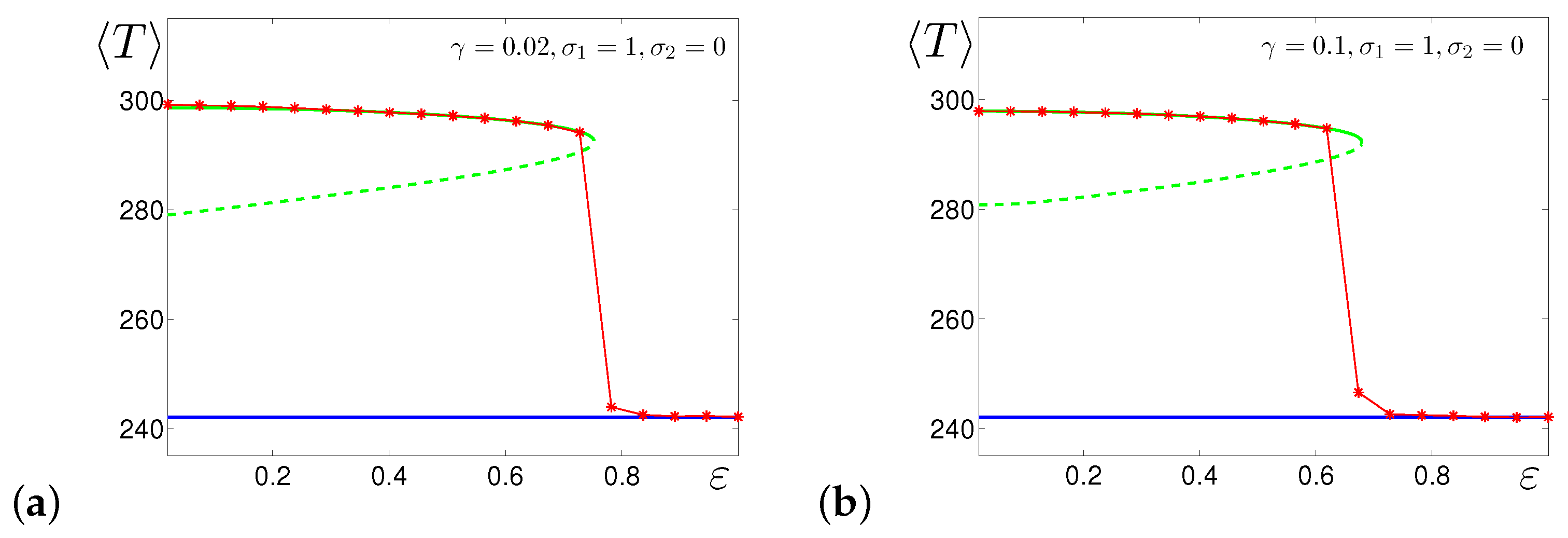
4.2. Multiplicative Noise
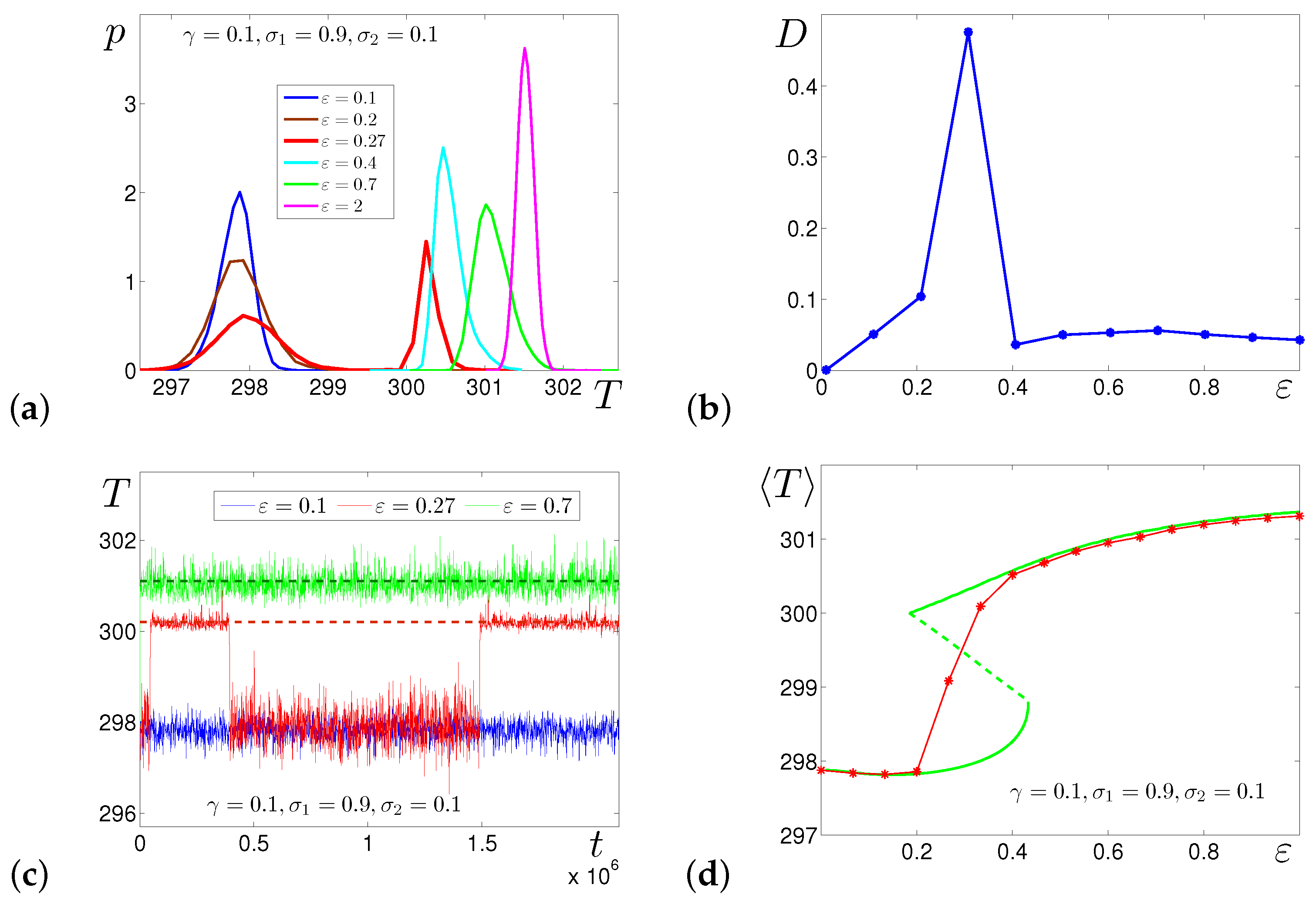
4.3. General Case
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Woodward, F. Climate and Plant Distribution; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Baudena, M.; D’Andrea, F.; Provenzale, A. A model for soil-vegetation-atmosphere interactions in water-limited ecosystems. Water Resour. Res. 2008, 44, W12429. [Google Scholar] [CrossRef]
- Claussen, M.; Bathiany, S.; Brovkin, V.; Kleinen, T. Simulated climate–vegetation interaction in semi-arid regions affected by plant diversity. Nat. Geosci. 2013, 6, 954–958. [Google Scholar] [CrossRef]
- Port, U.; Claussen, M. Transitivity of the climate–vegetation system in a warm climate. Clim. Past 2015, 11, 1563–1574. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Bashkirtseva, I.A.; Crucifix, M.; Ryashko, L.B. Nonlinear climate dynamics: From deterministic behaviour to stochastic excitability and chaos. Phys. Rep. 2021, 902, 1–60. [Google Scholar] [CrossRef]
- Rombouts, J.; Ghil, M. Oscillations in a simple climate–vegetation model. Nonlin. Process. Geophys. 2015, 22, 275. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Bashkirtseva, I.A.; Ryashko, L.B. Noise-induced transitions and shifts in a climate–vegetation feedback model. R. Soc. Open Sci. 2018, 5, 171531. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Bashkirtseva, I.A.; Ryashko, L.B. Anomalous climate dynamics induced by multiplicative and additive noises. Phys. Rev. E 2020, 102, 012217. [Google Scholar] [CrossRef] [PubMed]
- Anishchenko, V.; Astakhov, V.; Neiman, A.; Vadivasova, T.; Schimansky-Geier, L. Nonlinear Dynamics of Chaotic and Stochastic Systems. Tutorial and Modern Development; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. How environmental noise can contract and destroy a persistence zone in population models with Allee effect. Theor. Popul. Biol. 2017, 115, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Chen-Charpentier, B. Stochastic Modeling of Plant Virus Propagation with Biological Control. Mathematics 2021, 9, 456. [Google Scholar] [CrossRef]
- Arnold, L. Random Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Bashkirtseva, I.; Ryazanova, T.; Ryashko, L. Stochastic bifurcations caused by multiplicative noise in systems with hard excitement of auto-oscillations. Phys. Rev. E 2015, 92, 042908. [Google Scholar] [CrossRef]
- Horsthemke, W.; Lefever, R. Noise-Induced Transitions; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Bashkirtseva, I.; Chen, G.; Ryashko, L. Analysis of stochastic cycles in the Chen system. Int. J. Bifurc. Chaos 2010, 20, 1439–1450. [Google Scholar] [CrossRef]
- Lindner, B.; Garcia-Ojalvo, J.; Neiman, A.; Schimansky-Geier, L. Effects of noise in excitable systems. Phys. Rep. 2004, 392, 321–424. [Google Scholar] [CrossRef]
- Orcioni, S.; Paffi, A.; Apollonio, F.; Liberti, M. Revealing Spectrum Features of Stochastic Neuron Spike Trains. Mathematics 2020, 8, 1011. [Google Scholar] [CrossRef]
- Gao, J.; Hwang, S.; Liu, J. When can noise induce chaos? Phys. Rev. Lett. 1999, 82, 1132–1135. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. How additive noise forms and shifts phantom attractors in slow–fast systems. J. Phys. A 2020, 53, 375008. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. Noise-induced shifts in the population model with a weak Allee effect. Physica A 2018, 491, 28–36. [Google Scholar] [CrossRef]
- Alexandrov, D.; Bashkirtseva, I.; Ryashko, L. Anomalous stochastic dynamics induced by the slip-stick friction and leading to phantom attractors. Phys. D 2019, 399, 153–158. [Google Scholar] [CrossRef]
- Gardiner, C. Handbook of Stochastic Methods for Physics, Chemistry, and the Natural Sciences; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Roberts, A. Normal form transforms separate slow and fast modes in stochastic dynamical systems. Physica A 2008, 387, 12–38. [Google Scholar] [CrossRef]
- Bruna, M.; Chapman, S.J.; Smith, M.J. Model reduction for slow–fast stochastic systems with metastable behaviour. J. Chem. Phys. 2014, 140, 174107. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryashko, L.; Alexandrov, D.V.; Bashkirtseva, I. Analysis of Stochastic Generation and Shifts of Phantom Attractors in a Climate–Vegetation Dynamical Model. Mathematics 2021, 9, 1329. https://doi.org/10.3390/math9121329
Ryashko L, Alexandrov DV, Bashkirtseva I. Analysis of Stochastic Generation and Shifts of Phantom Attractors in a Climate–Vegetation Dynamical Model. Mathematics. 2021; 9(12):1329. https://doi.org/10.3390/math9121329
Chicago/Turabian StyleRyashko, Lev, Dmitri V. Alexandrov, and Irina Bashkirtseva. 2021. "Analysis of Stochastic Generation and Shifts of Phantom Attractors in a Climate–Vegetation Dynamical Model" Mathematics 9, no. 12: 1329. https://doi.org/10.3390/math9121329
APA StyleRyashko, L., Alexandrov, D. V., & Bashkirtseva, I. (2021). Analysis of Stochastic Generation and Shifts of Phantom Attractors in a Climate–Vegetation Dynamical Model. Mathematics, 9(12), 1329. https://doi.org/10.3390/math9121329