Abstract
Mathematical models of the human heart are evolving to become a cornerstone of precision medicine and support clinical decision making by providing a powerful tool to understand the mechanisms underlying pathophysiological conditions. In this study, we present a detailed mathematical description of a fully coupled multi-scale model of the human heart, including electrophysiology, mechanics, and a closed-loop model of circulation. State-of-the-art models based on human physiology are used to describe membrane kinetics, excitation-contraction coupling and active tension generation in the atria and the ventricles. Furthermore, we highlight ways to adapt this framework to patient specific measurements to build digital twins. The validity of the model is demonstrated through simulations on a personalized whole heart geometry based on magnetic resonance imaging data of a healthy volunteer. Additionally, the fully coupled model was employed to evaluate the effects of a typical atrial ablation scar on the cardiovascular system. With this work, we provide an adaptable multi-scale model that allows a comprehensive personalization from ion channels to the organ level enabling digital twin modeling.
1. Introduction
Cardiovascular diseases are the biggest contributors to the mortality and morbidity in the European Union, affecting millions of people every year [1]. While diagnostic tools and therapeutic options continuously improve and more data become available to researchers, the treatment of diseases, such as ischemic heart disease or atrial fibrillation remains difficult due to the highly complex nature of the human heart and cardiovascular system. Evidently, the complex mechanisms underlying these pathophysiological conditions are notoriously difficult to evaluate in the clinical environment due to ethical and technical limitations. Computational models of the human heart have the ability to avoid these limitations and provide a valuable tool for clinical research and practice [2]. Already today, these models can improve diagnosis [3], risk stratification [4], therapy planning [5,6], and intraprocedural support [7]. Furthermore, the vision of providing therapies customized to each individual patient heavily relies on mechanistic models to build a digital twin based on our knowledge of physiology and the fundamental laws of physics on the one hand and measured characteristics of the individual patient on the other hand [8]. An essential component of such a mechanistic model is the representation of the cardiac electrophysiology (EP) to reproduce the depolarization and repolarization sequence with a reaction-diffusion model. On the microscopic or cellular level, the reaction part was first described by Hodgkin and Huxley [9], while the diffusion on the macroscopic level can be modeled as described in [10]. Another essential component of the mechanistic model is cardiac mechanics (M) to describe the deformation, and the interplay between these systems described by myofilament models to drive the contraction and relaxation of the myocardium. The latter depends on the loading conditions imposed by the circulatory system, which is most accurately described by a fluid-structure interaction (FSI) problem, and the tissue that is surrounding the heart. Due to the complexity of this multi-physics problem, only a few cardiac simulation frameworks have been proposed that solve the complete EP-M-FSI system [11,12,13,14]. The most common way is to replace the FSI part by lumped parameter models of the circulatory system. More specifically, most simulations of the coupled EP-M problem focus on (bi-)ventricular models of a single heart beat and therefore only require isolated ventricular pre- and afterload models such as a 3- or 4-element Windkessel. To observe changes in cardiac function over multiple heartbeats, closed-loop models [15,16,17,18] are necessary and need to be coupled to the mechanical system [19,20,21,22,23,24,25]. EP-M models of the whole heart have been present for a few years now and have made impressive progress (e.g., [26,27,28,29,30]). However, only a few included the active contraction of the atria [31,32,33]. Land et al. [34] developed a model of active contraction for the atria based on human tissue preparations. This model can now be incorporated into coupled tissue level simulations, as was previously done for the ventricles [35,36].
Another aspect of such a complex model is the parameterization of all its components. With personalized heart models in mind, this is ideally done using patient-specific measurements. However, the majority of parameters can only be measured by invasive procedures, estimated indirectly, or not at all due technical limitations. Hence, efficient workflows are necessary to gain as much information as possible and incorporate them into digital twin models. Anatomically accurate heart models based on imaging data are created using (semi-)automatic workflows [37,38,39]. To make these heart models comparable to each other, universal coordinate systems have been proposed for the atria [40] and the ventricles [41,42]. Furthermore, we can build on already existing pipelines for the personalization of passive mechanical behavior of the heart [43,44], ventricular afterload models [45], and cardiac electrophysiology based on electrocardiograms [46,47,48,49] or electroanatomical mapping [50,51].
In this study, we present a detailed mathematical description of a fully coupled multi-scale model of the human heart building on previous work in cardiac mechanics [25,31,43,52,53,54,55] and cardiac electrophysiology [49,56,57,58,59,60]. We parameterize and use state-of-the-art myofilament models based on human physiology to describe membrane kinetics, excitation-contraction coupling and active tension generation in the atria and the ventricles. To solve the coupled EP-M problem, we apply a staggered scheme in time where the monodomain equation and the deformation are solved sequentially. Additionally, the proposed electro-mechanical whole-heart model is coupled to a novel 0D closed-loop model of the cardiovascular system. Here, we use a quasi Newton method to update the pressure values in all four chambers and reach convergence in fewer iterations compared to standard Newton methods. Furthermore, we briefly touch on the possibilities of such models to be tailored to patient-specific measurements and demonstrate their capabilities by simulating the complete heart cycle using an anatomical model of the heart of a healthy volunteer. Subsequently, the simulation data are evaluated and compared to magnetic resonance imaging (MRI) data with a focus on left ventricular function and atrio-ventricular plane displacement (AVPD). Finally, a typical radio-frequency ablation (RFA) scar is introduced into the left atrium and simulation results are compared to the healthy reference case. Hence, we demonstrate not only the possibility to adapt the model to pathological scenarios but the capability of the whole-heart model to respond to local changes in loading conditions.
2. Methods
2.1. Four-Chamber Heart Model
The geometric model used in this study is based on magnetic resonance imaging (MRI) data of a 32-year-old healthy volunteer provided by Heidelberg University Hospital. The data were acquired using a 1.5 T MR tomography system (Philips Medical Systems) and consist of a static whole heart image at diastasis, as well as time resolved MRI in 2-, 3-, and 4-chamber long axis view and 12 time resolved short axis slices with a 10 mm spacing. Endocardial and epicardial boundaries of the myocardial wall were segmented and labeled manually from the static whole heart image to create the atrial () and ventricular () domains. As in Fritz et al. [31], the heart is surrounded by a pericardial layer () representing the surrounding tissue in which the heart is embedded. Additionally, the tetrahedral mesh was extended by volumetric representations of the inferior and superior vena cava, the pulmonary veins, pulmonary artery, ascending aorta (further summarized in ), the mitral and tricuspidal valve (), and adipose tissue () around the base of the heart. Previously, the openings of the pulmonary veins and the venae cavae were fixed directly, which constrained atrial motion. This limitation was ameliorated by instead fixing the terminal ends of the major arteries and veins to allow for a free contraction of the atria [61]. Adipose tissue was added to the free space between the epicardial surface and the pericardium to obtain a continuous contact surface [32]. Two different discretizations are used: (1) the mechanical reference domain , as shown in Figure 1b; (2) the electrophysiological reference domain as a subset of .
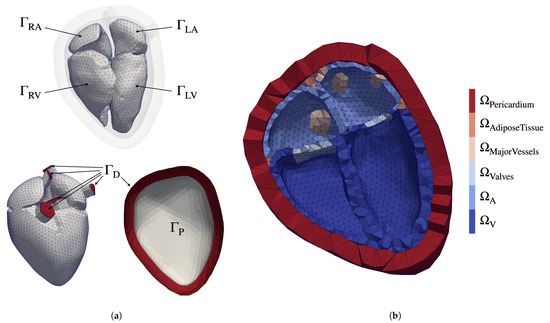
Figure 1.
(a) triangulated surfaces used for the boundary conditions: for the pressure in the
left and right ventricle and atrium; for the dirichlet boundary; for the pericardium. (b) clipped reference domain of the patient specific heart.
2.2. Cardiac Elasto-Mechanics
We consider the bounded reference domain for the human heart, which is deformed at time into the current configuration by the deformation vector
where is the displacement at a given position over time. The deformation on the continuum body is characterized by the axioms of conservation of mass, linear momentum and angular momentum. Following ([62], Chapter 3), the displacement is determined by the solution of the Navier–Cauchy equations for
with reference density , acceleration and the Cauchy stress . The vector-valued function represents applied boundary forces on all Neumann boundaries . The PDE (1) describes the deformation on the unknown domain . We therefore pull back the displacement onto the reference domain using the techniques provided in [62,63]: Denoting the Fréchet derivative in space by , we introduce the deformation gradient
and define the symmetric second Piola–Kirchhoff stress tensor
to obtain the following equations in the reference configuration for
The passive material properties of the cardiac tissue are described as follows: we assume that the material is hyperelastic, i.e., a stored energy function exists, such that the stress response is given by
As a consequence of objectivity, the material is frame-indifferent, i.e., there exist representations and , such that
The model is complemented by additional boundary conditions (Figure 1a), namely a Dirichlet boundary on on the distal end of the major vessels and the outer surface of the pericardium . On the inner surface of the pericardium , a contact boundary condition for the deformation is used (see Section 2.2.1). The Neumann boundary is given by the inner surfaces of the cardiac chambers , where a pressure
from the cardiovascular system (see Section 2.2.2) is applied.
With these assumptions, we obtain the equations of cardiac elasticity in the reference configuration for
The cardiac muscle tissue is nearly incompressible, i.e., . Therefore, we include, in the elastic energy, a penalty function with bulk modulus , which satisfies the conditions
For our applications, we use two different hyperelastic materials in subsets of . For the active part of the heart composed of cardiomyocytes, we use the anisotropic model of Guccione et al. [64]:
where is the shear modulus, , and is the transformation resulting from the orthogonal fiber, sheet and sheet-normal directions
and is a scalar function
with scaling parameters , , . Purely passive tissue is characterized by a Neo–Hookean material
with shear modulus and .
In addition to the passive material behavior, we model the active material response to electrical activation by an active stress approach. Given the deformed fiber directions , and the active tension generated by a cellular tension evolution model depending on and determined by (10c) and (12), we calculate the active stress response by
We use the additive decomposition to compute the stress.
2.2.1. Contact Boundary Conditions
Cardiac deformation is physiologically restricted by the pericardium and the surrounding tissue. In particular, it has been shown that including the interaction between ventricles, atria, and the pericardium during cardiac simulations allows one to better reproduce atrioventricular plane displacement (AVPD) [31,32] and thus cardiac motion. Realistic implementations of the interaction between the heart and surrounding tissue were first introduced by Fritz et al. [31]. They assumed frictionless and permanent contact between the epicardium and the pericardium using a penalty formulation. Other models describe these interactions using normal Robin boundary conditions on the epicardium with constant spring stiffness [26,32] or spatially varying spring stiffness [61] informed by image-derived motion. In this study, the sliding contact problem in Fritz et al. [31] between the epicardium and the inner pericardial surface (3c) is used by defining a contact energy
with the penalty parameter and the penalty functional
where is the surface normal of the epicardium and the projection of the deformed point onto the pericardium. This contact energy is then added to the hyperelastic energy functional.
2.2.2. Closed-Loop Circulatory Model
The heart’s main purpose is to effectively pump blood throughout the body. Therefore, it is important to define realistic hemodynamic boundary conditions for a computer model of cardiac mechanics. Most accurately, this is done by solving an FSI problem. To date, FSI models were typically restricted to a single chamber due to their computational complexity [11,12,13,14]. Since here, we are not interested in a detailed distribution of pressure and flow throughout all cardiac chambers, an alternative solution is to use a lumped parameter model of the circulatory system. For simulations spanning multiple heart beats, a closed-loop model is required to preserve the total blood volume in the circulatory system. Several closed-loop models of the circulatory system have been proposed [15,18,23,24,65] and all of them share some of their structure. However, in all cases, the circulatory system was only coupled to the finite element model of one or both of the ventricles, while the atria were represented by a time-varying elastance. To the best of our knowledge, there is no published work on coupling all four heart chambers with the circulatory model.
In the deformed configuration, the ventricular volume is computed from the reference domains for each chamber and the corresponding deformed chamber volumes are then denoted by with
We approximate the chamber volumes on the discrete geometry by summing up the volumes of all tetrahedrons constructed by a surface triangle and an inner point . We assume that each chamber is star-shaped around the point . By denoting the vectors of the vertices of K by , , , we obtain
To simulate the response of the circulatory system given the discrete volumes, we reinterpret the system as a series of transmissions [66] as shown in Figure 2. Our goal is to find a pressure vector (2) in such a way, that the chamber volumes of the circulatory model coincide with the discrete volumes of the mechanics simulation [20]. The circulatory chamber and vessel volumes are denoted by
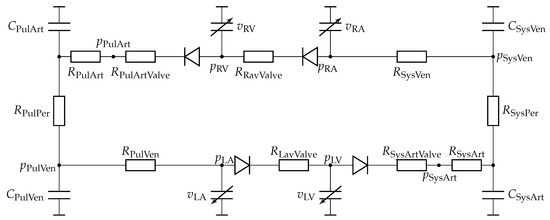
Figure 2.
Schematic of the circulatory system model with the pressure values of and , resistances R, fixed compliances C and volumes of variable compliances with .
A series of ODEs is solved to find a solution , to obtain
Let be the intermediate variables
describing the systemic venous, systemic arterial, pulmonary venous and pulmonary arterial pressures and flows. Then the closed-loop equations read
depending on
The evolution of in (7a) is determined by
The pressure values for the boundary condition (3d) are computed iteratively at each time step. Within one time step of the mechanical problem, we first find an approximated pressure through the closed-loop model. During the first time steps, we choose as a fixed increment of from the previous time step. After the fifth time step, we extrapolate using a 4th order Adams-Bashforth scheme:
with , . We then start the iteration to calculate the correct pressure: during each iteration cycle i, we update the mechanical and circulatory models for the given pressure boundary . The contraction is calculated as in Section 2.5. The ODEs of the circulatory model are updated with a Runge–Kutta 4 scheme. We compare the residual for each chamber
with for . If the absolute values of the residuals are below a threshold , the pressure is accepted and we move to the next time step. Otherwise, we update by a quasi-Newton method [67]:
where is the compliance matrix determined by
with , . Updating the compliance matrix by applying a quasi-Newton method is an improvement compared to the modified Newton method proposed by Kerckhoffs et al. [20], which makes it possible to reach convergence in fewer iterations.
2.3. Cardiac Electrical Activity
On the reference domain , the cardiac electric activity can be described by the monodomain model as explained by Keener and Sneyd [10]. This reaction-diffusion equation includes the transmembrane voltage coupled to ODEs describing the vector of gating variables and the vector of intracellular ion concentrations , so that the system in is given by
depending on the conductivity tensor , the external stimulus , the total ionic current , the functions and , the cellular surface-to-volume ratio and the membrane capacitance . The system (10) is complemented by initial values at for all
and homogeneous Neumann boundary conditions
The dimensions and , the ionic current , the vector functions and are specified by the choice of the cell model. According to the Hodgkin–Huxley model [9], the total ionic current can be written as
with the maximal conductance and the reversal potential for each ion channel i. More complex models add terms to the classical Hodgkin-Huxley model for additional ion channels. Those are of the form and increase the number k or are summarized in the function . The components of are typically given by
where for the positive functions and are fitted to the experimental data measured for the specific gate j. Due to different physiological properties on the cellular level for the atria and the ventricles, different models should be chosen on the domains and . The atrial and ventricular cell model used for simulations presented in this work are specified in Section 2.4.1.
The anisotropic conductivity tensor
depends on the fiber, sheet, and sheet-normal direction (5) with conductivity parameters . The depolarization waves are initiated by the stimuli in the stimulation area , and we set
depending on the starting time , duration , and amplitude .
2.4. Electro-Mechanical Coupling Mechanisms
2.4.1. Cellular Electro-Mechanical Model
The mathematical description of electrophysiological activity on the cellular level is represented by the term in Equation (10a) coupled to the ODEs (10b) and (10c). In general, Equation (10b,c) can represent any model that describes gating mechanisms and the transport of ions. Here, the models by Courtemanche et al. [68] and O’Hara et al. [69] are used for the atria and the ventricles, respectively. For the model by O’Hara et al., the modifications to the h- and j-gate as proposed by [70,71] were implemented.
Active tension development for is represented by a recent model for human cardiac contraction proposed by Land et al. [72]. It consists of a system of ODEs summarized as
where is the stretch in fiber direction. Bidirectional coupling between the models of electrophysiology and active stress is established by replacing the algebraic formulation of the troponin buffer in the Courtemanche et al. and O’Hara et al. models by the evolution of calcium bound to troponin from the Land et al. model. Therefore, the ion concentration depends on the stretch and Equation (10c) extends to
The components of (13) for the intracellular concentration of calcium ions change to
for the model by Courtemanche et al. and
for the model by O’Hara et al. with
CaTRPN is a component of and represents the fraction of troponin C units with calcium bound to its regulatory binding site in the Land et al. model, is the maximum concentration of troponin in the myoplasm, and is the length-dependent sensitivity to intra-cellular calcium.
The above modifications are introduced in [35,36] for the O’Hara et al. model. Parameters or equations not defined specifically are adopted from the original models and given in detail in the Supplementary Material.
Originally, the active stress model by Land et al. was developed and driven by experimentally measured human calcium transients (CaT) for the atria [34] and ventricles [72], respectively. Due to differences in the CaTs of the two models used in this study compared to the ones used by Land et al., a re-parameterization of the tension model is necessary to achieve physiologically correct active tension development. Based on the work of [34,36,72], we manually adjusted the parameters of the model to match key features of active tension to isometric twitch data of intact human tissue preparations from literature.
2.4.2. Mechano-Electric Feedback
As the conductivity tensor is oriented along the myocyte orientation , , , Equation (10a) has to be evaluated on the deformed geometry for
where the derivatives are dependent on the deformed variable . Applying the Piola transform on this equation, the corresponding Lagrange formulation reads
Furthermore, the existence of stretch-activated currents was first confirmed by Guharay and Sachs [73]. Different models were developed to describe the current carried by these channels [74,75,76,77,78,79]. In this case, is added to , so that the ion current also depends on the stretch. For the simulations presented in Section 4, the deformation was not considered for the calculation of electrophysiology and no stretch-activated channels were incorporated.
2.5. Electro-Mechanical Coupling Algorithm
The fully coupled whole heart model used for the numerical simulations in Section 4 is described by the following PDE-ODE system
with boundary conditions
This is complemented by the evaluation of the pressure vector and the intermediate variables as described in Section 2.2.2. As the cardiac electrophysiology is computed on and the elasto-mechanical equations are solved on , a mapping between the corresponding discrete meshes is required to couple the problem. This mapping from the vertices of the mesh of to the quadrature points of the finite element disctetization of is denoted as and the mapping vice versa as . Both mappings are realized via linear interpolation. In space, the PDEs in and are discretized with the finite element method, using linear conforming tetrahedral elements for the electrophysiology and quadratic elements for the elasto-mechanic part.
In time, we employ a staggered approach. First, the equations for the electrophysiology defined on are solved, updating , , , . This is realized via a first order operator splitting method as proposed by Sundnes et al. [80] where (10) is split in the reaction and diffusion part. The space-independent ODE system for the reaction is solved in time by explicit integration methods. The linear PDE modeling the diffusion is solved by a Crank-Nicolson scheme in time. The details are given in the supplement. The time step µs is used, so that the monodomain equation is computed times, before the mechanics is updated. Then, is mapped via to to evaluate the active stress response (6). Now, the equations for elasto-mechanics are solved on . Starting with the update of the pressure vector as explained in Section 2.2.2, a new displacement is computed with a Newmark -scheme, the details of which are again given in the Supplementary Material. Then, the chamber volumes of the discrete geometry are computed, cf. Section 2.2.2. Additionally, the volumes of the circulatory system are updated with a fourth order Runge–Kutta scheme and time step ms. Then, the new vector is computed. If the difference between the computed volumes is larger than a tolerance value, the procedure starts with an update of again. Else, the elasto-mechanics are finished for the time step and the stretch is mapped with to . The new stretch is used for the next update of the electrophysiology. The overall scheme is illustrated in Figure 3.
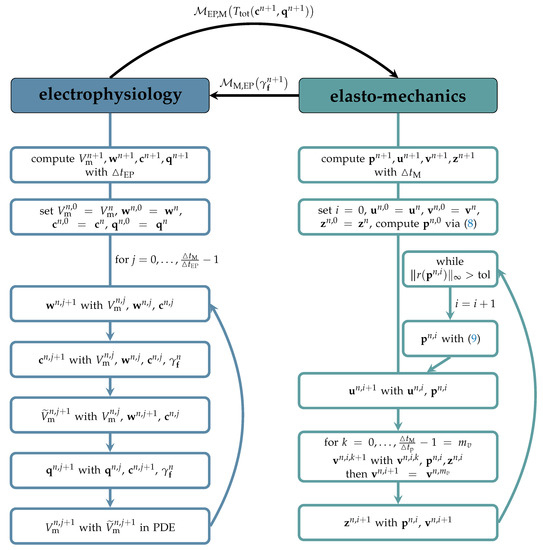
Figure 3.
Staggered algorithm for the fully coupled problem at time steps evaluating the solutions at with different time step sizes s, s and s for and mL.
3. Patient-Specific Simulation and Evaluation
3.1. Personalizing Electro-Mechanical Whole Heart Models: Building Digital Twins
Personalized in silico cardiology is evolving to become an important component of therapy planing and starts to inform the decision making process throughout the clinical workflow by maximizing the value of available clinical data [8]. Building a digital twin can comprise different aspects including statistical and mechanistic models. In the following, a brief overview of the important aspects of cardiac modeling is given and we highlight strategies on how to incorporate personalized information in our modeling framework.
3.1.1. Cardiac Anatomy
The first step to a personalized in silico model is to create an anatomically accurate representation of the heart in a discretized finite element model. Medical imaging data plays an important role in this step, since it provides the individuals shape of the heart and structural information such as the location of a scar, fiber architecture, and fibrosis in a non-invasive procedure [81,82]. In the case of whole heart models, a semi-automatic workflow has been proposed by Strocchi et al. [39]. However, a manual adjustment of the discretized model is still necessary and multiple tools are available to make this process more efficient (e.g., meshtool [83], vmtk [84]). Since anatomy is highly individualized, it is necessary to ensure the comparability between datasets. To solve this problem, a standardized 17 sector map of the ventricles can be used [85]. Similarly, universal coordinate systems have been proposed for the ventricles [41,42] and atria [40].
3.1.2. Fiber Orientation
Recovering patient-specific fiber and sheet orientation is possible through diffusion tensor MRI [86]. However, this kind of imaging data are only available from ex vivo measurements and is not acquired in vivo and thus, Laplace–Dirichlet rule-based (LDRB) methods are used to define fiber and sheet orientations in the ventricles [87,88,89] and atria [58,90]. Nevertheless, information about the transmural distribution of fiber and sheet angles from observations [91,92] can be used to parametrize LDRB methods to specify fiber and sheet angles at the endocardium and epicardium (,, ,).
3.1.3. Passive Stress
MRI data are typically acquired during the early diastolic state of the heart cycle when movement and chamber pressure are minimal. However, residual stress in the tissue cannot be measured with standard imaging techniques and the pressure inside the heart’s cavities can only be measured by invasive procedures. Therefore, a pressure and stress-free reference configuration of the heart has to be estimated to accurately model the biomechanical diastolic function. Methods applied in the context of cardiac mechanics try to find a stress-free reference configuration by using fixed-point iterations, as originally proposed by Sellier et al. [93]. Parameters for the constitutive model are mostly chosen manually [94] by utilizing the empirical end-diastolic pressure-volume relation (EDPVR) described by Klotz et al. [95] as a fitting target. In Kovacheva et al. [43], the constitutive parameters were determined by solving an optimization problem using a gradient-free method: the distance between the simulated EDPVR and the one proposed by Klotz et al. was minimized together with an additional condition imposed on the unloaded volume. The latter volume relation was again proposed by Klotz et al. However, values from different sources contradict each other [96]. Recently, Marx et al. [44] presented an automated method to match passive material parameters to the shape of a patient-specific EDPVR and to find an unloaded reference configuration of the heart simultaneously. Their method requires a mesh generated from clinical imaging data and at least one data point of the EDPVR.
3.1.4. Active Stress
Personalizing the systolic part of the heart cycle is done by adjusting the characteristics of the active tension model. This is done until the deformation of the heart is similar to the one observed in MRI data or until the ejected blood volume of the recorded heart beat is reached. Personalizing other characteristics of active tension development, such as the rate of contraction is more difficult in biophysically motivated models, due to the high number of parameters, which are typically not well constrained by the available experimental data [72]. Therefore, most personalized electro-mechanical models utilize a simplified model to drive contraction [33,61]. These models only comprise a small set of parameters that are linked to distinct characteristics (e.g., peak tension, rate of contraction and relaxation) of tension development, making them easier to fit to experimental data. As a consequence, these simpler models miss the important connection to calcium and are driven by activation times only.
3.1.5. Electrophysiology
Myocardial tissue in the atria and the ventricles shows regionally varying anisotropic properties with regard to conduction velocity (CV) [97]. Considering that CV is not a parameter of the momodomain equation, we cannot adjust it directly. However, assuming a planar wavefront propagation, Costa et al. [98] found that CV is proportionally related to the conductivity and the surface-to-volume ratio by . Since CV is much more likely to be measured in clinical scenarios than conductivity (e.g., [51,99]), one way to personalize the conduction model is to match CV. Costa et al. [98] realized this and proposed an automated parameterization strategy to find optimal conductivity values for a given CV. This strategy should be applied to each patient-specific mesh due to the dependency of CV on the spatial discretization [100] and the cellular models used in the study.
Mostly, atrial and ventricular activation is initiated by an externally applied stimulus mimicking the effect of the specialized cardiac conduction system at the sinus node and the Purkinje muscle junction. Timing and position of the stimulus are crucial for a proper depolarization pattern and orchestrated mechanical activation of the heart. In the atria, a stimulation at the sinus node is enough to initiate a heart beat. However, it is not trivial to properly activate the ventricles. This is due to the conduction of the depolarization wave through the atrio-ventricular node (AVN), the His–Purkinje system (HPS), and consequently the ventricular myocardium. Especially the HPS is highly individualized and rarely modeled explicitly [101] but rather implicitly by capturing its effect at the Purkinje muscle junctions [49,57,102]. Respective activation sequences can be personalized by using in-vivo measurements like electrocardiograms (ECG) or body surface potential maps (BSPM) to estimate sites of earliest activation [49,102,103]. Alternatively, the HPS can be modeled using N fascicular sites for the stimulus combined with a thin, fast conducting endocardial layer [104]. The conduction delay introduced by the AVN is typically represented by a predefined time delay between the onset of atrial and ventricular depolarization or by a model representing the AVN function [105].
3.2. Experimental Setup
Two simulations were conducted: one representing a normal heart beat as a reference and a second including a scar in the left atrium as a result of a typical radio-frequency ablation therapy for atrial fibrillation.
3.2.1. Parameterization
To capture the highly anisotropic characteristics of myocardial tissue, fiber and sheet architecture was incorporated into the model. For the ventricles, a method based on Bayer et al. [87] was applied. The original algorithm was adapted (https://github.com/KIT-IBT/LDRB_Fibers (accessed on 23 May 2021), release v0.1) [106] to eliminate a discontinuity of the fibers in the free walls and to yield a fiber rotation that is proportional to the transmural Laplace solution. As shown in Figure 4, fiber angles change linearly from at the endocardium to at the epicardium, as suggested by Streeter et al. [91]. Furthermore, the sheet angles change from to at the endo- and epicardium, respectively [87]. The atrial fiber and sheet orientation in this work are based on 22 seed points that define anatomical landmarks used to calculate numerous paths which split the atria in regions with distinct fiber orientation [58,59].

Figure 4.
Myocyte orientation in the fiber direction resulting from the algorithms in [58,106]. Fiber twist through the wall is shown in a slice through the ventricles.
Using the method proposed by Costa et al. [98], was optimized to achieve CVs that resulted in a realistic activation sequence. To simplify atrial activation, only three different conductivities were assigned to differentiate atrial bulk tissue, fast conducting bundles, and slow conducting regions [107]. The algorithm by Wachter et al. [58] was used to label the fast conducting regions including the crista terminalis, the pectinate muscles, Bachmann’s bundle, middle and upper posterior inter-atrial connection, the coronary sinus, and the scar in the left atrium (Figure 5).

Figure 5.
Anterior (left) and posterior (right) view of the atria with labels for fast conducting and slow conducting materials, as well as the scar. Transparant volumes represent the atrial bulk tissue.
They were assumed to be transversely isotropic with CVs of m/s in longitudinal direction and m/s in transverse direction. Slow regions were set to be isotropic with a CV of m/s, which is a commonly used simplification of the structural reality [107]. Atrial bulk tissue used the same value for a CV of m/s in longitudinal direction and m/s in transverse direction.
Ventricular myocardium was assumed to be orthotropic with CVs of m/s, m/s, m/s in longitudinal, transversal, and normal directions respectively. Additionally, a thin, fast-conducting endocardial layer was labeled using the consistent ventricular coordinates (Cobiveco) [42]. The CV in this layer was three times higher than in the rest of the ventricle to represent the effect of the HPS. All parameters used in the whole heart simulations are listed in Table 1.

Table 1.
Overview of electrophysiological parameters for the whole heart model.
The depolarization wave was initiated by a stimulus with a cycle length of s at the position of the most common sinus node exit site at the junction of the right atrial appendage and the superior vena cava [108]. Conduction between the left and right atrium was only possible via Bachmann’s bundle, a middle and upper posterior inter-atrial connection, and the coronary sinus. Otherwise, the tissue was isolated in the middle of the septal wall through duplicated vertices. 160 ms after the atrial stimulus, the ventricles were excited at five distinct positions. These five positions represent common sites of earliest activation in the ventricles and were chosen based on observations by Durrer et al. [109] and simulation results obtained in [104]. The activation pattern includes three sites of earliest activation in the LV (mid-posterior inferior , mid-posterior superior , basal anterior paraseptal ) and two in the RV (septal and free wall ). Their position is given in terms of universal coordinates in Table 2 and the resulting activation times are shown in Figure 6.

Table 2.
Sites of earliest activation in terms of the coordinate system Cobiveco [42]: a apicobasal; m transmural; r rotational; v transventricular.
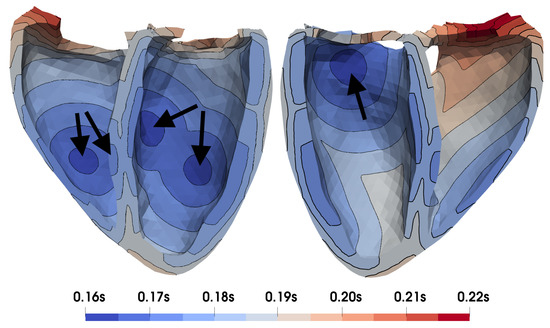
Figure 6.
Ventricular local activation times. Arrows indicate sites of earliest activation.
In the mechanical model, myocardial tissue in the atria and ventricles was modeled as a transversely isotropic material as defined in Equation (4). These parameters were determined using the method proposed by Kovacheva et al. [43] to match the empirical EDPVR of Klotz et al. [95]. Purely passive tissue was modeled as an isotropic Neo-Hookean solid using different material parameters. All mechanical parameters are listed in Table 3.

Table 3.
Overview of passive mechanical parameters in for the whole heart model.
For our particular subject, no measured data were available that can be related to circulatory system parameters. Therefore, all values were chosen based on models found in literature that share some of their structure with the model proposed in Section 2.2.2. The list of parameter values and corresponding references can be found in Table 4.

Table 4.
Overview of circulatory system parameters in Section 2.2.2 for the whole heart model.
The radio-frequency ablation scar only affected electrophysiological properties in this study. Specifically, the scar was assumed to be non-conducting and consists of a single lesion around all pulmonary veins isolating the whole roof of the left atrium plus a linear lesion towards the atrioventricular plane on the posterior side (Figure 5).
3.2.2. Initialization
As a first step, the cellular models were paced to a limit cycle at a cycle length of 1 s for a total of 1000 cycles. In this step, stretch and stretch rate were set to 1 and 0 respectively. The resulting values of the state variables were assigned to each vertex of as initial values. These values can be found in the Supplementary Material.
A backward displacement method [93,122] was used to find the unloaded configuration of for all four cavities simultaneously. As no measured pressure data was available, population-based values for the diastatic pressure were assumed ( mmHg, mmHg). The algorithm was stopped manually after 3 iterations with a residual norm of 0.0052 m and unloaded volumes with respect to the reference configuration. Afterwards, the unloaded configuration was inflated with the same pressure to pre-stress the tissue. Both, the unloaded and pre-stressed geometries are shown in the Supplementary Material together with the simulated EDPVR. To reduce the amount of heart beats that need to be run to reach a stable limit cycle of the circulatory system, purely mechanical simulations were done to find more suitable initial conditions for the circulatory model. The resulting initial values from which the coupled reference simulations was started are shown in Table 5.

Table 5.
Initial conditions for the circulatory system model.
3.2.3. Evaluation
To evaluate the simulation results, the deformation of the heart was analyzed in terms of atrio-ventricular valve displacement (AVPD), left ventricular blood volume, and intra-cavitary pressure-volume relationships. For the left ventricular volume and the AVPD, the in silico results were compared to time-resolved MR imaging data that were analyzed using the freely available software Segment (version 3.2 R8531, [123]). AVPD was measured by projecting the mean displacement of the surrounding tissue of the mitral- and tricuspidvalve onto the apico-basal heart axis. Pressure-volume relationships are provided as output by the circulatory system model. Since the circulatory model is a closed loop, all simulations were run for multiple cycles until the difference in stroke volumes of the left and right ventricle was less than 1 mL.
4. Results
4.1. Cellular Electro-Mechanical Model
The calcium transients (CaT) of the cell models differ from the experimental traces used by Land et al. to calibrate their model regarding key biomarkers such as time to peak of the calcium transient (TPCaT) and relaxation times to 50% and 90% decay from the peak calcium concentration (RT50, RT90). Therefore, a re-parameterization of the tension model by Land et al. was necessary after introducing the bidirectional coupling into the models of Courtemanche et al. and O’Hara et al.
For the atrial model, the parameters from Land et al. [34] were used. In tissue simulations this choice of parameters caused unphysiological behavior due to the introduction of length-dependent effects. An unphysiological rise in tension in the atria was observed during the contraction of the ventricles. The passive increase in volume and the atrio-ventricular plane displacement (AVPD) resulted in the atria being stretched by the ventricles, thus prolonging the time of contraction of the atria. Land et al. [34] encountered the same problem and suggested faster atrial contraction and crossbridge cycling rates as a solution. The CaT of the Courtemanche et al. electrophysiological model already promoted a faster contraction with faster TPCaT compared to physiological values. Therefore, calcium cycling rates were left unchanged. Instead, the change in calcium sensitivity with respect to was reduced to and the half-activation point was increased to µM. The re-parameterized atrial electro-mechanical model (Courtemanche–Land opt.) showed a time to peak tension TPT ms and RT50 ms after a total of 1000 cycles at a basic cycle length (BCL) of 1 s (Figure 7), which is in close agreement with atrial human tissue preparation data (Table 6).
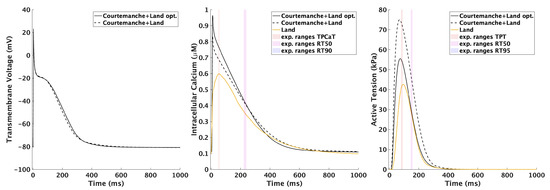
Figure 7.
Action potential (left), CaT (center), and active tension (right) of the optimized (solid line) and the original (dashed line) atrial model with reference experimental values from literature [129]. TPCaT: time to peak of calcium transient; TPT: time to peak tension; RT50/90/95: relaxation times to 50/90/95% decay from peak calcium/tension. Only the last cycle is visualized.

Table 6.
Literature values for time to peak of calcium transient (TPCaT) and active tension development (TPT) as well as relaxation time to 50%, 90% and 95% respectively (RT50, RT90, RT95) from human tissue preparations. The list of ventricular values were originally compiled in [36].
As a baseline for the ventricular model, the parameterization of [72] is used. First, the modifications suggested by Margara et al. [36] to the Hill coefficient of cooperative activation and the tropomyosin rate constant were adopted. Additionally, the same value for the half-activation point µM was used as for the atrial model. This reduced diastolic resting tension, which otherwise exceeded 2 kPa in tissue simulations in pre-stressed () conditions. The CaT and active tension development of the final ventricular model is shown in Figure 8. Compared to the original model by Land et al. [72], the optimized model (OHaraRudy+Land opt.) showed more physiological behavior compared to experimental data after stimulating the model for 1000 cycles at a BCL of 1 s (TPT ms, RT50 ms, RT95 ms). To achieve deformations comparable with MRI data, the parameter in the OHaraRudy+Land opt. model was set to 480 kPa in multi-scale simulations. All adjusted parameters are given in Table 7.
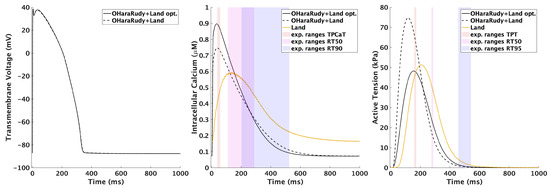
Figure 8.
Action potential (left), CaT (center), and active tension (right) of the optimized (solid line) and the original (dashed line) ventricular model with reference experimental values from literature [125]. TPCaT: time to peak of calcium transient; TPT: time to peak tension; RT50/90/95: relaxation times to 50/90/95% decay from peak calcium/tension. Only the last cycle is visualized.

Table 7.
Optimized parameters for the atrial and ventricular tension development model. The original values are taken from [34,72]. Values not listed in this table are unchanged from the original publications.
4.2. Electro-Mechanical Whole-Heart Simulation
The final discretizations were created using Gmsh [130]. consists of 26,681 quadratic tetrahedral elements with an average edge length of 7.2 mm, yielding 48,780 nodes with 135,897 degrees of freedom. Since electrophysiological simulations require a finer spatial discretization [100], a subset of was rediscretized to yield with 7,434,101 linear tetrahedral elements and an average edge length of 0.6 mm. All simulations were run on a 2019 Apple iMac™ using 8 MPI processes. A single heart beat took between 20 to 24 h to compute.
Starting from the pre-stressed reference geometry as described in Section 3.2, the reference heartbeat was simulated using the geometry shown in Figure 1. After eight beats, the simulation reached a stable limit cycle with a stroke volume (SV) difference between the two ventricles of less than 1 mL. As shown in Figure 9, the four major phases of the cardiac cycle were reproduced faithfully. After initiating the heart beat with an electrical stimulus at the location of the sinus node (Figure 9a), the atria contract and ventricular end-diastole later reached 180 ms (Figure 9b). Followed by a short time of isovolumetric contraction, the aortic and pulmonary valves open and the ejection of blood from the ventricles begins. Meanwhile, the atria relax and passively fill with blood (Figure 9c). During isovolumetric relaxation (Figure 9d), all valves close and the pressure reduces. As soon as the pressure is low enough, the mitral and tricuspid valves open and the ventricles fill with blood.
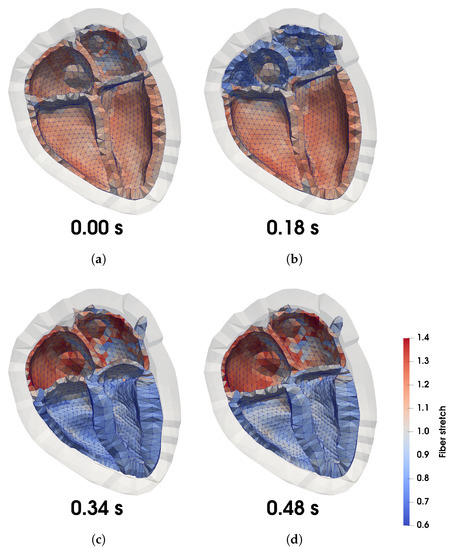
Figure 9.
Snapshots of the deformation of the heart during the final cycle. Visualized is the stretch in
fiber direction in a clipped long axis four chamber view. (a) at rest; (b) end-diastole; (c) end-systole;
(d) end of isovolumetric relaxation.
The results of the circulatory system are shown in Figure 10 for the last simulated heartbeat. Atrial PV-loops exhibit the typical figure-of-eight shape, with the A-wave and the V-wave both present. Additionally, a short spike in pressure with little change in volume (C-wave) can be observed in both atria immediately after the onset of ventricular contraction. With mL and mL, ventricular stroke volumes are close to the values derived from the imaging data ( mL, mL). However, systolic blood pressure is elevated in both the left ( mmHg) and the right ventricle ( mmHg). Flow through the mitral and tricuspid valve is observed during early diastolic filling (E-wave) and during atrial contraction (A-wave). With an E/A ratio of 1.11 in the left ventricle and 0.85 in the right ventricle, both are considered to function normally.
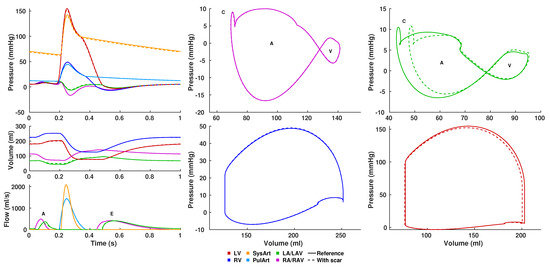
Figure 10.
Results of the circulatory system for the reference simulation (solid line) and the simulation with an ablation scar in the left atrium (dashed line) after reaching a stable limit cycle. First column from top to bottom: (1) Wiggers diagram showing pressure with respect to time; (2) cavity volume with respect to time; (3) flow through mitral valve (LAV), tricuspid valve (RAV), systemic arterial flow (SysArt), and pulmonary arterial flow (PulArt). The second and third column show the phase diagrams of the pressure-volume relationship for the left atrium (LA), left ventricle (LV), right atrium (RA), and right ventricle (RV).
The LV and RV volume at the beginning of the last heart beat demonstrates a discrepancy with respect to the segmented volumes from the MRI data and the initial volumes in the pre-stressed geometry. The volume reduced from 200.5 mL to 179.4 mL in the LV and increased from 188.5 mL to 224.8 mL in the RV during equilibration to a stable limit cycle. Therefore, LV volume was normalized for both simulated and MRI results for comparison (Figure 11). In both control and ablation cases, atrial systole contributed 11–13% to the end-diastolic ventricular blood volume. Major differences can be observed during ventricular systole and diastole. With a peak ejection rate (PER) of mL/s, it took only 160 ms until end-systole was reached. The mL/s in the MRI data was markedly lower resulting in a time to end-systole of 398 ms. The opposite behavior was observed during ventricular relaxation. Peak filling rate (PFR) in the MRI data was more than two times higher than in the simulation ( mL/s and mL/s). Hence, ventricular relaxation in the model was significantly slower than in the MRI data, taking 660 ms and 289 ms, respectively.
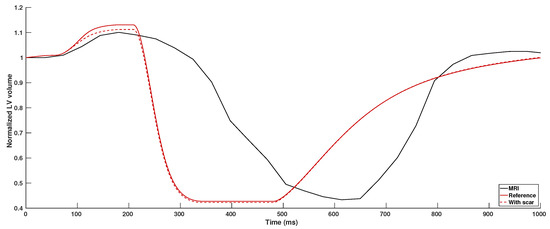
Figure 11.
Left ventricular (LV) cavity volume derived from imaging data (black) and numerical simulation (red). LV volume was normalized to the maximally measured volumes.
AVPD was measured relative to the position of the valves during diastasis and is shown in Figure 12. Negative values are associated with the movement of the valves towards the apex. During the contraction of the atria, both the mitral and the tricuspid valve were pulled up by 5 mm and 7 mm, respectively. Peak AVDP was reached at end-systole with a displacement of mm for the mitral valve and mm for the tricuspid valve. However, before moving towards the apex, the valves moved 2–3 mm in the opposite direction, which is associated with the bulging of the atrioventricular valves into the atria. This behavior could not be observed in the MRI data, since the temporal resolution was too low to capture it. Compared to the MRI data, the tricuspid valve is displaced 5 mm less during systole. However, valve displacement during atrial contraction is of the same magnitude. In contrast, the mitral valve is displaced 1.5 mm more during atrial contraction compared to the MRI data and differs only by mm during systole.
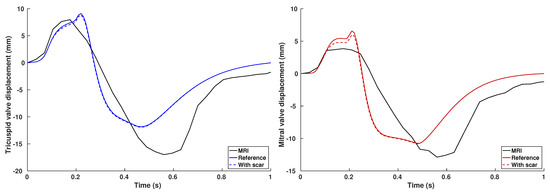
Figure 12.
Atrioventricular plane displacement from imaging data (dashed line) and numerical simulation (solid line).
Starting from the last cycle of the control heart beat simulation, an ablation scar was introduced in the left atrium. It took three heart cycles for the volumes in the circulatory system to adapt to the new conditions and to reach a limit cycle with a stroke volume difference of less than 1 mL. As shown in Figure 13, the scar isolates the whole roof of the left atrium from electrical signals. Since all the pathways between the left and right atrium are still intact, there is no measurable difference with regard to the electrical activation in the rest of the atrium. Due to the isolated area in the left atrium, a significant proportion of tissue is not developing any active tension hence reducing the overall contractile function of the left atrium. Less blood is pumped out of the LA into the LV, reducing the LV end-diastolic volume by 2.5 mL to 200.4 mL. This can be observed by a decreased flow through the mitral valve during atrial contraction and consequently by an increase of the E/A ratio to 1.46. Right atrial and ventricular pumping efficiency are unaffected by the ablation scar. Additionally, a decreased AVPD during atrial contraction is observed.
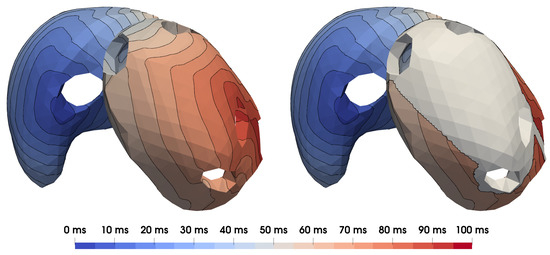
Figure 13.
Atrial local activation times from the reference simulation (left) and the simulation including an ablation scar in the left atrium (right).
5. Discussion
5.1. Bidirectional Coupling between the Mechanical and Electrophysiological Systems
Bidirectional coupling or strong coupling is required to simulate physiological behavior of the heart including mechano-electric feedback (MEF). Electrophysiological properties of cells are temporarily altered due to mechanical deformation. Currently, three major mechanisms are known to contribute to MEF: (1) the deformation of cardiac tissue during contraction and relaxation changes the electrical gradient ; (2) the transmembrane voltage is directly modified through stretch activated currents (SACs) ; (3) the stretch in the cells changes the binding affinity of calcium to troponin C, thus altering the intracellular levels of calcium. For the numerical experiments described in Section 3.2, we did not consider the effect of deformation on the electrical gradient. Its effect should be marginal during normal sinus rhythm, since large deformations only occur at times when the electrical gradient is small, i.e., during the action potential plateau phase or repolarization. However, this effect can alter the electrical activity of the heart, especially at shorter cycle lengths or reentry, and should be considered in such scenarios [131]. While SACs have been used extensively in simulation studies, the underlying mechanisms that relate stretch to changes in ion channel conductance are not well understood and the majority of published models of SACs are not well constrained by experimental data [74,75,76,77,78,79]. Since we use human electro-mechanical cell models and the parameterization of SACs is out of the scope of this study, we decided to exclude them from our model until more data from humans are available. Nevertheless, both of the currently missing effects can be easily added to the presented framework.
As illustrated in Figure 7 and Figure 8, the cellular electro-mechanical combination of models proposed in this study yields physiologically accurate active tension in line with data from human tissue preparations. However, when used in a multi-scale environment, it still has room for improvement as reflected in the time course of LV volume (Figure 11). The global behavior of the LV does not entirely reflect the contractile dynamics observed in MRI data. During relaxation, the reduction in stress and increase in ventricular volume is too slow. As a result, no clear diastasis phase can be observed in our model. Furthermore, the rate of contraction during systole is higher and the model reaches end-systole more than twice as fast as the MRI data suggests. This behavior can be observed in other simulation studies using the Land et al. tension model [72,132] or other tension models based on sliding filament theory [31,133], suggesting that not all mechanisms of cardiac contraction are fully represented in the most recent models. A simulation study by Campbell suggests that an acceleration of the relaxation can be achieved by introducing interfilamentory movement resulting from compliance in the sarcomere [134]. Possibly, a similar effect could result from an increase in myocardial stiffness and should be investigated further.
A limitation of our electro-mechanical model is that the dependence on stretch rate in Equation (12) had to be neglected by setting for all numerical experiments. Adding stretch rate dependence introduced strong unphysical oscillations in the multi-scale model resulting in an unstable numerical scheme. Regazzoni et al. [135] identified the source of these instabilities to be an inconsistent treatment of macroscopic and microscopic strains in staggered solution strategies of deformation in conjunction with an active stress model with a stretch rate dependence. This condition applies to the staggered approach used in this work (Section 2.5) and should be solved in the future either by implementing the proposed stabilization term in [135] or solving the whole system monolithically.
5.2. Circulatory System
As demonstrated in the numerical experiments, the closed-loop lumped-parameter model proposed in this manuscript is strongly coupled to the deformation problem and can reproduce major features of the human circulatory system. In the atria, the typical figure-of-eight shape is observed in the pressure-volume (PV) loops consisting of an A- and a V-loop corresponding to the atrial and ventricular contraction respectively. Additionally, a short increase in pressure in early systole known as the C-wave can be observed. Physiologically, this is the result of the atrioventricular valve’s cusps bulging into the atria during ventricular isovolumetric contraction. In the model, this observation was made possible by including physical representations of the valves in the mechanical mesh and was visible in the AVPD as well (Figure 12). In the ventricular PV-loops, the four major phases are present: (1) isovolumetric contraction; (2) ejection of blood from the ventricles; (3) isovolumetric relaxation; (4) passive filing with blood. Except for LV volume, no data related to the circulatory system were available from the healthy volunteer. Therefore, the parameterization of the lumped parameter model is motivated entirely by values obtained from literature and might not be fully representative to our specific case. The systolic pressures of the LV and the RV are too high for a healthy heart and are likely the result of the steep increase in stress due to the tension model. An optimized tension model could potentially address this issue and properly reflect systolic and diastolic behavior of the ventricles.
Using a closed-loop system makes it possible to study the influence of local changes in the cardiac tissue on the whole system. This was demonstrated by introducing an RFA scar into the left atrium (LA). The steady state of the circulatory system adapted to the decreased contractile function of the LA in a matter of 3 heart cycles and indicates that the general pumping efficiency of the ventricles is not heavily affected by the scar. Scar tissue typically shows an increased stiffness due to the higher collagen content compared to myocardial tissue. This could contribute to higher local stresses on the tissue in the atria and increasingly affect ventricular function. We did not consider this in our simulation setup and it should be included in further investigations of such scenarios. Studies like this can only be done with a whole heart model including the atria, the ventricles, and a circulatory system with a description of all necessary compartments. However, such a model is computationally very expensive and renders a patient-specific optimization of haemodynamic parameters challenging, especially since most of the parameters are unavailable from human measurements due to their invasive nature.
5.3. Numerical Considerations
The simulation framework proposed in this study was previously verified in N-version benchmarks that investigated the spatio-temporal convergence of the electrophysiological system [100] and the mechanical system [136], respectively.
For the solution of the monodomain equation, a small spatial resolution is required to avoid spatial undersampling artifacts leading to a reduction in conduction velocity or even conduction block. With an average spatial discretization of 0.6 mm of the electrophysiological domain , we use a coarser mesh than all values tested in [100]. Recently, Woodworth et al. published in [137] a convergence study for the monodomain problem coupled to the cell model of ten Tusscher et al. [138]. The spatial discretization needed to be in the convergence region is out of scope of the technical requirements for the simulations of this work. However, to match prescribed velocities [132] for the electrical activation pattern the conductivity values are increased for the whole heart simulations. As shown in Figure 6 and Figure 13, the resulting activation sequence matches normal patterns observed in humans [107,109].
The benchmark of the mechanical deformation problem only considered a simplified approach, which cannot be directly translated to a whole heart simulation scenario. However, it includes important aspects of cardiac function, such as the active contraction of the heart muscle, pressure boundary conditions, and a complex distribution of fiber orientations. We extended this benchmark problem to include different spatial resolutions and finite elements of a different order. The results are presented in the Supplementary Material and show negligible deviations in the solution for a similar spatial discretization as the left ventricle in our whole heart model as long as quadratic elements are used. Quadratic elements additionally reduce the effect of volumetric locking that is introduced by the penalty formulation used to enforce quasi-incompressability. For linear tetrahedral elements, volumetric locking is a major concern and would require a substantially smaller spatial discretization to achieve the large deformations required in cardiac mechanics.
To the best of our knowledge, there is currently no extensive existence result nor convergence study available for the fully coupled electro-mechanical problem. Some results were first presented by Andreianov et al. [139] and an extensive proof is given in [140], where an active strain decomposition was assumed in contrast to the active stress formulation used in this work. Moreover, the equations of finite elasticity were linearized and assumed to be isotropic. The authors mention that the proof is extensible to anisotropic and polyconvex material formulations, for which there are some existence results ([63], Chapter 7). Unfortunately, the material formulation and boundary conditions used in this work do not satisfy the necessary assumptions.
First, ideas to establish a benchmark for the coupled system were proposed by Quarteroni et al. [11] and Santiago et al. [12]. Their results implicate that the change in conduction velocity due the spatial discretization errors in the solution of the monodomain equation are the most prominent and cause a temporal shift in mechanical activation. The magnitude of the deformation itself was not affected for the tested scenarios. This supports the approach applied in this study to use different spatial resolutions for the mechanical and the electrophysiological problems. However, using two domains requires projection techniques to transfer values between these domains. To solve this, linear interpolation using shape functions was used. Extrapolation of values is avoided by ensuring that the boundaries of the domains are identical.
6. Conclusions
In this work, we propose a framework for the fully coupled cardiac electro-mechanical problem with a detailed description of appropriate boundary conditions such as a lumped parameter model of the human circulatory system and a contact handling that replicates the effects of the tissue surrounding the heart.
We provide parameterizations of a fully coupled excitation contraction model for cells of the atrial and ventricular myocardium. Both the intracellular calcium transient and the tension development match data of human tissue preparations from literature. Furthermore, the validity of the model is demonstrated through a simulation on a personalized heart geometry created from magnetic resonance imaging data of a healthy volunteer. Coupling the 0D lumped parameter model of human circulation to all four chambers of the 3D electromechanical model enables a faithful reproduction of the major phases of the cardiac cycle as well as the characteristic figure of eight shape in the atrial PV-loops and flow patterns observed in clinical practice. Including the influence of the surrounding tissue into the model yields an atrioventricular plane displacement close to that observed in the MRI data. Finally, we demonstrate the potential of the model to include pathological changes and predict effects of therapeutic interventions by introducing an ablation lesion in the left atrium which led to changes in the activation and contraction of the left atrium. As a result of the changed loading conditions, the end-diastolic volume, and thus, the cardiac output of the left ventricle was reduced as well.
The adaptability of the framework allows comprehensive personalization of the model and paves the way towards digital twin modeling.
Supplementary Materials
The following are available at https://www.mdpi.com/article/10.3390/math9111247/s1.
Author Contributions
Conceptualization, T.G. and A.L.; Data curation, T.G.; Formal analysis, T.G.; Funding acquisition, G.S., C.W. and A.L.; Investigation, T.G.; Methodology, T.G., S.S. and R.M.; Project administration, A.L.; Resources, G.S., C.W. and A.L.; Software, T.G., S.S., E.K., R.M. and E.M.W.; Supervision, G.S., C.W. and A.L.; Validation, T.G.; Visualization, T.G., S.S., J.F. and L.L.; Writing—original draft, T.G., J.F., L.L. and E.K.; Writing—review and editing, T.G., S.S., J.F., L.L., E.K., R.M., E.M.W., G.S., C.W. and A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 258734477—SFB 1173, HEiKA—Heidelberg Karlsruhe Research Partnership and the Federal Ministry of Education and Research, Germany, Grant Number: 05M2016.BMBF. We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The MATLAB code for the generation of the cardiac fiber orientation and the Consistent Biventricular Coordinates is available at https://github.com/KIT-IBT/LDRB_Fibers, accessed on 23 May 2021 and https://github.com/KIT-IBT/Cobiveco, accessed on 23 May 2021, respectively.
Acknowledgments
The authors would like to thank Olaf Dössel for valuable discussions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Timmis, A.; Townsend, N.; Gale, C.P.; Torbica, A.; Lettino, M.; Petersen, S.E.; Mossialos, E.A.; Maggioni, A.P.; Kazakiewicz, D.; May, H.T.; et al. European Society of Cardiology: Cardiovascular Disease Statistics 2019. Eur. Heart J. 2019, 41, 12–85. [Google Scholar] [CrossRef] [PubMed]
- Niederer, S.A.; Lumens, J.; Trayanova, N.A. Computational models in cardiology. Nat. Rev. Cardiol. 2019, 16, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Andlauer, R.; Seemann, G.; Baron, L.; Dössel, O.; Kohl, P.; Platonov, P.; Loewe, A. Influence of left atrial size on P-wave morphology: Differential effects of dilation and hypertrophy. Europace 2018, 20, iii36–iii44. [Google Scholar] [CrossRef] [PubMed]
- Arevalo, H.J.; Vadakkumpadan, F.; Guallar, E.; Jebb, A.; Malamas, P.; Wu, K.C.; Trayanova, N.A. Arrhythmia risk stratification of patients after myocardial infarction using personalized heart models. Nat. Commun. 2016, 7, 11437. [Google Scholar] [CrossRef]
- Prakosa, A.; Arevalo, H.J.; Deng, D.; Boyle, P.M.; Nikolov, P.P.; Ashikaga, H.; Blauer, J.J.E.; Ghafoori, E.; Park, C.J.; Blake, R.C.; et al. Personalized virtual-heart technology for guiding the ablation of infarct-related ventricular tachycardia. Nat. Biomed. Eng. 2018, 2, 732–740. [Google Scholar] [CrossRef]
- Loewe, A.; Poremba, E.; Oesterlein, T.; Luik, A.; Schmitt, C.; Seemann, G.; Dössel, O. Patient-Specific Identification of Atrial Flutter Vulnerability—A Computational Approach to Reveal Latent Reentry Paths. Front. Phys. 2018, 9, 1910. [Google Scholar] [CrossRef]
- Lehrmann, H.; Jadidi, A.S.; Minners, J.; Chen, J.; Müller-Edenborn, B.; Weber, R.; Dössel, O.; Arentz, T.; Loewe, A. Novel Electrocardiographic Criteria for Real-Time Assessment of Anterior Mitral Line Block. JACC Clin. Electrophysiol. 2018, 4, 920–932. [Google Scholar] [CrossRef]
- Corral-Acero, J.; Margara, F.; Marciniak, M.; Rodero, C.; Loncaric, F.; Feng, Y.; Gilbert, A.; Fernandes, J.F.; Bukhari, H.A.; Wajdan, A.; et al. The ‘Digital Twin’ to enable the vision of precision cardiology. Eur. Heart J. 2020, 41, 4556–4564. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Keener, J.; Sneyd, J. (Eds.) Mathematical Physology; I: Cellular Physiology; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2009; Volume 8/I. [Google Scholar]
- Quarteroni, A.; Lassila, T.; Rossi, S.; Ruiz-Baier, R. Integrated Heart–Coupling multiscale and multiphysics models for the simulation of the cardiac function. Comput. Methods Appl. Mech. Eng. 2017, 314, 345–407. [Google Scholar] [CrossRef]
- Santiago, A.; Zavala-Aké, M.; Aguado-Sierra, J.; Doste, R.; Gómez, S.; Arís, R.; Cajas, J.C.; Casoni, E.; Vázquez, M. Fully coupled fluid-electro-mechanical model of the human heart for supercomputers. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3140. [Google Scholar] [CrossRef]
- Sugiura, S.; Washio, T.; Hatano, A.; Okada, J.; Watanabe, H.; Hisada, T. Multi-scale simulations of cardiac electrophysiology and mechanics using the University of Tokyo heart simulator. Prog. Biophys. Mol. Biol. 2012, 110, 380–389. [Google Scholar] [CrossRef]
- Nordsletten, D.; McCormick, M.; Kilner, P.J.; Hunter, P.; Kay, D.; Smith, N.P. Fluid–solid coupling for the investigation of diastolic and systolic human left ventricular function. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 1017–1039. [Google Scholar] [CrossRef]
- Arts, T.; Delhaas, T.; Bovendeerd, P.; Verbeek, X.; Prinzen, F.W. Adaptation to mechanical load determines shape and properties of heart and circulation: The CircAdapt model. Am. J. Physiol. Heart Circul. Physiol. 2005, 288, H1943–H1954. [Google Scholar] [CrossRef]
- Paeme, S.; Moorhead, K.T.; Chase, J.G.; Lambermont, B.; Kolh, P.; D’orio, V.; Pierard, L.; Moonen, M.; Lancellotti, P.; Dauby, P.C.; et al. Mathematical multi-scale model of the cardiovascular system including mitral valve dynamics. Application to ischemic mitral insufficiency. Biomed. Eng. Online 2011, 10, 86. [Google Scholar] [CrossRef]
- Guidoboni, G.; Sala, L.; Enayati, M.; Sacco, R.; Szopos, M.; Keller, J.M.; Popescu, M.; Despins, L.; Huxley, V.H.; Skubic, M. Cardiovascular Function and Ballistocardiogram: A Relationship Interpreted via Mathematical Modeling. IEEE Trans. Bio-Med. Eng. 2019, 66, 2906–2917. [Google Scholar] [CrossRef] [PubMed]
- Regazzoni, F.; Salvador, M.; Africa, P.C.; Fedele, M.; Dede’, L.; Quarteroni, A. A cardiac electromechanics model coupled with a lumped parameters model for closed-loop blood circulation. Part I: Model derivation. arXiv 2020, arXiv:2011.15040. [Google Scholar]
- Sainte-Marie, J.; Chapelle, D.; Cimrman, R.; Sorine, M. Modeling and estimation of the cardiac electromechanical activity. Comput. Struct. 2006, 84, 1743–1759. [Google Scholar] [CrossRef]
- Kerckhoffs, R.C.P.; Neal, M.L.; Gu, Q.; Bassingthwaighte, J.B.; Omens, J.H.; McCulloch, A.D. Coupling of a 3D Finite Element Model of Cardiac Ventricular Mechanics to Lumped Systems Models of the Systemic and Pulmonic Circulation. Ann. Biomed. Eng. 2007, 35, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Gurev, V.; Lee, T.; Constantino, J.; Arevalo, H.; Trayanova, N.A. Models of cardiac electromechanics based on individual hearts imaging data: Image-based electromechanical models of the heart. Biomech. Model. Mechanobiol. 2011, 10, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Gurev, V.; Pathmanathan, P.; Fattebert, J.L.; Wen, H.F.; Magerlein, J.; Gray, R.A.; Richards, D.F.; Rice, J.J. A high-resolution computational model of the deforming human heart. Biomech. Model. Mechanobiol. 2015, 14, 829–849. [Google Scholar] [CrossRef] [PubMed]
- Hirschvogel, M.; Bassilious, M.; Jagschies, L.; Wildhirt, S.M.; Gee, M.W. A monolithic 3D-0D coupled closed-loop model of the heart and the vascular system: Experiment-based parameter estimation for patient-specific cardiac mechanics. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2842. [Google Scholar] [CrossRef]
- Augustin, C.M.; Gsell, M.A.F.; Karabelas, E.; Willemen, E.; Prinzen, F.; Lumens, J.; Vigmond, E.J.; Plank, G. Validation of a 3D-0D closed-loop model of the heart and circulation—Modeling the experimental assessment of diastolic and systolic ventricular properties. arXiv 2020, arXiv:2009.08802. [Google Scholar]
- Schuler, S.; Baron, L.; Loewe, A.; Dössel, O. Developing and Coupling a Lumped Element Model of the Closed Loop Human Vascular System to a Model of Cardiac Mechanics; BMTMedPhys 2017; de Gruyter: Dresden, Germany, 2017; Volume 62, p. S69. [Google Scholar]
- Gerbi, A.; Dedè, L.; Quarteroni, A. A monolithic algorithm for the simulation of cardiac electromechanics in the human left ventricle. Math. Eng. 2019, 1, 1. [Google Scholar] [CrossRef]
- Quarteroni, A.; Dedè, L.; Manzoni, A.; Vergara, C. Mathematical Modelling of the Human Cardiovascular System: Data, Numerical Approximation, Clinical Applications; Cambridge University Press: Cambridge, UK, 2019; Volume 33. [Google Scholar]
- Garcia-Blanco, E.; Ortigosa, R.; Gil, A.J.; Bonet, J. Towards an efficient computational strategy for electro-activation in cardiac mechanics. Comput. Methods Appl. Mech. Eng. 2019, 356, 220–260. [Google Scholar] [CrossRef]
- Garcia-Blanco, E.; Ortigosa, R.; Gil, A.J.; Lee, C.H.; Bonet, J. A new computational framework for electro-activation in cardiac mechanics. Comput. Methods Appl. Mech. Eng. 2019, 348, 796–845. [Google Scholar] [CrossRef]
- Augustin, C.M.; Crozier, A.; Neic, A.; Prassl, A.J.; Karabelas, E.; Ferreira da Silva, T.; Fernandes, J.F.; Campos, F.; Kuehne, T.; Plank, G. Patient-specific modeling of left ventricular electromechanics as a driver for haemodynamic analysis. EP Eur. 2016, 18, iv121–iv129. [Google Scholar] [CrossRef]
- Fritz, T.; Wieners, C.; Seemann, G.; Steen, H.; Dössel, O. Simulation of the Contraction of the Ventricles in a Human Heart Model Including Atria and Pericardium. Biomech. Model. Mechanobiol. 2014, 13, 627–641. [Google Scholar] [CrossRef]
- Pfaller, M.R.; Hörmann, J.M.; Weigl, M.; Nagler, A.; Chabiniok, R.; Bertoglio, C.; Wall, W.A. The importance of the pericardium for cardiac biomechanics: From physiology to computational modeling. Biomech. Model. Mechanobiol. 2019, 18, 503–529. [Google Scholar] [CrossRef]
- Augustin, C.M.; Fastl, T.E.; Neic, A.; Bellini, C.; Whitaker, J.; Rajani, R.; O’Neill, M.D.; Bishop, M.J.; Plank, G.; Niederer, S.A. The impact of wall thickness and curvature on wall stress in patient-specific electromechanical models of the left atrium. Biomech. Model. Mechanobiol. 2020, 19, 1015–1034. [Google Scholar] [CrossRef]
- Land, S.; Niederer, S.A. Influence of atrial contraction dynamics on cardiac function. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2931. [Google Scholar] [CrossRef] [PubMed]
- Levrero-Florencio, F.; Margara, F.; Zacur, E.; Bueno-Orovio, A.; Wang, Z.; Santiago, A.; Aguado-Sierra, J.; Houzeaux, G.; Grau, V.; Kay, D.; et al. Sensitivity analysis of a strongly-coupled human-based electromechanical cardiac model: Effect of mechanical parameters on physiologically relevant biomarkers. Comput. Methods Appl. Mech. Eng. 2020, 361, 112762. [Google Scholar] [CrossRef]
- Margara, F.; Wang, Z.J.; Levrero-Florencio, F.; Santiago, A.; Vázquez, M.; Bueno-Orovio, A.; Rodriguez, B. In-silico human electro-mechanical ventricular modelling and simulation for drug-induced pro-arrhythmia and inotropic risk assessment. Prog. Biophys. Mol. Biol. 2021, 159, 58–74. [Google Scholar] [CrossRef]
- Prassl, A.J.; Kickinger, F.; Ahammer, H.; Grau, V.; Schneider, J.E.; Hofer, E.; Vigmond, E.J.; Trayanova, N.A.; Plank, G. Automatically generated, anatomically accurate meshes for cardiac electrophysiology problems. IEEE Trans. Bio-Med. Eng. 2009, 56, 1318–1330. [Google Scholar] [CrossRef] [PubMed]
- Roney, C.; Beach, M.; Mehta, A.; Sim, I.; Corrado, C.; Bendikas, R.; Alonso Solis-Lemus, J.; Razeghi, O.; Whitaker, J.; O’Neill, L.; et al. Constructing Virtual Patient Cohorts for Simulating Atrial Fibrillation Ablation. In Proceedings of the 2020 Computing in Cardiology Conference (CinC), Rimini, Italy, 13–16 September 2020; Volume 47. [Google Scholar] [CrossRef]
- Strocchi, M.; Augustin, C.M.; Gsell, M.A.F.; Karabelas, E.; Neic, A.; Gillette, K.; Razeghi, O.; Prassl, A.J.; Vigmond, E.J.; Behar, J.M.; et al. A publicly available virtual cohort of four-chamber heart meshes for cardiac electro-mechanics simulations. PLoS ONE 2020, 15, e0235145. [Google Scholar] [CrossRef] [PubMed]
- Roney, C.H.; Pashaei, A.; Meo, M.; Dubois, R.; Boyle, P.M.; Trayanova, N.A.; Cochet, H.; Niederer, S.A.; Vigmond, E.J. Universal atrial coordinates applied to visualisation, registration and construction of patient specific meshes. Med. Image Anal. 2019, 55, 65–75. [Google Scholar] [CrossRef] [PubMed]
- Bayer, J.; Prassl, A.J.; Pashaei, A.; Gomez, J.F.; Frontera, A.; Neic, A.; Plank, G.; Vigmond, E.J. Universal ventricular coordinates: A generic framework for describing position within the heart and transferring data. Med. Image Anal. 2018, 45, 83–93. [Google Scholar] [CrossRef]
- Schuler, S.; Pilia, N.; Potyagaylo, D.; Loewe, A. Cobiveco: Consistent biventricular coordinates for precise and intuitive description of position in the heart—With MATLAB implementation. arXiv 2021, arXiv:2102.02898. [Google Scholar]
- Kovacheva, E.; Baron, L.; Schuler, S.; Gerach, T.; Dössel, O.; Loewe, A. Optimization Framework to Identify Constitutive Law Parameters of the Human Heart. Curr. Direct. Biomed. Eng. 2020, 6, 95–98. [Google Scholar] [CrossRef]
- Marx, L.; Niestrawska, J.A.; Gsell, M.A.F.; Caforio, F.; Plank, G.; Augustin, C.M. Efficient identification of myocardial material parameters and the stress-free reference configuration for patient-specific human heart models. arXiv 2021, arXiv:2101.04411. [Google Scholar]
- Marx, L.; Gsell, M.A.F.; Rund, A.; Caforio, F.; Prassl, A.J.; Toth-Gayor, G.; Kuehne, T.; Augustin, C.M.; Plank, G. Personalization of electro-mechanical models of the pressure-overloaded left ventricle: Fitting of Windkessel-type afterload models. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2020, 378, 20190342. [Google Scholar] [CrossRef]
- Pezzuto, S.; Prinzen, F.W.; Potse, M.; Maffessanti, F.; Regoli, F.; Caputo, M.L.; Conte, G.; Krause, R.; Auricchio, A. Reconstruction of three-dimensional biventricular activation based on the 12-lead electrocardiogram via patient-specific modelling. EP Eur. 2020, 23, 640–647. [Google Scholar] [CrossRef]
- Potse, M.; Krause, D.; Kroon, W.; Murzilli, R.; Muzzarelli, S.; Regoli, F.; Caiani, E.; Prinzen, F.W.; Krause, R.; Auricchio, A. Patient-specific modelling of cardiac electrophysiology in heart-failure patients. Europace 2014, 16 (Suppl. 4), iv56–iv61. [Google Scholar] [CrossRef] [PubMed]
- Gillette, K.; Prassl, A.; Bayer, J.; Vigmond, E.; Neic, A.; Plank, G. Automatic Generation of Bi-Ventricular Models of Cardiac Electrophysiology for Patient Specific Personalization Using Non-Invasive Recordings. In Proceedings of the 2018 Computing in Cardiology Conference (CinC), Maastricht, The Netherlands, 23–26 September 2018; Volume 45. [Google Scholar] [CrossRef]
- Kahlmann, W.; Poremba, E.; Potyagaylo, D.; Dössel, O.; Loewe, A. Modelling of patient-specific Purkinje activation based on measured ECGs. Curr. Direct. Biomed. Eng. 2017, 3, 171–174. [Google Scholar] [CrossRef]
- Corrado, C.; Williams, S.; Karim, R.; Plank, G.; O’Neill, M.; Niederer, S. A work flow to build and validate patient specific left atrium electrophysiology models from catheter measurements. Med. Image Anal. 2018, 47, 153–163. [Google Scholar] [CrossRef] [PubMed]
- Grandits, T.; Pezzuto, S.; Costabal, F.S.; Perdikaris, P.; Pock, T.; Plank, G.; Krause, R. Learning atrial fiber orientations and conductivity tensors from intracardiac maps using physics-informed neural networks. arXiv 2021, arXiv:2102.10863. [Google Scholar]
- Baron, L.; Fritz, T.; Seemann, G.; Dössel, O. Sensitivity study of fiber orientation on stroke volume in the human left ventricle. In Proceedings of the Computing in Cardiology 2014, Cambridge, MA, USA, 7–10 September 2014; Volume 41, pp. 681–684. [Google Scholar]
- Kovacheva, E.; Baron, L.; Dössel, O.; Loewe, A. Electro-Mechanical Delay in the Human Heart: A Study on a Simple Geometry. In Proceedings of the Computing in Cardiology 2018, Maastricht, The Netherlands, 23–26 September 2018; Volume 45. [Google Scholar] [CrossRef]
- Müller, A.; Kovacheva, E.; Schuler, S.; Dössel, O.; Baron, L. Effects of local activation times on the tension development of human cardiomyocytes in a computational model. Curr. Direct. Biomed. Eng. 2018, 4, 247–250. [Google Scholar] [CrossRef]
- Gerach, T.; Schuler, S.; Kovacheva, E.; Dössel, O.; Loewe, A. Consequences of Using an Orthotropic Stress Tensor for Left Ventricular Systole. In Proceedings of the Computing in Cardiology Conference (CinC) 2020, Rimini, Italy, 13–16 September 2020. [Google Scholar] [CrossRef]
- Seemann, G.; Sachse, F.B.; Karl, M.; Weiss, D.L.; Heuveline, V.; Dössel, O. Framework for modular, flexible and efficient solving the cardiac bidomain equation using PETSc. Math. Ind. 2010, 15, 363–369. [Google Scholar] [CrossRef]
- Keller, D.U.J.; Kalayciyan, R.; Dössel, O.; Seemann, G. Fast creation of endocardial stimulation profiles for the realistic simulation of body surface ECGs. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; Volume 25/4, pp. 145–148. [Google Scholar]
- Wachter, A.; Loewe, A.; Krueger, M.W.; Dössel, O.; Seemann, G. Mesh structure-independent modeling of patient-specific atrial fiber orientation. Curr. Direct. Biomed. Eng. 2015, 1, 409–412. [Google Scholar] [CrossRef]
- Loewe, A. Modeling Human Atrial Patho-Electrophysiology from Ion Channels to ECG: Substrates, Pharmacology, Vulnerability, and P-Waves. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2016. [Google Scholar] [CrossRef]
- Gerach, T.; Weiß, D.; Dössel, O.; Loewe, A. Observation Guided Systematic Reduction of a Detailed Human Ventricular Cell Model. In Proceedings of the 2019 Computing in Cardiology (CinC), Singapore, 8–11 September 2019. [Google Scholar]
- Strocchi, M.; Gsell, M.A.; Augustin, C.M.; Razeghi, O.; Roney, C.H.; Prassl, A.J.; Vigmond, E.J.; Behar, J.M.; Gould, J.S.; Rinaldi, C.A.; et al. Simulating Ventricular Systolic Motion in a Four-chamber Heart Model with Spatially Varying Robin Boundary Conditions to Model the Effect of the Pericardium. J. Biomech. 2020, 101, 109645. [Google Scholar] [CrossRef]
- Coman, C.D. Continuum Mechanics and Linear Elasticity; Springer: Dordrecht, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Ciarlet, P.G. (Ed.) Mathematical Elasticity; Volume I. Three-Dimensional Elasticity; Studies in Mathematics and Its Applications; North-Holland: Amsterdam, The Netherlands, 1988; Volume 20. [Google Scholar]
- Guccione, J.M.; McCulloch, A.D.; Waldman, L.K. Passive material properties of intact ventricular myocardium determined from a cylindrical model. J. Biomech. Eng. 1991, 113, 42–55. [Google Scholar] [CrossRef]
- Jafari, A.; Pszczolkowski, E.; Krishnamurthy, A. A framework for biomechanics simulations using four-chamber cardiac models. J. Biomech. 2019, 91, 92–101. [Google Scholar] [CrossRef] [PubMed]
- Milišić, V.; Quarteroni, A. Analysis of lumped parameter models for blood flow simulations and their relation with 1D models. ESAIM Math. Model. Numer. Anal. 2004, 38, 613–632. [Google Scholar] [CrossRef]
- Broyden, C.G. A class of methods for solving nonlinear simultaneous equations. Math. Comput. 1965, 19, 577–593. [Google Scholar] [CrossRef]
- Courtemanche, M.; Ramirez, R.J.; Nattel, S. Ionic mechanisms underlying human atrial action potential properties: Insights from a mathematical model. Am. J. Physiol.Heart Circul. Physiol. 1998, 275, H301–H321. [Google Scholar] [CrossRef] [PubMed]
- O’Hara, T.; Virag, L.; Varro, A.; Rudy, Y. Simulation of the undiseased human cardiac ventricular action potential: Model Formulation and experimental validation. PLoS Comput. Biol. 2011, 7, e1002061. [Google Scholar] [CrossRef]
- Passini, E.; Mincholé, A.; Coppini, R.; Cerbai, E.; Rodriguez, B.; Severi, S.; Bueno-Orovio, A. Mechanisms of pro-arrhythmic abnormalities in ventricular repolarisation and anti-arrhythmic therapies in human hypertrophic cardiomyopathy. J. Mol. Cell. Cardiol. 2016, 96, 72–81. [Google Scholar] [CrossRef]
- Dutta, S.; Mincholé, A.; Quinn, T.A.; Rodriguez, B. Electrophysiological properties of computational human ventricular cell action potential models under acute ischemic conditions. Prog. Biophys. Mol. Biol. 2017, 129, 40–52. [Google Scholar] [CrossRef] [PubMed]
- Land, S.; Park-Holohan, S.J.; Smith, N.P.; Dos Remedios, C.G.; Kentish, J.C.; Niederer, S.A. A model of cardiac contraction based on novel measurements of tension development in human cardiomyocytes. J. Mol. Cell. Cardiol. 2017, 106, 68–83. [Google Scholar] [CrossRef]
- Guharay, F.; Sachs, F. Stretch-activated single ion channel currents in tissue-cultured embryonic chick skeletal muscle. J. Physiol. 1984, 352, 685–701. [Google Scholar] [CrossRef]
- Niu, W.; Sachs, F. Dynamic properties of stretch-activated K+ channels in adult rat atrial myocytes. Prog. Biophys. Mol. Biol. 2003, 82, 121–135. [Google Scholar] [CrossRef]
- Zeng, T.; Bett, G.C.; Sachs, F. Stretch-activated whole cell currents in adult rat cardiac myocytes. Am. J. Physiol. Heart Circul. Physiol. 2000, 278, H548–H557. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Youm, J.B.; Sung, H.K.; Lee, S.H.; Ryu, S.Y.; Ho, W.K.; Earm, Y.E. Stretch-activated and background non-selective cation channels in rat atrial myocytes. J. Physiol. 2000, 523 Pt 3, 607–619. [Google Scholar] [CrossRef] [PubMed]
- Pueyo, E.; Orini, M.; Rodríguez, J.F.; Taggart, P. Interactive effect of beta-adrenergic stimulation and mechanical stretch on low-frequency oscillations of ventricular action potential duration in humans. J. Mol. Cell. Cardiol. 2016, 97, 93–105. [Google Scholar] [CrossRef]
- Tavi, P.; Han, C.; Weckström, M. Mechanisms of stretch-induced changes in [Ca2+]i in rat atrial myocytes: Role of increased troponin C affinity and stretch-activated ion channels. Circul. Res. 1998, 83, 1165–1177. [Google Scholar] [CrossRef] [PubMed]
- Kohl, P.; Sachs, F. Mechanoelectric feedback in cardiac cells. Philos. Trans. R. Soc. Lond. Ser. A 2001, 359, 1173–1185. [Google Scholar] [CrossRef]
- Sundnes, J.; Lines, G.T.; Tveito, A. An operator splitting method for solving the bidomain equations coupled to a volume conductor model for the torso. Math. Biosci. 2005, 194, 233–248. [Google Scholar] [CrossRef]
- Crozier, A.; Augustin, C.M.; Neic, A.; Prassl, A.J.; Holler, M.; Fastl, T.E.; Hennemuth, A.; Bredies, K.; Kuehne, T.; Bishop, M.J.; et al. Image-Based Personalization of Cardiac Anatomy for Coupled Electromechanical Modeling. Ann. Biomed. Eng. 2016, 44, 58–70. [Google Scholar] [CrossRef] [PubMed]
- Trayanova, N.A.; Doshi, A.N.; Prakosa, A. How personalized heart modeling can help treatment of lethal arrhythmias: A focus on ventricular tachycardia ablation strategies in post-infarction patients. Wiley Interdiscip. Rev. Syst. Biol. Med. 2020, 12, e1477. [Google Scholar] [CrossRef]
- Neic, A.; Gsell, M.A.; Karabelas, E.; Prassl, A.J.; Plank, G. Automating image-based mesh generation and manipulation tasks in cardiac modeling workflows using Meshtool. SoftwareX 2020, 11, 100454. [Google Scholar] [CrossRef]
- Fedele, M.; Quarteroni, A. Polygonal surface processing and mesh generation tools for the numerical simulation of the cardiac function. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3435. [Google Scholar] [CrossRef]
- Cerqueira, M.D. American Heart Association Writing Group on Myocardial Segmentation and Registration for Cardiac Imaging: Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart: A statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. Circulation 2002, 105, 539–542. [Google Scholar]
- Geerts, L.; Bovendeerd, P.; Nicolay, K.; Arts, T. Characterization of the normal cardiac myofiber field in goat measured with MR-diffusion tensor imaging. Am. J. Physiol. Heart Circ. Physiol. 2002, 283, 139. [Google Scholar] [CrossRef] [PubMed]
- Bayer, J.D.; Blake, R.C.; Plank, G.; Trayanova, N.A. A novel rule-based algorithm for assigning myocardial fiber orientation to computational heart models. Ann. Biomed. Eng. 2012, 40, 2243–2254. [Google Scholar] [CrossRef] [PubMed]
- Doste, R.; Soto-Iglesias, D.; Bernardino, G.; Alcaine, A.; Sebastian, R.; Giffard-Roisin, S.; Sermesant, M.; Berruezo, A.; Sanchez-Quintana, D.; Camara, O. A rule-based method to model myocardial fiber orientation in cardiac biventricular geometries with outflow tracts. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3185. [Google Scholar] [CrossRef] [PubMed]
- Wong, J.; Kuhl, E. Generating fibre orientation maps in human heart models using Poisson interpolation. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 1217–1226. [Google Scholar] [CrossRef]
- Piersanti, R.; Africa, P.C.; Fedele, M.; Vergara, C.; Dedè, L.; Corno, A.F.; Quarteroni, A. Modeling cardiac muscle fibers in ventricular and atrial electrophysiology simulations. Comput. Methods Appl. Mech. Eng. 2021, 373, 113468. [Google Scholar] [CrossRef]
- Streeter, D.D.; Spotnitz, H.M.; Patel, D.P.; J, R.J.; Sonnenblick, E.H. Fiber orientation in the canine left ventricle during diastole and systole. Circ. Res. 1969, 24, 339–347. [Google Scholar] [CrossRef]
- Streeter, D.D.; Bassett, D.L. An engineering analysis of myocardial fiber orientation in pig’s left ventricle in systole. Anat. Rec. 1966, 155, 503–511. [Google Scholar] [CrossRef]
- Sellier, M. An iterative method for the inverse elasto-static problem. J. Fluids Struct. 2011, 27, 1461–1470. [Google Scholar] [CrossRef]
- Genet, M.; Lee, L.C.; Nguyen, R.; Haraldsson, H.; Acevedo-Bolton, G.; Zhang, Z.; Ge, L.; Ordovas, K.; Kozerke, S.; Guccione, J.M. Distribution of normal human left ventricular myofiber stress at end diastole and end systole: A target for in silico design of heart failure treatments. J. Appl. Physiol. 2014, 117, 142–152. [Google Scholar] [CrossRef] [PubMed]
- Klotz, S.; Hay, I.; Dickstein, M.L.; Yi, G.H.; Wang, J.; Maurer, M.S.; Kass, D.A.; Burkhoff, D. Single-beat estimation of end-diastolic pressure-volume relationship: A novel method with potential for noninvasive application. Am. J. Physiol. Heart Circ. Physiol. 2006, 291, H403–H412. [Google Scholar] [CrossRef]
- Kallhovd, S.; Sundnes, J.; Wall, S.T. Sensitivity of stress and strain calculations to passive material parameters in cardiac mechanical models using unloaded geometries. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 664–675. [Google Scholar] [CrossRef] [PubMed]
- Kotadia, I.; Whitaker, J.; Roney, C.; Niederer, S.; O’Neill, M.; Bishop, M.; Wright, M. Anisotropic Cardiac Conduction. Arrhythm. Electrophysiol. Rev. 2020, 9, 202. [Google Scholar] [CrossRef] [PubMed]
- Mendonca Costa, C.; Hoetzl, E.; Martins Rocha, B.; Prassl, A.J.; Plank, G. Automatic parameterization strategy for cardiac electrophysiology simulations. In Proceedings of the Computing in Cardiology Conference (CinC) 2013, Zaragoza, Spain, 22–25 September 2013; pp. 373–376. [Google Scholar]
- Verma, B.; Oesterlein, T.; Loewe, A.; Luik, A.; Schmitt, C.; Dössel, O. Regional conduction velocity calculation from clinical multichannel electrograms in human atria. Comput. Biol. Med. 2018, 92, 188–196. [Google Scholar] [CrossRef] [PubMed]
- Niederer, S.A.; Kerfoot, E.; Benson, A.P.; Bernabeu, M.O.; Bernus, O.; Bradley, C.; Cherry, E.M.; Clayton, R.; Fenton, F.H.; Garny, A.; et al. Verification of cardiac tissue electrophysiology simulators using an N-version benchmark. Philos. Trans. R. Soc. A 2011, 369, 4331–4351. [Google Scholar] [CrossRef]
- Vigmond, E.J.; Stuyvers, B.D. Modeling our understanding of the His-Purkinje system. Prog. Biophys. Mol. Biol. 2016, 120, 179–188. [Google Scholar] [CrossRef]
- Gillette, K.; Prassl, A.; Bayer, J.; Vigmond, E.; Neic, A.; Plank, G. Patient-specific Parameterization of Left-ventricular Model of Cardiac Electrophysiology using Electrocardiographic Recordings. In Proceedings of the 2017 Computing in Cardiology Conference (CinC) 2017, Rennes, France, 24–27 September 2017; Volume 44. [Google Scholar] [CrossRef]
- Grandits, T.; Gillette, K.; Neic, A.; Bayer, J.; Vigmond, E.; Pock, T.; Plank, G. An Inverse Eikonal Method for Identifying Ventricular Activation Sequences from Epicardial Activation Maps. J. Comput. Phys. 2020, 419, 109700. [Google Scholar] [CrossRef]
- Cardone-Noott, L.; Bueno-Orovio, A.; Mincholé, A.; Zemzemi, N.; Rodriguez, B. Human ventricular activation sequence and the simulation of the electrocardiographic QRS complex and its variability in healthy and intraventricular block conditions. Europace 2016, 18, iv4–iv15. [Google Scholar] [CrossRef]
- Corino, V.D.A.; Sandberg, F.; Mainardi, L.T.; Sornmo, L. An atrioventricular node model for analysis of the ventricular response during atrial fibrillation. IEEE Trans. Bio-Med. Eng. 2011, 58, 3386–3395. [Google Scholar] [CrossRef]
- Schuler, S. KIT-IBT/LDRB_Fibers. Zenodo 2021. [Google Scholar] [CrossRef]
- Harrild, D.; Henriquez, C. A computer model of normal conduction in the human atria. Circ. Res. 2000, 87, E25–E36. [Google Scholar] [CrossRef]
- Loewe, A.; Krueger, M.W.; Holmqvist, F.; Dössel, O.; Seemann, G.; Platonov, P.G. Influence of the earliest right atrial activation site and its proximity to interatrial connections on P-wave morphology. EP Eur. 2016, 18, iv35–iv43. [Google Scholar] [CrossRef]
- Durrer, D.; van Dam, R.T.; Freud, G.E.; Janse, M.J.; Meijler, F.L.; Arzbaecher, R.C. Total excitation of the isolated human heart. Circulation 1970, 41, 899–912. [Google Scholar] [CrossRef]
- Smith, B.W.; Andreassen, S.; Shaw, G.M.; Jensen, P.L.; Rees, S.E.; Chase, J.G. Simulation of cardiovascular system diseases by including the autonomic nervous system into a minimal model. Comput. Methods Programs Biomed. 2007, 86, 153–160. [Google Scholar] [CrossRef]
- Hann, C.E.; Chase, J.G.; Desaive, T.; Froissart, C.B.; Revie, J.; Stevenson, D.; Lambermont, B.; Ghuysen, A.; Kolh, P.; Shaw, G.M. Unique parameter identification for cardiac diagnosis in critical care using minimal data sets. Comput. Methods Programs Biomed. 2010, 99, 75–87. [Google Scholar] [CrossRef] [PubMed]
- Stergiopulos, N.; Westerhof, B.E.; Westerhof, N. Total arterial inertance as the fourth element of the windkessel model. Am. J. Physiol. 1999, 276, H81–H88. [Google Scholar] [CrossRef] [PubMed]
- Murgo, J.P.; Westerhof, N.; Giolma, J.P.; Altobelli, S.A. Aortic input impedance in normal man: Relationship to pressure wave forms. Circulation 1980, 62, 105–116. [Google Scholar] [CrossRef] [PubMed]
- Segers, P.; Rietzschel, E.R.; De Buyzere, M.L.; Stergiopulos, N.; Westerhof, N.; Van Bortel, L.M.; Gillebert, T.; Verdonck, P.R. Three- and four-element Windkessel models: Assessment of their fitting performance in a large cohort of healthy middle-aged individuals. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2008, 222, 417–428. [Google Scholar] [CrossRef] [PubMed]
- Bovendeerd, P.H.M.; Kroon, W.; Delhaas, T. Determinants of left ventricular shear strain. Am. J. Physiol. Heart Circ. Physiol. 2009, 297, H1058–H1068. [Google Scholar] [CrossRef]
- Arts, T.; Reesink, K.; Kroon, W.; Delhaas, T. Simulation of adaptation of blood vessel geometry to flow and pressure: Implications for arterio-venous impedance. Mech. Res. Commun. 2012, 42, 15–21. [Google Scholar] [CrossRef]
- Slife, D.M.; Latham, R.D.; Sipkema, P.; Westerhof, N. Pulmonary arterial compliance at rest and exercise in normal humans. Am. J. Physiol. 1990, 258, H1823–H1828. [Google Scholar] [CrossRef] [PubMed]
- Lankhaar, J.W.; Westerhof, N.; Faes, T.J.C.; Marques, K.M.J.; Marcus, J.T.; Postmus, P.E.; Vonk-Noordegraaf, A. Quantification of right ventricular afterload in patients with and without pulmonary hypertension. Am. J. Physiol. Heart Circ. Physiol. 2006, 291, H1731–H1737. [Google Scholar] [CrossRef]
- Tanaka, T.; Arakawa, M.; Suzuki, T.; Gotoh, M.; Miyamoto, H.; Hirakawa, S. Compliance of human pulmonary “venous” system estimated from pulmonary artery wedge pressure tracings–comparison with pulmonary arterial compliance. Jpn. Circ. J. 1986, 50, 127–139. [Google Scholar] [CrossRef]
- Murgo, J.P.; Westerhof, N. Input impedance of the pulmonary arterial system in normal man. Effects of respiration and comparison to systemic impedance. Circ. Res. 1984, 54, 666–673. [Google Scholar] [CrossRef] [PubMed]
- Hadinnapola, C.; Li, Q.; Su, L.; Pepke-Zaba, J.; Toshner, M. The resistance-compliance product of the pulmonary circulation varies in health and pulmonary vascular disease. Physiol. Rep. 2015, 3, e12363. [Google Scholar] [CrossRef]
- Bols, J.; Degroote, J.; Trachet, B.; Verhegghe, B.; Segers, P.; Vierendeels, J. A computational method to assess the in vivo stresses and unloaded configuration of patient-specific blood vessels. J. Comput. Appl. Math. 2013, 246, 10–17. [Google Scholar] [CrossRef]
- Heiberg, E.; Sjögren, J.; Ugander, M.; Carlsson, M.; Engblom, H.; Arheden, H. Design and validation of Segment-freely available software for cardiovascular image analysis. BMC Med. Imaging 2010, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Coppini, R.; Ferrantini, C.; Yao, L.; Fan, P.; Del Lungo, M.; Stillitano, F.; Sartiani, L.; Tosi, B.; Suffredini, S.; Tesi, C.; et al. Late sodium current inhibition reverses electromechanical dysfunction in human hypertrophic cardiomyopathy. Circulation 2013, 127, 575–584. [Google Scholar] [CrossRef]
- Pieske, B.; Sütterlin, M.; Schmidt-Schweda, S.; Minami, K.; Meyer, M.; Olschewski, M.; Holubarsch, C.; Just, H.; Hasenfuss, G. Diminished post-rest potentiation of contractile force in human dilated cardiomyopathy. Functional evidence for alterations in intracellular Ca2+ handling. J. Clin. Investig. 1996, 98, 764–776. [Google Scholar] [CrossRef]
- Mulieri, L.A.; Hasenfuss, G.; Leavitt, B.; Allen, P.D.; Alpert, N.R. Altered myocardial force-frequency relation in human heart failure. Circulation 1992, 85, 1743–1750. [Google Scholar] [CrossRef] [PubMed]
- Rossman, E.I.; Petre, R.E.; Chaudhary, K.W.; Piacentino, V.; Janssen, P.M.L.; Gaughan, J.P.; Houser, S.R.; Margulies, K.B. Abnormal frequency-dependent responses represent the pathophysiologic signature of contractile failure in human myocardium. J. Mol. Cell. Cardiol. 2004, 36, 33–42. [Google Scholar] [CrossRef]
- Brixius, K.; Pietsch, M.; Hoischen, S.; Müller-Ehmsen, J.; Schwinger, R.H.G. Effect of inotropic interventions on contraction and Ca2+ transients in the human heart. J. Appl. Physiol. 1997, 83, 652–660. [Google Scholar] [CrossRef] [PubMed]
- Flesch, M.; Kilter, H.; Cremers, B.; Lenz, O.; Südkamp, M.; Kuhn-Regnier, F.; Böhm, M. Acute effects of nitric oxide and cyclic GMP on human myocardial contractility. J. Pharmacol. Exp. Ther. 1997, 281, 1340–1349. [Google Scholar]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Whiteley, J.P.; Bishop, M.J.; Gavaghan, D.J. Soft tissue modelling of cardiac fibres for use in coupled mechano-electric simulations. Bull. Math. Biol. 2007, 69, 2199–2225. [Google Scholar] [CrossRef]
- Augustin, C.M.; Neic, A.; Liebmann, M.; Prassl, A.J.; Niederer, S.A.; Haase, G.; Plank, G. Anatomically accurate high resolution modeling of human whole heart electromechanics: A strongly scalable algebraic multigrid solver method for nonlinear deformation. J. Comput. Phys. 2016, 305, 622–646. [Google Scholar] [CrossRef] [PubMed]
- Sachse, F.B.; Glänzel, K.; Seemann, G. Modeling of protein interactions involved in cardiac tension development. Int. J. Bifurc. Chaos 2003, 13, 3561–3578. [Google Scholar] [CrossRef]
- Campbell, K.S. Compliance Accelerates Relaxation in Muscle by Allowing Myosin Heads to Move Relative to Actin. Biophys. J. 2016, 110, 661–668. [Google Scholar] [CrossRef]
- Regazzoni, F.; Quarteroni, A. An oscillation-free fully staggered algorithm for velocity-dependent active models of cardiac mechanics. Comput. Methods Appl. Mech. Eng. 2021, 373, 113506. [Google Scholar] [CrossRef]
- Land, S.; Gurev, V.; Arens, S.; Augustin, C.M.; Baron, L.; Blake, R.; Bradley, C.; Castro, S.; Crozier, A.; Favino, M.; et al. Verification of cardiac mechanics software: Benchmark problems and solutions for testing active and passive material behaviour. Proc. R. Soc. Lond. A 2015, 471, 20150641. [Google Scholar] [CrossRef] [PubMed]
- Woodworth, L.A.; Cansız, B.; Kaliske, M. A numerical study on the effects of spatial and temporal discretization in cardiac electrophysiology. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3443. [Google Scholar] [CrossRef] [PubMed]
- ten Tusscher, K.H.; Noble, D.; Noble, P.J.; Panfilov, A.V. A model for human ventricular tissue. Am. J. Physiol. Heart Circ. Physiol. 2004, 286, H1573–H1589. [Google Scholar] [CrossRef] [PubMed]
- Andreianov, B.; Bendahmane, M.; Quarteroni, A.; Ruiz-Baier, R. Solvability analysis and numerical approximation of linearized cardiac electromechanics. Math. Models Methods Appl. Sci. 2015, 25, 959–993. [Google Scholar] [CrossRef]
- Mroue, F. Cardiac Electromechanical Coupling: Modeling, Mathematical Analysis and Numerical Simulation. Ph.D. Thesis, Ecole Centrale de Nantes (ECN). Université Libanaise, Beirut, Lebanon, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).