On S-Evolution Algebras and Their Enveloping Algebras

Abstract

In the present paper, we introduce S-evolution algebras and investigate their solvability, simplicity, and semisimplicity. The structure of enveloping algebras has been carried out through the attached graph of S-evolution algebras. Moreover, we introduce the concept of $\mathcal{E}$-linear derivation of S-evolution algebras, and prove such derivations can be extended to their enveloping algebras under certain conditions.

1. Introduction

It is well-known that several classes of non-associative algebras such as baric, evolution, Bernstein, train, stochastic, etc., were tied up with abstract algebra and biology [1,2,3]. The investigation of such kinds of algebras has offered many significant contributions to population genetics theory [3]. We point out that first population genetics problems can be traced back to the work of Bernstein [4] where evolution operators were examined, which naturally describe genetic algebras (see [3,5]). Evolution algebras are considered as a type of genetic algebras which are non-associative algebras with a dynamic nature. Such a type of algebras has been introduced in [6,7]. After that, in [8] the foundations of these algebras have been established. Later on, evolution algebras are used to model non-Mendelian genetics laws [9,10,11,12,13]. Moreover, these algebras are tightly connected with group theory, the theory of knots, dynamic systems, Markov processes and graph theory [14,15,16,17,18]. Evolution algebras allowed introduce useful algebraic techniques and methods into the investigation of some digraphs because such kind of algebras and weighted digraphs can be canonically identified [7,19]. In most investigations, considered evolution algebras were taken nilpotent [19,20,21,22,23,24]. A few papers are devoted to non-nilpotent evolution algebras [25,26,27]. In [28,29,30], a new class of evolution algebras, called Lotka–Volterra evolution algebras, has been introduced (see also [31]). It turns out that such kind of algebras are not nilpotent. Given an evolution algebra $\mathcal{E}$, then its enveloping algebra $M(\mathcal{E})$ is considered as a subalgebra of full matrix algebra $hom(\mathcal{E},\mathcal{E})$ of the endomorphism of linear space $\mathcal{E},$ generated by all left multiplications. The common properties between algebra and its enveloping algebra are essential tasks in algebra [32]. Therefore, it is natural to find which algebraic properties can be extended from the algebra to its enveloping. Some extendible properties among those algebras have been found (see [33] and the references given therein). It is worth pointing out that majority of studies constraint nilpotent algebras. In the present paper, we introduce a new class of evolution algebras called S-evolution algebras. These algebras are not nilpotent, but naturally extend Lotka–Volterra ones [30]. We point out that directed weighted graphs associated with S-evolution algebras have meaning while the Lotka–Volterra ones do not. Therefore, the study structure of these algebras may give some information about electrical circuits, find the shortest routes, and construct a model for analysis and solution of other problems [9,10,34].

One of this paper’s main aims is to study basic algebraic properties of S-evolution algebras such as simplicity, semisimplicity [25]. Up to now, there are not any investigations between evolution algebras and their enveloping algebras. Therefore, we will investigate the evolution algebras together with the specific properties of their enveloping algebras. Besides, the extendibility of derivations of S-evolution algebras will be examined as well. We notice that derivations of evolution algebras have been studied in [16,20,33,35,36,37,38].

Let us briefly highlight an organization of this paper. In Section 2, we provide ceratin basic properties of S-evolution algebras and their graphs. In Section 3, we study the structure of enveloping algebras generated by S-evolution algebras, whose attached graphs are complete. Furthermore, we prove that if two S-algebras are isomorphic, then their corresponding enveloping algebras are isomorphic, but the converse is not valid. In Section 4, we investigate properties of enveloping algebras generated by S-evolution algebras. Furthermore, in Section 5, a concept of $\mathcal{E}$-linear derivation is defined of enveloping algebras of S-evolution algebras. In the final Section 6, a description of all $\mathcal{E}$-linear derivations of enveloping algebra generated by 3-dimensional S-evolution algebras is provided.

2. S-Evolution Algebras and Their Graphs

Let us start with a definition of evolution algebras.

Definition 1.

Let $\mathcal{E}$ be a vector space over a field $\mathbb{K}$ with multiplication · and a basis $\{e_1,e_2,\dots ,e_n\}$ such that

$$e_i·e_j=0,i\ne j,$$

$$e_i·e_i={\displaystyle \sum _{k=1}^n}{a}_{ik}{e}_k,i\ge 1,$$

then $\mathcal{E}$ is called an evolution algebra and the basis $\{e_1,e_2,\dots ,e_n\}$ is said to be natural basis.

Here, the matrix $A={(a_{ij})}_{i,j=1}^n$ is called a structural matrix of the algebra $\mathcal{E}$ in the natural basis $\{e_1,\dots ,e_n\}.$

One can immediately see that every evolution algebra is commutative (therefore, flexible). Moreover, we have $rankA=dim(\mathcal{E}·\mathcal{E})$ this yields that for every finite-dimensional evolution algebra its rank of the matrix does not depend on the choice of natural basis. In what follows, we will consider non-degenerate evolution algebras, i.e., $e_i{e}_i\ne 0$ for any $i.$ For convenience, we write $\mathbf{u}\mathbf{v}$ instead of $\mathbf{u}·\mathbf{v}$ for any $\mathbf{u},\mathbf{v}\in \mathcal{E}$ and we shall write ${\mathcal{E}}^{\mathbf{2}}$ instead of $\mathcal{E}·\mathcal{E}$.

Definition 2.

A matrix $A={(a_{ij})}_{i,j=1}^n$ is called an S-matrix if

(i) 

$a_{ii}=0$ for all $1\le i\le n;$

(ii) 

$a_{ij}\ne 0$ if and only if $a_{ji}\ne 0$.

We notice that if $A={(a_{ij})}_{i,j=1}^n$ is an S-matrix, then there is a family of injective functions ${\{f_{ij}:\mathbb{K}\to \mathbb{K}\}}_{1\le i<j\le n}$ with $f_{ij}(0)=0$ such that $a_{ji}=f_{ij}(a_{ij})$ for all $1\le i<j\le n$. Hence, each S-matrix is uniquely defined by off diagonal upper triangular matrix ${(a_{ij})}_{i<j}$ and a family of functions ${(f_{ij})}_{i<j}$. This allows us to construct lots of examples of S-matrices.

Example 1.

Let ${(a_{ij})}_{i<j}$ be a given upper triangular matrix. Let us construct certain examples of S-matrices as follows:

1.

Assume that B is a symmetric matrix such that $b_{ij}=a_{ij}$ and $b_{ji}=a_{ij}$ for all $i<j$. In this setting, one can see that $f_{ij}(x)=x$;

2.

Assume that C is a skew-symmetric matrix such that $c_{ij}=a_{ij}$, $c_{ji}=-a_{ij}$ for all $i<j$. It is clear that $f_{ij}(x)=-x$;

3.

Assume that M is a matrix such that $m_{jj}=-a_{ij}$, $m_{ji}={(-1)}^{i+j}{a}_{ij}$ for all $i<j$. In this setting, we have $f_{ij}(x)={(-1)}^{i+j}x$.

Definition 3.

An evolution algebra $\mathcal{E}$ is called an S-evolution algebra if its structural matrix is an S-matrix.

Remark 1.

We note that evolution algebras corresponding to skew-symmetric matrices are called Lotka–Volterra (or Volterra) evolution algebras. Such kind of algebras have been investigated in [30,39]. From the given Example 1, we can see that Lotka–Volterra algebras and S-evolution algebras (different from those ones) may not share common properties. For example, if A is a skew-symmetric matrix, then its rank could be even, while if one considers an S-matrix which is symmetric, then its rank could be any positive integer.

Remark 2.

The motivation behind introducing S-evolution algebra is that such algebras have certain applications in the study of electrical circuits, find the shortest routes, and construct a model for analysis and solution of other problems [9,38]. From the physical point of view, if one considers $\{1,2,\dots ,n\}$ species than a pair $(i,j)$ interacts with $a_{ij}$ rate. Therefore, it is natural investigate algebraic properties of such kind of interactions. On the other hand, such kind of interactions lead us to the game theory like zero-sum games [40,41]. Moreover, recently, Lotka–Volterra matrices have been considered within the framework of phase transitions and Gibbs measures [42,43,44].

Example 2.

Let us provide a more concrete example. Let us consider two players A and B stochastic game, who move a token along one of the outgoing arcs [34]To determine whose turn, a coin is flipped. If head it is $A^{\prime }$s turn and if tail then $B^{\prime }$s turn. A pays to B the weight of the arc along which the token is moved. Such kinds of games have a lot of applications in economics, evolutionary biology, etc. One can see that the given weighted graph defines a matrix.

$$\left(\begin{array}{ccc}0& 1& 2\\ -3& 0& -2\\ -1& 3& 0\end{array}\right)$$

which is clearly an S-matrix. Hence, we can investigate the algebraic properties of the corresponding evolution algebra ( This is an S-evolution algebra). It is stressed that the evolution algebra is not Lotka–Volterra one. Therefore, it is natural to investigate such algebra, which may open some shed into these games from an algebraic point of view. Note that evolution algebra associated with the Markov process has been considered in [8,15,45]. However, the considered evolution algebra is not Markov evolution algebra, and hence, it is needed for the investigation (algebraic properties )

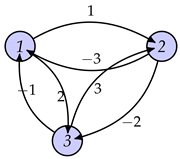Example 3.

Another implementation of S-evolution algebras could be in a face recognition. Suppose we are interested in designing a model to face recognition. The first step in any model of face recognition is devoted to finding out the coordinates of faces. If one person stands in front of the camera, the system will find the coordinates of the face and install them in a big matrix. If we assume that the region is related to the coordinate $A(i,i)=0$, this region is common and has the same properties in each person. One of the significant challenges of any face recognition system is the rotation of the person’s face when he stands in front of the camera. Usually, the company stored several images of its Customers in its database. The implementation of S-evolution algebra as follows:

Suppose the system took a picture of person A and installed it in the matrix, then the corresponding S-evolution algebra is denoted by ${\mathcal{E}}_n$ and if we assume that this person has ten pictures in the database, then each picture related to S-evolution algebra ${\mathcal{E}}_{n_i}$ where $i=1,\dots ,10.$ Now our model will check the isomorphism between ${\mathcal{E}}_n$ and all S-evolution algebras generated by the pictures in the database. Surely, the system will find ${\mathcal{E}}_n\cong {\mathcal{E}}_{n_i}$ where $i=1,\dots ,10.$ Hence, in this way, we can identify this person.

In what follows, for the sake of simplicity, we always assume that $\mathbb{K}$ is taken as the field of the complex numbers $\mathbb{C}$.

Let $\mathcal{E}$ be an S-evolution algebra w.r.t. natural basis$\{e_1,e_2,\dots ,e_n\}$, then the canonical form of the table of multiplications is given by

$$\begin{array}{ccc}& & e_i·e_j=0,i\ne j;\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill & & e_i·e_i={\displaystyle \sum _{k=1}^{i-1}}{f}_{ki}(a_{ki})e_k+{\displaystyle \sum _{m=i+1}^n}{a}_{im}{e}_m.\hfill \end{array}$$

(2)

We notice that if $i=1$ then the first summand of (2) is zero, if $i=n$ then the second summand is zero.

Let us define the following sequences:

$$\begin{array}{ccc}& & {\mathcal{E}}^{(1)}=\mathcal{E},{\mathcal{E}}^{(k+1)}={\mathcal{E}}^{(k)}{\mathcal{E}}^{(k)},\hfill \\ & & {\mathcal{E}}^{<1>}=\mathcal{E},{\mathcal{E}}^{<k+1>}={\mathcal{E}}^{<k>}\mathcal{E},\hfill \\ & & {\mathcal{E}}^1=\mathcal{E},{\mathcal{E}}^{k+1}={\displaystyle \sum _{i=1}^k}{\mathcal{E}}^i{\mathcal{E}}^{k+1-i},k\ge 1\hfill \end{array}$$

Next inclusions are true for $k\ge 1:$

$${\mathcal{E}}^{<k>}\subseteq {\mathcal{E}}^k,{\mathcal{E}}^{(k+1)}\subseteq {\mathcal{E}}^{2^k}.$$

Due to the commutativity of $\mathcal{E}$ one has ${\displaystyle {\mathcal{E}}^k=\sum _{1\le i\le k-i}{\mathcal{E}}^i{\mathcal{E}}^{k-i}.}$

Definition 4.

An evolution algebra $\mathcal{E}$ is called

(i) 

solvable if there exists $n\in \mathbb{N}$ such that ${\mathcal{E}}^{(n)}=0$ and the minimal such number is called index of solvability;

(ii) 

right nilpotent if there exists $n\in \mathbb{N}$ such that ${\mathcal{E}}^{<n>}=0$ and the minimal such number is called index of right nilpotency;

(iii) 

nilpotent if there exists $n\in \mathbb{N}$ such that ${\mathcal{E}}^n=0$ and the minimal such number is called index of nilpotency.

Remark 3.

We point out that the nilpotency of evolution algebra implies its right nilpotentcy and solvability. Moreover, the solvablity of evolution algebra does not imply its right nilpotency ([20], Example 2.4).

Definition 5.

Let $\mathcal{E}$ be an evolution algebra with a natural basis $B=\{e_1,\dots ,e_n\}$ and a structural matrix $A=\left({\alpha }_{ij}\right)$.

(i) 

A graph $\Gamma (\mathcal{E},B)=(V,E)$, with $V=\{1,\dots ,n\}$ and $E=\{(i,j)\in V\times V:{\alpha }_{ij}\ne 0\}$, is called the graph attached to the evolution algebra $\mathcal{E}$ relative to the natural basis B.

(ii) 

The triple ${\Gamma }^w(\mathcal{E},B)=(V,E,\omega )$, with $\Gamma (\mathcal{E},B)=(V,E)$ and where ω is the map $E\to \mathbb{F}$ given by $\omega \left((i,j)\right)={\alpha }_{ij}$, is called the weighted graph attached to the S-evolution algebra $\mathcal{E}$ relative to the natural basis B.

A graph $\Gamma (\mathcal{E},B)$ is called complete if every two vertices of the graph are connected by an edge. Moreover, $\Gamma (\mathcal{E},B)$ is connected if there is a path between any two vertices, otherwise is called disconnected.

Definition 6

([25]). An evolution subalgebra of an evolution algebra $\mathcal{E}$ is a subalgebra ${\mathcal{E}}^{\prime }\subseteq \mathcal{E}$ such that ${\mathcal{E}}^{\prime }$ is an evolution algebra, i.e., ${\mathcal{E}}^{\prime }$ has a natural basis.

We notice that the definition of evolution subalgebra, which is given in [7,8] has more restrictive than the Definition 6. The concepts of evolution subalgebra and evolution ideal in the sense of definition given in [7,8] are equivalent. However, they are not equivalent in the sense of Definition 6 (see Example 2.6 [25]). In this paper, we will consider the Definition 6.

Definition 7

([25]). An evolution ideal of an evolution algebra $\mathcal{E}$ is an ideal I of $\mathcal{E}$ such that I has a natural basis.

Recall that an evolution algebra $\mathcal{E}$ is called simple if ${\mathcal{E}}^2\ne 0$ and it has no non-trivial proper ideal, and it is called semisimple if it can be written as direct sum of simple subalgebras. An ideal is called simple if it does not contain any proper sub-ideal.

Remark 4.

In [46] a notion of basic ideals of evolution algebras is defined and corresponding basic simple evolution algebras are studied. A relation between simplicity and basic simplicity is established as well. These results allowed to describe four dimensional perfect non-simple evolution algebras over a field with mild restrictions.

Proposition 1

([25]). Let A be an evolution algebra and $B=\left\{e_i\right|i\in V\}$ be its natural basis. Consider the following conditions:

(i) 

$\mathcal{E}$ is simple.

(ii) 

$\mathcal{E}$ satisfies the following properties:

(a) 

$\mathcal{E}$ is non-degenerate.

(b) 

$\mathcal{E}=\mathrm{lin}\left\{e_i^2\right|i\in V\}$.

(c) 

$\mathrm{lin}\left\{e_i^2\right|i\in V^{\prime }\}$ is a non-zero ideal of A for a non-empty $V^{\prime }\subseteq V$ then $|V^{\prime }|=|V|.$

Then (i) ⇒ (ii) and (ii) ⇒ (i) if $\left|V\right|<\infty$.

In what follow, we always consider $\left|V\right|<\infty .$

3. Some Properties of S-Evolution Algebras

In this section, we are going to study some properties of S-evolution algebras.

In [30] we have recently proved the following fact.

Theorem 1

([30]). Let $\mathcal{E}$ be a non-trivial Lotka–Volterra evolution algebra then $\mathcal{E}$ is not nilpotent.

It turns out that this result could be extended for S-evolution algebras in a more general setting.

Theorem 2.

Let $\mathcal{E}$ be a non-trivial n-dimensional S-evolution algebra, then $\mathcal{E}$ is not solvable.

Proof. 

Let $\mathcal{E}=\mathrm{alg}\langle e_1,e_2,\dots ,e_n\rangle ,$ since $\mathcal{E}$ is non-degenerate, then there exists $e_i\in \mathrm{alg}\langle e_1,e_2,\dots ,e_n\rangle$ such that $e_i^2\ne 0.$ Therefore, one finds $k\ne i$ such that $a_{ik}\ne 0,$ since the structural matrix of $\mathcal{E}$ is a S-matrix, then $f(a_{ik})\ne 0,$ so, $\langle e_i,e_k\rangle \subseteq {\mathcal{E}}^{(2)}$. We claim that $\langle e_i,e_k\rangle \subseteq {\mathcal{E}}^{(n)},$ for any positive integer $n.$ Let us prove it by induction. Assume that $\langle e_i,e_k\rangle \subseteq {\mathcal{E}}^{(n-1)},$ due to ${\mathcal{E}}^{(n)}={\mathcal{E}}^{(n-1)}{\mathcal{E}}^{(n-1)}$ and $\langle e_i,e_k\rangle \subseteq {\mathcal{E}}^{(n-1)},$ we get $\langle e_i,e_k\rangle \subseteq {\mathcal{E}}^{(n)}$. This yields that ${\mathcal{E}}^{(n)}\ne 0$ for any positive $n.$ Hence, $\mathcal{E}$ is not solvable. □

The proved theorem together with Remark 3 implies that any non-degenerate S-evolution algebra is not nilpotent.

Let $B=\left\{e_i\right|i\in V\}$ be a natural basis of an evolution algebra $\mathcal{E}$ and let $i_0\in V.$ The first-generation descendants of $i_0$ are the elements of the subset $D^1(i_0)$ given by:

$$D^1(i_0):=\{j\in V|a_{j{i}_0}\ne 0\}.$$

Note that $j\in D^1(i_0)$ if and only if, ${\pi }_j(e_{i_0}^2)\ne 0$ (where ${\pi }_j$ is the canonical projection of $\mathcal{E}$ over $\mathbb{C}{e}_j$). Similarly, we say that j is a second-generation descendant of $i_0$ whenever $j\in D^1(k)$ for some $k\in D^1(i_0).$ Therefore,

$$D^2(i_0)=\bigcup _{k\in D^1(i_0)}{D}^1(k).$$

By recurrency, we define the set of mth-generation descendantsof $i_0$ as

$$D^m(i_0)=\bigcup _{k\in D^{m-1}(i_0)}{D}^1(k).$$

Finally, the set of descendants of $i_0$ is defined as the subset of ∨ given by

$$D(i_0)=\bigcup _{m\in \mathbb{N}}{D}^m(i_0).$$

On the other hand, we say that $j\in V$ is an ascendant of $i_0$ if $i_0\in D(j);$ that is, $i_0$ is a descendant of $j.$

Proposition 2.

Let $\mathcal{E}$ be an S-evolution algebra with natural basis $B=\left\{e_i\right|i\in V\}.$ If $\Gamma (\mathcal{E},B)$ is complete, then $D(i_0)=V$ for any $i_0\in V$.

Proof. 

Since the attached graph is complete, then, for any $i_0\in V$

$$D^1(i_0)=\{j\in V:j\ne i_0\}.$$

From $i_0\in D^1(j)$ we infer

$$D^2(i_0)=\bigcup _{k\in D^1(i_0)}{D}^1(k)=V.$$

Consequently,

$$D^m(i_0)=\bigcup _{k\in D^{m-1}(i_0)}{D}^1(k)=V.$$

Therefore,

$$D(i_0)=\bigcup _{m\in \mathbb{N}}{D}^m(i_0)=V.$$

Due to the arbitrariness of $i_0$ we get the assertion. □

Theorem 3.

Let $\mathcal{E}$ be an S-evolution algebra with $B=\{e_i:i\in V\}.$ Then $\mathcal{E}$ is simple if and only if $det(A)\ne 0,$ where A is the structural matrix of $\mathcal{E}.$

Proof. 

Let $\mathcal{E}$ be a simple algebra then by Proposition 1(b), we have $\mathcal{E}=\mathrm{lin}\left\{e_i^2\right|i\in V\}$. Hence, the set $\left\{e_i^2\right|i\in V\}$ contains linearly independent vectors, this implies that $det(A)\ne 0.$

Conversely, let us assume the contrary, i.e., $\mathcal{E}$ is not simple. Then, there exists $I\in \mathcal{E}$ such that $〈I〉$ is a non-zero proper ideal of $\mathcal{E}.$ Let $j\in V$ such that ${\pi }_j(I)\ne 0.$ Then $〈e_j^2〉$ is a non-zero ideal of $\mathcal{E}$ contained in $〈I〉$ but

$$〈e_j^2〉=\mathrm{lin}\{e_k^2:k\in D(j)\cup \left\{j\right\}\}$$

Due to $det(A)\ne 0$, we have

$$D(j)\cup \left\{j\right\}=V$$

which means $〈e_j^2〉=\mathcal{E}$ which is a contradiction as $〈e_j^2〉$ a proper ideal of $\mathcal{E}.$ This completes the proof. □

Corollary 1.

Let $\mathcal{E}$ be a simple S-evolution algebra with $B=\{e_i:i\in V\}.$ Then $\Gamma (\mathcal{E},B)$ is connected.

We stress that the converse of Corollary 1 is not true. For example, let us consider a three dimensional S-evolution algebra with a table of multiplication given by:

$$e_1^2=e_2,e_2^2=e_1+e_3,e_3^2=e_2.$$

It is clear that $\Gamma (\mathcal{E},B)$ is connected. However, $\mathcal{E}$ is not simple as $\mathrm{lin}\{e_1^2,e_2^2\}$ is a non-zero proper ideal of $\mathcal{E}.$

Proposition 3.

Let $\mathcal{E}$ be an n-dimensional S-evolution algebra with disconnected attached graphs, i.e., $\Gamma (\mathcal{E},B)={\displaystyle {\displaystyle \bigcup _{i=1}^p}}{A}_i$ and $A_m\cap A_k=\varphi ,$ for any $m\ne k,$ where p is the number of disconnected graphs. Then each graph $A_i$ corresponds to a proper ideal of $\mathcal{E}.$

Proof. 

As before, the attached graph of $\mathcal{E}$ is denoted by $\Gamma (\mathcal{E},B)$. Let $I_{A_i}:=\{e_i:i\in V(A_i)\}.$ We claim that $span\left\{I_{A_i}\right\}$ is an ideal. Since $I_{A_k}\cap I_{A_m}=\varphi$ for any $k\ne m$ one finds $e_r{e}_s=0$ for all $e_r\in I_{A_k}$ and $e_s\in I_{A_m}.$ Next, fix i and pick $e_r\in I_{A_i}$ then $e_r^2={\displaystyle \underset{e_l\in I_{A_i}}{\Sigma }}{\alpha }_l{e}_l.$ Hence, $e_r^2\in I_{A_i}$ whenever, $e_r\in I_{A_i}$ This means that $span\left\{I_{A_i}\right\}$ is an ideal of $\mathcal{E}.$ □

Example 4.

Let us consider an algebra $\mathcal{E}$ with the following structural matrix:

$$\left(\begin{array}{cc}\begin{array}{cc}0& a_1\\ -a_1& 0\end{array}& \mathbf{0}\\ \mathbf{0}& \begin{array}{cc}0& a_2\\ -a_2& 0\end{array}\end{array}\right)$$

The attached graphs areThen $span\left\{I_{A_1}\right\}=span\{e_1,e_2\}$ and $span\left\{I_{A_2}\right\}=span\{e_3,e_4\}$ are proper ideals of $\mathcal{E}.$

Corollary 2.

Let $\mathcal{E}$ be an n-dimensional S-evolution algebra with disconnected attached graphs,

$$\Gamma (\mathcal{E},B)={\displaystyle \bigcup _{i=1}^p}\Gamma ({\mathcal{E}}_i,B_i),$$

where $\Gamma ({\mathcal{E}}_k,B_k)\cap \Gamma ({\mathcal{E}}_m,B_m)=\varphi ,$ for any $k\ne m$ and p is the number of disconnected graphs. Then

$$\mathcal{E}\cong \underset{i}{⨁}{\mathcal{E}}_i,$$

if and only if each ${\mathcal{E}}_i$ is a simple S-evolution algebra.

Theorem 4.

If a non-trivial finite dimensional S-evolution algebra $\mathcal{E}$ is semisimple, then the attached graph $\Gamma (\mathcal{E},B)$ of $\mathcal{E}$ is disconnected.

Proof. 

Assume that $\mathcal{E}$ is semisimple, then there exists a non-trivial proper ideal I of $\mathcal{E}.$ Let us define the following set

$$A:=\{i:e_i\in I\}.$$

It follows that if $m\notin A$ then $e_m\notin I.$ Since $e_i^2\in I,$ one has that $a_{im}=0$ for any $i\in A.$ Hence, the vertex m is not connected to any vertex of A. Therefore, the attached graph is disconnected. □

Remark 5.

The converse of the Theorem 4 is, in general, not true. Namely, if the attached graph is disconnected then an evolution algebra may be not semisimple.

Example 5.

Let us consider an S-evolution algebra $\mathcal{E}$ with the following table of multiplication:

$$e_1^2=e_2,e_2^2=e_1,e_3^2=0.$$

It is clear that the attached graph is disconnected. However, $\mathcal{E}\ne {\mathcal{E}}_1\oplus {\mathcal{E}}_2$ where ${\mathcal{E}}_1=〈e_1,e_2〉,$ and ${\mathcal{E}}_2=〈e_3〉$. From ${\mathcal{E}}_2^2=0$ we infer that ${\mathcal{E}}_2$ is not simple.

In [30] we have established an isomorphism criteria of Lotka–Volterra evolution algebras.

Theorem 5

([30]). Let ${\mathcal{E}}_1,$ and ${\mathcal{E}}_2$ be two Lotka–Volterra evolution algebras whose attached graphs are complete. Then ${\mathcal{E}}_1\cong {\mathcal{E}}_2$ if and only if $\frac{a_{ij}}{bij}=\frac{a_{lm}}{b_{lm}},$ for any $1\le i\ne j\le n$ and $1\le l\ne m\le n.$

Next result extends the formulated one to S-evolution algebras.

Theorem 6.

Let ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$ be two S-evolution algebras with ${(a_{ij})}_{i,j=1}^n,{(b_{ij})}_{i,j=1}^n$ structural matrices, respectively, whose attached graphs are complete. Then ${\mathcal{E}}_1\cong {\mathcal{E}}_2$ if and only if the following conditions are satisfied

$$\begin{array}{ccc}\hfill {\left(\frac{a_{ij}}{b_{ij}}\right)}^2\left(\frac{f_{ij}(a_{ij})}{g_{ij}(b_{ij})}\right)& =& {\left(\frac{a_{ik}}{b_{ik}}\right)}^2\left(\frac{f_{ik}(a_{ik})}{g_{ik}(b_{ik})}\right),1\le i<j<k\le n.\hfill \\ \hfill \left(\frac{a_{pi}}{b_{pi}}\right){\left(\frac{f_{pi}(a_{pi})}{g_{pi}(b_{pi})}\right)}^2& =& {\left(\frac{a_{ik}}{b_{ik}}\right)}^2\left(\frac{f_{ik}(a_{ik})}{g_{ik}(b_{ik})}\right),1\le p<i<k\le n.\hfill \\ \hfill \left(\frac{a_{pi}}{b_{pi}}\right){\left(\frac{f_{pi}(a_{pi})}{g_{pi}(b_{pi})}\right)}^2& =& \left(\frac{a_{qi}}{b_{qi}}\right){\left(\frac{f_{qi}(a_{qi})}{g_{qi}(b_{qi})}\right)}^2,1\le p\le q<i\le n.\hfill \end{array}$$

Proof. 

Let ${\mathcal{E}}_1=\langle e_1,e_2,\dots ,e_n\rangle$ and ${\mathcal{E}}_2=\langle f_1,f_2,\dots ,f_n\rangle$. Assume that ${\mathcal{E}}_1\cong {\mathcal{E}}_2$, then one can write

$$f_i={\displaystyle \sum _{i=1}^n}{\alpha }_{ik}{e}_k.$$

From $f_i{f}_j=0$ for any $i\ne j,$ without loss of generality, we can assume that $f_i={\alpha }_{ii}{e}_i.$ Then

$$f_i^2={\alpha }_{ii}^2\left({\displaystyle \sum _{p=1}^{i-1}}{f}_{pi}(a_{pi})e_p+{\displaystyle \sum _{q=i+1}^n}{a}_{iq}{e}_q\right).$$

(3)

On the other hand,

$$f_i^2=\left({\displaystyle \sum _{p=1}^{i-1}}{\alpha }_{pp}{g}_{pi}(b_{pi})e_p+{\displaystyle \sum _{q=i+1}^n}{\alpha }_{qq}{b}_{iq}{e}_q\right).$$

(4)

Comparing (3) and (4), we obtain

$$\begin{array}{ccc}\hfill f_{pi}(a_{pi}){\alpha }_{ii}^2& =& g_{pi}(b_{pi}){\alpha }_{pp},p=\overline{1,i-1}\hfill \\ \hfill a_{iq}{\alpha }_{ii}^2& =& b_{iq}{\alpha }_{qq},q=\overline{i+1,n}.\hfill \end{array}$$

(5)

For any $i<j$, from (5) one finds

$$\begin{array}{cc}\hfill a_{ij}{\alpha }_{ii}^2& =b_{ij}{\alpha }_{jj}\hfill \\ \hfill f_{ij}(a_{ij}){\alpha }_{jj}^2& =g_{ij}(b_{ij}){\alpha }_{ii}\hfill \end{array}$$

Solving the above equations, we get

$$\begin{array}{cc}\hfill {\alpha }_{ii}& =\sqrt[3]{{\left(\frac{b_{ij}}{a_{ij}}\right)}^2\left(\frac{g_{ij}(b_{ij})}{f_{ij}(a_{ij})}\right)},or{\alpha }_{ii}=\sqrt[3]{{\left(\frac{b_{ij}}{a_{ij}}\right)}^2\left(\frac{g_{ij}(b_{ij})}{f_{ij}(a_{ij})}\right)}\left(\frac{1\pm \sqrt{3}i}{2}\right)\hfill \\ \hfill {\alpha }_{jj}& =\sqrt[3]{\left(\frac{b_{ij}}{a_{ij}}\right){\left(\frac{g_{ij}(b_{ij})}{f_{ij}(a_{ij})}\right)}^2},or{\alpha }_{jj}=\sqrt[3]{\left(\frac{b_{ij}}{a_{ij}}\right){\left(\frac{g_{ij}(b_{ij})}{f_{ij}(a_{ij})}\right)}^2}\left(\frac{1\pm \sqrt{3}i}{2}\right)\hfill \end{array}$$

(6)

The arbitrariness of j implies

$$\begin{array}{cc}\hfill {\left(\frac{a_{ij}}{b_{ij}}\right)}^2\left(\frac{f_{ij}(a_{ij})}{g_{ij}(b_{ij})}\right)& ={\left(\frac{a_{ik}}{b_{ik}}\right)}^2\left(\frac{f_{ik}(a_{ik})}{g_{ik}(b_{ik})}\right),1\le i<j<k\le n.\hfill \\ \hfill \left(\frac{a_{pi}}{b_{pi}}\right){\left(\frac{f_{pi}(a_{pi})}{g_{pi}(b_{pi})}\right)}^2& ={\left(\frac{a_{ik}}{b_{ik}}\right)}^2\left(\frac{f_{ik}(a_{ik})}{g_{ik}(b_{ik})}\right),1\le p<i<k\le n.\hfill \\ \hfill \left(\frac{a_{pi}}{b_{pi}}\right){\left(\frac{f_{pi}(a_{pi})}{g_{pi}(b_{pi})}\right)}^2& =\left(\frac{a_{qi}}{b_{qi}}\right){\left(\frac{f_{qi}(a_{qi})}{g_{qi}(b_{qi})}\right)}^2,1\le p\le q<i\le n.\hfill \end{array}$$

Conversely, the isomorphism between ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$ can be established by the following change of basis

$$\begin{array}{cc}\hfill f_1& =\sqrt[3]{{\left(\frac{b_{12}}{a_{12}}\right)}^2\left(\frac{g_{12}(b_{12})}{f_{12}(a_{12})}\right)}{e}_1\hfill \\ \hfill f_j& =\frac{a_{1j}}{b_{1j}}{\left(\sqrt[3]{{\left(\frac{b_{12}}{a_{12}}\right)}^2\left(\frac{g_{12}(b_{12})}{f_{12}(a_{12})}\right)}\right)}^2{e}_j,1<j\le n.\hfill \end{array}$$

□

4. Enveloping Algebras Generated by S-Evolution Algebras

Let us recall some notions from [32]. Let $\mathbf{E}$ be an evolution algebra, by $L_{\mathbf{a}}$ we denote the left multiplication operator by an element $\mathbf{a}$:

$$\begin{array}{c}{L}_{\mathbf{a}}:\mathbf{x}\mapsto \mathbf{x}·\mathbf{a}.\hfill \end{array}$$

By $Hom(\mathbf{E},\mathbf{E})$ we denote the full matrix algebra of endomorphisms of $\mathbf{E}$. A subalgebra of $Hom(\mathbf{E},\mathbf{E})$ generated by $\{L_{\mathbf{a}}:\mathbf{a}\in \mathbf{E}\}$, is called multiplication algebra of $\mathbf{E}$, denoted by $M(\mathbf{E})$.

Proposition 4.

Let $\mathcal{E}$ be an S-evolution algebra and $M(\mathcal{E})$ be its associative enveloping algebra. Then the vectors $R_{e_i}\circ R_{e_j},R_{e_i}\circ R_{e_k}\circ \dots \circ R_{e_m}\circ R_{e_j}$ are linearly dependent.

Proof. 

We first observe that

$$R_{e_i}\circ R_{e_j}=a_{ij}{\displaystyle \sum _{k=1}^n}{a}_{jk}{E}_{ik}.$$

and

$$R_{e_i}\circ R_{e_k}\circ \dots \circ R_{e_m}\circ R_{e_j}=a_{ik}\dots a_{mj}{\displaystyle \sum _{k=1}^n}{a}_{jk}{E}_{ik}.$$

If $a_{ij}=0,$ then $R_{e_i}\circ R_{e_j}=0$ which implies that these two vector are linearly dependent. If $a_{ij}\ne 0,$ one has that

$$R_{e_i}\circ R_{e_k}\circ \dots \circ R_{e_m}\circ R_{e_j}=\frac{a_{ik}\dots a_{mj}}{a_{ij}}{R}_{e_i}\circ R_{e_j}.$$

Hence, in both cases they are linearly dependent. □

For fixed $i,$ we define

$$A^{(i)}:=\{R_{e_i}\circ R_{e_j}:j\ne i,j=\overline{1,n}\}.$$

Proposition 5.

Let $\mathcal{E}$ be an S-evolution algebra whose attached graph is complete, with matrix of structural constants A and $M(\mathcal{E})$ be its associative enveloping algebra, then the following statements hold true:

(1) 

if $\mathcal{E}$ is simple then for each $i,$$\dim (\mathrm{span}(A^{(i)}))=\mathrm{Rank}(A)-1.$

(2) 

if $\mathcal{E}$ is not simple then for each $i,$$\dim (\mathrm{span}(A^{(i)}))=\mathrm{Rank}(A).$

(3) 

if the sets $A^{(i)},A^{(j)}$ contain linearly independent vectors then $A^{(i)}\cup A^{(j)}$ contains linearly independent vectors for any $i\ne j.$

Proof. (i) Consider

$$\sum _{j\ne i}{\alpha }_j(R_{e_i}\circ R_{e_j})=\sum _{j\ne i}{\alpha }_j{a}_{ij}{\displaystyle \sum _{k=1}^n}{a}_{jk}{E}_{ik}=0.$$

Since $a_{ij}\ne 0$ for any $1\le i\ne j\le n.$ Then one gets the following system of homogeneous linear equations:

$$\begin{array}{c}\hfill 〈a_{i1},a_{i2},\dots a_{ii-1},a_{ii+1},\dots ,a_{in}〉•〈{\mathbf{a}}_1^t,{\mathbf{a}}_2^t,\dots ,{\mathbf{a}}_{i-1}^t,{\mathbf{a}}_{i+1}^t,\dots ,{\mathbf{a}}_n^t〉\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_{i-1}\\ {\alpha }_{i+1}\\ ⋮\\ {\alpha }_n\end{array}\right]={\left[0\right]}_{n\times 1}\end{array}$$

(7)

where ${\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_{i-1},{\mathbf{a}}_{i+1},\dots ,{\mathbf{a}}_n$ are the row vectors of the structural matrix A without the ith row, and • stands for the dot product given by

$$〈a_{i1},a_{i2},\dots a_{ii-1},a_{ii+1},\dots ,a_{in}〉•〈{\mathbf{a}}_1^t,{\mathbf{a}}_2^t,\dots ,{\mathbf{a}}_{i-1}^t,{\mathbf{a}}_{i+1}^t,\dots ,{\mathbf{a}}_n^t〉=a_{i1}{\mathbf{a}}_1^t+a_{i2}{\mathbf{a}}_2^t+\dots +a_{in}{\mathbf{a}}_n^t.$$

Denote

$$A_{n\times n-1}^{\prime }:=a_{i1}{\mathbf{a}}_1^t+a_{i2}{\mathbf{a}}_2^t+\dots +a_{in}{\mathbf{a}}_n^t.$$

then we can rewrite (7) as follows

$$A_{n\times n-1}^{\prime }\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_{i-1}\\ {\alpha }_{i+1}\\ ⋮\\ {\alpha }_n\end{array}\right]={\left[0\right]}_{n\times 1}$$

Since $\det (A)\ne 0,$ then $\mathrm{Rank}(A^{\prime })=n-1.$ Therefore, the only solution of (7) is

$${\alpha }_1={\alpha }_2=\dots ={\alpha }_{i-1}={\alpha }_{i+1}=\dots ={\alpha }_n=0.$$

Hence, $A^{(i)}$ contains $\mathrm{Rank}(A)-1$ linearly independent vectors. Let $x,y\in A^{(i)}$ then one can easily show that $xy,x+y\in \mathrm{span}(A^{(i)}).$ Hence, $\dim (\mathrm{span}(A^{(i)}))=\mathrm{Rank}(A)-1.$

(ii) Next, assume that $\det (A)=0$ and $\mathrm{rank}(\mathrm{A})=m<n.$ Now, by removing dependent rows, we obtain a matrix $A_{m\times n}^{″}.$ Clearly, $\mathrm{Rank}(A_{m\times n}^{″})=m.$ Then, let us consider

$${\displaystyle \sum _{k=1,k\ne i}^{m+1}}{\alpha }_k(R_{e_i}\circ R_{e_k})={\left[0\right]}_{n\times n-m}.$$

From the last equation, we get

$$A_{n\times m}^{″}\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_{i-1}\\ {\alpha }_{i+1}\\ ⋮\\ {\alpha }_{m+1}\end{array}\right]={\left[0\right]}_{n\times 1}$$

The solution of the last system is trivial, hence a maximum number of independent vectors is $\mathrm{rank}(A)=m.$ Therefore, $\dim (\mathrm{span}(A^{(i)}))=\mathrm{rank}(A).$

(iii) Finally, assume that $A^{(i)}$ contains linearly independent elements for all $1\le i\le n.$ Then $\mathrm{span}(A^{(i)})$ is a subspace. Now let us suppose that $\mathrm{span}(A^{(i)})\cup \mathrm{span}(A^{(i)})$ are linearly dependent. It is clear that $A^{(i)}\cap A^{(j)}=\varphi$ for any $i\ne j,$ which yields $\mathrm{span}(A^{(i)})\cap \mathrm{span}(A^{(i)})=\left\{0\right\}.$ Assume that

$${\displaystyle \sum _{k\ne i}^n}{\alpha }_k(R_{e_i}\circ R_{e_k})+{\displaystyle \sum _{m\ne j}^n}{\beta }_m(R_{e_j}\circ R_{e_m})=0,k,m=\overline{1,n}.$$

Now, we consider the following cases:

If ${\alpha }_k=0$ for all k then we get $A^{(j)}$ is linearly dependent which is a contradiction. If ${\beta }_m=0$ for all m then we get $A^{(i)}$ is linearly dependent which is again a contradiction. Now, if

$${\displaystyle \sum _{k\ne i}^n}{\alpha }_k(R_{e_i}\circ R_{e_k})=-{\displaystyle \sum _{m\ne j}^n}{\beta }_m(R_{e_j}\circ R_{e_m})$$

then $-{\sum }_{m\ne j}^n{\beta }_m(R_{e_j}\circ R_{e_m})\in \mathrm{span}(A^{(i)})$, but it contradicts to $\mathrm{span}(A^{(i)})\cap \mathrm{span}(A^{(i)})=\left\{0\right\}.$ Hence, $A^{(i)}\cup A^{(j)}$ contains linearly independent vectors for any $i\ne j.$ □

Corollary 3.

Let $A^{(1)},A^{(2)},\dots ,A^{(n)}$ contain linearly independent vectors then ${\displaystyle \bigcup _{k=1}^n}{A}^{(k)}$ is linearly independent.

Proposition 6.

Let $M(\mathcal{E})$ be an associative enveloping algebra generated by an $S$-evolution algebra $\mathcal{E}$ whose attached graph $\Gamma (\mathcal{E},B)$ is complete. Then the following statements are true:

(i) 

vectors of $\mathcal{A}=\{R_{e_i}:1\le i\le n\}$ are linearly independent;

(ii) 

if $\mathcal{E}$ is simple then for each $i,$ the set $A^{(i)}\cup \left\{R_{e_i}\right\}$ is linearly independent;

(iii) 

if $\mathcal{E}$ is not simple then for each $i,$ the set $A^{(i)}\cup \left\{R_{e_i}\right\}$ is linearly dependent.

Proof. (i). Let us consider

$${\displaystyle \sum _{i=1}^n}{\alpha }_i{R}_{e_i}={\displaystyle \sum _{i=1}^n}{\alpha }_i\left({\displaystyle \sum _{k=1}^n}{a}_{ik}{E}_{ik}\right)={\left[0\right]}_{n\times n}.$$

Since $\Gamma (\mathcal{E},B)$ is complete, then $a_{ik}\ne 0$ for any $i\ne k,i,k=\overline{1,n}.$ This implies that ${\alpha }_i=0$ for all $1\le i\le n.$ Hence, the set $\mathcal{A}$ contains linearly independent vectors.

(ii) Consider the equality

$${\alpha }_1{R}_{e_i}+{\displaystyle \sum _{k=2}^n}{\alpha }_k(R_{e_i}\circ R_{e_k})={\left[0\right]}_{n\times n}.$$

Then

$$\begin{array}{c}\hfill 〈a_{i1},a_{i2},\dots ,1,a_{ii+1},\dots ,a_{in}〉•〈{\mathbf{a}}_1^t,{\mathbf{a}}_2^t,\dots ,{\mathbf{a}}_n^t〉\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_n\end{array}\right]={\left[0\right]}_{n\times n},\end{array}$$

(8)

here, as before, ${\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_n$ are row vectors of the structural matrix A. Now,

$$〈a_{i1},a_{i2},\dots ,1,a_{ii+1},\dots ,a_{in}〉•〈{\mathbf{a}}_1^t,{\mathbf{a}}_2^t,\dots ,{\mathbf{a}}_n^t〉\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_n\end{array}\right]=A^{\prime }\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_n\end{array}\right]={\left[0\right]}_{n\times n}.$$

(9)

with $\det (A^{\prime })=(a_{i1}{a}_{i2}\dots 1a_{ii+1}\dots a_{in})\det (A)$. Since $\det (A)\ne 0$ and the attached graph is complete, we find $\det (A^{\prime })\ne 0.$ Hence, the only solution of the system Equation (9) is trivial. Therefore, the set $A^{(i)}\cup \left\{R_{e_i}\right\}$ contains linearly independent vectors.

(iii) Due to the fact $\det (A^{\prime })=(a_{i1}{a}_{i2}\dots 1a_{ii+1}\dots a_{in})\det (A)$ and from $\det (A)=0,$ one has that there is a non-trivial solution of (9). Hence, in this case the set $A^{(i)}\cup \left\{R_{e_i}\right\}$ contains linearly dependent vectors. This completes the proof. □

Theorem 7.

Let $M(\mathcal{E})$ be an associative enveloping algebra generated by an S-evolution algebra $\mathcal{E}$ whose attached graph $\Gamma (\mathcal{E},B)$ is complete. Then the following statements are true:

(i) 

if $\mathcal{E}$ is simple then

$$M(\mathcal{E})={\displaystyle \bigcup _{i=1}^n}\left(A^{(i)}\cup \left\{R_{e_i}\right\}\right),dim(M(\mathcal{E}))=\dim (\mathcal{E})\dim ({\mathcal{E}}^2)=n^2$$

(ii) 

if $\mathcal{E}$ is not simple and $\mathrm{rank}(A)=m.$ Then

$$M(\mathcal{E})={\displaystyle \bigcup _{i=1}^n}\left({\overline{A}}^{(i)}\cup \left\{R_{e_i}\right\}\right),dim(M(\mathcal{E}))=\dim (\mathcal{E})\dim ({\mathcal{E}}^2)=nm,$$

where ${\overline{A}}^{(i)}=A^{(i)}\ominus \{R_{e_i}\circ R_{e_{m+1}}\}$

Proof. 

By compiling Propositions 5 and 6, we get the assertion. □

Definition 8.

If a graph Γ has a vertex with no edges, then such vertex is called isolated.

Let us denote the set of isolated vertices by $\mathrm{iso}(V).$ It is obvious that in a complete graph $|\mathrm{iso}(V)|=0,$ where $|\mathrm{iso}(V)|$ is the number of isolated vertices in $\Gamma (\mathcal{E},B).$

Remark 6.

If $i\in \mathrm{iso}(V),$ then $R_{e_i}=0.$ Hence, $R_{e_i}\circ R_{e_j}=R_{e_j}\circ R_{e_i}=0$ for all $1\le j\le n.$

Corollary 4.

Let $M(\mathcal{E})$ be an associative enveloping algebra generated by an n-dimensional S-evolution algebra $\mathcal{E}$ with disconnected attached graph $\Gamma (\mathcal{E},B)=\Gamma ({\mathcal{E}}_1,B_1)\cup \Gamma ({\mathcal{E}}_2,B_2)$ where $\Gamma ({\mathcal{E}}_1,B_1)$ is complete and $\Gamma ({\mathcal{E}}_2,B_2)$ contains the isolated vertices. Then the following statements hold true:

(i) 

If ${\mathcal{E}}_1$ is simple then $dim(M(\mathcal{E}))=2\left|E\right|+\left|V\right|-|\mathrm{iso}(V)|,$ where $\left|E\right|$ is the number of edges in $\Gamma (\mathcal{E},B)$.

(ii) 

If ${\mathcal{E}}_1$ is not simple and $\mathrm{rank}(A)=m.$ Then $dim(M(\mathcal{E}))=m\left(\left|V\right|-|\mathrm{iso}(V)|\right).$

Proof. 

Note that

$$\mathrm{span}(\mathcal{A})=〈R_{e_i}:i\notin \mathrm{iso}(V)〉.$$

Then,

$$\dim (\mathrm{span}(\mathcal{A}))=\left|V\right|-|\mathrm{iso}(V)|.$$

Consider

$$E=\{(i,j):w(i,j)\ne 0\}.$$

It is clear that $R_{e_i}\circ R_{e_j}\in A^{(i)}$ if and only if $(i,j)\in E.$ Since the structural matrix is an S-matrix, then $(i,j)\in E$ if and only if $(j,i)\in E$. This implies that $R_{e_i}\circ R_{e_j}\in A^{(i)}$ if and only if $R_{e_j}\circ R_{e_i}\in A^{(j)}.$ Then $\dim (\mathrm{span}({\cup }_{i=1}^n{A}^{(i)}))=2\left|E\right|.$ Therefore, by Theorem 7

$$\dim (M(\mathcal{E}))=\dim (\mathrm{span}({\cup }_{i=1}^n{A}^{(i)}))+\dim (\mathrm{span}(\mathcal{A}))=2\left|E\right|+\left|V\right|-|\mathrm{iso}(V)|.$$

Next, if $\det (A)=0,$ and $\mathrm{rank}(A)=m.$ Then

$$\mathrm{span}(\mathcal{A})=〈R_{e_i}:i\notin \mathrm{iso}(V)〉.$$

Then,

$$\dim (\mathrm{span}(\mathcal{A}))=\left|V\right|-|\mathrm{iso}(V)|.$$

Note that

$$\dim \left(\mathrm{span}(\mathcal{A})\cap (\mathrm{span}({\cup }_{i=1}^n{A}^{(i)}))\right)=m.$$

However,

$$\dim \left(\mathrm{span}(\mathcal{A})\cap (\mathrm{span}({\cup }_{i=1}^n{\overline{A}}^{(i)}))\right)=0.$$

Now, after removing dependent vectors from the structural matrix A we have a new structural matrix say $A_{n\times m}^{\prime }$ where its attached graph has n vertices such that the first m vertices will joint $m-1$ vertices and the rest will join m vertices. Hence,

$$\dim (\mathrm{span}({\cup }_{i=1}^n{\overline{A}}^{(i)}))=(m-1)(|V|-|\mathrm{iso}(V)|).$$

Consequently,

$$\begin{array}{ccc}\hfill \dim (M(\mathcal{E}))& =& \dim (\mathrm{span}({\cup }_{i=1}^n{\overline{A}}^{(i)}))+\dim \left(\mathrm{span}(\mathcal{A})\right)\hfill \\ & =& (|V|-|\mathrm{iso}(V)|)(m-1)+\left|V\right|-|\mathrm{iso}(V)|\hfill \\ & =& m\left(\left|V\right|-|\mathrm{iso}(V)|\right)\hfill \end{array}$$

This completes the proof. □

Remark 7.

We point out that a table of multiplication of the enveloping algebra $M(\mathcal{E})$ is given as follows:

$$\left\{\begin{array}{cc}{R}_{e_i}\circ (R_{e_l}\circ R_{e_m})=\frac{a_{il}{a}_{lm}}{a_{im}}(R_{e_i}\circ R_{e_m})\hfill & ifi<l<m.\hfill \\ R_{e_i}\circ (R_{e_l}\circ R_{e_i})=a_{il}{f}_{il}(a_{il})R_{e_i}\hfill & ifi<l.\hfill \\ (R_{e_i}\circ R_{e_j})\circ (R_{e_l}\circ R_{e_m})=\frac{a_{ij}{a}_{jl}{a}_{lm}}{a_{im}}(R_{e_i}\circ R_{e_m})\hfill & ifi<j<l<m.\hfill \\ (R_{e_i}\circ R_{e_j})\circ (R_{e_l}\circ R_{e_i})=a_{ij}{a}_{jl}{f}_{il}(a_{il})R_{e_i}\hfill & ifi<j<l.\hfill \end{array}\right.$$

(10)

Theorem 8.

Let $M(\mathcal{E})$ be an associative enveloping algebra generated by an n-dimensional simple S-evolution algebra $\mathcal{E}$ whose attached graph $\Gamma (\mathcal{E},B)$ is complete. Then

$$M(\mathcal{E})=\mathrm{lin}\{E_{ij}:1\le i,j\le n\}.$$

Proof. 

Let us denote $\tilde{M}:=\mathrm{lin}\{E_{ij}:1\le i,j\le n\}.$ Then $dim(\tilde{M})=n^2.$ Due to $R_{e_i}\in \tilde{M}$ for any $i=\overline{1,n},$ we infer that $M(\mathcal{E})$ is a subalgebra of $\tilde{M}.$ Now, let us pick any arbitrary element of $\tilde{M}$ say $E_{pq},$ we have to show that $E_{pq}\in M(\mathcal{E}).$ Indeed, if we consider the following equality

$$E_{pq}={\alpha }_p{R}_{e_p}+{\displaystyle \sum _{k\ne p}^n}{\alpha }_k(R_{e_p}\circ R_{e_k}).$$

Then we have the following system of equations:

$$\begin{array}{c}\hfill 〈a_{i1},a_{i2},\dots ,1,a_{ii+1},\dots ,a_{in}〉·〈{\mathbf{a}}_1^t,{\mathbf{a}}_2^t,\dots ,{\mathbf{a}}_n^t〉\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_n\end{array}\right]=E_{pq}.\end{array}$$

(11)

Now,

$$〈a_{i1},a_{i2},\dots ,1,a_{ii+1},\dots ,a_{in}〉·〈{\mathbf{a}}_1^t,{\mathbf{a}}_2^t,\dots ,{\mathbf{a}}_n^t〉\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_n\end{array}\right]=A^{\prime }\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_n\end{array}\right]=E_{pq}.$$

(12)

with $\det (A^{\prime })=\left({\displaystyle {\displaystyle \prod _{j=1,j\ne p}^n}{a}_{pj}}\right)\det (A)$. Now the simplicity of $\mathcal{E}$ (as $\det (A)\ne 0$) implies $\det (A^{\prime })\ne 0.$ Hence, by the Gaussian elimination of system (12) we obtain a unique solution. Therefore, $E_{pq}\in M(\mathcal{E})$, so $\tilde{M}\subseteq M(\mathcal{E}).$ This completes the proof. □

Corollary 5.

Let $M(\mathcal{E})$ be an enveloping algebra generated by a simple S-evolution algebra $\mathcal{E}$ whose attached graph is complete, then $M(\mathcal{E})=M_n(\mathbb{C}).$

Let us consider the following example.

Example 6.

Let $\mathcal{E}$ be a two dimensional S-evolution algebra with the following matrix of structural constants.

$$\left(\begin{array}{cc}0& a\\ -a& 0\end{array}\right)$$

The table of multiplication of enveloping algebra $M(\mathcal{E})$ is given by

$$\left\{\begin{array}{c}{R}_{e_1}\circ R_{e_2}=-a^2{E}_{11}.\hfill \\ R_{e_2}\circ R_{e_1}=-a^2{E}_{22}\hfill \\ (R_{e_1}\circ R_{e_2})\circ R_{e_1}=-a^2{R}_{e_1}\hfill \\ (R_{e_2}\circ R_{e_1})\circ R_{e_2}=-a^2{R}_{e_2}\hfill \\ (R_{e_1}\circ R_{e_2})\circ (R_{e_1}\circ R_{e_2})=-a^3(R_{e_1}\circ R_{e_2})\hfill \\ (R_{e_2}\circ R_{e_1})\circ (R_{e_2}\circ R_{e_1})=-a^3(R_{e_2}\circ R_{e_1})\hfill \end{array}\right.$$

(13)

then the attached graph as follows:Then $\mathcal{A}=\{R_{e_1},R_{e_2}\},A^{(1)}=\left\{R_{e_1}\circ R_{e_2}\right\},$ and $A^{(2)}=\left\{R_{e_2}\circ R_{e_1}\right\}$

$$M(\mathcal{E})=\mathrm{lin}〈\left\{\left(\begin{array}{cc}-a& 0\\ 0& 0\end{array}\right),\left(\begin{array}{cc}0& 0\\ 0& a\end{array}\right),\left(\begin{array}{cc}0& a\\ 0& 0\end{array}\right),\left(\begin{array}{cc}0& 0\\ -a& 0\end{array}\right)\right\}〉$$

with $\dim (M(\mathcal{E}))=2(1)+2=4.$ Furthermore, this algebra is simple.

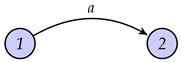Example 7.

Let $\mathcal{E}$ be a three dimensional S-evolution algebra with the following structural matrix:

$$\left(\begin{array}{ccc}0& a& 0\\ -a& 0& 0\\ 0& 0& 0\end{array}\right)$$

$$\left\{\begin{array}{c}{R}_{e_1}\circ R_{e_2}=-a^2{E}_{11}.\hfill \\ R_{e_2}\circ R_{e_1}=-a^2{E}_{22}\hfill \\ (R_{e_1}\circ R_{e_2})\circ R_{e_1}=-a^2{R}_{e_1}\hfill \\ (R_{e_2}\circ R_{e_1})\circ R_{e_2}=-a^2{R}_{e_2}\hfill \\ (R_{e_1}\circ R_{e_2})\circ (R_{e_1}\circ R_{e_2})=-a^3(R_{e_1}\circ R_{e_2})\hfill \\ (R_{e_2}\circ R_{e_1})\circ (R_{e_2}\circ R_{e_1})=-a^3(R_{e_2}\circ R_{e_1})\hfill \end{array}\right.$$

(14)

then the attached graph is:In this example, we have $|\mathrm{iso}(V)|=1,$ and $\left|V\right|=3$ then $\dim (M(\mathcal{E}))=2\left(3-1\right)=4.$ Furthermore, this algebra is neither simple nor semisimple.

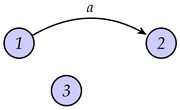Theorem 9

([47]). Every finite-dimensional simple algebra over $\mathbb{C}$ is isomorphic to $M_n(\mathbb{C}).$

Theorem 10.

Let $\mathcal{E}$ be an n-dimensional S-evolution algebra $\mathcal{E},$ whose attached graph $\Gamma (\mathcal{E},B)$ is complete. Then $\mathcal{E}$ is simple if and only if $M(\mathcal{E})$ is simple.

Proof. 

Let I be an ideal of $M(\mathcal{E})$ such the $I\ne \left\{0\right\}.$ We notice that one dimensional subalgebras $\langle R_{e_i}\rangle$ and $\langle R_{e_l}\circ R_{e_m}\rangle$ (for some $1\le i,m,l\le n$) are not ideals. As $R_{e_i}I\subseteq I,$ then any ideal of $M(\mathcal{E})$ should contain $R_{e_i}$ for some $1\le i\le n.$ This implies that the subalgebras $R_{e_i}M(\mathcal{E})$ and $M(\mathcal{E})R_{e_i}$ are contained in I. For fixed $i,$ let

$$K_i:=\langle R_{e_i},R_{e_i}\circ R_{e_{\ell }},R_{e_l}\circ R_{e_i}:\ell =1,\dots ,n,\ell \ne i\rangle .$$

It is easy to check that $K_i$ contains $R_{e_i}M(\mathcal{E})$ and $M(\mathcal{E})R_{e_i}$. Moreover,

$$dim(K_i)=\frac{\dim (\mathcal{E})\dim ({\mathcal{E}}^2)}{2}-1.$$

Since $R_{e_l}\circ R_{e_i}\in I,$ for all $1\le l\ne i\le n,$ then $(R_{e_l}\circ R_{e_i})M(\mathcal{E})$ is a sub-algebra. Let

$$K_l=\langle (R_{e_l}\circ R_{e_i})M(\mathcal{E})\rangle \ominus \langle R_{e_l}\circ R_{e_i}\rangle =\langle R_{e_l},R_{e_l}\circ R_{e_p}:p\ne i\rangle ,$$

where ⊖ stand for removing the subalgebra $\langle R_{e_l}\circ R_{e_i}\rangle$ from $K_l$. Note that $K_l$ is a sub-algebra. Moreover,

$${\displaystyle \bigcap _{l=1,\ne i}^n}{K}_l=\left\{0\right\}.$$

Assume that

$$N:={\displaystyle \bigcup _{l=1,\ne i}^n}{K}_l.$$

Then $dim(N)=\frac{\dim (\mathcal{E})\dim ({\mathcal{E}}^2)}{2}+1.$ Moreover, $N\cap K_i=\left\{0\right\}.$ Then

$$dim(K_i\cup N)=\frac{\dim (\mathcal{E})\dim ({\mathcal{E}}^2)}{2}-1+\frac{\dim (\mathcal{E})\dim ({\mathcal{E}}^2)}{2}+1=\dim (\mathcal{E})\dim ({\mathcal{E}}^2).$$

However, $K_i\cup N\subseteq I,$ then $dim(I)=\dim (\mathcal{E})\dim ({\mathcal{E}}^2)=dim(M(\mathcal{E})).$ Hence, $I=M(\mathcal{E}).$ This implies that $M(\mathcal{E})$ is simple.

Conversely, let us assume that $M(\mathcal{E})$ is simple, then by Theorem 8, we have $M(\mathcal{E})=\mathrm{Span}\{E_{ij}:1\le i,j\le n\}.$ Hence, for any $E_{pq}\in M(\mathcal{E})$ again by the proof of Theorem 8, one has

$$A^{\prime }\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_n\end{array}\right]=E_{pq}.$$

Then, $\det (A^{\prime })\ne 0$ but $\det (A^{\prime })=\left({\displaystyle {\displaystyle \prod _{j=1,j\ne p}^n}{a}_{pj}}\right)\det (A),$ as $\mathcal{E}$ has complete attached graph, so $\det (A)\ne 0.$ Therefore, Theorem 3 implies that $\mathcal{E}$ is simple. This completes the proof. □

Corollary 6.

If $M(\mathcal{E})$ is an enveloping algebra generated by an n-dimensional not simple S-evolution algebra, then $M(\mathcal{E})$ is not simple.

Proof. 

Since $\mathcal{E}$ is not simple and $\dim (M(\mathcal{E}))=nm,$ then $M(\mathcal{E})\ncong M_n(\mathbb{C}).$ Hence, by Theorem 9, we have $M(\mathcal{E})$ is not simple. □

Corollary 7.

Let ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$ be two n-dimensional simple S-evolution algebras, whose attached graphs are complete. Then $M({\mathcal{E}}_1)\cong M({\mathcal{E}}_2).$

Proof. 

As ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$ are simple. Hence, by Theorems 9 and 10, one gets $M({\mathcal{E}}_1)\cong M_n(\mathbb{C})$, $M({\mathcal{E}}_2)\cong M_n(\mathbb{C})$, so $M({\mathcal{E}}_1)\cong M({\mathcal{E}}_2).$ □

From the above corollary, we infer that if the attached graphs of two simple S-evolution algebras are complete, then the corresponding enveloping algebras are isomorphic. However, the corollary does not give an explicit isomorphism. Therefore, it will be interesting to find an explicit construction of the isomorphism. However, the job of finding explicit isomorphism between two enveloping algebra is tricky. In the next result, it turns out that such an isomorphism can be constructed explicitly for Lotka–Volterra evolution algebras.

Theorem 11.

Let ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$ be Lotka–Volterra evolution algebras whose attached graphs are complete. If ${\mathcal{E}}_1\cong {\mathcal{E}}_2$, then $M({\mathcal{E}}_1)\cong M({\mathcal{E}}_2).$ Moreover, the isomorphism can be explicitly constructed.

Proof. 

Let $M({\mathcal{E}}_1)=\langle R_{e_i}\circ R_{e_j},R_{e_i}:1\le i\ne j\le n\rangle ,$ and $M({\mathcal{E}}_2)=\langle R_{f_i}\circ R_{f_j},R_{f_i}:1\le i\ne j\le n\rangle .$ Define a mapping $\psi :M({\mathcal{E}}_1)\to M({\mathcal{E}}_2)$ by

$$\psi (R_{e_i})=R_{f_i}\mathrm{and}\psi (R_{e_i}\circ R_{e_j})=R_{f_i}\circ R_{f_j}.$$

Let us check that $\psi$ is a homomorphism. Indeed,

$$\psi (R_{e_i}\circ (R_{e_i}\circ R_{e_j}))=\psi \left(\frac{a_{il}{a}_{lm}}{a_{im}}(R_{e_i}\circ R_{e_m})\right)=\frac{a_{il}{a}_{lm}}{a_{im}}\left(R_{f_i}\circ R_{f_m}\right).$$

On the other hand,

$$\psi (R_{e_i})\circ \psi (R_{e_i}\circ R_{e_j})=R_{f_i}\circ (R_{f_l}\circ R_{f_m})=\frac{b_{il}{b}_{lm}}{b_{im}}\left(R_{f_i}\circ R_{f_m}\right).$$

Due to ${\mathcal{E}}_1\cong {\mathcal{E}}_2,$ by Theorem 5 we have $\frac{a_{il}{a}_{lm}}{a_{im}}=\frac{b_{il}{b}_{lm}}{b_{im}}.$ Hence,

$$\psi (R_{e_i}\circ (R_{e_i}\circ R_{e_j}))=\psi (R_{e_i})\circ \psi (R_{e_i}\circ R_{e_j})).$$

The equality of other elements in the table of multiplication are proceeded by the same way. Thus, $\psi$ is an algebra homomorphism from $M({\mathcal{E}}_1)$ into $M({\mathcal{E}}_2)$. Moreover, $ker(\psi )=\left\{0\right\}.$ This implies that the mapping $\psi$ is an isomorphism. □

Remark 8.

The converse of Theorem 11 is not true, i.e., if two S-evolution algebras are not isomorphic then their corresponding enveloping algebras could be isomorphic.

Example 8.

Let ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$ be two three dimensional S-evolution algebras with the following structural matrices:

$$\left(\begin{array}{ccc}0& 1& -2\\ -2& 0& 1\\ 2& -1& 0\end{array}\right),\left(\begin{array}{ccc}0& 1& -1\\ 1& 0& -1\\ 1& 1& 0\end{array}\right)$$

respectively. Then by Theorem 6, these algebras are not isomorphic. Since ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$ have complete attached graphs, and their determinates are not zero then Theorem 10 implies the corresponding enveloping algebras $M({\mathcal{E}}_1)$ and $M({\mathcal{E}}_2)$ are simple, then by Theorem 9, we have $M({\mathcal{E}}_1)\cong M({\mathcal{E}}_2).$

Theorem 12.

Any non-trivial finite dimensional S-evolution algebra $\mathcal{E}$ is semisimple if and only if its enveloping algebra $M(\mathcal{E})$ is semisimple.

Proof. 

Assume that $\mathcal{E}$ is semisimple, then by Theorem 4, its attached graph $\Gamma (\mathcal{E},B)$ is disconnected. Therefore, $\Gamma (\mathcal{E},B)={\displaystyle {\displaystyle \underset{i=1}{\overset{n}{\cup }}}}{\Gamma }_i,$ then by Proposition 3 each ${\Gamma }_i$ corresponds to a simple ideal, say $I_{{\Gamma }_i}.$ Due to the semisimplicity of $\mathcal{E}$ one has $\mathcal{E}={\displaystyle {\displaystyle \underset{i=1}{\overset{n}{\oplus }}}}{I}_{{\Gamma }_i}.$ Define

$$M({\mathcal{E}}_{I_{{\Gamma }_i}})=\{R_{e_k}:e_k\in I_{{\Gamma }_i}\}\cup \{R_{e_k}\circ R_{e_l}:e_l,e_k\in I_{{\Gamma }_i}\}.$$

We claim that $M({\mathcal{E}}_{I_{{\Gamma }_i}})$ is a proper simple ideal of $M(\mathcal{E}).$ First observe that $M^2({\mathcal{E}}_{I_{{\Gamma }_i}})\subseteq M({\mathcal{E}}_{I_{{\Gamma }_i}}).$ On the other hand, for any $e_p\notin I_{{\Gamma }_i},$ then by Theorem 4, we have $e_p{e}_k=0$ for any $e_k\in I_{{\Gamma }_i}.$ Consequently, $R_{e_p}M({\mathcal{E}}_{I_{{\Gamma }_i}})=0.$ Hence, $M({\mathcal{E}}_{I_{{\Gamma }_i}})$ is a proper simple ideal of $M(\mathcal{E})$, then $M(\mathcal{E})={\displaystyle {\displaystyle \underset{i=1}{\overset{n}{\oplus }}}}M({\mathcal{E}}_{I_{{\Gamma }_i}}).$ Thus, $M(\mathcal{E})$ is semisimple.

Conversely, assume that $M(\mathcal{E})$ is semisimple, then there exists a non-trivial proper ideal I of $M(\mathcal{E}).$ On the contrary, suppose that $\mathcal{E}$ is not semisimple, then by Theorem 4 $\Gamma (\mathcal{E},B)$ is connected. Hence, $dim(M(\mathcal{E}))=2\left|E\right|+n.$ Due to the connectivity of $\Gamma (\mathcal{E},B)$, then there is a path between any two different vertices. Fix $R_{e_i}\in I,$ then we have a non-zero element $R_{e_i}\circ R_{e_j},R_{e_j}\circ R_{e_i}\in I.$ Additionally, connectivity allows the existence of a cycle path, which means that there is a non-zero element, say $R_{e_k}\circ R_{e_l}\circ \dots \circ R_{e_k}=\alpha R_{e_k}\in I.$ This implies that $R_{e_k}\in I$ for all $1\le k\le n.$ Therefore, $dim(I)=2\left|E\right|+n=dim(M(\mathcal{E}))$ which contradicts to the simisimplicity of $M(\mathcal{E}).$ Thus, $\mathcal{E}$ is semisimple. □

Remark 9.

We emphasize that the above theorem is not valid for general evolution algebras, i.e., if an evolution algebra is semisimple then the corresponding enveloping algebra may not be semisimple. The following example ensures this fact.

Example 9.

Let $\mathcal{E}$ be an evolution algebra, with the following matrix of structural constant:

$$\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$$

It clear that $\mathcal{E}=\langle e_1\rangle \oplus \langle e_2\rangle ,$ where $\langle e_1\rangle ,\langle e_2\rangle$ are ideals of $\mathcal{E}.$ The corresponding enveloping algebra $M(\mathcal{E})=alg\langle R_{e_1},R_{e_2},R_{e_1}\circ R_{e_2},R_{e_2}\circ R_{e_1}\rangle$ which is simple.

5. $\mathcal{E}$-Linear Derivation of Enveloping Algebras Generated by S-Evolution Algebras

In this section, we are going to describe $\mathcal{E}$-linear derivations of enveloping algebras generated by S-evolution algebras.

Definition 9.

A linear mapping $\Delta :M(\mathcal{E})\to M(\mathcal{E})$ is called $\mathcal{E}$-linear if

$$\begin{array}{c}\hfill \Delta (R_{e_i})={\displaystyle \sum _{k=1}^n}{d}_{ik}{R}_{e_k},1\le i\le n.\end{array}$$

(15)

for some matrix $(d_{ik})$.

Definition 10.

A derivation Δ of $M(\mathcal{E})$ is called $\mathcal{E}$-derivation if Δ is $\mathcal{E}$-linear.

By $D_{M(\mathcal{E})}$ we denote the set of all $\mathcal{E}$-derivations of $M(\mathcal{E})$.

Theorem 13.

Let $M(\mathcal{E})$ be enveloping algebra generated by $\mathcal{E}$ whose attached graph is complete. Then the following assertions hold true:

(i) 

If $n=2,$ then

$$D_{M(\mathcal{E})}=\left\{\left(\begin{array}{cc}\alpha & 0\\ 0& -\alpha \end{array}\right):\alpha \in \mathbb{C}\right\}$$

(ii) 

If $n\ge 3,$ then $D_{M(\mathcal{E})}=\left\{0\right\}$, i.e., any $\mathcal{E}$-derivation is trivial.

Proof. (i) Assume that $n=2,$ then the structural matrix of $\mathcal{E}$ is given by

$$\left(\begin{array}{cc}0& a\\ f(a)& 0\end{array}\right).$$

Note that the attached graph is complete, therefore, $a\ne 0.$ Since $\Delta$ is $\mathcal{E}-$ linear, then

$$\Delta (R_{e_i}\circ R_{e_i})=\Delta (R_{e_i})\circ R_{e_i}+R_{e_i}\circ \Delta (R_{e_i})=d_{ij}(R_{e_j}\circ R_{e_i})+d_{ij}(R_{e_i}\circ R_{e_j})=0.$$

Since $R_{e_i}\circ R_{e_j},R_{e_j}\circ R_{e_i}$ are linearly independent, we have $d_{ij}=0,\mathrm{for} \mathrm{any}1\le i\ne j\le 2.$ Consequently,

$$\Delta (R_{e_i}\circ R_{e_j})=(d_{ii}+d_{jj})(R_{e_i}\circ R_{e_j}).$$

Next,

$$\Delta (R_{e_i}\circ R_{e_j}\circ R_{e_i})=\Delta (af(a)R_{e_i}).$$

Then

$$af(a)(d_{ii}+d_{jj})R_{e_i}+af(a)d_{ii}{R}_{e_i}=af(a)d_{ii}{R}_{e_i}.$$

So, one has $d_{ii}=-d_{jj}.$ This completes prove of $(i).$

(ii) Assume that $n\ge 3,$ for fixed i we have

$$\Delta (R_{e_i}\circ R_{e_i})={\displaystyle \sum _{i\ne j=1}^n}{d}_{ij}(R_{e_j}\circ R_{e_i})+{\displaystyle \sum _{i\ne j=1}^n}{d}_{ij}(R_{e_i}\circ R_{e_j})=0$$

Since the set $\left\{R_{e_i}\circ R_{e_j}\right\}$ and the set $\{R_{e_j}\circ R_{e_i}\}$ are linearly independent for any $1\le i\ne j\le n,$ then $d_{ij}=0.$ So,

$$D_{M(\mathcal{E})}\subseteq diag\{d_{ii}:1\le i\le n\}.$$

Now, consider

$$\Delta ((R_{e_i}\circ R_{e_j})\circ R_{e_i})=a_{ij}{f}_{ij}(a_{ij})(d_{ii}+d_{jj})R_{e_i}+a_{ij}{f}_{ij}(a_{ij})d_{ii}.$$

One the other hand,

$$\Delta ((R_{e_i}\circ R_{e_j})\circ R_{e_i})=a_{ij}{f}_{ij}(a_{ij})\Delta (R_{e_i})=a_{ij}{f}_{ij}(a_{ij})d_{ii}.$$

Since the attached graph is complete, then $f_{ij}(a_{ij})a_{ij}\ne 0,$ for any $1\le i\ne j\le n.$ Hence, $d_{ii}=-d_{jj}.$ This implies

$$D_{M(\mathcal{E})}\subseteq diag\{-d_{ii}:1\le i\le n\}.$$

Therefore,

$$D_{M(\mathcal{E})}\subseteq diag\{d_{ii}:1\le i\le n\}\cap diag\{-d_{ii}:1\le i\le n\}=\left\{0\right\}.$$

This completes the proof. □

In [30] we have established the following result.

Theorem 14

([30]). Let $\mathcal{E}$ be a Lotka–Volterra evolution algebra whose associated graph is complete. Then any derivation of $\mathcal{E}$ is trivial.

Theorem 15.

Let $M(\mathcal{E})$ be an enveloping algebra generated by an n-dimensional S-evolution algebra $\mathcal{E}$ whose attached graph is $\Gamma =H_1\cup H_2$ where $H_1$ is complete graph and $H_2$ contains all isolated vertices, and $|H_2|=k$. Then any $\mathcal{E}$-linear derivation of $M(\mathcal{E})$ has the following form

$$\left(\begin{array}{cc}{(\mathbf{0})}_{n-k\times n-k}& {(\mathbf{0})}_{n-k\times k}\\ {(\mathbf{0})}_{k\times n-k}& \left(\begin{array}{ccc}{d}_{k,k}& \dots & d_{k,n}\\ ⋮& \ddots & ⋮\\ d_{n,k}& \dots & d_{n,n}\end{array}\right)\end{array}\right)$$

Proof. 

From $\Delta (R_{e_i}\circ R_{e_i})=\Delta (R_{e_i})R_{e_i}+R_{e_i}\Delta (R_{e_i})$, due to the $\mathcal{E}$-linearity of $\Delta ,$ we have

$$\Delta (R_{e_i}\circ R_{e_i})={\displaystyle \sum _{i\ne j=1}^{k-1}}{d}_{ij}(R_{e_j}\circ R_{e_i})+{\displaystyle \sum _{i\ne j=1}^{k-1}}{d}_{ij}(R_{e_i}\circ R_{e_j})=0.$$

Since the set $\left\{R_{e_i}\circ R_{e_j}\right\},$ and the set $\{R_{e_j}\circ R_{e_i}\}$ are linearly independent for all $j\ne i,$ then $d_{ij}=0$ for all $1\le j\ne i\le k-1.$ Next, act $\Delta$ on the basis $R_{e_i}\circ R_{e_j},$ as

$$\Delta (R_{e_i}\circ R_{e_j})=(d_{ii}+d_{jj})(R_{e_i}\circ R_{e_j}).$$

Therefore,

$$\Delta ((R_{e_i}\circ R_{e_j})\circ R_{e_i})=-(2d_{ii}+d_{jj})R_{e_i}.$$

On the other hand, one has

$$\Delta ((R_{e_i}\circ R_{e_j})\circ R_{e_i})=-\Delta (R_{e_i})=-d_{ii}{R}_{e_i}+d_{ik}{R}_{e_k}+\dots +d_{in}{R}_{e_n}.$$

Comparing both sides, we obtain $d_{ik}=\dots =d_{in}=0,$ and $d_{ii}=-d_{jj},$ for any $1\le i\le k-1$. Since $(R_{e_i}\circ R_{e_j})\circ (R_{e_i}\circ R_{e_j})=a_{ij}{f}_{ij}(a_{ij})a_{ij}(R_{e_i}\circ R_{e_j})$, and applying $\Delta$ for both sides, one gets $d_{ii}=d_{jj}=0,$ for any $1\le i\le k-1.$ Finally, let $1\le m_0\le k-1$ and $k\le l_0\le n,$ then it is clear that $R_{e_{m_0}}\circ R_{e_{l_0}}=0.$ Consider $\Delta (R_{e_{m_0}}\circ R_{e_{l_0}})=R_{e_{m_0}}\Delta (R_{e_{l_0}})=0.$ This implies that $d_{l_{0}p}=0,$ for all $1\le p\le l_0-1.$ This completes the proof. □

Remark 10.

We point out that Theorem 13 is a particular case of Theorem 15 when $H_2$ is empty.

6. $\mathcal{E}$-Linear Derivation of Enveloping Algebras Generated by Three Dimensional S-Evolution Algebras

In this section we are going to fully describe all possible $\mathcal{E}$-linear derivations of enveloping algebras generated by three dimensional S-evolution algebras.

The possible graphs of three dimension non-isomorphic S-evolution algebras are the following ones

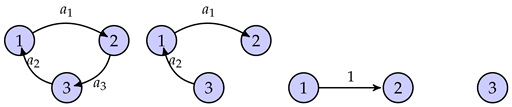Theorem 16.

Let $M(\mathcal{E})$ be an enveloping algebra generated by three dimensional S-evolution algebra $\mathcal{E},$ then the following statements hold true:

(i) 

If the attached graph is a complete, then any $\mathcal{E}$-linear derivation is trivial.

(ii) 

If the attached graph is disconnected, then any $\mathcal{E}$-linear derivation has the following form

$$D_{M(\mathcal{E})}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& d_{33}\end{array}\right).$$

(iii) 

If the attached graph is connected, but not complete, then any $\mathcal{E}$-linear derivation has the following form

$$D_{M(\mathcal{E})}=\left(\begin{array}{ccc}\alpha & 0& 0\\ 0& -\alpha & 0\\ 0& 0& -\alpha \end{array}\right)$$

Proof. (i) Since the graph is complete, then by Theorem 13 any $\mathcal{E}$-derivation of corresponding enveloping algebra is trivial. The attached graph of (ii) can be represent as $H_1\cup H_2,$ where $H_1$ is $K_2$ and $H_2$ is a graph containing the isolated vertex $e_3.$ Then by Theorem 15 the derivation in this case has the following form

$$D_{M(\mathcal{E})}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& d_{33}\end{array}\right).$$

Therefore, the only case left to prove is (iii), when the enveloping algebra generated by S-evolution algebra whose attached graph has no isolated vertex. Without lost of generality, we may assume that the structural matrix constant has the following form:

$$A_{\mathcal{E}}=\left(\begin{array}{ccc}0& a& b\\ f(a)& 0& 0\\ g(b)& 0& 0\end{array}\right)$$

Acting $\Delta$ on $R_{e_1}^2,$ yields that $d_{12}=d_{13}=0.$ Doing the same job for $R_{e_2}^2$ and $R_{e_3}^2$, one finds $d_{21}=d_{31}=d_{23}=d_{32}=0.$ Next, consider

$$\Delta (R_{e_1}\circ R_{e_2})=(d_{11}+d_{22})(R_{e_1}\circ R_{e_2})$$

and

$$\Delta (R_{e_1}\circ R_{e_3})=(d_{11}+d_{33})(R_{e_1}\circ R_{e_3}).$$

Therefore, applying $\Delta$ to $R_{e_1}\circ (R_{e_2}\circ R_{e_1}),$ we obtain

$$af(a)(d_{11}+d_{22})=0.$$

By the same argument, applying $\Delta$ to $R_{e_1}\circ (R_{e_3}\circ R_{e_1}),$ one gets

$$bg(b)(d_{11}+d_{33})=0.$$

Finally, from $\Delta (R_{e_2}\circ (R_{e_1}\circ R_{e_2})),$ and $\Delta (R_{e_3}\circ (R_{e_1}\circ R_{e_3})),$ we get $d_{11}+d_{22}=d_{11}+d_{33}=0.$ These imply that $d_{22}=d_{33}=-d_{11}$ which completes the proof. □

Remark 11.

From the proved theorem and ([30], Theorem 7.5), we infer that any derivation of Lotka–Volterra evolution algebra $\mathcal{E}$ can be extend to $\mathcal{E}$-linear derivation of enveloping algebra for the cases (i) and (ii), but it is not extendible for the case (iii).

Remark 12.

Here, we should point out that to describe derivations when $n>3$ is a tricky job, due to many cases and sub-cases of attached graphs will appear. Hence, we have demonstrated even in dimension 3, there are non-trivial derivations.

7. Conclusions

The main aim of this work was to introduce S-evolution algebra and discuss its solvability, simplicity, and semisimplicity. We have proved that such kind of algebras are not solvable, hence are not nilpotent. Moreover, we have demonstrated that if S-evolution algebras is simple, then the attached graph is connected. If S-evolution algebra is semisimple, then the attached graph is disconnected; this result motivates us to study when two S-evolution algebras are isomorphic. The second main aim was to study the enveloping algebras generated by S-evolution algebras, whose attached graph are complete. The main result in this direction was $\mathcal{E}$ is simple if and only if $M(\mathcal{E})$ is simple. However, in the case of $\mathcal{E}$ is semisimple, then $M(\mathcal{E})$ is semisimple, but the converse is not valid, and the counter-example has been introduced. Finally, the concept of $\mathcal{E}$-linear derivation has been introduced and proved such derivations can be extended to their enveloping algebra under certain conditions.