Abstract
This paper presents the application of three optimization algorithms to increase the chaotic behavior of the fractional order chaotic Chen system. This is achieved by optimizing the maximum Lyapunov exponent (MLE). The applied optimization techniques are evolutionary algorithms (EAs), namely: differential evolution (DE), particle swarm optimization (PSO), and invasive weed optimization (IWO). In each algorithm, the optimization process is performed using 100 individuals and generations from 50 to 500, with a step of 50, which makes a total of ten independent runs. The results show that the optimized fractional order chaotic Chen systems have higher maximum Lyapunov exponents than the non-optimized system, with the DE giving the highest MLE. Additionally, the results indicate that the chaotic behavior of the fractional order Chen system is multifaceted with respect to the parameter and fractional order values. The dynamical behavior and complexity of the optimized systems are verified using properties, such as bifurcation, LE spectrum, equilibrium point, eigenvalue, and sample entropy. Moreover, the optimized systems are compared with a hyper-chaotic Chen system on the basis of their prediction times. The results show that the optimized systems have a shorter prediction time than the hyper-chaotic system. The optimized results are suitable for developing a secure communication system and a random number generator. Finally, the Halstead parameters measure the complexity of the three optimization algorithms that were implemented in MATLAB. The results reveal that the invasive weed optimization has the simplest implementation.
1. Introduction
The nonlinear dynamical system is a branch in science, especially physics and mathematics, which is fundamental in the modelling of physical systems. Because of groudbreaking researches by pinoneering scientists in nonlinear dynamical system, a concept called chaos theory has emerged and, in the last few decades, the subject of chaos has attracted great interest from researchers. Initial studies on chaos have shown that the phenomenon has some unique properties in terms of sensitivity to initial conditions, complexity, ergodicity, transitivity, and determinism, which have been exploited in crucial areas, such as telecommunication [1,2,3], robotics [4,5,6], medicine [7,8,9], and so on. Therefore, investigations have led to the development of many chaotic systems, and there are several activities in areas, such as electronic realization, stability, synchronization, and chaos-based communication [10,11,12].
The level of unpredictability is of great importance in chaotic oscillators [13], which can be measured by computing the Lyapunov exponents (LEs) [14,15,16]. The LE is a quantity that measures the average rate of divergence or convergence of nearby trajectories in phase space. The number of state variables in a chaotic system determines the number of LEs that it possesses. For chaos to exist, at least one of the LEs must be positive. The largest positive LE is often called a Maximum Lyapunov exponent (MLE) and, the higher the MLE, the more chaotic the oscillator is.
However, there are not many researches in the literature regarding optimizing the MLE of chaotic oscillators. In the articles that are listed in [13,17,18,19], evolutionary algorithms (EAs) were used for global optimization of the MLE. In [13], the authors were able to maximize the MLE of multi-scroll chaotic oscillator based on saturated nonlinear function (SNLF) series (two to nine scrolls) by using differential evolution. Feasible solutions were found for the coefficients of the equations describing the SNLF-based oscillator. These optimized solutions produced higher MLEs than their original values. The work in [17] shows the comparison of the differential evolution and particle swarm optimization algorithms used to maximize the MLE of a multi-scroll chaotic oscillator that is based on SNLF series, from two to six scrolls. Although both algorithms gave similar results in terms of the optimized MLEs and execution times, it was discovered that the chaotic behavior is multimodal, in that different coefficient values maximized the MLEs. Additionally, differential evolution was applied in [18] and compared with a simple genetic algorithm to maximize the MLE of a 4-scroll chaotic oscillator of SNLF type. Differential evolution produced a slightly higher optimized MLE than the genetic algorithm. A multi-objective problem was solved in [19] by applying a non-dominated sorting genetic algorithm to simultaneously maximize the MLE and minimize the dispersion of the phase space portrait (PSP) of two multi-scroll chaotic oscillators based on piecewise-linear functions (PWLs), namely: SNLF and Chua’s diode (two to six scrolls were considered). In each case, the final chosen solutions were selected on the Pareto front, where the two objectives were traded. Because the two objectives are in conflict, the highest MLE (HMLE) could not be selected as the chosen solution. The investigations that are described above show the effectiveness of EAs in optimizing the dynamical behavior of integer order multi-scroll chaotic systems. Additionally, in a related investigation presented in [20], the authors proposed a two-dimensional (2D) modular chaotification system (2D-MCS) to improve the chaos complexity of any 2D chaotic map. The proposed system was applied to improve the complexity of chaos in Hénon Map, Zeraoulia-Sprott Map, and Duffing Map. The quantitative evaluation of the chaotic behaviors of the chaotic maps after the application of the 2D-MCS revealed improved complexity in the generated chaos. Likewise, in [21], time-delay linear feedback was combined with parameter perturbation to improve the complexity of a 1D logistic map and 2D Baker map, and was verified by numerical experiments. As a matter of fact, more effort is needed to optimize the MLE of other chaotic oscillators, especially of the recent ones having a fractional order, in order to guarantee the more chaotic regime in them.
Fractional calculus is a mathematical subject that has been widely applied in engineering and physics for centuries [22,23]. For instance, it is customary to describe physical systems or phenomena by fractional order differential equations. Many systems in aerodynamics, mechatronics, electrical circuits, biology, fluid flows, chemistry, electromagnetic waves, dielectric polarization, and many more are modeled as fractional order systems [24,25,26,27,28]. In this manner, fractional order chaotic systems have been investigated in recent times [29,30,31,32,33]. In [29], fractional order tangent systems were introduced to detect chaos in a fractional order simplified Lorenz system and fractional order Hénon map. A novel fuzzy-adaptive controller was applied in [30] to achieve a generalized projective synchronization of two incommensurate fractional modified coupled dynamic systems. The work in [31] was done to study the dynamical behavior and synchronization of a fractional order Genesio–Tesi system. The dynamics of the system was analyzed by LEs while synchronization was achieved by active control and sliding mode control. In [32], an active control technique was applied to stabilize the unstable equilibria of discontinuous fractional order Shimizu–Morioka system, while the dynamical behavior of a new hyperchaotic fractional order Rabinovich system was studied in [33].
Moreover, some more recent works on fractional order chaotic systems, their applications, and implementations are contained in [34,35,36,37,38,39,40]. The authors in [34] presented an analog approach towards implementing the fractional order derivates of a chaotic system, utilizing amplifiers and other passive circuit elements. In addition, the analog method includes the use of field-programmable analog arrays (FPAAs) to minimize the mismatch that may arise when using discrete devices. The work presented in [35] shows the application of a fractional order chaotic oscillator for secure communication systems based on the synchronization of two fractional order chaotic systems in a master–slave configuration. The secure communication system was applied to encrypt RGB and grayscale images. The work further shows fractional order chaotic systems as reliable for implementing random number generators for cryptographic applications. The authors presented the experimental field-programmable gate arrays (FPGAs) realization of four different fractional order chaotic systems in [36]. In the work, the Grünwald–Letnikov (GL) method was applied to solve the fractional order derivatives, while, in [37], the authors presented a work on numerical analysis of the Chen oscillator, whereby the computation of the LEs was a part of the results. The authors introduced an encryption, compression, and transmission scheme in [38], based on a fractional order chaotic system in conjunction with discrete wavelet transform (DWT) and quadrature phase shift keying (QPSK). The encrypted image file was wirelessly transmitted through a very small distance (7 cm). A novel multistable fractional order chaotic system, having an unstable equilibrium point of self-excited attractor and hidden attractors with no equilibrium point, was proposed in [39] with its digital signal processor (DSP) implementation, while the synchronization of two variable fractional orders chaotic systems using fuzzy modeling were considered in [40] with application in secure communications. In [41], the authors included a work on the optimization of the positive LE and Kaplan–Yorke Dimension of fractional order chaotic systems by differential evolution and particle swarm optimization. Here, the fractional order was fixed, while the system parameter values were varied within the search space, looking for the combination of values that increase MLE. This is probably the first attempt in this regard, because a rigorous search of the literature did not yield other works.
In the present investigation, the fractional order Chen system is considered with the primary objective of maximizing its MLE using EAs [42,43,44]. This effort will add to the pool of literatures that are available in the research area of optimizing the MLEs of fractional order chaotic systems. Specifically, the global optimization procedure presented in this work employs meta-heuristics to search for the values of the system parameters and fractional order that maximize the MLE. The dynamic properties and complexity of the optimized fractional order Chen chaotic system are theoretically and numerically verified. Bifurcation, LE spectrum, equilibrium point, eigenvalue, and sample entropy are the properties considered. The behavior of a system can change dramatically with a change in the values of its parameters. This is called bifurcation. The parameter values at which these changes occur are called bifurcation points. The spectrum of the LEs is a set of real numbers that are sorted in non-increasing order and equal to the dimension of the phase space. Knowledge of the complete LE spectrum gives more detailed analysis of a dynamical system. Geometrically, the equilibria are points in a system’s phase space that are calculated by solving the function . The stability of a dynamical system can be verified through the evaluation of the eigenvalues of the system. For instance, a saddle point is an equilibrium point in which at least one eigenvalue is located in the stable region and one eigenvalue is in the unstable region. An index 1 saddle point is the one in which only one eigenvalue is unstable and the others are stable. A saddle point of index 2 has one stable eigenvalue and two unstable eigenvalues.
The need to develop a more unpredictable and reliable fractional order chaotic Chen system for secure communication systems is the motivation behind this work [45,46,47,48,49]. The global optimization in this work is carried out using three single objective EAs, namely: differential evolution (DE), particle swarm optimization (PSO), and invasive weed optimization (IWO), and the results are then compared. In the light of this, the following contributions to the state of the art are hereby highlighted:
- (i)
- the optimization of the MLE of the fractional order chaotic Chen system by DE, PSO, and IWO, whereby the system’s fractional order q is not fixed, but it is considered to be a design variable and optimized alongside the conventional design variables, which are the system parameters. This was done because a slight change in the value of the fractional order q can also lead to a big change in the LEs; and,
- (ii)
- optimizing the system parameters and fractional order q gives up to an 80% increase in the value of the MLE over the non-optimized system. The highest optimized MLE is obtained from the DE optimization. Consequently, the optimized fractional order chaotic Chen systems are more complex and unpredictable, which makes them suitable for developing random number generators and secure communication systems for cryptographic applications.
This article is organized, as follows: Section 2 presents the theoretical framework, describing the fractional order chaotic Chen oscillator, the computation of the LEs, the applied EAs, and the complexity and instability analyses. Section 3 shows the results that were obtained in this work. The discussion of the results can be found in Section 4. Finally, the conclusion that is derived from the investigation is given in Section 5.
2. Theoretical Framework
This section describes some concepts and techniques that are relevant to this investigation. The following concepts are analyzed: fractional order chaotic Chen oscillator, LEs, the EAs under consideration, and time series complexity and instability of nonlinear systems.
In modeling fractional order systems, there are several definitions for the fractional derivative of order , but the Caputo’s definition is the most commonly used. Caputo’s definition includes initial conditions for the function f as well as its integer order derivatives. Therefore, using the Caputo’s derivative, the initial value problem (IVP) of a fractional order system is defined, as follows:
where is the Caputo’s differential operator of order and is a Lipschitz continuous nonlinear function, is the initial condition, and . If , then system (1) is called to have commensurate order; otherwise, non-commensurate order. is defined by:
where m has the smallest integer that is larger than is the m-order derivative in the usual sense, and is the Euler’s Gamma function. Numerical approximation methods, such as the Grünwald–Letnikov, Riemmann–Liouville, predictor-corrector Adams–Bashforth–Moulton (ABM), and optimized predictor-corrector ABM can be applied to evaluate the fractional differential equation in (1).
2.1. Fractional Order Chaotic Chen Oscillator
The Chen oscillator is a continuous nonlinear and autonomous dynamical system, and it is an initial value problem, either in integer or fractional order. Guanrong Chen and Tetsushi Ueta proposed the oscillator [50,51], and its fractional order version is modeled by Caputo’s fractional derivative, as follows:
where is the Caputo’s differential operator of order ; x, y, and z are the system dependent variables; and, a, b, and c are the system parameters with traditional values of 35, 3, and 28, respectively. We considered commensurate order in our work, hence, . The fractional order Chen system (3) has the same equilibrium points as its equivalent integer order. Hence, the three equilibria are [37]:
The Jacobian matrix of the fractional order Chen system (3) is:
2.2. Computation of Lyapunov Exponents
The LEs of continuous dynamical systems provide the most quantitative description of the presence of a deterministic non-periodic flow. The computation begins with determining their variational equation.
Definition 1.
Given a three-dimensional continuous fractional order system of the form:
where is the Caputo’s differential operator. If is the initial condition, a small perturbation to in x, y, and z directions will lead to the evolution of the initial perturbed condition vector in the direction of a different point, say, , , and , respectively.
The slopes of system (8) in each direction, which are described by the Jacobian matrix J, provide an indication of the evolution of the perturbation after a finite time t. The variation or perturbation in the three directions is defined by:
Generally, the variational equation in (9) can be written in the form:
where represents the matrix solution of system (8), , is the Jacobian of f, and I is the identity matrix. Because is non-singular, is non-singular for . The MLE is computed following the algorithm that is described in [45]. The methodology is based on the work shown in [52,53], in which a Gram–Schmidt orthogonalization procedure for computing LEs was proposed.
Definition 2.
Given j linearly independent set of vectors in , the Gram–Schmidt orthogonalization procedure generates an orthonormal set of vectors spanning the same subspace as . The volume of the parallelepiped that is covered by is:
The corresponding matrix of orthonormal vectors is calculated, the variational equation is integrated, and and are computed. The integration and orthonormalization continue until K is reached. A, Z, and e are the matrix, orthonormal vectors matrix, and initial condition, respectively. At k-th step of the process, the set of orthonormal vectors is . For a suitable value of T, the LEs are obtained by evaluating:
until a maximum iteration is attained or when convergence occurs.
2.3. Description of the Evolutionary Algorithms
In optimization, the function that is to be optimized is generally of the form: : . The global optimization problem of maximizing (or minimizing) the objective function is by optimizing the values of parameters , , where X is a vector comprising D objective function parameters. The parameters are bounded by lower and upper boundary constraints, i.e., .
Most of the EAs use mechanisms that are inspired by biological evolution, such as reproduction, mutation, recombination, and selection. The use of meta-heuristics search is a norm in global optimization problems because of the huge search space that is usually involved. The optimization algorithms that are applied in this investigation, DE, PSO, and IWO, are evolutionary and based on a meta-heuristic. An initialization of population is the first of the main activities of every EA. The others are random variation of individuals, evaluation of cost function, and selection. The last three activities are normally conducted in an iterative manner. Equation (15) shows the initialization of population of N individuals and V decision variables,
where l and u are the lower and upper bounds of the decision variables, respectively, and .
2.3.1. Differential Evolution
The DE was introduced and described in detail by the authors in [54,55]. It uses a set of vectors N called individuals as a population for each generation G. Each vector represents the potential solution for the global optimization problem. Currently, there exist several variants of DE, but the one used in this investigation is . DE uses the difference of solution vectors to create new candidate solutions, whereby the distribution of the population and its orientation are hidden in the differences in population members. As the population size increases, the distribution behind the DE sampling technique tends to a multi-variable Gaussian (normal) distribution, which is very common in the context of EAs. Specifically, the population of randomly created N solution vectors is successfully improved by applying genetic operators in the following order: mutation, crossover, and, finally, selection. Mutation is the main novelty of DE. This operation enables DE to explore the search space and maintain diversity. The mutation is explained in the following definition.
Definition 3.
For a given parameter vector , i.e., an individual i and a generation G, three vectors are randomly selected, and a mutant vector is then created, such that:
where random indexes , and is the scaling factor that controls the amplification of the differential variation .
The crossover operator is applied to the parent vector and mutant vector , in order to increase the diversity of the perturbed parameter vectors. Two crossover techniques are available, namely, binomial and exponential crossover. In binomial crossover, which is used in this investigation, the trial vector is formed, as follows:
where , is a random number within , , is the crossover probability, and D is the number of decision variables. is randomly chosen in order to ensure that obtains a minimum of one parameter from . The selection operator shown in Equation (18), for maximization problem, works by comparing the parent vector with the trial vector. The vector with the better fitness value is admitted to the next generation.
2.3.2. Particle Swarm Optimization
The PSO was developed by James Kennedy and Russel Eberhart, and described in [56,57]. PSO was inspired by the social behavior of birds and fish to solve optimization problems in a cooperative and intelligent framework. Unlike other EAs, PSO has no evolution operators, such as crossover and mutation. PSO uses a set of vectors N (that are called particles) as a population for each generation G. Potential solutions (particles) fly through the problem space by following the current optimum particles. Each particle keeps track of its coordinates in the problem space that are associated with the best solution (fitness) that it has achieved so far. The stored fitness value is called . When a particle takes all the population as its topological neighbours, the best value is a global best and it is called . The velocity of each particle, weighted by a random term, changes at each time step toward its and best location. The core of the PSO is the particle’s velocity and position update.
Definition 4.
Given a swarm of N dimensional population and D dimensional particles, the position and velocity of the j-th particle are represented by and , where , the following equations give the velocity update and position update of the particle, respectively:
where k is the current generation, w is the inertia weight, and are the cognitive and social coefficients, and are uniformly distributed random numbers in , is the personal best of a particle (the coordinates of the best solution obtained so far by a specific particle), and represents the global best, which is the overall best solution that was obtained in the swarm at generation k.
2.3.3. Invasive Weed Optimization
IWO is inspired by the spreading and colonizing strategy of weeds and it is described in [58]. Weeds represent the feasible solutions for the problem and population is the set of all weeds. A finite number of seeds (initial solutions) are randomly spread over the search area. This is the initialization stage. The reproduction stage follows, whereby the seeds grow to become flowering plants and produce seeds depending on their fitness obtained from the objective function [50]. Equation (21) represents the number of seeds to be produced by the plants,
where is the fitness of the i-th weed, and are the worst and best fitness in the weed population, and and represent the minimum and maximum number of seeds.
The spatial dispersal stage is next, during which the seeds produced are randomly dispersed over the search space by normally distributed random numbers with a mean equal to zero, but with a varying standard deviation . This is achieved by the following Equation (22):
where is the maximum number of iterations (generations), is the current iteration, and are the previously defined standard deviations, and n is the nonlinear modulation index. When the maximum number of plants is reached, the competitive exclusion technique is applied, whereby only the plants with high fitness can survive and produce seeds, and others are eliminated. The process continues until the maximum number of iterations is reached. The plant with the best fitness value is the optimized solution.
2.4. Complexity Analysis and Instability of Equilibria
The field of information theory studies the complexity in data series by analyzing its entropy. The entropy is a quantity that measures the degree of randomness in a system or data series to ascertain not only whether it is random or not, but also how random it is. As the level of randomness in a system increases, so does its complexity and unpredictability. There are several algorithms for measuring the randomness that exist in data series, chaotic time series inclusive. Examples of such algorithms incude approximate entropy, sample entropy, and permutation entropy. In this work, sample entropy [59,60] is applied to measure the time series complexity of the fractional order chaotic Chen system. Sample entropy measures the probability of generating new patterns in signals. The sample entropy is computed, as follows:
where m is the embedded dimension, r is the tolerance, N is the time series data, and A and B are template vector pairs.
The instability of an autonomous system, as in (1), is examined from the eigenvalues of the Jacobian matrix evaluated at each equilibrium point according to the following theorem [61]:
Theorem 1.
The equilibrium points of the autonomous fractional order system (1) are asymptotically stable if and only if
is strictly negative.
Remark 1.
If and the critical eigenvalues satisfying have a geometric multiplicity of one, then the equilibrium point is stable.
Remark 2.
If , then the equilibrium point is unstable and the system may exhibit chaotic behavior.
As a matter of fact, the system parameters that are used in the computation of the LE are the primary component for computing the eigenvalues upon which Theorem 1 is based. It is also safe to deduce that, if , then there may be a positive LE and chaotic attractor.
3. Results
The DE and PSO algorithms were randomly populated with 100 individuals, while IWO has an initial population size of 10 and maximum of 100. The number of generations was arbitrarily set from 50 to 500 with a step of 50. The values of the system parameters a, b, and c, as well as fractional order q in the search space, were kept within four decimal places. The initial condition is chosen in the basin of attraction of the system. For the step-size value, some tests were carried out on the simulation program, starting with a trial value and continuing to reduce the value until convergence occurs. The underlying numerical method adopted is the fast optimized ABM predictor-corrector [62]. The numerical evaluation of the LEs is by the Continuous Gram–Schmidt orthogonalization (CGSO) procedure, as justified in [62]. The configuration of the computer that was employed in the simulations and the specific parameters of each algorithm are given next:
- (i)
- Computer configuration: Intel(R) Core(TM) i7-4790, 3.60GHz; RAM: 12 GB; Operating System: Windows 10;
- (ii)
- DE: Crossover probability = 0.3;
- (iii)
- PSO: Constriction coefficient ; ; ; ; Damping ratio = 1;
- (iv)
- IWO: Minimum number of seeds = 0; Maximum number of seeds = 5; Variance reduction exponent = 4; Initial value of standard deviation = ; Final value of standard deviation = .
The chosen initial condition is , while the search spaces of the parameters are , , and . This investigation gives the best results at 400 to 500 generations for DE, and 450 to 500 generations for both PSO and IWO. Henceforth, any reference to the fractional order Chen oscillator DE, PSO, and IWO optimized results in the rest of the article refers to the best results obtained. Table 1 presents the optimized parameters and fractional order by the DE, PSO, and IWO, as well as the optimized LEs, against the non-optimized system. In addition, the table shows the equilibrium points, eigenvalues, sample entropy, and the asymptotic results applying Theorem 1. We note that the MLE of the non-optimized system that is computed in this work when is almost the same as the 2.0192 reported in [63] for integer order when using the same parameters. It can be seen that the slight difference of 0.0101 is caused by the q value. Generally, the LEs can be altered if there is a change in the value of a parameter or the fractional order.

Table 1.
The optimization results showing the optimized fractional order chaotic Chen system by DE, PSO, and IWO against the non-optimized system.
Figure 1 presents the evolution of the phase diagram in 3D planes of the best MLE obtained from DE, PSO, and IWO, respectively, which were simulated with a time-step and integration period s. Additionally, the chaos in the optimized system by each EA is compared in the time series presented in Figure 2.
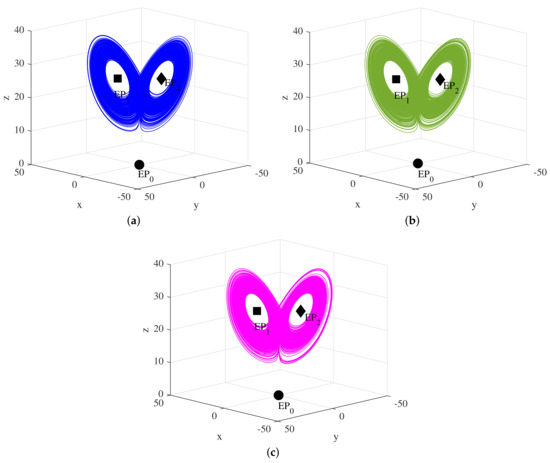
Figure 1.
Phase diagrams in 3D plane for the optimized fractional order Chen system for each EA. (a) DE: equilibrium points , (b) PSO: equilibrium points , and (c) IWO: equilibrium points .
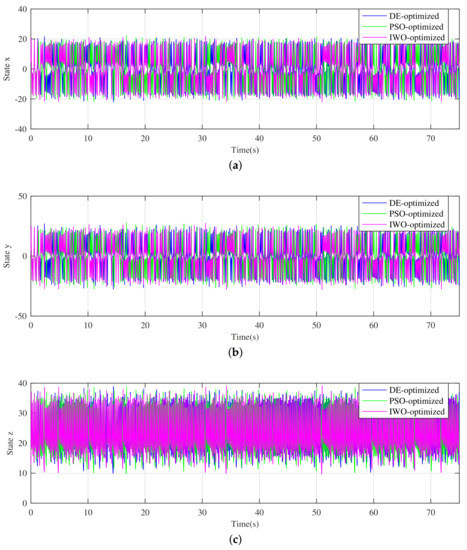
Figure 2.
Timeseries of the optimized fractional order chaotic Chen systems. Each state of the optimized system is superimposed in the respective graph, as indicated by the legend. (a) State x (b) State y (c) State z.
Furthermore, the dynamics of the non-optimized and optimized systems are examined with bifurcation diagrams of state x as well as the LE spectra against the varied values of parameters a, b, and c, and fractional order q. Figure 3, Figure 4, Figure 5 and Figure 6 display the results. The corresponding LE spectra in the figures show good agreement with the bifurcation diagrams.
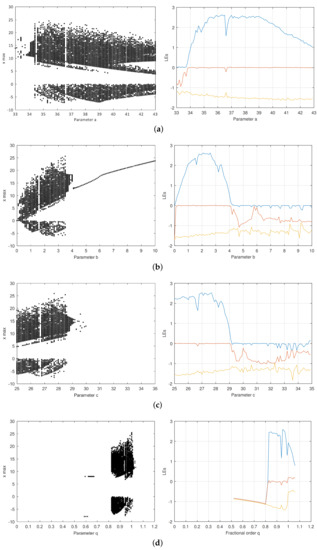
Figure 3.
Bifurcation diagram and LE spectra of non-optimized fractional order Chen system. For the LE spectra, is in blue color, in red, and in yellow. , , , and MLE . (a) Parameter a (b) Parameter b (c) Parameter c (d) Fractional order q.
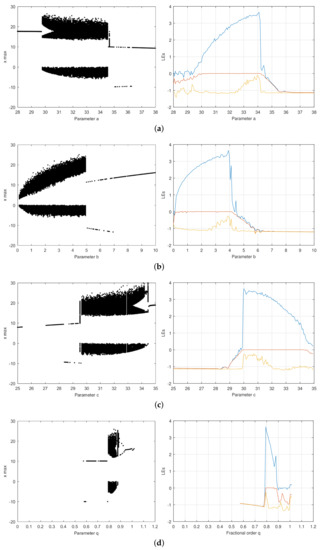
Figure 4.
Bifurcation diagram and LE spectra of fractional order Chen system for DE best result at 400 to 500 generations. For the LE spectra, is in blue color, in red, and in yellow. , , , and MLE . (a) Parameter a (b) Parameter b (c) Parameter c (d) Fractional order q.
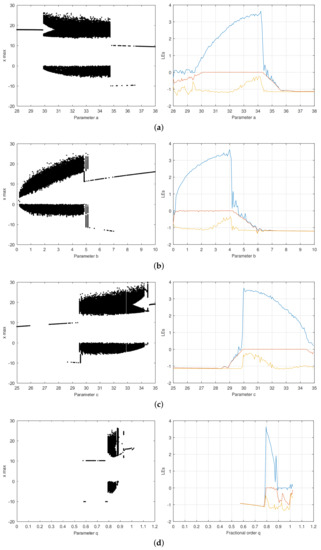
Figure 5.
Bifurcation diagram and LE spectra of fractional order Chen system for PSO best result at 450 and 500 generations. For the LE spectra, is in blue color, in red, and in yellow. , , , and MLE . (a) Parameter a (b) Parameter b (c) Parameter c (d) Fractional order q.
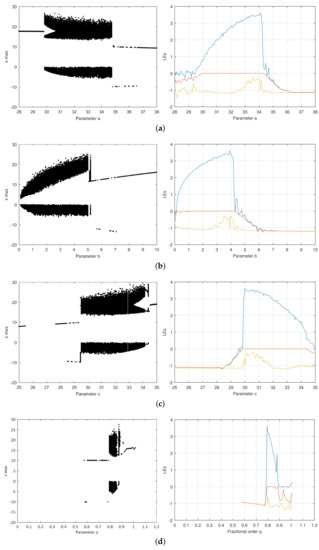
Figure 6.
Bifurcation diagram and LE spectra of fractional order Chen system for IWO best result at 450 and 500 generations. For the LE spectra, is in blue color, in red, and in yellow. , , , and MLE . (a) Parameter a (b) Parameter b (c) Parameter c (d) Fractional order q.
3.1. Comparison with Hyper-Chaotic Fractional Order System
The optimized parameters of Chen system that were obtained in this investigation are compared with a hyper-chaotic Chen system on the basis of their prediction times [64]. The hyper-chaotic system is a class of dynamical system with more than one positive Lyapunov exponent. They are usually more complicated than the traditional chaotic systems. The integer order of the compared hyper-chaotic Chen oscillator was described in [65] and the fractional order equivalent is represented, as follows:
where x, y, z, and w are the system dependent variables, a, b, c, and r are the system parameters with conventional values of 35, 3, 28, and 35 respectively, is the Caputo’s differential operator of order , and is a variable parameter that determines the chaotic attractor.
Figure 7 presents the LE spectrum of model (25), while the LEs of some selected states of the hyper-chaotic system are listed in Table 2. Generally, because hyper-chaotic system has two positive LEs, its prediction time is expected to be shorter than the original chaotic system [66]. The prediction time is given by:
where is the Kolmogorov–Sinai entropy (KS-Entropy). The sum of the positive LEs is the upper bound of the KS-Entropy [67]. The KS-Entropy is calculated, as follows [67]:
where are the LEs.
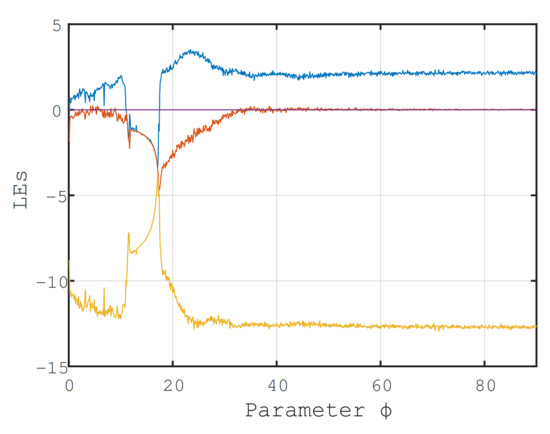
Figure 7.
The LE spectrum of hyper-chaotic fractional order Chen system. is in blue color, in purple, in red, and yellow color.

Table 2.
LEs of selected states of hyper-chaotic fractional order Chen system (the best hyper-chaotic state is italicized).
In this work, the prediction time of the hyper-chaotic system is computed for the best hyper-chaotic state, where . The computed Kolmogorov–Sinai entropies and prediction times of the chaotic and hyper-chaotic systems are: (1) non-optimized , ; (2) DE-optimized , ; (3) PSO-optimized , ; (4) IWO-optimized , ; and, (5) hyper-chaotic , . The results show that the optimized systems have a shorter prediction time than the non-optimized system and the hyper-chaotic system. The prediction time of the hyper-chaotic system is only shorter than the non-optimized system. Overall, DE-optimized system have the shortest prediction time.
3.2. Complexity of Optimization Codes
The complexity of the implemented algorithms in MATLAB were measured using the Halstead metrics, and the results are compared in Table 3. The procedure for determining the complexity begins with the counting of the distinct operators and operands that make up the software, where is the number of distinct operators, is the number of distinct operands, is the total number of operators, and is the total number of operands. Other parameters are derived from these four primary parameters. It should be noted that the metrics only measure the optimization algorithm, not including the numerical method to solve the fractional order system and numerical computation of the LEs.

Table 3.
Halstead complexity metrics for DE, PSO, and IWO.
IWO implementation is the least complex of the three algorithms, while PSO is the most complex, as shown, most importantly, by the program length, which is , and volume, which is a measure of the amount of codes written, based on the vocabulary () and length N. Other Halstead parameters in the table that show IWO to be the simplest are the values of the difficulty involved in writing and maintaining the codes, mental effort required to implement the algorithm in MATLAB, and the estimated time that is required to fully implement the algorithm, which is less than 4 h, as compared to DE of over 5 h. Additionally, the IWO’s estimated amount of delivered bugs is the least.
4. Discussion
The highest MLEs are obtained with optimized fractional order values that are above (Table 1). Although the three algorithms produce optimized MLEs within the same range of values , DE gives the overall best MLE. While the optimized parameters a, b, and q are slightly different in the three optimized results, the values of parameter c are the same. In the asymptotic analysis results shown in Table 1, it is seen that the equilibrium points , , and of the DE, PSO, and IWO optimized systems are saddle points, just like the non-optimized system. For each of them, is a saddle point of index 1, while and are the saddle points of index 2. According to the instability measure shown in Equation (24), at the saddle point of index 1 the systems are unstable for all the values of fractional order q, while the saddle points of index 2 become asymptotically stable below the following q values: for DE-optimized, for PSO-optimized, for IWO-optimized, and for non-optimized. Additionally, the measured complexity of the chaotic time series of the optimized systems and the non-optimized one shows consistency with the MLEs, with the DE-optimized system having the highest sample entropy and the non-optimized the lowest. This means that the DE-optimized system exhibits the most randomness in it. The improved randomness in the optimized systems makes them more suitable for developing a random number generator.
Table 4 compares this investigation with some other works in [13,18,19,68,69], which have been carried out for the global optimization of dynamical behavior and parameter estimation in chaotic systems. It could be seen that our investigation is the only one that measures the complexity of the implemented optimization algorithms. It uses more algorithms than the others to compare their performance in the optimization problem. Additionally, unlike others, the work is based on a chaotic system of fractional order.

Table 4.
A comparison of this investigation with some other works in chaotic behavior optimization.
In our work, the fractional order is a part of the design variables, making a total of four. Furthermore, we use wider search spaces for the design variables. Hence, the higher MLEs in the present investigation can be mostly accredited to the higher population size, higher number of generations, and wider search spaces. The bifurcation and LE spectra are studied while separately varying each of the parameters, including the fractional order, unlike the compared works presented in Table 4. The maximization of the MLE in this investigation further shows the effectiveness of EAs as a global optimization algorithm [13,18,19,68,69]. Our work shows that the three algorithms obtain system parameter and fractional order values that produced better MLE than the non-optimized fractional order Chen system. The higher MLEs obtained is an indication that the optimized fractional order Chen oscillators have greater unpredictability than the non-optimized one. In addition, the smaller prediction times obtained for the optimized systems are credited to the increased MLE value. A system with shorter prediction time is regarded as safer for designing security systems [66,70]. Therefore, an improved secure communication system is guaranteed in the optimized fractional order Chen system.
5. Conclusions
This work demonstrates the application of DE, PSO, and IWO evolutionary algorithms in optimizing the values of parameters a, b, and c, and fractional order q of the chaotic Chen system. The meta-heuristics produce optimized MLEs that fall with a range of values , but with completely different parameter and fractional order values. This underlines the fact that chaotic behavior in a fractional order Chen system is multifaceted with respect to the parameter and fractional order values. The dynamics and complexity of the optimized systems were verified with bifurcation, LE spectrum, asymptotic, and sample entropy analyses of the results. The optimized MLEs in this investigation are higher than the non-optimized system, which is an indication of greater unpredictability in the optimized systems, with the DE giving the best optimal MLE. Therefore, the most reliable secure communication system is guaranteed with the DE-optimized system. The optimized systems are compared with a Chen hyper-chaotic system using the prediction time. The optimized systems were found to have a shorter prediction time than the hyper-chaotic system, which is also promising for improved secure communication system. Additionally, the complexity of the three implemented algorithms is determined and the Halstead metrics reveal that IWO has the simplest implementation.
Author Contributions
Conceptualization, J.-C.N.-P., V.-A.A., F.-J.P.-P. and E.T.-C.; methodology, J.-C.N.-P., V.-A.A. and E.T.-C.; software, V.-A.A., Y.S.-I.; validation, J.-C.N.-P., Y.S.-I., F.-J.P.-P. and E.T.-C.; formal analysis, J.-C.N.-P., V.-A.A.; investigation, J.-C.N.-P., V.-A.A. and F.-J.P.-P.; resources, J.-C.N.-P. and E.T.-C.; writing—original draft preparation, J.-C.N.-P., V.-A.A. and E.T.-C.; writing—review and editing, J.-C.N.-P., V.-A.A., Y.S.-I., F.-J.P.-P. and E.T.-C.; visualization, V.-A.A. and Y.S.-I.; supervision, J.-C.N.-P. and E.T.-C.; project administration, J.-C.N.-P.; funding acquisition, J.-C.N.-P. All authors have read and agreed to the published version of the manuscript.
Funding
The authors wish to thank the Instituto Politecnico Nacional for its support provided through the project SIP-20210345. In addition, the authors would like to express their gratitude to the COFAA-IPN for its financial support.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sujarani, R.; Manivannan, D.; Manikandan, R.; Vidhyacharan, B. Lightweight Bio-Chaos Crypt to Enhance the Security of Biometric Images in Internet of Things Applications. Wirel. Pers. Commun. 2021. [Google Scholar] [CrossRef]
- Chen, H.; Ji, Q.; Wang, H.; Yang, Q.; Cao, Q.; Gong, Q.; Yi, X.; Xiao, Y. Chaos-assisted two-octave-spanning microcombs. Nat. Commun. 2020, 11. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Yu, W.; Wang, J.; Wang, J.; Chen, Y.; He, X.; Jiang, D. Dynamic analysis of seven-dimensional fractional-order chaotic system and its application in encrypted communication. J. Ambient Intell. Humaniz. Comput. 2020, 11, 5399–5417. [Google Scholar] [CrossRef]
- Freitas, V.; Yanchuk, S.; Zaks, M.; Macau, E. Synchronization-based symmetric circular formations of mobile agents and the generation of chaotic trajectories. Commun. Nonlinear Sci. Numer. Simul. 2021, 94, 105543. [Google Scholar] [CrossRef]
- Lian, J.; Yu, W.; Xiao, K.; Liu, W. Cubic Spline Interpolation-Based Robot Path Planning Using a Chaotic Adaptive Particle Swarm Optimization Algorithm. Math. Probl. Eng. 2020, 2020, 849240. [Google Scholar] [CrossRef]
- Sridharan, K.; Ahmadabadi, Z. A Multi-System Chaotic Path Planner for Fast and Unpredictable Online Coverage of Terrains. IEEE Robot. Autom. Lett. 2020, 5, 5268–5275. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Q.; Wei, D.; Li, G.; Wu, H.; Wang, Z.; Guo, B.; Zhang, J. Chaotic Ensemble of Online Recurrent Extreme Learning Machine for Temperature Prediction of Control Moment Gyroscopes. Sensors 2020, 20, 4786. [Google Scholar] [CrossRef] [PubMed]
- Shirzhiyan, Z.; Keihani, A.; Farahi, M.; Shamsi, E.; GolMohammadi, M.; Mahnam, A.; Haidari, M.; Jafari, A. Introducing chaotic codes for the modulation of code modulated visual evoked potentials (c-VEP) in normal adults for visual fatigue reduction. PLoS ONE 2019, 14, e0213197. [Google Scholar] [CrossRef]
- Nobukawa, S.; Shibata, N. Controlling Chaotic Resonance using External Feedback Signals in Neural Systems. Sci. Rep. 2019, 9, 4990. [Google Scholar] [CrossRef]
- Belmiloudi, A. Dynamical behavior of nonlinear impulsive abstract partial differential equations on networks with multiple time-varying delays and mixed boundary conditions involving time-varying delays. J. Dyn. Control Syst. 2015, 21, 95–146. [Google Scholar] [CrossRef]
- Demina, M.V.; Kuznetsov, N.S. Liouvillian integrability and the Poincaré problem for nonlinear oscillators with quadratic damping and polynomial forces. J. Dyn. Control. Syst. 2020, 27, 1–13. [Google Scholar] [CrossRef]
- Dawidowicz, A.L.; Poskrobko, A. On chaos behaviour of nonlinear Lasota equation in Lebesgue spaces. J. Dyn. Control. Syst. 2020, 27, 1–8. [Google Scholar] [CrossRef]
- Carbajal-Gómez, V.H.; Tlelo-Cuautle, E.; Fernández, F.V. Optimizing the positive Lyapunov exponent in multi-scroll chaotic oscillators with differential evolution algorithm. Appl. Math. Comput. 2013, 219, 8163–8168. [Google Scholar] [CrossRef]
- Xu, G.; Shekofteh, Y.; Akgül, A.; Li, C.; Panahi, S. A new chaotic system with a self-excited attractor: Entropy measurement, signal encryption, and parameter estimation. Entropy 2018, 20, 86. [Google Scholar] [CrossRef]
- Balibrea, F.; Caballero, M.V. Stability of orbits via Lyapunov exponents in autonomous and nonautonomous systems. Int. J. Bifurcat. Chaos. 2013, 23, 1350127. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, X. Simple estimation method for the largest Lyapunov exponent of continuous fractional-order differential equations. Phys. A Stat. Mech. Appl. 2021, 563, 125478. [Google Scholar] [CrossRef]
- De la Fraga, L.G.; Tlelo-Cuautle, E.; Carbajal-Gómez, V.H.; Muñoz-Pacheco, J.M. On maximizing positive Lyapunov exponents in a chaotic oscillator with heuristics. Rev. Mex. Fis. 2012, 58, 274–281. [Google Scholar]
- Carbajal-Gómez, V.H.; Tlelo-Cuautle, E.; Fernández, F.V.; de la Fraga, L.G.; Sánchez-López, C. Maximizing Lyapunov Exponents in a Chaotic Oscillator by Applying Differential Evolution. Int. J. Nonlinear Sci. Num. 2014, 15, 11–17. [Google Scholar] [CrossRef]
- De la Fraga, L.G.; Tlelo-Cuautle, E. Optimizing the maximum Lyapunov exponent and phase space portraits in multi-scroll chaotic oscillators. Nonlinear Dynam. 2014, 76, 1503–1515. [Google Scholar] [CrossRef]
- Hua, A.; Zhang, Y.; Zhou, Y. Two-Dimensional Modular Chaotification System for Improving Chaos Complexity. IEEE Trans. Signal Process. 2020, 68, 1937–1949. [Google Scholar] [CrossRef]
- Liu, B.; Xiang, H.; Liu, L. Reducing the dynamical degradation of digital chaotic maps with time-delay linear feedback and parameter perturbation. Math. Probl. Eng. 2020, 12, 4926937. [Google Scholar] [CrossRef]
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y.Q. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Srivastava, H.; Saxena, R.; Parmar, R. Some Families of the Incomplete H-Functions and the Incomplete H-Functions and Associated Integral Transforms and Operators of Fractional Calculus with Applications. Russ. J. Math. Phys. 2018, 25, 116–138. [Google Scholar] [CrossRef]
- Tolba, M.F.; AbdelAty, A.M.; Soliman, N.S.; Said, L.A.; Madian, A.H.; Azar, A.T.; Radwan, A.G. FPGA implementation of two fractional order chaotic systems. AEU-Int. J. Electron. C. 2017, 78, 162–172. [Google Scholar] [CrossRef]
- Bouzeriba, A.; Boulkroune, A.; Bouden, T. Projective synchronization of two different fractional-order chaotic systems via adaptive fuzzy control. Neural Compt. Appl. 2016, 27, 1349–1360. [Google Scholar] [CrossRef]
- Mescia, L.; Bia, P.; Caratelli, D. Fractional Calculus Based Electromagnetic Tool to Study Pulse Propagation in Arbitrary Dispersive Dielectrics. Phys. Status Solidi A 2018, 216, 1800557. [Google Scholar] [CrossRef]
- Gonzalez, E.A.; Petrás, I.; Ortigueira, M.D. Novel Polarization Index Evaluation Formula and Fractional-Order Dynamics in Electric Motor Insulation Resistance. Fract. Calc. Appl. Anal. 2018, 21, 613–627. [Google Scholar] [CrossRef]
- Ray, S.S.; Sahoo, S.; Das, S. Formulation and solutions of fractional continuously variable order mass–spring–damper systems controlled by viscoelastic and viscous–viscoelastic dampers. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Peng, Y. Detecting chaos in fractional-order nonlinear systems using the smaller alignment index. Phys. Lett. A 2019, 383, 2267–2271. [Google Scholar] [CrossRef]
- Boulkroune, A.; Bouzeriba, A.; Bouden, T. Fuzzy generalized projective synchronization of incommensurate fractional-order chaotic systems. Neurocomputing 2016, 173, 606–614. [Google Scholar] [CrossRef]
- Faieghi, M.R.; Delavari, H. Chaos in fractional-order Genesio–Tesi system and its synchronization. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 731–741. [Google Scholar] [CrossRef]
- Danca, M.F.; Garrapa, R. Suppressing chaos in discontinuous systems of fractional order by active control. Appl. Math. Comput. 2015, 257, 89–102. [Google Scholar] [CrossRef][Green Version]
- He, J.M.; Chen, F.Q. A new fractional order hyperchaotic Rabinovich system and its dynamical behaviors. Int. J. Nonlinear Mech. 2017, 95, 73–81. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillen-Fernandez, O.; Silva-Juarez, A. Analog Implementations of Fractional-Order Chaotic Systems. In Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer Nature: Cham, Switzerland, 2020; Chapter 4; pp. 93–114. [Google Scholar]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillen-Fernandez, O.; Silva-Juarez, A. Synchronization and Applications of Fractional-Order Chaotic Systems. In Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer Nature: Cham, Switzerland, 2020; Chapter 6; pp. 175–201. [Google Scholar]
- Pano-Azucena, A.; Ovilla-Martinez, B.; Tlelo-Cuautle, E.; Muñoz-Pacheco, J.; de la Fraga, L. FPGA-based implementation of different families of fractional-order chaotic oscillators applying Grünwald–Letnikov method. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 516–527. [Google Scholar] [CrossRef]
- Núñez Pérez, J.; Adeyemi, V.; Sandoval-Ibarra, Y.; Serrato-Andrade, R.; Cárdenas, J.; Tlelo-Cuautle, E. Mathematical and numerical analysis of the dynamical behavior of Chen oscillator. Int. J. Dyn. Control 2020, 8, 386–395. [Google Scholar] [CrossRef]
- Platas-Garza, M.; Zambrano-Serrano, E.; Rodríguez-Cruz, J.; Posadas-Castillo, C. Implementation of an encrypted-compressed image wireless transmission scheme based on chaotic fractional-order systems. Chin. J. Phys. 2021, 71, 22–37. [Google Scholar] [CrossRef]
- Liu, T.; Yan, H.; Banerjee, S.; Mou, J. A fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation. Chaos Solitons Fractals 2021, 145, 110791. [Google Scholar] [CrossRef]
- Soleimanizadeh, A.; Nekoui, M. Optimal type-2 fuzzy synchronization of two different fractional-order chaotic systems with variable orders with an application to secure communication. Soft Comput. 2021, 25, 6415–6426. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillen-Fernandez, O.; Silva-Juarez, A. Characterization and Optimization of Fractional-Order Chaotic Systems. In Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer Nature: Cham, Switzerland, 2020; Chapter 3; pp. 75–91. [Google Scholar]
- Goodarzi, M.; Mohades, A.; Forghani-elahabad, M. Improving the Gridshells’ Regularity by Using Evolutionary Techniques. Mathematics 2021, 9, 440. [Google Scholar] [CrossRef]
- Lu, N.; Yang, Y. Application of evolutionary algorithm in performance optimization of embedded network firewall. Microprocess. Microsyst. 2020, 76, 103087. [Google Scholar] [CrossRef]
- Turgut, M.; Sağban, H.; Turgut, O.; Özmen, T. Whale optimization and sine–cosine optimization algorithms with cellular topology for parameter identification of chaotic systems and Schottky barrier diode models. Soft Comput. 2021, 25, 1365–1409. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Carbajal-Gomez, V.; Obeso-Rodelo, P.; Rangel-Magdaleno, J.; Núñez-Pérez, J.C. FPGA realization of a chaotic communication system applied to image processing. Nonlinear Dynam. 2015, 82, 1879–1892. [Google Scholar] [CrossRef]
- Al-Saidi, N.M.G.; Younus, D.; Natiq, H.; Ariffin, M.R.K.; Asbullah, M.A.; Mahad, Z. A New Hyperchaotic Map for a Secure Communication Scheme with an Experimental Realization. Symmetry 2020, 12, 1881. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Higazy, M.; Althagafi, O.A. A Novel Strategy for Complete and Phase Robust Synchronizations of Chaotic Nonlinear Systems. Symmetry 2020, 12, 1765. [Google Scholar] [CrossRef]
- Anees, A.; Hussain, I. A Novel Method to Identify Initial Values of Chaotic Maps in Cybersecurity. J. Dyn. Control Syst. 2020, 11, 140. [Google Scholar] [CrossRef]
- Nuñez-Perez, J.; Adeyemi, V.; Sandoval-Ibarra, Y.; Pérez-Pinal, F.; Tlelo-Cuautle, E. FPGA Realization of Spherical Chaotic System with Application in Image Transmission. Math. Probl. Eng. 2021, 2021, 5532106. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurcat. Chaos. 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. Generating Lorenz-like and Chen-like attractors from a simple algebraic structure. Sci. China Inform. Sci. 2014, 57, 1–7. [Google Scholar] [CrossRef][Green Version]
- Benettin, G.; Galgani, L.; Giorgilli, A.; Strelcyn, J.M. Lyapunov characteristic exponents for smooth dynamical systems and for hamiltonian systems. A method for computing all of them. Part II: Numerical application. Meccanica 1980, 15, 21–30. [Google Scholar] [CrossRef]
- Benettin, G.; Pasquali, S.; Ponno, A. The Fermi-Pasta-Ulam problem and its underlying integrable dynamics: An approach through Lyapunov exponents. J. Stat. Phys. 2018, 171, 521–542. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution: A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Hamza, N.; Sarker, R.; Essam, D. Differential evolution with multi-constraint consensus methods for constrained optimization. J. Glob. Optim. 2013, 57, 583–611. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Swarm Intelligence, 1st ed.; Morgan Kaufmann Publishers: Burlington, VT, USA, 2001; p. 512. [Google Scholar]
- Baiquan, L.; Gaiqin, G.; Zeyu, L. The block diagram method for designing the particle swarm optimization algorithm. J. Glob. Optim. 2012, 52, 689–710. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, H.; Zhou, G. Invasive weed optimization algorithm for optimization no-idle flow shop scheduling problem. Neurocomputing 2017, 137, 285–292. [Google Scholar] [CrossRef]
- He, S.; Chen, H.; Lei, T.; Lu, S.; Dai, W.; Qiu, L.; Zhong, L. Dynamics and Complexity Analysis of Fractional-Order Chaotic Systems with Line Equilibrium Based on Adomian Decomposition. Complexity 2020, 2020, 5710765. [Google Scholar]
- Delgado-Bonal, A.; Marshak, A. Approximate Entropy and Sample Entropy: A Comprehensive Tutorial. Entropy 2019, 21, 541. [Google Scholar] [CrossRef]
- Danca, M.F. Hidden chaotic attractors in fractional-order systems. Nonlinear Dynam. 2017, 89, 577–586. [Google Scholar] [CrossRef]
- Danca, M.F.; Kuznetsov, N. Matlab code for Lyapunov exponents of fractional order systems. Int. J. Bifurcat. Chaos. 2018, 28, 1850067. [Google Scholar] [CrossRef]
- Khan, A.; Kumar, S. T–S fuzzy observed based design and synchronization of chaotic and hyper-chaotic dynamical systems. Int. J. Dyn. Control 2018, 6, 1409–1419. [Google Scholar] [CrossRef]
- Pesin, Y.B. Characteristic Lyapunov exponents and smooth ergodic theory. Russ. Math. Surv. 1977, 32, 55–114. [Google Scholar] [CrossRef]
- Zhu, Z.l.; Zhang, Q.; Yu, H.; Gao, J. A new hyper-chaos generated from Chen´s system via an external periodic perturbation. In Proceedings of the 2009 International Workshop on Chaos-Fractals Theories and Applications, Shenyang, China, 6–8 November 2009; pp. 260–266. [Google Scholar]
- Zhou, N.; Pan, S.; Cheng, S.; Zhou, Z. Image compression-encryption scheme based on hyper-chaotic system and 2D compressive sensing. Opt. Laser Technol. 2016, 82, 121–133. [Google Scholar] [CrossRef]
- Garner, D.M.; Ling, B.W.K. Measuring and locating zones of chaos and irregularity. J. Syst. Sci. Complex. 2014, 27, 494–506. [Google Scholar] [CrossRef]
- Lin, J.; Chen, C. Parameter estimation of chaotic systems by an oppositional seeker optimization algorithm. Nonlinear Dynam. 2014, 76, 509–517. [Google Scholar] [CrossRef]
- Zhang, H.; Li, B.; Zhang, J.; Qin, Y.; Feng, X.; Liu, B. Parameter estimation of nonlinear chaotic system by improved TLBO strategy. Soft. Comput. 2016, 20, 4965–4980. [Google Scholar] [CrossRef]
- Halstead, M.H. Elements of Software Science; Operating and Programming Systems Series; Elsevier: Amsterdam, The Netherlands, 1977; p. 127. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).