Steady Fluid–Structure Coupling Interface of Circular Membrane under Liquid Weight Loading: Closed-Form Solution for Differential-Integral Equations
Abstract
1. Introduction
2. Membrane Equation and Its Solution
3. Results and Discussions
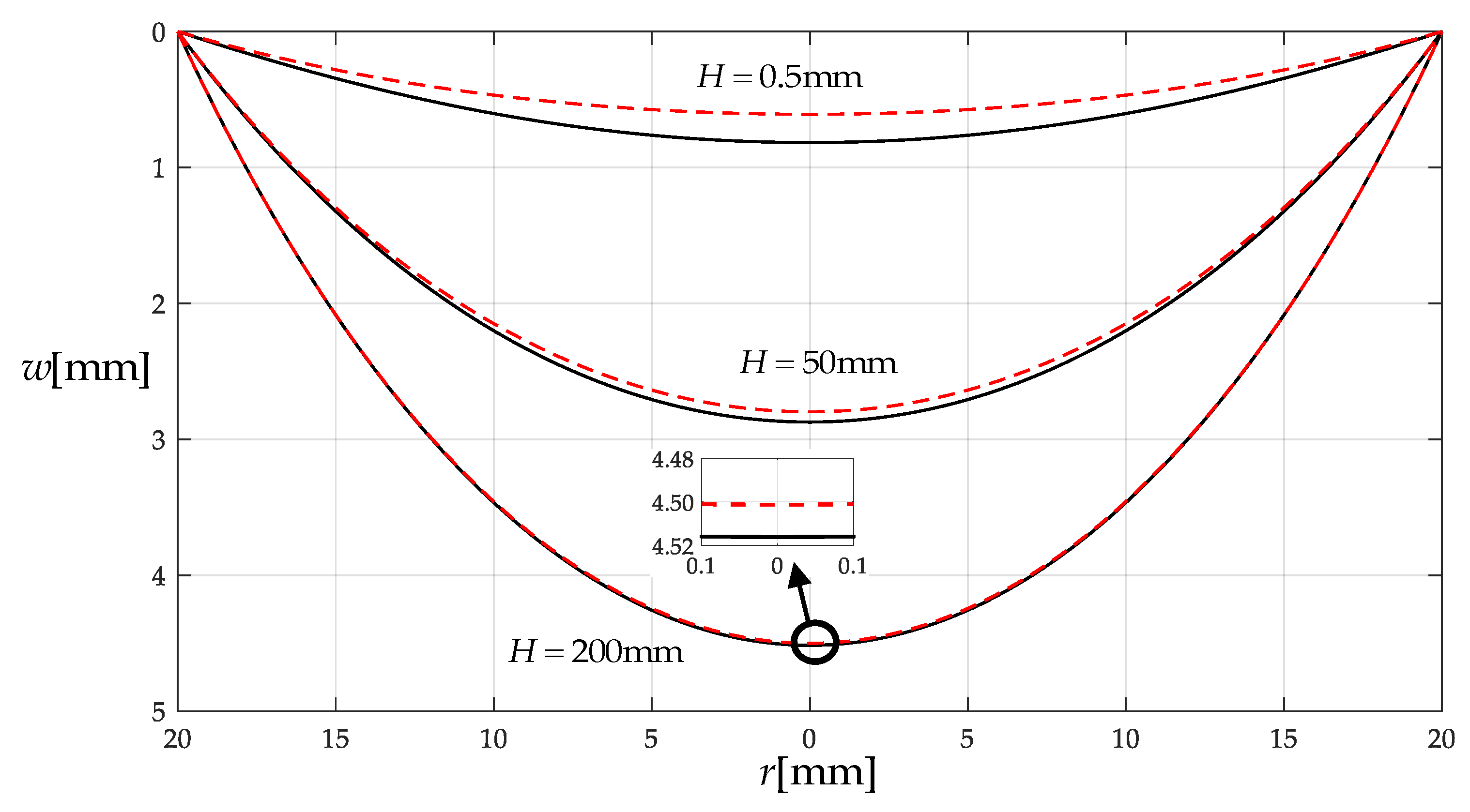
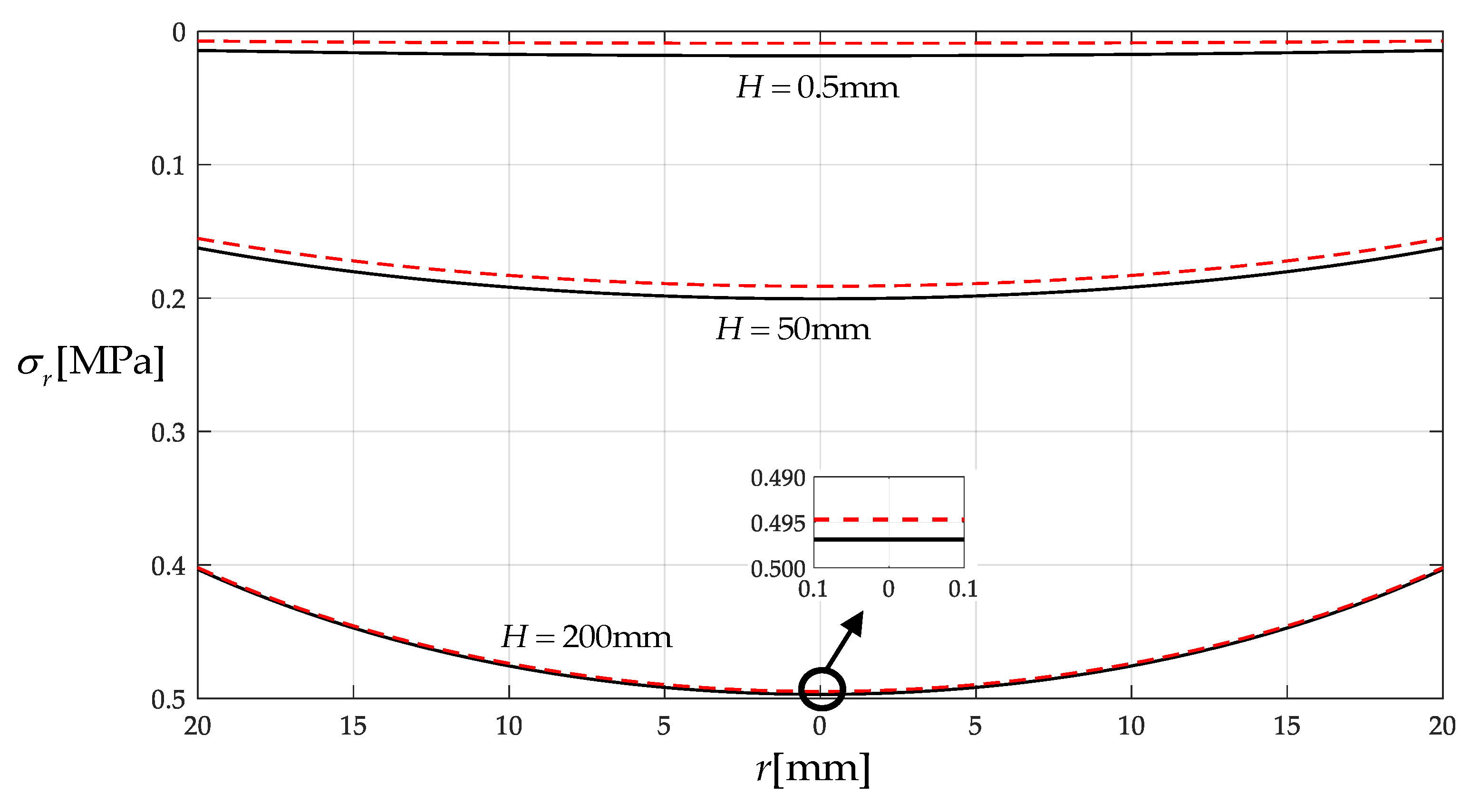
3.1. Comparison with the Well-Known Hencky Solution
3.2. Verification of Convergence of the Power Series Solution
4. Concluding Remarks
- i.
- The power series method is effective for the analytical solution to differential-integral equations.
- ii.
- When the amount of liquid applied onto the circular membrane is large enough, the difference between the solution presented in this paper and the well-known Hencky solution will become relatively small. If the requirement for calculation accuracy is not too high, the problem of axisymmetric deformation of the circular membrane under liquid self-weight loading may be treated as the well-known Hencky problem; the fluid–structure interaction may be neglected.
- iii.
- When the amount of liquid applied onto the circular membrane is relatively small, the solution presented in this paper will be quite different from the well-known Hencky solution. For a higher calculation accuracy, the fluid–structure interaction should be taken into account.
- iv.
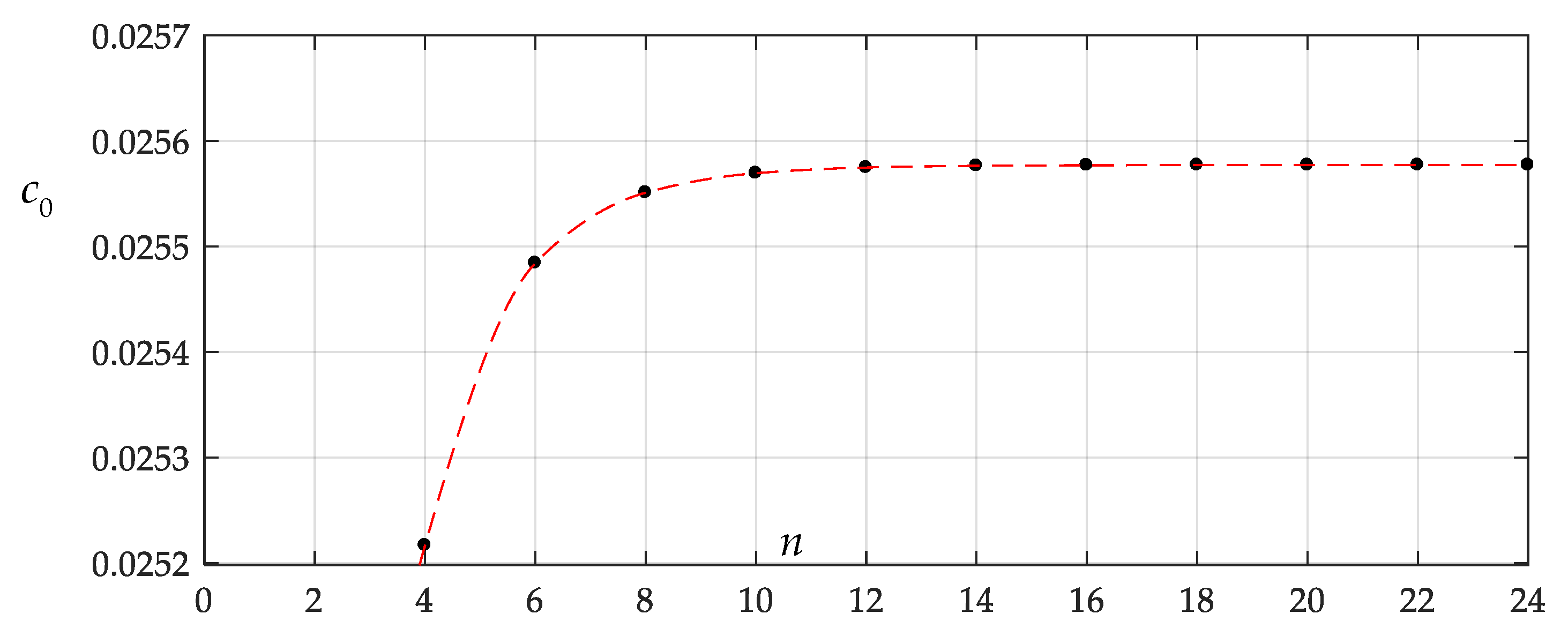
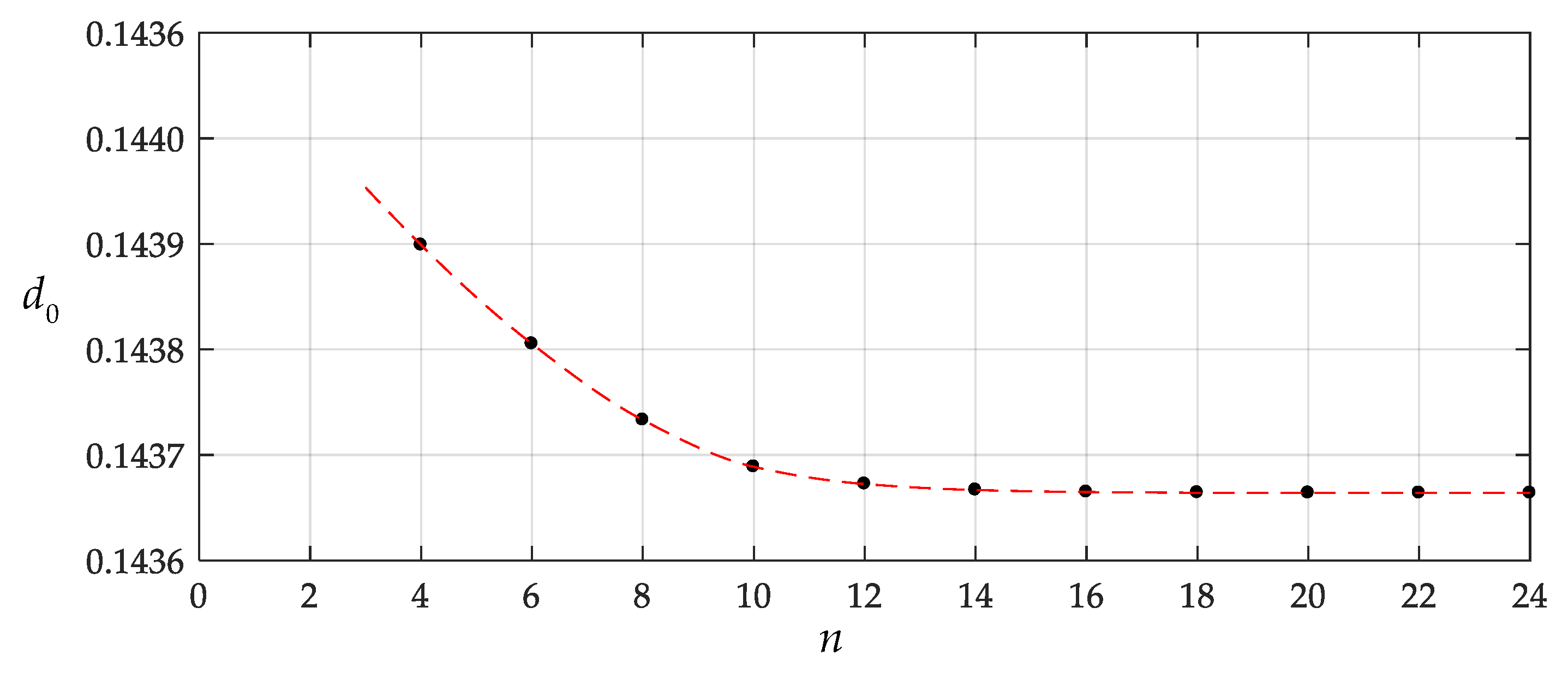
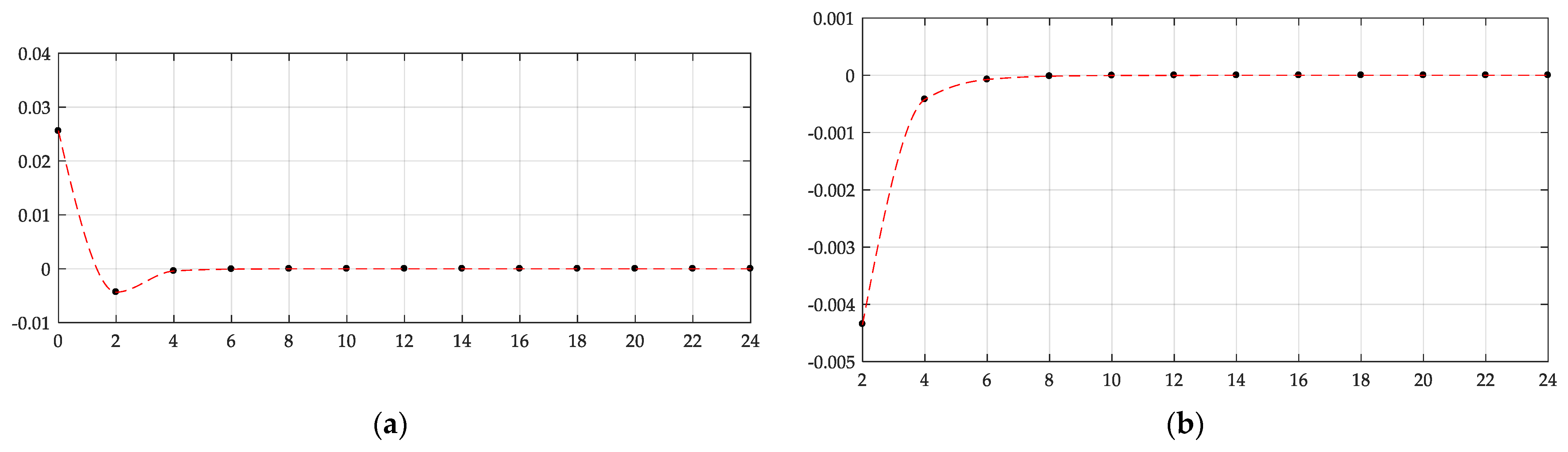
- The numerical example conducted shows that the closed-form solution obtained in this paper has good convergence.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclatures
| a | Radius of the circular membrane |
| h | Thickness of the circular membrane |
| E | Young’s modulus of elasticity |
| ν | Poisson’s ratio |
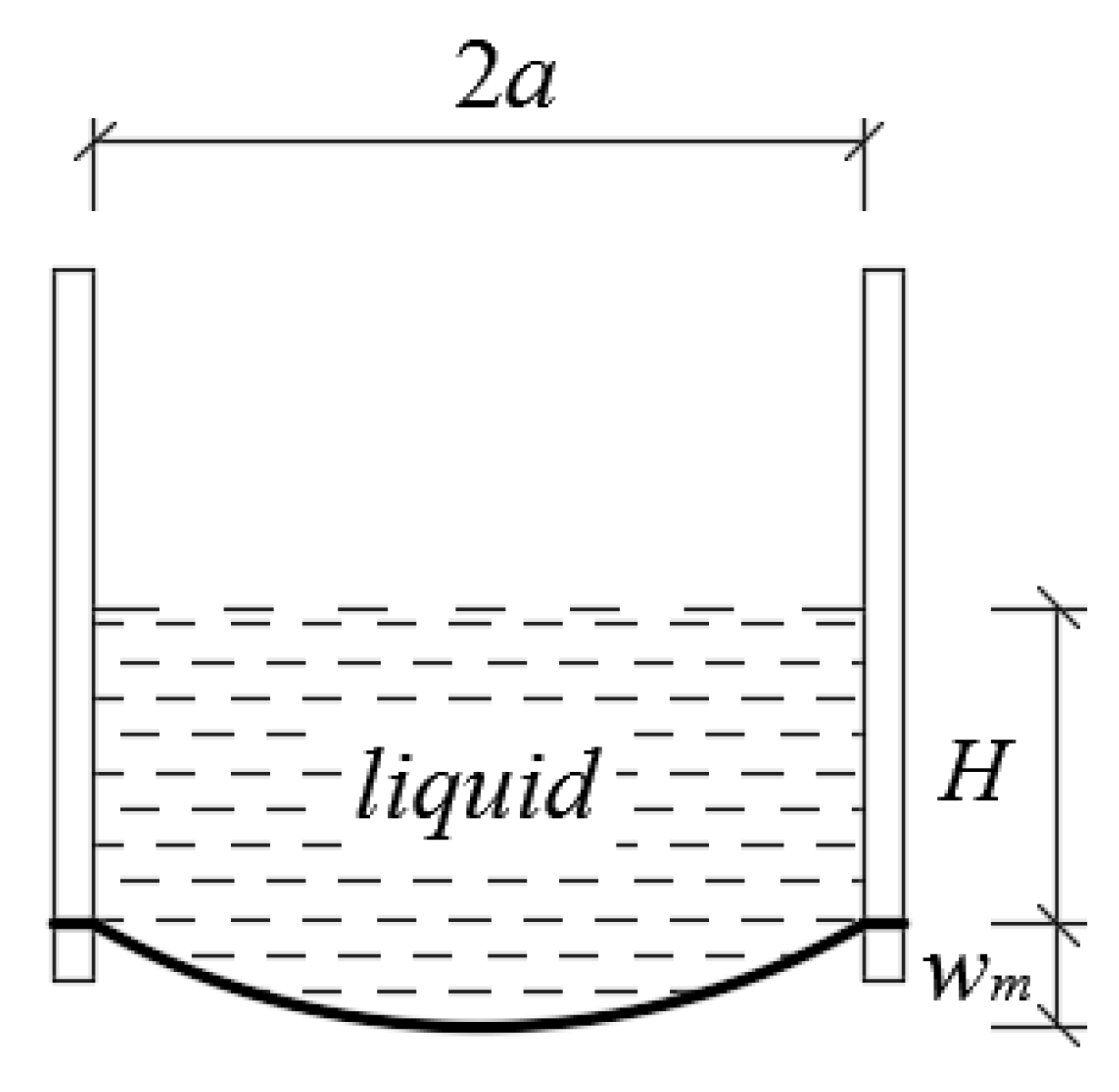
| H | Height of the liquid poured into the cup |
| ρ | Density of the poured liquid |
| g | Acceleration of gravity |
| r | Radial coordinate of the cylindrical coordinate system |
| φ | Circumferential coordinate of the cylindrical coordinate system |
| w | Axial coordinate of the cylindrical coordinate system as well as transverse displacement of a point on the deflected circular membrane |
| u | Radial displacement of a point on the deflected circular membrane |
| wm | Maximum deflection of the deflected circular membrane |
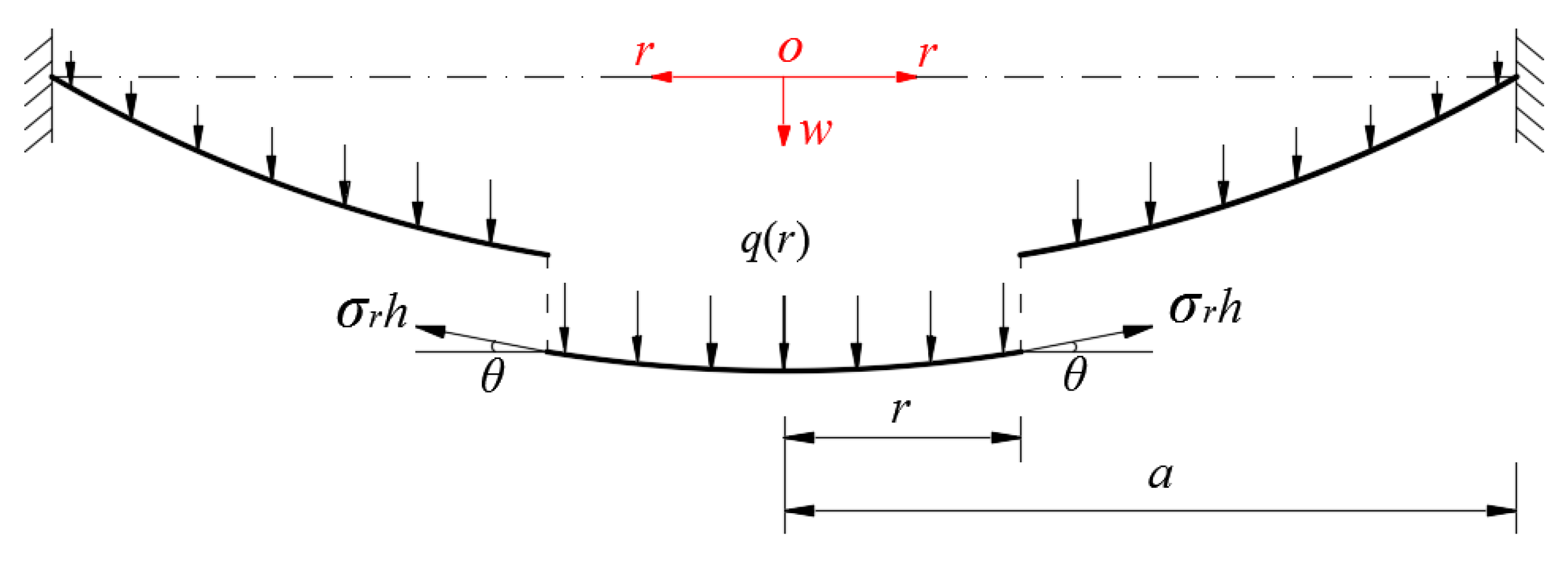
| q(r) | Transverse distributed loads over the circular membrane produced by the gravity of the liquid within radius r |
| F(r) | External force produced by q(r) within radius r |
| σr | Radial stress |
| σt | Circumferential stress |
| er | Radial strain |
| et | Circumferential strain |
| θ | Slope angle of the deflected membrane |
| π | Pi (ratio of circumference to diameter) |
| W | Dimensionless transverse displacement (w/a) |
| Sr | Dimensionless radial stress (σr/E) |
| St | Dimensionless circumferential stress (σt/E) |
| H0 | Dimensionless height of liquid (H/a) |
| G | Dimensionless quantity (ρga2/Eh) |
| x | Dimensionless radial coordinate (r/a) |
| ci | Coefficients of the power series for Sr |
| di | Coefficients of the power series for W |
Appendix A
Appendix B
References
- Dadgar-Rad, F.; Imani, A. Theory of gradient-elastic membranes and its application in the wrinkling analysis of stretched thin sheets. J. Mech. Phys. Solids 2019, 132, 103679. [Google Scholar] [CrossRef]
- Suresh, K.; Katara, N. Design and development of circular ceramic membrane for wastewater treatment. Mater. Today Proc. 2021, 43, 2176–2181. [Google Scholar] [CrossRef]
- Zhao, M.H.; Zheng, W.L.; Fan, C.Y. Mechanics of shaft-loaded blister test for thin film suspended on compliant substrate. Int. J. Solids Struct. 2010, 47, 2525–2532. [Google Scholar] [CrossRef][Green Version]
- Bernardo, P.; Iulianelli, A.; Macedonio, F.; Drioli, E. Membrane technologies for space engineering. J. Membr. Sci. 2021, 626, 119177. [Google Scholar] [CrossRef]
- Sun, H.X.; Bao, S.S.; Zhao, H.R.; Chen, Y.H.; Wang, Y.X.; Jiang, C.; Li, P.; Niu, Q.J. Polyarylate membrane with special circular microporous structure by interfacial polymerization for gas separation. Sep. Purif. Technol. 2020, 251, 117370. [Google Scholar] [CrossRef]
- Tsiatas, C.G.; Katsikadelis, J.T. Large deflection analysis of elastic space membranes. Int. J. Numer. Meth. Eng. 2006, 65, 264–294. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.Y.; Zhao, Z.H.; He, X.T. Large deflection analysis of axially symmetric deformation of prestressed circular membranes under uniform lateral loads. Symmetry 2020, 12, 1343. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Hien, T.D.; Nguyen-Thoi, T.; Lee, J. A unified adaptive approach for membrane structures: Form finding and large deflection isogeometric analysis. Comput. Method Appl. Mech. Eng. 2020, 369, 113239. [Google Scholar] [CrossRef]
- Mei, D.; Sun, J.Y.; Zhao, Z.H.; He, X.T. A closed-form solution for the boundary value problem of gas pressurized circular membranes in contact with frictionless rigid plates. Mathematics 2020, 8, 1017. [Google Scholar] [CrossRef]
- Arthurs, A.M.; Clegg, J. On the solution of a boundary value problem for the nonlinear Föppl-Hencky equation. Z. Angew. Math. Mech. 1994, 74, 281–284. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.Y.; Shi, B.B.; Zhao, Z.H.; He, X.T. A theoretical study on an elastic polymer thin film-based capacitive wind-pressure sensor. Polymers 2020, 12, 2133. [Google Scholar] [CrossRef]
- Dickey, R.W. A boundary value problem for a class of nonlinear ordinary differential equations. J. Differ. Equ. 1968, 4, 399–407. [Google Scholar] [CrossRef][Green Version]
- Versaci, M.; Angiulli, G.; Fattorusso, L.; Jannelli, A. On the uniqueness of the solution for a semi-linear elliptic boundary value problem of the membrane MEMS device for reconstructing the membrane profile in absence of ghost solutions. Int. J. Non-Linear Mech. 2019, 109, 24–31. [Google Scholar] [CrossRef]
- Hencky, H. Über den Spannungszustand in kreisrunden Platten mit verschwindender Biegungssteifigkeit. Z. Angew. Math. Phys. 1915, 63, 311–317. [Google Scholar]
- Chien, W.Z. Asymptotic behavior of a thin clamped circular plate under uniform normal pressure at very large deflection. Sci. Rep. Natl. Tsinghua Univ. 1948, 5, 193–208. [Google Scholar]
- Alekseev, S.A. Elastic circular membranes under the uniformly distributed loads. Eng. Corpus 1953, 14, 196–198. (In Russian) [Google Scholar]
- Lian, Y.S.; Sun, J.Y.; Zhao, Z.H.; Li, S.Z.; Zheng, Z.L. A refined theory for characterizing adhesion of elastic coatings on rigid substrates based on pressurized blister test methods: Closed-form solution and energy release rate. Polymers 2020, 12, 1788. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.Y.; Zhao, Z.H.; Li, S.Z.; He, X.T. A new solution to well-known Hencky problem: Improvement of in-plane equilibrium equation. Mathematics 2020, 8, 653. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, G.R.; Chen, Y.L.; Long, D.; Guan, Y.C.; Liu, L.Q.; Zhang, Z. Extended Hencky solution for the blister test of nanomembrane. Extrem. Mech. Lett. 2018, 22, 69–78. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Zhao, Z.H.; He, X.T.; Zheng, Z.L. A revisit of the boundary value problem for Föppl–Hencky membranes: Improvement of geometric equations. Mathematics 2020, 8, 631. [Google Scholar] [CrossRef]
- Sun, J.Y.; Rong, Y.; He, X.T.; Gao, X.W.; Zheng, Z.L. Power series solution of circular membrane under uniformly distributed loads: Investigation into Hencky transformation. Stuct. Eng. Mech. 2013, 45, 631–641. [Google Scholar] [CrossRef]
- Sun, J.Y.; Lian, Y.S.; Li, Y.M.; He, X.T.; Zheng, Z.L. Closed-form solution of elastic circular membrane with initial stress under uniformly-distributed loads: Extended Hencky solution. Z. Angew. Math. Mech. 2015, 95, 1335–1341. [Google Scholar] [CrossRef]
- Chien, W.Z.; Wang, Z.Z.; Xu, Y.G.; Chen, S.L. The symmetrical deformation of circular membrane under the action of uniformly distributed loads in its portion. Appl. Math. Mech. 1981, 2, 653–668. [Google Scholar]
- Alekseev, S.A. Elastic annular membranes with a stiff centre under the concentrated force. Eng. Corpus 1951, 10, 71–80. (In Russian) [Google Scholar]
- Chen, S.L.; Zheng, Z.L. Large deformation of circular membrane under the concentrated force. Appl. Math. Mech. 2003, 24, 28–31. [Google Scholar]
- Jin, C.R. Large deflection of circular membrane under concentrated force. Appl. Math. Mech. 2008, 29, 889–896. [Google Scholar] [CrossRef]
- Huang, P.F.; Song, Y.P.; Li, Q.; Liu, X.Q.; Feng, Y.Q. A theoretical study of circular orthotropic membrane under concentrated load: The relation of load and deflection. IEEE Access 2020, 8, 126127–126137. [Google Scholar] [CrossRef]
- Khapin, A.V.; Abdeev, B.M.; Makhiyev, B.E. Optimal size of an axisymmetric perfectly flexible membrane with a rigid centre loaded with a concentrated static force. IOP Conf. Ser. Mater. Sci. Eng. 2020, 775, 012138. [Google Scholar] [CrossRef]
- Strangeways, I. A history of rain gauges. Weather 2010, 65, 133–138. [Google Scholar] [CrossRef]
- Haselow, L.; Meissner, R.; Rupp, H.; Miegel, K. Evaluation of precipitation measurements methods under field conditions during a summer season: A comparison of the standard rain gauge with a weighable lysimeter and a piezoelectric precipitation sensor. J. Hydrol. 2019, 575, 537–543. [Google Scholar] [CrossRef]
- Saad Al-Wagdany, A. Intensity-duration-frequency curve derivation from different rain gauge records. J. King Saud Univ. Sci. 2020, 32, 3421–3431. [Google Scholar] [CrossRef]

| H | Maximum Deflection [mm] | Maximum Radial Stress [MPa] | ||||
|---|---|---|---|---|---|---|
| Presented Solution | Hencky Solution | Errors | Presented Solution | Hencky Solution | Errors | |
| 0.5 | 0.8169 | 0.6089 | 25.5% | 0.0184 | 0.0091 | 50.8% |
| 50 | 2.8733 | 2.7977 | 2.6% | 0.2005 | 0.1911 | 4.7% |
| 200 | 4.5161 | 4.5013 | 0.3% | 0.4969 | 0.4947 | 0.4% |
| (a) The values of ci at different n | ||||
| n | c0 | c2 | c4 | c6 |
| 4 | 2.5216650 × 10−2 | −4.4711868 × 10−3 | −4.5313948 × 10−4 | - |
| 6 | 2.5484214 × 10−2 | −4.3775807 × 10−3 | −4.2827528 × 10−4 | −7.5232361 × 10−5 |
| 8 | 2.5550954 × 10−2 | −4.3544054 × 10−3 | −4.2226218 × 10−4 | −7.3567411 × 10−5 |
| 10 | 2.5569445 × 10−2 | −4.3479638 × 10−3 | −4.2060234 × 10−4 | −7.3110446 × 10−5 |
| 12 | 2.5574842 × 10−2 | −4.3460754 × 10−3 | −4.2011702 × 10−4 | −7.2977069 × 10−5 |
| 14 | 2.5576464 × 10−2 | −4.3455055 × 10−3 | −4.1997075 × 10−4 | −7.2936900 × 10−5 |
| 16 | 2.5576960 × 10−2 | −4.3453305 × 10−3 | −4.1992585 × 10−4 | −7.2924572 × 10−5 |
| 18 | 2.5577114 × 10−2 | −4.3452760 × 10−3 | −4.1991189 × 10−4 | −7.2920739 × 10−5 |
| 20 | 2.5577163 × 10−2 | −4.3452589 × 10−3 | −4.1990751 × 10−4 | −7.2919536 × 10−5 |
| 22 | 2.5577178 × 10−2 | −4.3452535 × 10−3 | −4.1990612 × 10−4 | −7.2919156 × 10−5 |
| 24 | 2.5577183 × 10−2 | −4.3452518 × 10−3 | −4.1990568 × 10−4 | −7.2919035 × 10−5 |
| (b) The values of ci at different n | ||||
| n | c8 | c10 | c12 | c14 |
| 8 | −1.5488504 × 10−5 | - | - | - |
| 10 | −1.5357045 × 10−5 | −3.5823498 × 10−6 | - | - |
| 12 | −1.5318738 × 10−5 | −3.5710160 × 10−6 | −8.9013785 × 10−7 | - |
| 14 | −1.5307207 × 10−5 | −3.5676061 × 10−6 | −8.8910802 × 10−7 | −2.3216086 × 10−7 |
| 16 | −1.5303669 × 10−5 | −3.5665600 × 10−6 | −8.8879213 × 10−7 | −2.3206398 × 10−7 |
| 18 | −1.5302569 × 10−5 | −3.5662349 × 10−6 | −8.8869395 × 10−7 | −2.3203386 × 10−7 |
| 20 | −1.5302224 × 10−5 | −3.5661328 × 10−6 | −8.8866314 × 10−7 | −2.3202441 × 10−7 |
| 22 | −1.5302115 × 10−5 | −3.5661005 × 10−6 | −8.8865339 × 10−7 | −2.3202143 × 10−7 |
| 24 | −1.5302080 × 10−5 | −3.5660903 × 10−6 | −8.8865029 × 10−7 | −2.3202047 × 10−8 |
| (c) The values of ci at different n | ||||
| n | c16 | c18 | c20 | c22 |
| 16 | −6.2711514 × 10−8 | - | - | - |
| 18 | −6.2702167 × 10−8 | −1.7397329 × 10−8 | - | - |
| 20 | −6.2699234 × 10−8 | −1.7396410 × 10−8 | −4.9288360 × 10−9 | - |
| 22 | −6.2698306 × 10−8 | −1.7396119 × 10−8 | −4.9287442 × 10−9 | −1.4203606 × 10−9 |
| 24 | −6.2698011 × 10−8 | −1.7396027 × 10−8 | −4.9287150 × 10−9 | −1.4203513 × 10−9 |
| (d) The value of c24 at n = 24 | ||||
| n | c24 | - | - | - |
| 24 | −4.1511468 × 10−10 | - | - | - |
| (a) The values of di at different n | ||||
| n | d0 | d2 | d4 | d6 |
| 4 | 1.4389897 × 10−1 | −1.3373387 × 10−1 | −1.0165102 × 10−2 | - |
| 6 | 1.4380527 × 10−1 | −1.3232658 × 10−1 | −9.7095072 × 10−3 | −1.7991832 × 10−3 |
| 8 | 1.4373309 × 10−1 | −1.3197584 × 10−1 | −9.5986248 × 10−3 | −1.7643172 × 10−3 |
| 10 | 1.4368872 × 10−1 | −1.3187818 × 10−1 | −9.5679741 × 10−3 | −1.7547332 × 10−3 |
| 12 | 1.4367240 × 10−1 | −1.3184954 × 10−1 | −9.5590098 × 10−3 | −1.7519351 × 10−3 |
| 14 | 1.4366673 × 10−1 | −1.3184090 × 10−1 | −9.5563083 × 10−3 | −1.7510923 × 10−3 |
| 16 | 1.4366481 × 10−1 | −1.3183824 × 10−1 | −9.5554791 × 10−3 | −1.7508337 × 10−3 |
| 18 | 1.4366417 × 10−1 | −1.3183741 × 10−1 | −9.5552212 × 10−3 | −1.7507533 × 10−3 |
| 20 | 1.4366395 × 10−1 | −1.3183716 × 10−1 | −9.5551403 × 10−3 | −1.7507281 × 10−3 |
| 22 | 1.4366388 × 10−1 | −1.3183707 × 10−1 | −9.5551147 × 10−3 | −1.7507201 × 10−3 |
| 24 | 1.4366386 × 10−1 | −1.3183705 × 10−1 | −9.5551066 × 10−3 | −1.7507175 × 10−3 |
| (b) The values of di at different n | ||||
| n | d8 | d10 | d12 | d14 |
| 8 | −3.9431453 × 10−4 | - | - | - |
| 10 | −3.9128051 × 10−4 | −9.6550465 × 10−5 | - | - |
| 12 | −3.9039607 × 10−4 | −9.6267818 × 10−5 | −2.5251202 × 10−5 | - |
| 14 | −3.9012984 × 10−4 | −9.6182775 × 10−5 | −2.5223804 × 10−5 | −6.8962634 × 10−6 |
| 16 | −3.9004815 × 10−4 | −9.6156686 × 10−5 | −2.5215401 × 10−5 | −6.8935385 × 10−6 |
| 18 | −3.9002276 × 10−4 | −9.6148576 × 10−5 | −2.5212789 × 10−5 | −6.8926917 × 10−6 |
| 20 | −3.9001479 × 10−4 | −9.6146031 × 10−5 | −2.5211969 × 10−5 | −6.8924259 × 10−6 |
| 22 | −3.9001227 × 10−4 | −9.6145227 × 10−5 | −2.5211710 × 10−5 | −6.8923419 × 10−6 |
| 24 | −3.9001147 × 10−4 | −9.6144970 × 10−5 | −2.5211627 × 10−5 | −6.8923151 × 10−6 |
| (c) The values of di at different n | ||||
| n | d16 | d18 | d20 | d22 |
| 16 | −1.9420161 × 10−6 | - | - | - |
| 18 | −1.9417401 × 10−6 | −5.5954589 × 10−7 | - | - |
| 20 | −1.9416535 × 10−6 | −5.5951754 × 10−7 | −1.6411662 × 10−7 | - |
| 22 | −1.9416261 × 10−6 | −5.5950858 × 10−7 | −1.6411368 × 10−7 | −4.8827855 × 10−8 |
| 24 | −1.9416174 × 10−6 | −5.5950573 × 10−7 | −1.6411274 × 10−7 | −4.8827547 × 10−8 |
| (d) The value of d24 at n = 24 | ||||
| n | d24 | - | - | - |
| 24 | −1.4698279 × 10−8 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Sun, J.-Y.; Lu, X.-C.; Yang, Z.-X.; He, X.-T. Steady Fluid–Structure Coupling Interface of Circular Membrane under Liquid Weight Loading: Closed-Form Solution for Differential-Integral Equations. Mathematics 2021, 9, 1105. https://doi.org/10.3390/math9101105
Li X, Sun J-Y, Lu X-C, Yang Z-X, He X-T. Steady Fluid–Structure Coupling Interface of Circular Membrane under Liquid Weight Loading: Closed-Form Solution for Differential-Integral Equations. Mathematics. 2021; 9(10):1105. https://doi.org/10.3390/math9101105
Chicago/Turabian StyleLi, Xue, Jun-Yi Sun, Xiao-Chen Lu, Zhi-Xin Yang, and Xiao-Ting He. 2021. "Steady Fluid–Structure Coupling Interface of Circular Membrane under Liquid Weight Loading: Closed-Form Solution for Differential-Integral Equations" Mathematics 9, no. 10: 1105. https://doi.org/10.3390/math9101105
APA StyleLi, X., Sun, J.-Y., Lu, X.-C., Yang, Z.-X., & He, X.-T. (2021). Steady Fluid–Structure Coupling Interface of Circular Membrane under Liquid Weight Loading: Closed-Form Solution for Differential-Integral Equations. Mathematics, 9(10), 1105. https://doi.org/10.3390/math9101105






