Sign, Wilcoxon and Mann-Whitney Tests for Functional Data: An Approach Based on Random Projections

Abstract

Sign, Wilcoxon and Mann-Whitney tests are nonparametric methods in one or two-sample problems. The nonparametric methods are alternatives used for testing hypothesis when the standard methods based on the Gaussianity assumption are not suitable to be applied. Recently, the functional data analysis (FDA) has gained relevance in statistical modeling. In FDA, each observation is a curve or function which usually is a realization of a stochastic process. In the literature of FDA, several methods have been proposed for testing hypothesis with samples coming from Gaussian processes. However, when this assumption is not realistic, it is necessary to utilize other approaches. Clustering and regression methods, among others, for non-Gaussian functional data have been proposed recently. In this paper, we propose extensions of the sign, Wilcoxon and Mann-Whitney tests to the functional data context as methods for testing hypothesis when we have one or two samples of non-Gaussian functional data. We use random projections to transform the functional problem into a scalar one, and then we proceed as in the standard case. Based on a simulation study, we show that the proposed tests have a good performance. We illustrate the methodology by applying it to a real data set.

1. Introduction

Different phenomena in diverse fields can be modeled by means of random observations that are represented as curves. Since the beginning of the nineties, the functional data analysis (FDA) [1] has been used to describe, analyze and model this type of observations. The FDA is concerned with the study of realizations of functional random variables, that is, variables taking values in an infinite dimensional space [2]. Functional versions of a wide spectrum of statistical areas (as exploratory data analysis [3], linear models [4], sampling [5], time series [6], geostatistics [7] and multivariate analysis [8], among others) have been developed. A state-of-the-art review on methodological, practical and theoretical aspects of the FDA can be found in [9,10].

Statistical inference based on FDA has shown recently new theoretical developments [11,12]. There has been an increasing interest in methods for testing hypothesis using data from functional variables. Some basic inferential techniques in one-sample problems for functional data are given in [13]. In the case of two-sample problems, testing hypothesis that the generating distributions of two sets of curves are identical has been approached in several contexts, such as differences in mean curves, covariance functions or cumulative distribution functions (CDFs) [14]. In addition, in [1], a pointwise t-test is introduced, whereas in [15], a method to test whether two groups of curves have the same mean function is presented, when these curves are observed at different times without noise. Furthermore, a pseudolikelihood ratio test is derived in [16] and a $L_2$-norm-based test of the two-sample Behrens-Fisher problem for functional data is proposed and studied in [17] (note that it tests the equality of mean functions of two Gaussian processes with possibly unequal covariance functions). A review of several tests when two or more functional samples are involved is given in [13]. In a distribution-free context, the Anderson-Darling statistic for testing the null hypothesis that two samples of curves (observed with noise at discrete grids) have the same underlying distribution is derived in [14]. Many authors have treated the problem of testing hypothesis with more than two functional samples. Several alternatives for one-or-two-way ANOVA have been proposed in [18,19,20,21]. These methods can be applied to the two-sample case.

Some approaches to solve the two-sample problem for functional data are based on the Gaussianity assumption [13,15], that is, they assume that the sample at each group is a realization of a Gaussian stochastic process. Other approaches suppose that functional variables follow a Wishart process with some of them requiring homoscedasticity [13]. In a nonparametric context, some methods based on permutations and bootstrap have become very popular for testing hypothesis with functional data [15]. This is probably due to the flexibility of permutation methods to test complex hypothesis, especially when the asymptotic distributions are difficult to derive or the parametric assumptions are hard to justify. To the best of our knowledge, no studies on the adaptation of the sign, Wilcoxon and Mann-Whitney statistics [22,23] to the context of functional data have been conducted.

The objective of this paper is to derive the sign, Wilcoxon, and Mann-Whitney statistics using data from functional variables. We utilize random projections [21] to transform the functional problem into a scalar one, and then we proceed as in the standard case by using these statistics. As mentioned, there are several statistics that may be applied when the curves come from Gaussian processes. Consequently, the procedures proposed here are particularly useful when curves and random projections are realizations of non-Gaussian stochastic processes.

The rest of the paper is organized as follows. In Section 2, a review about both standard nonparametric tests for one-sample and two-sample problems, as well as some concepts on FDA, are provided. In Section 3, the sign, Wilcoxon and Mann-Whitney tests for functional data based on random projections are defined. In Section 4, the numerical results of this study are reported. First, a Monte Carlo simulation study is conducted to evaluate the performance of the results proposed, and then we provide an application of the proposed tests to a real data set. The paper ends with some conclusions, discussion and future research in Section 5.

2. Background

This section is based on the works presented in [1,21,22,23]. First, we provide an overview about the sign and Wilcoxon tests for one-sample and two-sample problems. Then, we present the pointwise t-test for functional data and hypothesis testing for Gaussian functional data based on random projections.

2.1. Sign, Wilcoxon and Mann-Whitney Tests

Let $X_1,\dots ,X_n$ be a random sample drawn from a symmetric distribution with CDF $F_X$ with median $\theta$. Suppose we are interested in testing the hypotheses given by

$${\mathrm{H}}_0:\theta ={\theta }_0\mathrm{versus}{\mathrm{H}}_1:\theta \ne {\theta }_0.$$

Defining $Z_i=X_i-{\theta }_0$, for $i=1,\dots ,n$, the above hypotheses can be written as

$${\mathrm{H}}_0:\theta =0\mathrm{versus}{\mathrm{H}}_1:\theta \ne 0,$$

where $\theta$ is the median of the random variable Z. Now, consider the absolute values $|Z_i|$, for $i=1,\dots ,n$, and order them increasingly. Let $R_i$ denote the rank of $|Z_i|$ in this ordering, for $i=1,\dots ,n$. To compute the sign (S) and Wilcoxon ($T^{+}$) statistics, for $i=1,\dots ,n$, define an indicator variable stated as

$${\psi }_i=\left\{\begin{array}{c}1,\mathrm{if}{Z}_i>0;\hfill \\ 0,\mathrm{if}{Z}_i\le 0;\hfill \end{array}\right.$$

and set

$$S=\sum _{i=1}^n{\psi }_i,T^{+}=\sum _{i=1}^n{R}_i{\psi }_i.$$

(1)

The statistic S defined in (1) is the number of positive values of Z and $T^{+}$ is the sum of signed ranks of $Z_i$ that are positive. At the level $\alpha$ of significance, ${\mathrm{H}}_0$ is rejected if $S\ge B_{1-\alpha /2}(n,1/2)$ or $S\le n-B_{1-\alpha /2}(n,1/2)$, where $B_{1-\alpha /2}(n,1/2)$ is the $(1-\alpha /2)\times$ 100-th percentile of the binomial distribution with sample size n and $p=1/2$ [23]. Analogously, ${\mathrm{H}}_0$ is rejected if $T^{+}\ge t_{1-\alpha /2}$ or $T^{+}\le n(n+1)/2-t_{1-\alpha /2}$, where $t_{1-\alpha /2}$ is chosen to make the type I error probability equal to $\alpha$. Values of $t_{1-\alpha /2}$ are given in Table A.4 of [23].

In the case of a paired sample $(X_{11},X_{12}),\dots ,(X_{n1},X_{n2})$ from a bivariate distribution with CDF $F_{X_1,X_2}$ with medians ${\theta }_1$ and ${\theta }_2$, the statistics S and $T^{+}$ defined in (1) may also be used to test the hypotheses established as

$${\mathrm{H}}_0:{\theta }_1={\theta }_2\mathrm{versus}{\mathrm{H}}_1:{\theta }_1\ne {\theta }_2,$$

by taking

$${\psi }_i=\left\{\begin{array}{c}1,\mathrm{if} X_{i2}>X_{i1};\hfill \\ 0,\mathrm{if} X_{i2}\le X_{i1};\hfill \end{array}\right.$$

and using again a binomial distribution or the critical values from the distribution of the statistic $T^{+}$ [23]. In this case, $|Z_i| = |X_{i2}-X_{i1}|$ and $R_i$ is the rank of $|Z_i|$, for $i=1,\dots ,n$. In both cases (one sample and paired sample), a large-sample approximation based on the standard Gaussian distribution can be used.

When $X_1,\dots ,X_m$ and $Y_1,\dots ,Y_n$ are two independent random samples from distributions with CDFs $F_X$ and $F_Y$, respectively, the Wilcoxon [24] or Mann-Whitney [25] statistics may be considered as alternatives to test the hypotheses stated as

$${\mathrm{H}}_0:F_X\left(\omega \right)=F_Y\left(\omega \right)\mathrm{versus}{\mathrm{H}}_1:F_X\left(\omega \right)\ne F_Y\left(\omega \right),\mathrm{for}\mathrm{every} \omega .$$

In this case, the Wilcoxon (W) and the Mann-Whitney (U) statistics are defined respectively as

$$W=\sum _{j=1}^n{R}_j,U=\sum _{i=1}^n\sum _{j=1}^m\varphi (X_i,Y_j),$$

with $R_j$ denoting the rank of $Y_j$, for $j=1,\dots ,n$, in the combined sample of size $N=m+n$, and

$$\varphi (X_i,Y_j)=\left\{\begin{array}{c}1,\mathrm{if}{X}_i>Y_j;\hfill \\ 0,\mathrm{if}{X}_i\le Y_j.\hfill \end{array}\right.$$

Note that ${\mathrm{H}}_0$ is rejected at the level $\alpha$ if $W\ge w_{1-\alpha /2}$ or if $W\le n(m+n+1)-w_{1-\alpha /2}$. The critical values $w_{1-\alpha /2}$ are given in Table A.6 of [23]. Mann and Whitney [25] showed that, in case of no ties, one has

$$U=W-\frac{n(n+1)}{2},$$

(2)

which implies that tests based on U are equivalent to tests based on W [23]. In both cases (Wilcoxon and Mann-Whitney statistics), large sample approximations based on Gaussianity of W and U allow us to carry out the tests using critical values of the standard Gaussian distribution.

2.2. Functional Data and Random Projections

A functional variable $X\left(t\right)$, for $t\in T$, is defined in [2] as a random variable taking values in a space of functions. Then, $X_1\left(t\right),\dots ,X_n\left(t\right)$ are a random sample of $X\left(t\right)$, that is, $X_i\left(t\right)$, for $i=1,\dots ,n$, are independent and identically distributed functional variables following the same underlying distribution of $X\left(t\right)$. Given that in practice the functions are known only for a finite number of measured values, a model is required to fit the function $X_i\left(t\right)$. Usually this modeling is carried out by using basis functions [1], which are a system of known functions ${\varphi }_1\left(t\right),\dots ,{\varphi }_k\left(t\right)$ that are mathematically independent of each other. This system approximates arbitrarily well any curve by a linear combination of a sufficiently large number K of these functions [9]. Fourier, B-splines and wavelet smoothing methods are widely used in this context [17]. Generally, the number of basis functions for smoothing is chosen by cross-validation [1].

In the case of one sample, the problem for functional data is described as follows. Suppose we have a random sample $X_1\left(t\right),\dots ,X_n\left(t\right)$ coming from a stochastic process with mean function $\mu \left(t\right)$, for $t\in T$, and covariance function $\gamma (s,t)$, for $s,t\in T$. Let $x_1\left(t\right),\dots ,x_n\left(t\right)$ be the observations of $X_1\left(t\right),\dots ,X_n\left(t\right)$ obtained after using a smoothing method. Now, the hypotheses of interest are stated as

$${\mathrm{H}}_0:\mu \left(t\right)={\mu }_0\left(t\right)\mathrm{versus}{\mathrm{H}}_1:\mu \left(t\right)\ne {\mu }_0\left(t\right),$$

(3)

where ${\mu }_0\left(t\right)$ is some known fixed function. A review of alternatives to test the hypothesis in (3) is given in [13], where pointwise, $L^2$-norm-based and F-type tests are introduced, among others. Almost all of these tests are based on the Gaussianity assumption, that is, they assume that $X\left(t\right)\sim \mathrm{N}(\mu ,\gamma )$, for each t. The simplest option in this case is the pointwise test. Under Gaussianity, we have

$$T\left(t\right)=\frac{\sqrt{n}\left(\overline{X}\left(t\right)-{\mu }_0\left(t\right)\right)}{\sqrt{\widehat{\gamma }(t,t)}}\sim t_{(n-1)},$$

(4)

with $\overline{X}\left(t\right)=(1/n){\sum }_{i=1}^n{X}_i\left(t\right)$. The null hypothesis is rejected whenever the observed absolute value of $T\left(t\right)$ defined in (4) and based on the observations $x_1\left(t\right),\dots ,x_n\left(t\right)$ is greater than $t_{1-\alpha /2,(n-1)}$, where $t_{1-\alpha /2,(n-1)}$ denotes the $(1-\alpha /2)\times 100$-th percentile of the Student-t distribution with $n-1$ degrees of freedom. The case of a paired sample $(X_{i1}\left(t\right),X_{i2}\left(t\right))$, for $i=1\dots ,n$, or two independent samples $(X_i\left(t\right),Y_j\left(t\right))$, for $i=1\dots ,n$ and $j=1,\dots ,m$, can be tested similarly defining the statistic $T\left(t\right)$ stated in (4) properly; see details in [15]. When the Gaussianity assumption is not satisfied, tests based on bootstrap [13] and permutations [26] may be applied.

Random projections refer to the technique of mapping a set of points from a high dimensional space to a randomly chosen low-dimensional space [27]. Given a set of functional data $x_1\left(t\right),\dots ,x_n\left(t\right)$, for $t\in T$, the hypotheses of interest can be tested projecting the functions on a one-dimensional subspace generated by $\nu \left(t\right)$ in H, where H is a separable Hilbert space of square integrable functions. Thus, $x_i={\int }_T^{}{x}_i\left(t\right)\nu \left(t\right)\mathrm{d}t$, for $i=1,\dots ,n$, where often $\nu \left(t\right)$ is a Brownian motion. Random projections have been recently applied in many contexts of the FDA [28], such as goodness-of-fit tests [29], clustering [30], and ANOVA [21], among others.

3. Sign, Wilcoxon and Mann Withney Tests for Functional Data

This section derives the sign, Wilcoxon and Mann-Whitney tests for functional data based on random projections for one-sample and two-sample problems.

3.1. The Case of One Sample

Let $X_1\left(t\right),\dots ,X_n\left(t\right)$ be a sample from a stochastic process with median function $\theta \left(t\right)$, for $t\in T$, defined in the space $C\left(I\right)$ of real continuous functions on the compact interval I. The hypotheses of interest are given by

$${\mathrm{H}}_0:\theta \left(t\right)={\theta }_0\left(t\right)\mathrm{versus}{\mathrm{H}}_1:\theta \left(t\right)\ne {\theta }_0\left(t\right),$$

(5)

where ${\theta }_0\left(t\right)$ is some particular function. In order to carry out the test:

• Define $Z_i\left(t\right)=X_i\left(t\right)-{\theta }_0\left(t\right)$, for $i=1\dots ,n$.
• Generate a Brownian motion $\nu \left(t\right)$, for $t\in T$.
• Obtain random projections $Z_i={\int }_T{Z}_i\left(t\right)\nu \left(t\right)\mathrm{d}t$, for $i=1,\dots ,n$.
• Let $\theta$ be the median of Z. Then, based on $Z_i$, for $i=1,\dots ,n$, test the hypotheses given by

  $${\mathrm{H}}_0:\theta =0\mathrm{versus}{\mathrm{H}}_1:\theta \ne 0,$$

  using the statistics S and $T^{+}$ defined in (1). The critical values are defined in the same way as in Section 2.1.

In the case of a paired functional sample $(X_{11}\left(t\right),X_{12}\left(t\right)),\dots ,(X_{n1}\left(t\right),X_{n2}\left(t\right))$ from a bivariate functional vector $(X_1\left(t\right),X_2\left(t\right))$ with medians ${\theta }_1\left(t\right)$ and ${\theta }_2\left(t\right)$, respectively, for $t\in T$, the statistics S and $T^{+}$ stated in (1) can be also used to test the hypotheses established as

$${\mathrm{H}}_0:{\theta }_1\left(t\right)={\theta }_2\left(t\right)\mathrm{versus}{\mathrm{H}}_0:{\theta }_1\left(t\right)\ne {\theta }_2\left(t\right),$$

(6)

defining $Z_i=|{\int }_T{X}_{i2}\left(t\right)\nu \left(t\right)\mathrm{d}t-{\int }_T{X}_{i1}\left(t\right)\nu \left(t\right)\mathrm{d}t|$ and ${\psi }_i$ as

$${\psi }_i=\left\{\begin{array}{c}1,\mathrm{if}{\int }_T{X}_{i2}\left(t\right)\nu \left(t\right)\mathrm{d}t>{\int }_T{X}_{i1}\left(t\right)\nu \left(t\right)\mathrm{d}t;\hfill \\ 0,\mathrm{if}{\int }_T{X}_{i2}\left(t\right)\nu \left(t\right)\mathrm{d}t\le {\int }_T{X}_{i1}\left(t\right)\nu \left(t\right)\mathrm{d}t;\hfill \end{array}\right.$$

with $\nu \left(t\right)$, for $t\in T$, being a Brownian motion. In both cases for the hypotheses defined in (5) and (6), a large sample approximation based on the Gaussian distribution may be used by standardizing the statistics S and $T^{+}$ [23].

3.2. The Case of Two Samples

Let $X_1\left(t\right),\dots ,X_m\left(t\right)$ and $Y_1\left(t\right),\dots ,Y_n\left(t\right)$ be two independent random samples from the functional variables $X\left(t\right)$ and $Y\left(t\right)$ with medians ${\theta }_X\left(t\right)$ and ${\theta }_Y\left(t\right)$, respectively. Suppose we want to test the hypotheses stated as

$${\mathrm{H}}_0:{\theta }_X\left(t\right)={\theta }_Y\left(t\right)\mathrm{versus}{\mathrm{H}}_0:{\theta }_X\left(t\right)\ne {\theta }_Y\left(t\right).$$

Then, the random projections given by

$$X_i={\int }_T{X}_i\left(t\right)\nu \left(t\right)\mathrm{d}t,i=1,\dots ,m,$$

and

$$Y_j={\int }_T{Y}_j\left(t\right)\nu \left(t\right)\mathrm{d}t,j=1,\dots ,n,$$

can be used once again to test these hypotheses using the Mann-Whitney and Wilcoxon statistics defined in (2).

4. Numerical Results

This section reports the numerical results of our study. First, a simulation study is conducted to evaluate the performance of the tests proposed, and then we apply these tests to a real data set.

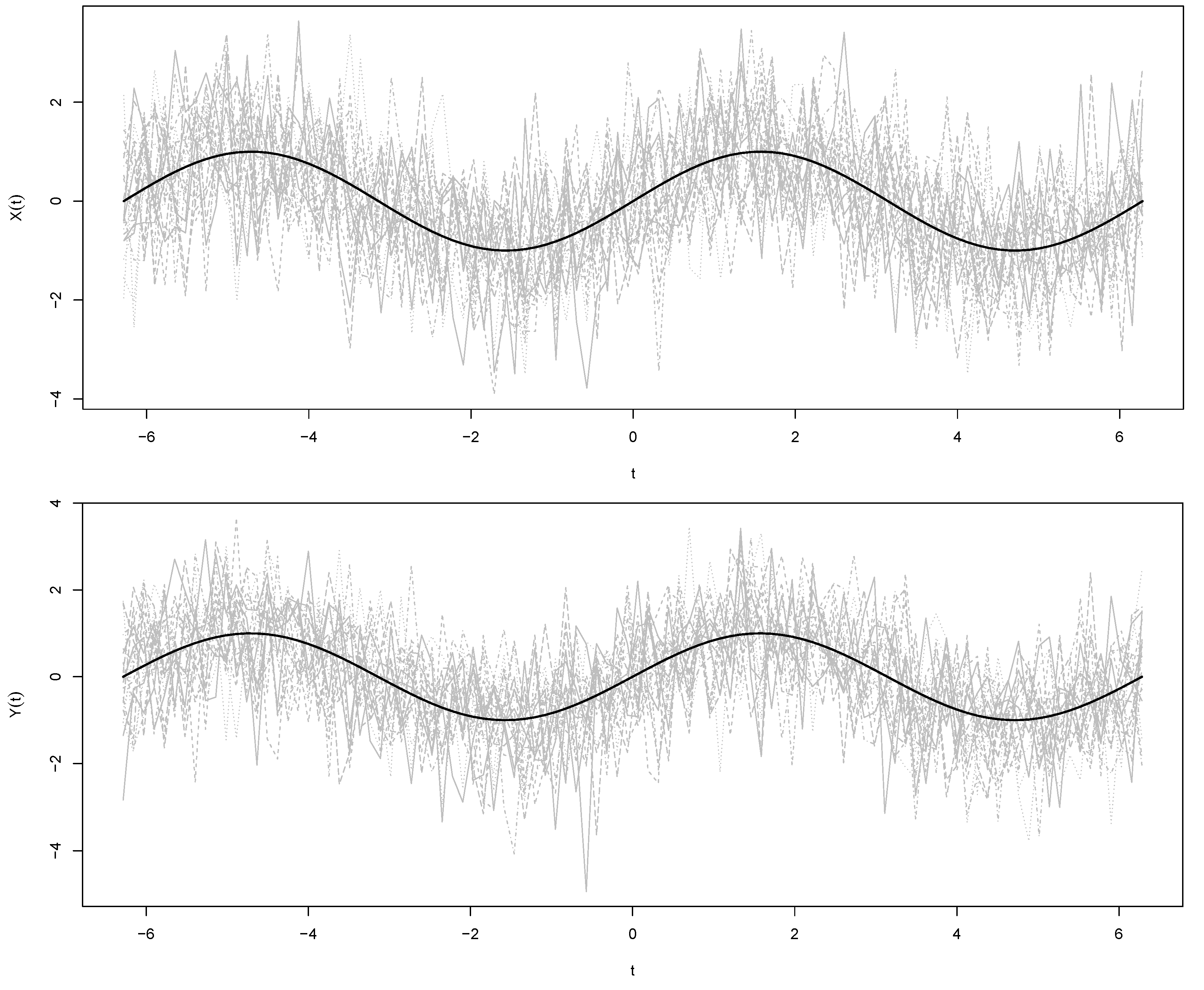
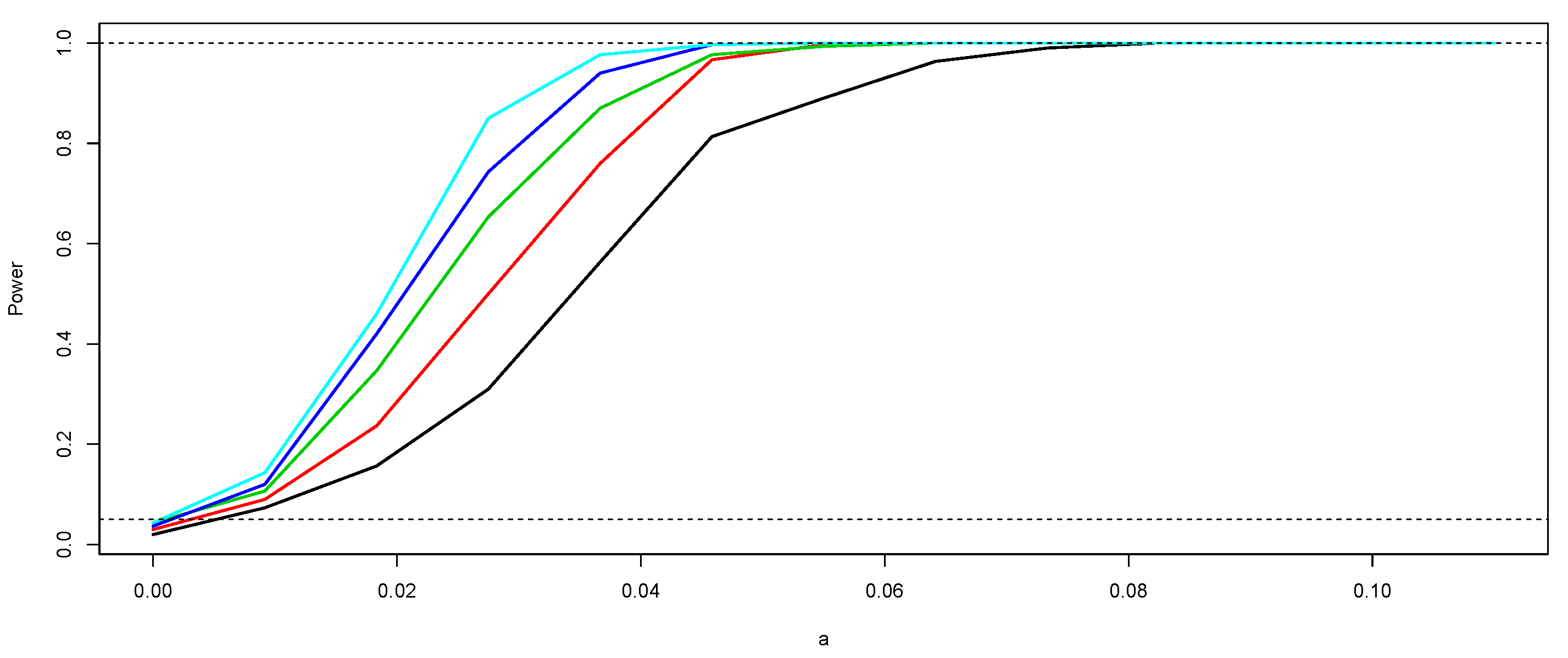
4.1. Simulation Study

We perform Monte Carlo simulations to evaluate the methodology presented in Section 3. We assess the power of the test for detecting differences between medians of two functional paired samples, with the one-sample problem being a particular case.

Consider a set of paired curves $(X_1\left(t\right),Y_1\left(t\right)),\dots ,(X_n\left(t\right),Y_n\left(t\right))$ with

$$X_i\left(t\right)=\mu \left(t\right)+{\epsilon }_{i1}\left(t\right),$$

(7)

and

$$Y_i\left(t\right)=\mu \left(t\right)+a\left(t\right)+{\epsilon }_{i2}\left(t\right),$$

(8)

where $\mu \left(t\right)=\sin \left(t\right)$, for $t\in [-2\pi ;2\pi ],$ is a common mean function, whereas ${\epsilon }_{i1}\left(t\right)$ and ${\epsilon }_{i2}\left(t\right)$ are a paired stochastic process with generalized Tukey-lambda distribution [31]. To obtain the realizations $(x_1\left(t\right),y_1\left(t\right)),\dots ,(x_n\left(t\right),y_n\left(t\right))$, the paired stochastic process $({\epsilon }_{i1}\left(t\right),{\epsilon }_{i2}\left(t\right))$, for $i=1,\dots ,n$, is simulated by using the function rpaired.gld of an R library named PairedData [32]. To simulate curves under the null hypothesis, consider the models defined in (7) and (8) with $a\left(t\right)=0\left(t\right)$, that is, a constant function at zero for all t, and $n=50$; see Figure 1.

In order to evaluate the power of the sign and Wilcoxon tests, we take $a\left(t\right)=a$, for all $t\in [-2\pi ;2\pi ]$, with $a=0.01,\dots ,0.11$. We consider five sample sizes $n=50,80,100,120,150$. At each case, 1000 realizations are generated and used to estimate empirically the power of the tests. Based on each sample size n, we conduct both a sign and Wilcoxon test as defined in Section 3. We utilize the libraries PASWR [33] and stats of R to carry out the tests at each iteration. At each case, the power of the test is obtained as the percentage of p-values less than 0.05. As an illustration, the simulations under the null hypothesis (with $n=50$) are shown in Figure 1. With the data of this simulation, the p-values obtained are 0.03 and 0.04, respectively. Following a similar procedure based on 1000 simulations, the p-values obtained were 0.03 (sign test) and 0.046 (Wilcoxon test). In Figure 2 and Figure 3, we show the empirical power curves of the tests for each one of the sampling sizes n and values $a\left(t\right)=a$. In both figures, note that the power of the tests increases when $a\left(t\right)$ and n increase, that is, the simulation study provides evidence that the sign and Wilcoxon tests for functional data proposed here are unbiased and consistent empirically. It is important to emphasize that, in the case of the Wilcoxon test, a symmetry test [34,35] must be performed beforehand. A comparison of the power curves in Figure 2 and Figure 3 indicates that, as in the standard case, the Wilcoxon test is slightly more powerful.

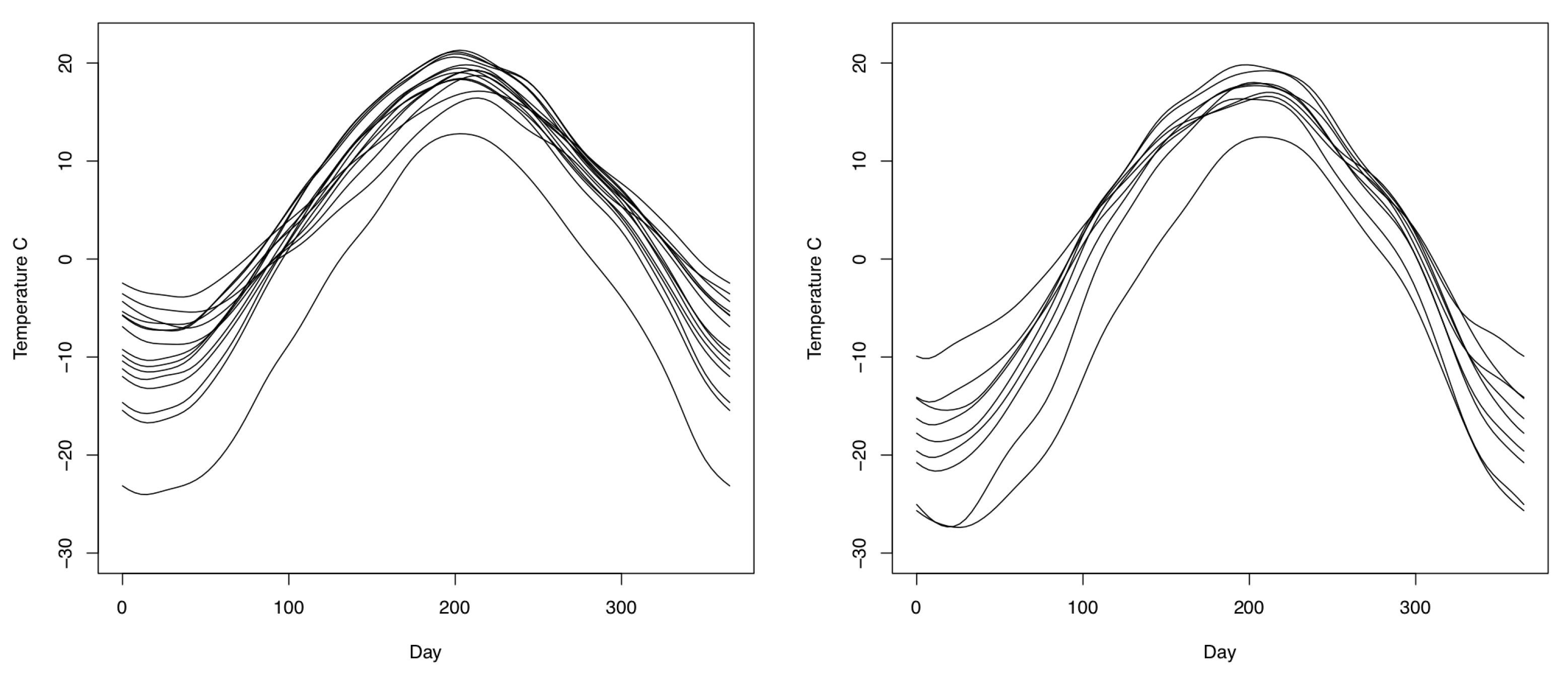
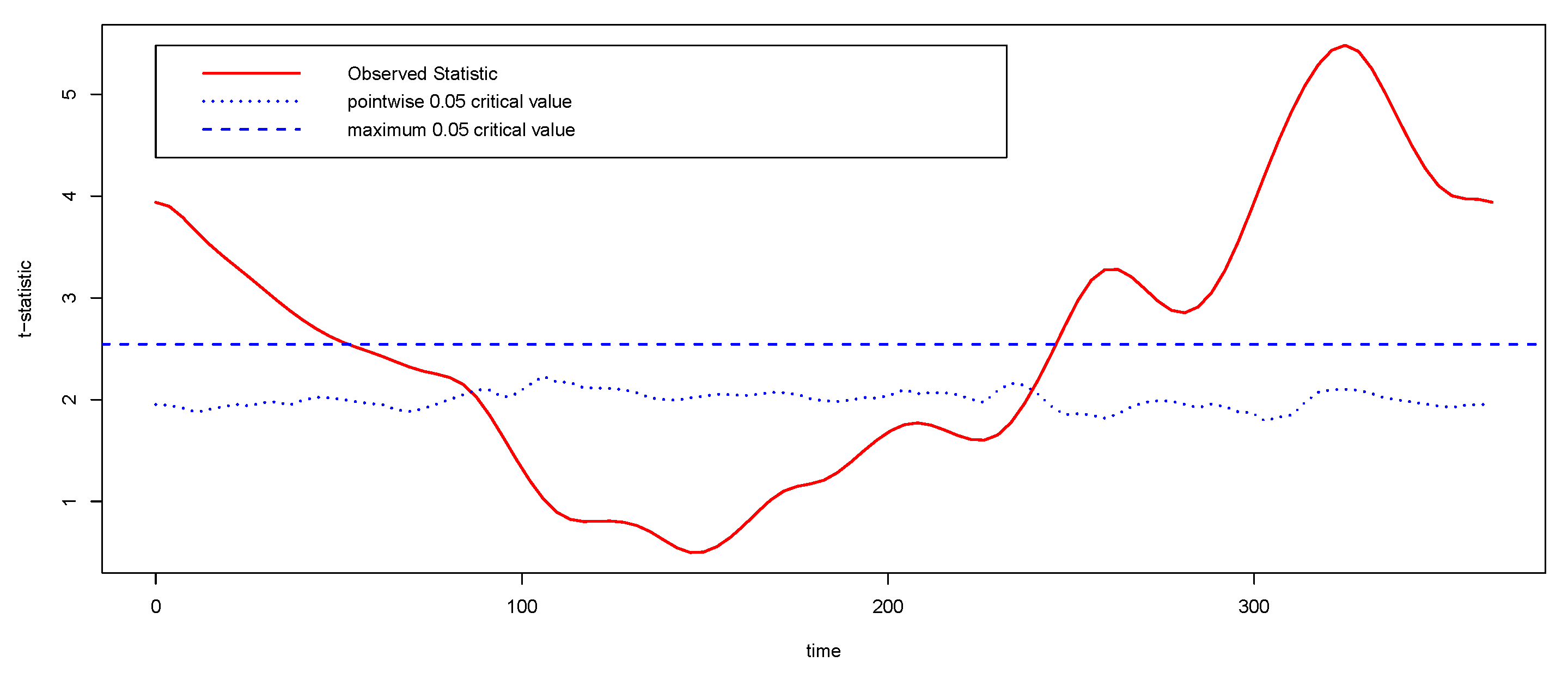
4.2. Application to Canadian Temperature Data

We apply the Mann-Whitney test of Section 3 to a meteorological data set widely used in FDA. This data set corresponds to daily average (30 years) of temperature (in Celsius degrees) at each one of 35 weather stations located across climate zones of Canada [1]. Some approaches for ANOVA, regression and cluster analysis [36] for functional data have been illustrated using this data set.

We show that statistical inference for functional data assuming Gaussianity can be unrealistic with these data and that the approaches presented here are valid alternatives under this scenario of non-Gaussianity. In order to carry out the analysis, we use the data from Atlantic and Continental zones (15 and 9 stations, respectively); see Figure 4. The data for each station are obtained from Ramsay and Silverman’s website (http://www.functionaldata.org). We smooth the data for each station using 65 Fourier basis functions. The number of basis functions is obtained by the generalized cross-validation criterion. According to [26], temperature curves of Atlantic coastal display little amplitude cool winters and summers. They appear to have a temperature around five Celsius degrees warmer than the Canadian average. In addition, the temperature of Continental stations show high amplitude and peakedness with cold winters and hot summers. Note that they are slightly warmer than average in the summer but are colder in the winter by about five Celsius degrees; see Figure 4. These descriptions suggest that there are heterogeneous patterns between these two data sets. In order to establish from a statistical point of view if there are significant differences between these zones, we apply a Mann-Whitney test for functional data as described in Section 3.

Initially, a Brownian motion $\nu \left(t\right)$ is generated. Then, we compute the random projections

$$X_i=\underset{T}{\int }{X}_i\left(t\right)\nu \left(t\right)\mathrm{d}t,i=1,\dots ,15,$$

and

$$Y_j=\underset{T}{\int }{Y}_j\left(t\right)\nu \left(t\right)\mathrm{d}t,j=1,\dots ,9,$$

where $X_i\left(t\right)$ and $Y_j\left(t\right)$ are the smoothed curves based on the Fourier basis. By using $X_i$ and $Y_j$, the Mann-Whitney test is applied. Before performing this test, the projections of each group are tested for Gaussianity using the Shapiro-Wilk test. The p-values of this test are 0.0013 (Atlantic zone) and 0.044 (Continental zone), respectively. This indicates that, in both cases we reject the hypothesis of Gaussianity at a level of significance $\alpha =0.05$, which suggests that using a two-sample t-test for these functional data is inadequate. In this scenario of non-Gaussianity, a Mann-Whitney test is a better alternative. The p-value for this test is 0.0013, that is, there are significant differences between the median temperature curves of both zones.

In order to establish in which periods of the year the differences occur, we apply a pointwise t-test for functional data based on permutations (a valid approach because this test does not assumes Gaussianity) using the function tperm.fd of the an R library named fda [26]; see Figure 5. The dotted line in this Figure suggests that differences between these zones are given in both January to March and September to December. The results found are consistent with the description of Canada’s climate variability, since the Atlantic and Continental regions have opposite temperature patterns. The Atlantic region of Canada is typically warmer during the winter and cooler during the summer, while in this season the parts of the country farthest from open water are the coldest ones. Note that our statistical analysis performed contributes to the explanation of these differences.

5. Conclusions, Discussion and Future Research

This paper reported the following findings:

(i)

An extension of the sign test to the functional data context was proposed.

(ii)

The Wilcoxon test in the functional data field was derived.

(iii)

The Mann-Whitney test for functional data analysis was stated.

(iv)

The power of the tests for detecting differences between medians of two functional paired samples was evaluated by Monte Carlo simulations.

(v)

An illustration with a real data set was considered to show potential applications of the results proposed.

In summary, we proposed nonparametric alternatives of methods used for testing hypothesis when one-sample, paired-sample and two-sample problems with non-Gaussian functional data are stated. We utilized random projections to become the functional problem into a scalar one, and then we proceeded as in the standard case. Based on a simulation study, we showed that the proposed tests have a good performance. Specifically, the empirical power curve for the sign test provided evidence that this test is unbiased and consistent. The same result was obtained with the Wilcoxon test. We illustrated our methods with a real data set. Thus, our proposal may be a knowledge addition to the tools of diverse practitioners, including engineers, statisticians and data scientists.

Some additional aspects which deserve study for future work in this field, which arose from the present investigation, are the following:

(i)

A power comparison between global tests for one-sample and two-sample problems with functional data can be considered.

(ii)

The extension to the case of a nonparametric test for the k-sample problem and designs in random blocks are also of interest.

(iii)

Applications to other models involving functional data are also of practical relevance [37,38,39,40,41,42,43].

(iv)

Usages of the methodology considered in this study may be of interest in diverse fields where the functional data analysis is employed [1].

Therefore, the proposed methodology in this study promotes new challenges and opens other issues to be considered in future research.