Abstract
In investment selection problems, the existence of contingency and uncertainty may result in the loss of attribute information. Then, how to make proper investment decision-making will be a tricky proposition. In this work, a multiattribute group decision making (MAGDM) method based on the generalized probabilistic hesitant fuzzy Bonferroni mean (GPHFBM) operator is constructed, which enables decision-makers to select the proper parameters in decision-making process. Firstly, the GPHFBM operator is proposed by combining the Bonferroni mean operator and Archimedean norm. Secondly, five excellent properties of the GPHFBM operator are discussed in detail. In view of applications, we further develop some special aggregation operators for GPHFBM with the various values of parameters b, d and additive operators g(t). Finally, we propose a probabilistic hesitant fuzzy MAGDM method based on the GPHFBM operator to analyze the aggregated information. A case study of the investment of social insurance funds is given to depict the validity and reasonability of the proposed method. Ultimately, the company is selected as the investment company with the best comprehensive indicator.
1. Introduction
Ageing of the population [1] is a prominent trend in social development and a reflection of the progress of human civilization. Population ageing has a profound impact on all areas of economic operation, social construction, social culture and even the overall strength and international competitiveness of the country, with both challenges [2] and opportunities [3]. Social insurance funds (SIFs) are mainly derived from social insurance premiums and the return on their investment, as well as appropriate inputs from the National Treasury. SIFs are established on the basis of the social security system and can be invested to obtain certain returns. SIFs generally take the form of social insurance funds, social welfare funds, social assistance funds etc., of which social insurance funds are the most important form of capital operation, and the funds can be used for investment, stocks and bonds [4]. Social insurance funds involve pensions, unemployment, medical insurance and so on. The investment of social insurance funds has a certain degree of selectivity [5]. Therefore, how to improve the return on investment is worthy of attention for social insurance fund managers.
Fund investment involves important financial decision-making that directly affects the development of the fund, and can be seen as a MAGDM problem. The development of decision-making theory has driven social and economic progress while facing some irreversible problems, such as the increasingly complex decision-making environment, the fuzzy uncertainty of human cognition and so on [6,7,8]. With the complexity and uncertainty of the real-world, it is challenging to describe practical decision-making problems with precise and clear numbers. It is worth noting that the environment of investment is full of uncertainty which is an important factor in MAGDM.
To overcome the issues in describing practical decision-making problems, Zadeh [9] proposed the theory of fuzzy sets (FSs). It has effectively solved some decision-making problems with fuzzy information and attracted many scholars’ attention and extended research on the problem of fuzzy decision-making. As an extension of FSs, Atanassov in [10] presented intuitionistic fuzzy sets (IFSs). Furthermore, Torra in [11,12] proposed hesitant fuzzy sets (HFSs), which described membership degree with several real values to express decision information. Some researchers also applied automatic techniques to the construction of fuzzy systems [13,14,15]. Although HFSs has some advantages in expressing decision-making, they cannot be accurate in depicting the original decision information and avoiding the loss of information.
In this regard, several researchers have taken the idea of probability into consideration in the hesitant fuzzy environment, some of them focused on information aggregation. For instance, some aggregation operators were presented by Zhang et al. [16], in which the average and geometric operators of probabilistic hesitant fuzzy sets (PHFSs) were shown. They deserve to be recognized but contain two flaws. One is that its operator does not satisfy idempotency, the other is that its integration algorithm process is more complicated. To solve this problem, Wu et al. [17] added the idea of an Archimedean norm in the probabilistic hesitant fuzzy environment and further defined new operational rules for probabilistic hesitant fuzzy elements. The Archimedean norm is an effective aggregation tool, which makes the aggregation method simpler and more flexible. Two aggregation operators, probabilistic hesitant fuzzy prioritized weighted average (PHFPWA) and probabilistic hesitant fuzzy prioritized weighted geometric (PHFPWG), were applied into an MADM problem by Li et al. [18]. Hao et al. [19] gave a definition of probabilistic dual hesitant fuzzy set (PDHFS), and further developed an approach of information fusion and visualization with some aggregation operators. Under the PDHFSs environment, Garg and Kaur [20] proposed several weighted ordered weighted averaging and geometric aggregation operators based on Einstein norm operation. Li et al. [21] introduced q-rung probabilistic dual hesitant fuzzy sets (q-RPDHFSs) to effectively depict DMs’ complicated evaluation information. Considering the importance of the correlation coefficient in data analysis, Song et al. [22] introduced a couple of new correlation coefficient expressions to measure the nexus between the PHFSs. Moreover, some of the researches have applied probability to linguistic term sets [23,24] and preference relations [25,26].
However, the indicators used for decision making do not exist independently in the investment process. None of the probabilistic hesitant fuzzy information aggregation operators described above take into account the situation that is often present in investment decision-making problems, namely that there is usually some interconnection between the decision-making information provided. During the process of information aggregation, the Bonferroni mean (BM) proposed by Bonferroni [27] considers the interrelationship between the input arguments, then some extended forms of BM are studied. Pamucar et al. [28] designed a new normalized interval rough numbers weighted geometric BM (IRNWGBM) operator. Based on the Archimedean t-norm and s-norm (ATS-), Wang et al. [29] developed two aggregation operators, hesitant Fermatean 2-tuple linguistic weighted Bonferroni mean (A-HF2TLWBM) operator and the hesitant Fermatean 2-tuple linguistic weighted geometric Bonferroni mean (A-HF2TLWGBM) operator, respectively. Combing the IFSs and the Dempster-Shafer Theory (DST), Liu and Gao [30] proposed the intuitionistic fuzzy power BM (IFPBMDST) operator, the intuitionistic fuzzy geometric power BM (IFGPBMDST) operator. Liu et al. [31] proposed a novel GSS method by combining Quality function deployment (QFD) with the partitioned BM (PBM) operator in the context of interval type-2 fuzzy sets (IT2FSs). Yin et al. [32] united the PBM operator into the interval grey triangular fuzzy numbers to aggregate interval grey triangular fuzzy numbers partitioned Bonferroni mean (IGTFPBM). Liang et al. [33] introduced the EBM into the interval-valued Pythagorean fuzzy environment, based on which, interval-valued Pythagorean fuzzy EBM (IVPFEBM) operator and its weighted form were developed. Moreover, some studies integrated Dombi norms and BM to better express subjective preferences of decision makers [34,35,36]. Compared to Dombi norms, the Archimedean norms are the generalizations of a lot of norms, such as Algebraic norms, Einstein norms, Hamacher norms and Frank norms. Archimedean norms also can reflect the decision-makers preference when the and are chosen as different functional forms. Therefore, Archimedean norms are more generalizable and more promising for a wider range of applications.
From the above analysis, there is growing recognition that probability should also be applied in fuzzy decision-making. Currently, some researchers have discussed BM aggregation operators under different fuzzy environments, but the results under probabilistic and hesitant fuzzy environments are still scarce. Zhu and Ma [37] developed the integration of BM operators, but they did not consider the probability of decision-making. In contrast, although Li and Chen [38] incorporated the idea of probability, the aggregation operators they proposed could not depict the correlation between the indicators. In this study, a new group decision-making method is presented by aggregating BM operators under a probabilistic hesitant fuzzy environment, which has the following advantages: (1) to better portray decision-making information; (2) to better express the correlation between aggregated values and (3) to be more generalizable and more promising for a wider range of applications.
The remainder of this paper is organized as follows. In Section 2, some fundamentals, including probabilistic hesitant fuzzy set, Bonferroni mean and Archimedean norm, are briefly reviewed. Section 3 defines the generalized probabilistic hesitant fuzzy Bonferroni mean (GPHFBM), and five desirable properties of the GPHFBM are discussed. Section 4 introduces several special forms of the GPHFBM, which considers the difference both parameters b, d and g(t) respectively. Then, Section 5 develops the generalized probabilistic hesitant fuzzy weighted Bonferroni mean (GPHFWBM) operator, and a group decision-making model is constructed. Section 6 presents one illustrative example of investment, and comparative analyses are implemented simultaneously on the proposed approach and other existing methods. In the last part, conclusions and contents are summarized in Section 7.
2. Preliminaries
This section briefly reviews some fundamentals, which includes PHFSs, BMs and Archimedean T-norm and S-norm.
2.1. Probabilistic Hesitant Fuzzy Sets
Definition 1.
[16] Suppose that is a given set, and the PHFSs is expressed as follows:
where is the probabilistic hesitant fuzzy element (PHFE). denotes the possible membership degrees of the element , and is the probability associated with .
For the convenience of application and description, PHFE will be denoted as , and is the set of all PHFE on .
Example 1.
A network distributor invites ten experts to evaluate the comprehensive conditions of a supplier. The satisfaction of four experts was 0.9, that of two experts was 0.7, that of three experts was 0.5, and that of the remaining one was 0.4. The above decision information can be expressed as a hesitant fuzzy element (HFE), that is . Obviously, the HFEs can only represent all possible decision information, but ignore the importance of each decision information. The PHFEs represent the above decision information as , which is a comprehensive representation of all the evaluation information given by the decision maker and the corresponding importance level.
In many practical applications, some decision-makers are unable to make assessments with certain and accurate information, so the following notes are shown:
Note 1 The elements in PHFE are arranged in descending order, where indicates the element corresponding to the k-th membership degree of .
Note 2 Let and be the numbers of elements in PHFEs and , respectively. If , then make the length of them be equal through adding elements and the probability of new element is 0.
Note 3 For convenience, let the number of elements in PHFEs be all equal.
Definition 2.
[16] Suppose that is a PHFE, and the score function of is defined below:
Definition 3.
[16] Suppose that is a PHFE, and its deviation degree is defined below:
Definition 4.
[16] Suppose that there are two PHFEs
and the rules are provided to compare and :
- 1.
- If , then .
- 2.
- If and , then .
- 3.
- If and , then .
- 4.
- If and , then .
2.2. Archimedean T-Norm and S-Norm
Archimedean norm is a simple and effective integration tool, which can make the aggregated method more selective and flexible.
Definition 5.
[39] Let T-norm be continuous in the domain of definition , and that for any
, , then is an Archimedean T-norm.
Definition 6.
[39] Let S-norm be continuous in the domain of definition , and that for any
, , then is an Archimedean S-norm.
For an additive operator in strictly monotone decrease, the strict Archimedean T-norm can be denoted as , where . In the light of the principle of duality, we can obtain which called the strict Archimedean S-norm, where . Hence, is a strictly monotonic increasing function, and .
Generally, is a T-norm function, is a T-conorm function, and are two functions, satisfying . For example, if , then , , .
2.3. Generalized Probabilistic Hesitant Fuzzy Operation Rules
Definition 7.
[17] Let and be three PHFEs, then:
- 1.
- ,
- 2.
- 3.
- 4.
- ,
- 5.
- .
where the standardized probability is , and it satisfies .
It’s not hard to prove that the above-mentioned operational rules for PHFEs satisfy the following theorem.
Theorem 1.
[17] Let be three PHFEs, then:
- 1.
- ,
- 2.
- ,
- 3.
- ,
- 4.
- ,
- 5.
- ,
- 6.
- .
Proof.
Based on Definition 7, the above theorems can be proved by the law of exchange, distribution, union and exponentiation.
2.4. Bonferroni Mean Operator
In MAGDM, DMs should not only consider the importance of various attributes but also take the interrelationship into account. As a useful aggregation operation, the Bonferroni mean operator considers the interrelationship among arguments.
Definition 8.
[27] Let , and
be a set of non-negative numbers, then the Bonferroni mean (BM) operator is shown as:
Generally, the BM has the following properties:
- 1.
- .
- 2.
- If for all , then .
- 3.
- If for all , then .
- 4.
where , and be a set of non-negative numbers.
Several special cases of the BM discussed by Dyckhoff and Pedrycz [40] are introduced as follows:
If , then
If and , then Equation (4) reduces to the arithmetic mean
If , then
If and , then
If and , then Equation (4) reduces to the geometric mean
If , then
3. Generalized Probabilistic Hesitant Fuzzy Bonferroni Mean Operator
To aggregate decision information while considering the intrinsic linkage between indicators, the Generalized Probabilistic Hesitant Fuzzy Bonferroni Mean operator is proposed and its related properties are investigated.
Definition 9.
Suppose that there is a set of PHFEs , for any , the Generalized Probabilistic Hesitant Fuzzy Bonferroni Mean (GPHFBM) operator is defined as follows:
Theorem 2.
Suppose that there are two parameters and , and is a set of PHFEs, then the aggregated value by using the GPHFBM is:
where .
Proof.
(1) By the Definition 3 and Theorem 1, we can get the following equations: , and
by Definition 5, we have
then
which completes the proof.
(2) To prove the value aggregated by the GPHFBM is a PHFE, we have the following discussions:
Since , and are all strictly monotone decreasing function. For all , we have
Simultaneous action of function on both sides of the above inequalities, we know
then, according to the expression of , we know .
To sum up, the aggregated value with the GPHFBM is a PHFE, which completes the proof.
In the follow-up part, let us discuss five properties of GPHFBM, i.e., monotonicity, idempotency, boundness, commutativity and symmetry.
Property 1.
(Monotonicity)Let and be two sets of PHFEs. If
for any and , then we have
Proof.
By the proof of Theorem 2, we can know the GPHFBM is monotonically increasing. When for all and , it follows that
i.e., , which completes the proof.
Property 2.
(Idempotency)Let be a set of PHFEs. If and , for any , then we have
Proof.
Since , we have
Since , we have
We complete the proof of Property 2.
Property 3.
(Boundedness)Let be a set of PHFEs, and . If and , then we have
Proof.
According to Property 1, we get , which finishes the proof of the property. □
Property 4.
(Commutativity)Let be a set of PHFEs, and be any permutation , then
Property 5.
(Symmetry)Let be a set of PHFEs and
, then
4. Some Special GPHFBM Operators
Considering the difference between parameters and additive operators, and several special forms will be studied in this part.
4.1. Different Combinations of Parameter Values b, d
Case 1. If , the GPHFBM operator is the generalized probabilistic hesitant fuzzy mean (GPHFM) operator:
Case 2. If and , the GPHFBM operator degenerates to the probabilistic hesitant fuzzy mean (PHFM) operator:
Case 3. If and , we get the generalized probabilistic hesitant fuzzy square mean (GPHFSM) operator:
Case 4. If and , the probabilistic hesitant fuzzy maximum mean (PHFMM) operator is:
Case 5. If , the generalized probabilistic hesitant fuzzy interactive square mean (GPHFISM) operator is:
4.2. Additive Operators with Different Functions
- (1)
- When , the GPHFBM operator degenerates to the probabilistic hesitant fuzzy Bonferroni mean (PHFBM) operator:
- (2)
- When , the GPHFBM operator is the probabilistic hesitant fuzzy Einstein Bonferroni mean (PHFEBM) operator:where
Example 2.
Suppose and are three PHFEs. We have:
Based on Equations (11) and (12), we get
Then, the corresponding score values can be obtained by the score function in Equation (2).
The score values changed with the variety of the parameters are shown in Figure 1,Figure 2 and Figure 3.
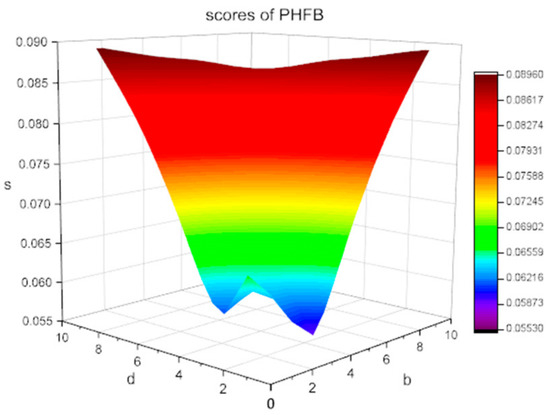
Figure 1.
Scores of the probabilistic hesitant fuzzy Bonferroni mean (PHFBM) varying with parameters b and d .
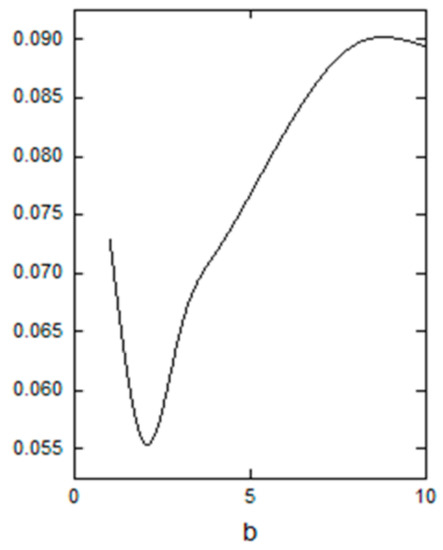
Figure 2.
Scores of the PHFBM .
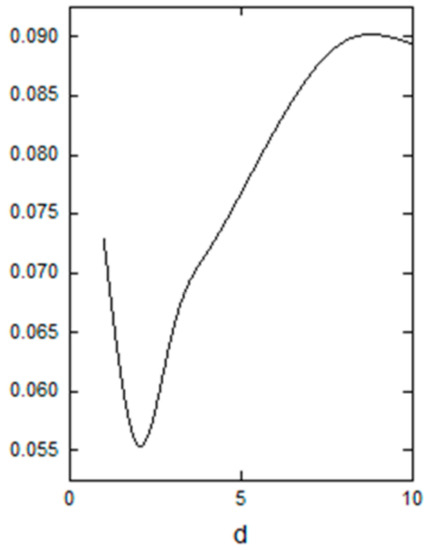
Figure 3.
Scores of the PHFBM .
5. The GPHFWBM and Its Approach in MAGDM
5.1. Generalized Probabilistic Hesitant Fuzzy Weighted Bonferroni Mean Operator
Considering the importance of attribute weights, we further introduce the generalized probabilistic hesitant fuzzy weighted Bonferroni mean (GPHFWBM) operator.
Definition 10.
Let be a set of PHFEs, and be the weight vector of them. For any , the generalized probabilistic hesitant fuzzy weighted Bonferroni mean (GPHFWBM) operator is defined as follows:
where denotes the important degree of , and it satisfies that and .
Theorem 3.
Let be a set of PHFEs, and the associated weight vector be , . The value aggregated by the GPHFWBM operator is also a PHFE, and is denoted as:
where denotes the important degree of , and it satisfies that and .
5.2. Model for Group Decision Making with the GPHFWBM Operator
Suppose that is a given set of alternatives, is attribute set with the weight vector satisfying and . Given the purpose for a complete and accurate description of the decision-making information provided by experts, we utilize the PHFE to depict the evaluation information under the attributes of the alternatives , and a probabilistic hesitant fuzzy decision matrix is constructed.
Generally, there are cost attributes and benefit attributes in a MAGDM problem. For the decision matrix , we have
Next, we further present an approach for MAGDM, which comprises the steps listed below.
Step 1. According to the decision-making evaluation information given by the experts, we construct the probabilistic hesitant fuzzy Bonferroni mean decision matrix
Step 2. Standardize decision matrix into matrix .
Step 3. Based on the standardized decision matrix , we aggregate the comprehensive attribute information of each alternative by using the GPHFWBM operator.
Step 4. By the Equation (2) calculate the score function values .
Step 5. Rank all the alternatives by , and the optimal comprehensive performance alternative is selected.
6. Application of Social Insurance Fund Investment
In this section, the proposed DM method is applied to solve the investment of SIFs and compared and analyzed with existing methods.
6.1. Illstrative Example
At present, with the continuous improvement of the social security system covering urban and rural areas in China, the accumulation of social insurance funds is increasing rapidly and the methods of bank deposits and the purchase of government bonds provided for in the current policy can no longer meet the need to preserve and increase the value of the funds. As China’s economic development enters a new normal, the population base is large, and the pace of ageing is rapid. The social insurance fund is an important tool for safeguarding the basic life of the aging population, maintaining social stability and promoting economic development, but is also an important issue related to national livelihood. China’s social insurance funds have such problems as small total volume, slow growth and large costs, and optimizing investment in basic pensions is of great importance.
It is assumed that the Fund Investment Department of the National Council of Social Security Funds needs to invest part of its capital in the market to increase its earnings in order to maintain the sustainable growth of the fund. Through the preliminary market research and technical screening conducted by relevant institutions, the following five companies which can be invested are initially identified as . The following five aspects should be considered in investment, with the weight vector .
- 1.
- Financial status. Finances are an effective guarantee for the normal operation of an enterprise. They consist mainly of the inventory turnover status, financial management rationality, asset-liability ratio, current asset-liability ratio and so on.
- 2.
- Production status. The capacity of production and supplying raw materials determines an enterprise’s construction and operation ability, and also determine its sustainable development ability.
- 3.
- Management capacity. An enterprise’s management mechanism and corporate culture determines its social influence, which affects the development of the enterprise in the future. Management capacity mainly includes enterprise mechanism system, organizational system rationality, advancement, corporate culture, and restraint and incentive mechanisms and so on.
- 4.
- Technology. Advanced technology not only can enhance the development potential of an enterprise, but also can safeguard the sustainable development of it. Technical factors include enterprise research and development conditions, follow-up research and development capabilities, emphasis on research and development personnel, etc.
- 5.
- Market. Market is a very important factor to consider in investment, which directly determines the efficiency of the investment return and the solution of the exit problem of the social security fund. Market factors include the evaluation of a company’s reputation, product competitiveness, market channels, market strategy, etc.
Through a series of preliminary work, the five investment companies finally selected met the above five criteria. Therefore, three experts from finance, insurance, and social security were invited to make the final score and decision on the five companies initially screened. The weight vector of experts was . Based on the above three relevant evaluation matrices (Table 1, Table 2 and Table 3), the decision-making steps were as follows.

Table 1.
Evaluation values given by financial expert.

Table 2.
Evaluation values given by insurance expert.

Table 3.
Evaluation values given by social security expert.
Step 1. Considering all the attributes are benefit type attributes and there is no necessary for standardization.
Step 2. Based on the decision-making evaluation information given by experts from Table 1, Table 2 andTable 3, the probabilistic hesitant fuzzy Bonferroni mean decision matrix is constructed by using the GPHFWBM (without losing generality, let and ),
which is shown in Table 4.

Table 4.
Probabilistic hesitant fuzzy Bonferroni mean decision matrix.
Step 3. The comprehensive attribute values of five alternatives are aggregated with the GPHFWBM operators. Without losing generality, let , parameters b and d take the following four cases respectively: (1) , (2) , (3) and (4) , see Table 5 for details.

Table 5.
Comprehensive attribute values of investment companies calculated by generalized probabilistic hesitant fuzzy weighted Bonferroni mean (GPHFWBM) operator.
Step 4. By the Equation (2) in Definition 2, the score values are calculated, respectively, as shown in Table 6.

Table 6.
Scores and ranking results of investment companies calculated by different operators.
Step 5. Rank all the alternatives sorted by in descending order. X4 is the optimal comprehensive performance (see Table 6).
The analysis shows that the best candidate is X4 and the proposed method is reasonable. For , one can get , which is different from the other result. When parameters b, d and g(t) are assigned different values and functional forms, various aggregation results can be obtained from different BM operators. Namely, the change of parameters b, d bring different decision results, and this can reflect the risk preference attitude of decision makers. When converges to zero, it can reflect the partial satisfaction relationship of aggregated values. Generally, we take in practice, which can grasp the interrelationship between arguments as much as possible. Nevertheless, the aggregated results with the proposed method are consistent, which shows the inherent consistency of them.
In terms of the results in Table 7, the fourth company is the most competent company for social insurance fund investment management, considering the five influencing factors in the case. However, the different values that are assigned to b, d lead to differences in the ranking of companies and . It also shows that the decision maker can choose different values of b, d according to the decision preference attitude.

Table 7.
Scores and ranking results of investment companies with
.
To more visually represent the aggregation results with b, d = [2,20], we plot Figure 4. Figure 4 represents the variation of the aggregated results with the value of d when b is a fixed value. As can be seen from the Figure 4, when b = 2, all five curves show a decreasing trend, and overall ranking is . Among them, the line X4 has the highest score values and X2 has the lowest score values. However, there is a slight difference in the ranking of X1 and X5, indicating that the different values of b, d affect the aggregation results.
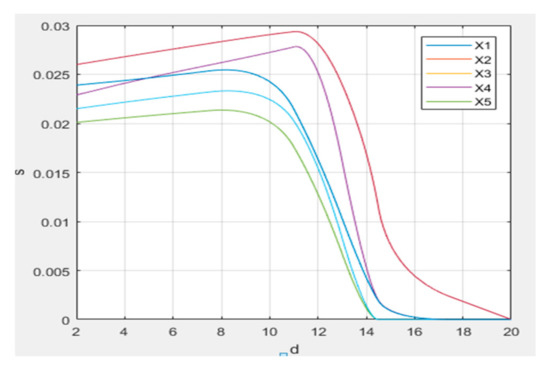
Figure 4.
Scores and ranking results of investment companies with .
- (1)
- As a whole, when b is fixed, the aggregation value decreases as the value of d increases.
- (2)
- By numerical simulation analysis, when , the aggregation results approach 0 and do not have an analytical value, so it is suggested that the values of b and d should satisfy .
- (3)
- For , is the best one. But when the aggregated results converge infinitely to 0. As b increases, the value of d should decrease if the result is meaningful.
6.2. Discussions
To testify reasonability and validity, we made a further comparison with the GHFWBM operators in [37] and the PHFWMSM in [38].
Zhu and Ma [37] developed a generalized hesitant fuzzy weighted Bonferroni mean (GHFWBM) operator:
According to the Equation (29), we aggregate attributes of the GHFWBM with conditions that
(1) , (2) , (3) and (4) . Then, the scores and the ranking of alternatives are shown in Table 8.

Table 8.
Score function values and ranking results of different candidates calculated by different operators.
Obviously, X4 is the best candidate, which is the same as the result of the proposed method. That is to say, the proposed method is reasonable and valid. Moreover, we took the probability of attribute values in the MAGDM problem into account, but the authors in [37] didn’t consider it. This further verifies that the proposed method can effectively reduce the loss of decision information.
Moreover, Li and Chen [38] presented a probabilistic hesitant fuzzy weighted Maclaurin symmetric mean operator:
Based on Equation (30), we aggregate attributes of the PHFWMSM with conditions that (1) , (2) . Then, the scores and the ranking of candidates are obtained in Table 8.
From the Table 8, it can be seen that the ranking result of the PHFMSM (when ) is consistent with that of the proposed method, which indicates the reasonability of this method. When , the ranking result of the PHFMSM changes, which shows that the proposed method is more stable than the PHFMSM operator. Otherwise, the BM, which has two parameters b and d, can capture the interrelationship of the individual arguments more than the MSM.
7. Conclusions
In practice, experts can not only make uncertain assessment of a given problem, but also describe their decision-making with some probabilistic information. Attribute information aggregation is a research hotspot. The main contributions of this paper are as follows. First, a new MAGDM method is constructed under the probabilistic hesitant fuzzy environment, which combines Archimedean norms and a BM operator. Then, based on the new operational rules, we propose a GPHFBM operator and discuss several desirable properties of the operator. In light of various values of parameters b, d and the additive operator g(t), several special cases of the GPHFBM operator are discussed. Finally, it is concluded that is the most suitable investment company by the application of investment of social insurance funds. Compared with the existing methods, the reasonability and reliability of the proposed method are verified.
However, the method proposed in this paper pays more attention to the cross-correlation between indicators in investment decision-making but ignores the overall correlation. Therefore, in future research, investment selection should be considered more from a holistic perspective. Besides, other norms can also be considered for aggregating the BM operator. Furthermore, how to obtain expert weights objectively is also worth studying in the future.
Author Contributions
Conceptualization, writing—original draft preparation, methodology, formal analysis, investigation, W.W. and Z.N.; writing—review and editing, W.W, F.J. and J.W.; supervision, Y.L. and P.L. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the National Natural Science Foundation of China (Nos. 71901001, 91546108, 71521001 and 71701061), Natural Science Foundation of Anhui Province (No. 2008085QG333), Key Research Project of Humanities and Social Sciences in Colleges and Universities of Anhui Province (No. SK2020A0038).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All authors declare that all data and materials generated or analyzed during this study are included in this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Verdiyeva, N. How the population of the Republic of Azerbaijan is ageing: Causes and potential for social and economic development. Popul. Econ. 2019, 3, 43–73. [Google Scholar] [CrossRef]
- Woo, J. Challenges of population ageing: Putting frailty as a cornerstone of health and social care systems. Eur. Geriatr. Med. 2018, 9, 273–276. [Google Scholar] [CrossRef]
- Lichtenstern, A.; Shevchenko, P.V.; Zagst, R. Optimal life-cycle consumption and investment decisions under age-dependent risk preferences. Math. Financ. Econ. 2020. [Google Scholar] [CrossRef]
- Shen, Y.; Zhu, K.H.; Wu, F.Y.; Chen, P. The Stock Investment Performance of Pension Funds in China. Emerg. Mark. Financ. Trade 2020, 56, 2732–2748. [Google Scholar] [CrossRef]
- Yang, T.; Meng, X.Z.; Zhang, H. Healthy, standardized and sustainable development—New features and trends of China’s foreign direct investment in 2018. J. Int. Econ. Coop. 2019, 1, 12–28. [Google Scholar]
- Krishankumar, R.; Ravichandran, K.S.; Ahmed, M.I.; Kar, S.; Peng, X. Interval-Valued Probabilistic Hesitant Fuzzy Set Based Muirhead Mean for Multi-Attribute Group Decision-Making. Mathematics 2019, 7, 342. [Google Scholar] [CrossRef]
- Zhang, Z.M. Multi-criteria group decision-making methods based on new intuitionistic fuzzy Einstein hybrid weighted aggregation operators. Neural Comput. Appl. 2017, 28, 3781–3800. [Google Scholar] [CrossRef]
- Zhang, C.; Li, D.Y.; Kang, X.P.; Liang, Y.; Broumi, S.; Sangaiah, A.K. Multi-Attribute Group Decision Making Based on Multigranulation Probabilistic Models with Interval-Valued Neutrosophic Information. Mathematics 2020, 8, 223. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009; pp. 1378–1382. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Rong, H.N.; Yi, K.; Zhang, G.X.; Dong, J.P.; Paul, P.; Huang, Z.W. Automatic Implementation of Fuzzy Reasoning Spiking Neural P Systems for Diagnosing Faults in Complex Power Systems. Complexity 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Lee, P.C.; Lo, T.P.; Tian, M.Y.; Long, D.B. An Efficient Design Support System based on Automatic Rule Checking and Case-based Reasoning. KSCE J. Civ. Eng. 2019, 23, 1952–1962. [Google Scholar] [CrossRef]
- Méndez, G.M.; Montes Dorantes, P.N.; Mexicano Santoyo, A. Interval type-2 fuzzy logic systems optimized by central composite design to create a simplified fuzzy rule base in image processing for quality control application. Int. J. Adv. Manuf. Technol. 2019, 102, 3757–3766. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Z.S.; He, Y. Operations and integrations of probabilistic hesitant fuzzy information in decision making. Inf. Fusion 2017, 38, 1–11. [Google Scholar] [CrossRef]
- Wu, W.Y.; Li, Y.; Jin, F.F.; Ni, Z.W.; Zhu, X.H. Probabilistic Interval-Valued Hesitant Fuzzy Information Aggregation Operators and Their Application to Multi-Attribute Decision Making. Algorithms 2018, 11, 120. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.X. Multi-attribute decision making based on prioritized operators under probabilistic hesitant fuzzy environments. Soft Comput. 2019, 23, 3853–3868. [Google Scholar] [CrossRef]
- Hao, Z.N.; Xu, Z.S.; Zhao, H.; Su, Z. Probabilistic dual hesitant fuzzy set and its application in risk evaluation. Knowl. Based Syst. 2017, 127, 16–28. [Google Scholar] [CrossRef]
- Garg, H.; Kaur, G. Algorithm for Probabilistic Dual Hesitant Fuzzy Multi-Criteria Decision-Making Based on Aggregation Operators with New Distance Measures. Mathematics 2018, 6, 280. [Google Scholar] [CrossRef]
- Li, L.; Lei, H.G.; Wang, J. Q-Rung Probabilistic Dual Hesitant Fuzzy Sets and Their Application in Multi-Attribute Decision-Making. Mathematics 2020, 8, 1574. [Google Scholar] [CrossRef]
- Song, C.Y.; Xu, Z.S.; Zhao, H. New Correlation Coefficients between Probabilistic Hesitant Fuzzy Sets and Their Applications in Cluster Analysis. Int. J. Fuzzy Syst. 2019, 21, 355–368. [Google Scholar] [CrossRef]
- Li, P.; Liu, J.; Yang, Y.J.; Wei, C.P. Evaluation of poverty-stricken families in rural areas using a novel case-based reasoning method for probabilistic linguistic term sets. Comput. Ind. Eng. 2020, 147, 106658. [Google Scholar] [CrossRef]
- Yue, N.; Xie, J.; Chen, S. Some new basic operations of probabilistic linguistic term sets and their application in multi-criteria decision making. Soft Comput. 2020, 24, 12131–12148. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, Z.S. Probability calculation and element optimization of probabilistic hesitant fuzzy preference relations based on expected consistency. IEEE Trans. Fuzzy Syst. 2018, 26, 1367–1378. [Google Scholar] [CrossRef]
- Jin, F.F.; Garg, H.; Pei, L.D.; Liu, J.P.; Chen, H.Y. Multiplicative Consistency Adjustment Model and Data Envelopment Analysis-Driven Decision-Making Process with Probabilistic Hesitant Fuzzy Preference Relations. Int. J. Fuzzy Syst. 2020, 22, 2319–2332. [Google Scholar] [CrossRef]
- Bonferroni, C. Sulle medie multiple di potenze. Bolletino Mat. Ital. 1950, 5, 267–270. [Google Scholar]
- Pamuar, D.; Boani, D.; Lukovac, V.; Komazec, N. Normalized weighted geometric Bonferroni mean operator of interval rough numbers—Application in interval rough DEMATEL-COPRAS model. Facta Univ. Ser. Mech. Eng. 2018, 16, 171–191. [Google Scholar]
- Wang, H.; Wang, X.; Wang, L. Multicriteria Decision Making Based on Archimedean Bonferroni Mean Operators of Hesitant Fermatean 2-Tuple Linguistic Terms. Complexity 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Liu, P.D.; Gao, H. Some intuitionistic fuzzy power Bonferroni mean operators in the framework of Dempster–Shafer theory and their application to multicriteria decision making. Appl. Soft Comput. 2019, 85, 105790. [Google Scholar] [CrossRef]
- Liu, P.D.; Gao, H.; Ma, J.H. Novel green supplier selection method by combining quality function deployment with partitioned Bonferroni mean operator in interval type-2 fuzzy environment. Inf. Sci. 2019, 490, 292–316. [Google Scholar] [CrossRef]
- Yin, K.D.; Yang, B.S.; Jin, X. Grey Fuzzy Multiple Attribute Group Decision-Making Methods Based on Interval Grey Triangular Fuzzy Numbers Partitioned Bonferroni Mean. Symmetry 2020, 12, 628. [Google Scholar] [CrossRef]
- Liang, D.C.; Darko, A.P.; Xu, Z.S. Interval-valued Pythagorean fuzzy extended Bonferroni mean for dealing with heterogenous relationship among attributes. Int. J. Intell. Syst. 2018, 33, 1381–1411. [Google Scholar] [CrossRef]
- Liu, P.D.; Liu, J.L.; Chen, S.M. Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J. Oper. Res. Soc. 2018, 69, 1–24. [Google Scholar] [CrossRef]
- Fan, J.P.; Jia, X.F.; Wu, M.Q. Green Supplier Selection Based on Dombi Prioritized Bonferroni Mean Operator with Single-Valued Triangular Neutrosophic Sets. Int. J. Comput. Intell. Syst. 2019, 12, 1091–1101. [Google Scholar] [CrossRef]
- Peng, X.D.; Smarandache, F. Novel neutrosophic Dombi Bonferroni mean operators with mobile cloud computing industry evaluation. Expert Syst. 2019, 36, 1–22. [Google Scholar] [CrossRef]
- Zhu, L.; Ma, Q.G. Generalized hesitant fuzzy Bonferroni mean and its application to multi-criteria group decision making. Comput. Eng. Appl. 2016, 52, 12–17. [Google Scholar]
- Li, B.P.; Chen, H.Y. Multi-attribute Group Decision Making Model Based on the Probabilistic Hesitant Fuzzy Maclaurin Symmetric Mean Operators. Fuzzy Syst. Math. 2018, 32, 130–142. [Google Scholar]
- Xia, M.M.; Xu, Z.S.; Zhu, B. Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm. Knowl. Based Syst. 2012, 31, 78–88. [Google Scholar] [CrossRef]
- Dyckhoff, H.; Pedrycz, W. Generalized means as model of compensative connectives. Fuzzy Sets Syst. 1984, 14, 143–154. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).