Dispersion Trading Based on the Explanatory Power of S&P 500 Stock Returns
Abstract
1. Introduction
2. Theoretical Framework
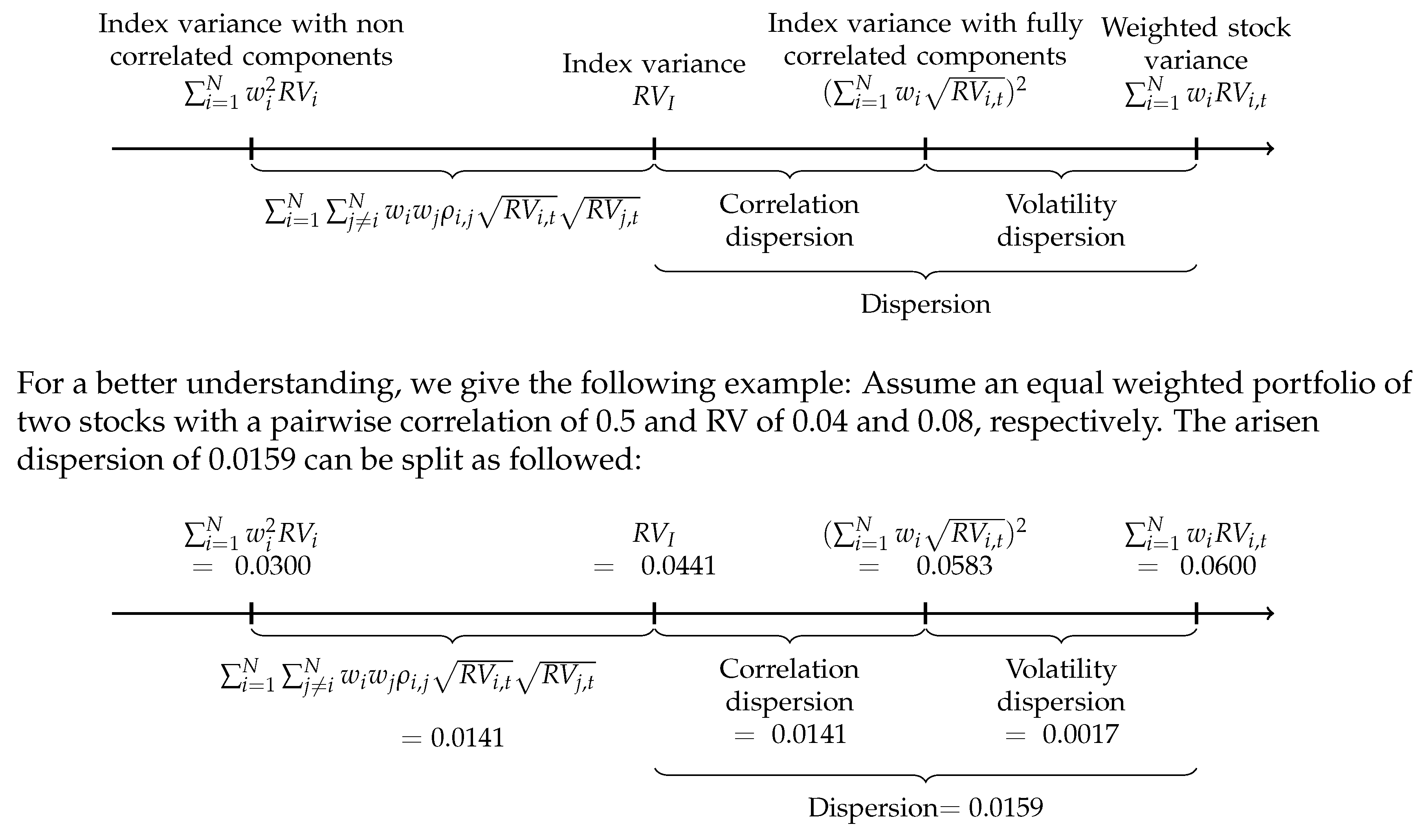
2.1. Dispersion Foundation and Trading Rational
2.2. Dispersion Trading Strategies
2.2.1. At-The-Money Straddle
2.2.2. At-the-Money Straddle with Delta Hedging
3. Back-Testing Framework
3.1. Data and Software
3.2. Formation Period
- Calculate the covariance matrix of all index members based on the trailing twelve month daily log returns.
- Decompose the covariance matrix into the eigenvector and order the principal components according to their explanatory power.
- Determine the first I principal components that cumulatively explain of the variance.
- Compute the explained variation of every index constituent through performing Steps 1 and 2 while omitting the specific index member and comparing the new explained variance of the I components to that of the full index member set.
- Select the top N stocks with the highest explained variation.
- Calculate the individual weights as the ratio of one index member’s explained variation to the total explained variation of the selected N stocks.
- Calculating the trailing 12 month return covariance matrix, after excluding stocks with missing data points, yields the following 410 × 410 matrix.
- Decomposing the covariance matrix from 1 into the eigenvectors results in 410 principal components. To keep this section concise, we report the selected components in Table 1 below.
- Examining the cumulative variance of the principal components in the last column of Table 1 shows that we have to set to explain of the variance.
- After repeating Steps 1 and 2 while omitting one index member at a time, we receive the new cumulative variance of the 36 components for every stock that enables us to calculate the individual explanatory power by comparing the new cumulative variance to that of the full index member set (Columns 3–5 in Table 2).
- We select the top five stocks with the highest explained variation, which in our example are Xcel Energy Inc. (XEL), Lincoln National Corporation (LNC), CMS Energy Corporation (CMS), Bank of America Corporation (BAC), and SunTrust Banks, Inc. (STI).
- Based on the explained variation of the top five stocks, we calculate the appropriate portfolio weights as the ratio of individually explained variation and total explained variation of the selected stocks. Eventually, we arrive in Table 2 at the reported portfolio weights.
3.3. Trading Period
- Whenever one month ATM options are available, a trading position is established.
- A trading position consists always of a single stock option basket and an index leg.
- Every position is held until expiry.
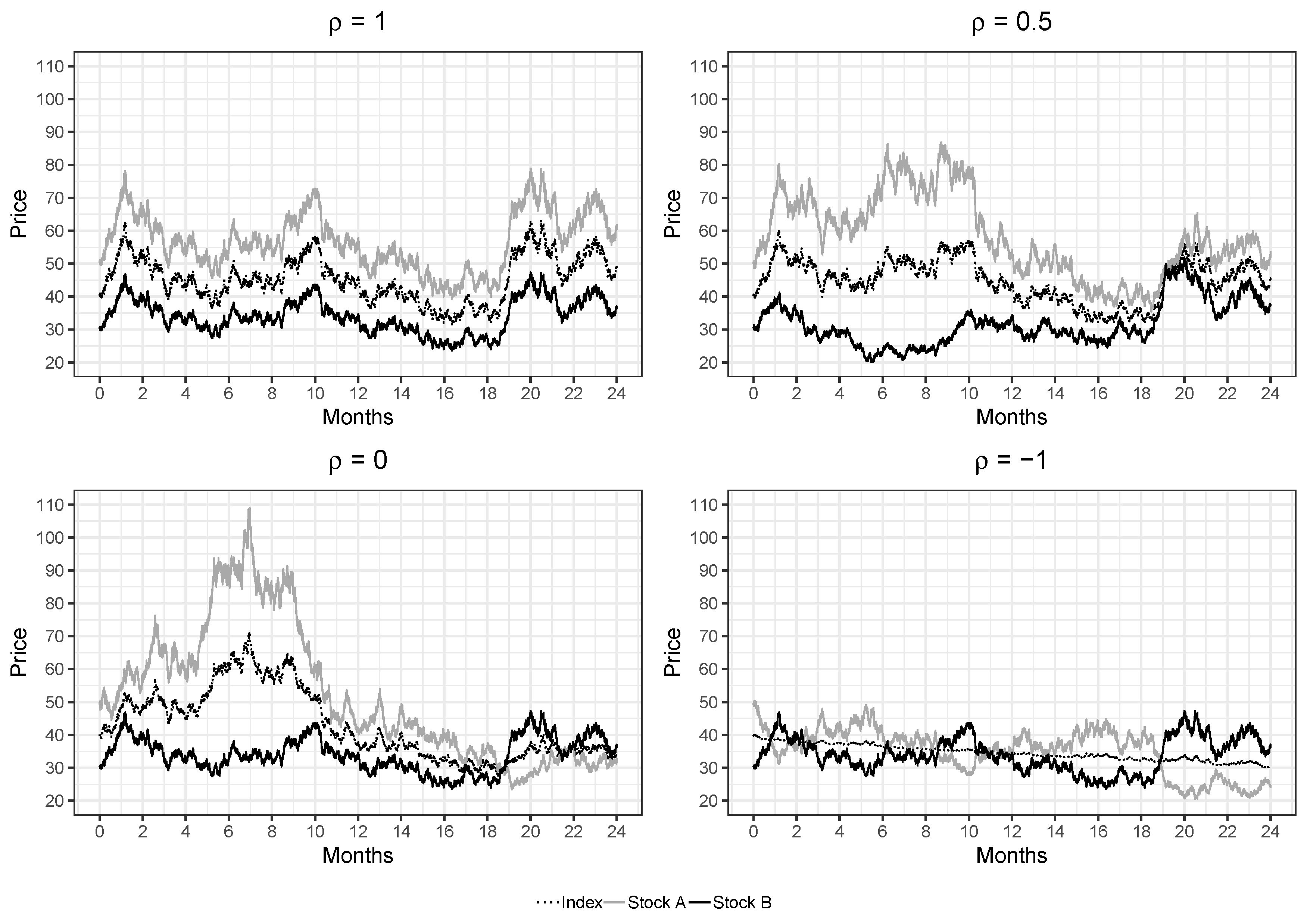
- PCA straddle delta hedged (PSD): The replicating portfolio of this strategy consists of the top five stocks that are selected with the statistical approach outlined in Section 3.2. A long straddle position of the basket portfolio is established while index straddles are sold. The overall position is delta hedged on a daily basis.
- PCA straddle delta unhedged (PSU): The selection process and the trade construction are similar to PSD. However, the directional exposure remains unhedged during the lifetime of the trade. This illustrates a simpler version of PSD.
- Largest constituents straddle delta hedged (LSD): The replicating portfolio of this strategy follows a naive subsetting approach and contains the top five largest constituents of the index at trade inception. Basket straddles are bought while index straddles are shorted. The directional exposure is delta hedged on a daily basis.
- Largest constituents straddle delta unhedged (LSU): The trade construction and selection process is identical to LSD. However, the overall delta position remains unhedged, hence representing a less sophisticated approach than LSD.
- Naive buy-and-hold strategy (MKT): This approach represents a simple buy-and-hold strategy. The index is bought in January 2000 and held during the complete back-testing period. MKT is the simplest strategy in our study.
3.4. Return Calculation
4. Results
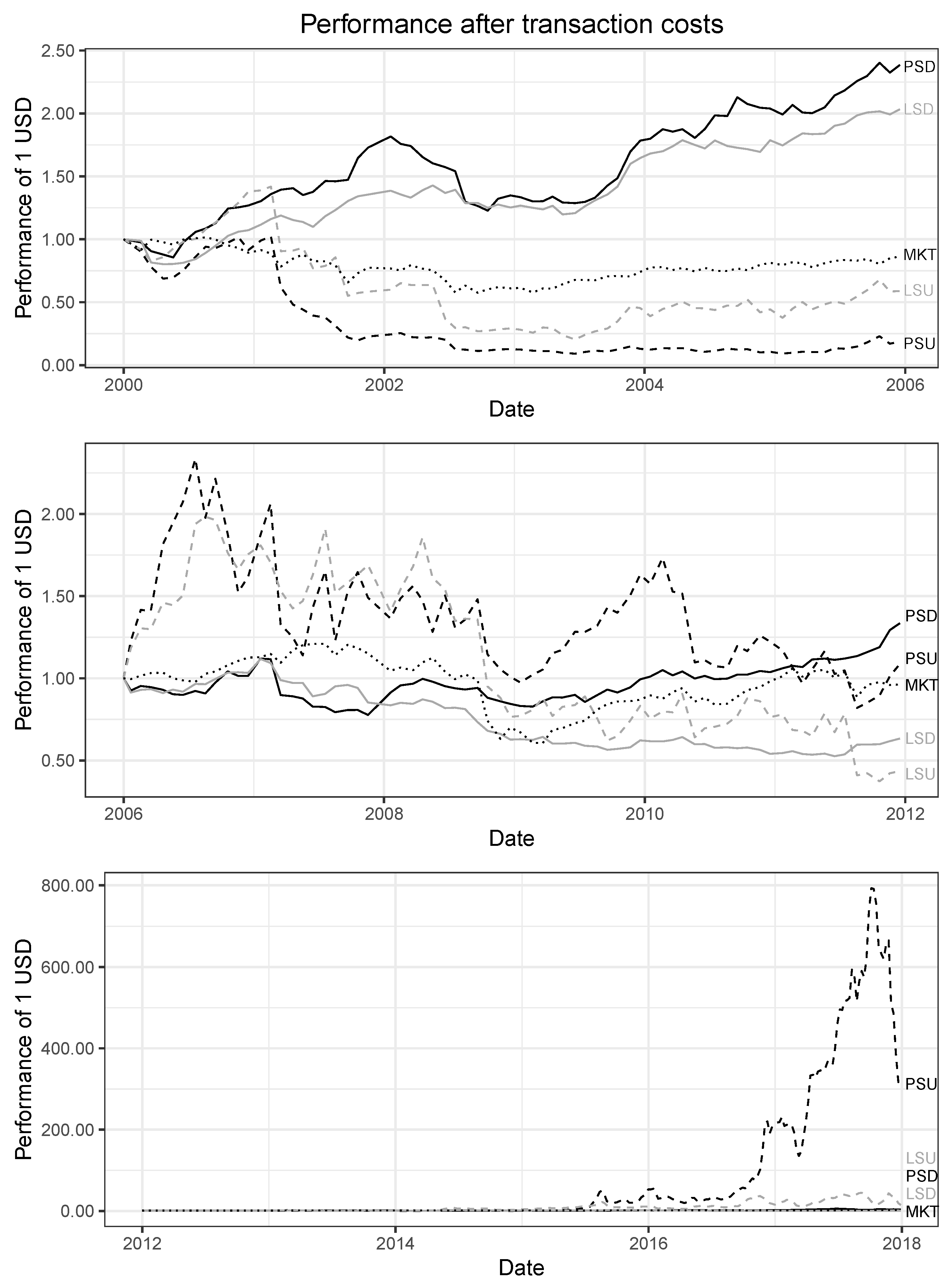
4.1. Strategy Performance
4.2. Sub-Period Analysis
4.3. Market Frictions
4.4. Robustness Check
4.5. Risk Factor Analysis
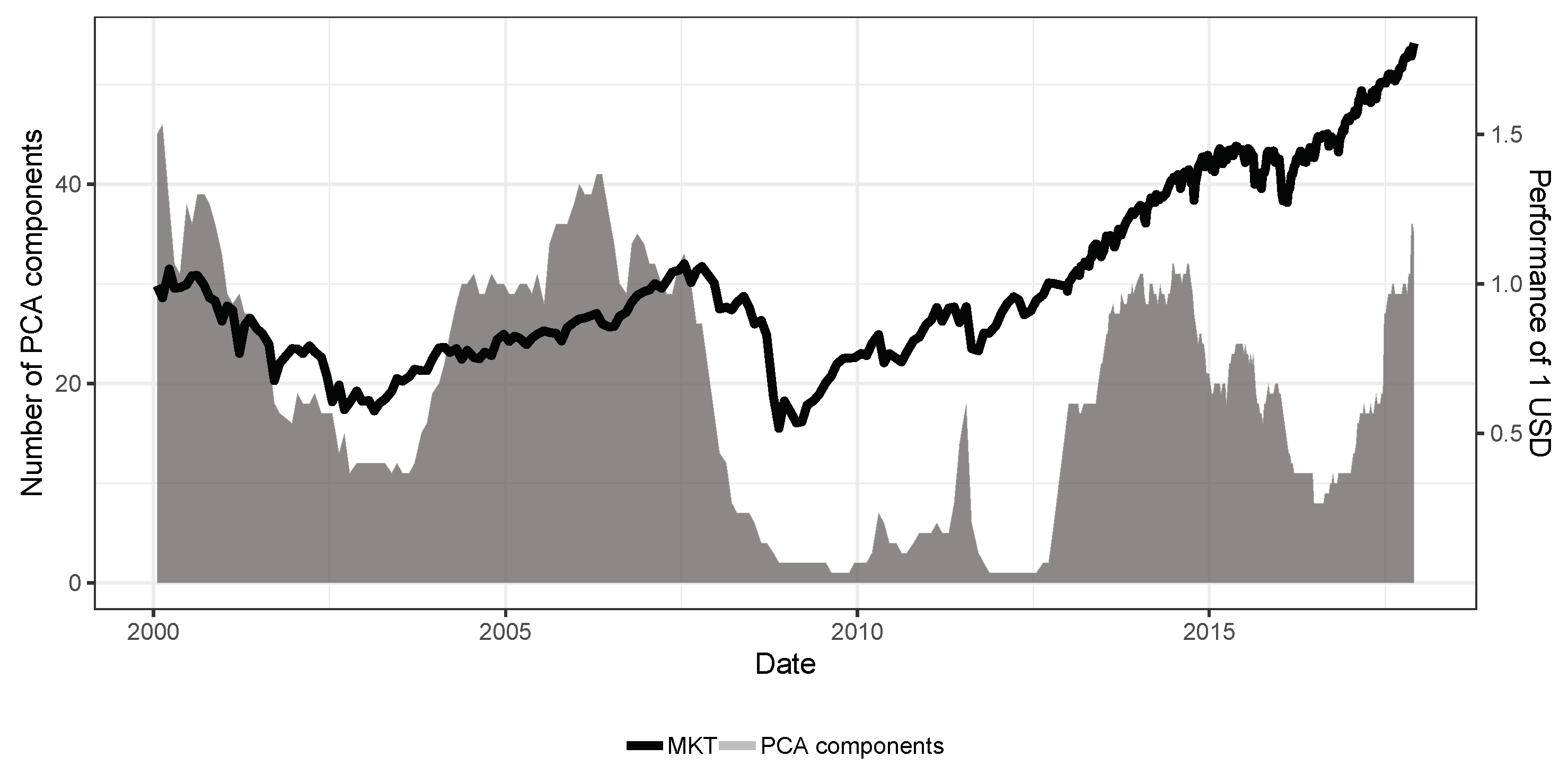
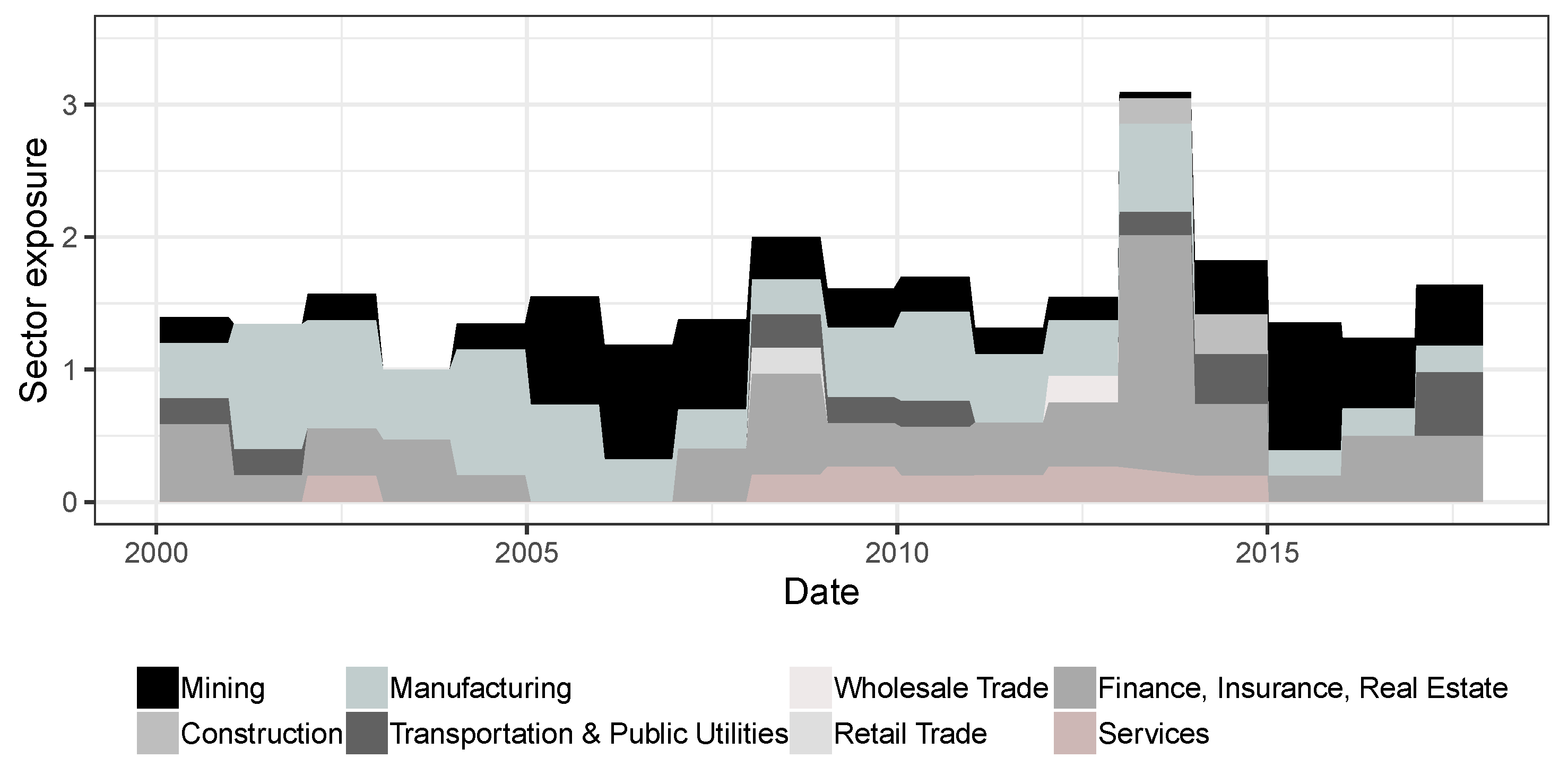
4.6. Analysis of PCA Components and Market Exposure
5. Conclusions and Policy Recommendations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pole, A. Statistical Arbitrage: Algorithmic Trading Insights and Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Gatev, E.; Goetzmann, W.N.; Rouwenhorst, K.G. Pairs trading: Performance of a relative-value arbitrage rule. Rev. Financ. Stud. 2006, 19, 797–827. [Google Scholar] [CrossRef]
- Do, B.; Faff, R. Does simple pairs trading still work? Financ. Anal. J. 2010, 66, 83–95. [Google Scholar] [CrossRef]
- Ramos-Requena, J.; Trinidad-Segovia, J.; Sánchez-Granero, M. Introducing Hurst exponent in pair trading. Phys. Stat. Mech. Its Appl. 2017, 488, 39–45. [Google Scholar] [CrossRef]
- Ramos-Requena, J.P.; Trinidad-Segovia, J.E.; Sánchez-Granero, M.Á. Some notes on the formation of a pair in pairs trading. Mathematics 2020, 8, 348. [Google Scholar] [CrossRef]
- Sánchez-Granero, M.; Balladares, K.; Ramos-Requena, J.; Trinidad-Segovia, J. Testing the efficient market hypothesis in Latin American stock markets. Phys. Stat. Mech. Its Appl. 2020, 540, 123082. [Google Scholar] [CrossRef]
- Bennett, C. Trading Volatility: Trading Volatility, Correlation, Term Structure and Skew; CreateSpace: Charleston, SC, USA, 2014. [Google Scholar]
- Nasekin, S.; Härdle, W.K. Model-driven statistical arbitrage on LETF option markets. Quant. Financ. 2019, 19, 1817–1837. [Google Scholar] [CrossRef]
- Glasserman, P.; He, P. Buy rough, sell smooth. Quant. Financ. 2020, 20, 363–378. [Google Scholar] [CrossRef]
- Gangahar, A. Smart Money on Dispersion. Financial Times. 2006. Available online: https://www.ft.com/content/a786ce1e-3140-11db-b953-0000779e2340 (accessed on 16 August 2020).
- Sculptor Capital Management Inc. Sculptor Capital Management Inc. website. 2020. Available online: https://www.sculptor.com/ (accessed on 16 August 2020).
- Alloway, T. A $12bn Dispersion Trade. Financial Times. 2011. Available online: https://ftalphaville.ft.com/2011/06/17/597511/a-12bn-dispersion-trade/ (accessed on 16 August 2020).
- Marshall, C.M. Dispersion trading: Empirical evidence from U.S. options markets. Glob. Financ. J. 2009, 20, 289–301. [Google Scholar] [CrossRef]
- Maze, S. Dispersion trading in south africa: An analysis of profitability and a strategy comparison. SSRN Electron. J. 2012. [Google Scholar] [CrossRef]
- Ferrari, P.; Poy, G.; Abate, G. Dispersion trading: An empirical analysis on the S&P 100 options. Invest. Manag. Financ. Innov. 2019, 16, 178–188. [Google Scholar]
- Deng, Q. Volatility dispersion trading. SSRN Electron. J. 2008. [Google Scholar] [CrossRef]
- Wilmott, P. Paul Wilmott Introduces Quantitative Finance, 2nd ed.; John Wiley: Chichester, UK, 2008. [Google Scholar]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Jiang, X. Return dispersion and expected returns. Financ. Mark. Portf. Manag. 2010, 24, 107–135. [Google Scholar] [CrossRef]
- Chichernea, S.C.; Holder, A.D.; Petkevich, A. Does return dispersion explain the accrual and investment anomalies? J. Account. Econ. 2015, 60, 133–148. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. Int. Econ. Rev. 1998, 39, 885. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X.; Labys, P. The distribution of realized exchange rate volatility. J. Am. Stat. Assoc. 2001, 96, 42–55. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Shephard, N. Estimating quadratic variation using realized variance. J. Appl. Econom. 2002, 17, 457–477. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77. [Google Scholar]
- Driessen, J.; Maenhout, P.J.; Vilkov, G. Option-implied correlations and the price of correlation risk. SSRN Electron. J. 2013. [Google Scholar] [CrossRef]
- Faria, G.; Kosowski, R.; Wang, T. The correlation risk premium: International evidence. SSRN Electron. J. 2018. [Google Scholar] [CrossRef]
- Bollen, N.P.B.; Whaley, R.E. Does net buying pressure affect the shape of implied volatility functions? J. Financ. 2004, 59, 711–753. [Google Scholar] [CrossRef]
- Shiu, Y.M.; Pan, G.G.; Lin, S.H.; Wu, T.C. Impact of net buying pressure on changes in implied volatility: Before and after the onset of the subprime crisis. J. Deriv. 2010, 17, 54–66. [Google Scholar] [CrossRef]
- Ruan, X.; Zhang, J.E. The economics of the financial market for volatility trading. J. Financ. Mark. 2020, 100556. [Google Scholar] [CrossRef]
- Bakshi, G.; Kapadia, N. Delta-hedged gains and the negative market volatility risk premium. Rev. Financ. Stud. 2003, 16, 527–566. [Google Scholar] [CrossRef]
- Ilmanen, A. Do financial markets reward buying or selling insurance and lottery tickets? Financ. Anal. J. 2012, 68, 26–36. [Google Scholar] [CrossRef]
- Gatheral, J. The Volatility Surface: A Practitioner’s Guide; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Crépey, S. Delta-hedging vega risk? Quant. Financ. 2004, 4, 559–579. [Google Scholar] [CrossRef]
- Jegadeesh, N.; Titman, S. Returns to buying winners and selling losers: Implications for stock market efficiency. J. Financ. 1993, 48, 65–91. [Google Scholar] [CrossRef]
- R Core Team. Stats: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2019. [Google Scholar]
- Do, B.; Faff, R. Are pairs trading profits robust to trading costs? J. Financ. Res. 2012, 35, 261–287. [Google Scholar] [CrossRef]
- Stübinger, J.; Schneider, L. Statistical arbitrage with mean-reverting overnight price gaps on high-frequency data of the S&P 500. J. Risk Financ. Manag. 2019, 12, 51. [Google Scholar]
- Korajczyk, R.A.; Sadka, R. Are momentum profits robust to trading costs? J. Financ. 2004, 59, 1039–1082. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Su, X. Hedging Basket Options by Using A Subset of Underlying Assets (Working Paper). 2006. Available online: https://www.econstor.eu/bitstream/10419/22959/1/bgse14_2006.pdf (accessed on 16 August 2020).
- von Beschwitz, B.; Massa, M. Biased short: Short sellers’ disposition effect and limits to arbitrage. J. Financ. Mark. 2020, 49, 100512. [Google Scholar] [CrossRef]
- Voya Investment Management. The Impact of Equity Market Fragmentation and Dark Pools on Trading and Alpha Generation. 2016. Available online: https://investments.voya.com (accessed on 16 August 2020).
- Frazzini, A.; Israel, R.; Moskowitz, T.J. Trading costs. SSRN Electron. J. 2018. [Google Scholar] [CrossRef]
- Henderson, R. Schwab Opens New front in Trading War by Slashing Rates to Zero. Financial Times. 2019. Available online: https://www.ft.com/content/cf644610-e45a-11e9-9743-db5a370481bc (accessed on 16 August 2020).
- Avellaneda, M.; Lee, J.H. Statistical arbitrage in the US equities market. Quant. Financ. 2010, 10, 761–782. [Google Scholar] [CrossRef]
- Cboe Global Markets, I. Chicago Board Options Exchange Margin Manual. 2000. Available online: https://www.cboe.com/learncenter/pdf/margin2-00.pdf (accessed on 16 August 2020).
- Stübinger, J.; Endres, S. Pairs trading with a mean-reverting jump-diffusion model on high-frequency data. Quant. Financ. 2018, 18, 1735–1751. [Google Scholar] [CrossRef]
- Mina, J.; Xiao, J.Y. Return to RiskMetrics: The evolution of a standard. Riskmetrics Group 2001, 1, 1–11. [Google Scholar]
- Stübinger, J.; Mangold, B.; Krauss, C. Statistical arbitrage with vine copulas. Quant. Financ. 2018, 18, 1831–1849. [Google Scholar] [CrossRef]
- Liu, B.; Chang, L.B.; Geman, H. Intraday pairs trading strategies on high frequency data: The case of oil companies. Quant. Financ. 2017, 17, 87–100. [Google Scholar] [CrossRef]
- Knoll, J.; Stübinger, J.; Grottke, M. Exploiting social media with higher-order factorization machines: Statistical arbitrage on high-frequency data of the S&P 500. Quant. Financ. 2019, 19, 571–585. [Google Scholar]
- Stübinger, J. Statistical arbitrage with optimal causal paths on high-frequency data of the S&P 500. Quant. Financ. 2019, 19, 921–935. [Google Scholar]
- Endres, S.; Stübinger, J. Regime-switching modeling of high-frequency stock returns with Lévy jumps. Quant. Financ. 2019, 19, 1727–1740. [Google Scholar] [CrossRef]
- Degiannakis, S.; Filis, G.; Hassani, H. Forecasting global stock market implied volatility indices. J. Empir. Financ. 2018, 46, 111–129. [Google Scholar] [CrossRef]
- Fang, T.; Lee, T.H.; Su, Z. Predicting the long-term stock market volatility: A GARCH-MIDAS model with variable selection. J. Empir. Financ. 2020, 58, 36–49. [Google Scholar] [CrossRef]
- Naimy, V.; Montero, J.M.; El Khoury, R.; Maalouf, N. Market volatility of the three most powerful military countries during their intervention in the Syrian War. Mathematics 2020, 8, 834. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. Multifactor explanations of asset pricing anomalies. J. Financ. 1996, 51, 55–84. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. A five-factor asset pricing model. J. Financ. Econ. 2015, 116, 1–22. [Google Scholar] [CrossRef]
- Yoshino, N.; Taghizadeh-Hesary, F. Analysis of credit ratings for small and medium-sized enterprises: Evidence from Asia. Asian Dev. Rev. 2015, 32, 18–37. [Google Scholar] [CrossRef]
- Bartlett, M.S. The effect of standardization on a χ2 approximation in factor analysis. Biometrika 1951, 38, 337–344. [Google Scholar] [CrossRef]
- Kaiser, H.F. A second generation little jiffy. Psychometrika 1970, 35, 401–415. [Google Scholar] [CrossRef]
- Kaiser, H. An index of factorial simplicity. Psychometrika 1974, 39, 31–36. [Google Scholar] [CrossRef]
- Kaiser, H.F.; Rice, J. Little jiffy, Mark Iv. Educ. Psychol. Meas. 1974, 34, 111–117. [Google Scholar] [CrossRef]
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar]
- Lintner, J. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Rev. Econ. Stat. 1965, 47, 13–37. [Google Scholar] [CrossRef]
| Principal Component | % of Variance | Cumulative Variance % |
|---|---|---|
| 1 | 32.01 | 32.01 |
| 2 | 17.02 | 49.03 |
| 3 | 6.32 | 55.35 |
| 4 | 5.65 | 61.00 |
| 5 | 4.74 | 65.73 |
| ⋮ | ⋮ | ⋮ |
| 35 | 0.34 | 89.82 |
| 36 | 0.33 | 90.16 |
| 37 | 0.31 | 90.47 |
| 38 | 0.30 | 90.77 |
| 39 | 0.29 | 91.06 |
| 40 | 0.28 | 91.34 |
| ⋮ | ⋮ | ⋮ |
| 410 | 0.00 | 100.00 |
| Cumulative Variance % | |||||
|---|---|---|---|---|---|
| Rank | Stock Ticker | All Constituents | Omitting Stocks | Explanatory Power % | Portfolio Weight % |
| 1 | XEL | 90.1576 | 90.1358 | 0.0219 | 20.2518 |
| 2 | LNC | 90.1576 | 90.1359 | 0.0217 | 20.1303 |
| 3 | CMS | 90.1576 | 90.1360 | 0.0216 | 20.0108 |
| 4 | BAC | 90.1576 | 90.1361 | 0.0215 | 19.9274 |
| 5 | STI | 90.1576 | 90.1364 | 0.0212 | 19.6797 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 406 | ULTA | 90.1576 | 90.2146 | −0.0570 | 0.0000 |
| 407 | ADM | 90.1576 | 90.2171 | −0.0595 | 0.0000 |
| 408 | NRG | 90.1576 | 90.2177 | −0.0601 | 0.0000 |
| 409 | HRB | 90.1576 | 90.2207 | −0.0631 | 0.0000 |
| 410 | EFX | 90.1576 | 90.2333 | −0.0757 | 0.0000 |
| Before Transaction Costs | After Transaction Costs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PSD | PSU | LSD | LSU | MKT | PSD | PSU | LSD | LSU | MKT | |
| Mean return | 0.0100 | 0.0228 | 0.0044 | 0.0140 | 0.0022 | 0.0084 | 0.0214 | 0.0030 | 0.0128 | 0.0022 |
| t-statistic (NW) | 2.2413 | 2.2086 | 0.8608 | 1.5083 | 1.2897 | 1.9069 | 2.0933 | 0.5809 | 1.3852 | 1.2897 |
| Standard error (NW) | 0.0044 | 0.0103 | 0.0051 | 0.0093 | 0.0017 | 0.0044 | 0.0102 | 0.0051 | 0.0093 | 0.0017 |
| Minimum | −0.2560 | −0.4539 | −0.2399 | −0.4798 | −0.2506 | −0.2556 | −0.4529 | −0.2396 | −0.4781 | −0.2506 |
| Quartile 1 | −0.0238 | −0.0640 | −0.0288 | −0.0704 | −0.0097 | −0.0251 | −0.0648 | −0.0300 | −0.0711 | −0.0097 |
| Median | 0.0097 | 0.0163 | 0.0037 | 0.0201 | 0.0037 | 0.0082 | 0.0150 | 0.0022 | 0.0188 | 0.0037 |
| Quartile 3 | 0.0489 | 0.1006 | 0.0374 | 0.0884 | 0.0170 | 0.0470 | 0.0988 | 0.0356 | 0.0866 | 0.0170 |
| Maximum | 0.3241 | 1.1694 | 0.3414 | 0.4270 | 0.1315 | 0.3202 | 1.1626 | 0.3373 | 0.4258 | 0.1315 |
| Standard deviation | 0.0678 | 0.1523 | 0.0730 | 0.1361 | 0.0363 | 0.0673 | 0.1515 | 0.0725 | 0.1353 | 0.0363 |
| Skewness | −0.0818 | 1.2340 | 0.2528 | −0.1259 | −1.5218 | −0.0806 | 1.2366 | 0.2546 | −0.1249 | −1.5218 |
| Kurtosis | 2.7042 | 8.9553 | 2.3025 | 0.9795 | 9.2676 | 2.7051 | 8.9824 | 2.3021 | 0.9806 | 9.2676 |
| Historical VaR 1% | −0.1955 | −0.3580 | −0.1820 | −0.3584 | −0.1431 | −0.1955 | −0.3570 | −0.1820 | −0.3574 | −0.1431 |
| Historical CVaR 1% | −0.2166 | −0.4080 | −0.2133 | −0.4068 | −0.1788 | −0.2165 | −0.4069 | −0.2132 | −0.4056 | −0.1788 |
| Historical VaR 5% | −0.1106 | −0.2091 | −0.1178 | −0.2052 | −0.0486 | −0.1113 | −0.2090 | −0.1184 | −0.2051 | −0.0486 |
| Historical CVaR 5% | −0.1573 | −0.2889 | −0.1632 | −0.2977 | −0.1000 | −0.1576 | −0.2884 | −0.1635 | −0.2971 | −0.1000 |
| Maximum drawdown | 0.6731 | 0.9358 | 0.8074 | 0.8534 | 0.4990 | 0.7053 | 0.9470 | 0.8201 | 0.8564 | 0.4990 |
| Trades with return ≥ 0 | 0.5747 | 0.5519 | 0.5342 | 0.5671 | 0.5975 | 0.5671 | 0.5468 | 0.5215 | 0.5646 | 0.5975 |
| Number of trades | 395 | 395 | 395 | 395 | 1 | 395 | 395 | 395 | 395 | 1 |
| Avg. trades per year | 21.9444 | 21.9444 | 21.9444 | 21.9444 | 0.0556 | 21.9444 | 21.9444 | 21.9444 | 21.9444 | 0.0556 |
| Before Transaction Costs | After Transaction Costs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PSD | PSU | LSD | LSU | MKT | PSD | PSU | LSD | LSU | MKT | |
| Mean return | 0.1841 | 0.2988 | 0.0401 | 0.1049 | 0.0347 | 0.1452 | 0.2651 | 0.0077 | 0.0779 | 0.0347 |
| Mean excess return | 0.1646 | 0.2794 | 0.0206 | 0.0854 | 0.0152 | 0.1257 | 0.2456 | −0.0117 | 0.0585 | 0.0152 |
| Standard deviation | 0.3192 | 0.7169 | 0.3438 | 0.6403 | 0.1710 | 0.3169 | 0.7128 | 0.3414 | 0.6367 | 0.1710 |
| Downside deviation | 0.2074 | 0.4110 | 0.2271 | 0.4264 | 0.1305 | 0.2090 | 0.4114 | 0.2287 | 0.4266 | 0.1305 |
| Sharpe ratio | 0.5157 | 0.3897 | 0.0599 | 0.1334 | 0.0890 | 0.3967 | 0.3446 | −0.0344 | 0.0918 | 0.0890 |
| Sortino ratio | 2.3481 | 2.0620 | 0.4254 | 0.6190 | 0.6389 | 1.7935 | 1.7911 | 0.0799 | 0.4518 | 0.6389 |
| Annualized Return | Sharpe Ratio | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PSD | PSU | LSD | LSU | MKT | PSD | PSU | LSD | LSU | MKT | ||
| Transaction costs | 0 | 0.1841 | 0.2988 | 0.0401 | 0.1049 | 0.0347 | 0.5157 | 0.3897 | 0.0599 | 0.1334 | 0.0890 |
| 1 | 0.1802 | 0.2954 | 0.0368 | 0.1022 | 0.0347 | 0.5037 | 0.3851 | 0.0504 | 0.1292 | 0.0890 | |
| 5 | 0.1645 | 0.2818 | 0.0238 | 0.0913 | 0.0347 | 0.4560 | 0.3670 | 0.0126 | 0.1126 | 0.0890 | |
| 10 | 0.1452 | 0.2651 | 0.0077 | 0.0779 | 0.0347 | 0.3967 | 0.3446 | −0.0344 | 0.0918 | 0.0890 | |
| 15 | 0.1262 | 0.2485 | −0.0080 | 0.0647 | 0.0347 | 0.3380 | 0.3222 | −0.0809 | 0.0712 | 0.0890 | |
| 20 | 0.1075 | 0.2321 | −0.0236 | 0.0516 | 0.0347 | 0.2798 | 0.3001 | −0.1271 | 0.0508 | 0.0890 | |
| 40 | 0.0356 | 0.1687 | −0.0836 | 0.0007 | 0.0347 | 0.0521 | 0.2130 | −0.3082 | −0.0299 | 0.0890 | |
| 50 | 0.0014 | 0.1381 | −0.1122 | −0.0238 | 0.0347 | −0.0589 | 0.1703 | −0.3967 | −0.0696 | 0.0890 | |
| 60 | −0.0318 | 0.1083 | −0.1400 | −0.0478 | 0.0347 | −0.1681 | 0.1283 | −0.4839 | −0.1088 | 0.0890 | |
| 90 | −0.1252 | 0.0232 | −0.2185 | −0.1166 | 0.0347 | −0.4852 | 0.0054 | −0.7380 | −0.2238 | 0.0890 | |
| 100 | −0.1544 | −0.0038 | −0.2431 | −0.1384 | 0.0347 | −0.5876 | −0.0345 | −0.8203 | −0.2613 | 0.0890 | |
| Reinvestment | 5% | 10% | 20% | 40% | 80% | 100% | |
|---|---|---|---|---|---|---|---|
| Mean return | |||||||
| Top 5 | Uncond.Correlation | 0.07120 | 0.11478 | 0.18411 | 0.23003 | NA | NA |
| Cond.Correlation | 0.05096 | 0.07288 | 0.09532 | 0.03780 | NA | NA | |
| Top 10 | Uncond. Correlation | 0.06976 | 0.11226 | 0.18090 | 0.23413 | −0.11755 | NA |
| Cond. Correlation | 0.04677 | 0.06481 | 0.08092 | 0.02113 | NA | NA | |
| Top 20 | Uncond. Correlation | 0.07394 | 0.12131 | 0.20171 | 0.28533 | 0.00145 | −0.59641 |
| Cond. Correlation | 0.05318 | 0.07825 | 0.11008 | 0.08608 | NA | NA | |
| Sharpe ratio | |||||||
| Top 5 | Uncond. Correlation | 0.6467 | 0.5969 | 0.5157 | 0.3298 | NA | NA |
| Cond. Correlation | 0.3902 | 0.3321 | 0.2361 | 0.0285 | NA | NA | |
| Top 10 | Uncond. Correlation | 0.6492 | 0.6004 | 0.5226 | 0.3475 | −0.1109 | NA |
| Cond. Correlation | 0.3496 | 0.2912 | 0.1976 | 0.0027 | NA | NA | |
| Top 20 | Uncond. Correlation | 0.7226 | 0.6774 | 0.6064 | 0.4424 | −0.0150 | −0.4100 |
| Cond. Correlation | 0.4432 | 0.3879 | 0.2994 | 0.1101 | NA | NA | |
| Maximum drawdown | |||||||
| Top 5 | Uncond. Correlation | 0.2146 | 0.4017 | 0.6731 | 0.9258 | 1.0000 | 1.0000 |
| Cond. Correlation | 0.2520 | 0.4943 | 0.8124 | 0.9908 | 1.0000 | 1.0000 | |
| Top 10 | Uncond. Correlation | 0.2363 | 0.4332 | 0.7053 | 0.9447 | 1.0000 | 1.0000 |
| Cond. Correlation | 0.2898 | 0.5403 | 0.8399 | 0.9920 | 1.0000 | 1.0000 | |
| Top 20 | Uncond. Correlation | 0.2282 | 0.4198 | 0.6885 | 0.9294 | 0.9999 | 1.0000 |
| Cond. Correlation | 0.2744 | 0.5187 | 0.8232 | 0.9897 | 1.0000 | 1.0000 |
| PSD | PSU | |||||
|---|---|---|---|---|---|---|
| FF3 | FF3+2 | FF5 | FF3 | FF3+2 | FF5 | |
| Intercept | 0.0075 ** | 0.0079 ** | 0.0074 ** | 0.0201 ** | 0.0222 *** | 0.0219 *** |
| (0.0035) | (0.0035) | (0.0035) | (0.0078) | (0.0080) | (0.0080) | |
| Market | 0.1200 | 0.1316 | 0.1517 * | 0.2128 | 0.4157 ** | 0.0560 |
| (0.0834) | (0.0926) | (0.0909) | (0.1894) | (0.2084) | (0.2056) | |
| SMB | 0.1626 | 0.1736 | 0.1325 | 0.1920 | ||
| (0.1359) | (0.1374) | (0.3085) | (0.3092) | |||
| HML | 0.2424 ** | 0.2360 ** | 0.0117 | 0.0767 | ||
| (0.1074) | (0.1146) | (0.2440) | (0.2579) | |||
| Momentum | −0.0225 | 0.0711 | ||||
| (0.0893) | (0.2008) | |||||
| Reversal | –0.0656 | −0.5416 ** | ||||
| (0.0968) | (0.2178) | |||||
| SMB5 | 0.1168 | 0.0847 | ||||
| (0.1551) | (0.3506) | |||||
| HML5 | 0.1383 | 0.3636 | ||||
| (0.1396) | (0.3157) | |||||
| RMW5 | −0.0216 | −0.2720 | ||||
| (0.1815) | (0.4102) | |||||
| CMA5 | 0.2194 | −0.8783 | ||||
| (0.2362) | (0.5340) | |||||
| 0.0256 | 0.0267 | 0.0264 | 0.0050 | 0.0243 | 0.0146 | |
| Adj. | 0.0181 | 0.0142 | 0.0139 | −0.0026 | 0.0118 | 0.0019 |
| No. obs. | 395 | 395 | 395 | 395 | 395 | 395 |
| RMSE | 0.0672 | 0.0674 | 0.0674 | 0.1527 | 0.1516 | 0.1523 |
| Kaiser-Meyer-Olkin Criterion | Bartlett’s Sphericity Test | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| KMO Value | p-Value | ||||||||
| Segment | 0–0.1 | 0.1–0.2 | 0.2–0.3 | 0.3–0.5 | ≥ 0.5 | Total | < 1% | ≥ 1% | Total |
| Count | 7 | 84 | 148 | 138 | 18 | 395 | 395 | 0 | 395 |
| Average | 0.0895 | 0.1600 | 0.2445 | 0.3725 | 0.5701 | 0.2833 | 0.0000 | NA | 0.0000 |
| Median | 0.0878 | 0.1668 | 0.2431 | 0.3530 | 0.5502 | 0.2619 | 0.0000 | NA | 0.0000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schneider, L.; Stübinger, J. Dispersion Trading Based on the Explanatory Power of S&P 500 Stock Returns. Mathematics 2020, 8, 1627. https://doi.org/10.3390/math8091627
Schneider L, Stübinger J. Dispersion Trading Based on the Explanatory Power of S&P 500 Stock Returns. Mathematics. 2020; 8(9):1627. https://doi.org/10.3390/math8091627
Chicago/Turabian StyleSchneider, Lucas, and Johannes Stübinger. 2020. "Dispersion Trading Based on the Explanatory Power of S&P 500 Stock Returns" Mathematics 8, no. 9: 1627. https://doi.org/10.3390/math8091627
APA StyleSchneider, L., & Stübinger, J. (2020). Dispersion Trading Based on the Explanatory Power of S&P 500 Stock Returns. Mathematics, 8(9), 1627. https://doi.org/10.3390/math8091627





