1. Introduction and Preliminaries
A directed graph G is a couple where is a set of vertices and is a set of directed edges. In our setting, each edge is labeled positive or negative. The set of positive (resp. negative) edges of the graph are denoted by (resp. ). A graph is called positive (resp. negative) if all labels on the edges are positive (resp. negative). If , the subgraph of G induced by S, denoted as , is the graph whose vertices set is and its edge set is . We denote by the subgraph of G induced by .
A graph is undirected if for every then . A graph is symmetric if it is undirected and for every then . That is, a symmetric graph is an undirected graph where each vertex has a (directed) selfloop.
If is an edge then we say that u is a predecessor of v and it is positive (resp. negative) if is a positive (resp. negative) edge. The set of positive (resp. negative) predecessors of a vertex v is denoted as (resp. ). The set of predecessors of v is .
The neighborhood of a vertex v in a graph G, denoted as is the set }. The closed neighborhood of v, denoted as is . The degree of a vertex is the number of vertices in its closed neighborhood and it is denoted by .
A dynamical system (DS) [
1,
2,
3,
4] or Boolean Network (BN) [
5,
6,
7]
is a couple
where
G is a directed graph called the dependency graph,
F is a set of functions
as defined below. We also define a
-dimensional vector
O of states.
where
,
. The vector
O will be referred as an orbit of
. We also consider the restriction (or the projection) of the vector
O on a subset of vertices
and we refer to it as
. Each function
is taken from the set of Boolean functions, where
h is the number of predecessors of
v. The argument of
is an
h-dimensional vector
where
when
, and,
when
being
the Boolean negation (or the complement modulo 2) of
. Although
can be an arbitrary Boolean function on
h variables, most pieces of research on DS and BN restrict the set of Boolean functions to AND, OR, NAND and NOR. This is motivated by the following.
An AND term (resp. OR term) is the logical AND (resp. logical OR) of a set of variables (where each variable can be either complemented or not complemented). Given a set of h Boolean variables , an AND term in which each of the h variables appears once (in either its complemented or not complemented form) is called a minterm. Analogously, an OR term in which each of the h variables appears once (in either its complemented or not complemented form) is called a maxterm. It is well known that every Boolean function can be expressed either by disjunction of uniquely minterms or by conjunction of just maxterms, among others. Furthermore, it is well known that the Boolean algebra using the binary operators AND, OR and NOT are equivalent to the algebra obtained by using either only NAND or only NOR.
In addition, the complexity of the problems involved in a DS dramatically changes when we modify either the structure of the dependency graph, or the type or distribution of the Boolean functions involved in the system. If the vertices of a DS use a function on a set then we refer to the dynamical system as an -DS. We also call a DS positive when its dependency graph is positive.
Given a vertex v of a DS, we may consider the state of the vertex as a function of a discrete time . Consequently, the global state O of the DS depends also on the time t. At time , we assign a value to each and if is the state of DS at time t then the state of a single vertex at time will be where is the restriction of O to the predecessors of v. If the states of the vertices are updated in parallel then we refer to the system as a parallel DS or PDS. In other settings, we want to update the state of exactly one vertex at time t. A permutation of the vertices is given and if is the vertex that is updated at time t then only (indices taken modulo n) will change its state at time and thus . In this case, we call the system a sequential DS or SDS.
Given a DS and an orbit O, we call O a fixed point orbit (FPO) of if and only if . When the set of functions F is clear from the context, we refer to O just as an FPO of G.
Fixed point orbits are particularly interesting since they correspond to stable states of the system. The problem of determining the existence of a fixed point orbit of a DS is called fixed point orbit existence (FPOE) problem. A number of works have explored the FPOE problem under the hypothesis that all the vertices have a selfloop. Some works put an additional restriction which requires the graph of the DS to be symmetric and/or either all the edges to be positive or all of them negative. Among others, the FPOE problem of an {AND}-DS, {OR}-DS, {NAND}-DS and {NOR}-DS is studied in [
2,
3,
4,
8,
9,
10]. In addition, the FPOE problem in an {AND, OR, NAND, NOR}-DS is polynomially solvable as shown in [
4,
11]. However, for {NAND, XNOR}-DS, {NAND, XOR}-DS,{NOR, XNOR}-DS and {NOR, XOR}-DS, the FPOE problem is NP-complete [
11]. The problem of counting the fixed point orbits in a DS whose dependency graph is symmetric and all edges are positive is studied in [
6] where it is proved that the problem of counting the FPOs in a
-DS is #P-complete under the hypothesis that the function associated to each node is arbitrary.
When the constraints that require the graph to be symmetric and positive are released, then the FPOE problem will be NP-complete in {AND, OR}-DS [
12,
13]. It remains NP-Complete even when the indegree of each vertex is at most two [
13]. It can be demonstrated that the problem remains NP-complete for {AND}-DS with all negative edges by using the transformation given in [
5].
In this paper, we present an algorithm for counting the FPOs in an AND-OR symmetric positive PDS. The algorithm has been designed by using more or less standard methodologies (such as the one used also in [
14,
15,
16,
17,
18,
19,
20,
21,
22,
23]) and by using both a greedy strategy and recursion. The paper is organized as follows. In
Section 2, we present some theoretical results about AND-OR PDS whose dependency graph is symmetric and positive. Based on them, we present an algorithm for counting all FPOs in AND-OR symmetric positive PDS and we prove its correctness. In
Section 3, we further develop the algorithm given in
Section 2 for building an algorithm which lists all FPOs in AND-OR symmetric PDS.
2. Algorithm for Computing the Number of FPOs in AND-OR Symmetric Positive PDS
In this section, we first determine the structure and the number of FPOs in {AND, OR}-DS whose dependency graph is symmetric and positive. It is well known that for this kind of graph the FPOE problem is polynomially solvable [
2,
3]. Let
be an {AND, OR}-DS where
G is a symmetric positive graph. We denote by
(resp.
) the vertices of
G such that
is OR (resp. AND). Furthermore, if for a vertex
v we have that
OR (resp.
AND) we refer to
v as an OR vertex (resp. AND vertex).
Since, in the following, we will limit our discussion to symmetric positive {AND, OR}-DS, for brevity we will often refer to them as DS without explicitly specifying that the dependency graph is symmetric positive and the set of Boolean functions {AND, OR}.
Lemma 1. Let be a DS and let O be an FPO of . Let and let be a DS whose dependency graph is . Then is an FPO of .
Proof. Let be the subgraph of G induced by U and let , that is, is the restriction of O to the vertices in U. We prove only that if then . The proof when can be obtained by applying a similar argument. Suppose first that . In this case clearly we have that . Suppose now that . Then, since O is an FPO of , for each we have that . Thus, in , for each we have that . Therefore, it follows that . □
Let be the set of the connected components of and let be the set of the connected components of . Let be the symmetric bipartite graph whose vertices set is with bipartition (we remark that can be disconnected or that or ). There is an edge in if and only if there is at least one edge with and . We will refer to as the AND-OR bipartition of G. Furthermore we associate to an {AND, OR}-DS referred to as the bipartite contraction of in which OR if and AND if .
Let us notice that can be achieved from just computing the connected components within the sub-graphs associated to and to . In order to do this it is sufficient with contracting all the vertices belonging to the same connected component in one.
The computational cost associated to this process is being .
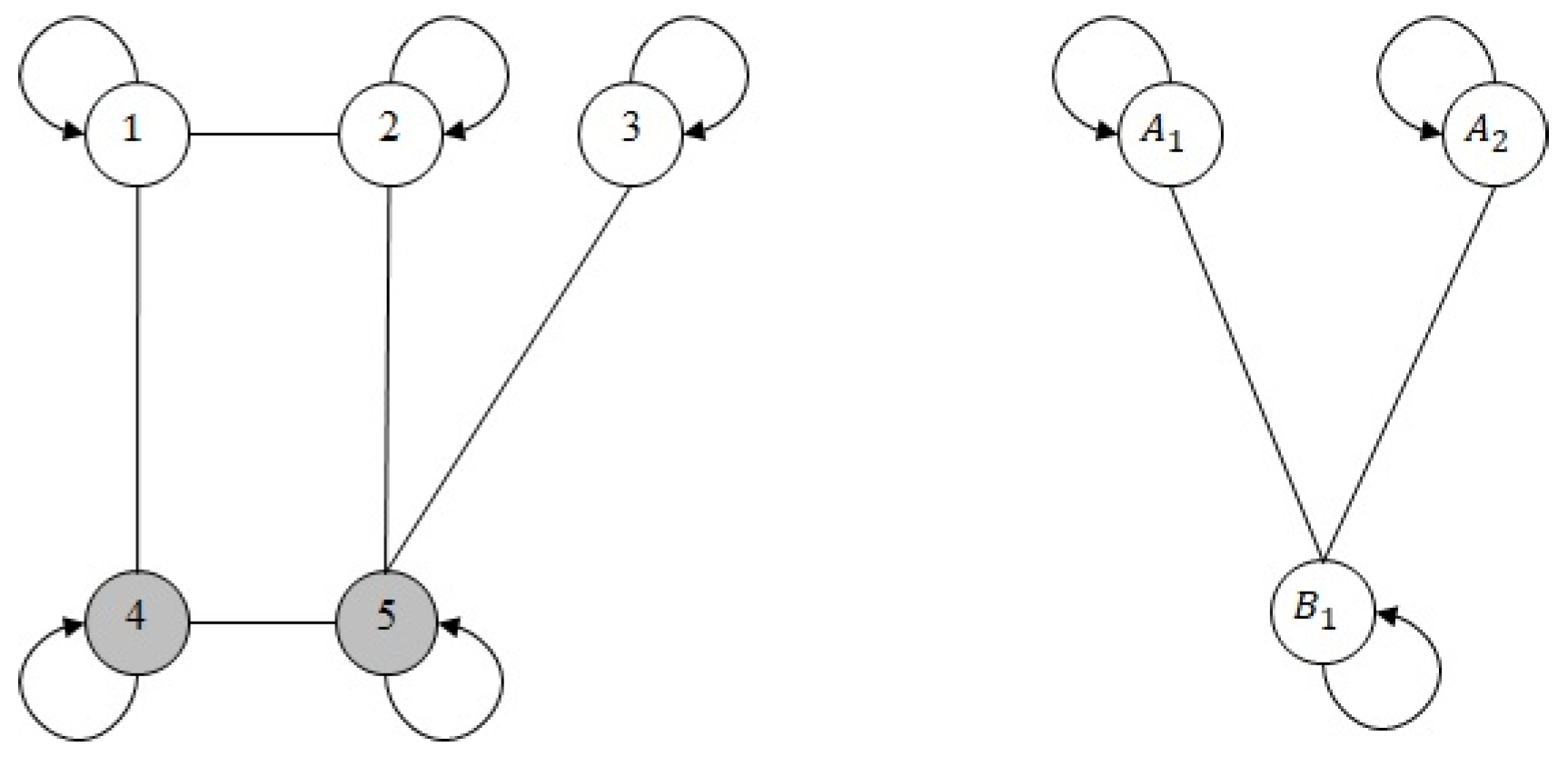
For example, in
Figure 1 on the left, there is an {AND, OR}-DS in which AND vertices are shaded grey and OR vertices are shaded white, whereas on the right its bipartite contraction appears.
Lemma 2. Let be a DS and let A be a connected component of such that . If O is an FPO of , then for all pairs of vertices we have that .
Proof. Let and suppose by contradiction that . Let P be a path in A connecting v to u. Then, there are two adjacent vertices, say w and z, on this path, such that . Suppose, without loss of generality, that . Since G is symmetric and positive there is an edge in G. Then O could not be an FPO since at time we would have that , a contradiction. □
By duality and in a similar way to Lemma 2, the following result is immediate to be proven:
Lemma 3. Let be a DS and let B be a connected component of such that . If O is an FPO of , then for all pairs of vertices we have that .
Now we show that FPOs of a DS are strictly related with FPOs of its corresponding bipartite contraction. In fact, we can prove the following two Lemmas.
Lemma 4. Let be a DS and let be the bipartite contraction of . If O is an FPO of then the orbit obtained from O by setting, for each , for any , is an FPO of .
Proof. Let O be an FPO of . Let be the set of the connected components of and be the set of the connected components of . If , by Lemma 2, for all pairs of vertices we have that . Similarly, by Lemma 3, if , for all pairs of vertices we have that . Let us suppose by contradiction that is not an FPO of . Then there is a vertex such that . Let us suppose that (the proof of the case in which is similar and omitted). By this assumption it cannot be that because otherwise since is symmetric and positive and OR. Therefore, we have that and C is adjacent, in , to a vertex such that . Then, by definition of bipartite contraction, there exists a vertex and a vertex such that and, by what said above, and . Furthermore . Then and O would not be an FPO of (a contradiction to the hypothesis). □
Lemma 5. Let be a DS and let be the bipartite contraction of . If is an FPO of then the orbit O obtained from by setting for all and for all is an FPO of .
Proof. Let us suppose by contradiction that O is not an FPO of . There must be at least a vertex such that . Suppose that and let A be the connected component of containing v. Since and , we must have that and that there exists a vertex such that . Since, by construction, for all , we have that . Let B be the connected component of containing u. By construction, and since and , we have that , and is an edge of . Then we have that contradicting the hypothesis that is an FPO of . The proof in which is quite similar and therefore omitted. □
Now we can give the following Lemma which states that the number of FPOs of a DS meets the number of FPOs of its bipartite contraction.
Lemma 6. Let be a DS and let be the bipartite contraction of . The number of FPOs of equals the number of FPOs of .
Proof. By Lemmas 4 and 5, there is a surjective relation from the set of FPOs of and the set of FPOs of . Therefore, we simply need to show that this relation is injective. That is, whenever we have two distinct FPOs and of S, then the corresponding orbits and in are distinct and vice versa. This is straightforward to prove and is left to the reader. □
The following algorithm will compute the number of FPOs of . In order to manage the base case we admit null graphs G (that is, graphs in which ) where we assume that null graphs have exactly one FPO (the empty vector).
Theorem 1. The procedure COUNT (Algorithm 1) correctly computes the number of FPOs in an {AND, OR}-DS with symmetric positive dependency graph.
Proof. Let G be the symmetric positive dependency graph of an {AND, OR}-DS . By Lemma 6, we simply need to count the number of FPOs in the bipartite contraction of . We prove the correctness of the algorithm by induction on the number n of vertices of .
Base. If
then there is only one connected component in
, that is, either all the vertices in
G are OR vertices or all of them are AND vertices. By [
2], there are only 2 FPOs in the DS. In this case, the algorithm will make two recursive calls with empty graphs as arguments, so returning 1 + 1 = 2. Thus, in the base case the algorithm is correct.
Induction. Let us suppose the algorithm correctly computes the number of FPOs of these DSs having graphs up to vertices. Let be a graph with n vertices and let be an OR vertex (v being an AND vertex requires so similar reasoning that it is omitted). In order to prove this part it is sufficient to show (1) a one-to-one correspondence between all FPOs O of the contraction of to in which , and all FPOs of the contraction of to and (2) a one-to-one correspondence between all FPOs O of the contraction of to in which , and all FPOs of the contraction of to .
Proof of (1). Let and let be an FPO of the contraction of to (FPO of over , to abbreviate). Let O be an orbit of obtained from by setting and setting . We show that O is an FPO of over . In fact, let since is bipartite and v is an OR vertex, u must be an AND vertex. If , this means that . Otherwise, if this means that, , we have that . Since , for all we have that . All the vertices not belonging to have the same neighborhood in and in . Thus, their value will not change with time t. This proves that O is an FPO of . To finish, let us consider O, an FPO O of over in which , by Lemma 1, is an FPO of over .
Proof of (2). Let . Let be an FPO of over and let O be an orbit of obtained from by setting and setting . Clearly each vertex in is an AND vertex, thus . v is adjacent in to only vertices u such that then . A vertex adjacent to a vertex in will not change its value. In fact, first we note that w is an OR vertex. Thus, if then . Otherwise, if , this means that w is adjacent in to only vertices z with and so remains in , since for all , . All the vertices neither in nor adjacent to any vertex in have their neighborhood which the same in and . Thus, their value will not change with time t. So that O is an FPO of over . To finish, let us consider O, an FPO O of over in which , by Lemma 1, is an FPO of over .
As we said in the beginning of the proof, we may analogously prove that if v is an AND vertex then there is (1) a one-to-one correspondence between all FPOs O of the contraction of to in which , and all FPOs of the contraction of to and (2) a one-to-one correspondence between all FPOs O of the contraction of to in which , and all FPOs of the contraction of to . This completes the proof. □
| Algorithm 1 Computing the number of FPOs of , an {AND, OR}-DS whose dependency graph G is symmetric positive |
- Input:
The AND-OR bipartition of G - Output:
The number of FPOs of - 1:
procedure Count() - 2:
if then return 1 - 3:
let - 4:
Count()+Count() - 5:
return - 6:
end procedure
|
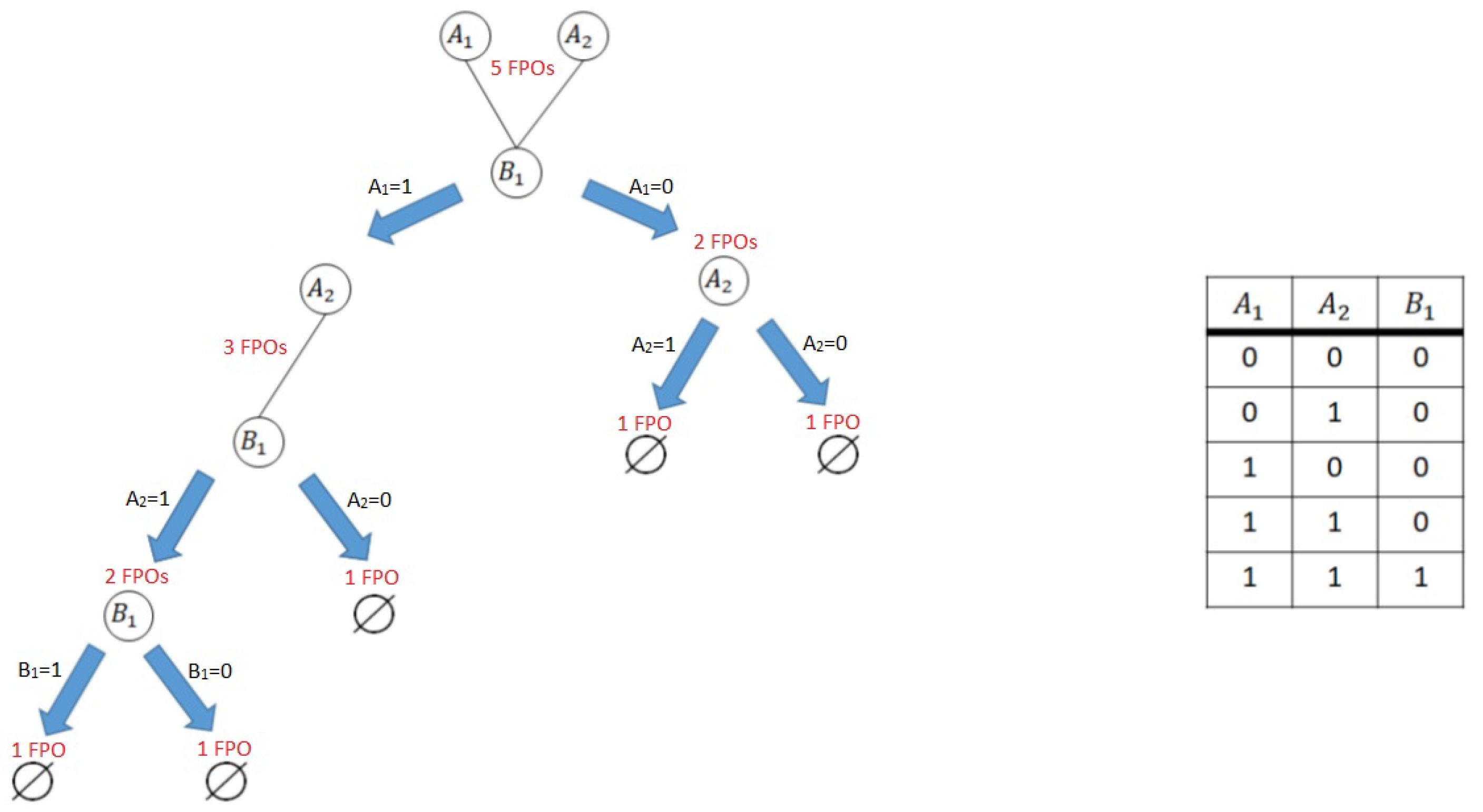
Figure 2 shows the recursive tree of calls of the Algorithm 1 applied to the bipartite contraction of the graph
G of
Figure 1. Numbers in red by the graphs compute the number of FPOs of the recursive call taking as argument the corresponding graph, so that the former call over the graph
appears on the top and outputs a total of 5 FPOs. The table on the right lists all the FPOs of
as the labels of the blue arrows show.
3. Algorithm for Listing All FPO in AND-OR Symmetric PDS
In this section, we provide a lower bound on Algorithm 1 and, based on it, we present an algorithm for listing all the FPOs of an AND-OR symmetric PDS.
We have the following:
Lemma 7. Let S be a DS and let be the bipartite contraction of . If is the bipartition of , then the number of FPOs of is .
Proof. By Lemma 6, it is sufficient to prove that where is the number of FPOs in the bipartite contraction of . Let O be an orbit of such that for all we have that . It is easy to check that if for any we set then since b is adjacent to vertices in A, while if then since b is an AND vertex. We can build different FPOs. A similar argument applies if we set for all . Since the FPO O in which for all and for all is present in both counts, we obtain the statement. □
From Lemma 7, the next corollary is immediately followed.
Corollary 1. Let S be a DS and let be the bipartite contraction of . If , then the number of FPOs of is not less than .
We also have the following result.
Lemma 8. Let S be a DS and let be the bipartite contraction of . If is a complete bipartite graph , then the number of FPOs of equals .
Proof. By Lemma 6, it is sufficient to prove that where is the number of FPOs in the bipartite contraction of . Let be the bipartition of where A is the set of OR vertices. Suppose w.l.o.g. that and . We show that given an FPO O of , only one of the following two cases can happen: (i) for all or (ii) for all . Suppose not and let be an FPO in which there is a vertex and a vertex such that and . Since is complete, v is adjacent to u so that and a contradiction to the hypothesis that is an FPO. Now, it is easy to see that in case (i), if we assign to each vertex in B any binary value, the orbit we obtain is a fixed point of (the same reasoning applies to case (ii)). Since there are, in case (i), of such orbits ( in case (ii)), the statement follows by the fact that the FPO O in which for all and for all is present in both counts. □
By Lemma 8, when the bipartite contraction of a DS is complete, listing all its FPOs requires a very simple algorithm for listing all the binary strings of a prefixed length. Therefore, in the following, we always assume that the bipartite contraction of a DS is not complete.
The Algorithm 1 can be modified in order to list in polynomial time all the FPOs of an {AND, OR}-DS whose dependency graph is symmetric positive as reported in Algorithm 2.
| Algorithm 2 Listing all the FPOs of the bipartite contraction of an {AND, OR}-DS whose dependency graph is symmetric positive |
- Input:
The AND-OR bipartite contraction of G with bipartition where A is the set of OR vertices and B the set of AND vertices of . An orbit O of (initially is undefined for all ) - Output:
All FPOs of - 1:
procedureFPO(, O) - 2:
if then output O - 3:
let - 4:
if then else - 5:
- 6:
- 7:
FPO(, ) - 8:
- 9:
For all - 10:
- 11:
FPO(, ) - 12:
end procedure
|
Theorem 2. Let be an {AND, OR}-DS whose dependency graph is symmetric positive. The Algorithm 2 lists all FPOs of the bipartite contraction of in polynomial time using linear space.
Proof. Let be the bipartite contraction of and the bipartition of . Let . The algorithm calls itself in line 7 and in line 11 and the argument, in each of the recursive call, is a graph with vertices, in the worst case. The for cycle (lines 9-10) takes at most times. Now we can have two cases: (i) in the degree of any vertex v is bounded by a constant c and (ii) is not bounded by constant, that is, we have that so we can find a constant such that for every .
Therefore, in case (i), the recursive relation of the time
, the algorithm spends for listing all the FPOs is:
Assuming that
, clearly this recursion solves in
, so that the algorithm has
complexity. In case (ii), the recursive relation is
The above recursion solves in so that the algorithm has complexity. By Corollary 1, we have that the number of FPOs is not less than and this completes the proof. □
As an example of the output of the algorithm, we refer to the table on the right hand side of
Figure 2.