1. Introduction
Boolean network models, either deterministic or probabilistic, have demonstrated to be a very useful tool to formalize several phenomena coming not only from computer sciences [
1,
2], but also from other sciences such as biology [
3,
4,
5,
6,
7,
8,
9,
10], chemistry [
11,
12], physics [
13,
14,
15,
16], mathematics [
17,
18] or social sciences [
19]. Hence, the study of the dynamical behavior of such models is of great interest, since it could help to understand the corresponding real phenomena.
From the theoretical point of view, deterministic Boolean networks can be seen as discrete dynamical systems of the form
where
is defined on the state space given by a cartesian product of
n copies of a Boolean algebra
. For this reason, in the literature, they are also known as Boolean dynamical systems [
20] or, more properly, as Boolean finite dynamical systems [
21,
22] to emphasize that they are considered on a finite set of elements, although without mentioning the term network.
Nevertheless, when modeling a real phenomenon, its elements are usually represented by nodes in a network in such a way that if an element
i is influenced by another one
j, then there exists an arc from
j to
i. These influences are then formalized by means of a (local) component function
. Frequently, the states of the elements can be only activated or deactivated (on–off) and the Boolean algebra
becomes appropriate to model such a framework. In this sense, it is natural to consider such an underlying graph, usually called a dependency graph, and call these kinds of systems (Boolean) graph dynamical systems (see [
23]). In particular, in this paper, we deal with Boolean graph dynamical systems whose dependency graph is a directed one
.
We will follow the notation given in some previous papers [
24,
25,
26,
27,
28], which we will revise next for the sake of completeness. Given a directed graph
and a vertex
,
is the set of vertices in V that influence
i, and
i itself. Analogously, given
, we define
The formal definition of a (Boolean) discrete dynamical system on a directed graph in which all the vertices update their states in a synchronous or parallel way is as follows.
Definition 1. Let be a directed graph on anda map where is the updated state value of the entity i by applying a local function over the state values of the vertices in . They constitute a discrete dynamical system called a parallel (Boolean) directed (graph) dynamical system over D, which will be denoted by or when specifying the dependency digraph is not necessary. Specifically, in this work, we focus on homogeneous systems defined on the Boolean algebra
, which are those induced by a (global) function
. That is, any component function
of
F is the restriction of the function
f to
. As an evolution operator, we deal with maxterms and minterms. Recall that a maxterm (resp. minterm) of
n variables is a Boolean function
where
or
, being
the negation of
. Thus, the simplest maxterms OR and NAND are given by
respectively, the simplest minterms AND and NOR are given by
According to the definition above, generic PDDS induced by a maxterm MAX (resp. minterm MIN) as evolution operator will be denoted by (resp. ).
On the other hand, in the case of sequential update, the definition is as follows.
Definition 2. Let be a directed graph on , a permutation on V anda map where updates the state value of the vertex from to considering the state values of the vertices belonging to and keeping the other states unaltered, i.e., , being the identity function over the vertex j and the local function which performs the update for the vertex . They constitute a discrete dynamical system called sequential (Boolean) directed (graph) dynamical system over D, which will be denoted by or when specifying the dependency graph is not necessary and the updating order is implicit in this context of sequential evolution. As in the case of PDDS, generic SDDS with a maxterm MAX (resp. minterm MIN) as evolution operator will be denoted by (resp. ).
The main purpose of this paper is to solve the problems of coexistence of periodic orbits in
,
,
and
. To determine the coexistence of periodic orbits is a classical problem in the study of dynamical systems. In fact, Sharkovsky’s Theorem [
29,
30] on the coexistence of periodic orbits in discrete dynamical systems associated with a continuous function defined on a compact interval is considered to be one of the most relevant theorems of the twentieth century.
In previous works [
31,
32,
33,
34,
35,
36], a complete study of the periodic structure of homogeneous parallel and sequential systems induced by maxterm and minterm Boolean functions over undirected dependency graphs were performed. More specifically, in [
36], the periodic structure of the simplest parallel systems, i.e., those induced by the maxterm OR (resp. minterm AND) and NAND (resp. NOR) was analyzed. In particular, it was shown that any parallel system inferred by OR (resp. AND) has only fixed points, while anyone induced by NAND (resp. NOR) only presents periodic orbits of period two. These results were generalized in [
31,
35], where it was demonstrated that any parallel (homogeneous) system induced by any maxterm (resp. minterm) can only present fixed points or two-periodic orbits, while fixed points and two-periodic orbits cannot coexist. Concerning the sequential case, in [
32], it was proved that, in contrast with the parallel case, sequential (homogeneous) systems induced by any maxterm (resp. minterm) can present periodic points of whichever period. Nevertheless, as in the parallel case, the existence of fixed points results incompatible with the existence of other periodic orbits. On the other hand, in [
33,
34], a study on the maximum number of coexisting periodic orbits of the same period is carried out for parallel and sequential systems, respectively.
For homogenous MAX-PDDS and MIN-PDDS over directed graphs, we can find some partial results in [
26,
27,
28]. In particular, in [
26], it was demonstrated that homogeneous MAX-PDDS and MIN-PDDS can present periodic orbits of any period and, in [
28], the periodic structures of such systems over special digraph classes were analyzed. In [
27], a matrix method was provided to calculate the (periodic) orbit of any initial state of a given system, allowing us to study the coexistent periods of such a system.
Likewise, some studies on the periodic or limit cycle structure of other kinds of Boolean graph dynamical systems, which are usually non-homogeneous, can be found in the literature. For instance, in [
37], the authors proved that, for the sequential case of Boolean graph dynamical systems whose evolution operators are given by threshold component functions, the only
-limit sets are fixed points, in contrast with the results for homogeneous sequential systems induced by maxterms and minterms shown in [
32]. After that, Mortveit [
38] studied the possible periodic structures and generalized these results for the case of standard threshold systems with block-sequential update schedules also known as mixed systems [
39]. Later, in [
40], the authors analyzed how the shape of the dependency graph influences the limit cycle structure of such block-sequential systems, deriving sufficient conditions on this shape which provides only fixed points as limit cycles. Finally, the limit cycle structure for systems whose evolution operator is composed by bi-threshold and multi-threshold functions were considered in [
41,
42] respectively.
More similar to our homogeneous systems, we can find some results on the periodic structure of non-homogeneous systems whose evolution operator is constituted by components which are maxterm or minterm Boolean functions [
43,
44]. In [
44], the authors determined the periodic structure of systems whose evolution operator consists of component functions which are the simplest maxterms OR, NAND and/or the simplest minterms AND, NOR. In [
43], these results were extended to more general Boolean functions, which induce systems with only fixed points as periodic orbits. These results, together with the ones in the present paper, could help to find the structure of periodic orbits for general non-homogeneous systems.
The main contribution of this paper is to show that periodic orbits of any period can exist and coexist together in , , and , which means a breaking of the pattern found in the case of their counterparts with undirected dependency graphs. These results complete the study of the periodic structure of homogeneous (Boolean) graph dynamical systems on maxterm and minterm Boolean functions.
The paper is organized as follows. In
Section 2, we demonstrate that a PDDS on a general maxterm or minterm Boolean function can present coexisting periodic orbits of any period, so breaking the pattern shown in the case over undirected graphs.
Section 3 is devoted to proving this same results in the case of SDDS. We finish the paper by showing the most important conclusions and future research directions which can be derived from these results.
2. Coexistence of Periodic Orbits in PDDS
In this section, we deal with the problem of the coexistence of periodic orbits in PDDS. In our previous work [
26], the existence of periodic orbits of different periods in
and
was studied and compared with their counterparts over undirected graphs.
In the simplest cases when MAX=OR and MIN=AND, recall that all
and
are fixed-point systems (see Theorems 1 and 2 in [
26]). Anyway, it is worth to point out that the number of fixed points for these PDDS systems increases with respect to the case of their counterparts over undirected graphs, usually denoted as
and
, where
(fixed point with all the vertices activated) and
(fixed point with all the vertices deactivated) are the only fixed points (see Remark 1 in [
26]), if the dependency graph of the system is connected.
Periodic orbits of any period and no fixed points can appear in a NAND-PDDS and a NOR-PDDS. This contrasts with the counterparts over undirected graphs, denoted NAND-PDS and NOR-PDS, where only two-periodic orbits can appear (see Theorems 3 and 4 in [
26]). To see that, given a natural number
n,
, a constructive method is detailed to obtain a
with a periodic orbit of period
n (the construction of a
with a periodic orbit of period
n is analogous). Next, we briefly revise how to construct such a PDDS, since we will use it later to prove our result on the coexistence of periodic orbits.
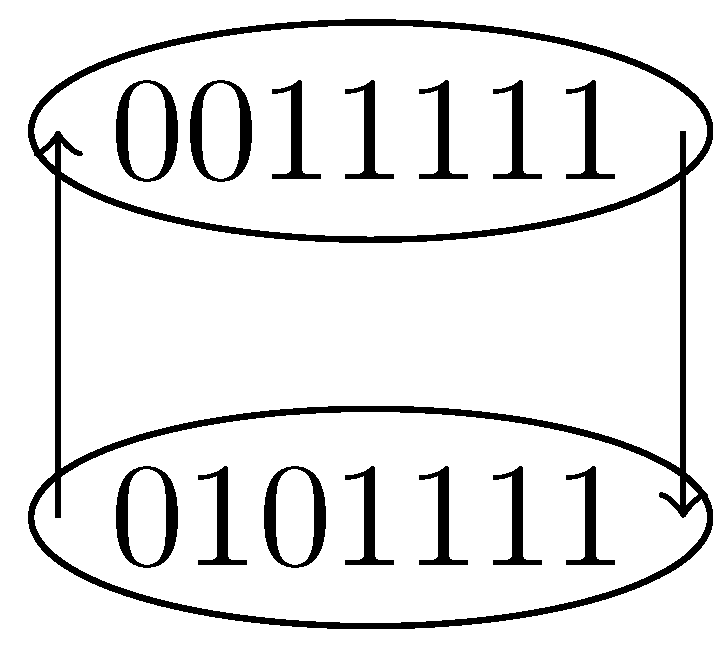
For
, the
defined over the digraph displayed in
Figure 1. It has two two-periodic orbits, namely:
and
.
In general, given , , consider the complete digraph , i.e., has n vertices and for any pair of vertices there is an arc form i to j and another one from j to i. Then we construct the directed graph as
.
.
and take .
Let us write to indicate the state value of the entity i after k iterations of the evolution operator and take the initial values for the variables and for all . It is a straightforward computation to check that the system evolves in the following way:
After k iterations, : , for all .
After n iterations, all the state values coincide with the initial ones, i.e., for all .
Namely, the PDDS constructed in this way presents a periodic orbit of period n.
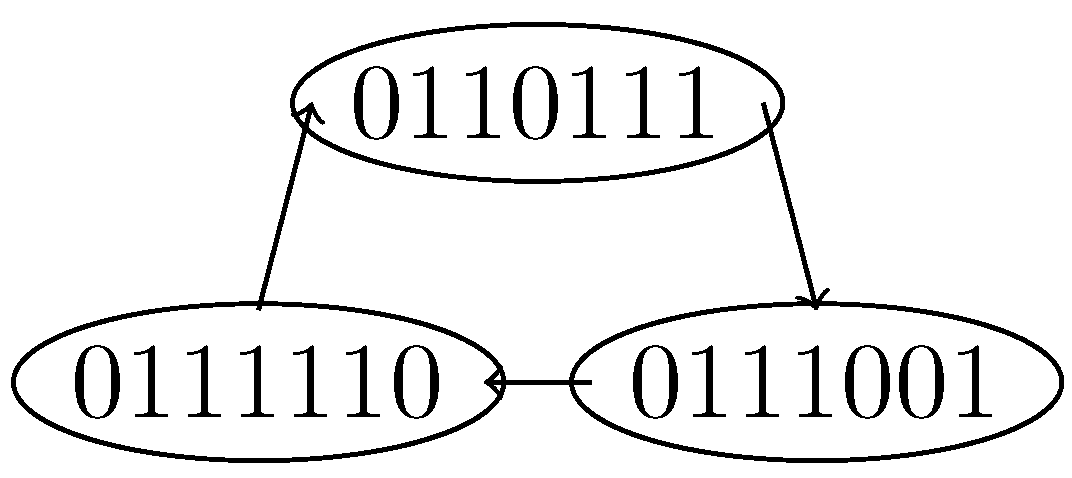
Figure 2 illustrates the designed digraphs for
,
,
and
.
Thus, following the description above:
For the case,
, the set of states
constitutes a periodic orbit of period 3.
For the case
,
is a periodic orbit of period 4.
For the case
,
is a periodic orbit of period 5.
For the case
,
is a periodic orbit of period 6.
Recall that the periodic orbits of
and
are fixed points and two-periodic orbits (see Theorems 3 and 4 in [
35]). Moreover, in such PDS, fixed points and two-periodic orbits cannot coexist (see Section 3 in [
31]).
On the other hand, in light of the mentioned results regarding PDDS, we have that
and
can have periodic orbits of whichever period (see Section 3 in [
31]). The coexistence of the periodic orbits for these PDDS remains an open problem, which we tackle next.
Theorem 1. (Coexistence of periods in ) Given , , there exists a MAX-PDDS which presents periodic orbits of periods simultaneously.
Proof. Let us construct a MAX-PDDS with orbits of periods .
Firstly, let us consider the case for all .
For each , let us take the digraph described above. To avoid duplication in the name of the vertices of each PDDS, we denote by the vertex j in the digraph . We also consider the following relations between the vertices of these digraphs: is adjacent (reciprocal influence) to for all j, m and . In this way we obtain the dependency graph D.
As evolution operator, we take .
As initial state values for the variables, we consider that the vertex is deactivated and the rest of vertices are activated.
This system evolves as follows:
After k iterations, , is deactivated and the rest of vertices are activated.
After iterations, all the state values coincide with the initial ones.
Namely, the constructed in this way presents a periodic orbit of period .
Thus, by considering the different r initial state values obtained by varying i in , r periodic orbits with periods result.
Assume now that there exists such that . Without loss of generality, we can assume . Let , , be the PDDS constructed above in which periodic orbits of period , , coexist. We take:
. Namely, is obtained from D by adding a new vertex which influences the rest of vertices and is only influenced by itself.
. Namely, we consider as evolution operator the disjuntion of MAX and a direct variable corresponding to the vertex .
Let us reason that has periodic orbits of periods .
Observe that, for such a PDDS, an initial state is preserved permanently and the system evolves as , appearing all the periodic orbits of periods greater than 1. On the other hand, an initial state reaches the fixed point after, at most, 1 iteration. □
Let us illustrate this result with the following example to clarify the notation.
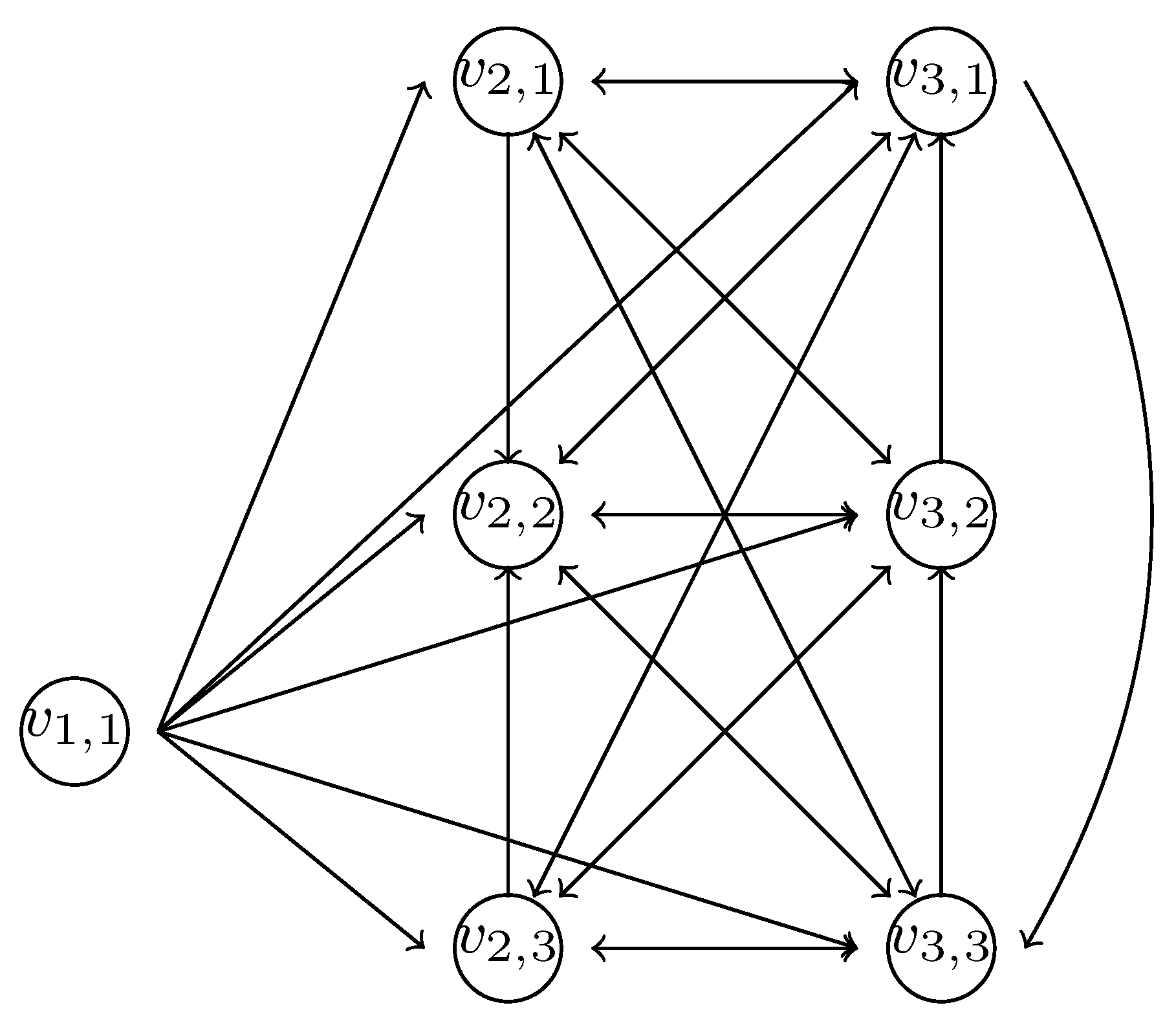
Example 1. The PDDS proposed by Theorem 1 in which a fixed point, a 2-periodic orbit and a 3-periodic orbit coexist, is defined by:
, ,
, and (see Figure 3), with - -
, and
- -
.
.
According to the notation in Theorem 1:
By fixing , the system evolves to the fixed point after, at most, 1 iteration.
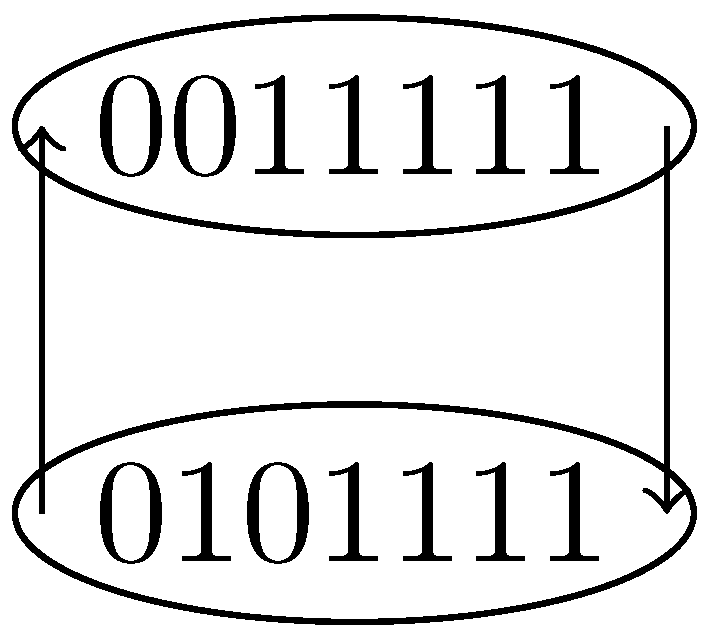
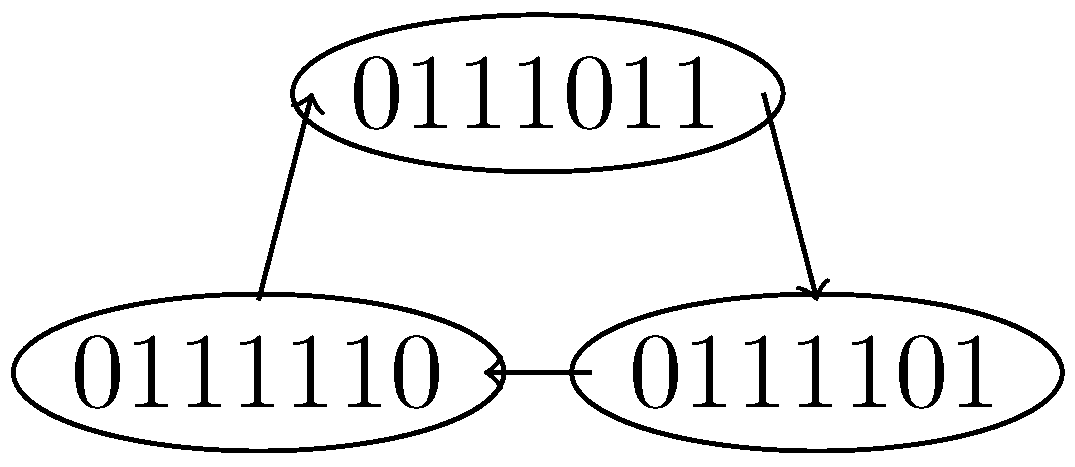
, , are the vertices which generate the 2-periodic orbit (see Figure 4). , , are the vertices which generate the 3-periodic orbit (see Figure 5).
Dually we have:
Theorem 2. (Coexistence of periods in ) Given , , there exists a MIN-PDDS which presents periodic orbits of periods simultaneously.
3. Coexistence of Periodic Orbits in SDDS
In
Section 2, some results about the orbital structure of PDDS with general maxterm (resp. minterm) functions as evolution operators have been shown, proving that periodic orbits of any period can appear in such systems. In this section, we analyze the case of SDDS with general maxterm (resp. minterm) functions as evolution operators, showing that this situation remains when considering a sequential update schedule.
In the case of sequential dynamical systems over undirected graphs, in Theorems 4 and 5 of [
32], it was shown that there exist MAX-SDS (resp. MIN-SDS) with periodic orbits of any period. As a direct consequence, since SDS are particular cases of SDDS, we can state that
(resp.
) can present periodic orbits of any period.
It is worth analyzing the particular relevant cases when the evolution operator of a discrete dynamical system is the maxterm OR or NAND (resp. minterm AND or NOR).
Recall that
(resp.
) are fixed points systems. More precisely,
and
are the only fixed points of such systems. Indeed, there are no differences between the orbital structures in
and
(resp.
and
). It happens because the fixed points of a
and those of the sequential counterpart
coincide (see Lemma 1 in [
32]), result that can be extended to the directed framework as follows:
Lemma 1. Any homogeneous sequential directed dynamical system induced by a maxterm or minterm F, , and its parallel counterpart, , have the same fixed points.
Proof. Let be a fixed point of the , where represents the (fixed) state value of the vertex . Since the updating of the state value of each i only depends on the state values of the vertices in and the restriction of F to that set, it is straightforward to check that, independently of the election of , is also a fixed point of .
Conversely, let be a fixed point for for a certain updating permutation . Since the state values of all the vertices remain equal in the successive updating steps determined by , it becomes clear that is also a fixed point of . □
As a consequence of Lemma 1, the fixed points of and (resp. and ) coincide. In the next two corollaries, we remark that, actually, and are fixed-point systems.
Corollary 1. Any is a fixed-point system. In fact, and are always fixed points of the system but, even if D is a (weakly) connected digraph, other fixed points can appear, in contrast with the property of with connected dependency graphs.
Proof. It is enough to show that there cannot be periodic orbits of a period greater that 1. In fact, we have only one of the following two possibilities for each :
, , i.e., the state value 0 is permanent for this entity from the initial configuration.
such that , being that the iteration T the first time that the variable takes the value 1. In this situation, the state value 1 is permanent from this iteration on.
Thus, after a certain number of iterations, all the vertices reach a fixed value that they preserve onwards. □
Dually, we have:
Corollary 2. Any is a fixed-point system. In fact, and are always fixed points of the system but, even if D is a (weakly) connected digraph, other fixed points can appear, in contrast with the property of with connected dependency graphs.
In Theorems 6 and 7 of [
32], it was proved that SDS over undirected dependency graphs with NAND (resp. NOR) as evolution operators can present periodic orbits of any period, except fixed points. For NAND-SDDS and NOR-SDS, we have:
Corollary 3. A can present periodic orbits of any period, except fixed points.
Proof. First, notice that such a SDDS cannot present fixed points. In fact, we know that PDDS with NAND as an evolution operator cannot present fixed points. Then, this first assertion follows from Lemma 1.
Furthermore, from Theorem 6 of [
32] and taking into account that SDS are particular cases of SDDS, this system can present periodic orbits of any period greater than 1. □
Dually, we have:
Corollary 4. A can present periodic orbits of any period, except fixed points.
Once the existence of periodic orbits in SDDS was studied, we continued analyzing the possible coexistence of them in these kinds of systems. In Theorem 1 (resp. Theorem 2), the coexistence of periods in (resp. ) is analyzed, proving that the coexistence of periodic orbits with different periods are possible, even with fixed points.
In line with the results for PDDS, in the context of SDDS with general maxterm (resp. minterm) functions as evolution operators, we will show that periodic orbits with different periods can coexist in an SDDS, even fixed points and periodic orbits of period greater than 1, in contrast with their counterparts over undirected dependency graphs.
Theorem 3. (Coexistence of periods in ) Given , , there exists a MAX-SDDS which presents periodic orbits of periods simultaneously.
Proof. If
for all
, the result is a direct consequence of Theorem 8 in [
32], since an SDS is a particular case of SDDS.
On the other hand, if there exists
with
, without loss of generality, we can assume
. Let
be the SDS constructed in Theorem 8 in [
32] (or in Theorem 6 in [
32] in the case
) in which the other periodic orbits
,
, coexist, being
. To make the comprehension of the following reasoning easier, and for the sake of completeness and clarity, next we reproduce the structure of these systems:
In the case , is the complete graph , with (note that denotes a non-directed complete graph, because an SDS is considered). As permutation on V, we take , the identity permutation. Finally, as the evolution operator, we take .
If
, the
proposed in Theorem 8 in [
32] is as follows:
Firstly, we construct : for each , let us take two complete graphs and of vertices. We will denote by and the vertices of and , respectively, for every . All these vertices constitute the vertex set V.
Now, the adjacency set E is constructed from the internal adjacencies in each complete graph and , considering additionally the following adjacency structure among the vertices:
is adjacent to for all k, m and . In other words, the vertices in are adjacent to all the vertices in for .
is adjacent to for all k, m and . In other words, the vertices in are adjacent to all the vertices in for .
is adjacent to for all k, m and . In other words, the vertices in are adjacent to all the vertices in for (but they are not adjacent to the vertices in ).
As permutation on the set of vertices, we will consider:
Namely, first, the state values of the vertices in are updated, then the ones in , next to the vertices in followed by the ones in , and so on until all the vertices are updated.
Finally, as evolution operator, we take .
Based on this SDS, let us consider the SDDS defined from these elements:
, the dependency digraph of the SDDS.
, the maxterm Boolean function of the SDDS.
, the order permutation of the SDDS.
In this case, an initial state will be preserved permanently (since no other vertex influences and it appears in MAX in its direct form), and the system will evolve as , where all the periodic orbits of period greater than 1 appear; while an initial state reaches the fixed point with all the vertices activated after, at most, one iteration due to the influence of the state of this vertex on the others. □
As in the case of PDDS, let us illustrate Theorem 3 with the following example.
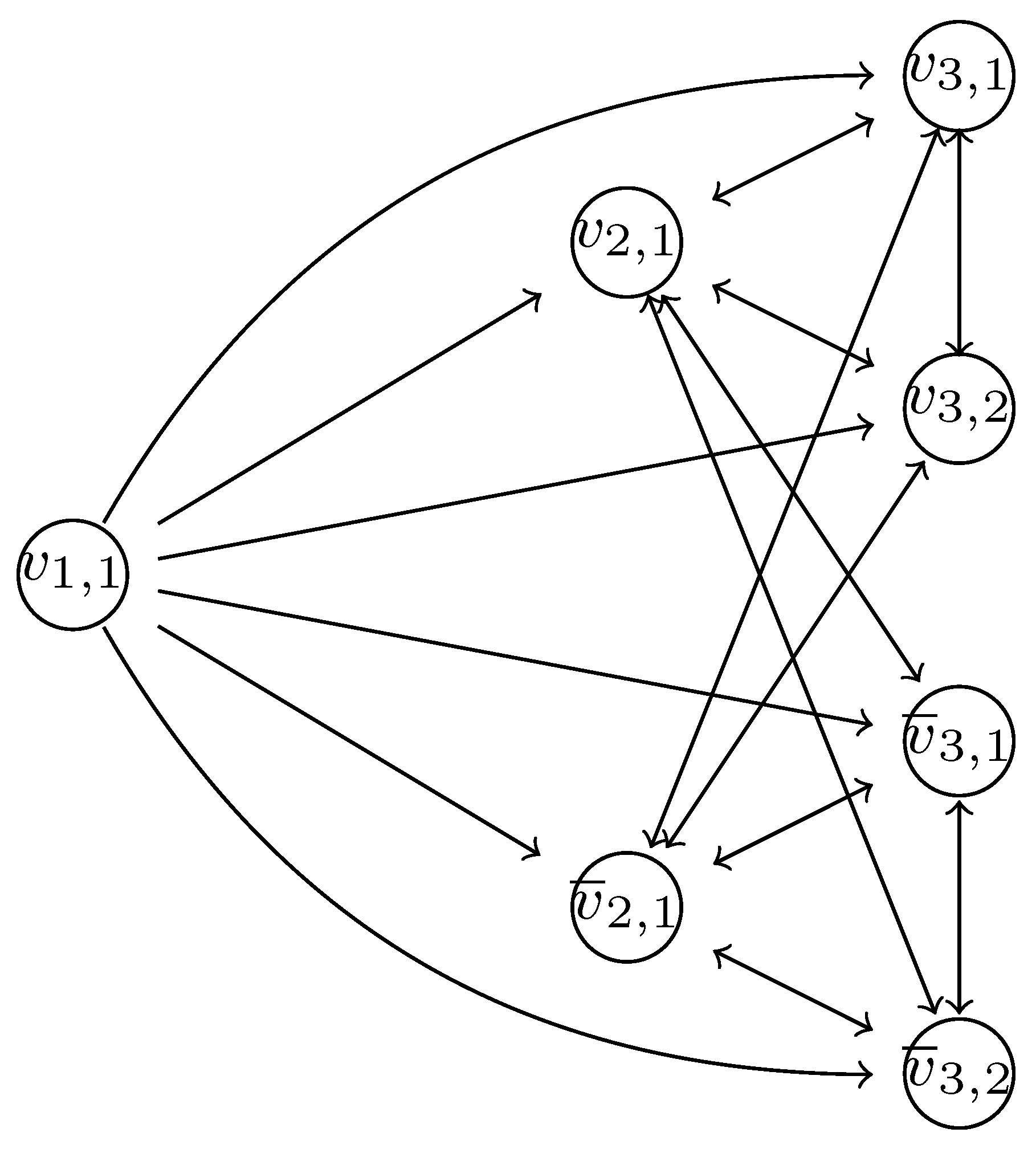
Example 2. The SDDS proposed by Theorem 3 in which a fixed point, a two-periodic orbit and a three-periodic orbit coexist, is defined by:
, , ,
, and (see Figure 6), with - -
, and
- -
.
.
.
According to the notation in Theorem 3:
By fixing , the system evolves to the fixed point after, at most, one iteration.
, are the vertices which generate the two-periodic orbit (see Figure 7). , , , are the vertices which generate the three-periodic orbit (see Figure 8).
Dually to Theorem 3, we have the following result.
Theorem 4. (Coexistence of periods in ) Given , , there exists awith a minterm as evolution operator which presents periodic orbits of periods simultaneously.
4. Conclusions and Future Research Directions
This work completes the study of the periodic structure of homogeneous Boolean graph dynamical systems induced by maxterm and minterm Boolean functions. Specifically, the results in this paper show that the existence and coexistence of periodic orbits in parallel and sequential Boolean dynamical systems, strongly depend on the character, undirected or directed, of the underlying dependency graph. In particular, for the directed case, fixed points can coexist with periodic points of any period, which supposes a drastic change in relation to the case of systems over undirected graphs. This difference could be relevant, especially when thinking in applications, since, in Boolean networks representing real phenomena, the relations between any two elements are usually unidirectional.
We think that these results could be useful to study the existence and coexistence of periodic orbits in non-homogeneous Boolean dynamical systems, mainly in the case of evolution operators consisting of independent component functions given by maxterms and minterms, also known as AND-OR-NOT systems.
Another future research line arising from this work could be to study conditions that guarantee the existence of a unique fixed point, which automatically becomes a global attractor of the system. In other words, to determine when fixed points are the only periodic orbits in the system and when there is only one. It would be also interesting to provide uniqueness results of periodic orbits of any period, or to count (or at least bound) the number of such periodic orbits.