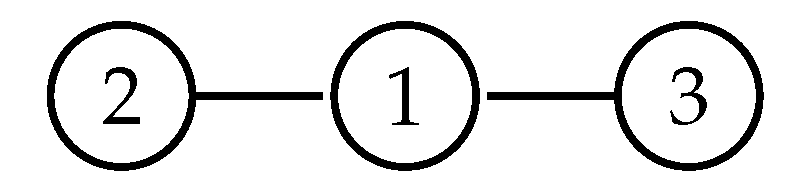On the Periodic Structure of Parallel Dynamical Systems on Generalized Independent Boolean Functions

Abstract

In this paper, based on previous results on AND-OR parallel dynamical systems over directed graphs, we give a more general pattern of local functions that also provides fixed point systems. Moreover, by considering independent sets, this pattern is also generalized to get systems in which periodic orbits are only fixed points or 2-periodic orbits. The results obtained are also applicable to homogeneous systems. On the other hand, we study the periodic structure of parallel dynamical systems given by the composition of two parallel systems, which are conjugate under an invertible map in which the inverse is equal to the original map. This allows us to prove that the composition of any parallel system on a maxterm (or minterm) Boolean function and its conjugate one by means of the complement map is a fixed point system, when the associated graph is undirected. However, when the associated graph is directed, we demonstrate that the corresponding composition may have points of any period, even if we restrict ourselves to the simplest maxterm OR and the simplest minterm AND. In spite of this general situation, we prove that, when the associated digraph is acyclic, the composition of OR and AND is a fixed point system.

1. Introduction

Discrete-time dynamical systems on a finite state space have an important role in several different branches of science and engineering. Examples of such systems include deterministic networks models, logical models, agent-based models, Petri nets, and finite state machines. Indeed, these kinds of systems have been used to model natural events such as gene regulatory networks [1,2,3,4,5,6], and processes coming from computer sciences [7,8], chemistry [9,10], physics [11,12,13,14], biology [15,16], and social sciences [17]. Although these systems can be simulated on a computer, only a few analytical results beyond simulation are available.

Let X be a non-empty finite set and $F:X\to X$ be a map. Then, the iterations of the function F evaluated on one point $x\in X$, given by $F^t\left(x\right),t\in \mathbb{N}$, can be seen as the description of the evolution of x in discrete steps of time. Thus, $(X,F)$ induces a discrete-time dynamical system when considering the iterations of the function F. To simplify, we usually say that F is a dynamical system on X. In this context, a point $x\in X$ is called a fixed point of F if $F\left(x\right)=x$, while x is called a periodic point of F of period $t>0$ when $F^t\left(x\right)=x$ and $F^s\left(x\right)\ne x$ for every $0<s<t$. Otherwise, x is said to be a non-periodic point. The set of fixed points of F is usually denoted by $\mathrm{Fix}\left(F\right)$ while the set of t-periodic points of F is denoted by ${\mathrm{Per}}_t\left(F\right)$. For any $x\in X$, the orbit of x is defined as $\mathrm{Orb}\left(x\right)=\{F^t\left(x\right):t\in \mathbb{N}\}.$ An eventually fixed point (resp. eventually periodic orbit) is a non-periodic point in which the orbit converges to a fixed point (resp. periodic orbit). One of the first problems in the study of the dynamics of a system is to find its fixed points and periodic points. In the literature, one can find several studies that have been carried out for different discrete-time dynamical systems on finite sets (see [18,19,20,21,22,23,24], for example).

We say that F is a fixed point system, if every $x\in X$ is a fixed point or an eventually fixed point. Likewise, F is called a t-periodic point system, if every $x\in X$ is t-periodic point or an eventually t-periodic point. One of the main objectives in this work is to find fixed point systems among a particular class of systems that can present periodic orbits of any period.

Let F and G be two discrete-time dynamical systems on X. We say that F and G are conjugate if there exists an invertible map $H:X⟶X$ such that $G=H^{-1}\circ F\circ H$. Observe that if F and G are conjugate then ${\mathrm{Per}}_t\left(F\right)=\{H\left(x\right):x\in {\mathrm{Per}}_t\left(G\right)\}$ for any positive integer t and, in particular $\mathrm{Fix}\left(F\right)=\left\{H\right(x):x\in \mathrm{Fix}(G\left)\right\}$. This means that the dynamics of both F and G are the same and, for this reason, F and G are said to be dynamically equivalent.

Specifically, in this work, we focus on dynamical systems induced by vector-valued Boolean functions on $X={\{0,1\}}^n$. Recall that a function

$$f:{\{0,1\}}^n⟶\{0,1\}$$

is said to be a Boolean function when $f(x_1,\dots ,x_n)$ is obtained from $x_1,\dots ,x_n\in \{0,1\}$ using the logical AND $(\wedge )$, the logical OR $(\vee )$ and the logical NOT ${(}^{\prime })$. In particular, a maxterm (resp. minterm) of n variables is a Boolean function

$$f(x_1,\dots ,x_n)=z_1\vee \cdots \vee z_n(\mathrm{resp}.f(x_1,\dots ,x_n)=z_1\wedge \cdots \wedge z_n),$$

where $z_i=x_i$ or $z_i=x_i^{\prime }$.

A dynamical system

$$F:{\{0,1\}}^n⟶{\{0,1\}}^n,F(x_1,\dots ,x_n)=(f_1(x_1,\dots ,x_n),\dots ,f_n(x_1,\dots ,x_n)),$$

where each $f_i$ is a Boolean function, is called a parallel dynamical system (PDS) over ${\{0,1\}}^n$.

Given a parallel dynamical system, we can consider a digraph associated with it by considering n vertices, $1,\dots ,n$, corresponding to the variables $x_1,\dots ,x_n$ of F and a directed edge (or arc) $(i,j)$, if the function $f_j$ depends on $x_i$. That is, the associated digraph encodes the variable dependencies in F. In the following, we shall assume that each $f_i$ depends on $x_i$ and avoid drawing the associated graph loops. If for every $i\ne j$, $f_j$ depends on $x_i$ if and only if $f_i$ depends on $x_j$, then the associated graph is a simple (undirected) one. Usually, the acronym PDS is used for parallel dynamical systems over undirected graphs, whereas if the associated graph is properly a digraph, F is said to be a parallel directed dynamical system (PDDS). As can be seen in the recent literature [25,26,27,28,29,30,31,32], the dynamics of PDDS are, in general, much more involved than the dynamics of PDS.

Let

$$F:{\{0,1\}}^n⟶{\{0,1\}}^n,F(x_1,\dots ,x_n)=(f_1(x_1,\dots ,x_n),\dots ,f_n(x_1,\dots ,x_n)),$$

be a PDS or a PDDS. If every $f_i$ is the restriction of a global function $f:{\{0,1\}}^n⟶\{0,1\}$ acting only over the state of the entity i and their related ones, then the system is called homogeneous. In this case, we say that F is a f-PDS or a f-PDDS depending on the associated graph. For example, when f is a maxterm function (resp. minterm function), the corresponding PDS or PDDS will be denoted by MAX-PDS or MAX-PDDS (resp. MIN-PDS or MIN-PDDS), as usually done in the previously cited references. Otherwise, if the local functions $f_1,\cdots ,f_n$ are independent and chosen from a set of Boolean functions, for instance, $\{g,h\}$, the corresponding PDS or PDDS will be denoted by g-h-PDS or g-h-PDDS, respectively.

In recent literature, some theoretical results have been obtained in relation to the periodic structure for PDS and PDDS. In particular, in [30], it is proved that any OR-PDS and AND-PDS are fixed point systems, while NAND-PDS and NOR-PDS are 2-periodic point systems, independently of the associated (simple) graph. Furthermore, these results are generalized in [25,26,27,28,29,33,34] where the authors study the periodic structure of MAX-PDS, MAX-PDDS, MIN-PDS, and MIN-PDDS. That is, parallel dynamical systems where the future state of each node is computed using the Boolean maxterm MAX or the Boolean minterm MIN. Specifically, it is proved that MAX-PDS and MIN-PDS are either fixed point systems or 2-periodic point systems, while MAX-PDDS and MIN-PDDS can present orbits of any period. The main idea in those papers is to study the dependency of the dynamics on the associated graph of the system. Indeed, it is shown that the dynamics of such systems strongly depend on the combinatorial properties of the corresponding associated graph. In particular, it is shown that AND-PDDS and OR-PDDS are fixed point systems like their PDS counterparts (whichever the associated graph is), while NAND-PDDS and NOR-PDDS are 2-periodic point systems if the associated digraph is acyclic.

In several previous works [19,28,35], the periodic structure of non-homogeneous systems, especially their fixed points, were studied. In particular, in [28], based on the mentioned results for homogeneous systems, it was demonstrated that AND-OR-PDS are also fixed point systems, while NAND-NOR-PDS are 2-periodic point systems. Regarding PDDS, AND-OR-PDDS are also fixed point systems, but NAND-NOR-PDDS can present periodic orbits of any period. Another interesting result obtained in this work is that AND-OR-NAND-NOR-PDS can only present fixed points and 2-periodic orbits as periodic orbits.

Inspired by these works, in this paper, we extend these results to systems with more general local Boolean functions as evolution operators. Specifically, based on the result on AND-OR-PDDS, we give a more general pattern of local Boolean functions that also provides fixed point systems. Moreover, by considering independent sets, the results on AND-NOR-NAND-NOR-PDDS are also generalized by providing a pattern to get parallel systems in which the periodic orbits are only fixed points or 2-periodic orbits. The results so obtained are also applicable to homogeneous systems.

On the other hand, we study the periodic structure of parallel dynamical systems given by the composition of two parallel systems that are conjugate by means of an invertible map whose inverse is equal to the original map. This allows us to prove that the composition of any parallel system on a maxterm (or minterm) Boolean function and its conjugate one by means of the complement map $\copyright :{\{0,1\}}^n⟶{\{0,1\}}^n$, such that $\copyright (x_1,\dots ,x_n)=(x_1^{\prime },\dots ,x_n^{\prime })$, is a fixed point system when the associated graph is undirected. However, when the associated graph is directed, we demonstrate that the corresponding composition may have points of any period, even for the simplest maxterm OR and the simplest minterm AND. In spite of this general situation, we prove that, when the associated digraph is acyclic, the composition of OR and AND is a fixed point system. As a consequence, it can be inferred that cycles in the associated digraph are the responsible of the appearance of periodic orbits with periods greater than 1.

The results here obtained could be of great relevance in applied models where the expression of the local functions are more general than maxterm or minterms.

The paper is organized as follows. In Section 2, first, we find a general class of fixed point PDDS. In the rest of this section, we complete the study by considering general independent local functions and prove that, although such systems can present periodic orbits of any period greater than one, under particular conditions related to independent sets, they can only present fixed points or 2-periodic orbits, as in the known case of AND-OR-NAND-NOR-PDS. Actually, both fixed and 2-periodic points can coexist, so breaking the pattern found for homogeneous PDS on any of these Boolean functions. In Section 3, we study the behavior of the composition of two PDDS, which are conjugate under an invertible map H such that $H^{-1}=H$, and give some applications of this result. In particular, we show that the composition of a MAX-PDS and a MIN-PDS, which are conjugate under the complement map, is a fixed point system. In contrast, if we consider directed dependency graphs, then we prove that the corresponding composition may have points of any period.

2. Periodic Structure of PDDS on Generalized Independent Local Functions

Let $D=(V,E)$ be the (directed) graph associated with a parallel dynamical system F. Given $j\in V$ and $Q\subseteq V$, we will use the following traditional terminology:

$$A_D\left(j\right)=\{i:(i,j)\in E\},\overline{A_D\left(j\right)}=A_D\left(j\right)\cup \left\{j\right\}$$

$$A_D\left(Q\right)={\cup }_{j\in Q}{A}_D\left(j\right),\overline{A_D\left(Q\right)}=A_D\left(Q\right)\cup Q$$

If D is a simple (undirected) graph, in the definition of $A_D\left(j\right)$, we should replace the arc $(i,j)$ by the edge $\{i,j\}$. Anyway, observe that a simple graph can be considered as a particular case of a digraph.

The next theorem gives a simple criterion in order to characterize a class of fixed point PDDS, which are not necessarily homogeneous. This theorem generalizes some classes of fixed point PDS and PDDS (for example, see [26] (Theorem 1, Theorem 2), [28] (Theorem 1) and [25] (Theorem 1, Theorem 2)).

Theorem 1.

Let F be a PDDS given by

$$F:{\{0,1\}}^n⟶{\{0,1\}}^n,F(x_1,\dots ,x_n)=(F_1(x_1,\dots ,x_n),\dots ,F_n(x_1,\dots ,x_n)).$$

If for each $1\le i\le n$, $F_i=x_i\vee M_{i}or{F}_i=x_i\wedge M_i$, and each $M_i$ is a Boolean function on $\{x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n\}$, then F is a fixed point system, independently of the associated graph of the system.

Proof. 

Let $x=(x_1^0,\cdots ,x_n^0)$ be a periodic point of F and let $t\ge 1$ be the smallest positive integer such that $F^t\left(x\right)=x$. Denote $F^m\left(x\right)=(x_1^m,\dots ,x_n^m)$ for $m\ge 1$ and

$$A_m=\{i:(x_i^m=1\mathrm{and}{F}_i=x_i\vee M_i)\mathrm{or}(x_i^m=0\mathrm{and}{F}_i=x_i\wedge M_i)\}.$$

Since $F^t\left(x\right)=x$, we have $A_0=A_t$. Observe that $A_m\subseteq A_{m+1}$ for each $m\ge 0$. In fact:

• If $i\in A_m$ is such that $x_i^m=1$ and $F_i=x_i\vee M_i$, then $x_i^{m+1}=1$ and so $i\in A_{m+1}$.
• If $i\in A_m$ is such that $x_i^m=0$ and $F_i=x_i\wedge M_i$, then $x_i^{m+1}=0$ and so $i\in A_{m+1}$.

Therefore,

$$A_0\subseteq A_1\subseteq \cdots \subseteq A_t=A_0,$$

and consequently $A_0=A_1$.

Finally, let us show that $(x_1^0,\dots ,x_n^0)=(x_1^1,\dots ,x_n^1)$, which means that $x=F\left(x\right)$. If $x_i^0=1$ and $i\in A_0=A_1$, then it is clear that $x_i^1=1$. Assume that $x_i^0=1$ and $i\notin A_0$. Then $F_i=x_i\wedge M_i$ for some Boolean function $M_i$ on $\{x_1,\dots ,x_{i-1},x_{i+1},\dots ,,x_n\}$. However, this implies that $x_i^1=1$, since otherwise $i\in A_1=A_0$, which is a contradiction. By a similar argument we get that if $x_i^0=0$ then $x_i^1=0$, which finishes the proof. □

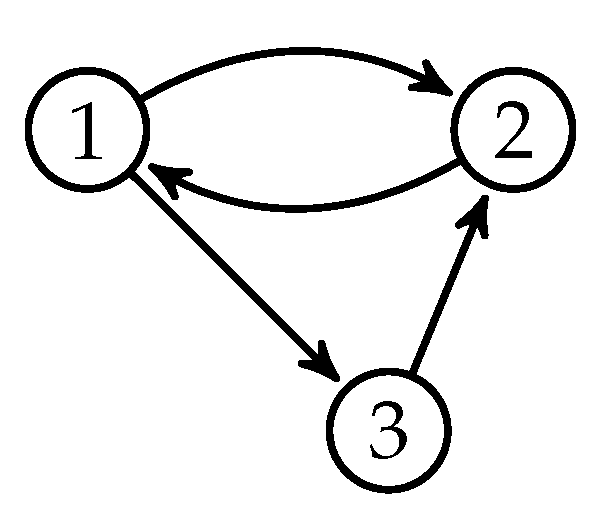
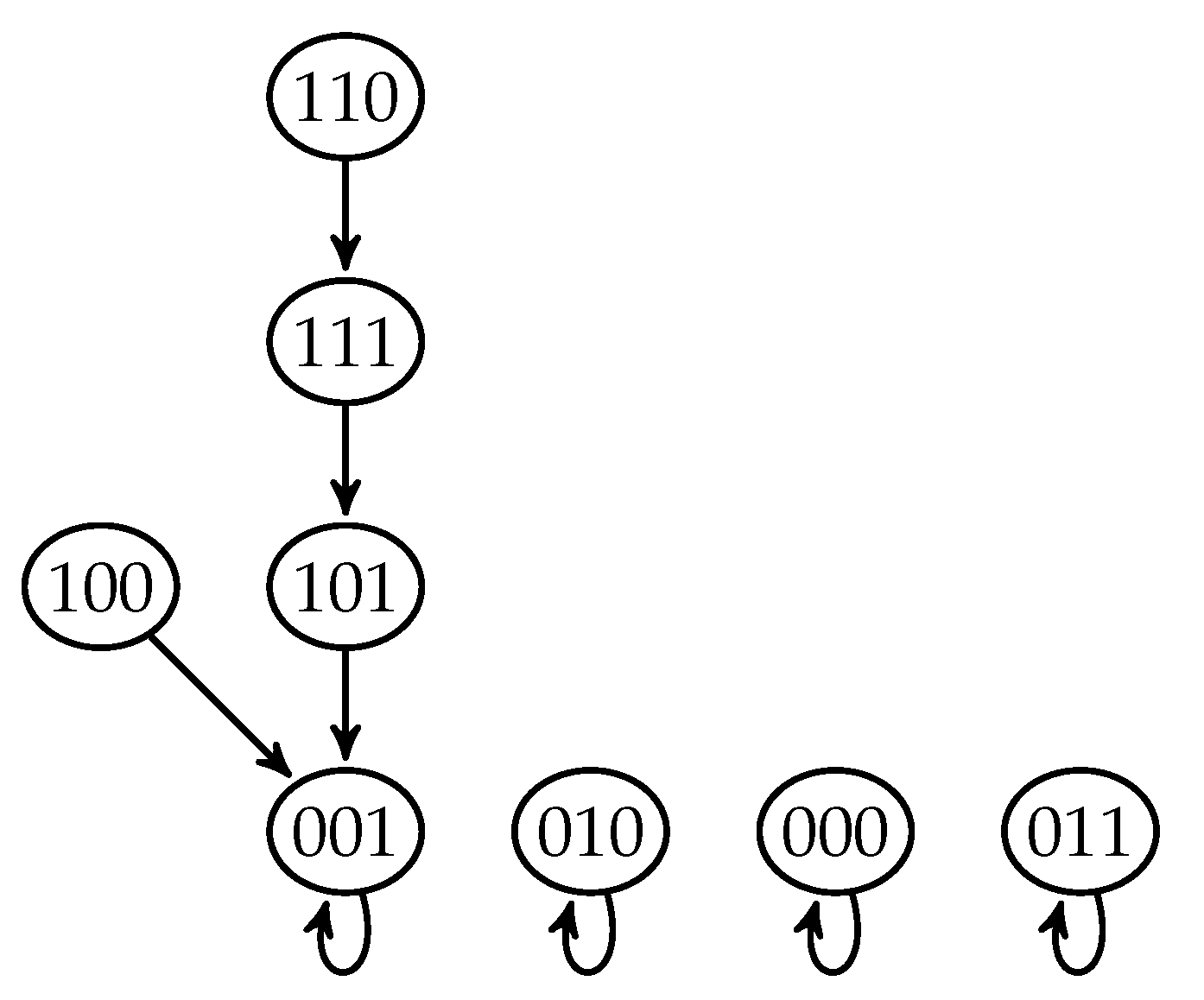
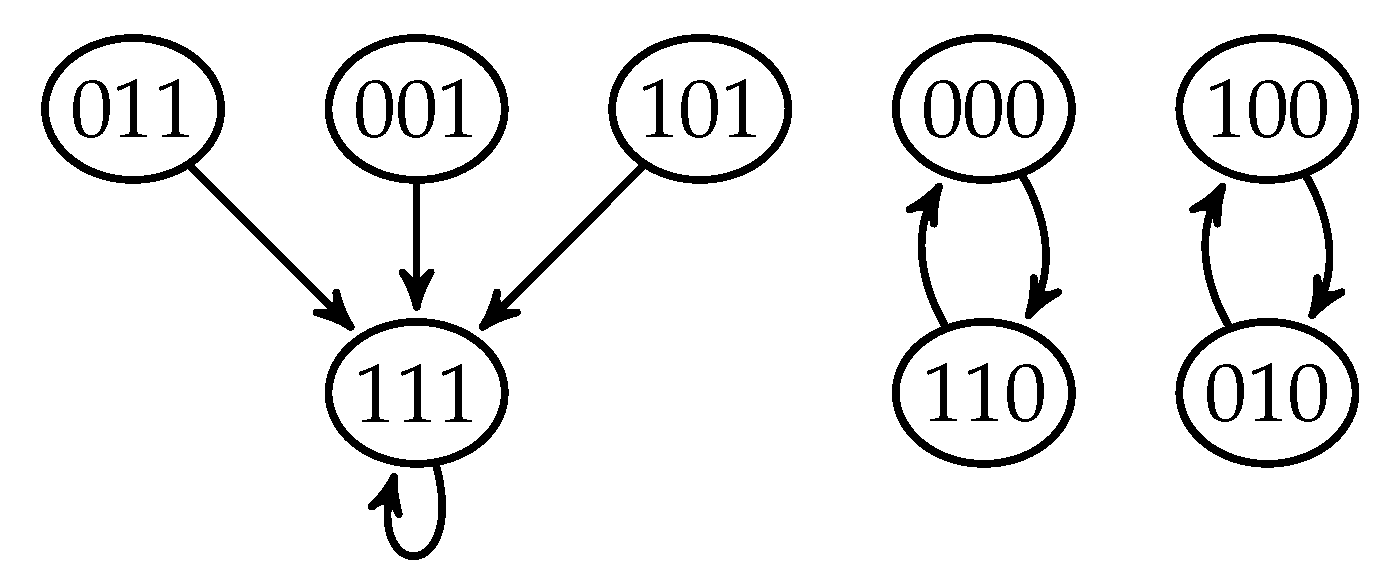
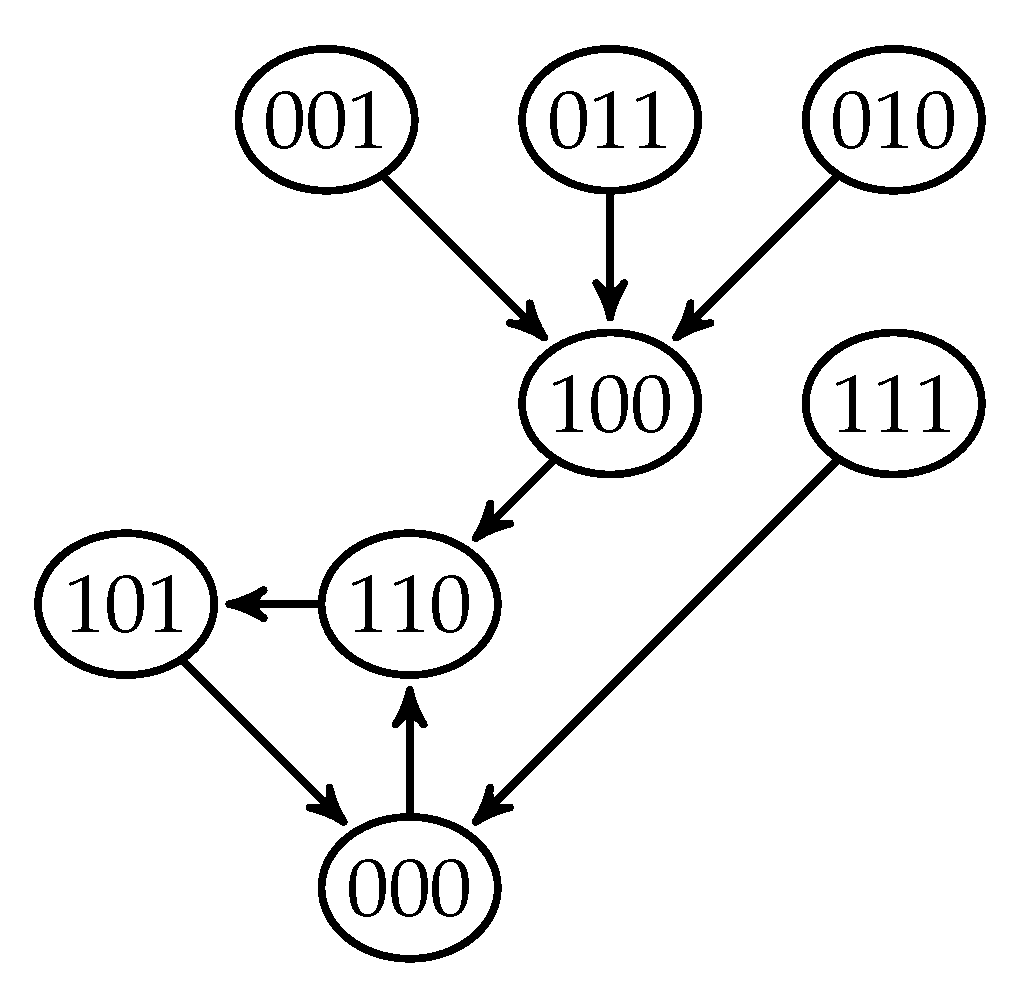
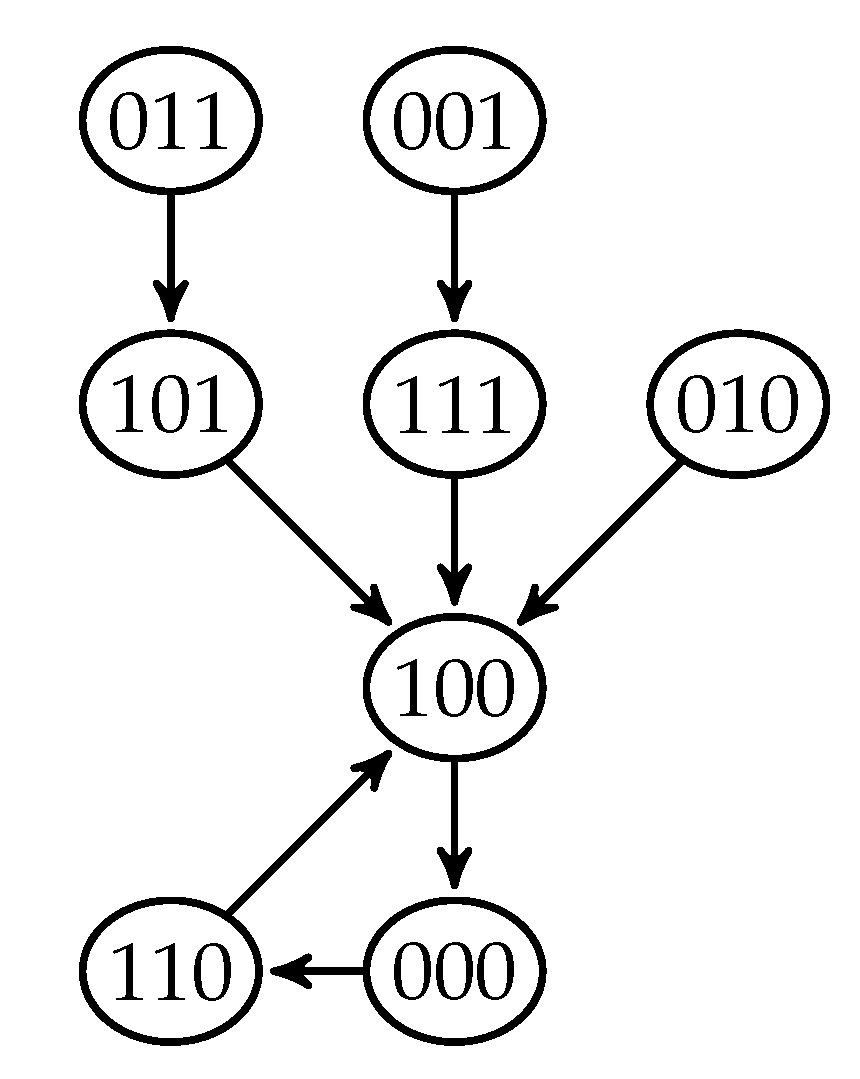
Example 1.

Let $F:{\{0,1\}}^3⟶{\{0,1\}}^3$ be

$$F(x_1,x_2,x_3)=(x_1\wedge (x_2\vee x_3),x_2\wedge (x_1^{\prime }\vee x_3^{\prime }),x_3\vee (x_2\wedge x_1)).$$

Then, its associated graph is given in Figure 1.

F is a fixed point system, as can be seen in its phase portrait (Figure 2).

As another example, let F be $F(x_1,x_2,x_3)=(x_1\wedge x_2,x_2\wedge (x_1^{\prime }\vee x_3^{\prime }),x_3\vee x_1)$. Then, its associated graph is given in Figure 3.

Again, F is a fixed point system as can be seen in its phase portrait (Figure 4).

Let $D=(V,E)$ be a (directed) graph and $Q\subseteq V$. We say that Q is an independent set of vertices of D, if there is no arc connecting two vertices in Q.

Then we have:

Theorem 2.

Let F be a PDDS given by

$$F:{\{0,1\}}^n⟶{\{0,1\}}^n,$$

$$F(x_1,\dots ,x_n)=(F_1(x_1,\dots ,x_n),\dots ,F_n(x_1,\dots ,x_n)).$$

Assume that for each $1\le i\le n$, $F_i=z_i\vee M_{i}or{F}_i=z_i\wedge M_i$ where $z_i=x_i$ or $z_i=x_i^{\prime }$, and each $M_i$ is a Boolean function on $\{x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n\}$. Let $D=(V,E)$ be a graph associated with F and

$$Z_F=\{i\in V:F_i=x_i^{\prime }\vee M_i\mathrm{or}{F}_i=x_i^{\prime }\wedge M_i\}.$$

Then, every periodic point of F is a fixed point or has period 2 provided that $Z_F$ is an independent set.

Proof. 

Let $x=(x_1^0,\dots ,x_n^0)$ be a periodic point for F and for each $m\ge 1$, $F^m\left(x\right)=(x_1^m,\dots ,x_n^m)$. Observe that if $Z_F=\varnothing$, the result follows from Theorem. On the other hand, if $Z_F=V$ then all the vertices in D are isolated since $Z_F$ is an independent set, and the result is immediate. Thus, let us assume that $Z_F\ne \varnothing$ and $Z_F\ne V$.

Without loss of generality, assume that $Z_F=\{1,\dots ,p\}$ for some $1\le p<n$. By a similar argument as the one in Theorem 1, it can be seen that $x_i^0=x_i^m$ for each $p+1\le i\le n$ and every $m\ge 1$. That is,

$$(x_{p+1}^0,\dots ,x_n^0)=(x_{p+1}^m,\dots ,x_n^m)\mathrm{for}\mathrm{each}m\ge 1.$$

(1)

Now, take $i\in Z_F$, i.e., $1\le i\le p.$ Since $Z_F$ is an independent set, there is no arc between i and any other vertex in $Z_F$. Therefore the Boolean function $M_i$ does not depend on the variables $x_1,\dots ,x_p$ and we can write $M_i(x_1,\dots ,x_n)=M_i(x_{p+1},\dots ,x_n)$. This observation and Equation (1) show that for the periodic point x we have

$$\begin{array}{ccc}\hfill M_i\left(x\right)& =& M_i(x_1^0,\dots ,x_n^0)=M_i(x_{p+1}^0,\dots ,x_n^0)\hfill \\ & =& M_i(x_{p+1}^m,\dots ,x_n^m)=M_i(x_1^m,\dots ,x_n^m)=M_i\left(F^m\left(x\right)\right)\hfill \end{array}$$

for each $m\ge 1$. Hence, for every $1\le i\le p$ one of the following situations happens:

Case 1:$F_i=x_i^{\prime }\vee M_i$ and $M_i\left(x\right)=M_i(x_{p+1}^0,\dots ,x_n^0)=1$. Then $x_i^m=1$ for each $m\ge 1$.

Case 2:$F_i=x_i^{\prime }\vee M_i$ and $M_i\left(x\right)=M_i(x_{p+1}^0,\dots ,x_n^0)=0$. Then $x_i^m={\left(x_i^{m-1}\right)}^{\prime }$ for each $m\ge 1$. In particular, for each $m\ge 1$ we have $x_i^m=\left\{\begin{array}{cc}{\left(x_i^0\right)}^{\prime },\hfill & \mathrm{if}m\mathrm{is}\mathrm{odd}\hfill \\ x_i^0,\hfill & \mathrm{if}m\mathrm{is}\mathrm{even}\hfill \end{array}\right.$.

Case 3:$F_i=x_i^{\prime }\wedge M_j$ and $M_i\left(x\right)=M_i(x_{p+1}^0,\dots ,x_n^0)=0$. Then $x_i^m=0$ for each $m\ge 1$.

Case 4:$F_i=x_i^{\prime }\wedge M_i$ and $M_i\left(x\right)=M_i(x_{p+1}^0,\dots ,x_n^0)=1$. Then $x_i^m={\left(x_i^{m-1}\right)}^{\prime }$ for each $m\ge 1$. In particular, for each $m\ge 1$ we have $x_i^m=\left\{\begin{array}{cc}{\left(x_i^0\right)}^{\prime },\hfill & \mathrm{if}m\mathrm{is}\mathrm{odd}\hfill \\ x_i^0,\hfill & \mathrm{if}m\mathrm{is}\mathrm{even}\hfill \end{array}\right.$.

Therefore, if there exists some $i\in Z_F$ in the Cases 2 or 4, then x is a 2-periodic point. Otherwise, x is a fixed point. With all of this, the thesis follows. □

Remark 1.

Let F be a PDDS as in Theorem 2. From the proof, it follows that if $x=(x_0,\dots ,x_n)$ is a fixed point of F, then for each $i\in Z_F$ we have $x_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{F}_i=x_i^{\prime }\vee M_i\hfill \\ 0,\hfill & \mathrm{if}{F}_i=x_i^{\prime }\wedge M_i\hfill \end{array}\right.$

Example 2.

Let F be a PDDS given by

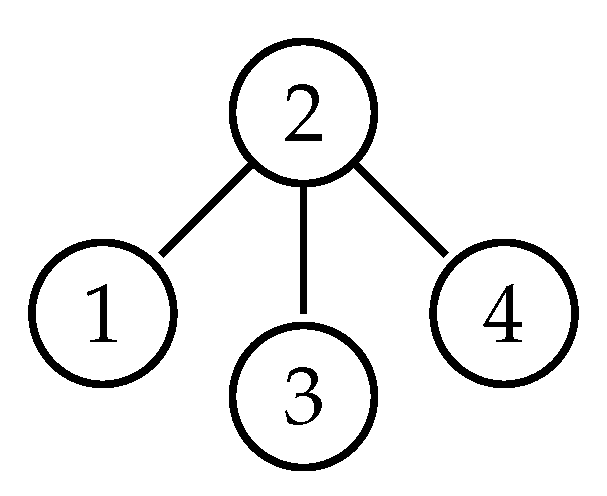
$$F:{\{0,1\}}^3⟶{\{0,1\}}^3,F(x_1,x_2,x_3)=(x_1^{\prime }\vee x_3,x_2^{\prime }\vee x_3,x_3).$$

We show its associated graph and its phase portrait in Figure 5 and Figure 6, respectively.

As can be easily checked, this system holds the conditions in Theorem 2, being $Z_F=\{1,2\}$ an independent set. Then, every periodic point of F is a fixed point or has period 2. Specifically, $(1,1,1)$ is the only fixed point of F, and $\left\{\right(0,0,0),(1,1,0\left)\right\}$, $\left\{\right(1,0,0),(0,1,0\left)\right\}$ are 2-periodic orbits.

Now, let F be a PDDS given by

$$F:{\{0,1\}}^3⟶{\{0,1\}}^3,F(x_1,x_2,x_3)=(x_1^{\prime }\wedge x_3,x_2^{\prime }\vee x_3^{\prime },x_1\vee x_3).$$

We show its associated graph and its phase portrait in Figure 7 and Figure 8, respectively.

Again, this system holds the conditions in Theorem 2, being $Z_F=\{1,2\}$ an independent set. Then, every periodic point of F is a fixed point or has period 2. Specifically, $(0,1,0)$ is the only fixed point of F, and $\left\{\right(0,1,1),(1,0,1\left)\right\}$, $\left\{\right(1,1,1),(0,0,1\left)\right\}$ are 2-periodic orbits.

Example 3.

Let F be a PDDS given by

$$F:{\{0,1\}}^n⟶{\{0,1\}}^n,F(x_1,\dots ,x_n)=(F_1(x_1,\dots ,x_n),\dots ,F_n(x_1,\dots ,x_n))$$

and assume that the set $Z_F$ is not independent. Note that it implies that $|Z_F|\ge 2$. Then F may have points of period bigger than two.

For example, take

$$F:{\{0,1\}}^3⟶{\{0,1\}}^3,F(x_1,x_2,x_3)=(x_1^{\prime }\vee x_3^{\prime },x_2^{\prime }\wedge x_3^{\prime },x_3^{\prime }\wedge x_1\wedge x_2).$$

Then, the associated graph of F is a line graph on three vertices (see Figure 9). Note that $Z_F=\{1,2,3\}$ is not an independent set of vertices.

The system has an orbit of period 3, as can be seen in the phase portrait (Figure 10).

As another example, take

$$F:{\{0,1\}}^3⟶{\{0,1\}}^3,F(x_1,x_2,x_3)=(x_1^{\prime }\vee x_2\vee x_3,x_2^{\prime }\wedge x_1^{\prime },x_3\wedge x_1^{\prime }).$$

The dependency graph and the phase portrait of F are given in Figure 11 and Figure 12, respectively.

Observe that $Z_F=\{1,2\}$ is not an independent set of vertices, and the system has a 3-period orbit.

3. Periodic Structure of the Composition of Conjugate PDDS

Recall that two discrete-time dynamical systems F and G on X are conjugate, if there exists an invertible map $H:X⟶X$ such that $G=H^{-1}\circ F\circ H$.

In this section, we assume that F and G are two conjugate PDDS or PDS under an invertible map H such that $H^{-1}=H$. In this context, we study the periodic structure of $F\circ G$ by means of F and H.

Theorem 3.

Let F and G be two conjugate PDDS under an invertible map H such that $H^{-1}=H$. Then,

(i) 

x is a periodic point of $F\circ G$ if, and only if, x is a periodic point of $F\circ H$.

(ii) 

${\mathrm{Per}}_t(F\circ H)={\mathrm{Per}}_t(F\circ G)$ provided that t is odd.

(iii) 

${\mathrm{Per}}_t(F\circ H)={\mathrm{Per}}_{\frac{t}{2}}(F\circ G)$ provided that t is even.

Proof. 

First of all, note that, under the assumptions of the theorem,

$$F\circ G={(F\circ H)}^2.$$

(i)

Let x be a periodic point of $F\circ G$. Then, for some $t\ge 1$, ${(F\circ G)}^t\left(x\right)=x$. Therefore ${(F\circ H)}^{2t}\left(x\right)=x$, which means that x is a periodic point of $F\circ H$.

Conversely, if x is a periodic point of $F\circ H$ then ${(F\circ H)}^s\left(x\right)=x$ for some $s\ge 1$. Therefore ${(F\circ G)}^s\left(x\right)={(F\circ H)}^{2s}\left(x\right)=x$, and so x is a periodic point of $F\circ G$.

On the other hand, observe that if $x\in {\mathrm{Per}}_t\left(F\right)$ and $F^s\left(x\right)=x$, then $t|s$. Of course, this assertion is true for whichever discrete dynamical system.

Let $x\in {\mathrm{Per}}_t(F\circ H)\cap {\mathrm{Per}}_{t^{\prime }}(F\circ G)$. Since ${(F\circ H)}^{2t^{\prime }}\left(x\right)={(F\circ G)}^{t^{\prime }}\left(x\right)=x$, then $t|2t^{\prime }$

(ii)

Assume that t is an odd number. Then, from $t|2t^{\prime }$ we get that $t|t^{\prime }$. Moreover, since ${(F\circ G)}^t\left(x\right)={(F\circ H)}^{2t}\left(x\right)=x$, we have that $t^{\prime }|t$. Hence, $t=t^{\prime }$ and the conclusion follows.

(iii)

Assume now that t is an even number. Then ${(F\circ G)}^{\frac{t}{2}}\left(x\right)={(F\circ H)}^t\left(x\right)=x$ and so $t^{\prime }|\frac{t}{2}$, which jointly $t|2t^{\prime }$ yields that $t^{\prime }=\frac{t}{2}$ and the proof finishes. □

Let F be a maxterm function (resp. a minterm function) and $D=(V,E)$ be the (directed or simple) graph associated with the corresponding discrete dynamical system MAX-PDDS or MAX-PDS (resp. MIN-PDDS or MIN-PDS). For such a dynamical system, we denote by $W_F\subseteq V$ (resp. $W_F^{\prime }\subseteq V$) the subset of vertices in V such that the corresponding variables in F appear in the direct (resp. complemented) form.

Consider the invertible map $\copyright :{\{0,1\}}^n⟶{\{0,1\}}^n$ such that $\copyright (x_1,\dots ,x_n)=(x_1^{\prime },\dots ,x_n^{\prime })$. Note that ${\copyright }^{-1}=\copyright$. Let F be a MAX-PDS (resp. MAX-PDDS) and G be a MIN-PDS (resp. MIN-PDDS) with the same associated graph $D=(V,E)$. Then, F and G are conjugate under © if, and only if, $W_F=W_G$.

Example 4.

Let F be the MAX-PDS system given by

$$F(x_1,x_2,x_3,x_4)=(x_1^{\prime }\vee x_2,x_1^{\prime }\vee x_2\vee x_3^{\prime }\vee x_4,x_2\vee x_3^{\prime },x_2\vee x_4)$$

and G the MIN-PDS system given by

$$G(x_1,x_2,x_3,x_4)=(x_1^{\prime }\wedge x_2,x_1^{\prime }\wedge x_2\wedge x_3^{\prime }\wedge x_4,x_2\wedge x_3^{\prime },x_2\wedge x_4).$$

Note that F and G are conjugate under © and $W_F=W_G$. In particular, both F and G are fixed point systems with a unique fixed point, as can be easily checked using [29] (Theorems 3 and 9). Specifically, $\mathrm{Fix}\left(F\right)=\left\{\right(1,1,1,1\left)\right\}$ and $\mathrm{Fix}\left(G\right)=\left\{\right(0,0,0,0\left)\right\}$.

It is well-known that if F is an arbitrary MAX-PDS or MIN-PDS over a graph D, then all the periodic points of this system are 2-periodic points or fixed points [26] (Theorem 3, Theorem 4). In particular, periodic orbits of different periods cannot coexist [29] (Theorem 7). Thus, based on these results, we have:

Corollary 1.

Let F be a MAX-PDS with associated graph D and G be the corresponding MIN-PDS conjugate with F under ©. Then, $F\circ G$ and $G\circ F$ are fixed point systems.

In particular

$$\mathrm{Fix}(F\circ G)=\mathrm{Fix}(F\circ \copyright )\cup {\mathrm{Per}}_2(F\circ \copyright )$$

$$\mathrm{Fix}(G\circ F)=\mathrm{Fix}(G\circ \copyright )\cup {\mathrm{Per}}_2(G\circ \copyright )$$

Proof. 

It is enough to prove the assertion for $F\circ G$. Note that $F\circ \copyright$ is also a MAX-PDS over D, and so $F\circ \copyright$ is a fixed point system or a 2-periodic point system. Therefore, by Theorem 3, it follows that $F\circ G$ is a fixed point system. □

Example 5.

Consider the conjugate dynamical systems F and G in Example 4. Observe that $F\circ \copyright$ is a 2-periodic point MAX-PDS because, as can be observed in the associated graph (Figure 13), the vertex 4 is in the complemented form and it is not adjacent to any vertex in the directed form.

In particular, as can be seen in its phase portrait (Figure 14),

$${\mathrm{Per}}_2(F\circ \copyright )=\{(1,1,0,0),(1,1,0,1),(0,1,1,0),(0,1,1,1),(1,1,1,0),(1,1,1,1)\}.$$

which coincides with $\mathrm{Fix}(F\circ G)$ by Corollary. Therefore, we have obtained $\mathrm{Fix}(F\circ G)$ through ${\mathrm{Per}}_2(F\circ \copyright )$.

In the study of MAX-PDS and MAX-PDDS (resp. MIN-PDS and MIN-PDDS) over a graph D, often researchers have focused on the simplest Boolean functions

$$\mathrm{OR}(x_1,x_2,\dots ,x_n)=x_1\vee x_2\vee \cdots \vee x_n$$

$$\mathrm{AND}(x_1,x_2,\dots ,x_n)=x_1\wedge x_2\wedge \cdots \wedge x_n$$

$$\mathrm{NAND}(x_1,x_2,\dots ,x_n)=x_1^{\prime }\vee x_2^{\prime }\vee \cdots \vee x_n^{\prime }$$

$$\mathrm{NOR}(x_1,x_2,\dots ,x_n)=x_1^{\prime }\wedge x_2^{\prime }\wedge \cdots \wedge x_n^{\prime }$$

The corresponding dynamical systems are called OR-PDS, AND-PDS, NAND-PDS and NOR-PDS (OR-PDDS, AND-PDDS, NAND-PDDS and NOR-PDDS in the case that D is a directed graph), respectively. Note that OR-PDS and AND-PDS are conjugate under ©. Also NAND-PDS and NOR-PDS are conjugate under © (the same holds for OR-PDDS and AND-PDDS, and also for NAND-PDDS and NOR-PDDS).

If $D=(V,E)$ is a connected graph and F is the NAND-PDS with associated graph D, then F is a 2-periodic point system (see [29] (Theorem 5)). The number of 2-periodic points of NAND-PDS has been computed in [34] (Proposition 3) as:

Proposition 1.

Let F be the NAND-PDS over the graph $D=(V,E)$ and $P\left(V\right)$ be the power set of V. Then, the number of 2-periodic points of this system is $\left|\mathsf{\Theta }\right|$, where

$$\mathsf{\Theta }=\{\overline{A_D\left(Q\right)}:Q\in P\left(V\right)\}.$$

Actually, as the proof of Proposition 1 shows, if F is an NAND-PDS, then $x=(x_1,\dots ,x_n)\in {\mathrm{Per}}_2\left(F\right)$ if and only if $\{j:x_j=1\}\in \mathsf{\Theta }$.

It is interesting to note that if $x=(x_1,\dots ,x_n)$ is an arbitrary point of ${\{0,1\}}^n$, then $F\left(x\right)=(x_1^1,\dots ,x_n^1)$ is a 2-periodic point for F. This happens because, if we let $Q=\{j:x_j=0\}$, then $\{j:x_j^1=1\}=\overline{A_D\left(Q\right)}$. Thus, we have the following result for the composition of AND-PDS and OR-PDS.

Corollary 2.

Let F be the OR-PDS and G be the AND-PDS over the same graph $D=(V,E)$. Then the following sentences are equivalent:

• $x=(x_1,\dots ,x_n)$ is a fixed point for $F\circ G$.
• x is a 2-periodic point of the NAND-PDS over D.
• $\{j:x_j=1\}\in \mathsf{\Theta }=\{\overline{A_D\left(Q\right)}:Q\in P\left(V\right)\}$.

Moreover, $\mathrm{Image}(F\circ G)=\mathrm{Fix}(F\circ G)$.

Proof. 

Observe that $F\circ \copyright$ is nothing but the NAND-PDS over the graph D. Then, since F and G are conjugate under ©, the result follows from Corollary 1 and Proposition 1. □

Dually, we have:

Corollary 3.

Let F be the OR-PDS and G be the AND-PDS over the same graph $D=(V,E)$. Then the following sentences are equivalent:

• $x=(x_1,\dots ,x_n)$ is a fixed point for $G\circ F$.
• x is a 2-periodic point of the NOR-PDS over D.
• $\{j:x_j=0\}\in \mathsf{\Theta }=\{\overline{A_D\left(Q\right)}:Q\in P\left(V\right)\}$.

Moreover, $\mathrm{Image}(G\circ F)=\mathrm{Fix}(G\circ F)$.

Next, we give some applications of Theorem 3 for the composition of AND-PDDS and OR-PDDS.

Corollary 4.

Let F be the OR-PDDS and G be the AND-PDDS over the same graph $D=(V,E)$. Then, $F\circ G$ and $G\circ F$ can present periodic points of any period.

Proof. 

It is a consequence of [25] (Theorem 3) and Theorem 3. □

The thesis of Corollary 4 is kind of surprising since both AND-PDDS and OR-PDDS are fixed point systems. As the following result shows, this is due to the existence of cycles.

Recall that an acyclic directed graph is a directed graph without (directed) cycles. In spite of the general result in Corollary 4, for this particular class of digraphs we have:

Corollary 5.

Let F be the OR-PDDS and G be the AND-PDDS over the same directed acyclic graph $D=(V,E)$. Then, $F\circ G$ and $G\circ F$ are fixed point systems.

Proof. 

Note that F and G are conjugate under ©. Moreover, $F\circ \copyright$ (resp. $G\circ \copyright$) is an NAND-PDDS (resp. NOR-PDDS) and by [27] (Propositions 7 and 8), it is a 2-periodic point system. Then the conclusion follows from Theorem 3. □

For the particular case when D is a (directed) cycle, we have:

Corollary 6.

The composition of an OR-PDDS and an AND-PDDS over directed cycles can present periodic points of any period except of period 2.

Proof. 

Let F and G be the OR-PDDS and the AND-PDDS, respectively, over a directed cycle of n nodes $C_n$. We know that F and G are conjugate under © and that $F\circ \copyright$ is the NAND-PDDS over $C_n$.

• It is easy to see that $x=(1,\dots ,1)$ is a 2-periodic point of $F\circ \copyright$. Hence, by Theorem 3, x is a fixed point of $F\circ G$.
• If $n=3$, $x=(1,1,0)$ is a point of period 3 of $F\circ \copyright$. Thus, by Theorem 3, x is a point of period 3 of $F\circ G$.
• Finally, if $n\ge 4$, $x=(1,1,0,\dots ,0)$ is a point of period $2n$ for $F\circ \copyright$ (see [27] (Corollary 3)). Therefore, by Theorem 3, x is a point of period n for $F\circ G$. □

As another application of Theorem 3 we have:

Corollary 7.

Let F be an OR-PDDS (or an AND-PDDS ) over a directed graph D and $\sigma :\{1,2,\dots ,n\}\to \{1,2,\dots ,n\}$ be a permutation such that ${\sigma }^{-1}=\sigma$. Let H be the map that sends $(x_1,\dots ,x_n)$ to $(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(n\right)})$. Then, any periodic point of $F\circ \sigma$ has period 2 or it is a fixed point.

Proof. 

Assume that F is an OR-PDDS over a directed graph $D=(V,E)$ and let $G={\sigma }^{-1}\circ F\circ \sigma$. It is easy to see that G is an OR-PDDS over the directed graph $D_1=(V,E_1)$ where $E_1=\{(i,j);(\sigma \left(i\right),\sigma \left(j\right))\in E\}$. Note that $F\circ G$ satisfies the necessary condition of Theorem, and so it is a fixed point system. Therefore, by Theorem 3, the conclusion follows. □

From Corollary 1, it is clear that the composition of NOR-PDS and NAND-PDS over the same undirected graph is a fixed point system. In the following result, we detail the fixed points of such composition.

Corollary 8.

Let F be the NOR-PDS and G be the NAND-PDS over the connected simple graph $D=(V,E)$. Then, $\mathrm{Fix}(F\circ G)=\mathrm{Fix}(G\circ F)=\left\{\right(1,\dots ,1),(0,\dots ,0\left)\right\}$.

Proof. 

It is enough to note that in this case $F\circ \copyright$ is the AND-PDS and $G\circ \copyright$ is the OR-PDS over the associated graph D. Then, since F and G are conjugate under ©, the conclusion follows from Corollary 1. □

Despite the fact that the composition of AND-PDDS and OR-PDDS over the same graph can have periodic points of any period, the composition of NAND-PDDS and NOR-PDDS are fixed point systems as we show in the following result.

Corollary 9.

Let F be the NOR-PDDS and G be the NAND-PDDS over the same graph $D=(V,E)$. Then, $F\circ G$ and $G\circ F$ are fixed point systems and $\left\{\right(1,\dots ,1),(0,\dots ,0\left)\right\}\subseteq \mathrm{Fix}(F\circ G)\cap \mathrm{Fix}(G\circ F)$.

Proof. 

Note that $F\circ \copyright$ and $G\circ \copyright$ are, respectively, the AND-PDDS and the OR-PDDS over D. It is well know that AND-PDDS and OR-PDDS are fixed point systems and $\left\{\right(1,\dots ,1),(0,\dots ,0\left)\right\}$ are always fixed points of these systems. Therefore, since F and G are conjugate under ©, the conclusion follows from Corollary 1. □

4. Conclusions

The results of this paper widely extend those known on the periodic structure for homogeneous parallel dynamical systems on certain types of Boolean functions. Specifically, a more general context is set out, by considering non-homogeneous parallel dynamical systems with general local Boolean functions as their evolution operators, and digraphs as dependency graphs instead of simple graphs. Thus, homogeneous parallel systems on (simple or directed) graphs can be seen as particular cases of the ones studied here. The results generalize the class of (non-homogeneous) parallel systems in which periodic orbits are only fixed points or 2-periodic orbits. Actually, some examples in this work show that, in such a class of parallel systems, fixed and 2-periodic points can coexist, thus breaking the pattern found for homogeneous parallel systems. Furthermore, in contrast with the homogeneous case, periodic points of a period greater than two can appear, as shown in some of the examples of this article.

On the other hand, as a novel research line in this field, we study the periodic structure of parallel dynamical systems given by the composition of two parallel systems that are conjugate under an invertible map in which the inverse is equal to the original map. In view of our results, it can be concluded that cycles in the associated digraph are responsible for the appearance of periodic orbits with periods greater than 1.

The results here obtained could be of great relevance for applied models, since in such models local functions are usually independent, giving as a result non-homogeneous systems, and the expression of the local functions could be more general than maxterm or minterms, threshold, monotone, or any other specific type of Boolean functions. Thus, our results could be a better support in the development of the study of such models.