Modelling of Alumina Splat Solidification on Preheated Steel Substrate Using the Network Simulation Method
Abstract
1. Introduction
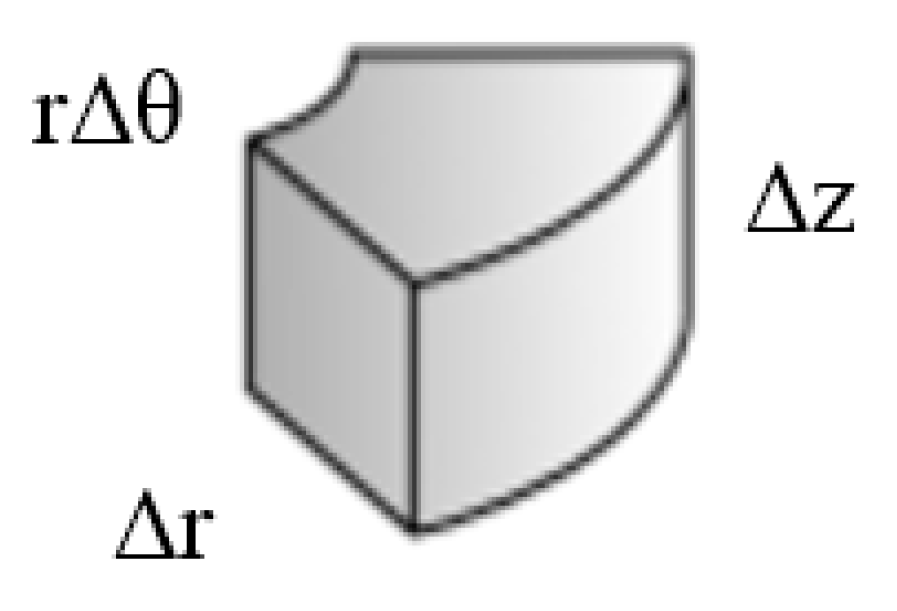
2. The Governing Equations
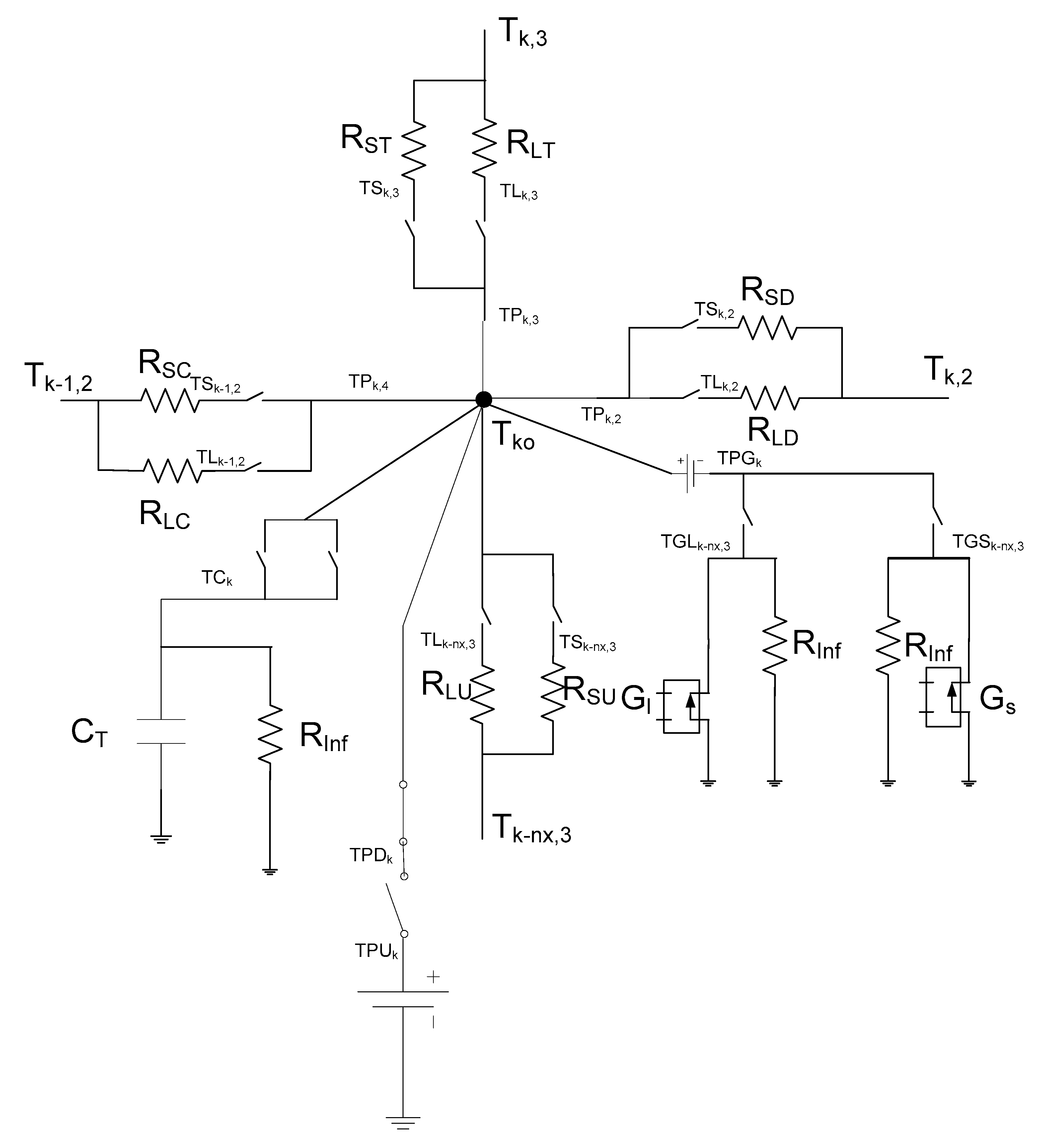
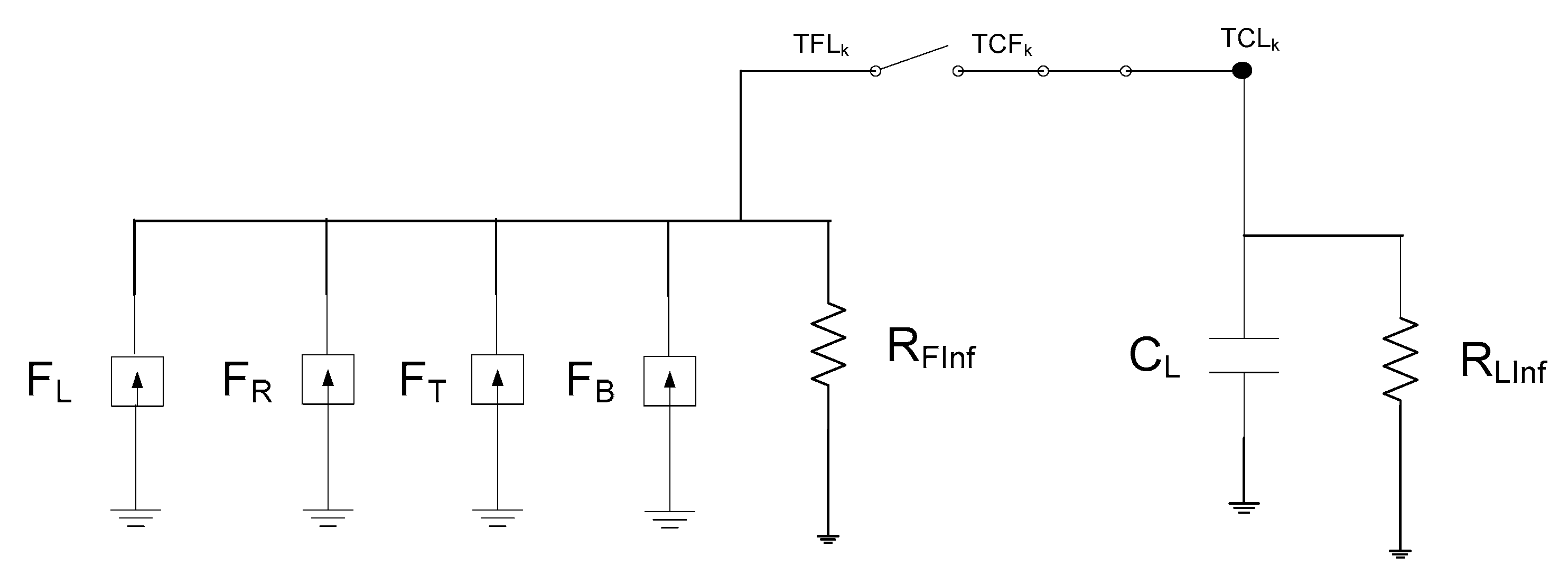
3. The Network Model
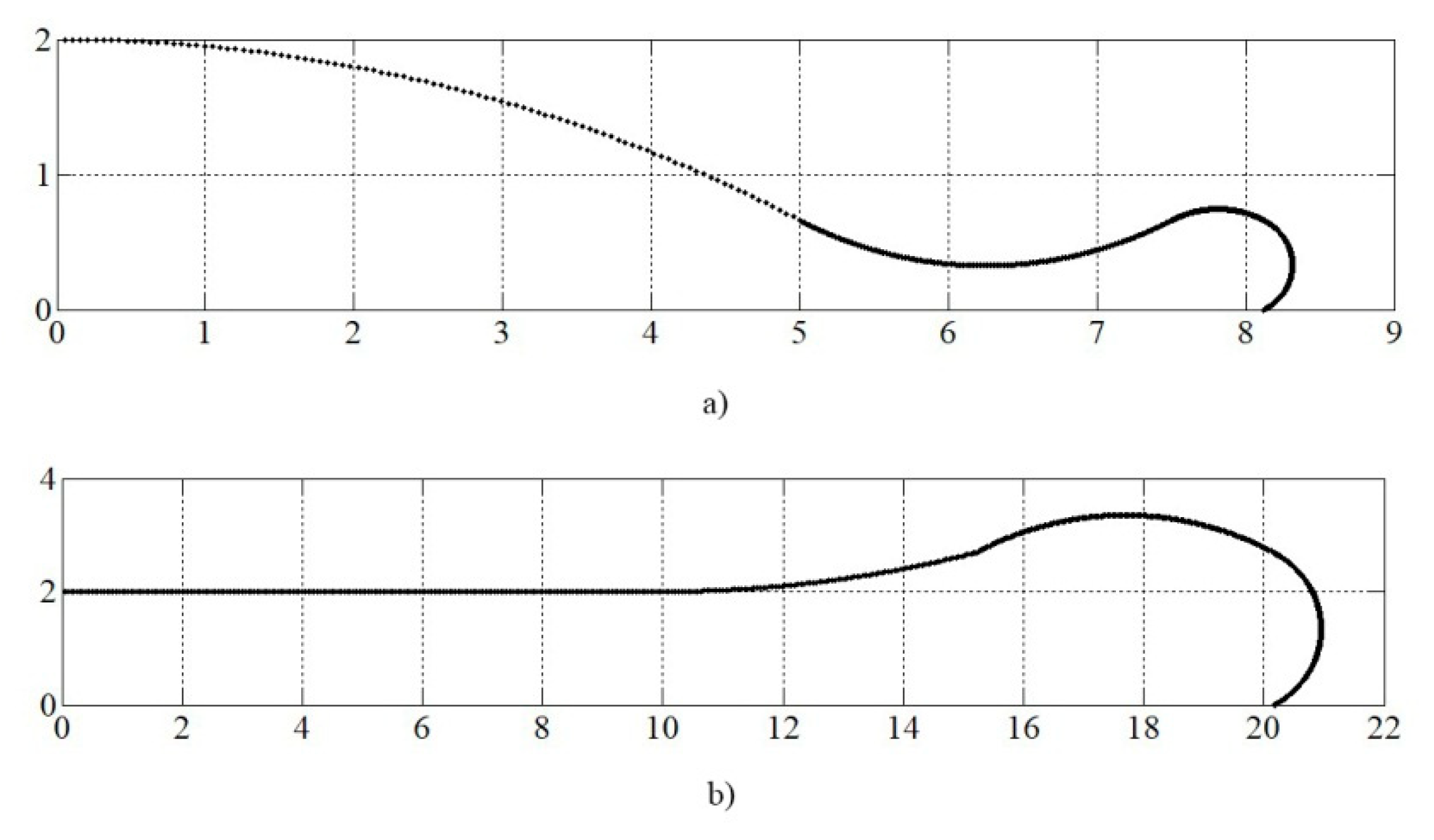
4. Simulation and Results
4.1. Simulation of Tin Splats Solidification
4.2. Simulation of Alumina Splats Solidification without Preheating Substrate
4.3. Simulation of Alumina Splats Solidification with Preheating the Substrate
4.4. Sensitive Study of the Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Abbreviations | |
| cp | specific heat capacity (J/K·kg) |
| D = k/(ρ cp) | thermal diffusivity (m2/s) |
| dp | particle diameter (m) |
| h | film coefficient (W/m·K) |
| hC | heat transfer coefficient between splat and subtract (W/m·K) |
| k | thermal conductivity (J/m·K) |
| L | latent heat (J/kg) |
| n | coordinate normal to the interface (m) |
| Q | heat (J) |
| r | radial coordinate (m) |
| R | resistance (Ω) |
| S | surface in contact with air (m2) |
| T | temperature (K) |
| un | interface displacement (m) |
| V | voltage (V) |
| z | axial coordinate (m) |
| ε | emissivity |
| ρ | density (kg/m3) |
| ξ | flattening rate |
| σ | Stefan–Boltzmann constant (W/m2·K4) |
| Ω | volume (m3) |
| Subscripts | |
| env | environment |
| int | interface between splat and substrate |
| k | cell number |
| l | liquid |
| nr | quantity of cells in a row |
| s | solid |
| surf | relative to surface in contact with air |
| subst | relative to substrate in contact with the splat |
References
- Chandra, S.; Fauchais, P. Formation of Solid Splats During Thermal Spray Deposition. J. Therm. Spray Technol. 2009, 18, 148–180. [Google Scholar] [CrossRef]
- Dhiman, R.; McDonald, A.G.; Chandra, S. Predicting splat morphology in a thermal spray process. Surf. Coat. Technol. 2007, 201, 7789–7801. [Google Scholar] [CrossRef]
- Fauchais, P.; Vardelle, M.; Goutier, S. Atmospheric Plasma Spraying Evolution Since the Sixties Through Modeling, Measurements and Sensors. Plasma Chem. Plasma Process. 2017, 37, 601–626. [Google Scholar] [CrossRef]
- Okumus, S.C. Microstructural and mechanical characterization of plasma sprayed Al2O3–TiO2 composite ceramic coating on Mo/cast iron substrates. Mater. Lett. 2005, 59, 3214–3220. [Google Scholar] [CrossRef]
- Houben, J. Relationship of the Adhesion of Plasma Sprayed Coatings to the Process Parameters: Size, Velocity and Heat Content of the Spray Particles. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 1988. [Google Scholar]
- Syed, A.; Denoirjean, A.; Hannoyer, B.; Fauchais, P.; Denoirjean, P.; Khan, A.; Labbe, J. Influence of substrate surface conditions on the plasma sprayed ceramic and metallic particles flattening. Surf. Coat. Technol. 2005, 200, 2317–2331. [Google Scholar] [CrossRef]
- Yin, Z.; Tao, S.; Zhou, X.; Ding, C. Particle in-flight behavior and its influence on the microstructure and mechanical properties of plasma-sprayed Al2O3 coatings. J. Eur. Ceram. Soc. 2008, 28, 1143–1148. [Google Scholar] [CrossRef]
- Zhang, C.; Li, C.-J.; Liao, H.; Planche, M.-P.; Li, C.-X.; Coddet, C. Effect of in-flight particle velocity on the performance of plasma-sprayed YSZ electrolyte coating for solid oxide fuel cells. Surf. Coat. Technol. 2008, 202, 2654–2660. [Google Scholar] [CrossRef]
- Zhang, C.; Kanta, A.F.; Li, C.-X.; Li, C.-J.; Planche, M.-P.; Liao, H.; Coddet, C. Effect of in-flight particle characteristics on the coating properties of atmospheric plasma-sprayed 8 mol% Y2O3–ZrO2 electrolyte coating studying by artificial neural networks. Surf. Coat. Technol. 2009, 204, 463–469. [Google Scholar] [CrossRef]
- Mantry, S.; Jha, B.; Mandal, A.; Mishra, D.K.; Chakraborty, M. Influence of in-flight particle state diagnostics on properties of plasma sprayed YSZ-CeO2nanocomposite coatings. Int. J. Smart Nano Mater. 2014, 5, 207–216. [Google Scholar] [CrossRef]
- Pershin, V.; Lufitha, M.; Chandra, S.; Mostaghimi, J. Effect of Substrate Temperature on Adhesion Strength of Plasma-Sprayed Nickel Coatings. J. Therm. Spray Technol. 2003, 12, 370–376. [Google Scholar] [CrossRef]
- Fukumoto, M.; Huang, Y. Flattening Mechanism in Thermal Sprayed Nickel Particle Impinging on Flat Substrate Surface. J. Therm. Spray Technol. 1999, 8, 427–432. [Google Scholar] [CrossRef]
- McDonald, A.; Moreau, C.; Chandra, S. Thermal contact resistance between plasma-sprayed particles and flat surfaces. Int. J. Heat Mass Transf. 2007, 50, 1737–1749. [Google Scholar] [CrossRef]
- Jiang, X.; Wan, Y.; Herman, H.; Sampath, S. Role of condensates and adsorbates on substrate surface on fragmentation of impinging molten droplets during thermal spray. Thin Solid Films 2001, 385, 132–141. [Google Scholar] [CrossRef]
- Tanaka, Y.; Fukumoto, M. Investigation of dominating factors on flattening behavior of plasma sprayed ceramic particles. Surf. Coat. Technol. 1999, 120, 124–130. [Google Scholar] [CrossRef]
- Tanaka, Y.; Fukumoto, M. Influence of Solidification and Wetting on Flattening Behavior of Plasma Sprayed Ceramic Particles. In ISAEM 2000: 2nd International Symposium on Designing, Processing and Properties of Advanced Engineering Materials; Inderscience Enterprises Ltd.: Guilin, China, 2000. [Google Scholar]
- Zhang, H.; Wang, X.; Zheng, L.; Jiang, X. Studies of splat morphology and rapid solidification during thermal spraying. Int. J. Heat Mass Transf. 2001, 44, 4579–4592. [Google Scholar] [CrossRef]
- Levi, C.G.; Jayaram, V.; Valencia, J.J.; Mehrabian, R. Phase selection in electrohydrodynamic atomization of alumina. J. Mater. Res. 1988, 3, 969–983. [Google Scholar] [CrossRef]
- Allen, R.F. The role of surface tension in splashing. J. Colloid Interface Sci. 1975, 51, 350–351. [Google Scholar] [CrossRef]
- Vardelle, A.; Fauchais, P.; Gobin, D.; Vardelle, M. Monitoring Particle Impact on a Substrate during Plasma Spray Process. Flash React. Process. 1995, 95–121. [Google Scholar] [CrossRef]
- Wang, S.-P.; Wang, G.-X.; Matthys, E. Melting and resolidification of a substrate in contact with a molten metal: Operational maps. Int. J. Heat Mass Transf. 1998, 41, 1177–1188. [Google Scholar] [CrossRef]
- Sun, D.W.; Xu, J.; Zang, H.; Wan, Y.P.; Prasad, V.; Wang, G.X. Effect of Contact Resistance and Substrate Melting on Thermal Spray Coating. In Thermal Spray: Surface Engineering via Applied Research; ASM International: Russell Township, OH, USA, 2000. [Google Scholar]
- Fauchais, P.; Vardelle, M.; Vardelle, A.; Bianchi, L. Parameters controlling the generation and properties of plasma sprayed zirconia coatings. Plasma Chem. Plasma Process. 1995, 16, S99–S125. [Google Scholar] [CrossRef]
- Sobolev, V.V.; Guilemany, J.M. Flattening of Droplets and Formation of Splats in Thermal Spraying: A Review of Recent Work—Part 1. J. Therm. Spray Technol. 1999, 8, 87–101. [Google Scholar] [CrossRef]
- Sobolev, V.V.; Guilemany, J.M. Flattening of Droplets and Formation of Splats in Thermal Spraying: A Review of Recent Work—Part 2. J. Therm. Spray Technol. 1999, 8, 301–314. [Google Scholar] [CrossRef]
- Maître, A.; Denoirjean, A.; Fauchais, P.; Lefort, P. Plasma-jet coating of preoxidized XC38 steel: Influence of the nature of the oxide layer. Phys. Chem. Chem. Phys. 2002, 4, 3887–3893. [Google Scholar] [CrossRef]
- Valette, S.; Denoirjean, A.; Lefort, P.; Fauchais, P. Influence of dc plasma preheating on oxide layers formed by furnace heating on low carbon steel substrates and resulting adhesion/cohesion of alumina coatings. High Temp. Mater. Process. Int. Q. High-Technol. Plasma Process. 2003, 7, 11–215. [Google Scholar] [CrossRef]
- Pech, J.; Hannoyer, B.; Lagnoux, O.; Denoirjean, A.; Fauchais, P. Influence of preheating parameters on the plasma-jet oxidation of a low-carbon steel. High Temp. Mater. Process. Int. Q. High-Technol. Plasma Process. 2011, 15, 51–60. [Google Scholar] [CrossRef]
- Valette, S.; Denoirjean, A.; Soulestin, B.; Trolliard, G.; Hannoyer, B.; Lefort, P.; Fauchais, P. Alumina coatings on preoxidized low carbon steel. Interfacial phenomena between alumina and iron oxide layer. In Proceedings of the International Thermal Spray Conference, Osaka, Japan, 10–12 May 2004. [Google Scholar]
- Haure, T. Multifunctional Layers by PACVD and Plasma Spraying. Ph.D. Thesis, University of Limoges, Limoges, France, 2003. [Google Scholar]
- Espie, G.; Fauchais, P.; Hannoyer, B.; Labbe, J.; Vardelle, A. Effect of metal particles oxidation during the APS on the wettability. Ann. N. Y. Acad. Sci. 1999, 891, 143–151. [Google Scholar] [CrossRef]
- Seyed, A.A.; Denoirjean, P.; Denoirjean, A.; Hannoyer, B.; Labbe, J.C.; Fauchais, P. Oxidation at different stages in stainless steel coatings developed by air plasma spraying on plain carbon steel. Progress in Plasma Processing of Materials 2003. In Proceedings of the seventh European Conference on Thermal Plasma Processes, Strasbourg, France, 18–21 June 2002. [Google Scholar]
- Pech, J.; Hannoyer, B.; Denoirjean, A.; Bianchi, L.; Fauchais, P. Influence of Substrate Preheating Monitoring on Alumina Splat Formation in D.C. Plasma Processes. In Thermal Spray: A United Forum for Scientific and Technological Advances; ASM International: Russell Township, OH, USA, 1999. [Google Scholar]
- Yang, E.-J.; Luo, X.-T.; Yang, G.-J.; Li, C.-X.; Li, C.-J.; Takahashi, M. Epitaxial grain growth during 8YSZ splat formation on polycrystalline YSZ substrates by plasma spraying. Surf. Coat. Technol. 2015, 274, 37–43. [Google Scholar] [CrossRef]
- Fukumoto, M.; Suzuki, D.; Maeda, N.; Jinbo, M.; Rang, T.; Northwood, D.; Brebbia, C.A. The splat formation issue in thermal spray processes. Mater. Contact Characterisation VIII 2017, 1, 181–185. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Bhola, R.; Chandra, S.; Mostaghimi, J. Deposition of tin droplets on a steel plate: Simulations and experiments. Int. J. Heat Mass Transf. 1998, 41, 2929–2945. [Google Scholar] [CrossRef]
- Robert, C.; Denoirjean, A.; Vardelle, A.; Wang, G.X.; Sampath, S. Nucleation and Phase Selection in Plasma-Sprayed Alumina: Modelling and Experiment. In Thermal Spray: Meeting the Challenges of the 21st Century; ASM International: Russell Township, OH, USA, 1998. [Google Scholar]
- Pasandideh-Fard, M.; Pershin, V.; Chandra, S.; Mostaghimi, J. Splat Shapes in a Thermal Spray Coating Process: Simulations and Experiments. J. Therm. Spray Technol. 2002, 11, 206–217. [Google Scholar] [CrossRef]
- Sourceforge. NgSpice. Available online: https://sourceforge.net/projects/ngspice/ (accessed on 10 August 2020).
- González-Fernández, C.F.; Alhama, F.; Sánchez, J.F.L.; Horno, J. Application of The Network Method To Heat Conduction Processes With Polynomial And Potential-Exponentially Varying Thermal Properties. Numer. Heat Transf. Part A Appl. 1998, 33, 549–559. [Google Scholar] [CrossRef]
- Horno, J.; González-Fernández, C.; Hayas, A. The Network Method for Solutions of Oscillating Reaction-Diffusion Systems. J. Comput. Phys. 1995, 118, 310–319. [Google Scholar] [CrossRef]
- Meca, A.S.; Alhama, F.; Fernández, C.G. An efficient model for solving density driven groundwater flow problems based on the network simulation method. J. Hydrol. 2007, 339, 39–53. [Google Scholar] [CrossRef]
- Zueco, J.; Alhama, F.; Fernández, C.G. Inverse determination of heat generation sources in two-dimensional homogeneous solids: Application to orthotropic medium. Int. Commun. Heat Mass Transf. 2006, 33, 49–55. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.F.; Marin, F.; Morales, J.L.; Canovas, M.; Alhama, F. Modeling and simulation of different and representative engineering problems using Network Simulation Method. PLoS ONE 2018, 13, e0193828. [Google Scholar] [CrossRef]
- Alhama, F.; García, F.M.; Nicolas, J.A.M. An efficient and reliable model to simulate microscopic mechanical friction in the Frenkel–Kontorova–Tomlinson model. Comput. Phys. Commun. 2011, 182, 2314–2325. [Google Scholar] [CrossRef]
- Marin, F.; Alhama, F.; Nicolas, J.A.M. Modelling of stick-slip behaviour with different hypotheses on friction forces. Int. J. Eng. Sci. 2012, 60, 13–24. [Google Scholar] [CrossRef]
- García, F.M.; Alhama, F.; Meroño, P.A.; Nicolas, J.A.M. Modelling of stick–slip behaviour in a Girling brake using network simulation method. Nonlinear Dyn. 2015, 84, 153–162. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.; Alhama, F.; Nicolas, J.A.M. An efficient and reliable model based on network method to simulate CO2 corrosion with protective iron carbonate films. Comput. Chem. Eng. 2012, 39, 57–64. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.; Nicolas, J.A.M.; Alhama, F.; Sanchez, J.F. Numerical Simulation of High-Temperature Oxidation of Lubricants Using the Network Method. Chem. Eng. Commun. 2014, 202, 982–991. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.; Alhama, F.; Nicolas, J.A.M.; Canovas, M. Study of main parameters affecting pitting corrosion in a basic medium using the network method. Results Phys. 2019, 12, 1015–1025. [Google Scholar] [CrossRef]
- Bejan, A.; Kraus, A.D. Heat Transfer Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- González-Fernández, F.; Alhama, C.F. Heat Transfer and the Network Simulation Method; Horno, J., Ed.; Transworld Research Network: Trivandrum, India, 2001. [Google Scholar]
- Perez, J.F.S.; Conesa, M.; Alhama, I. Solving ordinary differential equations by electrical analogy: A multidisciplinary teaching tool. Eur. J. Phys. 2016, 37, 65703. [Google Scholar] [CrossRef]
- Nagel, L.W. SPICE2: A Computer Program To Simulate Semiconductor Circuits. Ph.D Thesis, University of California and Available as Memorandum No ERL-M520, Electronics Research Laboratory, College of Engineering, University of California, Berkeley, CA, USA, 1975. [Google Scholar]
- Holger, N.V. Marcel Hendrix; Paolo, Ngspice User’s Manual Version 32. 2020. Available online: http://ngspice.sourceforge.net/index.html (accessed on 10 August 2020).
- Gear, C.W. The automatic integration of ordinary differential equations. Commun. ACM 1971, 14, 176–179. [Google Scholar] [CrossRef]
- Nagel, L.W.; Pederson, D.O. SPICE (Simulation Program with Integrated Circuit Emphasis); No ERLM382 Electronic Res. Lab.; EECS Department: Berkeley, CA, USA, 1973. [Google Scholar]
- Pasandideh-Fard, M. Droplet Impact and Solidification in a Thermal Spray Process. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1998. [Google Scholar]

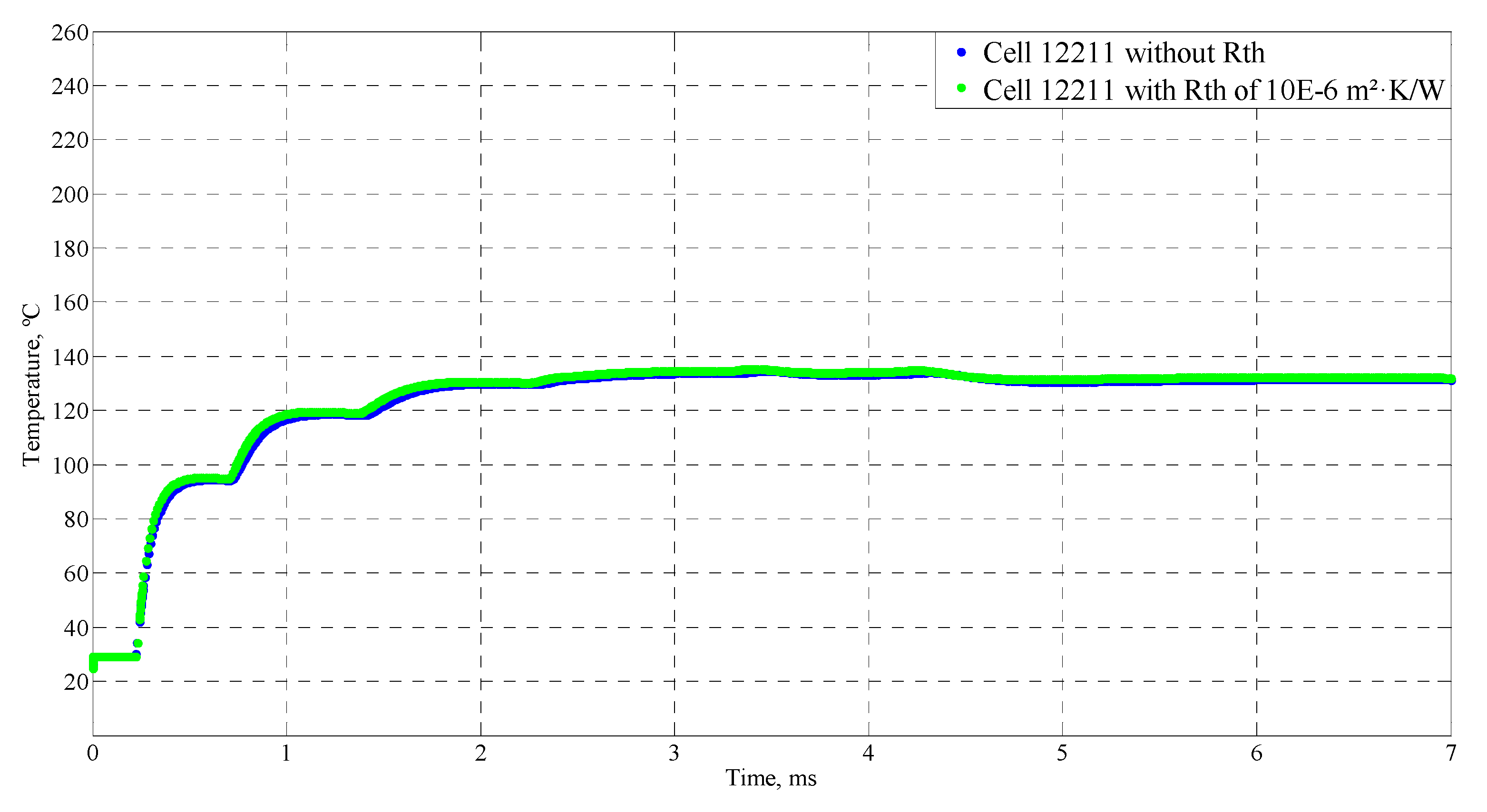
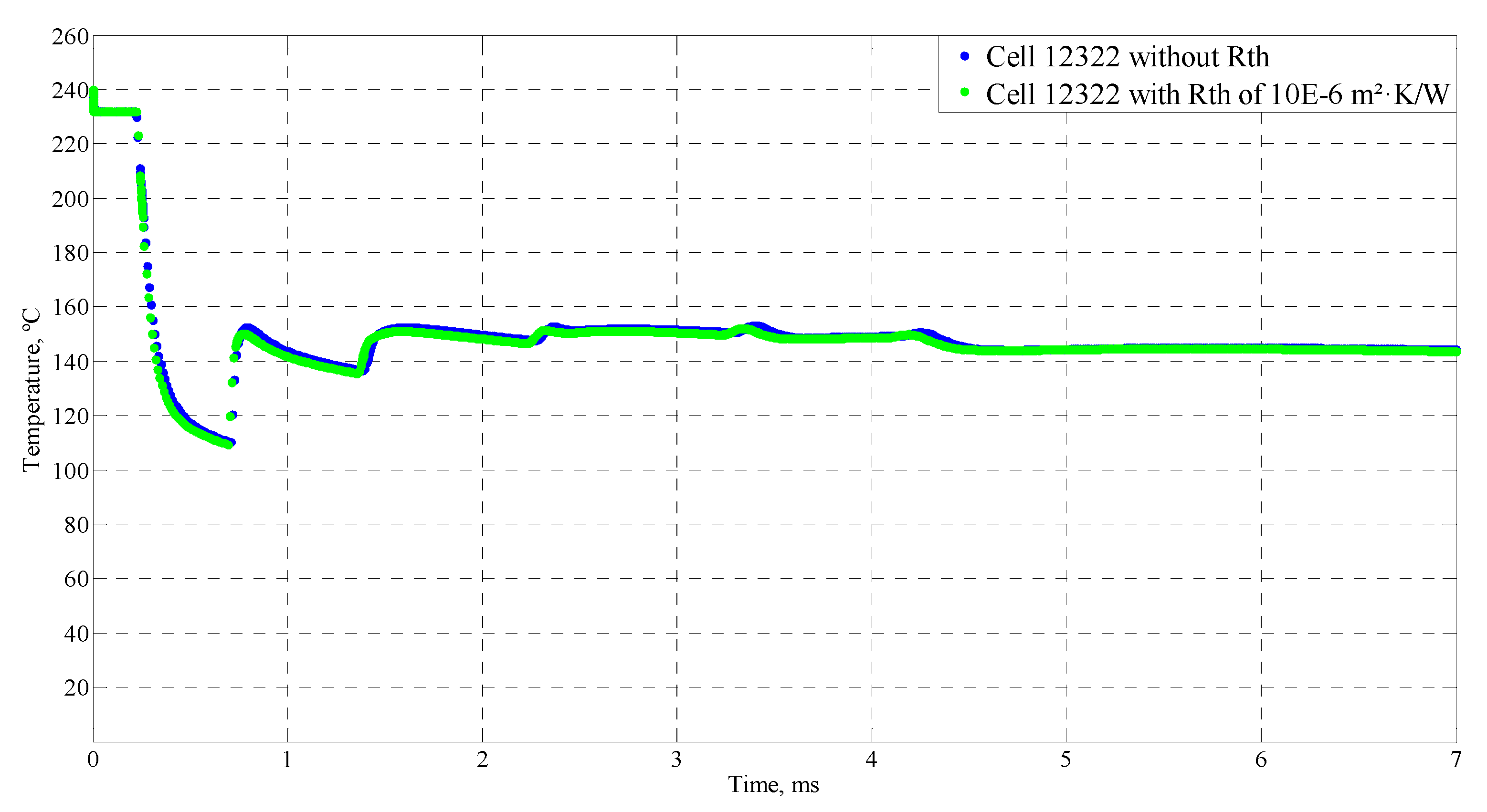
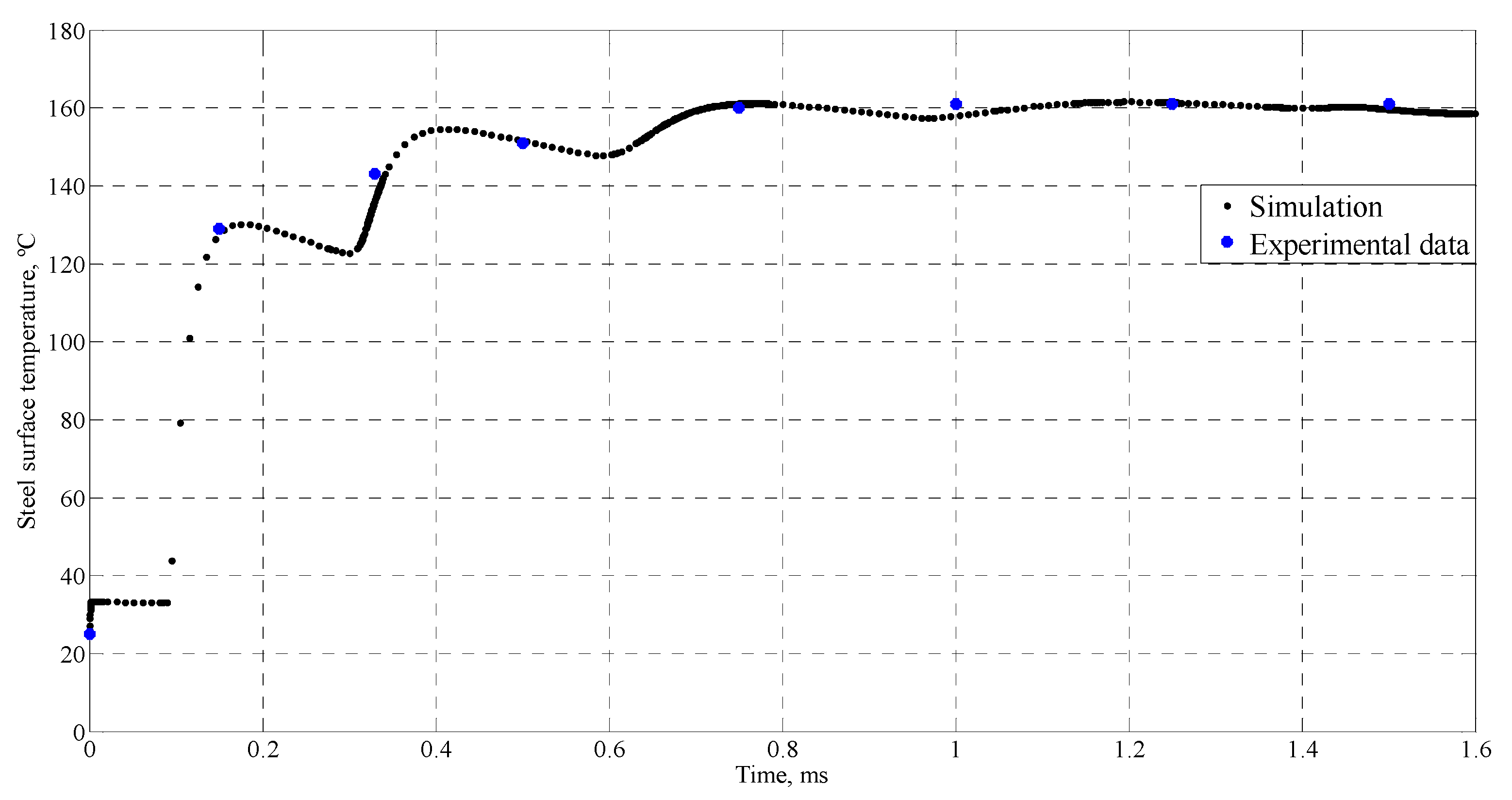
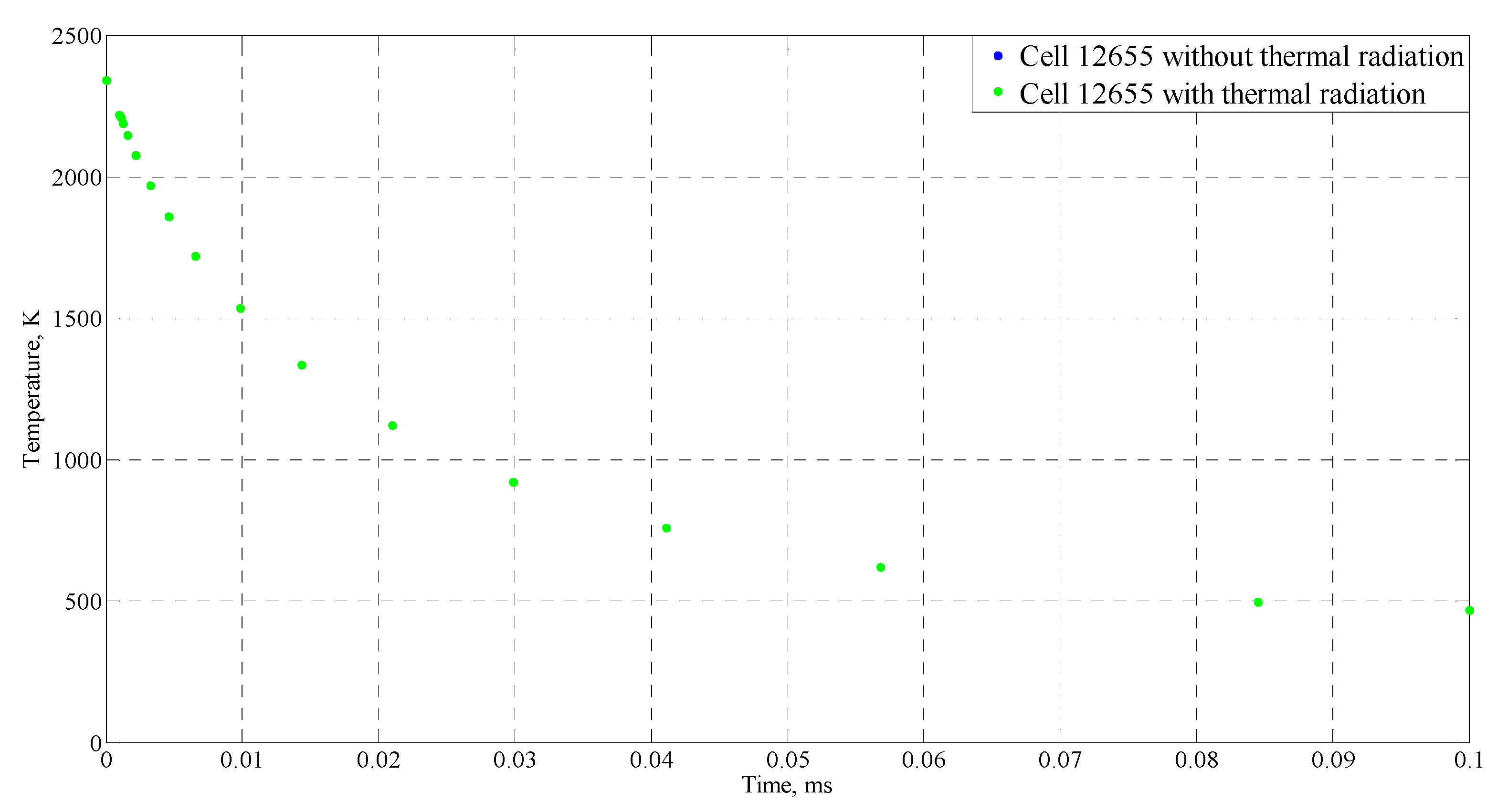
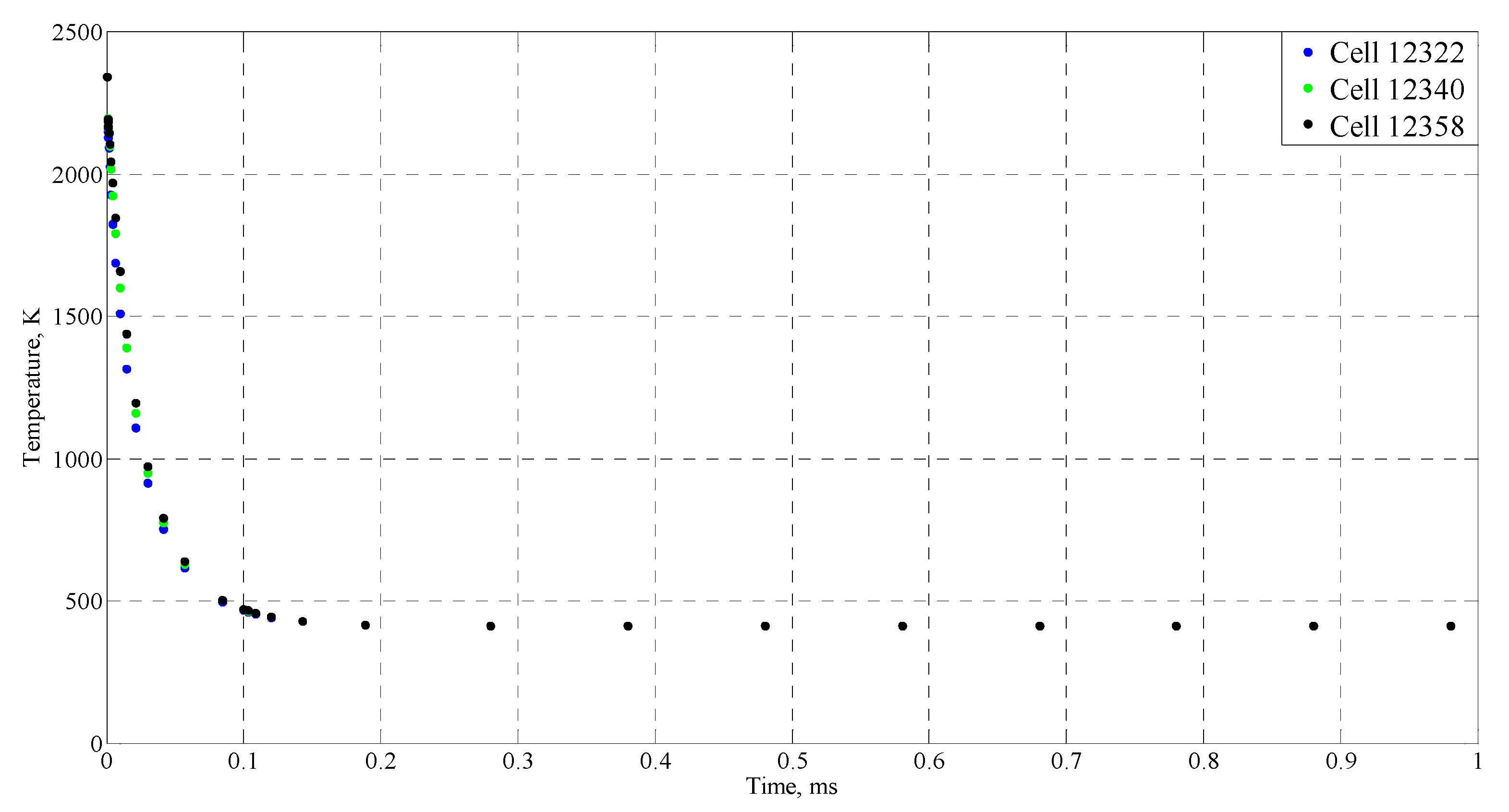
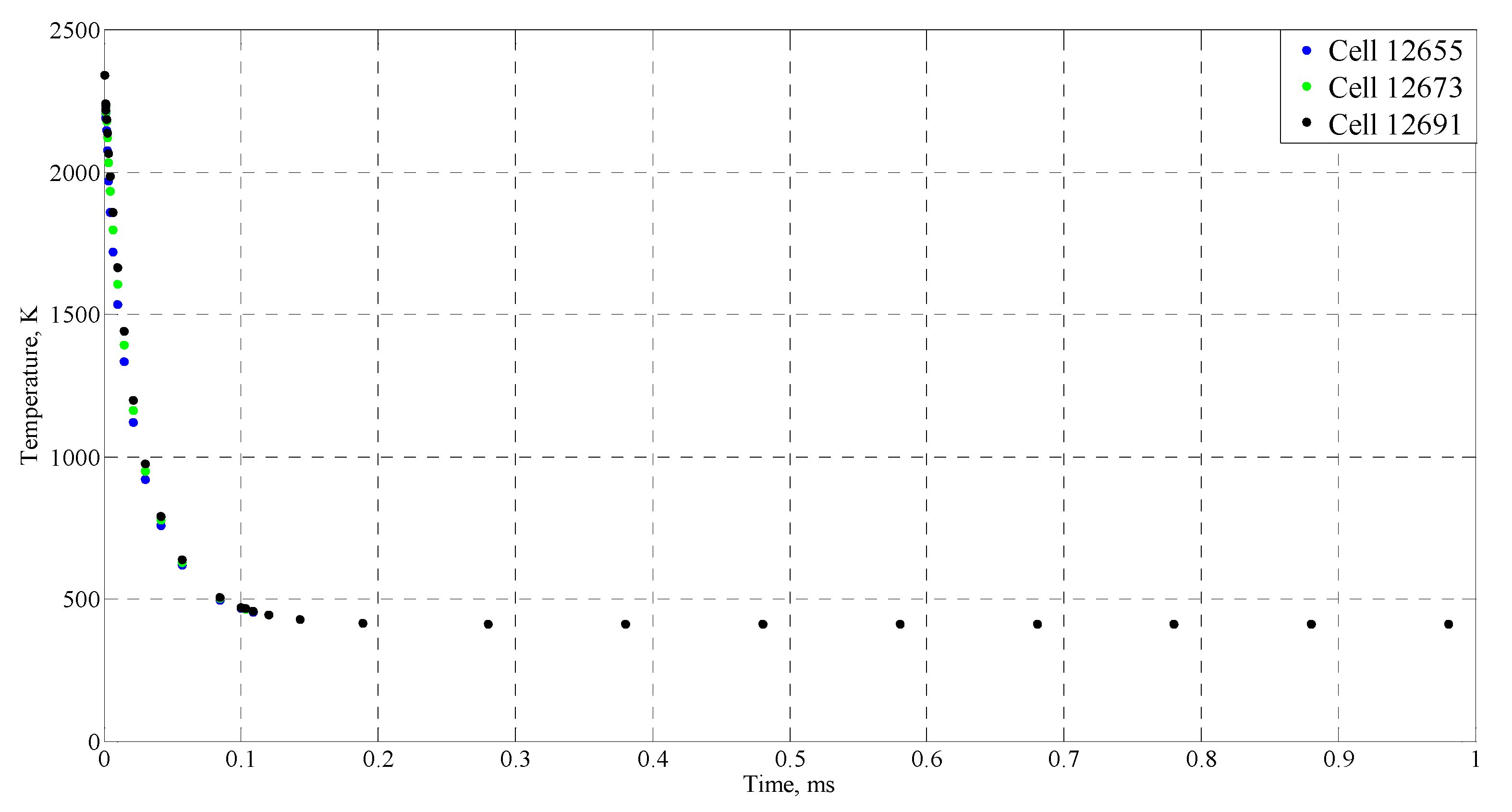
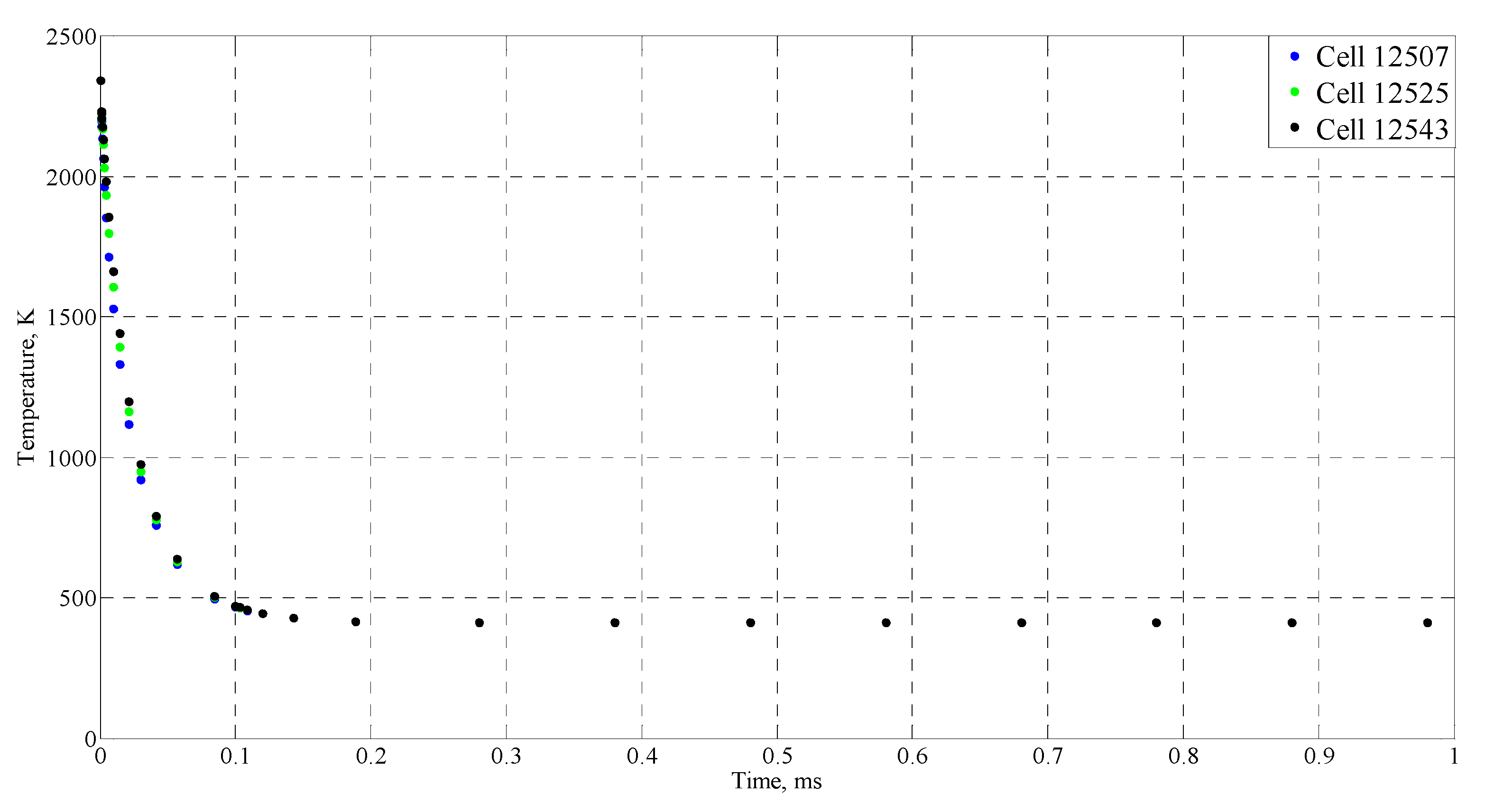
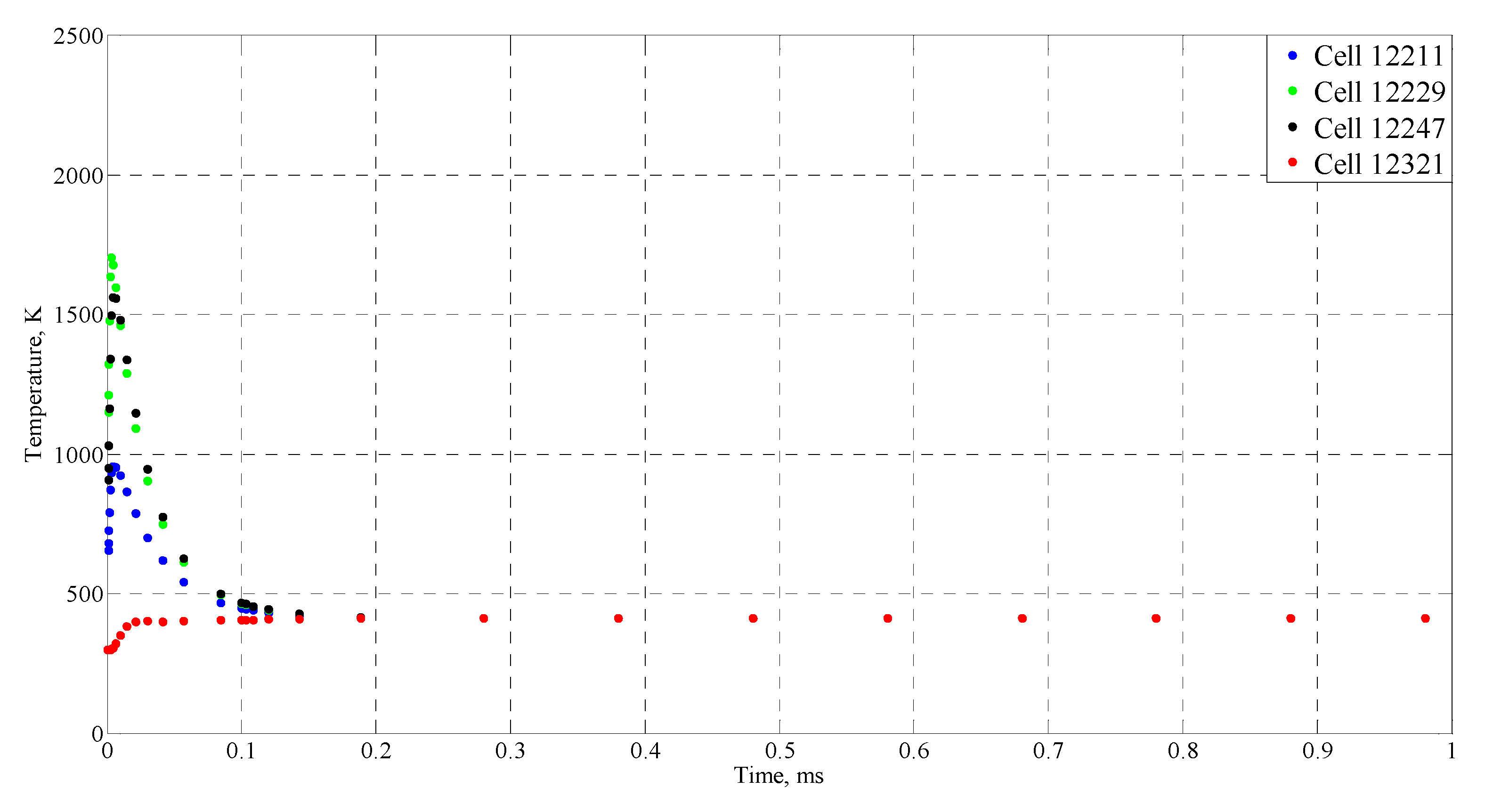
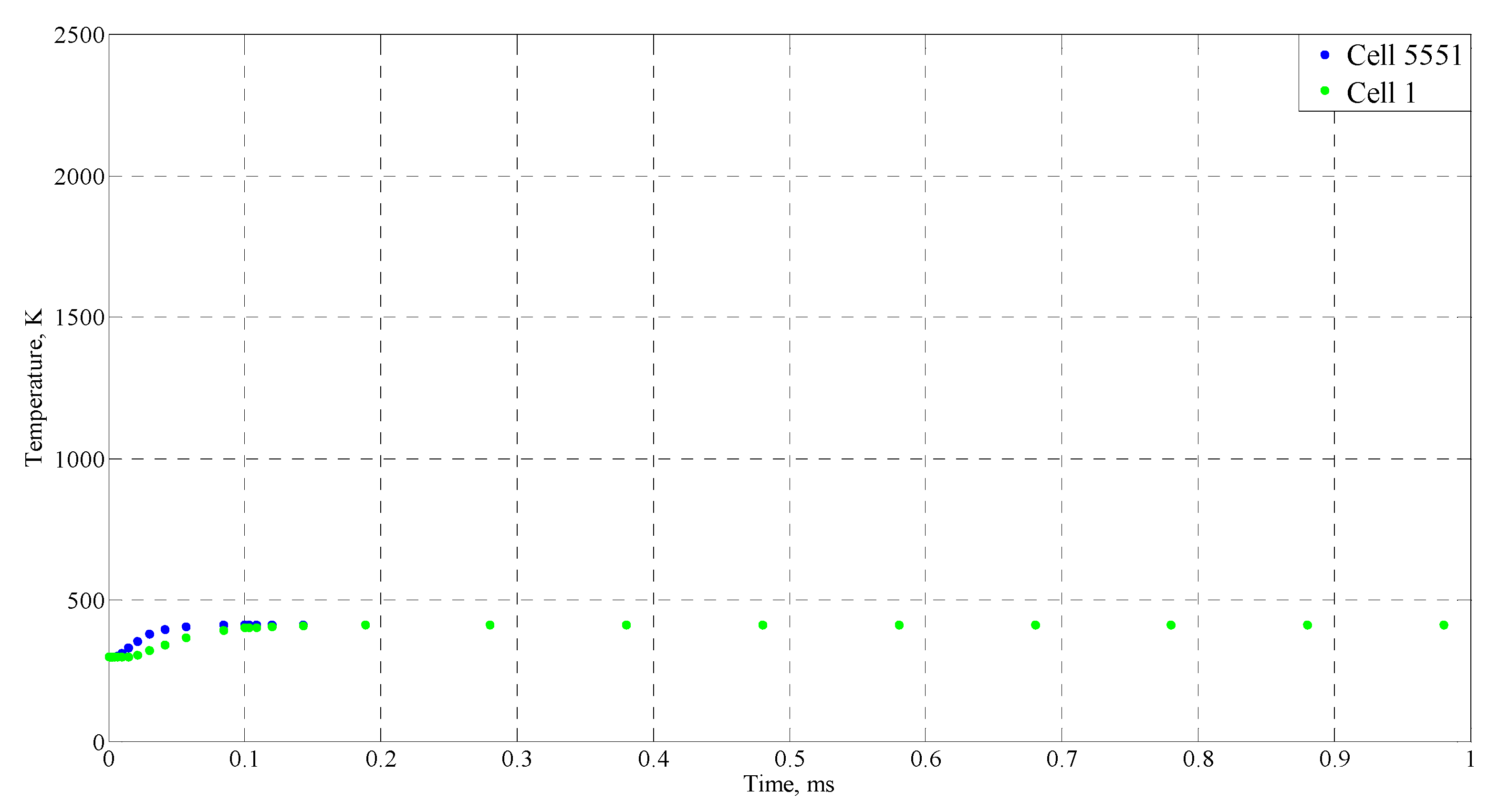
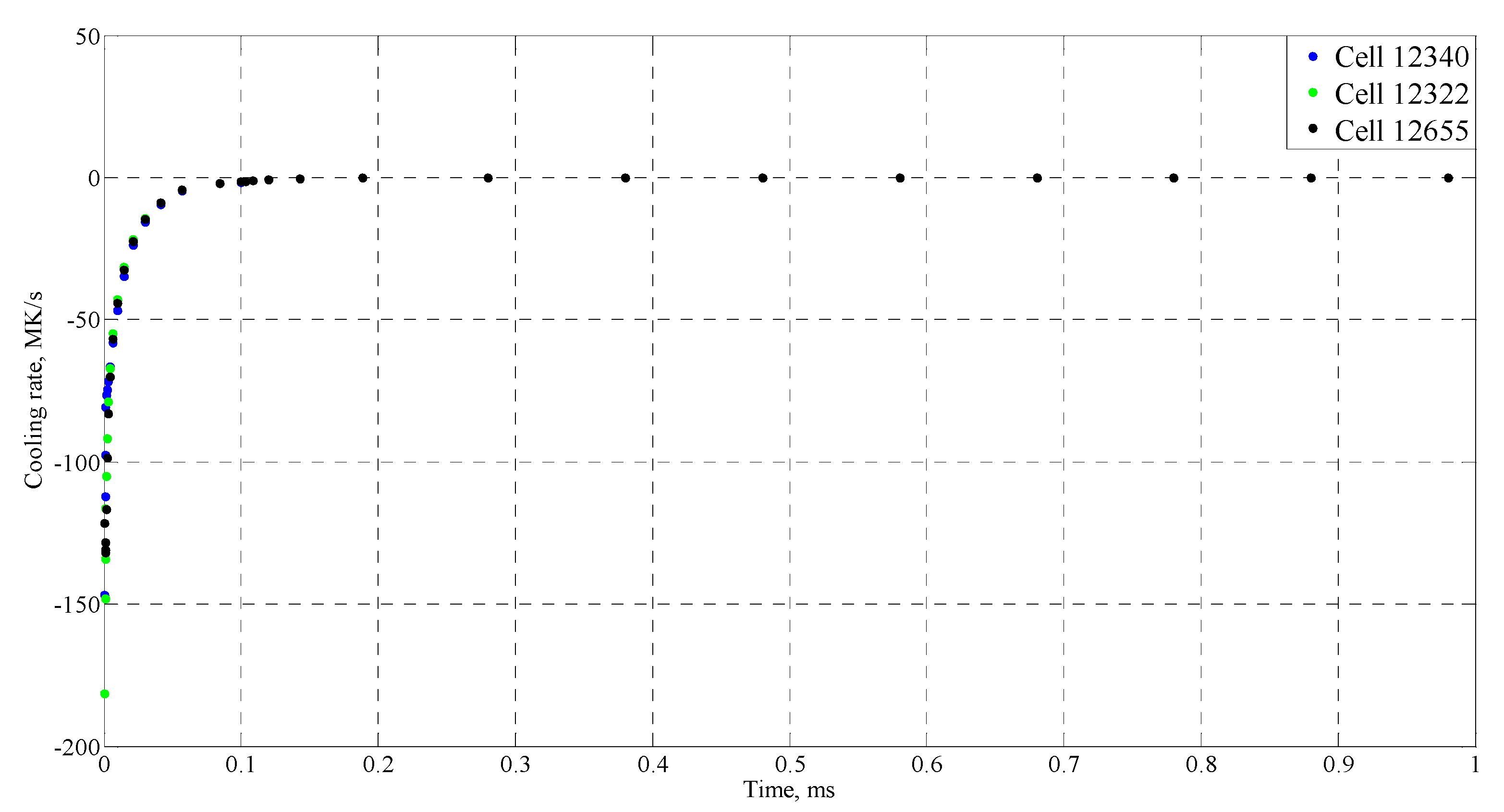
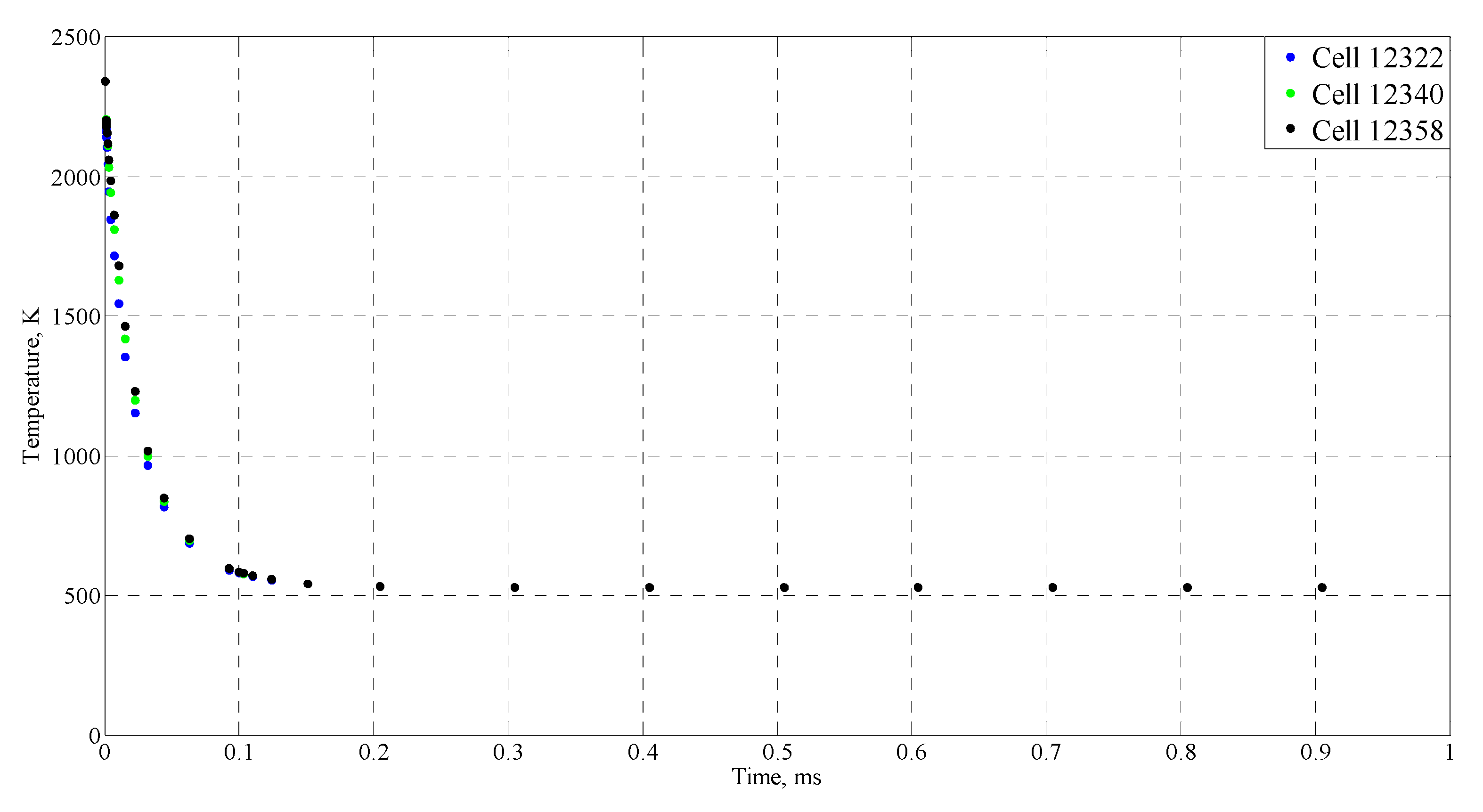


| Time (ms) | Temperature (°C) |
|---|---|
| 0 | 25 |
| 0.15 | 129 |
| 0.33 | 143 |
| 0.5 | 151 |
| 0.75 | 160 |
| 1 | 161 |
| 1.25 | 161 |
| 1.5 | 161 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González Morales, N.; Sánchez-Pérez, J.F.; Moreno Nicolás, J.A.; Killinger, A. Modelling of Alumina Splat Solidification on Preheated Steel Substrate Using the Network Simulation Method. Mathematics 2020, 8, 1568. https://doi.org/10.3390/math8091568
González Morales N, Sánchez-Pérez JF, Moreno Nicolás JA, Killinger A. Modelling of Alumina Splat Solidification on Preheated Steel Substrate Using the Network Simulation Method. Mathematics. 2020; 8(9):1568. https://doi.org/10.3390/math8091568
Chicago/Turabian StyleGonzález Morales, Noelia, Juan Francisco Sánchez-Pérez, Jose Andres Moreno Nicolás, and Andreas Killinger. 2020. "Modelling of Alumina Splat Solidification on Preheated Steel Substrate Using the Network Simulation Method" Mathematics 8, no. 9: 1568. https://doi.org/10.3390/math8091568
APA StyleGonzález Morales, N., Sánchez-Pérez, J. F., Moreno Nicolás, J. A., & Killinger, A. (2020). Modelling of Alumina Splat Solidification on Preheated Steel Substrate Using the Network Simulation Method. Mathematics, 8(9), 1568. https://doi.org/10.3390/math8091568







