Stability Assessment of Stochastic Differential-Algebraic Systems via Lyapunov Exponents with an Application to Power Systems

Abstract

In this paper, we discuss stochastic differential-algebraic equations (SDAEs) and the asymptotic stability assessment for such systems via Lyapunov exponents (LEs). We focus on index-1 SDAEs and their reformulation as ordinary stochastic differential equations (SDEs). Via ergodic theory, it is then feasible to analyze the LEs via the random dynamical system generated by the underlying SDEs. Once the existence of well-defined LEs is guaranteed, we proceed to the use of numerical simulation techniques to determine the LEs numerically. Discrete and continuous $QR$ decomposition-based numerical methods are implemented to compute the fundamental solution matrix and use it in the computation of the LEs. Important computational features of both methods are illustrated via numerical tests. Finally, the methods are applied to two applications from power systems engineering, including the single-machine infinite-bus (SMIB) power system model.

1. Introduction

Modeling the dynamic behavior of systems employing differential-algebraic equations is a mathematical representation paradigm that is widely used in many areas of science and engineering. On the other hand, the dynamics of systems perturbed by stochastic processes have been adequately modeled by stochastic differential equations (SDEs). The need of a generalized concept that covers both DAEs and SDEs, and allows the modeling and analysis of constrained systems subjected to stochastic disturbances, has led to the formulation of stochastic differential-algebraic equations (SDAEs). While there has been a broad and fruitful development both in the field of DAEs and SDEs (see, e.g., [1,2,3] and [4,5,6], respectively), studies of the concepts and the numerical treatment of SDAEs are rather limited, see e.g., [7,8,9]. The main reason for this is that the proper treatment of algebraic constraints in SDAEs pose many difficulties, except in the case that all of the constraints are explicitly given and can be resolved during the numerical integration process, which is the case that we will discuss.

As tool for the stability analysis we use Lyapunov exponents (LEs) introduced as characteristic exponents in [10]. The theory of LEs experienced a crucial development with the work [11], which, via the Multiplicative Ergodic Theorem (MET), ensures the regularity and existence of the LEs belonging to a linear cocycle over a metric dynamical system, see [12] for a detailed presentation of the theory. We review and extend the main concepts of this approach for asymptotic stability assessment of differential-algebraic equations driven by Gaussian white noise and apply the technique in the setting of power systems.

Following the ideas from [7,8,9,13,14], properties such as the existence and uniqueness of solutions are reviewed. Analogously to the DAE case, we define the class of strangeness-free (index-1) SDAEs and show that SDAE systems with this structure can be reduced to a classical SDE system that describes the dynamics of the original SDAE for which the MET can be applied to define the LEs of the system.

Once we have extended the theoretical framework that guarantees the existence of well-defined LEs, we study numerical methods, based on the $QR$ factorization of the fundamental solution matrix, which allow the numerical computation of spectral values that are associated to the Lyapunov spectra. The first technique requires computing the fundamental solution matrix and forming an orthogonal factorization, while the second one involves performing a continuous $QR$ decomposition of the fundamental solution matrix. Both techniques have been extensively studied in deterministic ODE and DAE systems, see [15,16,17,18,19,20]. This paper follows the ideas exposed in [21], where these $QR$-based methods were extended to the stochastic case.

Finally, these concepts and computational techniques are used to assess the asymptotic stability of power systems affected by stochastic fluctuations. We illustrate the results with elementary test cases, such as a single-machine infinite-bus system.

The paper is organized, as follows: in Section 2, we recall the main theory of strangeness-free SDAEs, their relation with the SDEs, and the existence of LEs generated by such SDEs. Section 3 presents the discrete and continuous $QR$-based decomposition methods and their evaluation. Interesting study-cases in the power systems area are presented in Section 4. We finish with some conclusions in Section 5.

2. Review of the Theory

2.1. Stochastic Differential-Algebraic Equations

Consider a system of quasi-linear stochastic differential-algebraic equations (SDAEs) of the form

$$\mathit{E}d{\mathit{x}}_t={\mathit{f}}_0({\mathit{x}}_t)dt+\sum _{j=1}^m{\mathit{f}}_j({\mathit{x}}_t)d{w}_t^j,t\in \mathbb{I},$$

(1)

with a singular matrix $\mathit{E}\in {\mathbb{R}}^{n\times n}$ of rank $d<n$. The function ${\mathit{f}}_0\in {\mathcal{C}}^k({\mathbb{D}}_{\mathit{x}},{\mathbb{R}}^n)$ (for some $k\ge 1$) is known as drift, and ${\mathit{f}}_1,\dots ,{\mathit{f}}_m\in {\mathcal{C}}^{k+1}({\mathbb{D}}_{\mathit{x}},{\mathbb{R}}^n)$ are the diffusions. Here, $\mathbb{I}:=[t_0,t_f]\subseteq {\mathbb{R}}^{+}$ is a closed time interval and ${\mathbb{D}}_{\mathit{x}}\subseteq {\mathbb{R}}^n$ is an open set. Furthermore, $w_t^j$ (for $j=1,\dots ,m$) form an m-dimensional Wiener process defined on the complete probability space $(\Omega ,\mathcal{F},\mathbb{P})$ with a filtration ${({\mathcal{F}}_t)}_{t\ge t_0}$, where $\mathcal{F}=\mathcal{B}(\Omega )$ is the $\sigma$-algebra of Borel sets in $\Omega$. Each j-th Wiener process $w_t$ is understood as a process such that $w_t(\omega )=\omega (t)$, where $\omega \in \Omega$, i.e., the elements of $\Omega$ are identified with the paths. We recall that the Wiener process has stationary independent increments, such that $(w_t-w_s)\sim \mathcal{N}(0,t-s)$, i.e., is a Gaussian random variable for all $0\le s<t$, such that

$$w_0=0,\mathbb{E}[w_t-w_s]=0,\mathbb{E}{[w_t-w_s]}^2=t-s.$$

Because the Wiener process is nowhere differentiable, it is more convenient to represent Equation (1) in its integral form as

$$\mathit{E}{\mathit{x}}_t=\mathit{E}{\mathit{x}}_{t_0}+{\int }_{t_0}^t{\mathit{f}}_0({\mathit{x}}_s)ds+\sum _{j=1}^m{\int }_{t_0}^t{\mathit{f}}_j({\mathit{x}}_s)d{w}_s^j,t\in \mathbb{I}.$$

(2)

Here, the first integral is a stochastic Riemann-Stieltjes integral, and the second one is a stochastic Itô-type integral, see e.g., [6].

We assume consistent initial values ${\mathit{x}}_{t_0}={\mathit{x}}_0$ independent of the Wiener processes $w_t^j$ and with finite second moments [6]. A solution ${\mathit{x}}_t=\mathit{x}(t,\omega )$ of (2) is an n-dimensional vector-valued Markovian stochastic process depending on $t\in \mathbb{I}$ and $\omega \in \Omega$ (the parameter $\omega$ is commonly omitted in the notation of $\mathit{x}$). Such a solution can be defined as strong solution if it fulfills the following conditions, see e.g., [9,13].

• $\mathit{x}(·)$ is adapted to the filtration ${({\mathcal{F}}_t)}_{t\ge t_0}$,
• ${\int }_{t_0}^{t_f}\left|f_0^{\ell }(x_s)\right|ds<\infty$ almost sure (a.s.), for all $\ell =1,\dots ,n$,
• ${\int }_{t_0}^{t_f}{\left|f_j^{\ell }(x_s)\right|}^{2}d{w}_s^j<\infty$ a.s., for all $j=1,\dots ,m$, and $\ell =1,\dots ,n$, and
• (2) holds for every $t\in \mathbb{I}$ a.s.

Because of the presence of the algebraic equations that are associated with the kernel of $\mathit{E}$, the solution components associated with these equations would be directly affected by white noise and not integrated. In order to avoid this, a reasonable restriction is to ensure that the noise sources do not appear in the algebraic constraints. According to [8,9], this assumption can be accomplished in SDAE systems whose deterministic part

$$\mathit{E}{\dot{\mathit{x}}}_t={\mathit{f}}_0({\mathit{x}}_t),t\in \mathbb{I},$$

(3)

is a DAE with tractability index-1 [9,22], in which the constraints are regularly and globally uniquely solvable for parts of the solution vector. We slightly modify this assumption and consider SDAE systems whose deterministic part (3) is a regular strangeness-free DAE [3] i.e., it has differentiation index-1. A system with these characteristics can be transformed into a semi-explicit form by means of an appropriate kinematic equivalence transformation [1,19], i.e., there exist pointwise orthogonal matrix functions $\mathcal{P}$ and $\mathcal{Q}$ such that, pre-multiplying (1) by $\mathcal{P}$, and changing the variables ${\mathit{x}}_t$ according to the transformation ${\mathit{x}}_t=\mathcal{Q}{\widehat{\mathit{x}}}_t$ one obtains a system in semi-explicit form

$$\begin{array}{cc}\hfill d{\widehat{\mathit{x}}}_t^D& ={\widehat{\mathit{f}}}_0^D({\widehat{\mathit{x}}}_t^D,{\widehat{\mathit{x}}}_t^A)dt+\sum _{j=1}^m{\widehat{\mathit{f}}}_j^D({\widehat{\mathit{x}}}_t^D,{\widehat{\mathit{x}}}_t^A)d{w}_t^j,\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill 0& ={\widehat{\mathit{f}}}_0^A({\widehat{\mathit{x}}}_t^D,{\widehat{\mathit{x}}}_t^A)dt+\sum _{j=1}^m{\widehat{\mathit{f}}}_j^A({\widehat{\mathit{x}}}_t^D,{\widehat{\mathit{x}}}_t^A)d{w}_t^j,\hfill \end{array}$$

(4b)

where ${\widehat{\mathit{x}}}_t^D$ and ${\widehat{\mathit{x}}}_t^A$ is a separation of the transformed state into differential and algebraic variables, respectively, which is performed in such a way that the Jacobian of the function ${\widehat{\mathit{f}}}_0^A$ with respect to the algebraic variables is nonsingular, see [3] for details of the construction. The condition that the noise sources do not appear in the constraints, implies that ${\sum }_{j=1}^m{\widehat{\mathit{f}}}_j^A\equiv 0$, so that the algebraic equation in (4b) can be solved as ${\widehat{\mathit{x}}}_t^A={\mathit{F}}^A({\widehat{\mathit{x}}}_t^D)$ and inserted in the dynamic Equation (4a) yielding an ordinary SDE

$$\begin{array}{cc}\hfill d{\widehat{\mathit{x}}}_t^D& ={\widehat{\mathit{f}}}_0^D({\widehat{\mathit{x}}}_t^D,{\mathit{F}}^A({\widehat{\mathit{x}}}_t^D))dt+\sum _{j=1}^m{\widehat{\mathit{f}}}_j^D({\widehat{\mathit{x}}}_t^D,{\mathit{F}}^A({\widehat{\mathit{x}}}_t^D))d{w}_t^j.\hfill \end{array}$$

(5)

This equation is called underlying SDE of the strangeness-free SDAE. It acts in the lower-dimensional subspace ${\mathbb{R}}^d$, with $d=n-a$ (where a denotes the number of algebraic equations). The SDE system (5) preserves the inherent dynamics of a strangeness-free SDAE system [22]. Note that, in this way, the algebraic equations have been removed from the system, but, whenever a numerical method is used for the numerical integration, then one has to make sure that the algebraic equations are properly solved at each time step, so that the back-transformation to the original state variables can be performed.

2.2. Random Dynamical Systems Generated by SDEs

In the previous section, we have discussed the reduction of an autonomous strangeness-free SDAE to its underlying SDE, which preserves the dynamic characteristics of the original system. Using the back-transformation, the definitions and properties attributed to the underlying SDE, and the analysis performed on it, can be extended to the original SDAE. For simplicity, we use the following representation, where the drift and diffusion terms are combined into one term.

$$d{\mathit{x}}_t={\mathit{f}}_0({\mathit{x}}_t)dt+\sum _{j=1}^m{\mathit{f}}_j({\mathit{x}}_t)d{w}_t^j=\sum _{j=0}^m{\mathit{f}}_j({\mathit{x}}_t)d{w}_t^j,t\in \mathbb{I},$$

(6)

where ${\mathit{f}}_0\in {\mathcal{C}}_b^{k,\delta }$, ${\mathit{f}}_1,\cdots ,{\mathit{f}}_m\in {\mathcal{C}}_b^{k+1,\delta }$ and ${\sum }_{j=1}^m{\sum }_{i=1}^d{f}_j^i\frac{\partial }{\partial x_i}{f}_j\in {\mathcal{C}}_b^{k,\delta }$ for some $k\ge 1$ and $\delta >0$. Here, ${\mathcal{C}}_b^{k,\delta }$ is the Banach space of ${\mathcal{C}}^k$ vector fields on ${\mathbb{R}}^d$ with linear growth and bounded derivatives up to order k and the k-th derivative is $\delta$-Hölder continuous. In addition, we assume that the differential operator $L:={\mathit{f}}_0+\frac{1}{2}{\sum }_{j=1}^m{({\mathit{f}}_j)}^2$ is strong hypoelliptic in the sense that the Lie algebra $\mathcal{L}({\mathit{f}}_0,{\mathit{f}}_1,\dots ,{\mathit{f}}_m)$ generated by the vector fields ${\mathit{f}}_j$ (with $j=0,\dots ,m$) has dimension d for all ${\mathit{x}}_t\in {\mathbb{R}}^d$ [12]. Once again, $w_t^j$ (for $j=0,\dots ,m$) is a m-dimensional Wiener process, this time with the convention $d{w}_t^0\equiv dt$.

For a given initial value, the solution process generates a Markovian stochastic process, and the SDE (6) generates a random dynamical system (RDS) $\Theta =(\theta ,\mathit{\phi })$ which is an object consisting of a metric dynamical system (MDS) $\theta$ for modeling the random perturbations, and a cocycle $\mathit{\phi }:{\mathbb{R}}^{+}\times \Omega \times {\mathbb{R}}^d\to {\mathbb{R}}^d$ over this system. The ergodic MDS is denoted by $\theta \equiv (\Omega ,\mathcal{F},\mathbb{P},{({\theta }_t)}_{t\in \mathbb{R}})$ with the filtration ${({\mathcal{F}}_t)}_{t\ge t_0}$, and defined by the Wiener shift

$${\theta }_t\omega (·)=\omega (t+·)-\omega (t),t\in \mathbb{I},$$

which means that a shift transformation given by $\theta$ is measure-preserving and ergodic [23].

Together with the SDE (6), we define the variational system

$$d{\mathit{v}}_t=\sum _{j=0}^m{\mathit{J}}_j({\mathit{x}}_t){\mathit{v}}_{t}d{w}_t^j,t\in \mathbb{I},\mathrm{with}{\mathit{J}}_j({\mathit{x}}_t):=\left(\frac{\partial {\mathit{f}}_j}{\partial \mathit{x}}\right){|}_{\mathit{x}(t;t_0)},$$

(7)

obtained after linearizing (6) along a solution. If we denote by $\mathit{\Phi }(t,\omega ,\mathit{x})$ the Jacobian of $\mathit{\phi }(t,\omega )$ at ${\mathit{x}}_t$, then $\mathit{\Phi }$ is the unique solution of the variational Equation (7), satisfying

$$\mathit{\Phi }(t,\omega ,\mathit{x})={\mathit{I}}_d+\sum _{j=0}^m{\int }_0^t{\mathit{J}}_j(\mathit{\phi }(s)\mathit{x})\mathit{\Phi }(s,\mathit{x})d{w}_s^j,t\in \mathbb{I},$$

(8)

where ${\mathit{I}}_d$ denotes the identity matrix of size d. Therefore, $\mathit{\Phi }$ it is a matrix cocycle over $\Theta$. The system (6) and (7) uniquely generates a ${\mathcal{C}}^{k-1}$ RDS $(\mathit{\phi },\mathit{\Phi })$ over $\theta$. Moreover, the determinant of $\mathit{\Phi }$ satisfies the Liouville equation

$$det\mathit{\Phi }=exp\left(\sum _{j=0}^m{\int }_0^{t}tr({\mathit{J}}_{\mathit{j}}(\mathit{\phi }(s)\mathit{x})d{w}_s^j\right),t\in \mathbb{I},$$

(9)

being then a scalar cocycle over $\Theta$ (see Theorems 2.3.32 and 2.3.39–40 in [12] for details).

2.3. Lyapunov Exponents of Ergodic RDSs

An important result of the theory of RDSs is the so-called Multiplicative Ergodic Theorem (MET) developed in [11]. This concept allows for the definition of LEs for linear cocycles over a ergodic MDS. First, the MET assumes for the linear cocycle $\mathit{\Phi }$ that the integrability condition

$${log}^{+}\parallel \mathit{\Phi }(t,\omega ,\mathit{x})\parallel \in {\mathcal{L}}^1(\Omega ,\mathcal{F},\mathbb{P}),$$

is satisfied (${log}^{+}$ denotes the positive part of log). This guarantees that the variational Equation (7) associated with (6) is well-posed. Additionally, let $\mu$ be an ergodic invariant measure with respect to the cocycle $\mathit{\phi }$ [12]. Subsequently, the MET assures the existence of an invariant set $\widehat{\Omega }\subset \Omega$ of full $\mu$-measure, such that, for each $\omega \in \widehat{\Omega }$, there is a measurable decomposition

$${\mathbb{R}}^d=L_1(\omega )\oplus \cdots \oplus L_p(\omega ),$$

of ${\mathbb{R}}^d$ into random linear subspaces $L_i(\omega )$, which are invariant under $\Theta$. Here $p\le d$, where $d_i\in \mathbb{N}$ denotes the dimension of the subspace $L_i(\omega )$ (with $1\le i\le p$), and ${\sum }_{i=1}^p{d}_i=d$. This splitting is dynamically characterized by real numbers ${\lambda }_1>\dots >{\lambda }_p$, which quantify the exponential growth rate of the subspaces. These are called Lyapunov exponents, and they are defined by

$${\lambda }_i:=\underset{t\to \infty }{lim}\frac{1}{t}log\parallel \mathit{\Phi }(t,\omega ,\mathit{x})\parallel \mathrm{whenever}\mathit{x}\in L_i(\omega )\backslash \left\{0\right\}.$$

According to [24], p. 118, the LEs ${\lambda }_i$ are independent of $(\omega ,\mathit{x})$ and thus they are universal constants of the cocycle generated by (7) under the ergodic invariant probability measure $\mu$. Finally, if the following identity holds for $\mathit{\Phi }$

$$\sum _{i=1}^d{\lambda }_i=\underset{t\to \infty }{lim}\frac{1}{t}log|det\mathit{\Phi }(t,\omega ,\mathit{x})|,$$

(10)

the system is said to be Lyapunov regular (Lyapunov regularity condition) [21,25]. In practice, it is hard (if not impossible) to verify Lyapunov regularity for a particular system [12]. One of the key statements of the MET is that linear RDS (whether these are constant, periodic, quasi-periodic, or almost-periodic) are a.s. Lyapunov regular.

The concept of LEs plays an important role in the asymptotic stability assessment of dynamical systems subjected to stochastic disturbances. Under appropriate regularity assumptions, the negativity of all LEs of the system of variational equations implies the exponential asymptotic stability of both the linear SDE and original nonlinear SDE system.

3. $\mathit{QR}$ Methods for Computing LEs

In this section, we derive the numerical techniques to compute the finite-time approximation of the LEs. Inspired by [21], the present paper proposes an adaptation of the ideas from the purely deterministic case [17,18,26] to noise-driven dynamical systems. The methods take advantage on the existence of a Lyapunov transformation of the linear RDS to an upper-triangular structure, and the feasibility to retrieve a numerical approximation of the LEs from that form. The transformation is performed through an orthogonal change of variables. The approach is made under the assumption of Lyapunov regularity of the system. In order to explain the methods, let us consider again the SDE as an initial value problem of the form

$$d{\mathit{x}}_t=\sum _{j=0}^m{\mathit{f}}_j({\mathit{x}}_t)d{w}_t^j,t\in \mathbb{I},{\mathit{x}}_{t_0}={\mathit{x}}_{t_0},$$

(11)

where ${\mathit{f}}_j$ are sufficiently smooth functions. The corresponding variational Equation (11) along with the solutions ${\mathit{x}}_t({\mathit{x}}_0)$, turned into a matrix initial value problem, is given by

$$d{\mathit{V}}_t=\sum _{j=0}^m{\mathit{J}}_j({\mathit{x}}_t){\mathit{V}}_{t}d{w}_t^j,{\mathit{V}}_0={\mathit{I}}_d,$$

(12)

with the identity matrix ${\mathit{I}}_d\in {\mathbb{R}}^{d\times d}$ as initial value, where ${\mathit{J}}_j({\mathit{x}}_t):=\frac{\partial {\mathit{f}}_j}{\partial \mathit{x}}$ are the Jacobians of the vector functions ${\mathit{f}}_j({\mathit{x}}_t)$, and $\mathit{V}\in {\mathcal{C}}^1(\mathbb{I}\times {\mathbb{R}}^{d\times d})$ is the fundamental solution matrix, whose columns are linearly independent solutions of the variational equation. A key theoretical tool for determining the LEs is the computation of the continuous $QR$ factorization of ${\mathit{V}}_t$,

$${\mathit{V}}_t={\mathit{Q}}_t{\mathit{R}}_t,$$

where ${\mathit{Q}}_t$ is orthogonal, i.e., ${\mathit{Q}}_t^T{\mathit{Q}}_t={\mathit{I}}_d$, and ${\mathit{R}}_t$ is upper triangular with positive diagonal elements $R_t^{ii}$ for $i=1,\dots ,d$. Applying the MET theory presented in Section 2.3, and taking into account the norm-preserving property of the orthogonal matrix function ${\mathit{Q}}_t$, we have

$${\lambda }_i=\underset{t\to \infty }{lim}\frac{1}{t}log\parallel {\mathit{V}}_t{\mathit{p}}_i\parallel =\underset{t\to \infty }{lim}\frac{1}{t}log\parallel {\mathit{R}}_t{\mathit{p}}_i\parallel ,$$

(13)

where $\{{\mathit{p}}_i\}$ is an orthonormal basis associated with the splitting of ${\mathbb{R}}^d$. Lyapunov regular systems preserve their regularity under kinematic similarity transformations. Subsequently, considering the regularity condition (10), the Liouville Equation (9), and performing some algebraic manipulations (see details in [21], p. 150), the LEs are given by

$${\lambda }_i=\underset{t\to \infty }{lim}\frac{1}{t}log\left|R_t^{ii}\right|\mathrm{a}.\mathrm{s}.,\mathrm{for}i=1,\dots ,d.$$

(14)

The $QR$ methods require to perform the $QR$ decomposition of ${\mathit{V}}_t$ for a long enough time, so that the $R_t^{ii}$ have started to converge. Depending on whether the decomposition is performed after or before integrating numerically the variational equation, the method is called discrete or continuous $QR$ method.

3.1. Discrete $QR$ Method

The discrete $QR$ method is a very popular method for computing LEs in ODEs and DAEs. In this approach, the fundamental solution matrix ${\mathit{V}}_t$ and its triangular factor ${\mathit{R}}_t$ are indirectly computed by a reorthogonalized integration of the variational Equation (12) through an appropriate $QR$ decomposition. Thus, given grid points $0=t_0<t_1<\dots <t_{N-1}<t_N=T$, we can write ${\mathit{V}}_{t_{\ell }}$ in terms of the state-transition matrices as

$${\mathit{V}}_{t_{\ell }}={\mathit{Z}}_{(t_{\ell },t_{\ell -1})}{\mathit{Z}}_{(t_{\ell -1},t_{\ell -2})}\cdots {\mathit{Z}}_{(t_2,t_1)}{\mathit{Z}}_{(t_1,t_0)}{\mathit{V}}_{t_0}.$$

(15)

At $t_0=0$, we perform a standard matrix $QR$ decomposition

$${\mathit{V}}_{t_0}={\mathit{Q}}_{t_0}{\mathit{R}}_{t_0},$$

and for $\ell =1,2,\cdots ,N$, we determine ${\mathit{Z}}_{(t_{\ell },t_{\ell -1})}$ as the numerical solution (via numerical integration) of the matrix initial value problem

$$d{\mathit{Z}}_{(t_{\ell },t_{\ell -1})}=\sum _{j=0}^m{\mathit{J}}_j({\mathit{x}}_t){\mathit{Z}}_{(t_{\ell },t_{\ell -1})}d{w}_t^j,{\mathit{Z}}_{(t_{\ell },t_{\ell -1})}={\mathit{Q}}_{t_{\ell -1}},t_{\ell -1}\le t\le t_{\ell },$$

(16)

and then compute the $QR$ decomposition

$${\mathit{Z}}_{(t_{\ell },t_{\ell -1})}={\mathit{Q}}_{t_{\ell }}{\mathit{R}}_{(t_{\ell },t_{\ell -1})},$$

where ${\mathit{R}}_{(t_{\ell },t_{\ell -1})}$ has positive diagonal elements. From (15), the value of the fundamental matrix ${\mathit{V}}_{t_{\ell }}$ is determined via

$${\mathit{V}}_{t_{\ell }}={\mathit{Q}}_{t_{\ell }}{\mathit{R}}_{(t_{\ell },t_{\ell -1})}{\mathit{R}}_{(t_{\ell -1},t_{\ell -2})}\cdots {\mathit{R}}_{(t_2,t_1)}{\mathit{R}}_{(t_1,t_0)}{\mathit{R}}_{t_0},$$

which is again a $QR$ factorization with positive diagonal elements. Because this is unique, for the $QR$ decomposition ${\mathit{V}}_{t_{\ell }}={\mathit{Q}}_{t_{\ell }}{\mathit{R}}_{t_{\ell }}$, we have

$${\mathit{R}}_{t_{\ell }}={\mathit{R}}_{(t_{\ell },t_{\ell -1})}{\mathit{R}}_{(t_{\ell -1},t_{\ell -2})}\cdots {\mathit{R}}_{(t_2,t_1)}{\mathit{R}}_{(t_1,t_0)}{\mathit{R}}_{t_0}=\prod _{\kappa =0}^{\ell }{\mathit{R}}_{\kappa }.$$

Here, we denote, as ${\mathit{R}}_{\kappa }$, the triangular transition matrices ${\mathit{R}}_{(t_{\ell },t_{\ell -1})}$ with $\kappa =0,1,\dots ,\ell$. From (14), the LEs are thus computed as

$${\lambda }_i=\underset{\ell \to \infty }{lim}\frac{1}{t_{\ell }}log\left|\prod _{\kappa =0}^{\ell }{R}_{\kappa }^{ii}\right|=\underset{\ell \to \infty }{lim}\frac{1}{t_{\ell }}\sum _{\kappa =0}^{\ell }log\left|R_{\kappa }^{ii}\right|,i=1,\dots ,d.$$

(17)

3.2. Continuous $QR$ Method

The implementation of the continuous $QR$ technique requires determining a system of SDEs for the $\mathit{Q}$ factor and the scalar equations for the logarithms of the diagonal elements of the $\mathit{R}$ factor elementwise. Subsequently, once the orthogonal matrix $\mathit{Q}$ is computed by numerical integration, the logarithms of the diagonal elements of $\mathit{R}$ can also be obtained.

By differentiating in the Itô sense the decomposition ${\mathit{V}}_t={\mathit{Q}}_t{\mathit{R}}_t$ and using the orthogonality ${\mathit{Q}}_t^T{\mathit{Q}}_t={\mathit{I}}_d$, we obtain

$$\begin{array}{cc}\hfill d{\mathit{V}}_t& =(d{\mathit{Q}}_t){\mathit{R}}_t+{\mathit{Q}}_t(d{\mathit{R}}_t),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \mathbf{0}& =(d{\mathit{Q}}_t^T){\mathit{Q}}_t+{\mathit{Q}}_t^T(d{\mathit{Q}}_t).\hfill \end{array}$$

(19)

Inserting (18) into the variational Equation (12), and multiplying by ${\mathit{Q}}_t^T$ from the left and by ${\mathit{R}}_t^{-1}$ from the right, we obtain

$${\mathit{Q}}_t^T(d{\mathit{Q}}_t)+(d{\mathit{R}}_t){\mathit{R}}_t^{-1}=\sum _{j=0}^m{\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_{t}d{w}_t^j.$$

(20)

Because $(d{\mathit{R}}_t){\mathit{R}}_t^{-1}$ is upper triangular, the skew-symmetric matrix $d{\mathit{S}}_t:={\mathit{Q}}_t^T(d{\mathit{Q}}_t)$ satisfies

$$d{\mathit{S}}_t^{il}=\left\{\begin{array}{cc}\sum _{j=0}^m{\left({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t\right)}^{jl}d{w}_t^j,\hfill & i>l,\hfill \\ 0,\hfill & i=l,\hfill \\ -\sum _{j=0}^m{\left({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t\right)}^{jl}d{w}_t^j,\hfill & i<l.\hfill \end{array}\right.$$

(21)

This results in an SDE for ${\mathit{Q}}_t$ given by

$$d{\mathit{Q}}_t={\mathit{Q}}_{t}d{\mathit{S}}_t=\sum _{j=0}^m{\mathit{Q}}_t{\mathit{T}}_t^j({\mathit{x}}_t,{\mathit{Q}}_t)d{w}_t^j,$$

(22)

where the matrices ${\mathit{T}}_t^j({\mathit{x}}_t,{\mathit{Q}}_t)$ (for $j=0,\dots ,m$) are defined via

$${\left({\mathit{T}}_t^j({\mathit{x}}_t,{\mathit{Q}}_t)\right)}^{il}=\left\{\begin{array}{cc}{\left({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t\right)}^{jl},\hfill & i>l,\hfill \\ 0,\hfill & i=l,\hfill \\ -{\left({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t\right)}^{jl},\hfill & i<l.\hfill \end{array}\right.$$

(23)

A corresponding SDE for ${\mathit{R}}_t$ can be obtained from (20) and (21) via

$$d{\mathit{R}}_t=\sum _{j=0}^m({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t-{\mathit{T}}_t^i({\mathit{x}}_t,{\mathit{Q}}_t)){\mathit{R}}_{t}d{w}_t^j,$$

(24)

and the equation for the ith diagonal element $R_t^{ii}$ is given by

$$d{R}_t^{ii}=\sum _{j=0}^m{({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t)}^{ii}{R}_t^{ii}d{w}_t^j,\mathrm{for}i=1,\dots ,d.$$

(25)

Because the computed LEs can be obtained from (14), we make use of the Itô Lemma to introduce the following SDE for the function ${\psi }_t^i=log{R}_t^{ii}$ from (25),

$$d{\psi }_t^i=d(log{R}_t^{ii})=\sum _{j=0}^m{({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t)}^{ii}d{w}_t^j-\frac{1}{2}{\left[\sum _{j=0}^m{({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t)}^{ii}d{w}_t^j\right]}^2.$$

(26)

If we assume that there are no correlations between the diffusion terms in the SDE system, then we do not have terms $d{w}_t^{k}d{w}_t^{\ell }$ (for $1<k<m$, and $1<\ell <m$, with $k\ne \ell$) in the SDE (26). Additionally, using that $dtdt\equiv 0$, $dtd{w}_t^k\equiv 0$, and $d{w}_t^{j}d{w}_t^j\equiv dt$ for $1<k<m$, the SDE (26) is reduced to

$$d{\psi }_t^i=\sum _{j=0}^m{({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t)}^{ii}d{w}_t^j-\frac{1}{2}\sum _{j=1}^m{\left[{({\mathit{Q}}_t^T{\mathit{J}}_j({\mathit{x}}_t){\mathit{Q}}_t)}^{ii}\right]}^{2}dt.$$

(27)

By integrating this SDE, it is possible to obtain the LEs ${\lambda }_i$ from

$${\lambda }_i=\underset{t\to \infty }{lim}\frac{1}{t}{\psi }_t^i,i=1,\dots ,d.$$

(28)

The alternative expressions (27) and (28), while easy to implement numerically, improve the numerical results in comparison to (25), and they lead to better robustness for large time intervals, as will be illustrated in the numerical examples.

In summary, the difference between the discrete and the continuous $QR$ method is that for the first one, the orthonormalization is performed numerically at every discrete time step, while the continuous $QR$ method maintains the orthogonality via solving differential equations that encode the orthogonality continuously.

3.3. Computational Considerations

In this section, we discuss additional aspects of the computational implementation of discrete and continuous $QR$-based methods to calculate LEs. The application of the discrete $QR$ technique mainly requires the numerical integration of the SDEs (11) and (16). This task is performed by using standard weak Euler-Maruyama and Milstein schemes, integrators for whom the ergodicity preservation property has been proved (see [27,28]).

On the other hand, the numerical integration of the SDEs (11), (22) and (27) in the computational implementation of the continuous $QR$ technique, must be performed in such a way that it preserves the orthogonality of the factor $\mathit{Q}$ in each integration step. This can be achieved via projected orthogonal schemes which consist of a two-step process in which first an approximation is computed via any standard scheme, and then the result is projected into the set of orthogonal matrices [29]. Again, we use the Euler-Maruyama and Milstein method, as in the discrete case.

We have implemented the two $QR$ methods in Matlab. However, to obtain a unique $QR$ factorization in each step, we have modified the $QR$ decomposition provided by Matlab to ensure this uniqueness, by forming a diagonal matrix $\mathcal{I}$ with ${\mathcal{I}}_{i,i}=\mathrm{sign}(R_{i,i})$, for $i=1,\dots ,d$; and, then setting $\mathit{Q}:=\mathit{Q}\mathcal{I}$ and $\mathit{R}:=\mathcal{I}\mathit{R}$.

3.4. Numerical Examples

In this section, we illustrate the described $QR$-based procedures via two strangeness-free SDAE systems in order to compare the computational efficiency, accuracy, and robustness of both the discrete and continuous $QR$-based methods using the numerical integration schemes Euler-Maruyama and Milstein. The four numerical methods will be denoted as D-EM, D-Milstein, C-EM, C-Milstein, respectively. The computations are carried out with Matlab Version 9.7.0(R2019b) on a computer with CPU Intel Core i7 composed by six cores of 2.20 GHz, and 16 GB of RAM.

3.4.1. Example 1

Let us consider the simple SDAE equation system

$$\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]·d\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}-x_2\\ -\alpha x_1+arctan(x_1)+x_2\end{array}\right]dt+\left[\begin{array}{c}{(x_1^2+1)}^{\frac{1}{2}}\\ 0\end{array}\right]d{w}_t,$$

(29)

with $\alpha \in {\mathbb{R}}^{+}$. The nonlinear functions in both the drift and diffusion part are continuous on ${\mathbb{R}}^{+}$, with continuous and bounded derivatives, and $w_t$ is a one-dimensional Wiener process. The underlying SDE of (29) is

$$d{\widehat{x}}_t=[-\alpha {\widehat{x}}_t+arctan({\widehat{x}}_t)]dt+{({\widehat{x}}_t^2+1)}^{\frac{1}{2}}d{w}_t,$$

(30)

whose LE exists and it can be explicitly represented as the following integral with respect to the solution of a stationary Fokker-Planck equation (see further details in [12])

$$\lambda =-\alpha +\frac{1}{2}{\int }_{\mathbb{R}}\frac{{\widehat{x}}^2-2}{{\widehat{x}}^2+1}p(x)dx,$$

(31)

where $p(x)$ is the stationary density of the unique invariant probability law of ${\widehat{x}}_t$. By solving numerically (31) for $\alpha =2$, we obtain the exact value of the LE associated to (30) and its original SDAE (29), which is $\lambda =-1.3385$. The accuracy of the $QR$-based methods will be assessed by comparing with this value as reference.

A large number of simulations have been carried out for stepsizes $h=1\times {10}^{-2},9\times {10}^{-3},\dots ,1\times {10}^{-3}$ with T = 1000, 2000,…, 12,000; to obtain computed approximations of the LE truncated at the final time $t_f:=T$, denoted by ${\lambda }_T$. To complete our stochastic numerical analysis of the LE, we have calculated the values of expectation $\mathbb{E}\left[{\lambda }_T\right]$, standard deviation $\sigma \left[{\lambda }_T\right]$, and variance $\mathbb{V}\left[{\lambda }_T\right]$; estimated from 100 independent realizations. Some results are presented in Table A1, Table A2, Table A3 and Table A4, taking T = 6000, 12,000, 20,000, and $h=1\times {10}^{-1},1\times {10}^{-2},1\times {10}^{-3},1\times {10}^{-4}$.

Observe that the time scale presented in Figure 1 has been conveniently adjusted to the range $[0,250]$, in order to show the exponential drop of the LE for the different realizations in the four methods, along the time evolution. While in Figure 2 the time scale has been adjusted to the range $[0,\mathrm{10,000}]$, to better display the convergence of the mean and variance of the LE.

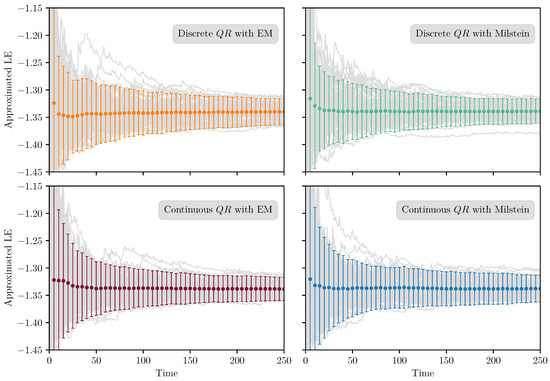
Figure 1. Discrete and continuous $QR$-based approximations of the Lyapunov exponent (LE) corresponding to stochastic differential-algebraic equation (SDAE) (29) via Euler-Maruyama and Milstein integrators, with a stepsize $h=1\times {10}^{-3}$ and $T=250$. The solid circles show mean and the whiskers the $95\%$ confidence intervals of the trajectories.

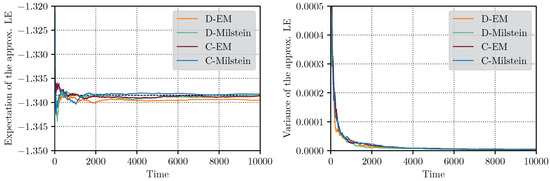
Figure 2. Discrete and continuous $QR$-based approximations of the LE corresponding to SDAE (29) via Euler-Maruyama and Milstein integrators, with a stepsize $h=1\times {10}^{-3}$ and T = 10,000. The black dashed line in the left-hand side subplot shows the analytic value of $\lambda$.

Based on the analytic expression of the LE, given by Equation (31), the LE $\lambda$ can be considered as a deterministic quantity. According to the numerical results obtained from the four $QR$-based methods, the sequences of random variables ${\lambda }_{t_{\ell }}$ reveal a trend towards null variance and convergence to the mean as ℓ tends to infinity. Such evolution can be seen in Figure 1, and more obviously in Figure 2. For all the methods, an exponential decay is illustrated in $\mathbb{E}\left[{\lambda }_{t_{\ell }}\right]$ and $\mathbb{V}\left[{\lambda }_{t_{\ell }}\right]$ as ℓ tends to infinite. This behavior indicates a mean square (m.s.) convergence of those sequences to a degenerate random variable, based on the implication that if ${\lambda }_{t_{\ell }}$ is such that $\mathbb{E}\left[{\lambda }_{t_{\ell }}\right]={\mu }_{\lambda }$, for all ℓ, and $\mathbb{V}\left[{\lambda }_{t_{\ell }}\right]\underset{\ell \to \infty }{\to }0$, then ${\lambda }_{t_{\ell }}\underset{\ell \to \infty }{\overset{\mathrm{m}.\mathrm{s}.}{\to }}{\mu }_{\lambda }$. This means that the limit of ${\lambda }_{t_{\ell }}$ can be interpreted as a deterministic value with probability 1. This enables us to state that the stochastic approximations ${\lambda }_{t_{\ell }}$ converge in m.s. sense to a number (a degenerate random variable), which is expected to represent the LE $\lambda$.

In Figure 3, we compare the relative error of the accuracy of the four numerical methods for different stepsize h and time interval $[0,T]$. From this graphical representation, we observe that continuous methods obtain better results than discrete ones, as expected. We also observe that the Milstein method has, in general, better accuracy than the Euler-Maruyma scheme, since its convergence order is higher, but requies more computational time. This latter fact is evidenced in Figure 4, where a comparison of CPU time (in seconds) is shown for different values of h and T. Here, we observe that all the methods are affected to the same extent by incrementing the simulation interval T, via a logarithmic increment, and by narrowing the stepsizes h, via an exponential increment. A more pronounced difference between the methods should be observed in higher dimensional systems.

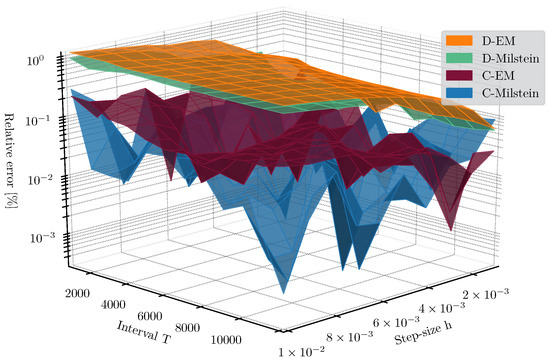
Figure 3. Comparison of relative errors for discrete and continuous $QR$-based approximations of the LE corresponding to SDAE (29) via Euler-Maruyama and Milstein integrators, with a range of stepsizes between $h=1\times {10}^{-2},\dots ,1\times {10}^{-3}$; and with T = 1000, …, 12,000.

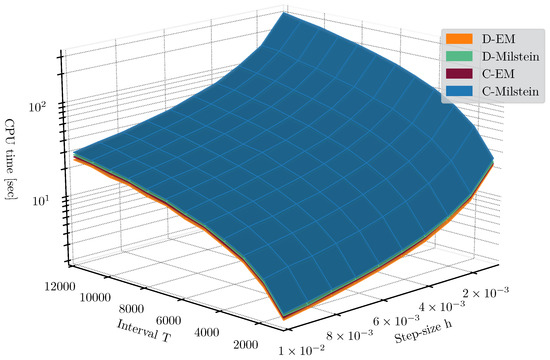
Figure 4. Comparison of the computing-time for discrete and continuous $QR$-based approximations of the LE corresponding to SDAE (29) via Euler-Maruyama and Milstein integrators, with a range of stepsizes between $h=1\times {10}^{-2},\dots ,1\times {10}^{-3}$; and with T = 1000, …, 12,000.

3.4.2. Example 2

In this example, we make use of the Chua’s circuit perturbed by noise, showed in the Figure 5. The Chua’s circuit is a simple electronic system that exhibits chaotic behavior due to its nonlinear negative resistance called Chua’s diode.

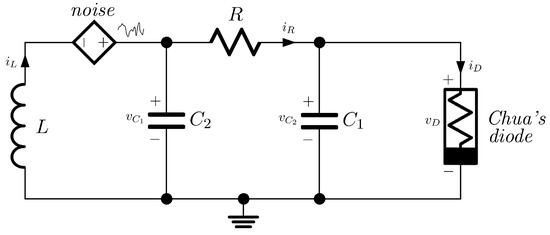
Figure 5. Chua’s circuit diagram.

For the purpose of our example, we consider the circuit is affected by an external noisy interference [30]. The noise, assumed to be coupled to the circuit in its left-hand side loop, is modeled as an additive voltage source, see Figure 5. On the other hand, the nonlinear relation between the voltage $v_D$ with the current $i_D$ in the Chua’s diode is modeled through the continuous cubic polynomial function $i_D:=K_a{v}_D^3-K_b{v}_D$, where $K_a$ and $K_b$ are positive constants, see [31]. By means of Kirchhoff’s circuit laws, the Chua’s circuit can be naturally written as an Itô-type strangeness-free SDAE system, as follows

$$\left[\begin{array}{cccccc}{C}_1& 0& 0& 0& 0& 0\\ 0& C_2& 0& 0& 0& 0\\ 0& 0& L& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]·d\left[\begin{array}{c}{v}_{C_1}\\ v_{C_2}\\ i_L\\ i_R\\ v_D\\ i_D\end{array}\right]=\left[\begin{array}{c}-i_R-i_D\\ i_R+i_L\\ -v_{C_2}\\ v_{C_1}-v_{C_2}-R{i}_R\\ v_{C_1}-v_D\\ K_a{v}_D^3-K_b{v}_D-i_D\end{array}\right]dt+\left[\begin{array}{c}0\\ 0\\ \epsilon \\ 0\\ 0\\ 0\end{array}\right]d{w}_t,$$

(32)

where ${\left[v_{C_1}{v}_{C_2}{i}_L\right]}^T$ are state variables and ${\left[i_R{v}_D{i}_D\right]}^T$ are algebraic variables, the subscript “t” has been omitted in this formulation for simplicity. The noise intensity constant is represented by $\epsilon$. The SDAE (32) can be reduced to its underlying SDE form

$$\begin{array}{cc}\hfill R{C}_{1}d{v}_{C_1}& =[-R{K}_a{v}_{C_1}^3+(R{K}_b-1)v_{C_1}+v_{C_2}]dt,\hfill \\ \hfill R{C}_{2}d{v}_{C_2}& =[v_{C_1}-v_{C_2}+R{i}_L]dt,\hfill \\ \hfill Ld{i}_L& =-v_{C_2}dt+\epsilon d{w}_t.\hfill \end{array}$$

(33)

For the numerical simulations, we have chosen as constants $R=1.00$; $C_1=0.0915$; $C_2=1.00$; $L=0.0714$; $K_a=0.0625$; $K_b=1.00$. Additionally, we have assigned the value $\epsilon =0.25$ to the noise intensity constant. Under these values the Chua’s system still tends to evolve around its characteristic double scroll attractor, but in a different way in comparison to the deterministic case (i.e., with $\epsilon =0.00$). The system presents a stochastic bifurcation, specifically a phenomenological bifurcation (or P-bifurcation), because of the qualitative changes in the stationary probability distributions of the system’s states [12,32]. Despite the qualitative changes in the Chua’s system due to the stochastic perturbation, its chaotic behavior remains, as can be seen in Figure 6.

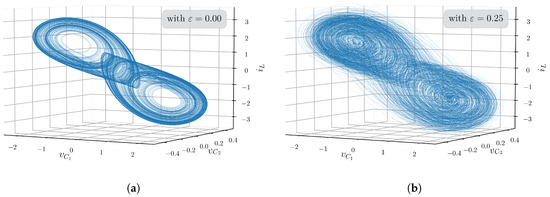
Figure 6. Chua’s system phase-portraits in chaotic regime, (a) without stochastic perturbation; (b) with stochastic perturbation.

Because the positiveness of the largest Lyapunov exponent (LLE) in a nonlinear dynamical is usually an indication (although not sufficient) that the system is chaotic, we make use of the $QR$-based methods to compute the LEs in order to test for the presence of chaos in the dynamics of the noise-driven oscillator (32). Furthermore, it is known the sum of all LEs allows for identifying dissipative dynamical systems. If $\mathcal{S}:={\sum }_{i=1}^d{\lambda }_i$ in negative, the system is dissipave [25].

Unfortunately, is unfeasible to analytically obtain LEs for the present example, doing a precision test of the methods impossible to perform. Therefore, the assessment of the $QR$-based techniques this time is rather focused on the observation of consistent, time-convergent, and homogeneous computed LEs for all of the numerical methods. In addition, the preservation of the dissipative characteristic of the system for all the simulations through the computed value $\mathcal{S}$ is verified as well.

Figure 7 shows the time evolution computed LEs by using the four $QR$-based methods. The simulation was carried out with the stepsize $h=1\times {10}^{-4}$ and the interval $T=6000$. It can be seen the convergence of each LE for a single realization. We additionally present the numerical values of $\mathcal{S}$. Here, the neganiveness of $\mathcal{S}$ evidences that, in our example, the stochastic Chua’s circuit is a dissipative system.

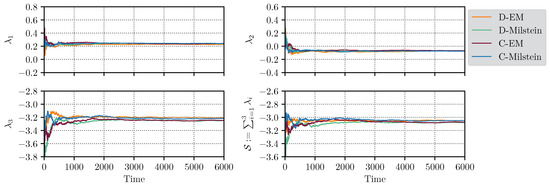
Figure 7. Time evolution of the computed LEs in stochastic Chua’s system (32) using the four $QR$-based methods for a stepsize $h=1\times {10}^{-4}$ and an interval $T=6000$.

As it can be seen, the computed LEs of the Chua’s system (32), and hence the sum of LEs $\mathcal{S}$ as well, exhibit a satisfactory convergence along the time even with a single realization. This is a suitable indicator of the numerical robustness and, a good performance of the proposed $QR$-based methods when they are implemented in complex situations, such as the positiveness of the computed LLE. Even though in Figure 7 we present results only for a stepsize $h=1\times {10}^{-4}$, similar satisfactory results can be obtained for wider stepsizes. In Table A5, we collect the numerical results corresponding to $h=1\times {10}^{-3},5\times {10}^{-4},1\times {10}^{-4}$.

4. Application of LEs to Power Systems Stability Analysis

The concept of stability (based on Lyapunov exponents) in power systems is, in essence, the same as that for a general dynamical system. In the literature, power system stability is defined as the stability to regain an equilibrium state after being subjected to physical disturbances [33,34]. Such equilibrium is characterized through three significant quantities during the power system operation: angles of nodal voltages, frequency, and nodal voltage magnitudes. Based on this triplet, there is an entire classification proposed by the Institute of Electrical and Electronics Engineers (IEEE) and the International Council on Large Electric Systems (CIGRE) in [34], which is illustrated in Figure 8. The test cases presented in this paper are oriented to evaluate the angle and voltage stability of power systems subjected to small or large disturbances. Studies considering small disturbances are commonly known as small-signal stability assessment (SSSA). Here, linear stability analysis via eigenvalues has been one of the traditional analysis tools to predict the degree of stability of the power system [33,35]. However, eigenvalue analysis is limited to linear time-invariant systems or systems close to a stationary solution. When time-varying systems are tested, as is the case of systems subjected to stochastic disturbances, then eigenvalue analysis is no longer applicable. On the other hand, the stability analysis of power systems affected by large disturbances, known as transient stability assessment, is mainly performed with verification strategies that are based on time-domain integration [34,36].

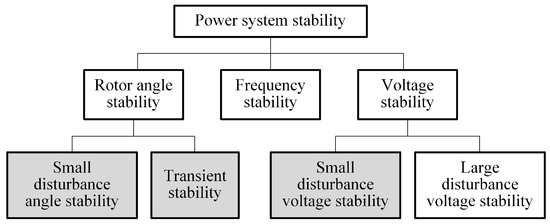
Figure 8. IEEE/CIGRE Power systems stability classification [34].

Because the concept of LEs is based on the trajectories of the dynamical systems, the method is an interesting measure of dynamic stability for power systems under stochastic disturbances in general. Accordingly, testing asymptotic stability of power systems via LEs has become an attractive approach for the two areas mentioned before, namely, the SSSA of rotor angles and voltages, by using the linearized set of SDAEs which model the system [37,38]; and strategies for the rotor angles via transient analysis using the nonlinear SDAE system and its variational equation [39,40]. For both cases, asymptotic stability is checked via approximations of the LLE of the system. In particular, a negative LLE indicates that the dynamics of the system is asymptotically stable. In the next subsections, test cases are presented that illustrate for strangenss-free SDAE systems the negativity of the LLE.

4.1. Modeling Power Systems through SDAEs

Under the assumption of deterministic dynamic behavior, power systems are typically modelled via a system of quasi-linear DAEs with partitioned variables, see [33,35], of the form

$$\begin{array}{cc}\hfill {\mathit{E}}_{11}d{\mathit{x}}_t^{D_1}& ={\mathit{f}}_0^{D_1}({\mathit{x}}_t^{D_1},{\mathit{x}}_t^A)dt,\hfill \end{array}$$

(34a)

$$\begin{array}{cc}\hfill 0& ={\mathit{f}}_0^A({\mathit{x}}_t^{D_1},{\mathit{x}}_t^A),\hfill \end{array}$$

(34b)

where ${\mathit{E}}_{11}\in {\mathbb{R}}^{d_1\times d_1}$ is a diagonal block matrix, ${\mathit{f}}_0^{D_1}\in {\mathcal{C}}^1({\mathbb{R}}^{d_1+a},{\mathbb{R}}^{d_1})$, ${\mathit{f}}_0^A\in {\mathcal{C}}^1({\mathbb{R}}^{d_1+a},{\mathbb{R}}^a)$, ${\mathit{x}}_t^{D_1}\in {\mathbb{R}}^{d_1}$ are the dynamic state variables, and ${\mathit{x}}_t^A\in {\mathbb{R}}^a$ are the algebraic state variables and we set $n_1=d_1+a$. The DAE system (34) is strangeness-free (or differentiation index-1).

The dynamic behavior of synchronous machines, system controllers, power converters, transmission lines, or power loads are adequately represented through such a DAE formulation. However, in current real world systems, the dynamic behavior of power systems is affected by disturbances of a stochastic nature, such as renewable stochastic power generation, rotor vibrations in synchronous machines, stochastic variations of loads, electromagnetic transients, or perturbations originated by the measurement errors of control devices, see [41]. Such disturbances can be modeled through Itô SDEs of the form

$$d{\mathit{x}}_t^{D_2}={\mathit{f}}_0^{D_2}({\mathit{x}}_t^{D_1},{\mathit{x}}_t^{D_2},{\mathit{x}}_t^A)dt+{\mathit{f}}_1^{D_2}({\mathit{x}}_t^{D_1},{\mathit{x}}_t^{D_2},{\mathit{x}}_t^A)d{w}_t.$$

(35)

Here, ${\mathit{f}}_0^{D_2}\in {\mathcal{C}}^1({\mathbb{R}}^{d_2+a},{\mathbb{R}}^{d_2})$ is the drift, ${\mathit{f}}_1^{D_2}\in {\mathcal{C}}^2({\mathbb{R}}^{d_2+a},{\mathbb{R}}^a)$ is the diffusion, ${\mathit{x}}_t^{D_2}\in {\mathbb{R}}^{d_2}$ are the stochastic variables, and $w_t$ is the Wiener process. By combining (34) and (35), and assuming that ${\mathit{x}}_t^{D_2}$ perturbs (34a) and (34b), we obtain a strangeness-free SDAE system of the form

$$\begin{array}{cc}\hfill {\mathit{E}}_{1}d{\mathit{x}}_t^{D_1}& ={\mathit{f}}_0^{D_1}({\mathit{x}}_t^{D_1},{\mathit{x}}_t^{D_2},{\mathit{x}}_t^A)dt,\hfill \end{array}$$

(36a)

$$\begin{array}{cc}\hfill d{\mathit{x}}_t^{D_2}& ={\mathit{f}}_0^{D_2}({\mathit{x}}_t^{D_1},{\mathit{x}}_t^{D_2},{\mathit{x}}_t^A)dt+{\mathit{f}}_1^{D_2}({\mathit{x}}_t^{D_1},{\mathit{x}}_t^{D_2},{\mathit{x}}_t^A)d{w}_t,\hfill \end{array}$$

(36b)

$$\begin{array}{cc}\hfill 0& ={\mathit{f}}_0^A({\mathit{x}}_t^{D_1},{\mathit{x}}_t^{D_2},{\mathit{x}}_t^A),\hfill \end{array}$$

(36c)

or in simplified notation, as

$$\mathit{E}d{\mathit{x}}_t={\mathit{f}}_0({\mathit{x}}_t)dt+{\mathit{f}}_1({\mathit{x}}_t)d{w}_t,{\mathit{x}}_{t_0}={\mathit{x}}_0,$$

(37)

with

$$\mathit{E}:=\left[\begin{array}{ccc}{\mathit{E}}_{11}& 0& 0\\ 0& {\mathit{I}}_{d_2}& 0\\ 0& 0& 0\end{array}\right],{\mathit{x}}_t:=\left[\begin{array}{c}{\mathit{x}}_t^{D_1}\\ {\mathit{x}}_t^{D_2}\\ {\mathit{x}}_t^A\end{array}\right],$$

drift ${\mathit{f}}_0\in {\mathcal{C}}^1({\mathbb{R}}^n,{\mathbb{R}}^n)$, and diffusion ${\mathit{f}}_1\in {\mathcal{C}}^2({\mathbb{R}}^n,{\mathbb{R}}^n)$, where $n=d_1+d_2+a$.

The study-cases that are presented below are formulated as the form (36). An alternative approach for including the stochastic disturbances is to directly implement the Wiener process in the underlying ODE of the system, turning them into SDEs (see [23,42] for examples).

4.2. Modeling Stochastic Perturbations

In this subsection, we discuss the modeling of stochastic variations via SDEs. We employ the well known mean-reverting process termed Ornstein-Uhlenbeck (OU) process [41,43]. The SDE that defines the OU process has the form

$$d{\eta }_t=\alpha (\mu -{\eta }_t)dt+\beta d{w}_t,{\eta }_{t_0}={\eta }_0,t\in \mathbb{I},$$

(38)

where $\alpha ,\mu ,\beta \in {\mathbb{R}}^{+}$. The OU process is a stationary autocorrelated Gaussian diffusion process distributed as $\mathcal{N}(\mu ,{\beta }^2/2\alpha )$. Another mean-reverting choice, similar to the OU process would be the Cox-Ingersoll-Ross (CIR) process, whose realizations are always nonnegative, in fact, it is a sum of squared OU process [44].

It is usually recommended to ensure the boundedness of the stochastic variations for the numerical implementations. In this regard, suitable resources are odd trigonometric functions, such as a sin or arctan, to guarantee boundedness. For example, if from (38) we generate a process with a normal distribution $\mathcal{N}(\mu ,{\sigma }^2)$, for $\mu =0$ and ${\sigma }^2=0.16$, this value of variance enables us to generate a mean-reverting stochastic trajectory, whose confidence interval of $95\%$ ($\pm 2\sigma$) is inside the threshold of $\pm 1$. Subsequently, through the functions

$$\xi ({\eta }_t)=sin{\eta }_t,\mathrm{or}\chi ({\eta }_t)=\frac{2}{\pi }arctan{\eta }_t,$$

(39)

we obtain a bounded stochastic variation inside the interval $[-1,1]$, and the OU SDEs, which generate the stochastic variations, are represented by (36b).

To couple the parameters of the system in (36a) and (36c) with a bounded stochastic disturbance, we use

$$p({\eta }_t)=p_0+\rho \xi ({\eta }_t),$$

where $p_0$ is a constant parameter, ${\eta }_t$ is the stochastic process that describes the variations of the parameter, and $\rho \in {\mathbb{R}}^{+}$ is a factor that controls the magnitude of the perturbation.

4.3. Test Cases

In this subsection, we present results of our implementation of the $QR$-based methods for the calculation of LEs at the hand of several test cases of power systems represented by strangeness-free SDAEs models of so-called single-machine-infinite-bus (SMIB) systems. This simplified model is frequently used in the area of power systems in order to understand the local dynamic behavior of a specific machine connected to a complex power network. The SMIB consists of a synchronous generator connected through a transmission line to a bus with a fixed bus voltage magnitude and angle, called infinite bus, which represents the grid. A diagram of the system is shown in Figure 9.

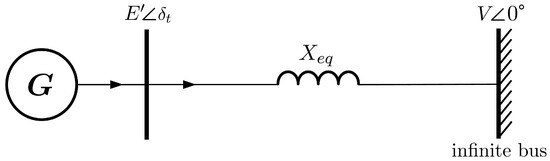
Figure 9. Single-machine infinite-bus (SMIB) scheme.

In each test case, we consider a different type of disturbance. For Case 1, the disturbance is a stochastic load connected to the system. In Case 2, the disturbance is due to noise caused by a measurement error in a transducer of the machine control system. In both cases, the maximum disturbance that the system can admit without loosing stability is analyzed, as well as the effect (positive or negative) of the disturbance for the system in the stable region. The whole SMIB system, i.e., the synchronous machine, system constraints, and stochastic disturbances; are modeled by a strangeness-free SDAE system. The dimension of this system is mainly defined by the type of model used in the synchronous machine; we use a classical model and a flux-decay model, see [33,35,36,45] for detailed descriptions.

4.3.1. Case 1: SMIB with Stochastic Load

In this test case, we make use of the LEs to assess the impact of stochastic disturbances associated with an active power load, over the rotor angle stability of a synchronous generator. Both the machine and load are connected to the same bus, and this bus, in turn, is linked to the grid through a transmission line. This kind of SMIB model is typically used to analyze the effects of renewable energy sources, or aggregated random power consumption, see Figure 10. For this version of SMIB system called classical model, the dynamic behavior of the synchronous machine is represented by the swing equations where the rotor angle ${\delta }_t$ and the rotor speed ${\omega }_t$ are the state variables, see [35,36]. The algebraic constraint in the system is given by the active power balance, expressed in terms of $P_m$ the mechanical power, $P_e$ the electrical power, and $P_L$ the constant power consumed by the load. A stochastic process ${\eta }_t$ is modeled by an OU SDE. We consider that $\rho {\eta }_t$ is the stochastic component of power consumption that perturbs additively the active power balance of the system, where $\rho$ is the size of the disturbance. This leads to the system

$$\begin{array}{cc}\hfill d{\delta }_t& =[{\omega }_t-{\omega }_s]dt,\hfill \end{array}$$

(40a)

$$\begin{array}{cc}\hfill 2Hd{\omega }_t& =[P_m-P_e-K_D({\omega }_t-{\omega }_s)]dt,\hfill \end{array}$$

(40b)

$$\begin{array}{cc}\hfill {\eta }_t& =-\alpha {\eta }_{t}dt+\beta d{w}_t,\hfill \end{array}$$

(40c)

$$\begin{array}{cc}\hfill 0& =\frac{E^{\prime }V}{X_{eq}}cos{\delta }_t+(P_L+\rho {\eta }_t)-P_e.\hfill \end{array}$$

(40d)

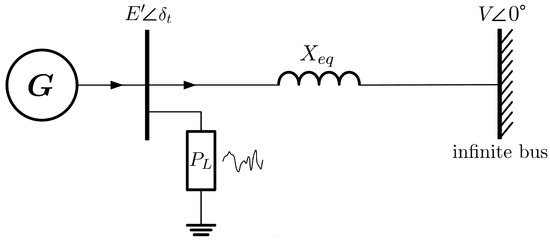
Figure 10. Scheme of a SMIB system with a stochastic load used in Test Case 1.

By computing the LEs of this SDAE system and checking the LLE, we can determine the maximal perturbation size $\rho$ (via successive increments of $\rho$) admitted by the SMIB system before loosing rotor angle stability. The numerical tests are performed for the values $P_m=0.8$; $P_L=0.3$; $X_{eq}=0.8$; $H=3.5$; $K_D=0.4$; ${\omega }_s=2\pi 50$; $V=1.0$; $E^{\prime }=1.05$; $\alpha =1.0$; $\beta =0.4$. Most of the values are expressed in the per-unit system (pu) [45]. The $QR$ methods are executed with step size $h=1\times {10}^{-3}$ and a simulation time T = 20,000. Figure 11 displays the computed LLE utilizing the four $QR$-based methods for incremental disturbance sizes $\rho =\mathrm{0.00,0.05},\dots ,2.00$. As expected, at $\rho =0.0$ when the system is not affected by a stochastic disturbance, i.e., the system is deterministic, the computed LEs match closely with the real parts of the eigenvalues obtained from the Jacobian matrix of the linearization of (40). When increasing $\rho$, all of the methods reveal the same monotonically increasing behavior of the calculated value of the LLE towards the unstable region. First, there is a slow increase for $0.00<\rho <0.60$, and then an abrupt increase of the LLE in the interval $0.60<\rho <0.75$. In the interval $0.75<\rho <1.20$, even though the LLE has not yet reached the instability region, for this particular case the characteristics, such as a low damping coefficient and the presence of the stochastic disturbance, provokes a behavior in the system called pole slipping. This is, in a certain sense, a different kind of instability because the system looses synchronism as it reaches another equilibrium point near another attractor, see ([35], Section 5.8) for further details. The different aspects of this study-case are better illustrated with the phase portraits in Figure 12. The charts display the trajectories of the dynamical system (40) projected onto the ${\delta }_t-{\omega }_t/{\omega }_s$ plane for the disturbance sizes $\rho =0.0,0.3,0.7,1.0,1.5$. Deatiled numerical data for this case are presented in Table A6.

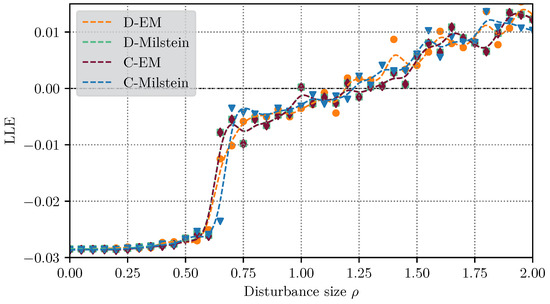
Figure 11. Largest Lyapunov exponent (LLE) considering different disturbance sizes $\rho$ for the SMIB Test Case 1, tested with four $QR$-based methods.

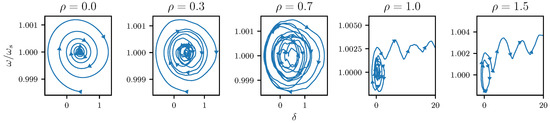
Figure 12. Phase portraits of the system (40) considering different disturbance sizes $\rho$ for the SMIB Test Case 1.

This test case shows the large potential of using LEs as an indicator of instability for nonlinear power systems. These could also be used in multi-machine study cases, where, however, the computational complexity has to be reduced, e.g., by model reduction.

4.3.2. Case 2: SMIB with Regulator Perturbed by Noise

In this subsection, we consider an SMIB system with a synchronous machine described by a third-order flux-decay model. Here, in addition to the rotor angle ${\delta }_t$ and the rotor speed ${\omega }_t$ associated to the swing equations, the system includes the effect of the field flux ${\psi }_{fd}$ described by the field circuit dynamic equations and constraints. In this model, the machine is equipped with an automatic voltage regulator (AVR) to keep the generator output voltage magnitude in a desirable range, and a power system stabilizer (PSS) to damp out low-frequency oscillations, see Figure 13. The AVR and PSS add to the system three more state variables $v_1$, $v_2$, and $v_s$; together with their corresponding DAEs, which describe the dynamic behavior and constraints of the controllers into the SMIB system. The resulting model is a nonlinear system of strangeness-free DAEs. We use the LEs to analyze the system stability at a specific operation point in the state-space when it is subjected to small-disturbances. Using the small-signal stability assessment (SSSA), the set of DAEs that describes the dynamics of the power system is linearized around the desired operating point. The final result is a linear DAE system. A comprehensive explanation of this model, its linearization, and reduction to an underlying ODE system can be found in [33] (ch. 12). We consider a disturbance of stochastic nature entering in the exciter block of the AVR as an error of the reference signal [33,37], by adding the stochastic variable $\eta$ to $v_1$ in Equation (41c). Resolving the algebraic constraints leads to the linearized system of SDEs

$$\begin{array}{cc}\hfill d\Delta \delta & ={\omega }_s\Delta \omega dt,\hfill \end{array}$$

(41a)

$$\begin{array}{cc}\hfill 2Hd\Delta \omega & =\left[-K_1\Delta \delta -K_D\Delta \omega -K_2\Delta {\psi }_{fd}+\Delta T_m\right]dt,\hfill \end{array}$$

(41b)

$$\begin{array}{cc}\hfill T_{3}d\Delta {\psi }_{fd}=& \left[-K_3{K}_4\Delta \delta -(1+K_3{K}_6{K}_A)\Delta {\psi }_{fd}-K_3{K}_A(1+\rho \eta )\Delta v_1\right.\hfill \\ & \left.+K_3{K}_A\Delta v_s\right]dt,\hfill \end{array}$$

(41c)

$$\begin{array}{cc}\hfill T_{R}d\Delta v_1& =\left[-K_5\Delta \delta +K_6\Delta {\psi }_{fd}-\Delta v_1\right]dt,\hfill \end{array}$$

(41d)

$$\begin{array}{cc}\hfill d\Delta v_2& =\left[-K_1{K}_{ST}\Delta \delta -K_D{K}_{ST}\Delta \omega -K_2{K}_{ST}\Delta {\psi }_{fd}-\frac{1}{T_W}\Delta v_2+\frac{K_{ST}}{2H}\Delta T_m\right]dt,\hfill \end{array}$$

(41e)

$$\begin{array}{cc}\hfill T_{2}d\Delta v_s=& \left[-K_1{K}_{ST}{T}_1\Delta \delta -K_D{K}_{ST}{T}_1\Delta \omega -K_2{K}_{ST}{T}_1\Delta {\psi }_{fd}+\left(\frac{T_1}{T_W}+1\right)\Delta v_2\right.\hfill \\ & \left.-\frac{1}{T_2}\Delta v_s+\frac{K_{ST}{T}_1}{2H}\Delta T_m\right]dt,\hfill \end{array}$$

(41f)

$$\begin{array}{cc}\hfill d\eta & =-\alpha \eta dt+\beta dw,\hfill \end{array}$$

(41g)

where $\Delta \delta ,\Delta \omega ,\Delta {\psi }_{fd},\Delta v_1,\Delta v_2,\Delta v_s,\eta$ are the state variables of the linear underlying SDE system (in the same way than Example 2 in Section 3.4.2, the subscript t has been omitted in the formulation for simplicity). Once again, the stochastic perturbation is generated via an OU SDE, and the size of the perturbation is controlled by the parameter $\rho$. The numerical analysis is done for the values ${\omega }_s=2\pi 60$; $H=3.0$; $K_1=1.591$; $K_2=1.50$; $K_D=0.0$; $K_3=0.333$; $K_4=1.8$; $K_5=-0.12$; $K_6=0.3$; $K_A=200.0$; $T_R=0.02$; $K_{ST}=9.5$; $T_1=0.154$; $T_2=0.033$; $T_3=1.91$; $T_W=1.4$; $\alpha =1.0$; $\beta =0.4$; $\Delta T_m=0.0$.

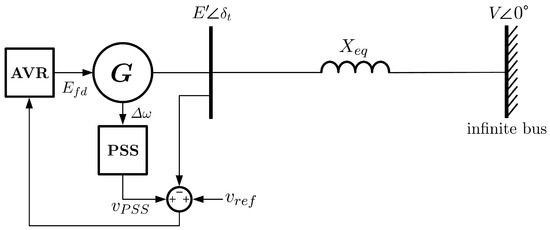
Figure 13. SMIB system scheme equipped with automatic voltage regulator (AVR) and power system stabilizer (PSS), corresponding to Test Case 2.

Based on the analysis of Section 3.4.1, we only consider the continuous Euler-Maruyama $QR$-based method. The results of computing the LLE of the SMIB system for incremental values of the perturbation size $\rho$, are presented graphically in Figure 14. The values of the LLE when increasing perturbation size $\rho$ clearly mark four defined intervals. In the leftmost interval with $0.00<\rho <0.40$, the calculated LLE is practically constant and equal to the real part of the right-most eigenvalue from the deterministic system. In this region, there is no impact of the disturbance on the system stability. In the interval $0.40<\rho <1.30$, a curious situation occurs, as the size of the disturbance increases, the distance from the LLE to the positive region increases, in other words, the noise improves the stability of the system. In the interval $1.30<\rho <2.60$, the situation changes completely, and the LLE converges to zero. Finally, from $\rho \approx 2.60$ onward, the system is unstable. Table A7 shows the numerical values of this test case.

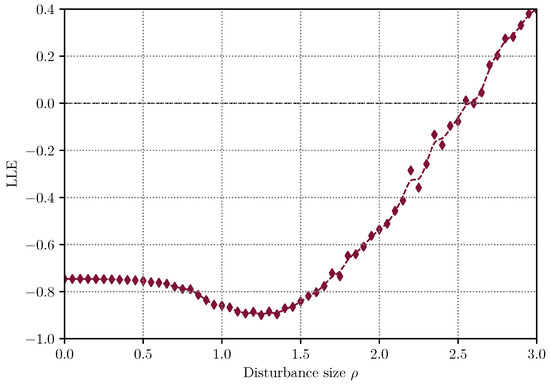
Figure 14. Computed LLE for the dimension 7 SMIB system of Test Case 2, considering different disturbance sizes and using the continuous Euler-Maruyama $QR$-based method.

Finally, we have evaluated the computing-times for this 7-dimensional test case. The results are shown in Figure 15. Although the computational cost for all method is similar for the different methods as a factor of the step sizes h and time interval $[0,T]$, the computational costs strongly increase.

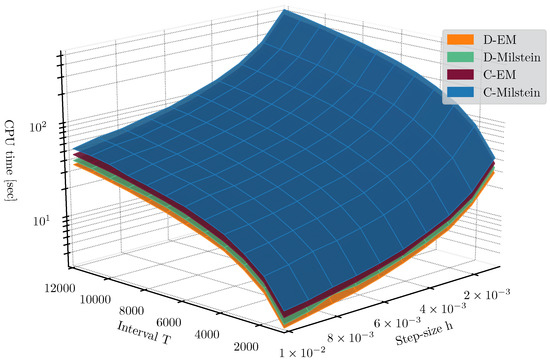
Figure 15. Computing-time comparison of LE calculation for the dimension 7 SMIB Test Case 2. Comparison performed for the four $QR$-based methods in a range of step sizes between $h=[1\times {10}^{-2},1\times {10}^{-3}]$ and with $T=[1000,\mathrm{12,000}]$.

Even though the present work has been oriented for testing the asymptotic stability of transmission power systems under uncertainty through the computation of LEs, as shown in the last two study-cases, the numerical $QR$-based techniques for computing the LEs in stochastic dynamical systems can also be a suitable assessment tool in a vast range of fields, such as physics, chemistry, biology, sociology, economics, etc. Moreover, beyond its use as a tool for the asymptotic stability assessment, LEs are useful for other quantitative studies, such as the characterization of synchronization or chaos.

5. Conclusions

We have revisited the theory of strangeness-free SDAE systems, as well as the concepts of LEs associated with the RDEs generated via such SDAEs. We have adapted and implemented stochastic versions of continuous and discrete $QR$-based methods to calculate approximations of the LEs, and assessed them by using Euler-Maruyama and Milstein schemes over the corresponding underlying SDE. The results obtained from our numerical experiments illustrate the approximations of the corresponding LE converge to degenerate random variables, i.e., the LE can be interpreted as a deterministic value, since in the limit the variance of the approximations tends to zero. Both $QR$-based method provide reliable results, but, in general, continuous methods provide better accuracy than the discrete counterpart at the expenses of higher computational cost and higher memory requirement. We have illustrated the $QR$-based methods for SMIB power system problems and shown the usefulness of the LEs as a stability indicator for the rotor angle and voltage stability analysis of power systems affected by bounded stochastic disturbances.

As future work, we suggest the use of discretization schemes for SDAEs in order to directly apply the numerical integration to the SDAE system. Furthermore, methods for computing the LEs based on Singular Value Decompositions, a combination with model reduction, and a careful comparison with $QR$-based methods would be of interest. Concerning to the applications to power systems and dynamical network systems in general, stability assessment of large-scale cases are remarkable works to be performed. Although the aim of this paper has been to develop reliable computational methods to compute the LEs associated to SDAEs with no correlated noises modeling power systems, as future work it would be interesting to extend our analysis to SDAEs with correlated noises, including their applications to other engineering problems.