Systematic Review of Geometrical Approaches and Analytical Integration for Chen’s System

Abstract

The main goal of this paper is to present an analytical integration in connection with the geometrical frame given by the Hamilton–Poisson formulation of a specific case of Chen’s system. In this special case we construct an analytic approximate solution using the Multistage Optimal Homotopy Asymptotic Method (MOHAM). Numerical simulations are also presented in order to make a comparison between the analytic approximate solution and the corresponding numerical solution.

1. Introduction

In the last decades, the study of chaotic systems became an important part of the study of dynamical systems due to their important applications in electrical engineering, medicine or economics. The Chen system [1] was first proposed in 1999, and it has collected a long list of important studies, especially about its chaotic behavior, synchronization issues (see [2]), and the possible prediction of chaos but also for analyzing stochastic cycles using the stochastic sensitivity function (SSF) technique (see [3] for details). The goal of this paper is to present an analytical integration in connection with the geometrical frame proposed in [4].

Let us briefly recall our last results regarding the Poisson structure of Chen’s system [1], which is given by the following differential equations on ${\mathbf{R}}^3:$

$$\left\{\begin{array}{c}\stackrel{.}{\mathrm{x}}=a\left(y-x\right)\hfill \\ \stackrel{.}{\mathrm{y}}=\left(c-a\right)x-xz+cy,\hfill \\ \stackrel{.}{\mathrm{z}}=-bz+xy\hfill \end{array}\right.$$

(1)

where $a,b,$ and c are real parameters. The system is chaotic when $a=35,b=3,$ and $c=28$ ([5]).

If $a=0$ and $b=c$, the system admits a Hamilton–Poisson realization, as we have proven in [6]. In the same paper, the Casimir functions were found and some stability problems were discussed. Numerical integration was performed using symplectic or non-symplectic integrators (Lie–Trotter integrator and Kahan’s integrator).

If the Hamiltonian function (H) and the Casimir function (C) are known, then the phase curves of the dynamical system are the intersections of the surfaces $H=cst$ and $C=cst$.

On the other hand, if $b\ne c,$ the problem of finding a Hamilton–Poisson realization is still an open one.

In all that follows we will focus on the special case $a\in R^{*},b=c=0$.

If $a\in R^{*},b=c=0$, System (1) becomes:

$$\left\{\begin{array}{c}\dot{x}=a(y-x)\hfill \\ \dot{y}=-ax-xz\hfill \\ \dot{z}=xy\hfill \end{array}\right..$$

(2)

In this specific case, the Hamiltonian function is presented in [6] but finding the Casimir functions remains an open problem. Therefore, the exact solution written as an intersection between the surfaces $H=cst$ and $C=cst$ is impossible.

Therefore, in this case we construct an analytic approximate solution using the Multistage Optimal Homotopy Asymptotic Method (MOHAM), denoted by MOHAM solution.

In the literature, a class of degenerate differential equations in Banach space with unbounded operators possessing the converging properties was isolated and can be found in [2,3,7].

2. Analytic Approximate Solutions of the Chen System (2) Using the Multistage Optimal Homotopy Asymptotic Method

In order to find the analytical approximate solutions of the nonlinear differential system (2) with the boundary conditions

$$\begin{array}{c}x\left(0\right)=A_1,y\left(0\right)=A_2,z\left(0\right)=A_3,A_1,A_2,A_3\in \mathbf{R},\hfill \end{array}$$

(3)

we will use the Multistage Optimal Homotopy Asymptotic Method (MOHAM) [8], as follows:

(a)

We divide the theoretical interval $[t_0,T]$ into some subintervals, such as $[t_0,t_1),\dots ,[t_{j-1},t_j),\dots ,$ where $t_0=0$ and $t_j=T$;

(b)

The approximate analytic solution $\overline{F}\left(t\right)$ has the form

$$\overline{F}\left(t\right)=\left\{\begin{array}{cccc}{F}^{\left(1\right)}\left(t\right)\hfill & ,\hfill & t\in I^{\left(1\right)}:=[t_0,t_1]\hfill & \\ F^{\left(2\right)}\left(t\right)\hfill & ,\hfill & t\in I^{\left(2\right)}:=[t_1,t_2]\hfill & \\ \dots \dots \dots \hfill & \hfill & \hfill & ,\hfill \\ F^{\left(k\right)}\left(t\right)\hfill & ,\hfill & t\in I^{\left(k\right)}:=[t_{k-1},t_k]\hfill & \\ \dots \dots \dots \hfill & \end{array}\right.$$

(4)

with $F^{\left(k\right)}\left(t\right)=\overline{F}{|}_{[t_{k-1},t_k]}\left(t\right)$, $k\ge 1$, and $\overline{F}\left(t\right)$ is continuous differentiable function;

(c)

We apply the Optimal Homotopy Asymptotic Method (OHAM) [9,10] to find the first-order approximate solutions $F^{\left(k\right)}\left(t\right)$, $k\ge 1$ using only one iteration.

The initial approximation in each interval $[t_{j-1},t_j)$, $j\in {\mathbf{N}}^{*}$ is provided by the solution from the previous interval, so the analytical approximate solutions can be obtained for equations of the general form:

$$\begin{array}{c}\hfill \mathcal{L}\left(F\left(t\right)\right)+\mathcal{N}\left(F\left(t\right)\right)=0,\end{array}$$

(5)

subject to the initial conditions (3), where $\mathcal{L}$ is an arbitrary linear operator and $\mathcal{N}$ is the corresponding nonlinear one.

Let the fixed interval be $[0,t_1]$.

Now, choosing the linear operators $\mathcal{L}$ as:

$$\begin{array}{c}\mathcal{L}\left[x\left(t\right)\right]=\dot{x}+Kx\left(t\right)-\left[-{\omega }_0{A}_{1}sin\left({\omega }_{0}t\right)+{\omega }_0{a}_{2}cos\left({\omega }_{0}t\right)\right]·e^{-Kt},\hfill \\ \mathcal{L}\left[y\left(t\right)\right]=\dot{y}+Ky\left(t\right)-\left[-{\omega }_0{B}_{1}sin\left({\omega }_{0}t\right)+{\omega }_0{a}_{4}cos\left({\omega }_{0}t\right)\right]·e^{-Kt},\hfill \\ \mathcal{L}\left[z\left(t\right)\right]=\dot{z}+Kz\left(t\right)-\left[-{\omega }_0{C}_{1}sin\left({\omega }_{0}t\right)+{\omega }_0{a}_{6}cos\left({\omega }_{0}t\right)\right]·e^{-Kt},\hfill \end{array}$$

(6)

and the nonlinear operators $\mathcal{N}\left[F\left(t\right)\right]$ as:

$$\begin{array}{c}\mathcal{N}\left[x\left(t\right)\right]=-Kx\left(t\right)+\left[-{\omega }_0{A}_{1}sin\left({\omega }_{0}t\right)+{\omega }_0{a}_{2}cos\left({\omega }_{0}t\right)\right]·e^{-Kt}-a·(y\left(t\right)-x\left(t\right)),\hfill \\ \mathcal{N}\left[y\left(t\right)\right]=-Ky\left(t\right)+\left[-{\omega }_0{A}_{2}sin\left({\omega }_{0}t\right)+{\omega }_0{a}_{4}cos\left({\omega }_{0}t\right)\right]·e^{-Kt}+a·x\left(t\right)+x\left(t\right)z\left(t\right),\hfill \\ \mathcal{N}\left[z\left(t\right)\right]=-Kz\left(t\right)-\left[-{\omega }_0{A}_{3}sin\left({\omega }_{0}t\right)+{\omega }_0{a}_{6}cos\left({\omega }_{0}t\right)\right]·e^{-Kt}-x\left(t\right)y\left(t\right),\hfill \end{array}$$

(7)

$K,a_2,a_4,a_6,{\omega }_0\in \mathbf{R}$ are unknown parameters.

If $p\in [0,1]$ is the embedding parameter and $H(t,B_j,C_j)\ne 0)$ is an auxiliary convergence-control function, depending on the variable t and the parameters $B_1,B_2,\dots ,B_{s_1}$, $C_1,C_2,\dots ,C_{s_2}$, then by means of the homotopy relation [9,11], given by:

$$\begin{array}{c}\hfill \mathcal{H}\left[\mathcal{L}\left(F(t,p)\right),H(t,B_j,C_j),\mathcal{N}\left(F(t,p)\right)\right]=\mathcal{L}\left(F_0\left(t\right)\right)+\\ \hfill +p\left[\mathcal{L}\left(F_1(t,B_j,C_j)\right)-H(t,B_j,C_j)\mathcal{N}\left(F_0\left(t\right)\right)\right]\equiv 0,\end{array}$$

(8)

we construct the functions F of the form:

$$\begin{array}{c}\hfill F(t,p)=F_0\left(t\right)+p{F}_1(t,B_j,C_j).\end{array}$$

(9)

Now, using the linear operators given by Equation (6), the solutions of the equation

$$\begin{array}{c}\hfill \mathcal{L}\left(F_0\left(t\right)\right)=0,\mathcal{B}\left(F_0\left(t\right),\frac{d{F}_0\left(t\right)}{dt}\right)=0,\end{array}$$

(10)

for the initial approximations $F_0$ are:

$$\begin{array}{c}{x}_0\left(t\right)=\left[A_{1}cos\left({\omega }_{0}t\right)+a_{2}sin\left({\omega }_{0}t\right)\right]·e^{-Kt},\hfill \\ y_0\left(t\right)=\left[A_{2}cos\left({\omega }_{0}t\right)+a_{4}sin\left({\omega }_{0}t\right)\right]·e^{-Kt},\hfill \\ z_0\left(t\right)=\left[A_{3}cos\left({\omega }_{0}t\right)+a_{6}sin\left({\omega }_{0}t\right)\right]·e^{-Kt}.\hfill \end{array}$$

(11)

Additionally, to compute $F_1(t,C_i)$ we solve the equation

$$\begin{array}{c}\hfill \begin{array}{c}\mathcal{L}\left(F_1(t,B_j,C_j)\right)=H(t,B_j,C_j)\mathcal{N}\left(F_0\left(t\right)\right),\hfill \\ \mathcal{B}\left(F_1(t,B_j,C_j),\frac{d{F}_1(t,B_j,C_j)}{dt}\right)=0,i=\overline{1,s}.\hfill \end{array}\end{array}$$

(12)

by taking into consideration that the nonlinear operator N presents the general form:

$$\begin{array}{c}\mathcal{N}\left(x_0\left(t\right)\right)=\left[M_{1}cos\left({\omega }_{0}t\right)+N_{1}sin\left({\omega }_{0}t\right)\right]·e^{-Kt},\hfill \end{array}$$

(13)

where

$$M_1=a(A_1-A_2)-K{A}_1+a_2{\omega }_0,$$

$$N_1=a(a_2-a_4)-K{a}_2-A_1{\omega }_0.$$

Analogue for $\mathcal{N}\left(y_0\left(t\right)\right)$ and $\mathcal{N}\left(z_0\left(t\right)\right)$, respectively.

Although Equation (12) is a nonhomogeneous linear one, in most cases its solution cannot be found.

In order to compute the function $F_1(t,B_j,C_j)$, we will use the OHAM technique (see [9] for details), consisting of the following steps:

• we choose the auxiliary convergence-control functions H such that $H·\mathcal{N}\left[F_0\left(t\right)\right]$ and $\mathcal{N}\left[F_0\left(t\right)\right]$ have the same form. For example, if H has the form:

$$H={\alpha }_1+\left[{\alpha }_{2}cos\left(p_{1}t\right)+{\alpha }_{3}cos\left(p_{2}t\right)+{\alpha }_{4}cos\left(p_{3}t\right)\right]+\left[{\alpha }_{5}sin\left(p_{1}t\right)+{\alpha }_{6}sin\left(p_{2}t\right)+{\alpha }_{7}sin\left(p_{3}t\right)\right]+$$

$$+\left[{\beta }_{2}cos\left(p_{4}t\right)+{\beta }_{3}cos\left(p_{5}t\right)+{\beta }_{4}cos\left(p_{6}t\right)\right]·e^{Kt}+\left[{\beta }_{5}sin\left(p_{4}t\right)+{\beta }_{6}sin\left(p_{5}t\right)+{\beta }_{7}sin\left(p_{6}t\right)\right]·e^{Kt},$$

then by a simple computation the first approximation $x_1$ becomes:

$$\begin{array}{c}{\displaystyle x_1\left(t\right)=B_{1}cos\left({\omega }_{1}t\right)+B_{2}cos\left({\omega }_{2}t\right)+B_{3}cos\left({\omega }_{3}t\right)+B_{4}cos\left({\omega }_{4}t\right)+B_{5}cos\left({\omega }_{5}t\right)+B_{6}cos\left({\omega }_{6}t\right)+}\hfill \\ +\left[B_{7}cos\left({\omega }_{7}t\right)+B_{8}cos\left({\omega }_{8}t\right)+B_{9}cos\left({\omega }_{9}t\right)+B_{10}cos\left({\omega }_{10}t\right)+B_{11}cos\left({\omega }_{11}t\right)+B_{12}cos\left({\omega }_{12}t\right)\right]·e^{-Kt}+\hfill \\ +C_{1}sin\left({\omega }_{1}t\right)+C_{2}sin\left({\omega }_{2}t\right)+C_{3}sin\left({\omega }_{3}t\right)+C_{4}sin\left({\omega }_{4}t\right)+C_{5}sin\left({\omega }_{5}t\right)+C_{6}sin\left({\omega }_{6}t\right)+\left[C_{7}sin\left({\omega }_{7}t\right)+\right.\hfill \\ \left.+C_{8}sin\left({\omega }_{8}t\right)+C_{9}sin\left({\omega }_{9}t\right)+C_{10}sin\left({\omega }_{10}t\right)+C_{11}sin\left({\omega }_{11}t\right)+C_{12}sin\left({\omega }_{12}t\right)\right]·e^{-Kt},\hfill \end{array}$$

(14)

where $B_{12}=-{\sum }_{i=1}^{11}{B}_i$ and the following relations hold:

$${\alpha }_1·M_1=-a_2·{\omega }_0,{\alpha }_1·N_1=A_1·{\omega }_0,p_1=\frac{1}{2}({\omega }_7+{\omega }_8),p_2=\frac{1}{2}({\omega }_9+{\omega }_{10}),$$

$$p_3=\frac{1}{2}({\omega }_{11}+{\omega }_{12}),p_4=\frac{1}{2}({\omega }_1+{\omega }_2),p_5=\frac{1}{2}({\omega }_3+{\omega }_4),p_6=\frac{1}{2}({\omega }_5+{\omega }_6),$$

$${\beta }_2=\frac{1}{M_1}(B_2+B_1),{\beta }_3=\frac{1}{M_1}(B_4+B_3),{\beta }_4=\frac{1}{M_1}(B_6+B_5),{\beta }_5=\frac{1}{N_1}(B_2-B_1),$$

$${\beta }_6=\frac{1}{M_1}(B_4-B_3),{\beta }_7=\frac{1}{N_1}(B_6-B_5),{\alpha }_2=\frac{1}{M_1}(B_8+B_7),{\alpha }_3=\frac{1}{M_1}(B_{10}+B_9),$$

$${\alpha }_4=\frac{1}{M_1}(B_{12}+B_{11}),{\alpha }_5=\frac{1}{N_1}(B_8-B_7),{\alpha }_6=\frac{1}{N_1}(B_{10}-B_9),{\alpha }_7=\frac{1}{N_1}(B_{12}-B_{11}),$$

$${\beta }_2=\frac{1}{N_1}(C_1-C_2),{\beta }_3=\frac{1}{N_1}(C_3-C_4),{\beta }_4=\frac{1}{N_1}(C_5-C_6),{\beta }_5=\frac{1}{M_1}(C_2+C_1),$$

$${\beta }_6=\frac{1}{M_1}(C_4+C_3),{\beta }_7=\frac{1}{M_1}(C_6+C_5),{\alpha }_2=\frac{1}{N_1}(C_7-C_8),{\alpha }_3=\frac{1}{N_1}(C_9-C_{10}),$$

$${\alpha }_4=\frac{1}{N_1}(C_{11}-C_{12}),{\alpha }_5=\frac{1}{M_1}(C_8+C_7),{\alpha }_6=\frac{1}{M_1}(C_{10}+C_9),{\alpha }_7=\frac{1}{M_1}(C_{12}+C_{11}).$$

In an analogous manner, the unknown functions $y\left(t\right)$ and $z\left(t\right)$ can be of the same form as Equation (14).

• next, by taking into account Equation (9), the first-order analytical approximate solution of Equations (3)–(5) is:

$$\begin{array}{c}\hfill \overline{F}(t,C_i)=F(t,1)=F_0\left(t\right)+F_1(t,B_j,C_j),\end{array}$$

(15)

where $\overline{F}$ can be $\overline{x}$, $\overline{y}$, or $\overline{z}$, $F_0$ can be $x_0$, $y_0$, or $z_0$, and $F_1$ can be $x_1$, $y_1$, or $z_1$;

• finally, the convergence-control parameters $a_2,a_4,a_6$, ${\omega }_0$, ${\omega }_1-{\omega }_{12}$, $B_1-B_{12}$, $C_1-C_{12}$, which determine the first-order approximate solution (15), can be optimally computed by means of various methods, such as: the least squares method, the Galerkin method, the collocation method, the Kantorowich method, or the weighted residual method.

By means of the MOHAM procedure, the approximate analytic solutions have the final form:

$$\overline{F}\left(t\right)=\left\{\begin{array}{ccc}{F}^{\left(1\right)}\left(t\right):=F_0\left(t\right)+F_1(t,B_j,C_j)\hfill & ,\hfill & t\in I^{\left(1\right)}:=[0,t_1]\hfill \\ F^{\left(2\right)}\left(t\right):=F_0(t-t_1)+F_1(t-t_1,B_j,C_j)\hfill & ,\hfill & t\in I^{\left(2\right)}:=[t_1,t_2]\hfill \\ \dots \dots \dots \hfill \\ F^{\left(k\right)}\left(t\right):=F_0(t-t_{k-1})+F_1(t-t_{k-1},B_j,C_j)\hfill & ,\hfill & t\in I^{\left(k\right)}:=[t_{k-1},t_k],\hfill \\ \dots \dots \dots \hfill \end{array}\right.$$

(16)

with $F_0$ and $F_1$ given by Equations (11) and (14), respectively.

Let us recall briefly the following definitions regarding the tools we use:

Definition 1

([11]). We call an ϵ-approximate solution of the problem (2) on the domain $(0,\infty )$ a smooth function $\overline{F}(t,C_i)$ of the form (16), which satisfies the following condition:

$$\begin{array}{c}\hfill \left|R\right(t,\overline{F}(t,C_i)\left)\right|<ϵ,\end{array}$$

together with the initial conditions from Equation (3), where the residual function $R(t,\overline{F}(t,C_i))$ is obtained by substituting Equation (16) into Equation (2), i.e.,

$$R(t,\overline{F}(t,C_i))=L\left(\overline{F}(t,C_i)\right)+N\left(\overline{F}(t,C_i)\right).$$

Definition 2

([11]). We call an week ϵ-approximate solution of the problem (2) on the domain $(0,\infty )$ a smooth function $\overline{F}(t,C_i)$ of the form (16), which satisfies the following condition:

$$\begin{array}{c}\hfill {\displaystyle {\int }_0^{\infty }{R}^2(t,\overline{F}(t,C_i))dt<ϵ,}\end{array}$$

together with the initial conditions from Equation (3).

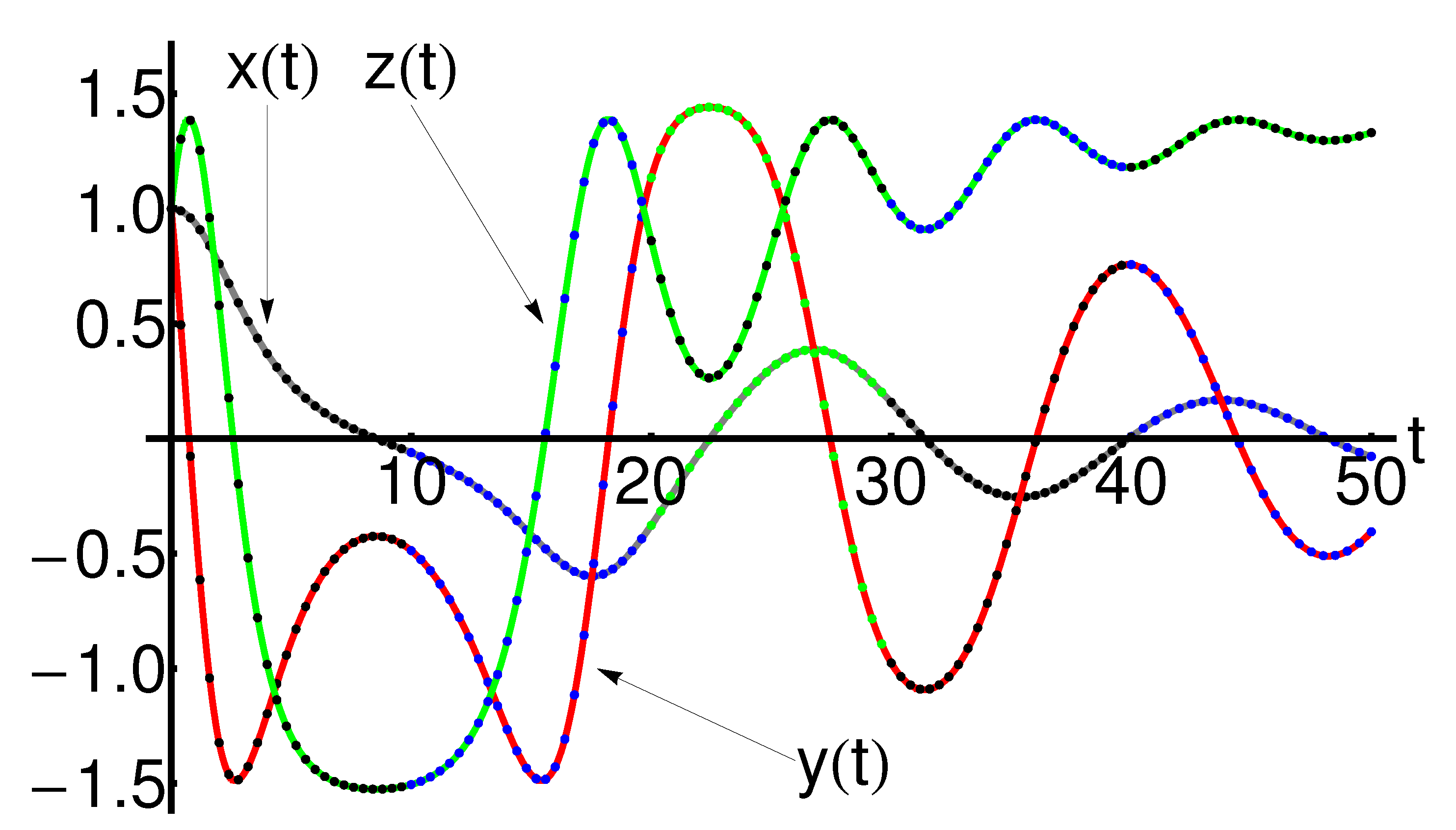
3. Numerical Examples and Discussions

In this section, the accuracy and validity of the MOHAM technique is proved using a comparison of our approximate solutions with numerical results obtained via the fourth-order Runge–Kutta method in the following case: we consider the initial value problem given by (2) with the initial conditions $A_i=1$, $i=\overline{1,3}$, $a=0.1$, and $b=c=0$.

The convergence-control parameters $a_2$, $a_4$, $a_6$, ${\omega }_0$, ${\omega }_1$-${\omega }_{12}$, $\left\{B_i\right\}{|}_{i=\overline{1,11}}$, and $\left\{C_i\right\}{|}_{i=\overline{1,12}}$ were optimally determined by means of the least-squares method using the Wolfram Mathematica software.

• For $\overline{x}:$ the convergence-control parameters on the interval $\left[0,10\right]$ are:

$$\begin{array}{cccc}{a}_2=6.8055011983,\hfill & a_4=0.0690513427,\hfill & a_6=-0.0906614599,\hfill & B_1=0.2718467394,\hfill \\ B_2=0.2291741991,\hfill & B_3=0.3018306965,\hfill & B_4=0.2759625955,\hfill & B_5=-0.2101658214,\hfill \\ B_6=0.2295677909,\hfill & B_7=3.7209890201,\hfill & B_8=-5.7548207759,\hfill & B_9=2.5337891462,\hfill \\ B_{10}=8.6828087318,\hfill & B_{11}=-4.3671936746,\hfill & C_1=-0.0511602388,\hfill & C_2=0.5086593478,\hfill \\ C_3=-0.0025199973,\hfill & C_4=-0.1713785049,\hfill & C_5=0.0633388390,\hfill & C_6=-0.0131773159,\hfill \\ C_7=-0.3378351530,\hfill & C_8=1.6026008049,\hfill & C_9=0.1188311898,\hfill & C_{10}=0.3381005413,\hfill \\ C_{11}=2.9102306589,\hfill & C_{12}=-0.7847237621,\hfill & K=1.4400054767,\hfill & {\omega }_0=0.2234064158,\hfill \\ {\omega }_1=0.2497624701,\hfill & {\omega }_2=-0.4185118688,\hfill & {\omega }_3=0.1577572753,\hfill & {\omega }_4=0.0710545480,\hfill \\ {\omega }_5=0.5052081236,\hfill & {\omega }_6=-0.2077991963,\hfill & {\omega }_7=1.0334164879,\hfill & {\omega }_8=1.2705537996,\hfill \\ {\omega }_9=1.1181026599,\hfill & {\omega }_{10}=1.4572785295,\hfill & {\omega }_{11}=-0.8937207901,\hfill & {\omega }_{12}=1.4910109360;\hfill \end{array}$$

(17)

• For $\overline{y}:$ the convergence-control parameters on the interval $\left[0,10\right]$ are:

$$\begin{array}{cccc}{a}_2=-0.35453520867,\hfill & a_4=4279.4014051576,\hfill & a_6=0.2195540378,\hfill & B_1=-2.6778492773,\hfill \\ B_2=12.73554840731,\hfill & B_3=-3.6791846385,\hfill & B_4=-11.5644476631,\hfill & B_5=7.8492678717,\hfill \\ B_6=-4.05628732378,\hfill & B_7=-87426.3195868320,\hfill & B_8=357516.0915550593,\hfill & B_9=357482.3789750056,\hfill \\ B_{10}=-87441.381199899,\hfill & B_{11}=-0.3590179440,\hfill & C_1=1289.0983931220,\hfill & C_2=497.9664617740,\hfill \\ C_3=1307.0097022384,\hfill & C_4=403.3739838437,\hfill & C_5=-485.8315351459,\hfill & C_6=1313.3923419982,\hfill \\ C_7=1853.9691656451,\hfill & C_8=-871.2310294911,\hfill & C_9=-868.2429406691,\hfill & C_{10}=1856.3597093276,\hfill \\ C_{11}=-0.0588538394,\hfill & C_{12}=-36593.9049799201,\hfill & K=1.3174536718,\hfill & {\omega }_0=0.0714437544,\hfill \\ {\omega }_1=-0.0057209185,\hfill & {\omega }_2=0.0159139573,\hfill & {\omega }_3=-0.0057097573,\hfill & {\omega }_4=0.0168401697,\hfill \\ {\omega }_5=-0.0160539714,\hfill & {\omega }_6=-0.0057054444,\hfill & {\omega }_7=0.0811125817,\hfill & {\omega }_8=0.0420766422,\hfill \\ {\omega }_9=0.0420768388,\hfill & {\omega }_{10}=0.0811113137,\hfill & {\omega }_{11}=-1.7355944044,\hfill & {\omega }_{12}=0.0145305787;\hfill \end{array}$$

(18)

• For $\overline{z}:$ the convergence-control parameters on the interval $\left[0,10\right]$ are:

$$\begin{array}{cccc}{a}_2=-0.3016232723,\hfill & a_4=-0.7603198858,\hfill & a_6=-20.6255017667,\hfill & B_1=0.1808851801,\hfill \\ B_2=1.1264813659,\hfill & B_3=0.9324855663,\hfill & B_4=-0.5791427510,\hfill & B_5=-0.2867368085,\hfill \\ B_6=-0.8831723072,\hfill & B_7=2.6011520027,\hfill & B_8=-2.2941481383,\hfill & B_9=3.6012308545,\hfill \\ B_{10}=-4.4967363700,\hfill & B_{11}=495027.8924551586,\hfill & C_1=-1.2898161045,\hfill & C_2=-0.3643788431,\hfill \\ C_3=-0.2327588930,\hfill & C_4=-1.4624089394,\hfill & C_5=0.2646964440,\hfill & C_6=0.4452722088,\hfill \\ C_7=-6.5398744159,\hfill & C_8=-5.9322280208,\hfill & C_9=-59.5497961075,\hfill & C_{10}=6.4783741818,\hfill \\ C_{11}=-0.6507196670,\hfill & C_{12}=-0.5356495284,\hfill & K=1.2239244253,\hfill & {\omega }_0=-0.0407806907,\hfill \\ {\omega }_1=0.4879808745,\hfill & {\omega }_2=-0.3275696752,\hfill & {\omega }_3=0.3075462783,\hfill & {\omega }_4=0.2388987261,\hfill \\ {\omega }_5=0.5977816602,\hfill & {\omega }_6=0.4006197580,\hfill & {\omega }_7=-0.2729051465,\hfill & {\omega }_8=-0.6938446861,\hfill \\ {\omega }_9=-0.0173005679,\hfill & {\omega }_{10}=-0.8174062684,\hfill & {\omega }_{11}=2.2531872831,\hfill & {\omega }_{12}=-2.2531873404.\hfill \end{array}$$

(19)

Proposition 1.

The functions $\overline{x}\left(t\right)$, $\overline{y}\left(t\right)$, and $\overline{z}\left(t\right)$ given by Formula (16), with corresponding parameters from Equations (17)–(19), respectively, represent a week ϵ-approximation solution of the system (2) on $[0,10]$, with initial conditions $A_i=1$, $i=\overline{1,3}$, $a=0.1$ and $b=c=0$.

Proof. 

The relative errors are presented in Table 1, Table 2, Table 3, Table 4 and Table 5. Then the corresponding residual functions relative to the interval $I^{\left(1\right)}=[0,10]$ are:

$$\begin{array}{c}{R}_x^{\left(1\right)}(t,\overline{x}(t,C_i))=\dot{\overline{x}}\left(t\right)-a\left(\overline{y}\left(t\right)-\overline{x}\left(t\right)\right),\hfill \end{array}$$

(20)

$$\begin{array}{c}{R}_y^{\left(1\right)}(t,\overline{y}(t,C_i))=\dot{\overline{y}}\left(t\right)+a\overline{x}\left(t\right)+\overline{x}\left(t\right)\overline{z}\left(t\right),\hfill \end{array}$$

(21)

$$\begin{array}{c}{R}_z^{\left(1\right)}(t,\overline{z}(t,C_i))=\dot{\overline{z}}\left(t\right)-\overline{x}\left(t\right)\overline{y}\left(t\right).\hfill \end{array}$$

(22)

Table 1. Comparison between the approximate solutions $\overline{x}$ given by Equation (17) and the corresponding numerical solutions for $a=0.1$ and $b=c=0$ (relative errors: ${ϵ}_x=|x_{numerical}-{\overline{x}}_{MOHAM}|$).

t	${\mathit{x}}_{\mathit{numerical}}$	${\overline{\mathit{x}}}_{\mathit{MOHAM}}$	${\mathit{ϵ}}_{\mathit{x}}$
		Given by Equation (17) on $[0,10]$
0	1	1	0
1	0.9364117165	0.9364116923	2.418795 $·{10}^{-8}$
2	0.7598648489	0.7598648112	3.773508 $·{10}^{-8}$
3	0.5496634288	0.5496634002	2.856912 $·{10}^{-8}$
4	0.3696539068	0.3696539545	4.768122 $·{10}^{-8}$
5	0.2361306278	0.2361305711	5.672768 $·{10}^{-8}$
6	0.1417808360	0.1417808950	5.904862 $·{10}^{-8}$
7	0.0744693389	0.0744692855	5.335994 $·{10}^{-8}$
8	0.0235417451	0.0235417987	5.357260 $·{10}^{-8}$
9	−0.0193274185	−0.0193274710	5.247476 $·{10}^{-8}$
10	−0.0607564092	−0.0607563471	6.213179 $·{10}^{-8}$

Table 2. Comparison between the approximate solutions $\overline{y}$ given by Equation (18) and the corresponding numerical solutions for $a=0.1$ and $b=c=0$ (relative errors: ${ϵ}_y=|y_{numerical}-{\overline{y}}_{MOHAM}|$).

t	${\mathit{y}}_{\mathit{numerical}}$	${\overline{\mathit{y}}}_{\mathit{MOHAM}}$	${\mathit{ϵ}}_{\mathit{y}}$
		Given by Equation (18) on $[0,10]$
0	1	0.999999999935	6.445688 $·{10}^{-11}$
1	−0.3553574878	−0.3553406469	1.684093 $·{10}^{-5}$
2	−1.3222633236	−1.3222267995	3.652404 $·{10}^{-5}$
3	−1.4627365880	−1.4627655007	2.891273 $·{10}^{-5}$
4	−1.1965325679	−1.1965069538	2.561406 $·{10}^{-5}$
5	−0.8833863981	−0.8834211067	3.470861 $·{10}^{-5}$
6	−0.6467691477	−0.6467410965	2.805123 $·{10}^{-5}$
7	−0.5010248753	−0.5010288335	3.958216 $·{10}^{-6}$
8	−0.4332635221	−0.4332863552	2.283315 $·{10}^{-5}$
9	−0.4308009782	−0.4307717036	2.927459 $·{10}^{-5}$
10	−0.4872360436	−0.4872559270	1.988340 $·{10}^{-5}$

Table 3. Comparison between the approximate solutions $\overline{z}$ given by Equation (19) and the corresponding numerical solutions for $a=0.1$ and $b=c=0$ (relative errors: ${ϵ}_z=|z_{numerical}-{\overline{z}}_{MOHAM}|$).

t	${\mathit{z}}_{\mathit{numerical}}$	${\overline{\mathit{z}}}_{\mathit{MOHAM}}$	${\mathit{ϵ}}_{\mathit{z}}$
		Given by Equation (19) on	$[0,10]$
0	1	1.000000000007	7.753353 $·{10}^{-12}$
1	1.3435098520	1.3435117225	1.870482 $·{10}^{-6}$
2	0.5794256998	0.5794264180	7.182044 $·{10}^{-7}$
3	−0.3653327889	−0.3653338194	1.030464 $·{10}^{-6}$
4	−0.9822187335	−0.9822190522	3.187262 $·{10}^{-7}$
5	−1.2956707043	−1.2956700418	6.625175 $·{10}^{-7}$
6	−1.4385401687	−1.4385409624	7.936812 $·{10}^{-7}$
7	−1.4996335886	−1.4996327358	8.528737 $·{10}^{-7}$
8	−1.5220698429	−1.5220705915	7.486002 $·{10}^{-7}$
9	−1.5228177923	−1.5228170129	7.794542 $·{10}^{-7}$
10	−1.5044931170	−1.5044943712	1.254174 $·{10}^{-6}$

Table 4. Comparison between the approximate solutions $\overline{y}$ given by Equation (A5) and the corresponding numerical solutions for $a=0.1$ and $b=c=0$ (relative errors: ${ϵ}_y=|y_{numerical}-{\overline{y}}_{MOHAM}|$).

t	${\mathit{y}}_{\mathit{numerical}}$	${\overline{\mathit{y}}}_{\mathit{MOHAM}}$	${\mathit{ϵ}}_{\mathit{y}}$
		Given by Equation (A5) on $[10,20]$
10	−0.4872360436	−0.4872559270	1.988340 $·{10}^{-5}$
11	−0.6020163945	−0.6019673252	4.906934 $·{10}^{-5}$
12	−0.7769448025	−0.7769582240	1.342157 $·{10}^{-5}$
13	−1.0076845857	−1.0076745905	9.995179 $·{10}^{-6}$
14	−1.2647930513	−1.2648497330	5.668172 $·{10}^{-5}$
15	−1.4608323548	−1.4607292187	1.031360 $·{10}^{-4}$
16	−1.4275878870	−1.4275819492	5.937881 $·{10}^{-6}$
17	−0.9926160834	−0.9924248087	1.912747 $·{10}^{-4}$
18	−0.2018262566	−0.2017968869	2.936977 $·{10}^{-5}$
19	0.6069402387	0.6070773469	1.371082 $·{10}^{-4}$
20	1.1347132559	1.1347995011	8.624522 $·{10}^{-5}$

Table 5. Comparison between the approximate solutions $\overline{z}$ given by Equation (A11) and the corresponding numerical solutions for $a=0.1$ and $b=c=0$ (relative errors: ${ϵ}_z=|z_{numerical}-{\overline{z}}_{MOHAM}|$).

t	${\mathit{z}}_{\mathit{numerical}}$	${\overline{\mathit{z}}}_{\mathit{MOHAM}}$	${\mathit{ϵ}}_{\mathit{z}}$
		Given by Equation (A11) on $[30,40]$
30	1.0212205896	1.0213459275	1.253379 $·{10}^{-4}$
31	0.9180981076	0.9182408746	1.427670 $·{10}^{-4}$
32	0.9306470486	0.9308026898	1.556412 $·{10}^{-4}$
33	1.0435260411	1.0436704899	1.444488 $·{10}^{-4}$
34	1.2025755175	1.2027255256	1.500081 $·{10}^{-4}$
35	1.3353033803	1.3354462611	1.428807 $·{10}^{-4}$
36	1.3865223388	1.3866649002	1.425614 $·{10}^{-4}$
37	1.3509108877	1.3510545089	1.436211 $·{10}^{-4}$
38	1.2706560671	1.2707974871	1.414199 $·{10}^{-4}$
39	1.2013516479	1.2014949451	1.432972 $·{10}^{-4}$
40	1.1798239453	1.1799651910	1.412457 $·{10}^{-4}$

Hence, we have:

$$\begin{array}{c}\hfill {\displaystyle {\int }_0^{10}{\left(R_x^{\left(1\right)}\right)}^2(t,\overline{x}(t,C_i))dt=6.476023959919411·{10}^{-11},}\end{array}$$

$$\begin{array}{c}\hfill {\displaystyle {\int }_0^{10}{\left(R_y^{\left(1\right)}\right)}^2(t,\overline{y}(t,C_i))dt=2.316094653837801·{10}^{-7},}\end{array}$$

$$\begin{array}{c}\hfill {\displaystyle {\int }_0^{10}{\left(R_x^{\left(1\right)}\right)}^2(t,\overline{y}(t,C_i))dt=2.4866219416720193·{10}^{-9}.}\end{array}$$

Following this procedure, we can find other week $ϵ$-approximate solutions of the system (2) over the intervals $[10,20]$, $[20,30]$, and so on.

Finally, Table 1, Table 2, Table 3, Table 4 and Table 5 emphasize the accuracy of the MOHAM technique by comparing the approximate analytic solutions $\overline{x}$, $\overline{y}$, and $\overline{z}$ presented above with the corresponding numerical integration values (via the 4th-order Runge–Kutta method). These comparisons show the effectiveness, reliability, applicability, efficiency, and accuracy of the MOHAM.

All of the convergence-control parameters, corresponding to the intervals $[10,20]\cup [20,30]\cup [30,40]\cup [40,50],$ are presented in Appendix A.  □

Remark 1.

Figure 1 presents the comparisons between the analytical approximate solutions given by MOHAM and numerical results provided by the Runge–Kutta 4th-order integrator. We can see that the analytical approximate solutions and Runge–Kutta 4th order integrator’s results were quite similar.

Figure 1. Profiles of the functions $\overline{x}$ given by Equations (17), (A1)–(A4), $\overline{y}$ given by Equations (18), (A5)–(A8) and $\overline{z}$ given by Equations (19), (A9)–(A12), on $[0,10]\bigcup [10,20]\bigcup [20,30]\bigcup [30,40]\bigcup [40,50]$: $---------------$ numerical solution, $···········$ MOHAM solution.

4. Conclusions

The Hamilton–Poisson realizations of a dynamical system allows us to study it from mechanical geometry point of view (see for instance Toda Lattice [12], Lagrange system [13], Lotka–Volterra system [14], Kowalevski top dynamics [15], the battery model [6], and others [16]).

The Poisson geometry offers us a different point of view, unlike other old approaches, and specific tools to study our dynamics. In addition, the phase portrait, as the intersection between the surfaces $H=const.$ and $C=const.$ gives us the exact solution of the system.

Chen’s system rose from the electrical engineering field. Its chaotic behavior makes it good to apply in secure communications, complete synchronization, or optimization of nonlinear system performance, but finding its exact solution may be difficult. This problem can be solved using a Hamilton–Poisson realization of the system. Unfortunately, like other chaotic systems studied before—e.g., the Rikitake system [17], the Lü system [18], and the Lorenz system [19]—finding the corresponding Poisson structure implies the study of particular values for its parameters.

For the specific values of its parameters, for which finding the exact solutions is impossible, the approximate solutions obtained using the multistage optimal homotopy asymptotic method and the corresponding numerical results were analyzed. We summarize that the MOHAM’s analytic solutions were proven to be the best.