Modeling and Simulation of Impact and Control in Social Networks with Application to Marketing

Abstract

The problems of social networks analysis and calculation of the resulting opinions of network agents are considered. Algorithms for identifying strong subgroups and satellites as well as for calculating some quantitative characteristics of a network are implemented by the R programming language and tested on model examples. A new algorithm for calculating the resulting opinions of agents is developed by the R toolkit and tested on model examples. It is important that control actions that exert impact to the opinions should be applied exclusively to the members of strong subgroups (opinion leaders of a target audience), since they fully determine the stable resulting opinions of all network members. This approach allows saving control resources without significantly affecting its efficiency. Much attention is paid to the original models of optimal control (single subject) and conflict control (several competing subjects) under the assumption that the members of strong subgroups (opinion leaders) are already identified at the previous stage of network analysis. Models of optimal opinion control on networks are constructed and investigated by computer simulations using the author’s method of qualitatively representative scenarios. Differential game-based models of opinion control on networks with budget constraints in the form of equalities and inequalities are constructed and analytically investigated. All used notions, approaches and results of this paper are interpreted in terms of marketing problems.

1. Introduction

French [1] and Harary [2] proposed the pioneer models of influence in social networks. The most famous basic model, which is also adopted in this paper, belongs to De Groot [3]. Later on, a number of modifications and refinements of this model were presented, including, e.g., the case of time-dependent mutual influence of agents [4,5,6,7], the convergence conditions of opinions [8,9,10], the rate of convergence [4,10] and conditions of the resulting opinion (consensus) uniqueness [4,5].

In [11], the Markov model of influence in a social group described by a dynamic Bayesian network with a two-level structure (individual agents and the entire group) was introduced. This model is closely connected with a number of other models of the same class, e.g., mixed memory Markov models [12], implicit paired Markov models [13] and the tree-like models of dynamical systems [14].

The most complete survey of influence models over networks can be found in the monograph [15] and paper [16] by Jackson. Communication and coordination in social networks were analyzed in [17]. The papers [18,19,20] were dedicated to the modeling of the word-of-mouth effects. The relative influence of network nodes was studied in [21]. A systematic approach to network analysis was applied in [22]. Models of social influence were also described in the papers [23,24].

A detailed analysis of influence models and some formulations of control models were given in the monograph [25]. A closest approach to the one developed below was presented in [26,27], where linear-quadratic game-theoretic models were constructed and investigated on a network with two influence nodes. In [26], the Nash equilibrium for two independent nodes was found; in [27], the Stackelberg equilibrium for hierarchically ordered nodes.

Also, there exists other approaches to the mathematical modeling and computer simulation of networks, including gene-environment networks, eco-finance networks, Markov switching models, rumor propagation, and others. A detailed survey was given the paper [28], where modern trends in the development and use of operations research methods were considered; in particular, optimization methods for gene-environment and eco-finance networks based on finite time series, with special attention to uncertainty and interaction between model elements, were described there. In the paper [29], the gene-environment networks were further overviewed, which contributed to the contemporary understanding of the foundations and interdisciplinary consequences of introducing this class of networks; moreover, a relevant topic of carbon dioxide emission reduction was generalized to the context of networks and dynamic systems. In [30], dynamic gene-environment networks under ellipsoidal uncertainty were considered and the corresponding set-theoretic regression models were discussed.

Eco-finance networks under uncertainty were studied in [31]. A mathematical model describing the propagation of true information and rumors was presented in [32]. The existence of equilibria, the local and global asymptotic stability as well as the threshold values for the propagation of rumors were investigated. The results were illustrated using numerical calculations.

Markov switching models in the economic analysis are discussed in [33]. They have become very popular in the economic studies of manufacturing, interest rates, wholesale prices and the rate of unemployment. As for the contribution of [34], a characterization of the moments and serial correlation of the level as well as the squares of the Markov switching processes should be mentioned. In [35], the stochastic optimal control problem for a Markov regime-switching jump-diffusion model with delay was considered and the necessary and sufficient conditions of maximum under complete and partial information about such a system were established. In the paper [36], the boundary-value problems on extremely large periodic networks arising in many applications were examined; as a model example, the singularly perturbed elliptic differential equations of the second order were considered. The results established there were further developed in [37]. The authors of [38] were the first to introduce and analyze rough discrete-time control systems of the “goal–environment” type with polyhedral uncertainty through robust optimization. The goal of the paper [39] was to obtain a mathematical framework for analyzing the cooperation of nodes and determining strategies that lead to the optimal behavior of nodes in the networks created for a particular case.

The goal of the paper [40] is to analyze a relation between the number of actions performed by an agent embedded in a social system; that is, his activity (A), and the number of reactions that these actions imply in his peers, or response (R). For the quantitative characteristics the authors generalize the efficiency metric (η = R/A). The theoretical distributions of efficiency are calculated by three different methodologies: the method of Monte-Carlo simulation, direct computation with discrete probability distributions and derivation of an analytical expression.

A big stream of literature relates to the problem of controllability of networks [41,42,43]. A comprehensive review is presented in [44]. An interesting review of the models of information diffusion in networks is given in the paper [45].

This paper extends the author’s postulates from [46]. The key idea is that control actions (impact) should be applied exclusively to the members of strong subgroups (opinion leaders), since they fully determine the stable resulting opinions of all network members. This approach allows saving control resources without significantly affecting its efficiency. Much attention is paid to the development and investigation of original models of optimal control (single control subject) and conflict control (competing control subjects) under the assumption that the members of strong subgroups (opinion leaders) are already identified at the previous stage of network analysis. Thus, the paper makes the following contributions:

• The problems of analyzing networks and calculating the resulting opinions of network agents are interpreted in terms of marketing problems. No doubt, they will find applications in other fields such as politics and sociology [47].
• Algorithms for identifying strong subgroups (representing opinion leaders) and satellites (other members of the target audience) as well as for calculating some quantitative characteristics of a network using the R programming language [48] are implemented and tested on model examples.
• A new algorithm for calculating the resulting opinions of agents is developed, implemented in the R language and tested on model examples.
• Models of optimal opinion control on networks are constructed and investigated by computer simulations using the author’s method of qualitatively representative scenarios [49].
• Differential game-based models of opinion control on networks with budget constraints in the form of equalities and inequalities are constructed and analytically investigated. Some marketing interpretations are made.

In Section 2, the basic model of influence in a social group is described, including an interpretation to marketing problems; in addition, the corresponding problems of analysis and prediction are formulated, and some illustrative examples are given. Section 3 and Section 4 are dedicated to the analytical investigation of the optimal control problems and game-theoretic models of opinion control on networks, respectively. The results and possible future prospects are summarized in Section 5.

2. Network Analysis and Calculation of Resulting Opinions of Agents

Following [50], we describe the basic model of influence in a social network. A group of $n$ agents $y_1,\dots ,y_n$ makes a decision on some issue. At the initial time instant $t=0$, each agent $y_i$ has some opinion $x_i(0)$ on this issue; the vector of initial opinions $x^0=x(0)=(x_1(0),\dots ,x_n(0))$ is given. Denote by $a_{ij}\ge 0$ the influence level of $y_i$ on $y_j$ (equivalently, the degree of trust of $y_j$ to $y_i$). Generally speaking, the values $a_{ij}$ can be called the coefficients of interaction of network agents. A network is described by an influence digraph $D=(Y,A),\hspace{1em}Y=\{y_1,\dots ,y_n\},\hspace{1em}A=\left|\right|a_{ij}|{|}_{i,j=1}^n$. We make the following assumptions: $D$ remains invariable during the decision process; all decisions are made at discrete time instants $t=0,1,2,\dots$; the opinions of different agents evolve in accordance with the rule

$$x_j(t+1)={\displaystyle \sum _{i=1}^n{a}_{ij}{x}_i(t)},\hspace{1em}j=1,\dots ,n.$$

(1)

The natural questions are:

(i)

is there a stable resulting opinion $x_i^{\infty }=\underset{t\to \infty }{\lim }{x}_i(t)$ for each agent?

(ii)

will the entire group converge to the same resulting opinion (consensus) $x^{\infty }=x_i^{\infty },\hspace{0.33em}i=1,\dots ,n$?

A set of nodes $\{y_1,\dots ,y_k\}$ of an influence digraph $D=(Y,A)$ will be called a strong subgroup if it represents a strong component of $D$ that enters the node base $B*$ of the condensation $D*$. Let us recall the definitions [50]. The subdigraph $K$ of a digraph $D=(Y,A)$ is called a strong component in $D$ if it is (1) strongly connected; (2) generated by the respective set of nodes; (3) maximal by inclusion of nodes. The set $B*$ is called a node base in a digraph $D=(Y,A)$ if (1) for any node $b\in Y\backslash B*$ there is a node $a\in B*$ such that there is a path from $a$ to $b$; (2) $B*$ is a minimal set having the property (1). The digraph $D*=(Y*,B*)$ is called the condensation of a digraph $D$ if(1) $Y*=\{K_1,\dots ,K_p\}$, where $K_1,\dots ,K_p$ are strong components in $D$; (2) $(K_i,K_j)\in A*\iff \exists a\in K_i,b\in K_j:(a,b)\in A$.We compile a list of strong subgroups $S_1,\dots ,S_z$ and number all nodes sequentially, for the sake of definiteness in the following way:

$S_1=\{y_{11},\dots ,y_{1n_1}\},S_2=\{y_{21},\dots ,y_{2n_2}\},\dots ,S_z=\{y_{z1},\dots ,y_{z{n}_z}\}$, where z is a number of strong subgroups. We also number the nodes from the transition set (i.e., all other nodes):

$T=\{y_{z+1,1},\dots ,y_{z+1,n_{z+1}}\}$. If a node $y_{ij}$ belongs to $S_i$, then

$$x_{ij}^{\infty }={\displaystyle \sum _{k=1}^{n_i}{w}_k^{(i)}{x}_{ik}(0)=x_i^{\infty }}.$$

(2)

Therefore, the resulting opinion of each member of a strong subgroup depends on the initial opinions of its other members only, being the same for the entire subgroup. If a node $y_{z+1,j}$ belongs to $T$, then

$$x_{z+1,j}^{\infty }={\displaystyle \sum _{i=1}^r{b}_{ji}\left({\displaystyle \sum _{k=1}^{n_i}{w}_k^{(i)}{x}_{ik}(0)}\right)}={\displaystyle \sum _{i=1}^r{b}_{ji}{x}_i^{\infty }}.$$

(3)

Thus, the resulting opinion of each member of a transition set (called satellite) depends on the opinions of all strong subgroup members. Other satellites have no impact on it. The resulting opinion is a linear convolution of the common resulting opinions of all strong subgroups [50].

The algorithms for identifying strong subgroups and satellites as well as for calculating the resulting opinions of agents were developed and implemented using the R programming language in [48]. Consider a model example to illustrate the above concepts and test the algorithms.

A small IT firm consists of fifteen employees and a manager. The manager is going to celebrate his birthday, and the staff has decided to chip in on a gift for him. Each employee has an individual opinion on appropriate contribution, which forms the initial opinions. There are social relations in the firm: some employees are on friendly terms, considering the opinions of each other. Let the influence matrix be given by

$$\begin{array}{l}{a}_{21}=a_{22}=1;a_{23}=1/4;a_{210}=1/6;a_{33}=1/4;a_{34}=1/2;a_{43}=a_{44}=1/2;a_{45}=1/3;\\ a_{65}=2/3;a_{66}=a_{68}=1/2;a_{69}=1/4;a_{76}=a_{77}=1/2;a_{87}=a_{88}=1/2;a_{89}=1/4;\\ a_{99}=1/4;a_{910}=1/12;a_{109}=1/4;a_{1010}=a_{1012}=a_{1013}=1/2;a_{1011}=1;a_{1110}=1/12;a_{1115}=1/3;\\ a_{1210}=1/12;a_{1212}=1/4;a_{1310}=1/12;a_{1313}=1/2;a_{1314}=1/4;a_{1414}=3/4;a_{1415}=1/3;\\ a_{1512}=1/4;a_{1515}=1/3;a_{ij}=0\hspace{0.33em}\mathrm{for}\hspace{0.33em}\mathrm{other}\hspace{0.33em}i,j.\end{array}$$

The initial opinions on the appropriate contributions to the gift (in conditional units) form the vector (500, 900, 500, 400, 400, 500, 800, 500, 600, 400, 100, 200,200, 300, 500). This network is shown in Figure 1.

The strong subgroups and satellites obtained using the algorithm can be seen in Figure 2. Node 10 (analyst) has a strong influence on nodes 11–15 (programmers), that is, people from the same financial category, with the same interests, who communicate only with each other and with the analyst as a link between them and the rest of the staff. Nodes 6–8 (the first strong subgroup) correspond to the marketing and sales department. Node 9 is the project manager; node 2 is the implementation department (the second strong subgroup). The other nodes correspond to ordinary employees.

The resulting opinions of the agents calculated by the developed algorithm are given by

$$\begin{array}{l}{x}_1^{\infty }=x_2^{\infty }=x_3^{\infty }=x_4^{\infty }=900;x_5^{\infty }=700;x_6^{\infty }=x_7^{\infty }=x_8^{\infty }=600;x_9^{\infty }=675;\\ x_{10}^{\infty }=x_{11}^{\infty }=x_{12}^{\infty }=x_{13}^{\infty }=x_{14}^{\infty }=x_{15}^{\infty }=825.\end{array}$$

Based on the analysis of the model example, we can conclude that the opinion leaders of this IT firm (except for the manager) are employees 2, 6, 7 and 8 becausethe sets {2} and {6,7,8} are strong subgroups. Despite the fact that the subgroup of employees 9–15 is quite large and has close communication, their resulting opinions are still formed by the leaders; moreover, employees 9 and 10 are a kind of bridge between this subgroup and the leaders. Accordingly, employees 2, 6–8 indirectly influence agents 11–15, forming their opinion.

One way or another, all employees listen to the opinion of leaders, changing their own ones; at the same time, the leaders listen to the opinions of each other (as in the case of employees 6–8), or do not change their opinion at all (as in the case of employee 2). Therefore, the opinions of the entire staffcan be controlled (e.g., for increasing the contribution to the gift) by affecting the opinions of employees 2, 6–8 only, not all the fifteen agents.

Summarizing the outcomes of this section, we note that influence models over networks can be used for solving analysis and prediction problems. The former class of problems includes identification of strong subgroups and satellites as well as calculation of quantitative characteristics of networks [51]. The latter class of problems is focused on predicting the opinion dynamics of social group members based on its structure identified in the course of analysis (

Table 1. Interpretation of different elements of the models of influence and control on networks in marketing.

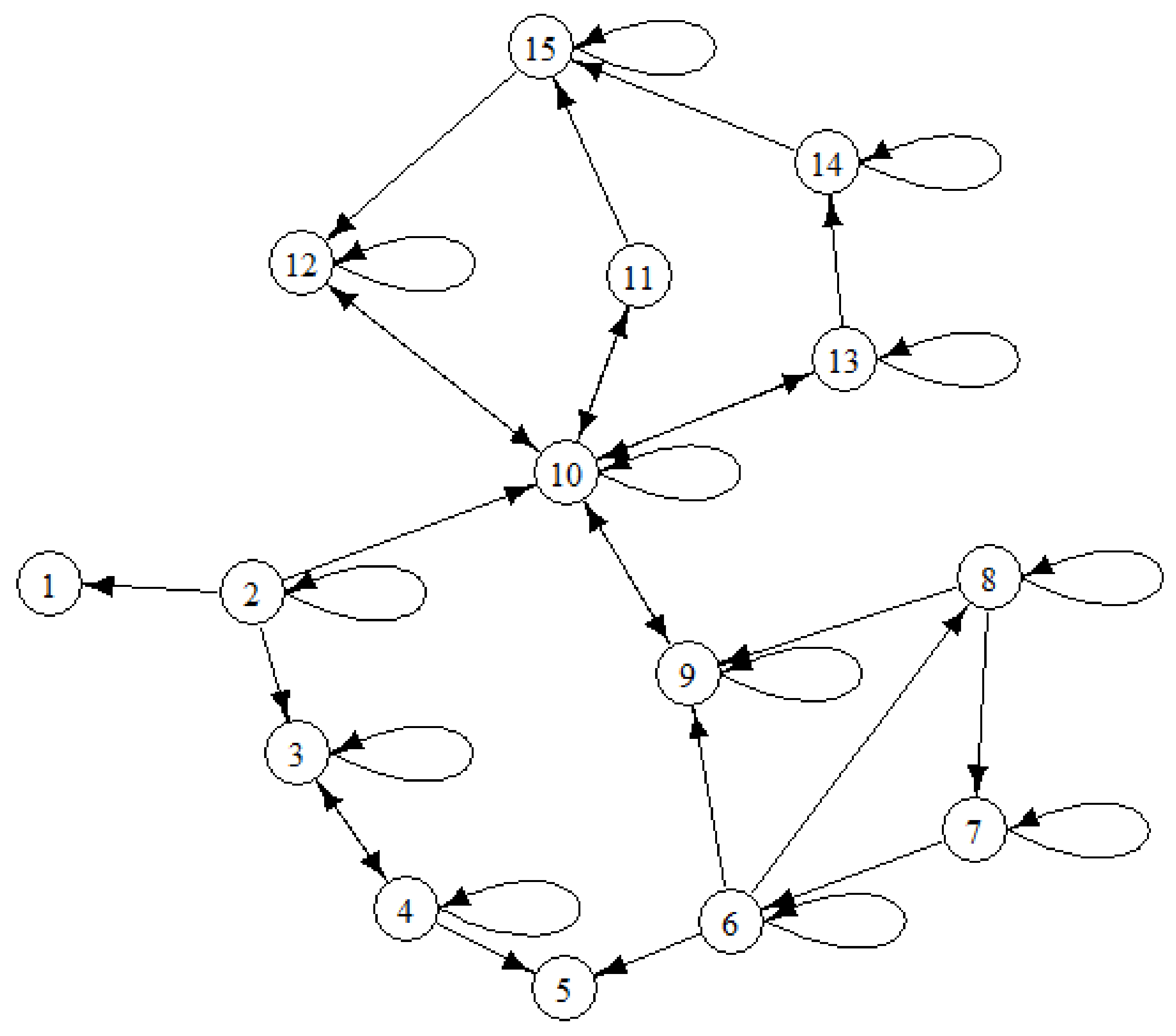
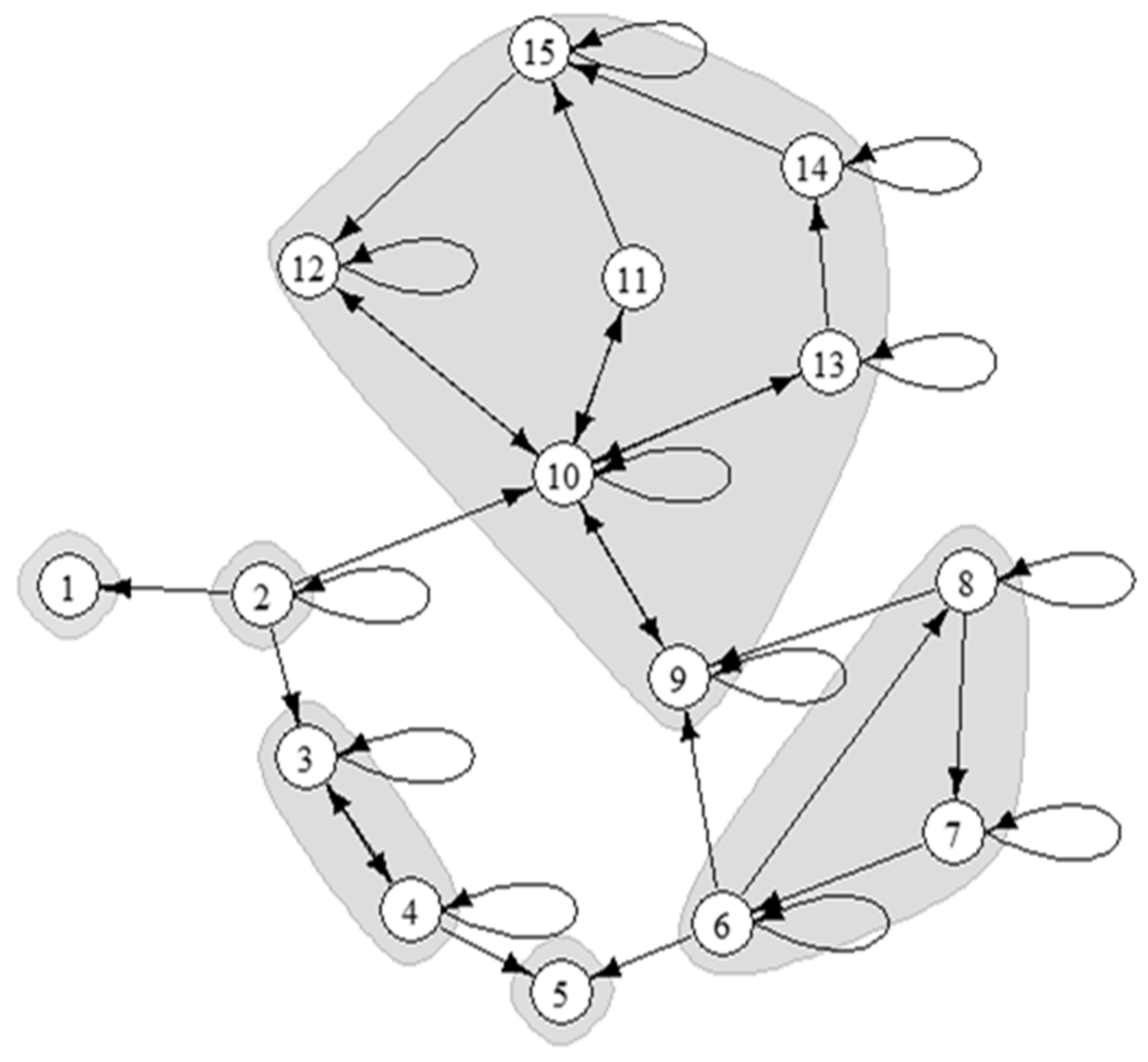
Model Element	Mathematical Sense	Interpretation in Marketing
Basic agent	Network node	Segment of audience
Influencing agent	Network node	Market participants (firms), advertising agencies, mass media, etc.
Opinion of basic agent	Real value associated with each node (basic agent) that varies with time	Agent’s monthly (annual) expenses on firm’s products, or the number of visits to firm’s enterprises, or some numerical score of firm’s products (services)
Trust (influence)	Arc between initial and terminal nodes (initial trusts terminal, terminal influences initial)	Word-of-mouth, other communications of agents
Degree of trust of basic agent to another one (degree of influence of another agent on basic agent)	Real value associated with each network arc	Quantitative characteristic of trust
Resulting opinion	Limiting value of opinion over infinite time horizon	Stable resulting opinion over long period of time
Strong subgroup	Nondegenerate strong network component	Determines its own resulting opinions and also the dependent opinions of other agents
Satellite	Subset of nodes representing degenerate strong components	Resulting opinions are completely determined by strong subgroups
Impact on opinions	Additive term of opinion vector (more complex cases are also possible)	Marketing action plan
Impact on degrees of trust (influence)	Additive term of influence matrix (more complex cases are also possible)	Marketing action plan
Goal of control	Domain in state space of network	Range of desired opinions

).

3. Optimal Control over Networks

Thus, the main control hypothesis in both cases (a single subject or several competing subjects) is that control actions (marketing strategies) should be applied only to the members of strong subgroups (opinion leaders), since they alone determine the resulting opinions of all network members. In Section 3, we consider the models of optimal opinion control over networks in which a monopolistic firm is the subject of control. We assume that all opinion leaders have been already identified and the control actions are applied to them only.

More specifically, consider the optimal control problem

$$J={\displaystyle \sum _{t=1}^T{e}^{-\rho t}\left[{\displaystyle \sum _{j=1}^n{x}_j^t-{\displaystyle \sum _{k=1}^m{u}_k^t}}\right]}\to \max ;$$

(4)

$${\displaystyle \sum _{t=1}^T{\displaystyle \sum _{j=1}^m{e}^{-\rho t}{u}_j^t\le R}};$$

(5)

$$x_j^{t+1}=b_j\sqrt{u_j^t}+{\displaystyle \sum _{i=1}^n{a}_{ij}{x}_i^t,\hspace{0.33em}{x}_j^0=x_{j0},\hspace{0.33em}j=1,\dots ,n,\hspace{0.33em}t=0,1,\dots ,T.}$$

(6)

The notations are the following: $x_j^t$,$x_j^{t+1}$ are the opinions of agent $j$ at time instants $t$, $t+1$ respectively; $u_j^t$ as the control action applied to agent $j$ at a time instant $t$; $R$ as the marketing budget of the firm; $a_{ij}$ as the coefficients of interaction of agents i and j; $b_j$ as the cost coefficient to control agent $j$; $m$ as the number of strong subgroups members; $n$ as the total number of agents; $T$ as the time horizon; finally, $\mathsf{\rho }$ as the discount factor; $x_{j0}$ is an initial opinion of the agent j.

Computer simulations with model (4)–(6) were performed to answer two questions as follows. First, is it possible to hypothesize that when introducing control (e.g., by rule (6)), the resulting opinions of all agents will still be determined only by the initial opinions of strong subgroups members, like in the case of the natural opinion dynamics (1)?

To answer this question, numerical experiments were carried out for three model examples [51] with different values of the model parameters. As an illustration we consider the following data set for the model example of Section 2: the marketing budget $R=$ 60,000 (conditional units); the time horizons $T=200,\hspace{0.33em}500,\hspace{0.33em}\mathrm{20,000}$; the total number of agents $n=15$; the vector of initial opinions x₀ = (500, 900, 500, 400, 400, 500, 800, 500, 600, 400, 100, 200,200, 300, 500). For each agent, the control action was calculated by the formula $u_j=\frac{R}{T\cdot n},j=1,\dots ,n$. The resulting opinions and payoffs of the monopolistic firm are combined in

Table 2. Resulting opinions and payoffs in model example.

	T = 200	T = 500	T = 20,000
Impact on all agents	x1 = … = x4 = 1794; x5 = 1595; x6 = x7 = x8 = 1494; x9 = 1569; x10 = … = x15 = 1719 J = 283,253.3	x1 = … = x4 = 2314; x5 = 2114; x6 = x7 = x8 = 2014; x9 = 2089; x10 = … = x15 = 2239 J = 272,897.1	x1 = … = x4 = 29,184; x5 = 28,984; x6 = x7 = x8 = 28,884; x9 = 28,959; x10 = … = x15 = 29,109 J = 251,515.4
Impact on strong subgroups members only	x1 = x2 = 2623; x3 = 2562; x4 = 2545; x5 = 2394; x6 = x7 = x8 = 2632; x9 = 2374; x10 = 2494; x11 = 2485; x12 = 2468; x13 = 2477; x14 = 2442; x15 = 2451 J = 307,121.9	x1 = 3633; x2 = 3639; x3 = 3595; x4 = 3584; x5 = 3415; x6 = x7 = x8 = 3339; x9 = 3393; x10 = 3524; x11 = 3518; x12 = 3507; x13 = 3513; x14 = 3491; x15 = 3497 J = 288,059.9	x1 = 55,612; x2 = 55,672; x3 = x4 = 55,670; x5 = 55,471; x6 = x7 = x8 = 55,372; x9 = 55,466; x10 = x11 = 55,595; x12 = 55,594; x13 = 55,595; x14 = x15 = 55,594 J = 252,273

. Here the second row corresponds to the impact exerted on all agents while the third row to the impact exerted on the strong subgroups members only.

In accordance with Table 2, the impact on the strong subgroups members only is more effective than the impact on all agents, both in terms of the payoff and the resulting opinions. Similar results were obtained for the other data sets, which gives an affirmative answer to the first question of the study.

The second question concerns the minimum number of simulation scenarios required for making an acceptable qualitative forecast. To answer this question, the author’s method of qualitatively representative scenarios of simulation modeling was adopted; see [49].

A collection of scenarios $QRS=\{u^1,u^2,\dots u^m\}$ is said to be a set of qualitatively representative scenarios for the optimal control problem with an accuracy Δ if:

(a)

for any two scenarios $u^i,u^j\in QRS$,

$$|J_{}^{(i)}-J_{}^{(j)}|>\Delta ;$$

(7)

(b)

for any other scenario $u^l\notin QRS$ there exists a scenario $u^j\in QRS$ such that

$$|J_{}^{(l)}-J_{}^{(j)}|\le \Delta .$$

(8)

We check that in the model example, the values T = {200, 500, 200,000} are a set of qualitatively representative scenarios. The corresponding data are presented in

Table 3. Checking qualitative representativeness conditions for scenarios in model example.

Time Horizon T	Payoff J
200	2,937,211
500	2,917,487
1000	2,906,170
20,000	2,883,652
40,000	2,881,675
60,000	2,880,795
80,000	2,880,269
100,000	2,879,910
120,000	2,879,645
140,000	2,879,438
160,000	2,879,272
180,000	2,879,134
200,000	2,879,017

. The scenarios for which the conditions of qualitative representativeness were checked are set in boldface.

Let Δ = 19,000. Then, condition (7) takes the form

$$\begin{array}{c}|J_{}^{(200)}-J_{}^{(500)}|=\mathrm{19,724}>\Delta ;|J_{}^{(200)}-J_{}^{(\mathrm{200,000})}|=\mathrm{58,194}>\Delta ;\\ |J_{}^{(500)}-J_{}^{(\mathrm{200,000})}|=\mathrm{38,470}>\Delta .\end{array}$$

Condition (8) takes the form

$$\begin{gathered} |J_{}^{(1000)}-J_{}^{(500)}|=\mathrm{11,317}<\Delta ;|J_{}^{(\mathrm{20,000})}-J_{}^{(\mathrm{200,000})}|=4635<\Delta ; \\ |J_{}^{(\mathrm{40,000})}-J_{}^{(\mathrm{200,000})}|=2658<\Delta ;|J_{}^{(\mathrm{60,000})}-J_{}^{(\mathrm{200,000})}|=1778<\Delta ; \\ |J_{}^{(\mathrm{80,000})}-J_{}^{(\mathrm{200,000})}|=1252<\Delta ;|J_{}^{(\mathrm{100,000})}-J_{}^{(\mathrm{200,000})}|=893<\Delta ; \\ |J_{}^{(\mathrm{120,000})}-J_{}^{(\mathrm{200,000})}|=628<\Delta ;|J_{}^{(\mathrm{140,\; 000})}-J_{}^{(\mathrm{200,000})}|=421<\Delta ; \\ |J_{}^{(\mathrm{160,000})}-J_{}^{(\mathrm{200,000})}|=255<\Delta ;|J_{}^{(\mathrm{180,000})}-J_{}^{(\mathrm{200,000})}|=117<\Delta . \end{gathered}$$

Thus, the qualitative representativeness conditions in this example are really satisfied with an accuracy of $\Delta$ = 19,000, which is small compared to the values of the payoffs. Similar checks were performed for the other parameters of this example (as well as of the two other model examples) and confirmed a proper choice of qualitatively representative scenarios in all cases.

4. Game-Theoretic Models of Opinion Control over Networks

In this section, we consider differential game-based models of opinion control over networks in which players are competing firms. We study the cases of budget constraints in the form of equality and inequality. In both cases, we compare the independent (individual) and cooperative behavior of players (the latter setup reduces the game-theoretic model to an optimal control problem). We use the Hamilton–Jacobi–Bellman equations and Lagrange’s method of multipliers in the case of equality constraints, reducing the case of inequality constraints to it.

Model 1 (budget constraint in form of equality)

First, consider the independent behavior of the players. The problem of firm i has the form

$$\begin{gathered} J_i={\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{x}_j\left(t\right)}dt}\to \max , \\ {\dot{x}}_j={\displaystyle \sum _{i=1}^r{b}_j^i\sqrt{u_j^i\left(x_j\left(t\right)\right)}}+{\displaystyle \sum _{l=1}^N{a}_{lj}{x}_l\left(t\right)}, x_j\left(0\right)=x_{j0},j=1,2,\dots ,N, \\ {\displaystyle \sum _{j=1}^N{u}_j^i\left(x_j\left(t\right)\right)=R_i^t}, {\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{R}_i^t}dt=R_i, \end{gathered}$$

where serial numbers j and i are associated with agents and firms, respectively; N and r give the total number of agents and firms, respectively; the other notations are the same as in Section 3. Different firms separately decide which agents of strong subgroups to influence. Therefore, we let $b_j^i=0$ if firm i does not affect agent j.

We write the Hamilton–Jacobi–Bellman equation

$$\mathsf{\rho }{V}_i-\frac{\partial V_i}{\partial t}=\underset{u_j^i,1\le j\le N}{{\displaystyle \max }}\underset{}{{\displaystyle \left\{{\displaystyle \sum _{j=1}^N{x}_j\left(t\right)+{\displaystyle \sum _{j=1}^N\frac{\partial V_i}{\partial x_j}\left[{\displaystyle \sum _{i=1}^r{b}_j^i\sqrt{u_j^i\left(x_j\right)}}+{\displaystyle \sum _{l=1}^N{a}_{lj}{x}_l}\right]}}\right\}}}$$

(9)

subject to the constraint ${\displaystyle \sum _{j=1}^N{u}_j^i\left(x_j\left(t\right)\right)=R_i^t}$. Maximization over $u_j^i$, $j=1,2,\dots ,N$, yields

$$\frac{\partial V}{\partial x_j}{b}_j^i\frac{1}{2}{\left(u_j^i\right)}^{-\frac{1}{2}}=\mathsf{\mu },$$

where $\mathsf{\mu }$ is the Lagrange multiplier. After simple transformations, we obtain

$$u_j^i=\frac{R_i^t{\left(b_j^i\frac{\partial V}{\partial x_j}\right)}^2}{{\displaystyle \sum _{j=1}^N{\left(b_j^i\frac{\partial V}{\partial x_j}\right)}^2}}.$$

(10)

Let the Bellman functions be linear:

$$V_i\left(x,t\right)={\displaystyle \sum _{j=1}^N{\mathsf{\alpha }}_j\left(t\right)x_j+\mathsf{\beta }\left(t\right)}.$$

Then Equation (9) can be written as

$$\begin{array}{c}\mathsf{\rho }{\displaystyle \sum _{j=1}^N{\mathsf{\alpha }}_j\left(t\right)x_j+\mathsf{\rho }\mathsf{\beta }\left(t\right)-{\displaystyle \sum _{j=1}^N{{\mathsf{\alpha }}^{\prime }}_j\left(t\right)x_j-{\mathsf{\beta }}^{\prime }\left(t\right)=}}\\ ={\displaystyle \sum _{j=1}^N{x}_j\left(t\right)+{\displaystyle \sum _{j=1}^N{\displaystyle \sum _{l=1}^N{\mathsf{\alpha }}_j\left(t\right)a_{lj}{x}_l+{\displaystyle \sum _{i=1}^r\sqrt{R_i^t}\sqrt{{\displaystyle \sum _{j=1}^N{\left({\mathsf{\alpha }}_j\left(t\right)b_j^i\right)}^2}}}}}}\end{array}$$

Equalizing the factors at the identical powers of x, we arrive at the differential equations

$${{\mathsf{\alpha }}^{\prime }}_j\left(t\right)-\mathsf{\rho }{\mathsf{\alpha }}_j\left(t\right)+{\displaystyle \sum _{l=1}^N{\mathsf{\alpha }}_l\left(t\right)a_{jl}}=-1$$

(11)

for the factors at x, $j=1,2,\dots ,N$, and

$${\mathsf{\beta }}^{\prime }\left(t\right)-\mathsf{\rho }\mathsf{\beta }\left(t\right)=-{\displaystyle \sum _{i=1}^r\sqrt{R_i^t}\sqrt{{\displaystyle \sum _{j=1}^N{\left({\mathsf{\alpha }}_j\left(t\right)b_j^i\right)}^2}}}$$

(12)

for the free term. Now, we write the system of Equation (11) in matrix form:

$${\mathsf{\alpha }}^{\prime }=\left(\mathsf{\rho }I-A\right)\mathsf{\alpha }-\mathsf{\epsilon },$$

(13)

where A is the influence matrix; the column vector $\mathsf{\alpha }$ consists of the factors ${\mathsf{\alpha }}_j$, $j=1,2,\dots ,N$; I denotes an identity matrix of compatible dimensions; finally, $\mathsf{\epsilon }$ is the N-dimensional column vector of unities. Solving the system of differential Equations (13) gives

$$\overline{\mathsf{\alpha }}={\left(\mathsf{\rho }I-A\right)}^{-1}\mathsf{\epsilon }, \mathsf{\alpha }=e^{\left(\mathsf{\rho }I-A\right)t}C+{\left(\mathsf{\rho }I-A\right)}^{-1}\mathsf{\epsilon }.$$

The column vector of the integration constants can be found from the boundary-value conditions

$$\mathsf{\alpha }\left(T\right)=0,$$

which lead to

$$C=-e^{-\left(\mathsf{\rho }I-A\right)t}{\left(\mathsf{\rho }I-A\right)}^{-1}\mathsf{\epsilon }.$$

As a result,

$$\mathsf{\alpha }=-e^{\left(\mathsf{\rho }I-A\right)\left(t-T\right)}{\left(\mathsf{\rho }I-A\right)}^{-1}\mathsf{\epsilon }+{\left(\mathsf{\rho }I-A\right)}^{-1}\mathsf{\epsilon }=\left(e^{\left(A-\mathsf{\rho }I\right)\left(T-t\right)}-I\right){\left(A-\mathsf{\rho }I\right)}^{-1}\mathsf{\epsilon }.$$

For $t=0$,

$$\mathsf{\alpha }\left(0\right)=\left(e^{\left(A-\mathsf{\rho }I\right)T}-I\right){\left(A-\mathsf{\rho }I\right)}^{-1}\mathsf{\epsilon }.$$

(14)

We solve Equation (12) by the method of variation of constants:

$$\mathsf{\beta }\left(t\right)=e^{\mathsf{\rho }t}C\left(t\right).$$

Then

$${\mathsf{\beta }}^{\prime }=C^{\prime }{e}^{\mathsf{\rho }t}+C\mathsf{\rho }{e}^{\mathsf{\rho }t}-C\mathsf{\rho }{e}^{\mathsf{\rho }t}=-{\displaystyle \sum _{i=1}^r\sqrt{R_i^t{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}},$$

and hence it follows that

$$C\left(t\right)=-{\displaystyle \sum _{i=1}^r{\displaystyle \underset{0}{\overset{t}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R_i^{\mathsf{\tau }}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}}d\mathsf{\tau }+C.$$

Because

$$C\left(T\right)=0,$$

we have

$$C={\displaystyle \sum _{i=1}^r{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R_i^{\mathsf{\tau }}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}}d\mathsf{\tau },$$

and consequently

$$C\left(t\right)={\displaystyle \sum _{i=1}^r{\displaystyle \underset{t}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R_i^{\mathsf{\tau }}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}}d\mathsf{\tau }.$$

Therefore,

$$\mathsf{\beta }\left(t\right)={\displaystyle \sum _{i=1}^r{\displaystyle \underset{t}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\left(\mathsf{\tau }-t\right)}\sqrt{R_i^{\mathsf{\tau }}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}}d\mathsf{\tau }.$$

For $t=0$,

$$\mathsf{\beta }\left(0\right)={\displaystyle \sum _{i=1}^r{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R_i^{\mathsf{\tau }}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}}d\mathsf{\tau }.$$

Thus,

$$\underset{u_j^i,1\le j\le N}{{\displaystyle \max J_i}}=V_i\left(x\left(0\right),0\right)={\displaystyle \sum _{j=1}^N{\mathsf{\alpha }}_j\left(0\right)x_j\left(0\right)}+{\displaystyle \sum _{i=1}^r{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R_i^{\mathsf{\tau }}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}}d\mathsf{\tau },$$

(15)

where ${\mathsf{\alpha }}_j\left(0\right)$, $j=1,2,\dots ,N$, are the components of the vector $\mathsf{\alpha }\left(0\right)$; see (14).

It remains to solve an isoperimetric problem: for each firm i, allocate resources over time so that the i-th term of (15) achieves maximum,

$${\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R_i^{\mathsf{\tau }}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }\to \max$$

subject to the constraint

$${\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{R}_i^{\mathsf{\tau }}}d\mathsf{\tau }=R_i.$$

The Lagrange function for this problem is given by

$$L\left(t,R_i^t,{\left(R_i^t\right)}^{\prime },\lambda \right)=e^{-\mathsf{\rho }t}\sqrt{R_i^t{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}+\lambda e^{-\mathsf{\rho }t}{R}_i^t.$$

The Euler equation takes the form

$$\frac{\partial L\left(t,R_i^t,{\left(R_i^t\right)}^{\prime },\lambda \right)}{\partial R_i^t}=\frac{e^{-\mathsf{\rho }t}\sqrt{{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}{2\sqrt{R_i^t}}+\lambda e^{-\mathsf{\rho }t}=0.$$

Hence,

$$R_i^t=\frac{{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}{4{\lambda }^2}.$$

The Lagrange multiplier can be calculated from the budget constraint

$$\frac{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}{4{\lambda }^2}=R_i.$$

We have:

$$\frac{1}{4{\lambda }^2}=\frac{R_i}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt},$$

which yields

$$R_i^t=\frac{R_i{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}.$$

Finally,

$$\begin{gathered} \mathsf{\beta }\left(0\right)={\displaystyle \sum _{i=1}^r{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R_i}\frac{\sqrt{{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}\sqrt{{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}{\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}d\mathsf{\tau }}}= \\ ={\displaystyle \sum _{i=1}^r\sqrt{R_i}\frac{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^{2}d\mathsf{\tau }}}}{\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}}={\displaystyle \sum _{i=1}^r\sqrt{R_i}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}. \end{gathered}$$

With independent behavior, the payoff of each player makes up

$${\displaystyle \sum _{j=1}^N{x}_{j0}{\mathsf{\alpha }}_j\left(0\right)+}{\displaystyle \sum _{i=1}^r\sqrt{R_i}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}-R_i,$$

where ${\mathsf{\alpha }}_j\left(0\right)$ are the components of vector (14), $j=1,2,\dots ,N$.

Substituting the expression of $R_i^t$ into (10), we obtain the optimal control formula

$$\begin{gathered} u_j^i=\frac{{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}{{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}\cdot \frac{R_i{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}=\frac{R_i{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}, \\ i=1,2,\dots ,r; j=1,2,\dots ,N. \end{gathered}$$

Now, consider the cooperative behavior of the players, under which the original game is reduced to the optimal control problem

$$\begin{gathered} J={\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{x}_j\left(t\right)}dt}\to \max , \\ {\dot{x}}_j={\displaystyle \sum _{i=1}^r{b}_j^i\sqrt{u_j^i\left(x_j\left(t\right)\right)}}+{\displaystyle \sum _{l=1}^N{a}_{lj}{x}_l\left(t\right)}, x_j\left(0\right)=x_{j0}, j=1,2,\dots ,N, \\ {\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{u}_j^i\left(x_j\left(t\right)\right)=R^t}}, {\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{R}^t}dt=R={\displaystyle \sum _{i=1}^r{R}_i}, \end{gathered}$$

where serial numbers j and i are associated with agents and firms, respectively; N and r give the total number of agents and firms, respectively. Different firms separately decide which agents of strong subgroups to influence. Therefore, we let $b_j^i=0$ if firm i does not affect agent j.

We write the Hamilton–Jacobi–Bellman equation

$$\mathsf{\rho }V-\frac{\partial V}{\partial t}=\underset{\begin{array}{l}{u}_j^i,1\le j\le N,\\ 1\le i\le r\end{array}}{{\displaystyle \max }}\underset{}{{\displaystyle \left\{{\displaystyle \sum _{j=1}^N{x}_j\left(t\right)+{\displaystyle \sum _{j=1}^N\frac{\partial V}{\partial x_j}\left[{\displaystyle \sum _{i=1}^r{b}_j^i\sqrt{u_j^i\left(x_j\right)}}+{\displaystyle \sum _{l=1}^N{a}_{lj}{x}_l}\right]}}\right\}}}$$

(16)

subject to the constraint ${\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{u}_j^i\left(x_j\left(t\right)\right)=R^t}}$. Maximization over $u_j^i$, $i=1,2,\dots ,r$, $j=1,2,\dots ,N$, yields

$$\frac{\partial V}{\partial x_j}{b}_j^i\frac{1}{2}{\left(u_j^i\right)}^{-\frac{1}{2}}=\mathsf{\mu },$$

where $\mathsf{\mu }$ is the Lagrange multiplier. Then for any $1\le i_1,i_2\le r$ and $1\le j_1,j_2\le N$,

$$\frac{u_{j_1}^{i_1}}{{\left(b_{j_1}^{i_1}\frac{\partial V}{\partial x_{j_1}}\right)}^2}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i\frac{\partial V}{\partial x_j}\right)}^2}}=R^t,$$

and hence

$$u_j^i=\frac{R^t{\left(b_j^i\frac{\partial V}{\partial x_j}\right)}^2}{{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i\frac{\partial V}{\partial x_j}\right)}^2}}}.$$

(17)

Let the Bellman function be linear:

$$V\left(x,t\right)={\displaystyle \sum _{j=1}^N{\mathsf{\alpha }}_j\left(t\right)x_j+\mathsf{\beta }\left(t\right)}.$$

By analogy with the previous case, we may write Equation (16) as

$$\begin{gathered} \mathsf{\rho }{\displaystyle \sum _{j=1}^N{\mathsf{\alpha }}_j\left(t\right)x_j+\mathsf{\rho }\mathsf{\beta }\left(t\right)-{\displaystyle \sum _{j=1}^N{{\mathsf{\alpha }}^{\prime }}_j\left(t\right)x_j-{\mathsf{\beta }}^{\prime }\left(t\right)=}} \\ ={\displaystyle \sum _{j=1}^N{x}_j\left(t\right)+{\displaystyle \sum _{j=1}^N{\displaystyle \sum _{l=1}^N{\mathsf{\alpha }}_j\left(t\right)a_{lj}{x}_l+\sqrt{R^t}\sqrt{{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left({\mathsf{\alpha }}_j\left(t\right)b_j^i\right)}^2}}}}}}. \end{gathered}$$

Equalizing the factors at the identical powers of x, we arrive at the differential equations

$${{\mathsf{\alpha }}^{\prime }}_j\left(t\right)-\mathsf{\rho }{\mathsf{\alpha }}_j\left(t\right)+{\displaystyle \sum _{l=1}^N{\mathsf{\alpha }}_l\left(t\right)a_{jl}}=-1$$

(18)

for the factors at x,$j=1,2,\dots ,N$, and

$${\mathsf{\beta }}^{\prime }\left(t\right)-\mathsf{\rho }\mathsf{\beta }\left(t\right)=-\sqrt{R^t{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left({\mathsf{\alpha }}_j\left(t\right)b_j^i\right)}^2}}}$$

(19)

for the free term. Now, we write the system of Equation (18) in matrix form:

$${\mathsf{\alpha }}^{\prime }=\left(\mathsf{\rho }I-A\right)\mathsf{\alpha }-\mathsf{\epsilon },$$

(20)

where A is the influence matrix; the column vector $\mathsf{\alpha }$ consists of the factors ${\mathsf{\alpha }}_j$, $j=1,2,\dots ,N$; I denotes an identity matrix of compatible dimensions; finally, $\mathsf{\epsilon }$ is the N-dimensional column vector of unities. Solving the system of differential Equation (20) gives

$$\overline{\mathsf{\alpha }}={\left(\mathsf{\rho }I-A\right)}^{-1}\mathsf{\epsilon }, \mathsf{\alpha }=e^{\left(\mathsf{\rho }I-A\right)t}C+{\left(\mathsf{\rho }I-A\right)}^{-1}\mathsf{\epsilon }.$$

Due to the boundary-value conditions

$$\mathsf{\alpha }\left(T\right)=0,$$

we have

$$\mathsf{\alpha }=-e^{\left(\mathsf{\rho }I-A\right)\left(t-T\right)}{\left(\mathsf{\rho }I-A\right)}^{-1}\mathsf{\epsilon }+{\left(\mathsf{\rho }I-A\right)}^{-1}\mathsf{\epsilon }=\left(e^{\left(A-\mathsf{\rho }I\right)\left(T-t\right)}-I\right){\left(A-\mathsf{\rho }I\right)}^{-1}\mathsf{\epsilon }.$$

For $t=0$,

$$\mathsf{\alpha }\left(0\right)=\left(e^{\left(A-\mathsf{\rho }I\right)T}-I\right){\left(A-\mathsf{\rho }I\right)}^{-1}\mathsf{\epsilon }.$$

(21)

We solve Equation (19) by the method of variation of constants:

$$\mathsf{\beta }\left(t\right)=e^{\mathsf{\rho }t}C\left(t\right),$$

which gives

$$C\left(t\right)=-{\displaystyle \underset{0}{\overset{t}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R^{\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left({\mathsf{\alpha }}_j\left(t\right)b_j^i\right)}^2}}}}d\mathsf{\tau }+C.$$

Because

$$C\left(T\right)=0,$$

we have

$$C\left(t\right)={\displaystyle \underset{t}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R^{\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left({\mathsf{\alpha }}_j\left(t\right)b_j^i\right)}^2}}}}d\mathsf{\tau }.$$

Therefore,

$$\mathsf{\beta }\left(t\right)={\displaystyle \underset{t}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\left(\mathsf{\tau }-t\right)}\sqrt{R^{\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left({\mathsf{\alpha }}_j\left(t\right)b_j^i\right)}^2}}}}d\mathsf{\tau }.$$

For $t=0$,

$$\mathsf{\beta }\left(0\right)={\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R^{\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left({\mathsf{\alpha }}_j\left(t\right)b_j^i\right)}^2}}}}d\mathsf{\tau }.$$

Since

$$\underset{\begin{array}{l}{u}_j^i,1\le j\le N,\\ 1\le i\le r\end{array}}{{\displaystyle \max J}}=V\left(x\left(0\right),0\right),$$

we obtain

$$\underset{\begin{array}{l}{u}_j^i,1\le j\le N,\\ 1\le i\le r\end{array}}{{\displaystyle \max J}}={\displaystyle \sum _{j=1}^N{\mathsf{\alpha }}_j\left(0\right)x_j\left(0\right)}+{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R^{\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}}d\mathsf{\tau },$$

(22)

where ${\mathsf{\alpha }}_j\left(0\right)$, $j=1,2,\dots ,N$, are the components of the vector $\mathsf{\alpha }\left(0\right)$; see (21). Once again, it remains to solve a simple isoperimetric problem: allocate resources over time so that the last term of (22) achieves maximum.

$${\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\sqrt{R^{\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}}d\mathsf{\tau }\to \max$$

subject to the constraint

$${\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{R}^{\mathsf{\tau }}}d\mathsf{\tau }=R.$$

The Lagrange function for this problem is given by

$$L\left(t,R^t,{\left(R^t\right)}^{\prime },\lambda \right)=e^{-\mathsf{\rho }t}\sqrt{R^t{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}+\lambda e^{-\mathsf{\rho }t}{R}^t.$$

The Euler equation takes the form

$$\frac{\partial L\left(t,R^t,{\left(R^t\right)}^{\prime },\lambda \right)}{\partial R^t}=\frac{e^{-\mathsf{\rho }t}\sqrt{{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}}{2\sqrt{R^t}}+\lambda e^{-\mathsf{\rho }t}=0.$$

Hence,

$$R^t=\frac{{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}{4{\lambda }^2}.$$

The Lagrange multiplier can be calculated from the budget constraint

$$\frac{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}dt}{4{\lambda }^2}=R.$$

We have

$$\frac{1}{4{\lambda }^2}=\frac{R}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}dt},$$

which yields

$$R^t=\frac{R{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}dt}.$$

Finally,

$$\begin{gathered} \mathsf{\beta }\left(0\right)=\sqrt{R}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}\frac{\sqrt{{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}\sqrt{{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}}{\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}dt}}}d\mathsf{\tau }= \\ =\sqrt{R}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }}. \end{gathered}$$

In the case of cooperative behavior, the total payoff makes up

$${\displaystyle \sum _{j=1}^N{x}_{j0}{\mathsf{\alpha }}_j\left(0\right)+}\sqrt{R}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }}-R,$$

(23)

where ${\mathsf{\alpha }}_j\left(0\right)$ are the components of vector (21), $j=1,2,\dots ,N$.

Substituting the expression of $R^t$ into (17), we obtain the optimal control formula

$$\begin{gathered} u_j^i=\frac{{\left(b_j^i\frac{\partial V}{\partial x_j}\right)}^2}{{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i\frac{\partial V}{\partial x_j}\right)}^2}}}\cdot \frac{R{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}dt}=\frac{R{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}}dt}, \\ i=1,2,\dots ,r; j=1,2,\dots ,N. \end{gathered}$$

Let us compare the payoffs in the cases of independent behavior and cooperation of the players. With independent behavior, the total payoff is given by

$${\displaystyle \sum _{j=1}^N{x}_{j0}{\mathsf{\alpha }}_j\left(0\right)+}{\displaystyle \sum _{i=1}^r\sqrt{R_i}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}-{\displaystyle \sum _{i=1}^r{R}_i}.$$

(24)

In other words, we have to compare the term

$${\displaystyle \sum _{i=1}^r\sqrt{R_i}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}$$

for the case of independent behavior with the term

$$\sqrt{R}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }}$$

for the case of cooperation.

In accordance with the Holder inequality, for r pairs of positive numbers $u_i$, $v_i$, $i=1,2,\dots ,r$,

$${{\displaystyle \sum _{i=1}^r{u}_i{v}_i\le \left({\displaystyle \sum _{i=1}^r{\left(u_i\right)}^p}\right)}}^{\frac{1}{p}}{\left({\displaystyle \sum _{i=1}^r{\left(v_i\right)}^q}\right)}^{\frac{1}{q}}$$

if $p>1$ and $\frac{1}{p}+\frac{1}{q}=1$, or

$${{\displaystyle \sum _{i=1}^r{u}_i{v}_i\ge \left({\displaystyle \sum _{i=1}^r{\left(u_i\right)}^p}\right)}}^{\frac{1}{p}}{\left({\displaystyle \sum _{i=1}^r{\left(v_i\right)}^q}\right)}^{\frac{1}{q}},$$

if $p<1$, $p\ne 0$ and $\frac{1}{p}+\frac{1}{q}=1$.

Denoting

$$u_i=\sqrt{R_i}, v_i=\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt},$$

and letting $p=q=2$, by the Holder inequality we establish that

$${\displaystyle \sum _{i=1}^r\sqrt{R_i}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}\le \sqrt{R}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }},$$

i.e., the total payoff of all firms with independent behavior does not exceed its counterpart in the case of their cooperation.

Model 2 (budget constraint in form of inequality)

First, consider the independent behavior of the players. The problem of firm i has the form

$$\begin{gathered} J_i={\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}\left({\displaystyle \sum _{j=1}^N{x}_j\left(t\right)-{\displaystyle \sum _{j=1}^N{s}_j^i{u}_j^i\left(x_j\left(t\right)\right)}}\right)dt}\to \max , \\ {s}_j^i=\left\{\begin{array}{c}1\hspace{1em}if\hspace{1em}{b}_j^i\ne 0,\\ 0\hspace{1em}if\hspace{1em}{b}_j^i=0,\end{array}\right. \\ {\dot{x}}_j={\displaystyle \sum _{i=1}^r{b}_j^i\sqrt{u_j^i\left(x_j\left(t\right)\right)}}+{\displaystyle \sum _{l=1}^N{a}_{lj}{x}_l\left(t\right)}, x_j\left(0\right)=x_{j0},j=1,2,\dots ,N, \\ {\displaystyle \sum _{j=1}^N{u}_j^i\left(x_j\left(t\right)\right)\le R_i^t}, {\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{R}_i^t}dt\le {\Re }_i, \end{gathered}$$

where serial numbers j and i are associated with agents and firms, respectively; N and r give the total number of agents and firms, respectively. Different firms separately decide which agents of strong subgroups to influence. Therefore, we let $b_j^i=0$ if firm i does not affect agent j.

For solving this problem with inequality constraints, consider the following set of problems with equality constraints:

$$\begin{gathered} J_i={\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}\left({\displaystyle \sum _{j=1}^N{x}_j\left(t\right)-{\displaystyle \sum _{j=1}^N{s}_j^i{u}_j^i\left(x_j\left(t\right)\right)}}\right)dt}\to \max , \\ {s}_j^i=\left\{\begin{array}{c}1\hspace{1em}if\hspace{1em}{b}_j^i\ne 0,\\ 0\hspace{1em}if\hspace{1em}{b}_j^i=0,\end{array}\right. \\ {\dot{x}}_j={\displaystyle \sum _{i=1}^r{b}_j^i\sqrt{u_j^i\left(x_j\left(t\right)\right)}}+{\displaystyle \sum _{l=1}^N{a}_{lj}{x}_l\left(t\right)}, x_j\left(0\right)=x_{j0}, j=1,2,\dots ,N, \\ {\displaystyle \sum _{j=1}^N{u}_j^i\left(x_j\left(t\right)\right)=R_i^t}, {\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{R}_i^t}dt=R_i \end{gathered}$$

with an arbitrary value of the parameter $R_i$, $0\le R_i\le {\Re }_i$. Later, we will choose an appropriate value of $R_i$ for which the solution is achieved. By analogy with the previous case, we calculate the payoff of each player i with independent behavior in the form

$${\displaystyle \sum _{j=1}^N{x}_{j0}{\mathsf{\alpha }}_j\left(0\right)+}{\displaystyle \sum _{i=1}^r\sqrt{R_i}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}-R_i,$$

where ${\mathsf{\alpha }}_j\left(0\right)$ are the components of the vector $\mathsf{\alpha }\left(0\right)=\left(e^{\left(A-\mathsf{\rho }I\right)T}-I\right){\left(A-\mathsf{\rho }I\right)}^{-1}\mathsf{\epsilon }$,$j=1,2,\dots ,N$, and also the optimal control action

$$u_j^i=\frac{R_i{(b_j^i{\alpha }_j(t))}^2}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N(b_j^i{\alpha }_j(t))dt}}}, i=1,2,\dots ,r; j=1,2,\dots ,N.$$

Now, we get back to the original statement of the problem with inequality constraints, trying to find for which value of the parameter $R_i$ from the range $\left[0,{\Re }_i\right]$ the payoff of firm i achieves maximum. From this point onwards, $R_i^t$ denotes the costs of firm i at a time instant t, while $R_i$ are the total costs over the entire time horizon (taking into account the discounting effect). Moreover, we assume that the total costs $R_i$ are distributed over time, i.e., for any $R_i$ the function $R_i^t$ is chosen in an optimal way. As a matter of fact, we varied the resulting solution in $R_i^t$ for each $R_i$.

Thus, we consider the problem

$${\displaystyle \sum _{j=1}^N{x}_{j0}{\mathsf{\alpha }}_j\left(0\right)+}{\displaystyle \sum _{l=1}^r\sqrt{R_l}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^l{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}-R_i\underset{R_i}{\to }\max ,$$

subject to the constraint $0\le R_i\le {\Re }_i$. The first-order optimality condition with respect to $R_i$ yields

$$\frac{\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}{2\sqrt{R_i}}-1=0,$$

or

$$R_i=\frac{1}{4}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt.$$

Hence, the optimal total costs of firm i are given by

$$R_i^{*}=\left\{\begin{array}{c}\frac{1}{4}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt\hspace{1em}if\hspace{1em}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt<4{\Re }_i,\\ {\Re }_i\hspace{1em}if\hspace{1em}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt\ge 4{\Re }_i.\end{array}\right.$$

To proceed, we study the cooperative behavior of the players, which reduces the original game to the optimal control problem

$$\begin{gathered} J={\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}\left({\displaystyle \sum _{j=1}^N{x}_j\left(t\right)-{\displaystyle \sum _{j=1}^N{s}_j^i{u}_j^i\left(x_j\left(t\right)\right)}}\right)dt}\to \max , \\ {s}_j^i=\left\{\begin{array}{c}1\hspace{1em}if\hspace{1em}{b}_j^i\ne 0,\\ 0\hspace{1em}if\hspace{1em}{b}_j^i=0,\end{array}\right. \\ {\dot{x}}_j={\displaystyle \sum _{i=1}^r{b}_j^i\sqrt{u_j^i\left(x_j\left(t\right)\right)}}+{\displaystyle \sum _{l=1}^N{a}_{lj}{x}_l\left(t\right)}, x_j\left(0\right)=x_{j0}, j=1,2,\dots ,N, \\ {\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{u}_j^i\left(x_j\left(t\right)\right)\le R^t}}, {\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{R}^t}dt\le \Re ={\displaystyle \sum _{i=1}^r{\Re }_i}, \end{gathered}$$

where serial numbers j and i are associated with agents and firms, respectively; N and r give the total number of agents and firms, respectively. Different firms separately decide which agents of strong subgroups to influence. Therefore, we let $b_j^i=0$ if firm i does not affect agent j.

For solving this problem with inequality constraints, consider the following set of problems with equality constraints:

$$\begin{gathered} J={\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{x}_j\left(t\right)}dt}\to \max , \\ {\dot{x}}_j={\displaystyle \sum _{i=1}^r{b}_j^i\sqrt{u_j^i\left(x_j\left(t\right)\right)}}+{\displaystyle \sum _{l=1}^N{a}_{lj}{x}_l\left(t\right)}, x_j\left(0\right)=x_{j0}, j=1,2,\dots ,N, \\ {\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{u}_j^i\left(x_j\left(t\right)\right)=R^t}}, {\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{R}^t}dt=R, \end{gathered}$$

with an arbitrary value of the parameter $R$, $0\le R\le \Re$. Later, we will choose an appropriate value of $R$ for which the optimal solution is achieved. By analogy with the previous case, we calculate the payoff of each player i with cooperative behavior in the form

$${\displaystyle \sum _{j=1}^N{x}_{j0}{\mathsf{\alpha }}_j\left(0\right)+}\sqrt{R}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }}-R,$$

(25)

where ${\mathsf{\alpha }}_j\left(0\right)$ are the coordinates of the vector $\mathsf{\alpha }\left(0\right)=\left(e^{\left(A-\mathsf{\rho }I\right)T}-I\right){\left(A-\mathsf{\rho }I\right)}^{-1}\mathsf{\epsilon }$, $j=1,2,\dots ,N$, and the optimal control action

$$u_j^i=\frac{R{(b_j^i{\alpha }_j(t))}^2}{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{(b_j^i{\alpha }_j(t))}^{2}dt}}}}, i=1,2,\dots ,r; j=1,2,\dots ,N.$$

Reverting to the original statement of the problem with inequality constraints, we find for which value of the parameter $R$ from the range $\left[0,\Re \right]$ the total payoff achieves maximum. From this point onwards, $R^t$ denotes the total costs at a time instant t, while $R$ are the total costs over the entire time horizon (taking into account the discounting effect). Moreover, we assume that the total costs $R$ are distributed over time, i.e., for any $R$ the function $R^t$ is chosen in an optimal way. (As a matter of fact, we varied the resulting solution in $R^t$ for each $R$.)

Thus, we consider the problem

$${\displaystyle \sum _{j=1}^N{x}_{j0}{\mathsf{\alpha }}_j\left(0\right)+}\sqrt{R}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }}-R\underset{R}{\to }\max$$

subject to the constraint $0\le R\le \Re$. The first-order optimality condition with respect to $R$ yields

$$\frac{\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }}}{2\sqrt{R}}-1=0,$$

or

$$R=\frac{1}{4}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }.$$

Hence, the optimal total costs are given by

$$R^{\ast }=\left\{\begin{array}{c}\frac{1}{4}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }\hspace{1em}if\hspace{1em}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}dt<4\Re ,\\ \Re \hspace{1em}if\hspace{1em}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}dt\ge 4\Re .\end{array}\right.$$

Thus, the total payoff has the following form:

-

in the first case,

$${\displaystyle \sum _{j=1}^N{x}_{j0}{\mathsf{\alpha }}_j\left(0\right)+}\frac{1}{4}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau };$$

-

in the second case,

$${\displaystyle \sum _{j=1}^N{x}_{j0}{\mathsf{\alpha }}_j\left(0\right)+}\sqrt{\Re }\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }}-\Re .$$

We compare the total payoffs in the cases of independent behavior and cooperation of the players. First, we do it for the problem with equality constraints and ${\displaystyle \sum _{i=1}^r{R}_i=R}$. In this problem, the total payoff in the case of cooperation is described by formula (25); in the case of independent behavior, by formula (24). In other words, we have to compare the term

$${\displaystyle \sum _{i=1}^r\sqrt{R_i}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}$$

in (24) for the case of independent behavior with the term

$$\sqrt{R}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }}$$

in (25) for the case of cooperation.

Lemma 1.

In the problem with equality constraints, the total payoff of all firms with independent behavior does not exceed its counterpart in the case of their cooperation.

 Proof. 

In accordance with the Holder inequality, for r pairs of positive numbers $u_i$, $v_i$, $i=1,2,\dots ,r,$

$${{\displaystyle \sum _{i=1}^r{u}_i{v}_i\le \left({\displaystyle \sum _{i=1}^r{\left(u_i\right)}^p}\right)}}^{\frac{1}{p}}{\left({\displaystyle \sum _{i=1}^r{\left(v_i\right)}^q}\right)}^{\frac{1}{q}}$$

if $p>1$ and $\frac{1}{p}+\frac{1}{q}=1$, or

$${{\displaystyle \sum _{i=1}^r{u}_i{v}_i\ge \left({\displaystyle \sum _{i=1}^r{\left(u_i\right)}^p}\right)}}^{\frac{1}{p}}{\left({\displaystyle \sum _{i=1}^r{\left(v_i\right)}^q}\right)}^{\frac{1}{q}},$$

if $p<1$, $p\ne 0$ and $\frac{1}{p}+\frac{1}{q}=1$.

Denoting

$$u_i=\sqrt{R_i}, v_i=\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt},$$

and letting $p=q=2$, by the Holder inequality we establish that

$${\displaystyle \sum _{i=1}^r\sqrt{R_i}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt}}\le \sqrt{R}\sqrt{{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}d\mathsf{\tau }},$$

i.e., in the problem with equality constraints, the total payoff of all firms with independent behavior does not exceed its counterpart in the case of their cooperation. The proof of this lemma is complete. □

Let us consider the problem with inequality constraints, i.e., ${\displaystyle \sum _{i=1}^r{\Re }_i=\Re }$. We introduce the following terminology. If firm i with independent behavior satisfies the inequality ${\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt\le 4{\Re }_i$, then it will be said that firm i has enough marketing resources. Otherwise, i.e., ${\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }t}{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(t\right)\right)}^2}}dt>4{\Re }_i$, it will be said that firm i has a lack of marketing resources. If in the case of cooperation the inequality ${\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\mathsf{\rho }\mathsf{\tau }}{\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^N{\left(b_j^i{\mathsf{\alpha }}_j\left(\mathsf{\tau }\right)\right)}^2}}}dt\le 4\Re$ holds, then it will be said that there are enough marketing resources in total, both in the cases of cooperative and independent behavior. Otherwise (meaning that the opposite inequality is true), it will be said that there is a lack of marketing resources in total, in both cases.

As before, ${\Re }_i$ denotes the total quantity of marketing resource allocated to firm i while $R_i$ the total quantity of marketing resource used by firm i in the optimal solution. In the same fashion, in the case of cooperation, $\Re$ denotes the total quantity of marketing resource of all firms while R the total quantity of marketing resource used in the optimal solution. In the case of independent behavior, if firm i has a lack of marketing resources, then ${\Re }_i=R_i$ and its payoff monotonically depends on ${\Re }_i$; if firm i has enough marketing resources, then ${\Re }_i>R_i$ and its payoff becomes independent of $R_i$ (as a result, marketing resources are redundant and the shadow price of marketing resource $\mathsf{\mu }$ is 0). In the case of cooperation, if there is a lack of marketing resources in total, then $\Re =R$ and the total payoff monotonically depends on $\Re$; if there are enough marketing resources in total, then $\Re =R$ and the total payoff becomes independent of $\Re =R$ (as a result, marketing resources are redundant and the shadow price of marketing resource $\mathsf{\mu }$ is 0).

In terms of resource availability, four cases are possible as follows:

(1)

There are enough marketing resources in total, and they are allocated among the firms so that each firm has enough marketing resources. In this case, the total payoff of all firms with independent behavior coincides with the total payoff in the case of their cooperation.

(2)

There are enough marketing resources in total, but they are poorly allocated among the firms: some firms have a lack of marketing resources. In this case, the total quantity of marketing resource used by the firms in independent behavior is less than the total quantity of marketing resource used in cooperation. On the interval corresponding to the lack of marketing resources, the dependence of payoffs on the quantity of resource used is strictly monotonic; hence, the total payoff of all firms with independent behavior is smaller than the total payoff in the case of their cooperation.

(3)

There is a lack of marketing resources in total, but they are allocated so that some firms have enough marketing resources. In this case, the total quantity of marketing resource used by the firms in independent behavior is smaller than the total quantity of marketing resource used in cooperation. Consequently, the total payoff of all firms with independent behavior is smaller than the total payoff in the case of cooperation.

(4)

Each firm has a lack of marketing resources. Then, there is a lack of marketing resources in total. In this case, by the lemma the total payoff of all firms with independent behavior does not exceed the total payoff in the case of cooperation.

Thus, the models of influence and control in social groups have the following applications in marketing; see

Table 4. Models of influence and control over networks and their applications to marketing.

Model Problems	Applications to Marketing
Network analysis	1. Audience segmentation, identification of strong subgroups that determine the inner common resulting opinions of subgroups members and also the individual resulting opinions of other agents as a linear combination of resulting opinions of strong subgroups 2. Calculation of centrality, prestige and other characteristics of audience
Prediction over network	Calculation of resulting opinions of all agents without purposeful impact on them
Optimal control over network	Choice of optimal marketing actions (impact) for audience by one firm
Dynamic games over networks	Choice of compromise impact on audience in the case of competition and/or cooperation of firms

[46].

5. Conclusions

Social networks have been a popular object of mathematical modeling and computer simulation since the second half of the 20th century. There are various approaches to the mathematical modeling and simulation of networks, based on a diverse mathematical apparatus, including discrete and continuous, deterministic and stochastic models of different nature. Among them are graph-theoretic and dynamical systems models, optimization and optimal control problems, and game-theoretic models, as well as the gene-environment models, eco-finance models, Markov switching models, and rumor propagation models.

This paper develops the basic De Groot model and formulates the problems of analysis, prediction, optimal and conflict control in social groups with a given network of interactions. These problems have been interpreted in terms of marketing applications and also illustrated on a model example. At the stage of structural analysis, the target audience is segmented into strong subgroups and satellites. The initial opinions of strong subgroups members (opinion leaders) determine both the common resulting opinions of strong subgroups and the individual resulting opinions of satellites, which in fact solves the prediction problem.

In the authors’ opinion, the solution of the analysis and prediction problems is only the first stage of an integrated approach to the study of social networks that forms input data for the second stage. Namely, a natural continuation is to formulate and solve optimal and conflict control problems for the opinions of network agents. As is stressed above, it suffices to exert control actions only on the members of strong subgroups (opinion leaders) identified at the analysis stage, which allows saving control resources while significantly affecting its efficiency.

In general, the following conclusions can be made:

• A system of descriptive, optimal control, and game-theoretic models for a conceptual analysis of social networks in various fields has been constructed. The marketing interpretation of the results has been given as an example. In this case, one or more influence agents model the competitive firms as marketing agents, and the basic agents describe the target audience of this/those influence agent(s). Of course, applications to politics, organizational and regional control, and other areas are also possible.
• Algorithms for analyzing the network and calculating the resulting opinions of agents have been developed, implemented in the R programming language and tested on model examples.
• Computer simulations of the optimal opinion control problems over networks have been performed using model examples in the domain of marketing and the hypothesis of sufficient impact on the members of strong subgroups (opinion leaders of the target audience) has been experimentally confirmed. The qualitatively representative scenarios of simulation have been identified.
• Explicit solutions to the differential games of opinion control over networks with marketing budget constraints in the form of equalities and inequalities have been analytically constructed. For the case of inequalities, a special method for solving the problem has been proposed.
• A comparative analysis of the independent and cooperative behavior of the players has been carried out, and the results have been interpreted in terms of marketing problems. In the sense of total payoff, cooperation is more profitable. Some conclusions regarding the optimal allocation of the marketing budget have been made. Namely, there are four possible cases in terms of the marketing resources availability: when there are enough marketing resources in total or not, and when each firm has enough resources, or some firms have a lack of marketing resources. The posed game theoretic problem is solved for all cases.

In the future, the problems of optimal and conflict control should be supplemented with the viability conditions, which establish social requirements to a controlled active dynamic system. Typically, these requirements contradict the direct economic interests of control subjects and therefore can be included in the problem statement either with the voluntary self-restriction of the subjects (social responsibility), or by introducing an additional control authority (principal) that will ensure viability through administrative or economic impact on other control subjects. Both options lead to the consideration of dynamic games with state-space constraints.

We are going to investigate dynamic game-theoretic models of opinion control over networks for the cases of independent and cooperative behavior and a hierarchy of players under various nonlinear control actions. Undoubtedly, the development of a simulation approach based on the method of qualitatively representative scenarios for the problems of opinion control and resource allocation over networks will make sense as well. Also, the study of uncertainty in various aspects is of great interest.