Hierarchical Clustering with Spatial Constraints and Standardized Incidence Ratio in Tuberculosis Data
Abstract
1. Introduction
2. Material and Methods
2.1. Study Design and Data Sources
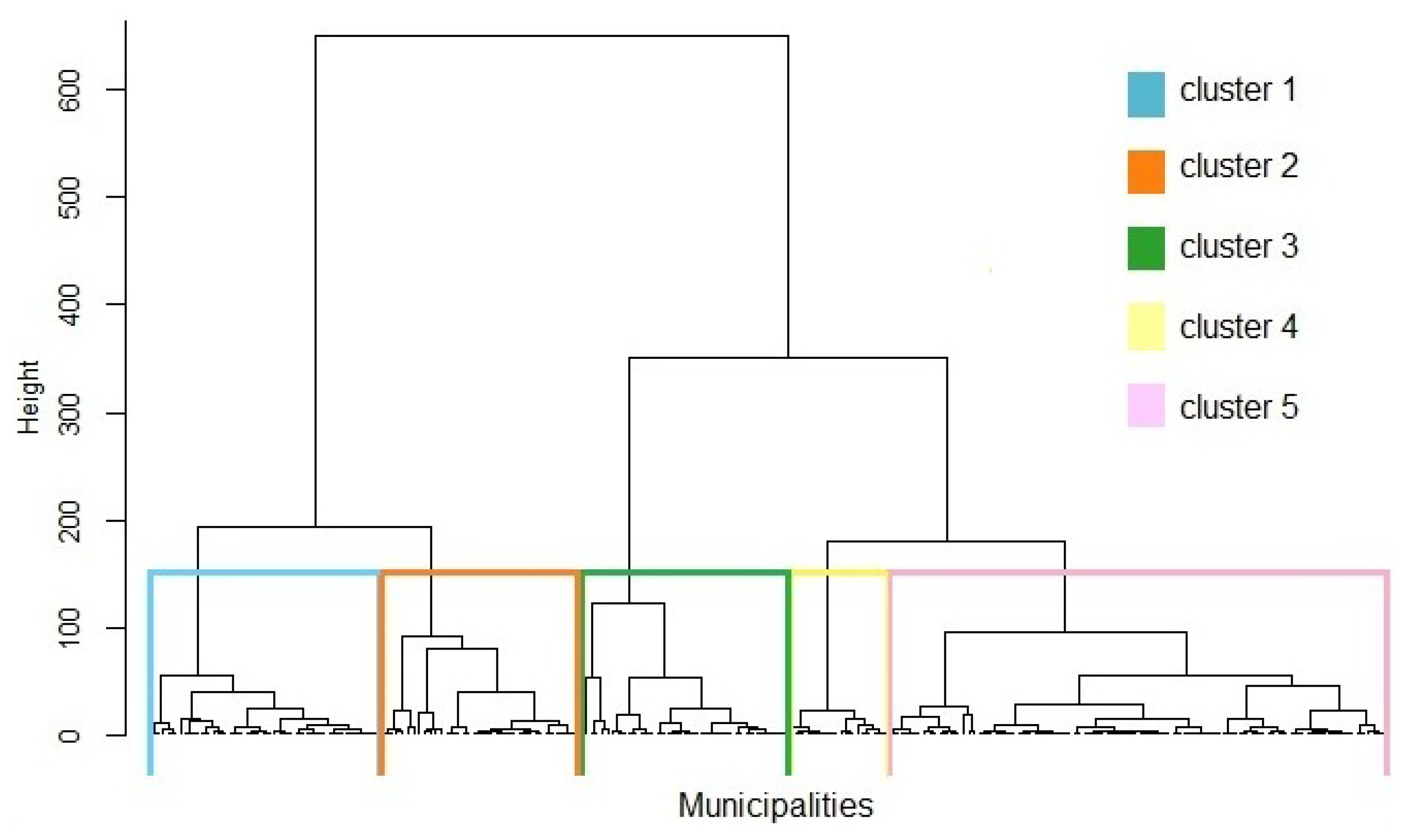
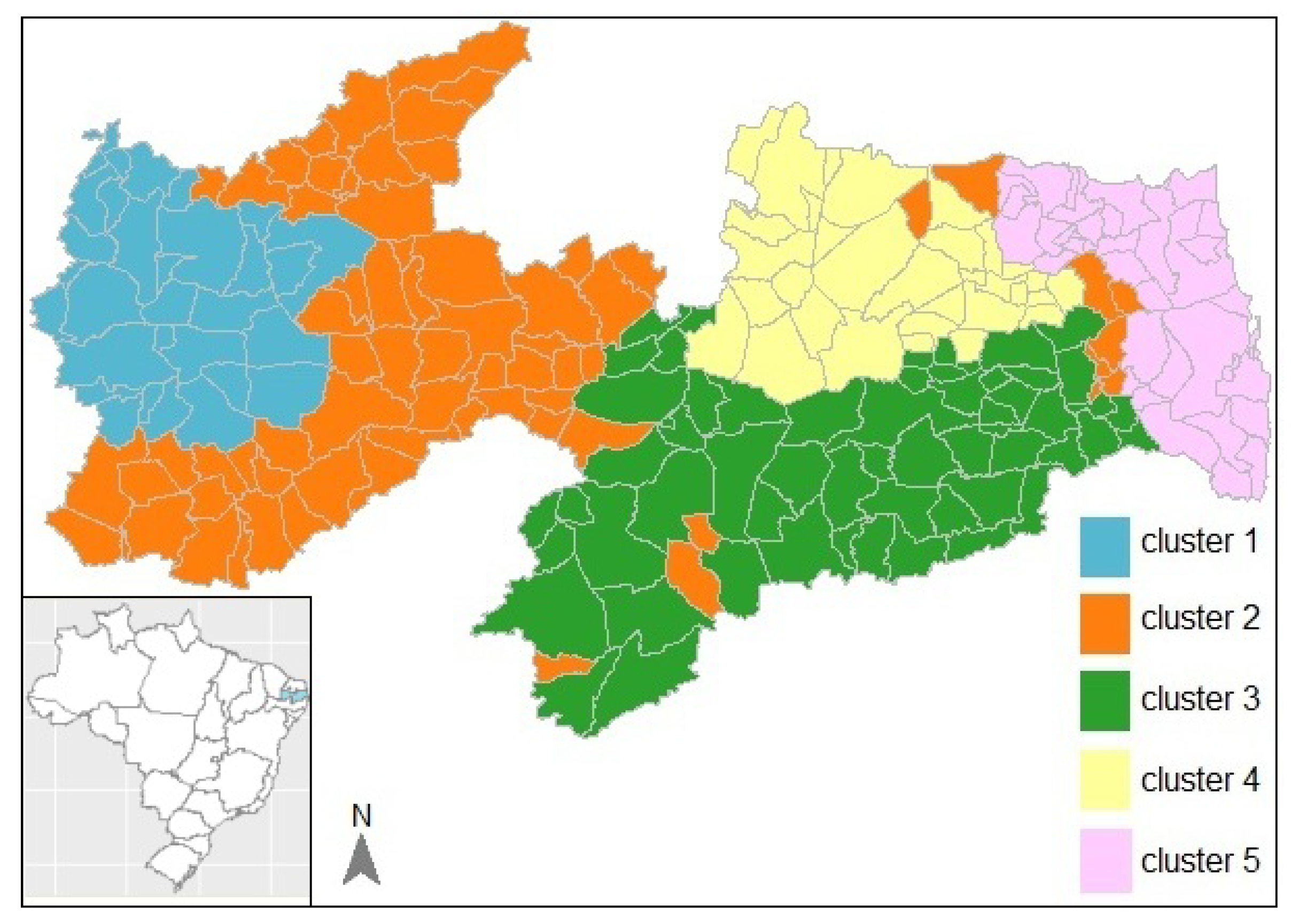
2.2. Constrained Hierarchical Clustering
2.3. Ward-Like Hierarchical Clustering
2.4. Manhattan Distance
2.5. Standardized Incidence Ratio
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DATASUS | Department of the Unified Health System |
| IBGE | Brazilian Institute of Geography and Statistics |
| SIR | standardized incidence ratio |
| TB | tuberculosis |
| WHO | World Health Organization |
Appendix A
References
- Vandewalle, V. Multi-Partitions Subspace Clustering. Mathematics 2020, 8, 597. [Google Scholar] [CrossRef]
- Wierzchoń, S.T.; Kłopotek, M.A. Cluster Analysis. In Modern Algorithms of Cluster Analysis; Janusz, K., Ed.; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 9–66. [Google Scholar]
- Chavent, M.; Kuentz-Simonet, V.; Labenne, A.; Saracco, J. ClustGeo: Hierarchical Clustering with Spatial Constraints, R Package Version 2.0; 2017. Available online: https://CRAN.R-project.org/package=ClustGeo (accessed on 17 May 2020).
- WHO—World Health Organization. Global Tuberculosis Report 2019; World Health Organization: Geneva, Switzerland, 2019. [Google Scholar]
- Reis-Santos, B.; Shete, P.; Bertolde, A.; Sales, C.M.; Sanchez, M.N.; Arakaki-Sanchez, D.; Andrade, K.B.; Gomes, M.G.M.; Boccia, D.; Lienhardt, C.; et al. Tuberculosis in Brazil and Cash Transfer Programs: A Longitudinal Database Study of the Effect of Cash Transfer on Cure Rates. PLoS ONE 2019, 14, e0212617. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Global Tuberculosis Report 2017; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Ministério da Saúde. Brasil Livre da Tuberculose: Evolução dos Cenários Epidemiológicos e Operacionais da Doença; Boletim Epidemiológico; Secretaria de Vigilância em Saúde: Brasília, Brasil, March 2019; Volume 50.
- Aguiar, D.C.; Silva Camelo, E.L.; Carneiro, R.O. Análise estatística de indicadores da tuberculose no Estado da Paraíba. Rev. Aten. Saúde. 2019, 17, 5–12. [Google Scholar]
- IBGE. Instituto brasileiro de geografia e Estatística. In Paraíba–Panorama; 2019. Available online: https://cidades.ibge.gov.br (accessed on 8 May 2020).
- Santos Neto, M.; Sousa, M.R.; da Silva, F.B.G.; Santos, F.S.; Ferreira, A.G.N.; Pascoal, L.M.; Costa, A.C.P.d.; Bezerra, J.M.; Serra, M.A.A.d.O.; Dias, I.C.C.M.; et al. Spatial distribution of tuberculosis cases in a priority Brazilian northeast municipality for control of the disease. Int. J. Dev. Res. 2017, 7, 10611. [Google Scholar]
- Moraga, P. Small Area Disease Risk Estimation and Visualization Using R. R J. 2018, 10, 495–506. [Google Scholar] [CrossRef]
- SINAN. Sistema de Informação de Agravos de Notificação. In Tuberculose–Casos Confirmados; Ministério da Saúde, Brazil: Brasília, Barzil, 2020. Available online: http://www2.datasus.gov.br/ (accessed on 5 April 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 15 May 2020).
- Duque, J.C.; Dev, B.; Betancourt, A.; Franco, J.L. ClusterPy: Library of Spatially Constrained Clustering Algorithms, RiSE-Group (Research in Spatial Economics). 2011. Version 0.9.9; Available online: http://www.rise-group.org/risem/clusterpy/ (accessed on 15 May 2020).
- Bécue-Bertaut, M.; Alvarez-Esteban, R.; Sánchez-Espigares, J.A. Xplortext: Statistical Analysis of Textual Data R Package, R Package Version 1.0. 2017. Version 0.9.9; Available online: https://cran.r-project.org/package=Xplortext (accessed on 7 June 2020).
- Dehman, A.; Ambroise, C.; Neuvial, P. Performance of a blockwise approach in variable selection using linkage disequilibrium information. BMC Bioinform. 2015, 16, 148. [Google Scholar] [CrossRef] [PubMed]
- Legendre, P. const.clust: Space-and Time-Constrained Clustering Package. R Package Version 1.2. 2011. Available online: http://adn.biol.umontreal.ca/numericalecology/Rcode/ (accessed on 20 May 2020).
- Ambroise, C.; Govaert, G. Convergence of an EM-type algorithm for spatial clustering. Pattern Recognit. Lett. 1998, 19, 919–927. [Google Scholar] [CrossRef]
- Ambroise, C.; Dang, M.; Govaert, G. Clustering of Spatial Data by the EM Algorithm. In geoENV I-Geostatistics for Environmental Applicattions; Soares, A.O., Gomez-Hernandez, J.J., Froidevaux, R., Eds.; Kluwer: Dordrecht, The Netherland, 1997; pp. 493–504. [Google Scholar]
- Aguiar, D.C.; Sánchez, R.G.; Silva Camêlo, E.L. Hierarchical clustering with spatial constraints in tuberculosis data. IJDR 2020, 10, 35374–35380. [Google Scholar]
- Aguiar, D.C.; Sánchez, R.G.; Silva Camêlo, E.L. Ward-like hierarchical clustering with dissimilarities and non-uniform weights in cases of tuberculosis in Paraíba, Brazil. IJDR 2020, 10, 35478–35483. [Google Scholar]
- Miele, V.; Picard, F.; Dray, S. Spatially constrained clustering of ecological networks. Methods Ecol. Evol. 2014, 5, 771–779. [Google Scholar] [CrossRef]
- Chavent, M.; Kuentz-Simonet, V.; Labenne, A.; Saracco, J. ClustGeo: An R package for hierarchical clustering with spatial constraints. Comput. Stat. 2018, 33, 1799–1822. [Google Scholar] [CrossRef]
- Majure, J.J.; Gebhardt, A. sgeostat: An Object-Oriented Framework for Geostatistical Modeling in S+, R Package Version 1.0-27; 2016. Available online: https://CRAN.R-project.org/package=sgeostat (accessed on 7 June 2020).
- Hijmans, R.J. Geosphere: Spherical Trigonometry, R Package Version 1.5-10; 2019. Available online: https://CRAN.R-project.org/package=geosphere (accessed on 7 June 2020).
- Wallace, J.R. Imap: Interactive Mapping, R Package Version 1.32; 2012. Available online: https://CRAN.R-project.org/package=Imap (accessed on 7 June 2020).
- Strauss, T.; von Maltitz, M.J. Generalising Ward’s Method for Use with Manhattan Distances. PLoS ONE 2017, 12, e0168288. [Google Scholar] [CrossRef] [PubMed]

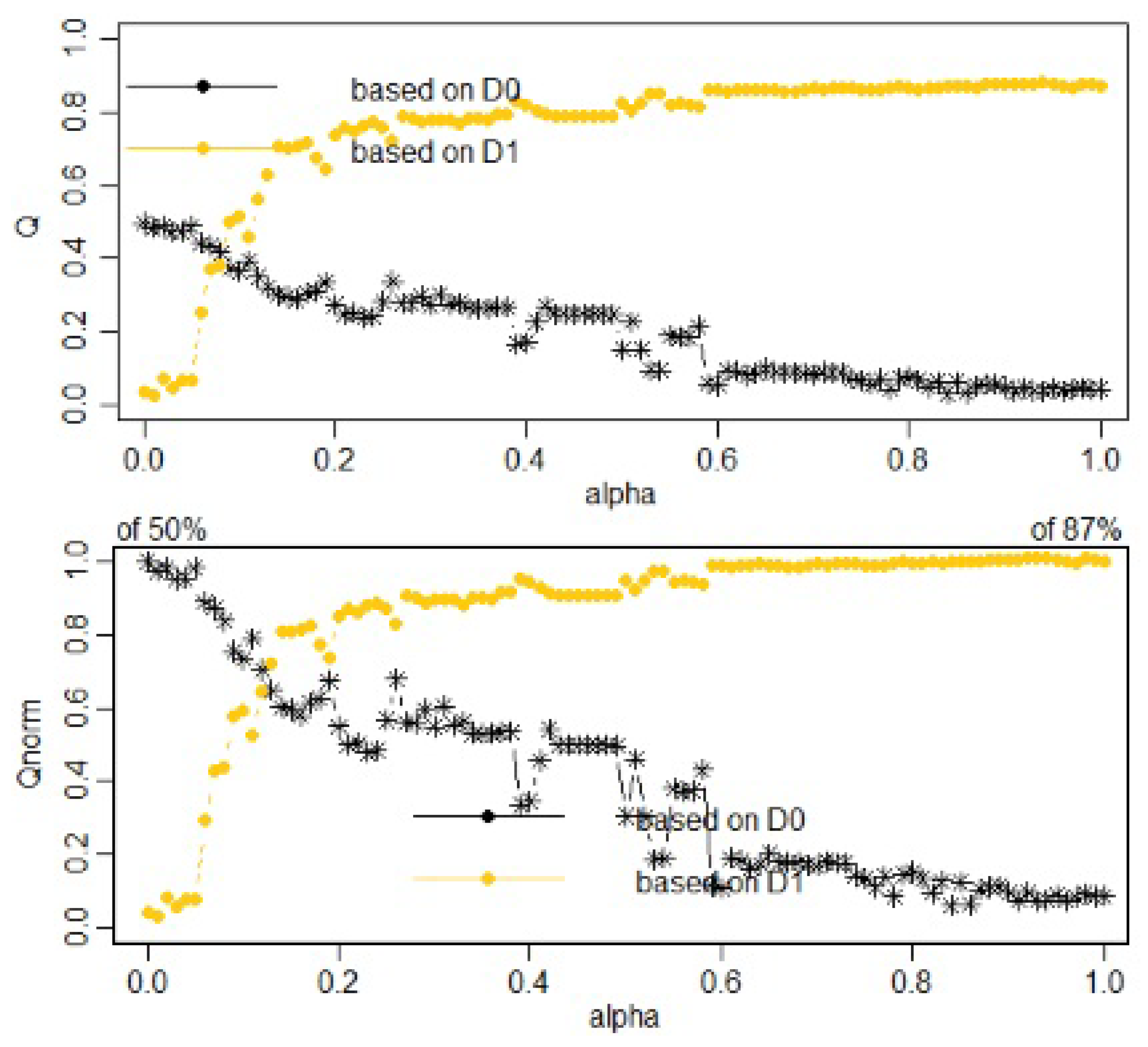
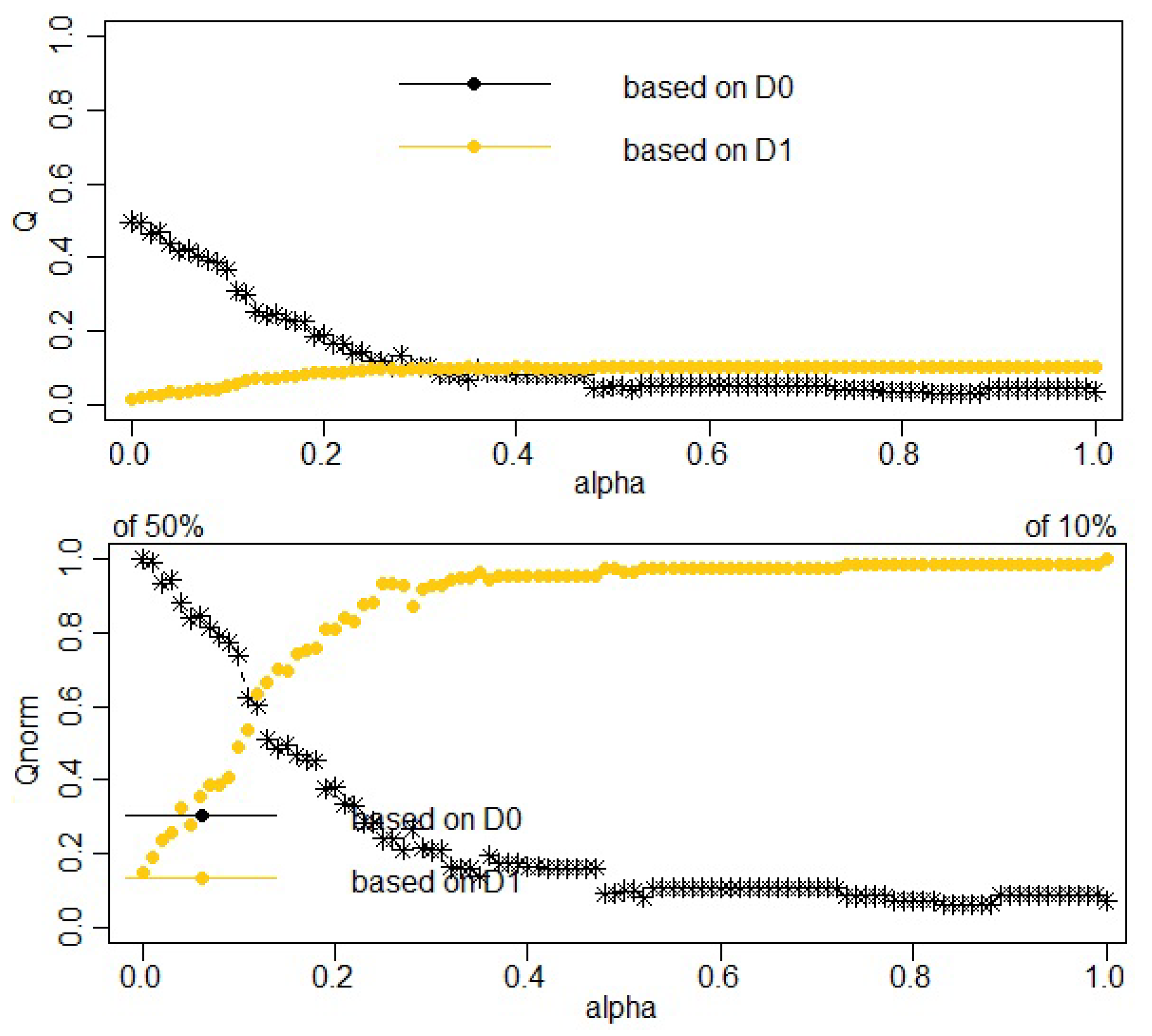

| Alpha Values | Q0norm | Q1norm |
|---|---|---|
| = 0.16 | 0.57808701 | 0.81167272 |
| = 0.17 | 0.61407565 | 0.82247147 |
| = 0.18 | 0.62478207 | 0.77433402 |
| = 0.19 | 0.67296737 | 0.73850413 |
| = 0.20 | 0.54877711 | 0.84948899 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camêlo Aguiar, D.; Gutiérrez Sánchez, R.; Silva Camêlo, E.L. Hierarchical Clustering with Spatial Constraints and Standardized Incidence Ratio in Tuberculosis Data. Mathematics 2020, 8, 1478. https://doi.org/10.3390/math8091478
Camêlo Aguiar D, Gutiérrez Sánchez R, Silva Camêlo EL. Hierarchical Clustering with Spatial Constraints and Standardized Incidence Ratio in Tuberculosis Data. Mathematics. 2020; 8(9):1478. https://doi.org/10.3390/math8091478
Chicago/Turabian StyleCamêlo Aguiar, Dalila, Ramón Gutiérrez Sánchez, and Edwirde Luiz Silva Camêlo. 2020. "Hierarchical Clustering with Spatial Constraints and Standardized Incidence Ratio in Tuberculosis Data" Mathematics 8, no. 9: 1478. https://doi.org/10.3390/math8091478
APA StyleCamêlo Aguiar, D., Gutiérrez Sánchez, R., & Silva Camêlo, E. L. (2020). Hierarchical Clustering with Spatial Constraints and Standardized Incidence Ratio in Tuberculosis Data. Mathematics, 8(9), 1478. https://doi.org/10.3390/math8091478






