On the Δ n 1 Problem of Harvey Friedman ^†

Abstract

In this paper, we prove the following. If $n\ge 3$, then there is a generic extension of $\mathbf{L}$, the constructible universe, in which it is true that the set $\mathcal{P}\left(\omega \right)\cap \mathbf{L}$ of all constructible reals (here—subsets of $\omega$) is equal to the set $\mathcal{P}\left(\omega \right)\cap {\Delta }_n^1$ of all (lightface) ${\Delta }_n^1$ reals. The result was announced long ago by Leo Harrington, but its proof has never been published. Our methods are based on almost-disjoint forcing. To obtain a generic extension as required, we make use of a forcing notion of the form $\mathbb{Q}=\mathbb{C}ℂ\times {\prod }_{\nu }{\mathbb{Q}}_{\nu }$ in $\mathbf{L}$, where $\mathbb{C}$ adds a generic collapse surjection b from $\omega$ onto $\mathcal{P}\left(\omega \right)\cap \mathbf{L}$, whereas each ${\mathbb{Q}}_{\nu }$, $\nu <{\omega }_2^{\mathbf{L}}$, is an almost-disjoint forcing notion in the ${\omega }_1$-version, that adjoins a subset $S_{\nu }$ of ${\omega }_1^{\mathbf{L}}$. The forcing notions involved are independent in the sense that no ${\mathbb{Q}}_{\nu }$-generic object can be added by the product of $\mathbb{C}$ and all ${\mathbb{Q}}_{\xi }$, $\xi \ne \nu$. This allows the definition of each constructible real by a ${\Sigma }_n^1$ formula in a suitably constructed subextension of the $\mathbb{Q}$-generic extension. The subextension is generated by the surjection b, sets $S_{\omega ·k+j}$ with $j\in b\left(k\right)$, and sets $S_{\xi }$ with $\xi \ge \omega ·\omega$. A special character of the construction of forcing notions ${\mathbb{Q}}_{\nu }$ is $\mathbf{L}$, which depends on a given $n\ge 3$, obscures things with definability in the subextension enough for vice versa any ${\Delta }_n^1$ real to be constructible; here the method of hidden invariance is applied. A discussion of possible further applications is added in the conclusive section.

1. Introduction

Problem 87 in Harvey Friedman’s treatise One hundred and two problems in mathematical logic [1] requires proof that for each n in the domain $2<n\le \omega$ there is a model of

$$\mathbf{ZFC}+“\mathrm{the}\mathrm{constructible}\mathrm{reals}\mathrm{are}\mathrm{precisely}\mathrm{the}{\Delta }_n^1\mathrm{reals}”.$$

(1)

(For $n\le 2$ this is definitely impossible e.g., by the Shoenfield’s absoluteness theorem.) This problem was generally known in the early years of forcing, see, e.g., problems 3110, 3111, 3112 in an early survey [2] (the original preprint of 1968) by Mathias. At the very end of [1], it is noted that Leo Harrington had solved this problem affirmatively. For a similar remark, see [2] (p. 166), a comment to P 3110. And indeed, Harrington’s handwritten notes [3] (pp. 1–4) contain a sketch of a generic extension of $\mathbf{L}$, based on the almost-disjoint forcing of Jensen and Solovay [4], in which it is true that ${\omega }^{\omega }\cap \mathbf{L}={\Delta }_3^1$. Then a few sentences are added on page 5 of [3], which explain, as how Harrington planned to get a model in which ${\omega }^{\omega }\cap \mathbf{L}={\Delta }_n^1$ holds for a given (arbitrary) natural index $n\ge 3$, and a model in which ${\omega }^{\omega }\cap \mathbf{L}={\Delta }_{\infty }^1$, where ${\Delta }_{\infty }^1={\bigcup }_n{\Delta }_n^1$ (all analytically definable reals). This positively solves Problem 87, including the case $n=\infty$. Different cases of higher order definability are observed in [3] as well.

Yet no detailed proofs have ever emerged in Harrington’s published works. An article by Harrington, entitled “Consistency and independence results in descriptive set theory”, which apparently might have contained these results among others, was announced in the References list in Peter Hinman’s book [5] (p. 462) to appear in Ann. of Math., 1978, but in fact, this or similar article has never been published by Harrington.

One may note that finding a model for (1) belongs to the “definability of definable” type of mathematical problems, introduced by Alfred Tarski in [6], where the definability properties of the set $D_{1M}$, of all sets $x\subseteq \omega$ definable by a parameter-free type-theoretic formula with quantifiers bounded by type M, are discussed for different values of $M<\omega$. In this context, case $n=\infty$ in (1) is equivalent to case $M=1$ in the Tarski problem, whereas cases $n<\infty$ in (1) can be seen as refinements of case $m=1$ in the Tarski problem, because classes ${\Delta }_n^1$ are well-defined subclasses of $D_{11}={\bigcup }_{n<\omega }{\Delta }_n^1$.

The goal of this paper is to present a complete proof of the following part of Harrington’s statement that solves the mentioned Friedman’s problem. No such proof has been known so far in mathematical publications, and this is the motivation for our research.

Theorem 1

(Harrington). If $2\le 𝕟<\infty$ then there is a generic extension of $\mathbf{L}$ in which it is true that the constructible reals are precisely the ${\Delta }_{𝕟+1}^1$ reals.

The ${\Delta }_{\infty }^1$ case of Harrington’s result, as well as different results related to Tarski’s problems in [6], will be subject of a forthcoming publication.

This paper is dedicated to the proof of Theorem 1. This will be another application of the technique introduced in our previous paper [7] in this Journal, and in that sense this paper is a continuation and development of the research started in [7]. However, the problem considered here, i.e., getting a model for (1), is different from and irreducible to the problems considered in [7] and related to definability and constructability of individual reals. Subsequently the technique applied in [7] is considerably modified and developed here for the purposes of this new application. In particular, as the models involved here by necessity satisfy ${\omega }_1^{\mathbf{L}}<{\omega }_1$ (unlike the models considered in [7], which satisfy the equality ${\omega }_1^{\mathbf{L}}={\omega }_1$), the almost-disjoint forcing is combined with a cardinal collapse forcing in this paper. And hence we will have to substantially deviate from the layout in [7], towards a modification that shifts the whole almost-disjoint machinery from $\omega$ to ${\omega }_1$.

Section 2: we set up the almost-disjoint forcing in the ${\omega }_1$-version. That is, we consider the sets $\mathbf{S}\mathbf{EQ}={\left({\omega }_1\right)}^{<{\omega }_1}$ and $\mathbf{F}\mathbf{UN}={\left({\omega }_1\right)}^{{\omega }_1}$ in $\mathbf{L}$, the constructible universe, and, given $u\subseteq \mathbf{F}\mathbf{UN}$, we define a forcing notion $Q\left[u\right]$ which adds a set $G\subseteq \mathbf{S}\mathbf{EQ}$ such that if $f\in \mathbf{F}\mathbf{UN}$ in $\mathbf{L}$ then G covers f iff $f\notin u$, where covering means that $f\upharpoonright \xi \in G$ for unbounded-many $\xi <{\omega }_1^{\mathbf{L}}$. We also consider two types of transformations related to forcing notions of the form $Q\left[u\right]$.

Section 3. We let $\mathcal{I}={{\omega }_2}^{\mathbf{L}}$ be the index set. Arguing in $\mathbf{L}$, we consider systems $U={\left\{U\left(\nu \right)\right\}}_{\nu \in \mathcal{I}}$, where each $U\left(\nu \right)\subseteq \mathbf{F}\mathbf{UN}$ is dense. Given such U, the product almost-disjoint forcing $\mathbf{Q}\left[U\right]=\mathbb{C}\times {\prod }_{\nu \in {\mathcal{I}}^{+}}Q\left[U\left(\nu \right)\right]$ (with finite support) is defined in $\mathbf{L}$, where $\mathbb{C}={\left(\mathcal{P}\left(\omega \right)\right)}^{<\omega }$ is a version of Cohen’s collapse forcing. Such a forcing notion adjoins a generic map ${\mathit{b}}_G:\omega \stackrel{\mathrm{onto}}{⟶}\mathcal{P}\left(\omega \right)\cap \mathbf{L}$ to $\mathbf{L}$, and adds an array of sets $G\left(\nu \right)\subseteq \mathbf{S}\mathbf{EQ}$ (where $\nu \in \mathcal{I}$) as well, so that each $G\left(\nu \right)$ is a $Q\left[U\left(\nu \right)\right]$-generic set over $\mathbf{L}$. We also investigate the structure of related product-generic extensions and their subextensions, and transformations of forcing notions of the form $\mathbf{Q}\left[U\right]$.

Section 4. Given $𝕟\ge 2$, we define a system $\mathbb{U}\in \mathbf{L}$ as above, which has some remarkable properties, in particular, (1) being $Q\left[\mathbb{U}\left(\nu \right)\right]$-generic is essentially a ${\Pi }_{𝕟}^1$ property in all suitable generic extensions, (2) if $\nu \in \mathcal{I}$ and $G\subseteq \mathbf{Q}\left[\mathbb{U}\right]$ is generic over $\mathbf{L}$, then the extension $\mathbf{L}[{\mathit{b}}_G,{\left\{G\left({\nu }^{\prime }\right)\right\}}_{{\nu }^{\prime }\ne \nu }]$ contains no $Q\left[\mathbb{U}\left(\nu \right)\right]$-generic reals, and (3) all submodels of $\mathbf{L}\left[G\right]$ of certain kind are elementarily equivalent w. r. t. ${\Sigma }_{𝕟}^1$ formulas. The latter property is summarized in the key technical instrument, Theorem 4 (the elementary equivalence theorem), whose proof is placed in a separate Section 6. To prove Theorem 1, we make use of a related generic extension $\mathbf{L}[{\mathit{b}}_G,{\left\{G\left(\nu \right)\right\}}_{\nu \in W\left[G\right]}]$, where

$$W\left[G\right]=w\left[G\right]\cup W=\{\omega ·k+2^j:j\in {\mathit{b}}_G\left(k\right)\}\cup \{\omega ·k+3^j:j,k<\omega \}\cup \{\nu \in \mathcal{I}:\nu \ge {\omega }^2\}$$

(see Lemma 23), and · is the ordinal multiplication. The first term in $W\left[G\right]$ provides a suitable definition of each set $x={\mathit{b}}_G\left(k\right)\in \mathbf{L}$ in the model $\mathbf{L}[{\mathit{b}}_G,{\left\{G\left(\nu \right)\right\}}_{\nu \in W\left[G\right]}]$, namely

$${\mathit{b}}_G\left(k\right)=\left\{j:\mathrm{there}\mathrm{exists}\mathrm{a}Q\left[U\left(\nu \right)\right]-\mathrm{generic}\mathrm{set}\mathrm{over}\mathbf{L}\right\},$$

while the second and third terms in $W\left[G\right]$ are added for technical reasons. The proof itself goes on in Section 4.5, modulo Theorem 4.

We introduce forcing approximations in Section 5, a forcing-like relation used to prove the elementary equivalence theorem. Its key advantage is the invariance under some transformations, including the permutations of the index set $\mathcal{I}$, see Section 5.4. The actual forcing notion $\mathbb{Q}=\mathbf{Q}\left[\mathbb{U}\right]$ is absolutely not invariant under permutations, but the $𝕟$-completeness property, maintained through the inductive construction of $\mathbb{U}$ in $\mathbf{L}$, allows us to prove that the auxiliary forcing relation is connected to the truth in $\mathbb{Q}$-generic extensions exactly as the true $\mathbb{Q}$-forcing relation does—up to the level ${\Sigma }_{𝕟}^1$ of the projective hierarchy (Lemma 33). We call this construction the hidden invariance technique (see Section 6.1).

Finally, Section 6 presents the proof of the elementary equivalence theorem, with the help of forcing approximations, and hence completes the proof of Theorem 1.

The flowchart can be seen in Figure 1 on page 3. And we added the index and contents as Supplementary Materials for easy reading.

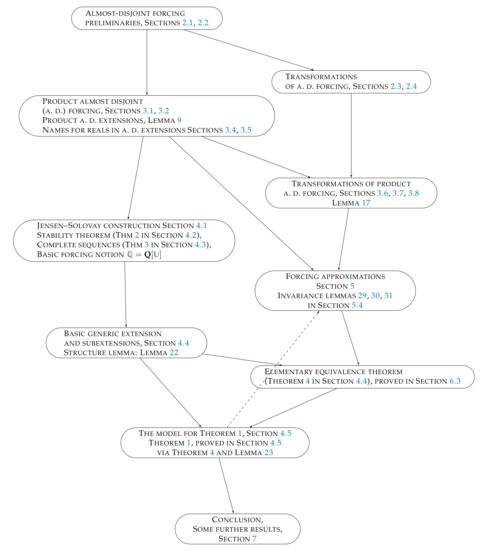
Figure 1. Flowchart.

2. Almost-Disjoint Forcing

Almost-disjoint forcing as a set theoretic tool was invented by Jensen and Solovay [4]. It has been applied in many research directions in modern set theory, in particular, in our paper [7] in this Journal. Here we make use of a considerably different version of the almost-disjoint forcing technique, which, comparably to [7], (1) considers countable cardinality instead of finite cardinalities in some key positions, (2) accordingly considers cardinality ${\omega }_1$ instead of countable cardinality. In particular, sequences of finite length change to those of length $<{\omega }_1$. And so on.

Assumption 1.

During arguments in this section, we assume that the ground set universe is $\mathbf{L}$, the constructible universe. Recall that in $\mathbf{L}$, $\mathrm{HC}={\mathbf{L}}_{{\omega }_1}$ and $\mathrm{H}{\omega }_2={\mathbf{L}}_{{\omega }_2}$. □

For the sake of brevity, we call ${\omega }_1$-size sets those X satisfying $\mathtt{card}X\le {\omega }_1$.

2.1. Almost-Disjoint Forcing: ${\omega }_1$-Version

This subsection contains a review the basic notation related to almost-disjoint forcing in the ${\omega }_1$- version. Arguing in $\mathbf{L}$, we put $\mathbf{F}\mathbf{UN}={{\omega }_1}^{{\omega }_1}$ = all ${\omega }_1$-sequences of ordinals $<{\omega }_1$.

• A set $X\subseteq \mathbf{F}\mathbf{UN}$ is dense iff for any $s\in \mathbf{S}\mathbf{EQ}$ there is $f\in X$ such that $s\subset f$.
• We let $\mathbf{S}\mathbf{EQ}={{\omega }_1}^{<{\omega }_1}\setminus \{\Lambda \}$, the set of all non-empty sequencess of ordinals $<{\omega }_1$, of length $\mathtt{lh}s=\mathtt{dom}s<{\omega }_1$. We underline that $\Lambda$, the empty sequence, does not belong to $\mathbf{S}\mathbf{EQ}$.
• If $S\subseteq \mathbf{S}\mathbf{EQ},f\in \mathbf{F}\mathbf{UN}$ then let $S/f=\mathtt{sup}\{\xi <{\omega }_1:f\upharpoonright \xi \in S\}$. If $S/f$ is unbounded in ${\omega }_1$ then say that S covers f, otherwise S does not cover f.

The following or very similar version of the almost-disjoint forcing was defined by Jensen and Solovay in [4] ([§ 5]). Its goal can be formulated as follows: given a set $u\subseteq \mathbf{F}\mathbf{UN}$ in the ground universe, find a generic set $S\subseteq \mathbf{S}\mathbf{EQ}$ such that the equivalence

$$f\in u⟺S\mathrm{does}\mathrm{not}\mathrm{cover}f$$

(2)

holds for each $f\in \mathbf{F}\mathbf{UN}$ in the ground universe.

Definition 1 (in $\mathbf{L}$).

$Q^{*}$ is the set of all pairs $p=⟨S_p;F_p⟩$ of finite sets $F_p\subseteq \mathbf{F}\mathbf{UN}$, $S_p\subseteq \mathbf{S}\mathbf{EQ}$. Elements of $Q^{*}$ will be called (forcing) conditions. If $p\in Q^{*}$ then put

$$F_p^{\vee }=\{f\upharpoonright \xi :f\in F_p\wedge 1\le \xi <{\omega }_1\},$$

a tree in $\mathbf{S}\mathbf{EQ}$. If $p,q\in Q^{*}$ then let $p\wedge q=⟨S_p\cup S_q;F_p\cup F_q⟩$; a condition in $Q^{*}$.

Let $p,q\in Q^{*}$. Define $q\le p$ (that is, q is stronger as a forcing condition) iff $S_p\subseteq S_q,F_p\subseteq F_q$, and the difference $S_q\setminus S_p$ does not intersect $F_p^{\vee }$, i.e., $S_q\cap F_p^{\vee }=S_p\cap F_p^{\vee }$. Clearly, we have $q\le p$ iff $S_p\subseteq S_q,F_p\subseteq F_q$, and $S_q\cap F_p^{\vee }=S_p\cap F_p^{\vee }$. □

Lemma 1 (in $\mathbf{L}$).

Conditions $p,q\in Q^{*}$ are compatible in $Q^{*}$ iff $\left(1\right)$ $S_q\setminus S_p$ does not intersect $F_p^{\vee }$, and $\left(2\right)$$S_p\setminus S_q$ does not intersect $F_q^{\vee }$. Therefore any $p,q\in P^{*}$ are compatible in $P^{*}$ iff $p\wedge q\le p$ and $p\wedge q\le q$.

Proof. 

If (1), (2) hold then $p\wedge q\le p$ and $p\wedge q\le q$, thus $p,q$ are compatible. □

If $u\subseteq \mathbf{F}\mathbf{UN}$ then put $Q\left[u\right]=\{p\in Q^{*}:F_p\subseteq u\}$.

Any conditions $p,q\in Q\left[u\right]$ are compatible in $Q\left[u\right]$ iff they are compatible in $Q^{*}$ iff the condition $p\wedge q=⟨S_p\cup S_q;F_p\cup F_q⟩\in Q\left[u\right]$ satisfies both $p\wedge q\le p$ and $p\wedge q\le q$. Therefore, we can say that conditions $p,q\in Q^{*}$ are compatible (or incompatible) without an explicit indication which forcing notion $Q\left[u\right]$ containing $p,q$ is considered.

Lemma 2 (in $\mathbf{L}$).

If $u\subseteq \mathbf{F}\mathbf{UN}$ and $A\subseteq Q\left[u\right]$ is an antichain then $\mathtt{card}A\le {\omega }_1$.

Proof. 

Suppose towards the contrary that $\mathtt{card}A>{\omega }_1$. If $p\ne q$ in A are incompatible then obviously $S_p\ne S_q$. Yet $\{S_p:p\in Q^{*}\}=$ all finite subsets of $\mathbf{S}\mathbf{EQ}$, is a set of cardinality ${\omega }_1$, a contradiction. □

2.2. Almost-Disjoint Generic Extensions

To work with $\mathbf{L}$-sets $\mathbf{F}\mathbf{UN}$ and $\mathbf{S}\mathbf{EQ}$ in generic extensions of $\mathbf{L}$, possibly in those obtained by means of cardinal collapse, we let

$$\mathbf{F}{\mathbf{UN}}^{\mathbf{L}}={\left({\omega }_1^{\mathbf{L}}\right)}^{{\omega }_1^{\mathbf{L}}}\cap \mathbf{L}\mathrm{and}\mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}=({\left({\omega }_1^{\mathbf{L}}\right)}^{<{\omega }_1^{\mathbf{L}}}\cap \mathbf{L})\setminus \{\Lambda \}$$

(3)

—in other words, $\mathbf{F}{\mathbf{UN}}^{\mathbf{L}}$ and $\mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}$ are just $\mathbf{F}\mathbf{UN}$ and $\mathbf{S}\mathbf{EQ}$ defined in $\mathbf{L}$.

Lemma 3.

Suppose that in $\mathbf{L}$, $u\subseteq \mathbf{F}\mathbf{UN}$ is dense. Let $G\subseteq Q\left[u\right]$ be a set $Q\left[u\right]$-generic over $\mathbf{L}$. We define $S_G={\bigcup }_{p\in G}{S}_p;$ thus $S_G\subseteq \mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}$. Then

(i)

if $f\in \mathbf{F}{\mathbf{UN}}^{\mathbf{L}}$ then $f\in u$ iff $S_G$ does not cover $f;$

(ii)

if $p\in Q\left[u\right]$ then $p\in G$ iff $S_p\subseteq S_G\wedge (S_G\setminus S_p)\cap F_p^{\vee }=⌀$.

(iii)

$\mathbf{L}\left[G\right]=\mathbf{L}\left[S_G\right];$

(iv)

if $f\in \mathbf{F}{\mathbf{UN}}^{\mathbf{L}}\setminus u$ then $X_f=\{\xi <{\omega }_1^{\mathbf{L}}:f\upharpoonright \xi \in S_G\}$ is a cofinal subset of ${\omega }_1^{\mathbf{L}}$ of order type $\omega ;$

(v)

${\omega }_1^{\mathbf{L}\left[G\right]}={\omega }_2^{\mathbf{L}}$.

Proof. 

(i) Consider any $f\in u$. We claim that $D_f=\{p\in P\left[u\right]:f\in F_p\}$ is dense in $P\left[u\right]$. (Indeed if $q\in P\left[u\right]$ then define $p\in P\left[u\right]$ by $S_p=S_q$ and $F_p=F_q\cup \left\{f\right\}$; we have $p\in D_f$ and $p\le q$.) It follows that $D_f\cap G\ne ⌀$. Choose any $p\in D_f\cap G$; we have $f\in F_p$. Each condition $r\in G$ is compatible with p, therefore, by Lemma 1, $S_r/f\subseteq S_p/f$. We conclude that $S_G/f=S_p/f$.

Now assume that $f\notin u$. The set $D_{fl}=\{p\in P\left[u\right]:\mathtt{sup}\left(S_p/f\right)>l\}$ is dense in $P\left[u\right]$ for any $l<\omega$. (Let $q\in P\left[u\right]$. Then $F_q$ is finite. There exists $m>l$ with $f\upharpoonright m\notin F_q^{\vee }$, since $f\notin u$. Define a condition p by $F_p=F_q$ and $S_p=S_q\cup \left\{f\upharpoonright m\right\}$; we have $p\in D_{fl}$ and $p\le q$.) Pick, by the density, any $p\in D_{fl}\cap G$. Then $\mathtt{sup}\left(S_G/f\right)>l$. We conclude that $S_G/f$ is infinite because l is arbitrary.

(ii) Let $p\in G$. Then obviously $s_p\subseteq S_G$. If there exists $s\in (S_G\setminus S_p)\cap F_p^{\vee }$ then $s\in S_q$ for some $q\in G$. Then conditions $p,q$ are incompatible by Lemma 1, which is a contradiction.

Now assume that $p\in P\left[u\right]\setminus G$. There is a condition $q\in G$ incompatible with p. We have two cases by Lemma 1. First, there is some $s\in (S_q\setminus S_p)\cap F_p^{\vee }$. Then $s\in S_G\setminus S_p$, so p is not compatible with $S_G$. Second, there is some $s\in (S_p\setminus S_q)\cap F_q^{\vee }$. In this case, $s\notin S_r$ holds for any condition $r\le q$. It follows that $s\notin S_G$, hence $S_p⊈S_G$, and p cannot be compatible with $S_G$.

Further it follows from (ii) that $G=\{p\in P\left[u\right]:s_p\subseteq S_G\wedge (S_G\setminus s_p)\cap F_p^{\vee }=⌀\}$, hence, we have (iii). Claim (v) is an immediate corollary of (iv) since ${\omega }_2^{\mathbf{L}}$ remains a cardinal in $\mathbf{L}\left[G\right]$ by Lemma 2.

Finally, to prove (iv) let $f\in \mathbf{F}{\mathbf{UN}}^{\mathbf{L}}\setminus u$ and $\lambda <{\omega }_1^{\mathbf{L}}$. The set $D_{f\lambda }$ of all conditions $p\in Q\left[u\right]$, such that $f\upharpoonright \lambda \subset g$ for some $g\in S_p$, is dense in $\mathbf{Q}\left[u\right]$. Therefore G contains some $p\in D_{f\lambda }$. Let this be witnessed by some $g\in S_p$. Now, if $\xi <\lambda$ belongs to $X_f$, so that $s=f\upharpoonright \xi \in S_G$, then s must belong to $S_p$ by (ii), therefore $\xi$ belongs to the finite set $\{\mathtt{lh}s:s\in S_p\}$. Thus, $X_f\cap \lambda$ is finite. That $X_f\cap {\omega }_1^{\mathbf{L}}$ is infinite follows from (i) (recall that $f\notin u$). □

Now we consider two types of transformations related to the forcing notion $Q^{*}$.

2.3. Lipschitz Transformations

We argue in $\mathbf{L}$. Let $\mathbf{L}\mathbf{IP}$ be the group of all $\subseteq$-automorphisms of $\mathbf{S}\mathbf{EQ}$, called Lipschitz transformations. Any $\mathit{\lambda }\in \mathbf{L}\mathbf{IP}$ preserves the length $\mathtt{lh}$ of sequences, i.e., $\mathtt{lh}s=\mathtt{lh}\left(\mathit{\lambda }·s\right)$ for all $s\in \mathbf{S}\mathbf{EQ}$. Any transformation $\mathit{\lambda }\in \mathbf{L}\mathbf{IP}$ acts on:

–

sequences $s\in \mathbf{S}\mathbf{EQ}$: by $\mathit{\lambda }·s=\mathit{\lambda }\left(s\right)$;

–

functions $f\in \mathbf{F}\mathbf{UN}$: by $\mathit{\lambda }·f\in \mathbf{F}\mathbf{UN}$ and $\left(\mathit{\lambda }·f\right)\upharpoonright \xi =\mathit{\lambda }·\left(f\upharpoonright \xi \right)$ for all $\xi <{\omega }_1$;

–

sets $S\subseteq \mathbf{S}\mathbf{EQ},F\subseteq \mathbf{F}\mathbf{UN}$: by $\mathit{\lambda }·S=\{\mathit{\lambda }·s:s\in S\}$, $\mathit{\lambda }·F=\{\mathit{\lambda }·f:f\in F\}$;

–

conditions $p\in Q^{*}$: by $\mathit{\lambda }·p=⟨\mathit{\lambda }·S_p;\mathit{\lambda }·F_p⟩\in Q^{*}$.

Lemma 4 (routine).

The action of any $\mathit{\lambda }\in \mathbf{L}\mathbf{IP}$ is an order-preserving automorphism of $Q^{*}.$ If $u\subseteq \mathbf{F}\mathbf{UN}$ and $p\in Q\left[u\right]$ then $\mathit{\lambda }·p\in Q\left[\lambda ·u\right]$. □

We proceed with an important existence lemma. If $f\ne g$ belongs to $\mathbf{F}\mathbf{UN}$ then let $\beta (f,g)$ be equal to the least ordinal $\beta <{\omega }_1$ such that $f\left(\beta \right)\ne g\left(\beta \right)$ (or, similarly, the largest ordinal $\beta$ with $f\upharpoonright \beta =g\upharpoonright \beta$). Say that sets $X,Y\subseteq \mathbf{F}\mathbf{UN}$ are intersection-similar, or i-similar for brevity, if there is a bijection $b:X\stackrel{\mathrm{onto}}{⟶}Y$ such that $\beta (f,g)=\beta \left(b\right(f),b(g\left)\right)$ for all $f\ne g$ in X—such a bijection b will be called an i-similarity bijection.

Lemma 5.

Suppose that $u,v\subseteq \mathbf{F}\mathbf{UN}$ are ${\omega }_1$-size sets, dense in $\mathbf{F}\mathbf{UN}$. Then $u,v$ are i-similar. Moreover, if $X\subseteq u$, $Y\subseteq v$ are finite and i-similar then

(i)

there is an i-similarity bijection $b:u\stackrel{\mathrm{onto}}{⟶}v$ such that $b\left[X\right]=Y$,

(ii)

there exists a transformation $\mathit{\lambda }\in \mathbf{L}\mathbf{IP}$ such that $\mathit{\lambda }·u=v$ and $\mathit{\lambda }·X=Y$.

Proof. 

The key argument is that if $A\subseteq u$, $B\subseteq v$ are at most countable, $b:A\stackrel{\mathrm{onto}}{⟶}B$ is an i-similarity bijection, and $f\in u\setminus A$, then by the density of v there is $g\in v\setminus B$ such that the extended map $b\cup \{⟨f,g⟩\}:A\cup \left\{f\right\}\stackrel{\mathrm{onto}}{⟶}B\cup \left\{g\right\}$ is still an i-similarity bijection. This allows proof of (i), iteratively extending an initial i-similarity bijection $b_0:X\stackrel{\mathrm{onto}}{⟶}Y$ by a ${\omega }_1$-step back-and-forth argument involving eventually all elements $f\in u$ and $g\in v$, to an i-similarity bijection $u\stackrel{\mathrm{onto}}{⟶}v$ required. See the proof of Lemma 5 in [7] for more detail.

To get (ii) from (i), consider any sequence $s\in \mathbf{S}\mathbf{EQ}$. Let $\beta =\mathtt{lh}s$. As u is dense, there exist $f,f^{\prime }\in u$ such that $\beta (f,f^{\prime })=\beta$ and $s\subset f,s\subset f^{\prime }$. Put $g=b\left(f\right),g^{\prime }=b\left(f^{\prime }\right)$. Then still $\beta (g,g^{\prime })=\beta$, hence $g\upharpoonright \beta =g^{\prime }\upharpoonright \beta$. Therefore, we can define $\mathit{\lambda }\left(s\right)=g\upharpoonright \beta =g^{\prime }\upharpoonright \beta$. □

2.4. Substitution Transformations

We continue to argue in $\mathbf{L}$. Assume that conditions $p,q\in Q^{*}$ satisfy

$$F_p=F_q\mathrm{and}{S}_p\cup S_q\subseteq F_p^{\vee }=F_q^{\vee }.$$

(4)

We define a transformation $h_{pq}$ acting as follows.

If $p=q$ then define $h_{pq}\left(r\right)=r$ for all $r\in Q^{*}$, the identity.

Suppose that $p\ne q$. Then $p,q$ are incompatible by (4) and Lemma 1. Define $d_{pq}=\{r\in Q^{*}:r\le p\vee r\le q\}$,the domain of $h_{pq}$. Let $r\in d_{pq}$. We put $h_{pq}\left(r\right)=r^{\prime }:=⟨S_{r^{\prime }},F_{r^{\prime }}⟩$, where $F_{r^{\prime }}=F_r$ and

$$S_{r^{\prime }}=\left\{\begin{array}{ccc}\hfill (S_r\setminus S_p)\cup S_q& \mathrm{in}\mathrm{case}& r\le p,\hfill \\ \hfill (S_r\setminus S_q)\cup S_p& \mathrm{in}\mathrm{case}& r\le q.\hfill \end{array}\right.$$

(5)

Thus, assuming (4), the difference between $S_r$ and $S_{r^{\prime }}$ lies entirely within the set $X=F_p^{\vee }=F_q^{\vee }$, so that if $r\le p$ then $S_r\cap X=S_p$ but $S_{r^{\prime }}\cap X=S_q$, while if $r\le q$ then $S_r\cap X=S_q$ but $S_{r^{\prime }}\cap X=S_p$.

Lemma 6.

(i) If $u\subseteq \mathbf{F}\mathbf{UN}$ is dense and $p_0,q_0\in Q\left[u\right]$ then there exist conditions $p,q\in Q\left[u\right]$ with $p\le p_0$, $q\le q_0$, satisfying (4).

(ii)

Let $p,q\in Q^{*}$ satisfy (4). If $p=q$ then $h_{pq}$ is the identity transformation. If $p\ne q$ then $h_{pq}$ an order automorphism of $d_{pq}=\{r\in Q^{*}:r\le p\vee r\le q\}$, satisfying $h_{pq}\left(p\right)=q$ and $h_{pq}={\left(h_{pq}\right)}^{-1}=h_{qp}$.

(iii)

If $u\subseteq \mathbf{F}\mathbf{UN}$ and $p,q\in Q\left[u\right]$ satisfy (4) then $h_{pq}$ maps the set $Q\left[u\right]\cap d_{pq}$ onto itself order-preserving.

Proof. 

(i) By the density of u there is a finite set $F\subseteq \mathbf{F}\mathbf{UN}$ satisfying $F_p\cup F_q\subseteq F$ and $S_p$. Put $p=⟨S_p,F⟩$ and $q=⟨S_q,F⟩$. Claims (ii), (iii) are routine. □

Please note that unlike the Lipschitz transformations above, transformations of the form $h_{pq}$, called substitutions in this paper, act within any given forcing notion of the form $Q\left[u\right]$ by claim (iii) of the lemma, and hence the forcing notions of the form $Q\left[u\right]$ considered are sufficiently homogeneous.

3. Almost-Disjoint Product Forcing

Here we review the structure and basic properties of product almost-disjoint forcing and corresponding generic extensions in the ${\omega }_1$-version. There is an important issue here: a forcing $\mathbb{C}$, which collapses ${\omega }_1$ to $\omega$, enters as a factor in the product forcing notions considered.

3.1. Product Forcing

In $\mathbf{L}$, we define $\mathbb{C}={\mathcal{P}\left(\omega \right)}^{<\omega }$, the set of all finite sequences of subsets of $\omega$, an ordinary forcing to collapse $\mathcal{P}\left(\omega \right)\cap \mathbf{L}$ down to $\omega$. We will make use of an ${\omega }_2$-product of $Q^{*}$ with $\mathbb{C}$ as an extra factor. (In fact, $\mathbb{C}$ can be eliminated since $Q^{*}$ collapses ${\omega }_1^{\mathbf{L}}$ anyway by Lemma 3 (v). Yet the presence of $\mathbb{C}$ somehow facilitates the arguments since $\mathbb{C}$ has a more transparent forcing structure.)

Technically, we put $\mathcal{I}={\omega }_2$ (in $\mathbf{L}$) and consider the index set ${\mathcal{I}}^{+}=\mathcal{I}\cup \{-1\}$. Let ${\mathbf{Q}}^{*}$ be the finite-support product of $\mathbb{C}$ and $\mathcal{I}$ copies of $Q^{*}$ (Definition 1 in Section 2.1), ordered componentwise. That is, ${\mathbf{Q}}^{*}$ consists of all maps p defined on a finite set $\mathtt{dom}p={\left|p\right|}^{+}\subseteq {\mathcal{I}}^{+}$ so that $p\left(\nu \right)\in Q^{*}$ for all $\nu \in \left|p\right|:={\left|p\right|}^{+}\setminus \{-1\}$, and if $-1\in {\left|p\right|}^{+}$ then ${\mathit{b}}_p:=p(-1)\in \mathbb{C}$. If $p\in {\mathbf{Q}}^{*}$ then put $F_p\left(\nu \right)=F_{p\left(\nu \right)}$ and $S_p\left(\nu \right)=S_{p\left(\nu \right)}$ for all $\nu \in \left|p\right|$, so that $p\left(\nu \right)=⟨S_p\left(\nu \right);F_p\left(\nu \right)⟩$.

We order ${\mathbf{Q}}^{*}$ componentwise: $p\le q$ (p is stronger as a forcing condition) iff ${\left|q\right|}^{+}\subseteq {\left|p\right|}^{+}$, ${\mathit{b}}_q\subseteq {\mathit{b}}_p$ in case $-1\in {\left|q\right|}^{+}$, and $p\left(\nu \right)\le q\left(\nu \right)$ in $Q^{*}$ for all $\nu \in \left|q\right|$. Put

$$F_p^{\vee }\left(\nu \right)=F_{p\left(\nu \right)}^{\vee }=\{f\upharpoonright \xi :f\in F_p\left(\nu \right)\wedge 1\le \xi <{\omega }_1\}.$$

In particular, ${\mathbf{Q}}^{*}$ contains the empty condition $\odot \in {\mathbf{Q}}^{*}$ satisfying ${|\odot |}^{+}=⌀$; obviously ⊙ is the $\le$-least (and weakest as a forcing condition) element of ${\mathbf{Q}}^{*}$.

Because of the factor $\mathbb{C}$, it takes some effort to define $p\wedge q$ for $p,q\in {\mathbf{Q}}^{*}$, and only assuming that ${\mathit{b}}_p,{\mathit{b}}_q$ are compatible, i.e., ${\mathit{b}}_p\subseteq {\mathit{b}}_q$ or ${\mathit{b}}_q\subseteq {\mathit{b}}_p$. In such a case define $p\wedge q\in {\mathbf{Q}}^{*}$ as follows. First, ${|p\wedge q|}^{+}={\left|p\right|}^{+}\cup {\left|q\right|}^{+}$. If $\nu \in {\left|p\right|}^{+}\setminus {\left|q\right|}^{+}$ then put $(p\wedge q)\left(\nu \right)=p\left(\nu \right)$, and similarly if $\nu \in {\left|q\right|}^{+}\setminus {\left|p\right|}^{+}$ then $(p\wedge q)\left(\nu \right)=q\left(\nu \right)$. Now suppose that $\nu \in {\left|p\right|}^{+}\cap {\left|q\right|}^{+}$.

If $\nu \ne -1$ then $(p\wedge q)\left(\nu \right)=p\left(\nu \right)\wedge q\left(\nu \right)$ in the sense of Definition 1 in Section 2.1.

If $\nu =-1\in {\left|p\right|}^{+}\cap {\left|q\right|}^{+}$, then, by the compatibility, either ${\mathit{b}}_p\subseteq {\mathit{b}}_q$—and then define ${\mathit{b}}_{p\wedge q}={\mathit{b}}_q$, or ${\mathit{b}}_q\subseteq {\mathit{b}}_p$—and then accordingly ${\mathit{b}}_{p\wedge q}={\mathit{b}}_p$.

Lemma 7.

Let $p,q\in {\mathbf{Q}}^{*}$ be compatible. Then $(p\wedge q)\in {\mathbf{Q}}^{*}$, $(p\wedge q)\le p$, $(p\wedge q)\le q$, and if $r\in {\mathbf{Q}}^{*}$, $r\le p$, $r\le q$, then $r\le (p\wedge q)$. □

3.2. Systems

Arguing in $\mathbf{L}$, we consider certain subforcings of the total product forcing notion ${\mathbf{Q}}^{*}$.

Let a system be any map $U:\left|U\right|\to \mathcal{P}\left(\mathbf{F}\mathbf{UN}\right)$ such that $\left|U\right|\subseteq \mathcal{I}$, each set $U\left(\nu \right)$ ($\nu \in \left|U\right|$) is dense in $\mathbf{F}\mathbf{UN}$, and the components $U\left(\nu \right)\subseteq \mathbf{F}\mathbf{UN}(\nu \in |U\left|\right)$ are pairwise disjoint.

• A system U is small, if both $\left|U\right|$ and each set $U\left(\nu \right)(\nu \in |U\left|\right)$ has cardinality $\le {\omega }_1$.
• If $U,V$ are systems, $\left|U\right|\subseteq \left|V\right|$, and $U\left(\nu \right)\subseteq V\left(\nu \right)$ for all $\nu \in \left|U\right|$, then say that VextendsU, in symbol $U\preccurlyeq V$.
• If ${\left\{U_{\xi }\right\}}_{\xi <\lambda }$ is a $\preccurlyeq$-increasing sequence of systems then define a system $U={\bigvee }_{\xi <\lambda }{U}_{\xi }$ by $\left|U\right|={\bigcup }_{\xi <\lambda }\left|U_{\xi }\right|$ and $U\left(\nu \right)={\bigcup }_{\xi <\lambda ,\nu \in |U_{\xi }|}{U}_{\xi }\left(\nu \right)$ for all $\nu \in \left|U\right|$.
• If U is a system, then $\mathbf{Q}\left[U\right]$ is the finite-support product of $\mathbb{C}$ and sets $Q\left[U\left(\nu \right)\right],\nu \in \left|U\right|$, i.e.,

  $$\mathbf{Q}\left[U\right]=\{p\in {\mathbf{Q}}^{*}:|p|\subseteq |U|\wedge \forall \nu \in |p\left|(F_p\left(\nu \right)\subseteq U\left(\nu \right))\right\}.$$

Suppose that $c\subseteq {\mathcal{I}}^{+}$. If $p\in {\mathbf{Q}}^{*}$ then define $p^{\prime }=p\upharpoonright c\in {\mathbf{Q}}^{*}$ so that $|p^{\prime }{|}^{+}=c\cap {\left|p\right|}^{+}$ and $p^{\prime }\left(\nu \right)=p\left(\nu \right)$ whenever $\nu \in |p^{\prime }{|}^{+}$. A special case: if $\nu \in {\mathcal{I}}^{+}$ then let $p{\upharpoonright }_{\ne \nu }=p\upharpoonright \left(\right|p{|}^{+}\setminus \left\{\nu \right\})$. Similarly, if U is a system then define a system $U^{\prime }=U\upharpoonright c$ so that $|U^{\prime }|=c\cap |U|$ and $U^{\prime }\left(\nu \right)=U\left(\nu \right)$ whenever $\nu \in |U^{\prime }|$. A special case: if $\nu \in {\mathcal{I}}^{+}$ then let $U{\upharpoonright }_{\ne \nu }=U\upharpoonright \left(\right|p|\setminus \{\nu \left\}\right)$. And if $Q\subseteq {\mathbf{Q}}^{*}$ then let $Q\upharpoonright c=\left\{p\in Q:\right|p{|}^{+}\subseteq c\}$ (will usually coincide with $\{p\upharpoonright c:p\in Q\}$.

Writing $p\upharpoonright c$, $U\upharpoonright c$ etc., it is not assumed that $c\subseteq {\left|p\right|}^{+}$.

Lemma 8 (in $\mathbf{L}$).

If U is a system and $A\subseteq \mathbf{Q}\left[U\right]$ is an antichain then $\mathtt{card}A\le {\omega }_1$.

Proof. 

Suppose that $\mathtt{card}A>{\omega }_1$. As $\mathtt{card}\mathbb{C}={\omega }_1$, we can w.l.o.g. assume that ${\mathit{b}}_p={\mathit{b}}_q$ for all $p,q\in A$. It follows by the $\Delta$-system lemma that there is a set $A^{\prime }\subseteq A$ of the same cardinality $\mathtt{card}{A}^{\prime }=\mathtt{card}A>{\omega }_1$, and a finite set $d\subseteq {\mathcal{I}}^{+}$, such that ${\left|p\right|}^{+}=d$ for all $p\in A^{\prime }$. Then we have $S_p\ne S_q$ for all $p\ne q$ in $A^{\prime }$, easily leading to a contradiction, as in the proof of Lemma 2. □

3.3. Outline of Product Extensions

We consider sets of the form $\mathbf{Q}\left[U\right]$, U being a system in $\mathbf{L}$, as forcing notions over $\mathbf{L}$. Accordingly, we’ll study $\mathbf{Q}\left[U\right]$-generic extensions $\mathbf{L}\left[G\right]$ of the ground universe $\mathbf{L}$. Define some elements of these extensions. Suppose that $G\subseteq {\mathbf{Q}}^{*}$. Put $\left|G\right|={\bigcup }_{p\in G}\left|p\right|$;$\left|G\right|\subseteq \mathcal{I}$. Let

$${\mathit{b}}_G={\bigcup }_{p\in G}{\mathit{b}}_p,\mathrm{and}{S}_G\left(\nu \right)=S_{G\left(\nu \right)}={\bigcup }_{p\in G}{S}_p\left(\nu \right)$$

for any $\nu \in \left|G\right|$, where $G\left(\nu \right)=\{p\left(\nu \right):p\in G\}\subseteq Q^{*}$.

Thus, $S_G\left(\nu \right)\subseteq \mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}$, and $S_G\left(\nu \right)=⌀$ for any $\nu \notin \left|G\right|$.

By the way, this defines a sequence ${\overrightarrow{S}}_G={\left\{S_G\left(\nu \right)\right\}}_{\nu \in \mathcal{I}}$ of subsets of $\mathbf{S}\mathbf{EQ}$.

If $c\subseteq {\mathcal{I}}^{+}$ then let $G\upharpoonright c=\left\{p\in G:\right|p{|}^{+}\subseteq c\}$. It will typically happen that $G\upharpoonright c=\{p\upharpoonright c:p\in G\}$. Put $G{\upharpoonright }_{\ne \nu }{=\{p\in G:\nu \notin |p|}^{+}\}=G\upharpoonright ({\mathcal{I}}^{+}\setminus \left\{\nu \right\})$.

If U is a system in $\mathbf{L}$, then any $\mathbf{Q}\left[U\right]$-generic set $G\subseteq \mathbf{Q}\left[U\right]$ splits into the family of sets $G\left(\nu \right),\nu \in \mathcal{I}$, and a separate map ${\mathit{b}}_G:\omega \stackrel{\mathrm{onto}}{⟶}\mathcal{P}\left(\omega \right)\cap \mathbf{L}$. It will follow from (ii) of the next lemma that $\mathbf{Q}\left[U\right]$-generic extensions of $\mathbf{L}$ satisfy ${\omega }_1={\omega }_2^{\mathbf{L}}$.

Lemma 9.

Let U be a system in $\mathbf{L}$, and $G\subseteq \mathbf{Q}\left[U\right]$ be a set $\mathbf{Q}\left[U\right]$-generic over $\mathbf{L}$. Then:

(i)

${\mathit{b}}_G$ is a $\mathbb{C}$-generic map from ω onto $\mathcal{P}\left(\omega \right)\cap \mathbf{L};$

(ii)

if $\nu \in \mathcal{I}$ then $\mathbf{L}\left[G\left(\nu \right)\right]=\mathbf{L}\left[S_G\left(\nu \right)\right]$ and ${\omega }_1^{\mathbf{L}\left[{\mathit{b}}_G\right]}={\omega }_1^{\mathbf{L}\left[G\right(\nu \left)\right]}={\omega }_2^{\mathbf{L}}={\omega }_1^{\mathbf{L}\left[G\right]};$

(iii)

$\mathbf{L}\left[G\right]=\mathbf{L}[{\overrightarrow{S}}_G]$ and ${\left|G\right|}^{+}=\mathcal{I};$

(iv)

if $\nu \in \mathcal{I}$ and $c\in \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right]$, $\nu \notin c\subseteq {\mathcal{I}}^{+}$, then $\mathbf{L}\left[G\upharpoonright c\right]\subseteq \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right];$

(v)

if $\nu \in \mathcal{I}$ then $S_G\left(\nu \right)\notin \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right];$

(vi)

if $\nu \in \mathcal{I}$ then the set $G\left(\nu \right)=\{p\left(\nu \right):p\in G\}\in \mathbf{L}\left[G\right]$ is $P\left[U\left(\nu \right)\right]$-generic over $\mathbf{L}$, hence if $f\in \mathbf{F}{\mathbf{UN}}^{\mathbf{L}}$ then $f\in U\left(\nu \right)$ iff $S_G\left(\nu \right)\mathrm{does}\mathrm{not}\mathrm{cover}f.$

Proof. 

Proofs of (i) and (iii)–(vi) are similar to ([7] (Lemma 9)). To prove ${\omega }_1^{\mathbf{L}\left[G\right(\nu \left)\right]}={\omega }_2^{\mathbf{L}}$ in (ii) apply Lemma 3 (v). Finally, to see that ${\omega }_2^{\mathbf{L}}$ remains a cardinal in $\mathbf{L}\left[G\right]$ apply Lemma 8. □

3.4. Names for Sets in Product Extensions

The next definition introduces names for elements of product-generic extensions of $\mathbf{L}$ considered.

Assume that in $\mathbf{L}$, $K\subseteq {\mathbf{Q}}^{*}$, e.g., $K=\mathbf{Q}\left[U\right]$, where U is a system, and X is any set. By ${\mathbf{N}}_X\left(K\right)$ ($K$-names for subsets of X) we denote the set of all sets $\tau \subseteq K\times X$ in $\mathbf{L}$. Furthermore, ${\mathbf{SN}}_X\left(K\right)$ (small names) consist of all ${\omega }_1$-size names $\tau \in {\mathbf{SN}}_X\left(K\right)$; in other words, it is required that $\mathtt{card}\tau \le {\omega }_1$.

Suppose that $\tau \in {\mathbf{N}}_X({\mathbf{Q}}^{*})$. We put

$$\mathtt{dom}\tau =\{p:\exists x(⟨p,x⟩\in \tau \},|\tau {|}^{+}=\bigcup _{p\in \mathtt{dom}\tau }|p{|}^{+},|\tau |=\bigcup _{p\in \mathtt{dom}\tau }|p|.$$

If $G\subseteq {\mathbf{Q}}^{*}$ then define

$$\tau \left[G\right]=\left\{x\in X:\right(\tau ’’x)\cap G\ne ⌀\},\mathrm{where}\tau ’’x=\{p:⟨p,x⟩\in \tau \},$$

so that $\tau \left[G\right]\subseteq X$. If $\phi$ is a formula in which some names $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$ occur, and $G\subseteq {\mathbf{Q}}^{*}$, then accordingly $\phi \left[G\right]$ is the result of substitution of $\tau \left[G\right]$ for each name $\tau$ in $\phi$.

Lemma 10.

Suppose that $X\in \mathbf{L}$, $\mathtt{card}X\le {\omega }_1$ in $\mathbf{L}$, U is a system in $\mathbf{L}$, and $G\subseteq \mathbf{Q}\left[U\right]$ is a set $\mathbf{Q}\left[U\right]$-generic over $\mathbf{L}$. Then for any set $Y\in \mathbf{L}\left[G\right],Y\subseteq X,$ there is a name $\tau \in {\mathbf{SN}}_X\left(\mathbf{Q}\left[U\right]\right)$ in $\mathbf{L}$ such that $Y=\tau \left[G\right]$. If in addition $c\in \mathbf{L},c\subseteq {\mathcal{I}}^{+}$, and $Y\in \mathbf{L}\left[G\upharpoonright c\right]$, then there is a name $\tau \in {\mathbf{SN}}_X\left(\mathbf{Q}\left[U\right]\upharpoonright c\right)$ in $\mathbf{L}$ such that $Y=\tau \left[G\right]$.

Proof. 

It follows from general forcing theory that there is a name $\sigma \in {\mathbf{N}}_X\left(\mathbf{Q}\left[U\right]\right)$, not necessarily an ${\omega }_1$-size name, such that $X=\sigma \left[G\right]$. Let $Q_x=\sigma ’’x$ for all $x\in X$. Arguing in $\mathbf{L}$, put

$$\tau =\{⟨p,x⟩\in \sigma :x\in X\wedge p\in A_x\},$$

where $A_x\subseteq Q_x$ is a maximal antichain for any x. We observe that $\mathtt{card}{A}_x\le {\omega }_1$ in $\mathbf{L}$ for all x by Lemma 8, hence $\tau \in {\mathbf{SN}}_X\left(\mathbf{Q}\left[U\right]\right)$. And on the other hand, we have $\tau \left[G\right]=\sigma \left[G\right]=Y$.

To prove the additional claim, note that by the product forcing theorem if $Y\in \mathbf{L}\left[G\upharpoonright c\right]$ then the original name $\sigma$ can be chosen in ${\mathbf{N}}_X\left(\mathbf{Q}\left[U\right]\upharpoonright c\right)$, and repeat the argument. □

3.5. Names for Reals in Product Extensions

Now we introduce names for reals (elements of ${\omega }^{\omega }$) in generic extensions of $\mathbf{L}$ considered. This is an important particular case of the content of Section 3.4.

Assume that in $\mathbf{L}$, $K\subseteq {\mathbf{Q}}^{*}$, e.g., $K=\mathbf{Q}\left[U\right]$, where U is a system. By ${\mathbf{N}}_{\omega }^{\omega }\left(K\right)$ ($K$-names for reals in ${\omega }^{\omega }$)we denote the set of all $\tau \subseteq K\times (\omega \times \omega )$ such that the sets $\tau ’’⟨j,k⟩=\{p:⟨p,⟨j,k⟩⟩\in \tau \}$ satisfy the following requirement:

$$\mathrm{if}\hspace{1em}k\ne k^{\prime }p\in \tau ’’⟨j,k⟩p^{\prime }\in \tau ’’⟨j,k^{\prime }⟩,\hspace{1em}\mathrm{then} \mathrm{conditions} p,p^{\prime } \mathrm{are} \mathrm{incompatible}.$$

We let $\tau ’’j={\bigcup }_k\tau ’’⟨j,k⟩$, $\mathtt{dom}\tau ={\bigcup }_{j,k<\omega }\tau ’’⟨j,k⟩$, ${\left|\tau \right|}^{+}=\bigcup \{{\left|p\right|}^{+}:p\in \mathtt{dom}\tau \}$.

Let ${\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$ (small names) consist of all ${\omega }_1$-size names $\tau \in {\mathbf{N}}_{\omega }^{\omega }\left(K\right)$; in other words, it is required that $\mathtt{card}(\tau ’’⟨j,k⟩)\le {\omega }_1$ for all $j,k<\omega$.

Define the restrictions ${\mathbf{SN}}_{\omega }^{\omega }\left(K\right)\upharpoonright c=\{\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\right):{\left|\tau \right|}^{+}\subseteq c\}$.

A name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$ is $K$-full iffthe set $\tau ’’j$ is pre-dense in K for any $j<\omega$. A name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$ is $K$-full below some $p_0\in K$, iff all sets $\tau ’’j$ are pre-dense in K below $p_0$, i.e., any condition $q\in K,q\le p_0$, is compatible with some $r\in {\tau }_j$ (and this holds for all $j<\omega$).

Suppose that $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$. A set $G\subseteq K$ is minimally $\tau$-generic iff it is compatible in itself (if $p,q\in G$ then there is $r\in G$ with $r\le p,r\le q$), and intersects each set $\tau ’’x,x\in X$. In this case, put

$$\tau \left[G\right]=\{⟨j,k⟩\in {\omega }^{\omega }\times {\omega }^{\omega }:\left(\tau ’’⟨j,k⟩\right)\cap G\ne ⌀\},$$

so that $\tau \left[G\right]\in {\omega }^{\omega }$ and $\tau \left[G\right]\left(j\right)=k⟺\tau ’’⟨j,k⟩\cap G\ne ⌀$. If $\phi$ is a formula in which some names $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$ occur, and a set $G\subseteq {\mathbf{Q}}^{*}$ is minimally $\tau$-generic for any name $\tau$ in $\phi$, then accordingly $\phi \left[G\right]$ is theresult of substitution of $\tau \left[G\right]$ for each name $\tau$ in $\phi$.

Lemma 11.

Suppose that U is a system in $\mathbf{L}$, and $G\subseteq \mathbf{Q}\left[U\right]$ is $\mathbf{Q}\left[U\right]$-generic over $\mathbf{L}$. Then for any real $x\in \mathbf{L}\left[G\right]\cap {\omega }^{\omega }$ there is a $\mathbf{Q}\left[U\right]$-full name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$ in $\mathbf{L}$ such that $x=\tau \left[G\right]$. If in addition $c\in \mathbf{L},c\subseteq {\mathcal{I}}^{+}$, and $x\in \mathbf{L}\left[G\upharpoonright c\right]$, then there is a $\mathbf{Q}\left[U\right]$-full name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\upharpoonright c\right)$ in $\mathbf{L}$ such that $x=\tau \left[G\right]$. □

Proof. 

It follows from general forcing theory that there is a $\mathbf{Q}\left[U\right]$-full name $\sigma \in {\mathbf{N}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$, not necessarily an ${\omega }_1$-size name, such that $f=\sigma \left[G\right]$. Then all sets $Q_j=\sigma ’’j,j<\omega$, are pre-dense in $\mathbf{Q}\left[U\right]$. Arguing in $\mathbf{L}$, put $\tau =\{⟨p,⟨j,k⟩⟩\in \sigma :j,k<\omega \wedge p\in A_j\}$, where $A_j\subseteq Q_j$ is a maximal antichain for any $j<\omega$. We conclude by Lemma 8 that $\mathtt{card}{A}_j\le {\omega }_1$ in $\mathbf{L}$ for all j, hence in fact $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$. And on the other hand, we have $\tau \left[G\right]=\sigma \left[G\right]=f$. □

Equivalent names. Names $\tau ,\mu \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$ are equivalent iff conditions $q,r$ are incompatiblewhenever $q\in \tau ’’⟨j,k⟩$ and $r\in \mu ’’⟨j,k^{\prime }⟩$ for some j and $k^{\prime }\ne k$. Names $\tau ,\mu$ are equivalent below some $p\in {\mathbf{Q}}^{*}$ iff the triple ofconditions $p,q,r$ is incompatible (that is, no common strengthening) whenever $q\in \tau ’’⟨j,k⟩$ and $r\in \mu ’’⟨j,k^{\prime }⟩$ for some j and $k^{\prime }\ne k$.

Lemma 12.

Suppose that in$\mathbf{L}$, $p\in {\mathbf{Q}}^{*}$, and names$\mu ,\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$are equivalent (resp., equivalent below p). If$G\subseteq {\mathbf{Q}}^{*}$is minimally$\mu$-generic and minimally$\tau$-generic (resp., and containing p), then$\mu \left[G\right]=\tau \left[G\right]$.

Proof. 

Suppose that this is not the case. Then by definition there exist numbers j and $k^{\prime }\ne k$ and conditions $q\in G\cap (\tau ’’⟨j,k⟩)$ and $r\in G\cap \left(\mu ’’⟨j,k^{\prime }⟩\right)$. Then $p,q,r$ are compatible (as elements of the same generic set), contradiction. □

The next lemma provides a useful transformation of names. Recall that $p^{\prime }\wedge p$ is defined in Section 3.1.

Lemma 13 (in $\mathbf{L}$).

If $p\in {\mathbf{Q}}^{*}$ and $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$, then

$${\tau }_{\le p}=\{⟨p^{\prime }\wedge p,⟨j,k⟩⟩:⟨p^{\prime },⟨j,k⟩⟩\in \tau \mathrm{and}{p}^{\prime }\mathrm{is}\mathrm{compatible}\mathrm{with}p\}$$

is still a name in ${\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$, equivalent to τ below p, and $|{\tau }_{\le p}{|}^{+}\subseteq {\left|\tau \right|}^{+}\cup {\left|p\right|}^{+}$.

If U is a system and $p\in \mathbf{Q}\left[U\right]$, $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$, then ${\tau }_{\le p}\in {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$.

Moreover, if τ is $\mathbf{Q}\left[U\right]$-full below p then ${\tau }_{\le p}$ is $\mathbf{Q}\left[U\right]$-full below p, too.

Proof. 

Routine. □

3.6. Permutations

We continue to argue in $\mathbf{L}$. There are three important families of transformations of the whole system of objects related to product forcing, considered in this Subsection and the two following ones.

We begin with permutations, the first family. Let $\mathbf{B}\mathbf{IJ}$ be the set of all bijections $\pi :\mathcal{I}\stackrel{\mathrm{onto}}{⟶}\mathcal{I}$, i.e., permutations of the set $\mathcal{I}$,such that the set $\left|\pi \right|=\left\{\nu \in \mathcal{I}:\pi \right(\nu )\ne \nu \}$ (the essential domain) satisfies $\mathtt{card}\left|\pi \right|\le {\omega }_1$. Please note that $\pi$ is the identity outside of $\left|\pi \right|$. Any permutation $\pi \in \mathbf{B}\mathbf{IJ}$ acts onto:

–

sets $e\subseteq \mathcal{I}$: by $\pi ·e:=\{\pi \left(\nu \right):\nu \in e\}$;

–

systems U: by $\left(\pi ·U\right)\left(\pi \right(\nu \left)\right):=U\left(\nu \right)$ for all $\nu \in \left|U\right|$—then $\left|\pi ·U\right|=\pi ·\left|U\right|$;

–

conditions $p\in {\mathbf{Q}}^{*}$: if $-1\in {\left|p\right|}^{+}$ then $-1\in {\left|\pi ·p\right|}^{+}$ and ${\mathit{b}}_{\pi ·p}={\mathit{b}}_p$, and if $\nu \in \left|p\right|$ then $\left(\pi ·p\right)\left(\pi \right(\nu \left)\right):=p\left(\nu \right)$, so $\left|\pi ·p\right|=\pi ·\left|p\right|$;

–

sets $G\subseteq {\mathbf{Q}}^{*}$: by $\pi ·G:=\{\pi ·p:p\in G\}$—then $\pi ·G\subseteq {\mathbf{Q}}^{*}$;

–

names $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$: by $\pi ·\tau :=\{⟨\pi ·p,⟨\ell ,k⟩⟩:⟨p,⟨\ell ,k⟩⟩\in \tau \}\in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right).$

Lemma 14 (routine).

If $\pi \in \mathbf{B}\mathbf{IJ}$ then $p⟼\pi ·p$ is an order-preserving bijection of ${\mathbf{Q}}^{*}$ onto ${\mathbf{Q}}^{*}$, and if U is a system then $p\in \mathbf{Q}\left[U\right]⟺\pi ·p\in \mathbf{Q}\left[\pi ·U\right]$. □

3.7. Multi-Lipschitz Transformations

Still arguing in $\mathbf{L}$, we let $\mathbf{L}{\mathbf{IP}}^{\mathcal{I}}$ be the $\mathcal{I}$-product of the group $\mathbf{L}\mathbf{IP}$ (see Section 2.3), this will be our second family of transformations, called multi-Lipschitz. Thus, a typical element $\lambda \in \mathbf{L}{\mathbf{IP}}^{\mathcal{I}}$ is $\lambda ={\left\{{\lambda }_{\nu }\right\}}_{\nu \in \left|\lambda \right|}$, where $\left|\lambda \right|=\mathtt{dom}\lambda \subseteq {\mathcal{I}}^{+}$ has ${\omega }_1$-size, ${\lambda }_{\nu }\in \mathbf{L}\mathbf{IP},\forall \nu$. Define the action of any $\lambda \in \mathbf{L}{\mathbf{IP}}^{\mathcal{I}}$ on:

–

systems U: $\left|\lambda ·U\right|:=\left|U\right|$, and $\left(\lambda ·U\right)\left(\nu \right):={\lambda }_{\nu }·U\left(\nu \right)$ for all elements $\nu \in \left|\lambda \right|\cap \left|U\right|$, but $\left(\lambda ·U\right)\left(\nu \right):=U\left(\nu \right)$ for all $\nu \in \left|U\right|\setminus \left|\lambda \right|$;

–

conditions $p\in {\mathbf{Q}}^{*}$: ${\left|\lambda ·p\right|}^{+}={\left|p\right|}^{+}$, if $-1\in {\left|p\right|}^{+}$ then ${\mathit{b}}_{\lambda ·p}={\mathit{b}}_p$, if $\nu \in \left|p\right|\cap \left|\lambda \right|$ then $\left(\lambda ·p\right)\left(\nu \right)={\lambda }_{\nu }·p\left(\nu \right)$, but if $\nu \in \left|p\right|\setminus \left|\lambda \right|$, then $\left(\lambda ·p\right)\left(\nu \right)=p\left(\nu \right)$;

–

sets $G\subseteq {\mathbf{Q}}^{*}$: $\lambda ·G:=\{\lambda ·p:p\in G\}$;

–

names $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$: $\lambda ·\tau :=\{⟨\lambda ·p,⟨n,k⟩⟩:⟨p,⟨n,k⟩⟩\in \tau \}$;

In the first two items, we refer to the action of ${\lambda }_{\nu }\in \mathbf{L}\mathbf{IP}$ on sets $u\subseteq \mathbf{F}\mathbf{UN}$ and on forcing conditions, as defined in Section 2.3.

Lemma 15 (routine).

If $\lambda \in \mathbf{L}{\mathbf{IP}}^{\mathcal{I}}$ then $p⟼\pi ·p$ is an order-preserving bijection of ${\mathbf{Q}}^{*}$ onto ${\mathbf{Q}}^{*}$, and if U is a system then $p\in \mathbf{Q}\left[U\right]⟺\lambda ·p\in \mathbf{Q}\left[\lambda ·U\right]$. □

Lemma 16.

Suppose that $U,V$ are systems, $\left|U\right|=\left|V\right|$, $p\in \mathbf{Q}\left[U\right],q\in \mathbf{Q}\left[V\right]$, $\left|p\right|=\left|q\right|$, and sets $F_p^{\vee }\left(\nu \right)$, $F_q^{\vee }\left(\nu \right)$ are i-similar for all $\nu \in \left|p\right|=\left|q\right|$. Then there is $\lambda \in \mathbf{L}{\mathbf{IP}}^{\mathcal{I}}$ such that $\left|\lambda \right|=\left|U\right|=\left|V\right|$, $\lambda ·U=V$, and $F_q^{\vee }\left(\nu \right)=F_{\lambda ·p}^{\vee }\left(\nu \right)$ for all $\nu \in \left|p\right|=\left|q\right|$.

Proof. 

Apply Lemma 5 componentwise for every $\nu \in \mathcal{I}$. □

3.8. Multi-Substitutions

Assume that conditions $p,q\in {\mathbf{Q}}^{*}$ satisfy the following:

$$\left.\begin{array}{cc}\left(6\mathrm{i}\right)\hfill & -1\in {\left|p\right|}^{+}={\left|q\right|}^{+}\mathrm{and}\mathtt{lh}{\mathit{b}}_p=\mathtt{lh}{\mathit{b}}_q,\mathrm{and}\hfill \\ \left(6\mathrm{ii}\right)\hfill & \mathrm{if}\nu \in \left|p\right|\mathrm{then}{F}_p\left(\nu \right)=F_q\left(\nu \right)\mathrm{and}{S}_p\left(\nu \right)\cup S_q\left(\nu \right)\subseteq F_p^{\vee }\left(\nu \right)=F_q^{\vee }\left(\nu \right).\hfill \end{array}\right\}$$

(6)

In particular, (4) of Section 2.4 holds for all $\nu$. We define a transformation $H_{pq}$ acting as follows. First, we let ${\mathbf{D}}_{pq}$, the domain of $H_{pq}$, contain all conditions $r\in {\mathbf{Q}}^{*}$ such that

(a)

if $-1\in {\left|r\right|}^{+}$ and ${\mathit{b}}_p\ne {\mathit{b}}_q$, then ${\mathit{b}}_p\subseteq {\mathit{b}}_r$ or ${\mathit{b}}_q\subseteq {\mathit{b}}_r$;

(b)

if $\nu \in \left|r\right|\cap \left|p\right|$ and $p\left(\nu \right)\ne q\left(\nu \right)$, then $r\left(\nu \right)\le p\left(\nu \right)$ or $r\left(\nu \right)\le q\left(\nu \right)$, thus, in other words, $r\left(\nu \right)\in d_{p\left(\nu \right)p\left(\nu \right)}$ in the sense of Section 2.4.

Please note that all conditions $r\le p$ and all $r\le p$ belong to ${\mathbf{D}}_{pq}$. On the other hand, if $r\in {\mathbf{Q}}^{*}$ satisfies $\left|r\right|\cap \left|p\right|=⌀$ and (a), then r belongs to ${\mathbf{D}}_{pq}$ as well. In particular, $\odot \in {\mathbf{D}}_{pq}$.

If $r\in {\mathbf{D}}_{pq}$, then define $r^{\prime }=H_{pq}\left(r\right)\in {\mathbf{Q}}^{*}$ so that $|r^{\prime }{|}^{+}={\left|r\right|}^{+}$ and:

(a1)

if $-1\in {\left|r\right|}^{+}$ and ${\mathit{b}}_p={\mathit{b}}_q$ then simply ${\mathit{b}}_{r^{\prime }}={\mathit{b}}_r$,

(a2)

if $-1\in {\left|r\right|}^{+}$ and ${\mathit{b}}_p\ne {\mathit{b}}_q$, then by (a) either ${\mathit{b}}_r={\mathit{b}}_{p}s$ or ${\mathit{b}}_r={\mathit{b}}_{q}s$, where $s\in \mathcal{P}{\left(\omega \right)}^{<\omega }$—we put ${\mathit{b}}_{r^{\prime }}={\mathit{b}}_{q}s$ in the first case, and ${\mathit{b}}_{r^{\prime }}={\mathit{b}}_{p}s$ in the second case;

(b1)

if either $\nu \in \left|r\right|\setminus \left|p\right|$, or $\nu \in \left|r\right|\cap \left|p\right|\wedge p\left(\nu \right)=q\left(\nu \right)$, then put $r^{\prime }\left(\nu \right)=r\left(\nu \right)$,

(b2)

if $\nu \in \left|p\right|=\left|q\right|$ and $p\left(\nu \right)\ne q\left(\nu \right)$, then we put $r^{\prime }\left(\nu \right)=h_{p\left(\nu \right)q\left(\nu \right)}\left(r\left(\nu \right)\right)$, where $h_{p\left(\nu \right)q\left(\nu \right)}$ is defined in Section 2.4.

Transformations of the form $H_{pq}$ will be called multi-substitutions.

Lemma 17 (in L).

(i)

If U is a system and $p_0,q_0\in \mathbf{Q}\left[U\right]$ then there exist conditions $p,q\in \mathbf{Q}\left[U\right]$ with $p\le p_0$, $q\le q_0$, satisfying (6).

(ii)

If conditions $p,q\in {\mathbf{Q}}^{*}$ satisfy (6), then $H_{pq}$ is an order automorphism of ${\mathbf{D}}_{pq}={\mathbf{D}}_{qp}$, and we have $H_{pq}={\left(H_{pq}\right)}^{-1}=H_{qp}$ and $H_{pq}\left(p\right)=q$.

(iii)

If U is a system, and $p,q\in \mathbf{Q}\left[U\right]$ satisfy (6), then $H_{pq}$ maps the set $\mathbf{Q}\left[U\right]\cap {\mathbf{D}}_{pq}$ onto itself order-preserving.

Proof. 

Apply Lemma 6 componentwise. □

Corollary 1 (of Lemma 17).

If U is a system then$\mathbf{Q}\left[U\right]$ishomogeneousin the following sense: if $p_0,q_0\in \mathbf{Q}\left[U\right]$ then there exist stronger conditions $p\le p_0$ and $q\le q_0$ in $\mathbf{Q}\left[U\right]$, such that the according lower cones $\{p^{\prime }\in \mathbf{Q}\left[U\right]:p^{\prime }\le p\}$ and $\{q^{\prime }\in \mathbf{Q}\left[U\right]:q^{\prime }\le q\}$ are order-isomorphic. □

Action of$H_{pq}$on names. Assume that conditions $p,q\in {\mathbf{Q}}^{*}$ satisfy (6). Let ${{\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)}_{pq}$ contain all names $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$ such that $\mathtt{dom}\tau \subseteq {\mathbf{D}}_{pq}$. If $\tau \in {\mathbf{SN}}_{\omega }^{\omega }{\left({\mathbf{Q}}^{*}\right)}_{pq}$ then put

$$H_{pq}·\tau =\{⟨H_{pq}\left(p^{\prime }\right),⟨n,k⟩⟩:⟨p^{\prime },⟨n,k⟩⟩\in \tau \}.$$

Then obviously $H_{pq}·\tau \in {\mathbf{SN}}_{\omega }^{\omega }{\left({\mathbf{Q}}^{*}\right)}_{qp}$.

4. The Basic Forcing Notion and the Model

In this paper, we let ${\mathbf{ZFC}}^{-}$ be $\mathbf{ZFC}$ minus the Power Set axiom, with the schema of Collection instead of Replacement, with AC is assumed in the form of well-orderability of every set, and with the axiom: “${\omega }_1$ exists”. See [8] on versions of $\mathbf{ZFC}$ sans the Power Set axiom in detail.

Let ${\mathbf{ZFC}}_2^{-}$ be ${\mathbf{ZFC}}^{-}$ plus the axioms: $\mathbf{V}=\mathbf{L}$, and the axiom “every set x satisfies $\mathtt{card}x\le {\omega }_1$”.

4.1. Jensen—Solovay Sequences

Arguing in $\mathbf{L}$, let $U,V$ be systems. Suppose that M is any transitive model of ${\mathbf{ZFC}}_2^{-}$. Define $U{\preccurlyeq }_M{U}^{\prime }$ iff $U\preccurlyeq U^{\prime }$ and the following holds:

(a)

the set $\Delta (U,U^{\prime })={\bigcup }_{\nu \in \left|U\right|}(U^{\prime }\left(\nu \right)\setminus U\left(\nu \right))$ is multiply $\mathbf{S}\mathbf{EQ}$-generic over M,in the sense that every sequence $⟨f_1,\dots f_m⟩$ of pairwise different functions $f_{\ell }\in \Delta (U,U^{\prime })$ is generic over M in the sense of $\mathbf{S}\mathbf{EQ}={{\omega }_1}^{<{\omega }_1}$ as the forcing notion in $\mathbf{L}$, and

(b)

if $\nu \in \left|U\right|$ then $U^{\prime }\left(\nu \right)\setminus U\left(\nu \right)$ is dense in $\mathbf{F}\mathbf{UN}$, therefore uncountable.

Let $\mathbf{JS}$, Jensen—Solovay pairs, be the set of all pairs $⟨M,U⟩$ of:

−

a transitive model $M\vDash {\mathbf{ZFC}}_2^{-}$, and a system U,

−

such that the sets ${\omega }_1$ and U belong to M—then sets $\mathbf{S}\mathbf{EQ},\mathbf{Q}\left[U\right]$ also belong to M.

Let $\mathbf{sJS}$, small Jensen—Solovay pairs, be the set of all pairs $⟨M,U⟩\in \mathbf{JS}$ such that both U and M have cardinality $\le {\omega }_1$. We define:

• $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩$ ($⟨M^{\prime },U^{\prime }⟩$ extends $⟨M,U⟩$) iff $M\subseteq M^{\prime }$ and $U{\preccurlyeq }_M{U}^{\prime }$;
• $⟨M,U⟩\prec ⟨M^{\prime },U^{\prime }⟩$ (strict extension) iff $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩$ and $\forall \nu \in \mathcal{I}(U\left(\nu \right)⫋U^{\prime }\left(\nu \right))$.

Lemma 18 (in L).

If $⟨M,U⟩\in \mathbf{sJS}$ and $z\subseteq \mathcal{I}$, $\mathtt{card}z\le {\omega }_1$, then there is a pair $⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$, such that $⟨M,U⟩\prec ⟨M^{\prime },U^{\prime }⟩$ and $z\subseteq |U^{\prime }|$.

Proof. 

Let $d=\left|U\right|\cup z$. By definition $\mathbf{S}\mathbf{EQ}$ is $\omega$-closed as a forcing: any $\subseteq$-increasing sequence ${\left\{s_n\right\}}_{n<\omega }$ of $s_n\in \mathbf{S}\mathbf{EQ}$ has the least upper bound in $\mathbf{S}\mathbf{EQ}$, equal to the union of all $s_n$. It follows that the countable-support product $\mathbf{S}{\mathbf{EQ}}^{(d\times {\omega }_1)}$ is $\omega$-closed, too. Therefore, as $\mathtt{card}M\le {\omega }_1$, there exists a system $\overrightarrow{f}={\left\{f_{\nu \xi }\right\}}_{\nu \in d,\xi <{\omega }_1}\in {\left(\mathbf{Fun}\right)}^{d\times {\omega }_1}$, $\mathbf{S}{\mathbf{EQ}}^{(d\times {\omega }_1)}$-generic over M. Now define $U^{\prime }\left(\nu \right)=U\left(\nu \right)\cup \{f_{\nu \xi }:\xi <{\omega }_1\}$ for each $\nu \in d$ (assuming that $U\left(\nu \right)=⌀$ in case $\nu \notin \left|U\right|$), and let $M^{\prime }\vDash {\mathbf{ZFC}}_1^{-}$ be any transitive model of cardinality ${\omega }_1$, satisfying $M\subseteq M^{\prime }$ and containing $U^{\prime }$. □

Lemma 19 (in $\mathbf{L}$).

Suppose that pairs $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩\preccurlyeq ⟨M^{\prime \prime },U^{\prime \prime }⟩$ belong to $\mathbf{JS}$. Then $⟨M,U⟩\preccurlyeq ⟨M^{\prime \prime },U^{\prime \prime }⟩$. Thus ≼ is a partial order on $\mathbf{JS}$.

Proof. 

We claim that $F={\bigcup }_{\nu \in \left|U\right|}(U^{\prime \prime }\left(\nu \right)\setminus U\left(\nu \right))$ is multiply $\mathbf{S}\mathbf{EQ}$-generic over M. Suppose, for the sake of brevity, that $F=\{f,g\}$, where $f\in U^{\prime }\left(\nu \right)\setminus U\left(\nu \right)$—then $f\in M^{\prime }$, $g\in U^{\prime \prime }\left(\mu \right)\setminus U^{\prime }\left(\mu \right)$, and $\nu ,\mu \in \left|U\right|$. (The general case does not differ much.) By definition, f is Cohen generic over M and g is Cohen generic over $M^{\prime }$. Therefore, g is Cohen generic over $M\left[f\right]$, because $M\left[f\right]\subseteq M^{\prime }$ (as $f\in M^{\prime }$). It remains to apply the product forcing theorem. □

Now, still in $\mathbf{L}$, a Jensen—Solovay sequence of length $\lambda \le {\omega }_2$ is any strictly $\prec$-increasing $\lambda$-sequence ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <\lambda }$ of pairs $⟨M_{\xi },U_{\xi }⟩\in \mathbf{sJS}$, satisfying $U_{\eta }={\bigvee }_{\xi <\eta }{U}_{\xi }$ on limit steps. Let ${\overrightarrow{\mathbf{JS}}}_{\lambda }$ be the set of all such sequences.

Lemma 20 (in $\mathbf{L}$).

Let λ be a limit ordinal, and${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <\lambda }\in {\overrightarrow{\mathbf{JS}}}_{\lambda }$. Put$U={\bigvee }_{\xi <\lambda }{U}_{\xi }$. Then

(i)

$U_{\xi }{\preccurlyeq }_{M_{\xi }}U$ for every ξ.

(ii)

If moreover $\lambda <{\omega }_2$ and $M\vDash {\mathbf{ZFC}}_2^{-}$ is a transitive model containing ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <\lambda }$ then $⟨M,U⟩\in \mathbf{sJS}$ and $⟨M_{\xi },U_{\xi }⟩\prec ⟨M,U⟩,\forall \xi$.

(iii)

The same is true in case $\lambda ={\omega }_2$, but then the model M is not necessarily a ${\omega }_1$-size model, and we require $⟨M,U⟩\in \mathbf{JS}$ rather than $\mathbf{sJS}$, of course.

Proof. 

The same arguments work as in the proof of Lemma 19. □

4.2. Stability of Dense Sets

If U is a system, D is a pre-dense subset of $\mathbf{P}\left[U\right]$, and $U^{\prime }$ is another system extending U, then in principle D does not necessarily remain maximal in $\mathbf{P}\left[U^{\prime }\right]$, a bigger set. This is where the genericity requirement (a) in Section 4.1 plays its role to seal the pre-density of sets in M w. r. t. further extensions. This is the content of the following key theorem. Moreover, the product forcing arguments will allow us to extend the stability result in pre-dense sets not necessarily in M, as in items (ii), (iii) of the theorem.

Theorem 2 (stability of dense sets).

Assume that, in $\mathbf{L}$, $⟨M,U⟩\in \mathbf{sJS}$, $U^{\prime }$ is a system, and $U{\preccurlyeq }_M{U}^{\prime }$. If D is a pre-dense subset of $\mathbf{Q}\left[U\right]$ (resp., pre-dense below some $p\in \mathbf{Q}\left[U\right]$) then D remains pre-dense in $\mathbf{Q}\left[U^{\prime }\right]$ (resp., pre-dense below p) in each of the following three cases:

(i)

$D\in M;$

(ii)

$D\in M\left[G\right]$, where $G\subseteq P$ is $P$-generic over $\mathbf{L}$, and $P\in M$ is a PO set;

(iii)

$D\in M\left[H\right]$, where $H\subseteq U^{\prime }\left({\nu }_1\right)$ is finite, ${\nu }_1\in \mathcal{I}$ is fixed, and $D\subseteq \mathbf{Q}\left[U\right]{\upharpoonright }_{\ne {\nu }_1}=\{q\in \mathbf{Q}\left[U\right]:{\nu }_1\notin \left|q\right|\}$.

Proof. 

Arguing in $\mathbf{L}$, we consider only the case of sets D pre-dense in $\mathbf{Q}\left[U\right]$ itself; the case of pre-density below some $p\in \mathbf{Q}\left[U\right]$ is treated similarly.

(i) Suppose, towards the contrary, that a condition $p\in \mathbf{Q}\left[U^{\prime }\right]$ is incompatible with each $q\in D$. As $D\subseteq \mathbf{P}\left[U\right]$, we can w.l.o.g. assume that $\left|p\right|\subseteq \left|U\right|$.

We are going to define a condition $p^{\prime }\in \mathbf{Q}\left[U\right]$, also incompatible with each $q\in D$, contrary to the pre-density. To maintain the construction, consider the finite sequence $\overrightarrow{f}=⟨f_1,\dots ,f_m⟩$ of all elements $f\in \mathbf{F}\mathbf{UN}$ occurring in ${\bigcup }_{\nu \in \left|p\right|}{F}_p\left(\nu \right)$ but not in U. It follows from $U{\preccurlyeq }_M{U}^{\prime }$ that $\overrightarrow{f}$ is $\mathbf{S}{\mathbf{EQ}}^m$-generic over M. Moreover, p being incompatible with D is implied by the fact that $\overrightarrow{f}$ meets a certain family of dense sets in $\mathbf{S}{\mathbf{EQ}}^m$, of cardinality $\le {\omega }_1$ in M. Therefore, we will be able to simulate this in M, getting a sequence $\overrightarrow{g}\in M$ which meets the same dense sets, and hence yields a condition $p^{\prime }\in \mathbf{Q}\left[U\right]$, also incompatible with each $q\in D$.

To present the key idea in sufficient detail in a rather simplified subcase, we assume that

$$\left|p\right|=\left\{{\nu }_0\right\}\mathrm{is}\mathrm{a}\mathrm{singleton};{\nu }_0\in \left|U\right|.$$

(7)

Then $p\left({\nu }_0\right)=⟨S_p\left({\nu }_0\right);F_p\left({\nu }_0\right)⟩\in Q\left[U^{\prime }\left({\nu }_0\right)\right]$, where $S_p\left({\nu }_0\right)\subseteq \mathbf{S}\mathbf{EQ}$ and $F_p\left({\nu }_0\right)\subseteq U^{\prime }\left({\nu }_0\right)$ are finite sets. The (finite) set $X=F_p\left({\nu }_0\right)\setminus U\left({\nu }_0\right)$ is multiply $\mathbf{S}\mathbf{EQ}$-generic over M since $U{\preccurlyeq }_M{U}^{\prime }$. To make the argument even more transparent, we suppose that

$$X=\{f,g\},\mathrm{where}f\ne g\mathrm{and}\mathrm{the}\mathrm{pair}⟨f,g⟩\mathrm{is}\mathbf{S}{\mathbf{EQ}}^2-\mathrm{generic}\mathrm{over}M.$$

(8)

(The general case follows the same idea and can be found in [4]; we leave it to the reader.)

Thus, $F_p\left({\nu }_0\right)=F\cup \{f,g\}$, where $F=F_p\left({\nu }_0\right)\cap U\left({\nu }_0\right)\in M$ is by definition a finite set.

The plan is to replace the functions $f,g$ by some functions $f^{\prime },g^{\prime }\in U\left({\nu }_0\right)$ so that the incompatibility of p with conditions in D will be preserved.

It holds by the choice of p and Lemma 1 that $D=D_1(f,g)\cup D_2$, where

$$\begin{array}{ccc}\hfill D_1(f,g)& =& \{q\in D:A_q\cap F_p^{\vee }\left({\nu }_0\right)\ne ⌀\},\mathrm{where}{A}_q=S_q\left({\nu }_0\right)\setminus S_p\left({\nu }_0\right)\subseteq \mathbf{S}\mathbf{EQ};\hfill \\ \hfill D_2& =& \{q\in D:(S_p\left({\nu }_0\right)\setminus S_q\left(\nu \right))\cap F_q^{\vee }\left({\nu }_0\right)\ne ⌀\}\in M;\hfill \end{array}$$

and $D_1$ depends on $f,g$ via $F_p\left({\nu }_0\right).$ The equality $D=D_1(f,g)\cup D_2$ can be rewritten as $\Delta \subseteq D_1(f,g)$, where $\Delta =D\setminus D_2\in M$. Furthermore, $\Delta \subseteq D_1(f,g)$ is equivalent to

$$\forall A\in \mathcal{A}(A\cap F_p^{\vee }\left(\nu \right)\ne ⌀),\mathrm{where}\mathcal{A}=\{A_q:q\in D\}\in M,$$

(9)

and each $A_q=S_q\left({\nu }_0\right)\setminus S_p\left({\nu }_0\right)\subseteq \mathbf{S}\mathbf{EQ}$ is finite. Recall that $F_p\left({\nu }_0\right)=F\cup \{f,g\}$, therefore $F_p^{\vee }\left({\nu }_0\right)=Z\cup S(f,g)$, where $Z=\{h\upharpoonright \mu :1\le \mu <{\omega }_1\wedge h\in F\}\in M$ and $S(f,g)={\bigcup }_{1\le \mu <{\omega }_1}\{f\upharpoonright \mu ,g\upharpoonright \mu \}$. Thus, (9) is equivalent to

$$\forall A^{\prime }\in {\mathcal{A}}^{\prime }(A^{\prime }\cap S(f,g)\ne ⌀),\mathrm{where}{\mathcal{A}}^{\prime }=\{A_q\setminus Z:q\in D\}\in M.$$

(10)

Please note that each $A^{\prime }\in {\mathcal{A}}^{\prime }$ is a finite subset of $\mathbf{S}\mathbf{EQ}$, so we can re-enumerate ${\mathcal{A}}^{\prime }=\{A_{\kappa }^{\prime }:\kappa <{\omega }_1\}$ in M and rewrite (10) as follows:

$$\forall \kappa <{\omega }_1(A_{\kappa }^{\prime }\cap S(f,g)\ne ⌀),\mathrm{where}\mathrm{each}{A}_{\kappa }^{\prime }\subseteq \mathbf{S}\mathbf{EQ}\mathrm{is}\mathrm{finite}.$$

(11)

As the pair $⟨f,g⟩$ is $\mathbf{S}\mathbf{EQ}$-generic, there is an index ${\mu }_0<{\omega }_1$ such that (11) is forced over M by $⟨{\sigma }_0,{\tau }_0⟩$, where ${\sigma }_0=f\upharpoonright {\mu }_0$ and ${\tau }_0=g\upharpoonright {\mu }_0$. In other words, $A_{\kappa }^{\prime }\cap S(f^{\prime },g^{\prime })\ne ⌀$ holds for all $\kappa <{\omega }_1$ whenever $⟨f^{\prime },g^{\prime }⟩$ is $\mathbf{S}\mathbf{EQ}$-generic over M and ${\sigma }_0\subset f^{\prime }$, ${\tau }_0\subset g^{\prime }$. It follows that for any $\kappa <{\omega }_1$ and sequences $\sigma ,\tau \in \mathbf{S}\mathbf{EQ}$ extending resp. ${\sigma }_0,{\tau }_0$ there are sequences ${\sigma }^{\prime },{\tau }^{\prime }\in \mathbf{S}\mathbf{EQ}$ extending resp. $\sigma ,\tau$, at least one of which extends one of sequences $w\in A_{\kappa }^{\prime }$. This allows us to define, in M, a pair of sequences $f^{\prime },g^{\prime }\in \mathbf{F}\mathbf{UN}$, such that ${\sigma }_0\subset f^{\prime }$, ${\tau }_0\subset g^{\prime }$, and for any $\kappa <{\omega }_1$ at least one of $f^{\prime },g^{\prime }$ extends one of $w\in A_k^{\prime }$. In other words, we have

$$\forall \kappa <{\omega }_1(A_{\kappa }^{\prime }\cap S(f^{\prime },g^{\prime })\ne ⌀)\mathrm{and}\forall A^{\prime }\in {\mathcal{A}}^{\prime }(A^{\prime }\cap S(f^{\prime },g^{\prime })\ne ⌀).$$

It follows that the condition $p^{\prime }$ defined by $|p^{\prime }|=\left\{{\nu }_0\right\}$, $S_{p^{\prime }}\left({\nu }_0\right)=S_p\left({\nu }_0\right)$, $F_{p^{\prime }}\left({\nu }_0\right)=F\cup \{f^{\prime },g^{\prime }\}$, still satisfies $\forall A\in \mathcal{A}(A\cap F_{p^{\prime }}^{\vee }\left({\nu }_0\right)\ne ⌀)$ (compare with (9)), and further $D=D_1(f^{\prime },g^{\prime })\cup D_2$, thus $p^{\prime }$ is incompatible with each $q\in D$. Yet $p^{\prime }\in M$ since $f^{\prime },g^{\prime }\in M$, which contradicts the pre-density of D.

(ii)The above proof works with $M\left[G\right]$ instead of M since the set X as in the proof is multiple $\mathbf{S}\mathbf{EQ}$-generic over $M\left[G\right]$ by the product forcing theorem.

(iii) Assuming w.l.o.g. that $H\subseteq U^{\prime }\left({\nu }_1\right)\setminus U\left({\nu }_1\right)$, we conclude that $M\left[H\right]$ is a $\mathbf{S}\mathbf{EQ}$-generic extension of M. Now, if $p\in \mathbf{Q}\left[U^{\prime }\right]{\upharpoonright }_{\ne {\nu }_1}$, then, following the above argument, let ${\nu }_0\in \left|p\right|,{\nu }_0\ne {\nu }_1$. By the definition of ≼ the set $F=F_p\left({\nu }_0\right)\setminus U\left({\nu }_0\right)$ is multiply $\mathbf{S}\mathbf{EQ}$-generic not only over M but also over $M\left[H\right]$. This allows the carrying out of the same argument as above. □

Corollary 2.

Under the assumptions of Theorem 2, if a set $G\subseteq \mathbf{Q}\left[U^{\prime }\right]$ is $\mathbf{Q}\left[U^{\prime }\right]$-generic over a transitive model $M^{\prime }\vDash {\mathbf{ZFC}}_2^{-}$ containing M and $U^{\prime }$ (including the case $M^{\prime }=\mathbf{L}$), then the intersection $G\cap \mathbf{Q}\left[U\right]$ is $\mathbf{Q}\left[U\right]$-generic over M.

Proof. 

If a set $D\in M$, $D\subseteq \mathbf{Q}\left[U\right]$, is pre-dense in $\mathbf{Q}\left[U\right]$, then it is pre-dense in $\mathbf{Q}\left[U^{\prime }\right]$ by Theorem 2, and hence $G\cap D\ne ⌀$ by the genericity. □

Corollary 3 (in $\mathbf{L}$).

Under the assumptions of Theorem 2, if $\tau \in M\cap {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$ is a $\mathbf{Q}\left[U\right]$-full name then τ remains $\mathbf{Q}\left[U^{\prime }\right]$-full, and if $p\in \mathbf{Q}\left[U\right]$ and τ is $\mathbf{Q}\left[U\right]$-full below p, then τ remains $\mathbf{Q}\left[U^{\prime }\right]$-full below p.□

4.3. Complete Sequences and the Basic Forcing Notion

In $\mathbf{L}$, we say that a pair $⟨M,U⟩\in \mathbf{sJS}$ solves a set $D\subseteq \mathbf{sJS}$ iff either $⟨M,U⟩\in D$ or there is no pair $⟨M^{\prime },U^{\prime }⟩\in D$ that extends $⟨M,U⟩$. Let $D^{\mathrm{solv}}$ be the set of all pairs $⟨M,U⟩\in \mathbf{sJS}$ whichsolve a given set $D\subseteq \mathbf{sJS}$. A sequence ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <{\omega }_2}\in {\overrightarrow{\mathbf{JS}}}_{{\omega }_2}$ is called $n$-complete ($n\ge 3$) iff it intersects every set of the form $D^{\mathrm{solv}}$, where $D\subseteq \mathbf{sJS}$ is a ${\Sigma }_{n-2}^{\mathrm{H}{\omega }_2}\left(\mathrm{H}{\omega }_2\right)$ set.

Recall that $\mathrm{H}{\omega }_2$ is the collection of all sets x whose transitive closure $\mathrm{TC}\left(x\right)$ has cardinality $\mathtt{card}\left(\mathrm{TC}\right(x\left)\right)<{\omega }_2$. Furthermore, ${\Sigma }_{n-2}^{\mathrm{H}{\omega }_2}\left(\mathrm{H}{\omega }_2\right)$ means definability by a ${\Sigma }_{n-2}^{}$ formula of the $\in$-language, in which any definability parameters in $\mathrm{H}{\omega }_2$ are allowed, while ${\Sigma }_{n-2}^{\mathrm{H}{\omega }_2}$ means parameter-free definability. Similarly, ${\Delta }_{n-1}^{\mathrm{H}{\omega }_2}\left(\left\{{\omega }_1\right\}\right)$ in the next theorem means that ${\omega }_1$ is allowed as a sole parameter. It is a simple exercise that sets $\left\{\mathbf{S}\mathbf{EQ}\right\}$ and $\mathbf{S}\mathbf{EQ}$ are ${\Delta }_1^{\mathrm{H}{\omega }_2}\left(\left\{{\omega }_1\right\}\right)$ under $\mathbf{V}=\mathbf{L}$.

Generally, we refer to e.g., ([9] (Part B, 5.4)), or ([10] (Chapter 13)) on the Lévy hierarchy of ∈-formulas and definability classes ${\Sigma }_n^H$, ${\Pi }_n^H$, ${\Delta }_n^H$ for any transitive set H.

Theorem 3 (in $\mathbf{L}$).

Let $n\ge 2$. There is a sequence ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <{\omega }_2}\in {\overrightarrow{\mathbf{JS}}}_{{\omega }_2}$ of class ${\Delta }_{n-1}^{\mathrm{H}{\omega }_2}\left(\left\{{\omega }_1\right\}\right)$, hence, ${\Delta }_{n-1}^{\mathrm{H}{\omega }_2}$ in case $n\ge 3$, $n$-complete in case $n\ge 3$, and such that $\xi \in |U_{\xi +1}|$ for all $\xi <{\omega }_2$.

Proof. 

To account for ${\omega }_1$ as a parameter, note that the set ${\omega }_1$ is ${\Sigma }_1^{\mathrm{H}{\omega }_2}$, and hence the singleton $\left\{{\omega }_1\right\}$ is ${\Delta }_2^{\mathrm{H}{\omega }_2}$. Indeed “being ${\omega }_1$” is equivalent to the conjunction of “being uncountable”—which is ${\Pi }_1^{\mathrm{H}{\omega }_2}$, and “every smaller ordinal is countable”—which is ${\Sigma }_1^{\mathrm{H}{\omega }_2}$ since the quantifier “for all smaller ordinals” is bounded, hence, it does not increase the complexity.

It follows that ${\Delta }_{n-1}^{\mathrm{H}{\omega }_2}\left(\left\{{\omega }_1\right\}\right)={\Delta }_{n-1}^{\mathrm{H}{\omega }_2}$ in case $n\ge 3$, supporting the “hence” claim of the theorem.

Then, it can be verified that the sets $Q^{*},{\mathbf{Q}}^{*},\mathbf{sJS}$ are ${\Delta }_1^{\mathrm{H}{\omega }_2}\left(\left\{{\omega }_1\right\}\right)$. (Indeed “being finite” and “being countable” are ${\Delta }_1^{\mathrm{H}{\omega }_2}$ relations, while “being of cardinality ${\omega }_1$” is ${\Delta }_1^{\mathrm{H}{\omega }_2}\left(\left\{{\omega }_1\right\}\right)$; the ${\Pi }_1^{}$ definition says that there is no injection from ${\omega }_1$ into a given set.)

Define pairs $⟨M_{\xi },U_{\xi }⟩,\xi <{\omega }_2$, by induction. Let $U_0$ be the null system with $|U_0|=⌀$, and $M_0$ be the least CTM of ${\mathbf{ZFC}}_2^{-}$. If $\lambda <{\omega }_1$ is a limit, then put $U_{\lambda }={\bigvee }_{\xi <\lambda }{U}_{\xi }$ and let $M_{\lambda }$ be the least CTM of ${\mathbf{ZFC}}_2^{-}$ containing the sequence ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <\lambda }$. If $⟨M_{\xi },U_{\xi }⟩\in \mathbf{sJS}$ is defined, then by Lemma 18 there is a pair $⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$ with $⟨M_{\xi },U_{\xi }⟩\prec ⟨M^{\prime },U^{\prime }⟩$ and $\xi \in |U^{\prime }|$. Further let $\Theta \subseteq {\omega }_1\times \mathrm{H}{\omega }_2$ be a universal ${\Sigma }_{n-2}^{\mathrm{H}{\omega }_2}$ set, and if $\xi <{\omega }_2$ then $D_{\xi }=\{z\in \mathbf{sJS}:⟨\xi ,z⟩\in \Theta \}$. Let $⟨M_{\xi +1},U_{\xi +1}⟩$ be the ${<}_{\mathbf{L}}$-least pair $⟨M,U⟩\in {D_{\xi }}^{\mathrm{solv}}$ satisfying $⟨M^{\prime },U^{\prime }⟩\preccurlyeq ⟨M,U⟩$, where ${<}_{\mathbf{L}}$ isthe Gödel wellordering of $\mathbf{L}$, the constructible universe. This completes the inductive construction of $⟨M_{\xi },U_{\xi }⟩\in \mathbf{sJS}$, $\xi <{\omega }_2$.

To check the definability property, make use of the well-known fact that the restriction ${<}_{\mathbf{L}}\upharpoonright \mathrm{H}{\omega }_2$ is a ${\Delta }_1^{\mathrm{H}{\omega }_2}$ relation, and if $n\ge 1$, $p\in {\omega }^{\omega }$ is any parameter, and $R(x,y,z,\dots )$ is a finitary ${\Delta }_n^{\mathrm{H}{\omega }_2}\left(p\right)$ relation on $\mathrm{HC}$ then the relations $\exists x{<}_{\mathbf{L}}yR(x,y,z,\dots )$ and $\forall x{<}_{\mathbf{L}}yR(x,y,z,\dots )$ (with arguments $y,z,\dots$) are ${\Delta }_n^{\mathrm{H}{\omega }_2}\left(p\right)$ as well. □

Definition 2 (in $\mathbf{L}$).

Fix a number$𝕟\ge 2$during the proof of Theorem 1.

• Let $\overrightarrow{\mathbb{js}}={\left\{⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩\right\}}_{\xi <{\omega }_2}\in {\overrightarrow{\mathbf{JS}}}_{{\omega }_2}$ be any $𝕟$-complete Jensen–Solovay sequenceof class ${\Delta }_{𝕟-1}^{\mathrm{H}{\omega }_2}$ as in Theorem 3—in case $𝕟\ge 3$, or just any Jensen–Solovay sequence of class ${\Delta }_1^{\mathrm{H}{\omega }_2}\left(\left\{{\omega }_1\right\}\right)$—in case $𝕟=2$, as in Theorem 3, including $\xi \in |{\mathbb{U}}_{\xi +1}|$ for all ξ in both cases.
• Put $\mathbb{U}={\bigvee }_{\xi <{\omega }_1}{\mathbb{U}}_{\xi }$, so $\mathbb{U}\left(\nu \right)={\bigcup }_{\xi <{\omega }_2,\nu \in \left|{\mathbb{U}}_{\xi }\right|}{\mathbb{U}}_{\xi }\left(\nu \right)$ for all $\nu \in \mathcal{I}$. Thus, $\mathbb{U}\in \mathbf{L}$ is a system and $\left|\mathbb{U}\right|=\mathcal{I}$ since $\xi \in |{\mathbb{U}}_{\xi +1}|$ for all ξ.

We define $\mathbb{Q}=\mathbf{Q}\left[\mathbb{U}\right]$ (the basic forcing notion), and ${\mathbb{Q}}_{\xi }=\mathbf{Q}\left[{\mathbb{U}}_{\xi }\right]$ for $\xi <{\omega }_2$. Thus, $\mathbb{Q}$ is the finite-support product of the set $\mathbb{C}$ and sets $\mathbb{Q}\left(\nu \right)=Q\left[\mathbb{U}\left(\nu \right)\right],i\in \mathcal{I}$; so that $\mathbb{Q}\in \mathbf{L}$. □

Corollary 4.

Suppose that in $\mathbf{L}$, $\xi <{\omega }_2$ and M is a TM of ${\mathbf{ZFC}}_2^{-}$ containing the sequence $\overrightarrow{\mathbb{js}}$. Then

(i)

$⟨M,\mathbb{U}⟩\in \mathbf{JS}$, $⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩\prec ⟨M,\mathbb{U}⟩$, and if $\nu \in \mathcal{I}$ then $\mathtt{card}\left({\mathbb{U}}_{\xi }\left(\nu \right)\right)={\omega }_1<{\omega }_2=\mathtt{card}\left(\mathbb{U}\left(\nu \right)\right)$ in $\mathbf{L}$.

(ii)

If $G\subseteq \mathbb{Q}$ is a set $\mathbb{Q}$-generic over $\mathbf{L}$ then the set $G^{\xi }=G\cap {\mathbb{Q}}_{\xi }$ is ${\mathbb{Q}}_{\xi }$-generic over ${\mathbb{M}}_{\xi }$.

Proof. 

Make use of Lemma 20 and Corollary 2 in Section 4.2. □

Lemma 21 (in $\mathbf{L}$).

The binary relation $f\in \mathbb{U}\left(\nu \right)$, the sets $\mathbb{Q}$ and ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbb{Q}\right)$ ($\mathbb{Q}$-names for reals in ${\omega }^{\omega }$), and the set of all $\mathbb{Q}$-full names in ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbb{Q}\right)$ are ${\Delta }_{𝕟-1}^{\mathrm{H}{\omega }_2}\left(\left\{{\omega }_1\right\}\right)$, and even ${\Delta }_{𝕟-1}^{\mathrm{H}{\omega }_2}$ in case $𝕟\ge 3$.

Proof. 

The sequence ${\left\{⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩\right\}}_{\xi <{\omega }_1}$ is ${\Delta }_{𝕟-1}^{\mathrm{H}{\omega }_2}$ by definition, hence the relation $f\in \mathbb{U}\left(\nu \right)$ is ${\Sigma }_{𝕟-1}^{\mathrm{H}{\omega }_2}$. On the other hand, if $f\in \mathrm{Fun}$ belongs to some ${\mathbb{M}}_{\xi }$ then $f\in \mathbb{U}\left(\nu \right)$ obviously implies $f\in {\mathbb{U}}_{\xi }\left(\nu \right)$, leading to a ${\Pi }_{𝕟-1}^{\mathrm{HC}}$ definition of the relation $f\in \mathbb{U}\left(\nu \right)$. To prove the last claim, note that by Corollary 3 if a name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbb{P}}_{\xi }\right)\cap {\mathbb{M}}_{\xi }$ is ${\mathbb{P}}_{\xi }$-full then it remains $\mathbb{P}$-full. □

4.4. Basic Generic Extension

The proof of Theorem 1 makes use of a generic extension of the form $\mathbf{L}\left[G\upharpoonright z\right]$, where $G\subseteq \mathbb{Q}$ is a set $\mathbb{Q}$-generic over $\mathbf{L}$, and $z\subseteq {\mathcal{I}}^{+},z\notin \mathbf{L}$. The following two theorems will play the key role in the proof. Define formulas ${ℾ}_{\nu }$ ($\nu \in \mathcal{I}$) as follows:

$${ℾ}_{\nu }\left(S\right):{=}_{\mathrm{def}}S\subseteq \mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}\wedge \forall f\in \mathbf{F}{\mathbf{UN}}^{\mathbf{L}}(f\in \mathbb{U}\left(\nu \right)⟺S\mathrm{does}\mathrm{not}\mathrm{cover}f).$$

Lemma 22.

Suppose that a set $G\subseteq \mathbb{Q}$ is $\mathbb{Q}$-generic over $\mathbf{L}$, and $\nu \in \mathcal{I}$, $c\in \mathbf{L}\left[G\right],⌀\ne c\subseteq {\mathcal{I}}^{+}$. Then

(i)

${\omega }_1^{\mathbf{L}\left[G\upharpoonright c\right]}={\omega }_2^{\mathbf{L}}$,

(ii)

if $-1\in c$ then ${\mathit{b}}_G\in \mathbf{L}\left[G\upharpoonright c\right]$, and if $\nu \in c$ then $S_G\left(\nu \right)\in \mathbf{L}\left[G\upharpoonright c\right]$,

(iii)

${ℾ}_{\nu }\left(S_G\left(\nu \right)\right)$ holds,

(iv)

$S_G\left(\nu \right)\notin \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right]$, and generally, there are no sets $S\subseteq \mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}$ in $\mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right]$ satisfying ${ℾ}_{\nu }\left(S\right)$.

Proof. 

To prove (i) apply Lemma 9 (ii) (ii); is easy. Furthermore, Lemma 9 (vi) immediately implies (iii).

To prove (iv), we need more work. Let $X=\mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}$. Suppose towards the contrary that some $S\in \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right],S\subseteq X=\mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}$ satisfies ${ℾ}_{\nu }\left(S\right)$. It follows from Lemma 10 (with $U=\mathbb{U}$ and $c={\mathcal{I}}^{+}\setminus \left\{\nu \right\}$), that there is a name $\tau \in {\mathbf{SN}}_X\left(\mathbb{Q}\right){\upharpoonright }_{\ne \nu }$ in $\mathbf{L}$ such that $S=\tau \left[G{\upharpoonright }_{\ne \nu }\right]$. There is an ordinal $\xi <{\omega }_1$ satisfying $\tau \in {\mathbb{M}}_{\xi }$ and $\tau \in {\mathbf{SN}}_X\left({\mathbb{Q}}_{\xi }{\upharpoonright }_{\ne \nu }\right)$. Then $S=\tau \left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$, where $G^{\xi }=G\cap {\mathbb{P}}_{\xi }$ is ${\mathbb{P}}_{\xi }$-generic over ${\mathbb{M}}_{\xi }$ by Corollary 4 (ii), and by the way S belongs to ${\mathbb{M}}_{\xi }\left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$ by the choice of $\xi$.

Please note that $F=\mathbb{U}\left(\nu \right)\setminus {\mathbb{U}}_{\xi }\left(\nu \right)\ne ⌀$ by Corollary 4 (i). Let $f\in F$. Then f is Cohen generic over the model ${\mathbb{M}}_{\xi }$ by Corollary 4. On the other hand, $G^{\xi }{\upharpoonright }_{\ne \nu }$ is ${\mathbb{P}}_{\xi }{\upharpoonright }_{\ne \nu }$-generic over ${\mathbb{M}}_{\xi }\left[f\right]$ by Theorem 2 (iii). Therefore f is Cohen generic over ${\mathbb{M}}_{\xi }\left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$ as well.

Recall that $S\in {\mathbb{M}}_{\xi }\left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$ and ${ℾ}_{\nu }\left(S\right)$ holds, hence S does not cover f. As f is Cohen generic over ${\mathbb{M}}_{\xi }\left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$, it follows that there is a sequence $s\in \mathbf{S}{\mathbf{EQ}}^{\mathbf{L}},s\subset f$, such that S contains no subsequences of f extending s. Take any $\mu \in \mathcal{I},\mu \ne \nu$. By Corollary 4 (i), there exists a function $g\in \mathbb{U}\left(\mu \right)\setminus {\mathbb{U}}_{\xi }\left(\mu \right),g\notin \mathbb{U}\left(\nu \right)$, satisfying $s\subset g$. Then, S covers g by ${ℾ}_{\nu }\left(S\right)$. However, this is absurd by the choice of s. □

The proof of the next important elementary equivalence theorem will be given below in Section 6.3.

Theorem 4 (elementary equivalence theorem).

Assume that in $\mathbf{L}$, $-1\in d\subseteq {\mathcal{I}}^{+}$, sets $Z^{\prime },Z\subseteq \mathcal{I}\setminus d$ satisfy $\mathtt{card}(\mathcal{I}\setminus Z)\le {\omega }_1$ and $\mathtt{card}(\mathcal{I}\setminus Z^{\prime })\le {\omega }_1$, the symmetric difference $Z\Delta Z^{\prime }$ is at most countable, and the complementary set $\mathcal{I}\setminus (d\cup Z\cup Z^{\prime })$ is infinite.

Let $G\subseteq \mathbb{Q}$ be $\mathbb{Q}$-generic over $\mathbf{L}$, and $x_0\in \mathbf{L}\left[G\upharpoonright d\right]$ be any real. Then any closed ${\Sigma }_{𝕟}^1$ formula φ, with real parameters in $\mathbf{L}\left[x_0\right]$, is simultaneously true in $\mathbf{L}[x_0,G\upharpoonright Z]$ and in $\mathbf{L}[x_0,G\upharpoonright Z^{\prime }]$.

4.5. The Main Theorem Modulo the Elementary Equivalence Theorem: The Model

Here we begin the proof of Theorem 1 on the base of Theorem 4 of Section 4.4. We fix a number $𝕟\ge 2$ during the proof. The goal is to define a generic extension of $\mathbf{L}$ in which for any set $x\subseteq \omega$ the following is true: $x\in \mathbf{L}$ iff $x\in {\Delta }_{𝕟+1}^1$. The model is a part of the basic generic extension defined in Section 4.4.

In the notation of Definition 2 in Section 4.3, consider a set $G\subseteq \mathbb{Q}$, $\mathbb{Q}$-generic over $\mathbf{L}$. Then ${\mathit{b}}_G=\bigcup G(-1)$ is a $\mathbb{C}$-generic map from $\omega$ onto $\mathcal{P}\left(\omega \right)\cap \mathbf{L}$ by Lemma 9 (i). We define

$$w\left[G\right]=\{\omega k+2^j:k<\omega \wedge j\in {\mathit{b}}_G\left(k\right)\}\cup \{\omega k+3^j:j,k<\omega \}\subseteq {\omega }^2,$$

(12)

and $w^{+}\left[G\right]=\{-1\}\cup w\left[G\right]$. We also define, for any $m<\omega$,

$$w_{\ge m}\left[G\right]=\{\omega k+\ell \in w\left[G\right]:k\ge m\},w_{<m}\left[G\right]=\{\omega k+\ell \in w\left[G\right]:k<m\},$$

and accordingly $w_{\ge m}^{+}\left[G\right]=\{-1\}\cup w_{\ge m}\left[G\right]$ and $w_{<m}^{+}\left[G\right]=\{-1\}\cup w_{<m}\left[G\right]$.

With these definitions, each kth slice

$$w_k\left[G\right]=\{\omega k+2^j:j\in {\mathit{b}}_G\left(k\right)\}\cup \{\omega k+3^j:j<\omega \}$$

(13)

of $w\left[G\right]$ is necessarily infinite and coinfinite, and it codes the target set ${\mathit{b}}_G\left(k\right)$ since

$${\mathit{b}}_G\left(k\right)=\{j<\omega :\omega k+2^j\in w_k\left[G\right]\}=\{j<\omega :\omega k+2^j\in w^{+}\left[G\right]\}.$$

(14)

It will be important below that definition (12) is monotone w. r. t. ${\mathit{b}}_G$, i.e., if ${\mathit{b}}_G\left(k\right)\subseteq {\mathit{b}}_{G^{\prime }}\left(k\right)$ for all k, then $w\left[G\right]\subseteq w\left[G^{\prime }\right]$ and $w^{+}\left[G\right]\subseteq w^{+}\left[G^{\prime }\right]$. Non-monotone modifications, like e.g.,

$$w\left[G\right]=\{\omega k+2^j:j\in {\mathit{b}}_G\left(k\right)\}\cup \{\omega k+3^j:j\notin {\mathit{b}}_G\left(k\right)\}$$

would not work. Finally, let

$$W=[{\omega }^2,{\omega }_2)=\{\zeta :{\omega }^2\le \zeta <{\omega }_2\}.$$

Anyway, $w^{+}\left[G\right]\subseteq {\omega }^2=\omega ·\omega$ (the ordinal product) is a set in the model $\mathbf{L}\left[{\mathit{b}}_G\right]=\mathbf{L}\left[w^{+}\left[G\right]\right]=\mathbf{L}\left[w\left[G\right]\right]=\mathbf{L}\left[w_{\ge m}\left[G\right]\right]$ for each m, containing $-1$, while $w_{<m}\left[G\right]\in \mathbf{L}$ for all m. We are going to prove the following lemma:

Lemma 23.

The model $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$ witnesses Theorem 1. That is, let a set $G\subseteq \mathbb{Q}$ be $\mathbb{Q}$-generic over $\mathbf{L}$. Then it holds in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$ that

(i)

$w\left[G\right]$ is ${\Sigma }_{𝕟+1}^1$ and each set $x\in \mathbf{L},\left[0\right]x\subseteq \omega$ is ${\Delta }_{𝕟+1}^1;$

(ii)

if $x\subseteq \omega$ is ${\Delta }_{𝕟+1}^1$ then $x\in \mathbf{L}$.

Recall that if $Z\subseteq {\mathcal{I}}^{+}$ then $G\upharpoonright Z=\left\{p\in G:\left[0\right]\right|p{|}^{+}\subseteq Z\}$.

Proof (Claim (i) of the lemma).

Consider an arbitrary ordinal $\nu =\omega k+\ell$; $k,\ell <\omega$. We claim that

$$\nu \in w\left[G\right]⟺\exists S{ℾ}_{\nu }\left(S\right)$$

(15)

holds in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$. Indeed, assume that $\nu \in w\left[G\right]$. Then $S=S_G\left(\nu \right)\in \mathbf{L}\left[G\upharpoonright w^{+}\left[G\right]\right]$, and we have ${ℾ}_{\nu }\left(S\right)$ in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$ by Lemma 22 (ii), (iii). Conversely assume that $\nu \notin w\left[G\right]$. Then we have $w^{+}\left[G\right]\in \mathbf{L}\left[{\mathit{b}}_G\right]\subseteq \mathbf{L}\left[G\upharpoonright w^{+}\left[G\right]\right]\subseteq \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right]$, but $\mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right]$ contains no S with ${ℾ}_{\nu }\left(S\right)$ by Lemma 22 (iv).

However, the right-hand side of (15) defines a ${\Sigma }_{𝕟}^{\mathrm{H}{\omega }_2}\left(\{{\omega }_1^{\mathbf{L}},\mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}\}\right)$ relation in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$ by Lemma 21. (Indeed, ${\left(\mathrm{H}{\omega }_2\right)}^{\mathbf{L}}={\mathbf{L}}_{{{\omega }_2}^{\mathbf{L}}}={\mathbf{L}}_{{\omega }_1}$ in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$, therefore ${\left(\mathrm{H}{\omega }_2\right)}^{\mathbf{L}}$ is ${\Sigma }_1^{\mathrm{H}{\omega }_2}$ in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$.) On the other hand, the sets $\left\{{\omega }_1^{\mathbf{L}}\right\}$ and $\left\{\mathbf{S}{\mathbf{EQ}}^{\mathbf{L}}\right\}$ remain ${\Delta }_2^{\mathrm{H}{\omega }_2}$ singletons in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$, so they can be eliminated since $𝕟\ge 2$. This yields $w\left[G\right]\in {\Sigma }_{𝕟}^{\mathrm{HC}}$ in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$. It follows that $w\left[G\right]\in {\Sigma }_{𝕟+1}^1$ by ([10] (Lemma 25.25)), as required.

Consider an arbitrary set $x\in \mathbf{L},x\subseteq \omega$. By genericity there exists $k<\omega$ such that ${\mathit{b}}_G\left(k\right)=x$. Then $x=\{j:\omega k+2^j\in w\left[G\right]\}$ by (12), therefore x is ${\Sigma }_{𝕟+1}^1$ as well. However, $\omega \setminus x\in {\Sigma }_{𝕟+1}^1$ by the same argument. Thus, x is ${\Delta }_{𝕟+1}^1$ in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$, as required.      (Claim (i) of Lemma 23) □

4.6. Proof of the Key Claim of Lemma 23

The proof of Lemma 23 (ii) is based on several intermediate lemmas.

Recall that $W=[{\omega }^2,{\omega }_2)=\{\xi :{\omega }^2\le \xi <{\omega }_2\}$.

Lemma 24

(compare with Lemma 33 in [7]). Suppose that $G\subseteq \mathbb{Q}$ is $\mathbb{Q}$-generic over $\mathbf{L}$, and $m<\omega$. Let $c\subseteq w_{<m}\left[G\right]$ be any set in $\mathbf{L}$. Then any closed ${\Sigma }_{𝕟}^1$ formula Φ, with reals in $\mathbf{L}\left[G\upharpoonright (c\cup w_{\ge m}^{+}\left[G\right]\cup W)\right]$ as parameters, is simultaneously true in $\mathbf{L}\left[G\upharpoonright (c\cup w_{\ge m}^{+}\left[G\right]\cup W)\right]$ and in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$.

It follows that if $c^{\prime }\subseteq c\subseteq w_{<m}\left[G\right]$ in $\mathbf{L}$, then any closed ${\Sigma }_{𝕟+1}^1$ formula Ψ, with parameters in $\mathbf{L}\left[G\upharpoonright (c^{\prime }\cup w_{\ge m}^{+}\left[G\right]\cup W)\right]$, true in $\mathbf{L}\left[G\upharpoonright (c^{\prime }\cup w_{\ge m}^{+}\left[G\right]\cup W)\right]$, is true in $\mathbf{L}\left[G\upharpoonright (c\cup w_{\ge m}^{+}\left[G\right]\cup W)\right]$ as well.

Proof (Lemma 24)).

There is an ordinal $\xi <{\omega }_2$ such that all parameters in $\phi$ belong to $\mathbf{L}\left[G\upharpoonright Y\right]$, where $Y=c\cup w_{\ge m}^{+}\left[G\right]\cup X$ and $X=[{\omega }^2,\xi )=\{\gamma :\left[0\right]{\omega }^2\le \gamma <\xi \}$. The set Y belongs to $\mathbf{L}\left[{\mathit{b}}_G\right]$, in fact, $\mathbf{L}\left[Y\right]=\mathbf{L}\left[{\mathit{b}}_G\right]$. Therefore $G\upharpoonright Y$ is equi-constructible with the pair $⟨{\mathit{b}}_G,{\left\{S_G\left(\nu \right)\right\}}_{\nu \in X^{\prime }}⟩$, where ${\mathit{b}}_G$ is a map from $\omega$ onto, essentially, ${\omega }_1^{\mathbf{L}}$. It follows that there is a real $x_0$ with $\mathbf{L}\left[G\upharpoonright Y\right]=\mathbf{L}\left[x_0\right]$. Then all parameters of $\phi$ belong to $\mathbf{L}\left[x_0\right]$.

To prepare for Theorem 4 of Section 4.4, put $Z^{\prime }=[\xi ,{\omega }_2)$, $e=w_{<m}\left[G\right]\setminus c$, $Z=e\cup Z^{\prime }$,

$$d=\{-1\}\cup \{\omega k+j:k\ge m\wedge j<\omega \}\cup X.$$

As $w_{\ge m}^{+}\left[G\right]\subseteq \{-1\}\cup \{\omega k+j:k\ge m\wedge j<\omega \}$, we have $Y=c\cup w_{\ge m}^{+}\left[G\right]\cup X\subseteq d$, and hence $x_0\in \mathbf{L}\left[G\upharpoonright d\right]$. It follows by Theorem 4 that $\phi$ is simultaneously true in $\mathbf{L}[x_0,G\upharpoonright Z]$ and in $\mathbf{L}[x_0,G\upharpoonright Z^{\prime }]$. However, $\mathbf{L}[x_0,G\upharpoonright Z^{\prime }]=\mathbf{L}\left[G\upharpoonright (Y\cup Z^{\prime })\right]=\mathbf{L}\left[G\upharpoonright (c\cup w_{\ge m}^{+}\left[G\right]\cup W)\right]$ by construction, while $\mathbf{L}[x_0,G\upharpoonright Z]=\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$, and we are done. □

In continuation of the proof of Lemma 23 (ii), suppose that

(†)

$\phi (·)$ and $\psi (·)$ are parameter-free ${\Sigma }_{n+1}^1$ formulas that provide a ${\Delta }_{n+1}^1$ definition for a set $x\subseteq \omega ,x\in \mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$, i.e., we have

$$x=\left\{\ell <\omega :\phi \right(\ell \left)\right\}=\{\ell <\omega :\neg \psi (\ell \left)\right\}$$

in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$. Thus, the equivalence $\forall \ell \left(\phi \right(\ell )⟺\neg \psi (\ell \left)\right)$ is forced to be true in $\mathbf{L}\left[\underline{G}\upharpoonright (w^{+}\left[\underline{G}\right]\cup \check{W})\right]$ by a condition $p_0\in G$.

Here, $\underline{G}$ is the canonical $\mathbb{Q}$-name for the generic set $G\subseteq \mathbb{Q}$, as usual, while $\check{W}$ is a name for $W\in \mathbf{L}$.

Lemma 25.

Assume (†). If $\ell <\omega$ then the sentence “$\mathbf{L}\left[\underline{G}\upharpoonright (w^{+}\left[\underline{G}\right]\cup \check{W})\right]\vDash \phi \left(\ell \right)$” is $\mathbb{Q}$-decided by $p_0$.

Proof. 

Suppose, for the sake of simplicity, that $p_0$ is the empty condition ⊙ (i.e., $|p_0{|}^{+}=⌀$); the general case does not differ much. Then $\forall \ell \left(\phi \right(\ell )⟺\neg \psi (\ell \left)\right)$ holds in $\mathbf{L}\left[G\upharpoonright (w^{+}\left[G\right]\cup W)\right]$ for any generic set $G\subseteq \mathbb{Q}$.

Say that conditions $p,q\in \mathbb{Q}=\mathbf{Q}\left[\mathbb{U}\right]$ are close neighbours iff $-1\in {\left|p\right|}^{+}\cap {\left|q\right|}^{+}$ and one of the following holds:

(I)

${\mathit{b}}_p={\mathit{b}}_q$ (recall that ${\mathit{b}}_p=p(-1)$), or

(II)

$p{\upharpoonright }_{\ne -1}=q{\upharpoonright }_{\ne -1}$, $\mathtt{lh}{\mathit{b}}_p=\mathtt{lh}{\mathit{b}}_q$, and either (a) ${\mathit{b}}_p\left(k\right)\subseteq {\mathit{b}}_q\left(k\right)$ for all $k<\mathtt{lh}{\mathit{b}}_p$, or (b) ${\mathit{b}}_q\left(k\right)\subseteq {\mathit{b}}_p\left(k\right)$ for all $k<\mathtt{lh}{\mathit{b}}_p$.

Proposition 1.

If conditions $p,q\in \mathbb{Q}$ are close neighbours, satisfying (6) in Section 3.8, $\ell <\omega$, and p $\mathbb{Q}$-forces the sentence“$\mathbf{L}\left[\underline{G}\upharpoonright (w^{+}\left[\underline{G}\right]\cup \check{W})\right]\vDash \phi \left(\ell \right)$”, then so does q.

Proof (Proposition).

Suppose on the contrary that q does not force “$\mathbf{L}\left[\underline{G}\upharpoonright (w^{+}\left[\underline{G}\right]\cup \check{W})\right]\vDash \phi \left(\ell \right)$”. As $p,q$ satisfy (6), the associated transformation $H_{pq}$ maps the set ${\mathbb{Q}}_{\le p}=\{p^{\prime }\in \mathbb{Q}:p^{\prime }\le p\}$ onto ${\mathbb{Q}}_{\le q}=\{q^{\prime }\in \mathbb{Q}:q^{\prime }\le q\}$ order-preserving by Lemma 17 (with $U=\mathbb{U}$). By the choice of q, there is a set $G_q\subseteq {\mathbb{Q}}_{\le q}$, generic over $\mathbf{L}$, containing q, and such that $\phi \left(\ell \right)$ is false in $\mathbf{L}\left[G_q\upharpoonright (w^{+}\left[G_q\right]\cup W)\right]$. Then $\psi \left(\ell \right)$ is true in $\mathbf{L}\left[G_q\upharpoonright (w^{+}\left[G_q\right]\cup W)\right]$ by (†) (and the assumption that $p_0=\odot$).

The set $G_p=\{\left(H_{pq}\right){}^{-1}\left(q^{\prime }\right):q^{\prime }\in G_q\wedge q^{\prime }\le q\}\subseteq {\mathbb{Q}}_{\le p}$ is $\mathbb{Q}$-generic over $\mathbf{L}$ as well (as $H_{pq}$ is an order isomorphism), and contains p, and hence $\phi \left(\ell \right)$ is true and $\psi \left(\ell \right)$ false in $\mathbf{L}\left[G_p\upharpoonright (w^{+}\left[G_p\right]\cup W)\right]$.

Case 1: (I) holds, i.e., ${\mathit{b}}_p={\mathit{b}}_q$. Then by definition ${\mathit{b}}_{G_p}={\mathit{b}}_{G_q}$, so that $w^{+}\left[G_p\right]=w^{+}\left[G_q\right]$. On the other hand, the sets $G_p$ and $G_q$ are equi-constructible by means of the application of $H_{pq}$, and hence $G_p\upharpoonright (w^{+}\left[G_p\right]\cup W)$ and $G_q\upharpoonright (w^{+}\left[G_q\right]\cup W)$ are equi-constructible, that is, the classes $\mathbf{L}\left[G_p\upharpoonright (w^{+}\left[G_p\right]\cup W)\right]$ and $\mathbf{L}\left[G_q\upharpoonright (w^{+}\left[G_q\right]\cup W)\right]$ coincide. However, $\phi \left(\ell \right)$ is true in one of them and false in the other one, a contradiction.

Case 2: (II) holds. Let $m=\mathtt{lh}{\mathit{b}}_p=\mathtt{lh}{\mathit{b}}_q$. Then ${\mathit{b}}_{G_p}\left(k\right)={\mathit{b}}_{G_q}\left(k\right)$ for all $k\ge m$ via $H_{pq}$. This implies $\mathbf{L}\left[{\mathit{b}}_{G_p}\right]=\mathbf{L}\left[{\mathit{b}}_{G_q}\right]$, and also implies $w_{\ge m}^{+}\left[G_p\right]=w_{\ge m}^{+}\left[G_q\right]$, while the difference between the sets $w_{<m}\left[G_p\right]$, $w_{<m}\left[G_q\right]$ is that for any $k<m$ and any j,

$$\omega k+2^j\in w_{<m}\left[G_q\right]⟺j\in {\mathit{b}}_q\left(k\right)\mathrm{and}\omega k+2^j\in w_{<m}\left[G_p\right]⟺j\in {\mathit{b}}_p\left(k\right).$$

(16)

Moreover, (II) implies $G_p{\upharpoonright }_{\ne -1}=G_q{\upharpoonright }_{\ne -1}$, and hence $S_{G_p}\left(\nu \right)=S_{G_q}\left(\nu \right)$ for all $\nu \in \mathcal{I}$ via $H_{pq}$. We conclude that $\mathbf{L}\left[G_p\upharpoonright Z\right]=\mathbf{L}\left[G_q\upharpoonright Z\right]$ for any set $Z\in \mathbf{L}\left[{\mathit{b}}_{G_p}\right],Z\subseteq {\mathcal{I}}^{+}$, in particular, $\mathbf{L}\left[G_p\upharpoonright (w^{+}\left[G_q\right]\cup W)\right]=\mathbf{L}\left[G_q\upharpoonright (w^{+}\left[G_q\right]\cup W)\right]$.

If now (II) (a) holds, then $c^{\prime }=w_{<m}\left[G_p\right]\subseteq c=w_{<m}\left[G_q\right]=c^{\prime }\cup z$ by (16), where

$$z=\{\omega k+2^j:k<m\wedge j\in {\mathit{b}}_q\left(k\right)\setminus {\mathit{b}}_p\left(k\right)\}\in \mathbf{L}.$$

However, $\phi \left(\ell \right)$ holds in $\mathbf{L}\left[G_p\upharpoonright (w^{+}\left[G_p\right]\cup W)\right]$, see above. It follows by Lemma 24 that $\phi \left(\ell \right)$ holds in $\mathbf{L}\left[G_p\upharpoonright (w^{+}\left[G_q\right]\cup W)\right]$. However, we know that $\mathbf{L}\left[G_p\upharpoonright (w^{+}\left[G_q\right]\cup W)\right]=\mathbf{L}\left[G_q\upharpoonright (w^{+}\left[G_q\right]\cup W)\right]$. Thus, $\phi \left(\ell \right)$ holds in $\mathbf{L}\left[G_q\upharpoonright (w^{+}\left[G_q\right]\cup W)\right]$, which is a contradiction to the above. If (II) (b) holds, then argue similarly using the formula $\psi \left(\ell \right)$.              (Proposition 1) □

Coming back to Lemma 25, suppose towards the contrary that “$\mathbf{L}\left[\underline{G}\upharpoonright (w^{+}\left[\underline{G}\right]\cup \check{W})\right]\vDash \phi \left(\ell \right)$” is not $\mathbb{Q}$-decided by $p_0=\odot$. There are two conditions $p,q\in \mathbb{Q}$ such that p $\mathbb{Q}$-forces “$\mathbf{L}\left[\underline{G}\upharpoonright (w^{+}\left[\underline{G}\right]\cup \check{W})\right]\vDash \phi \left(\ell \right)$” while q$\mathbb{Q}$-forces the negation. We may w.l.o.g. assume, by Lemma 17 (i), that $p,q$ satisfy (6) of Section 3.8. We claim that p, q can be connected by a finite chain of conditions in $\mathbb{Q}$ in which each two consecutive terms are close neighbours in the sense above, satisfying (6) in Section 3.8— then Proposition 1 implies a contradiction and concludes the proof of Lemma 25.

Thus, it remains to prove the connection claim. Let $p^{\prime }\in \mathbb{Q}$ be defined by ${\mathit{b}}_{p^{\prime }}={\mathit{b}}_p$ and $p^{\prime }{\upharpoonright }_{\ne -1}=q{\upharpoonright }_{\ne -1}$. Then $p,p^{\prime }$ are close neighbours and (6) holds for this pair as it holds for $p,q$. Let $r\in \mathbb{Q}$ be defined by ${\mathit{b}}_r\left(k\right)={\mathit{b}}_p\left(k\right)\cup {\mathit{b}}_q\left(k\right)$ for all $k<\ell =\mathtt{lh}{\mathit{b}}_p=\mathtt{lh}{\mathit{b}}_q$ and $p^{\prime }{\upharpoonright }_{\ne -1}=q{\upharpoonright }_{\ne -1}$. Still r is a close neighbour to both $p^{\prime }$ and q, and (6) holds for $p^{\prime },r$ and $q,r$. Thus, the chain p—$p^{\prime }$—r—q proves the connection claim.                         (Lemma 25) □

Now, to accomplish the proof of Lemma 23 (ii), apply Lemma 25.

                                                 (Lemma 23) □

                                  (Theorem 1 modulo Theorem 4 of Section 4.4) □

5. Forcing Approximation

To prove Theorem 4 of Section 4.4 and thus complete the proof of Theorem 1 in the next Section 6, we define here a forcing-like relation forc, and exploit certain symmetries of objects related to forc. This similarity will allow us to only outline really analogous issues but concentrate on several things which bear some difference.

We argue under Blanket Assumption 1.

Recall that ${\mathbf{ZFC}}^{-}$ is $\mathbf{ZFC}$ minus the Power Set axiom, with the schema of Collection instead of Replacement, with the axiom “${\omega }_1$ exists”, and with AC in the form of wellorderability of every set, and ${\mathbf{ZFC}}_2^{-}$ is ${\mathbf{ZFC}}^{-}$ plus the axioms: $\mathbf{V}=\mathbf{L}$, and “every set x satisfies $\mathtt{card}x\le {\omega }_1$”.

5.1. Formulas

Here we introduce a language that will help us to study analytic definability in $\mathbf{Q}\left[U\right]$-generic extensions, for different systems U, and their submodels.

Let $\mathcal{L}$ be the 2nd order Peano language, with variables of type 1 over ${\omega }^{\omega }$. If $K\subseteq {\mathbf{Q}}^{*}$ then an $\mathcal{L}\left(K\right)$ formula is any formula of $\mathcal{L}$, with somefree variables of types $0,1$ replaced by resp. numbers in $\omega$ and names in ${\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$, and some type 1 quantifiers are allowed to have bounding indices B (i.e., ${\exists }^B,{\forall }^B$) such that $B\subseteq {\mathcal{I}}^{+}$ satisfies either $\mathtt{card}B\le {\omega }_1$ or $\mathtt{card}(\mathcal{I}\setminus B)\le {\omega }_1$ (in $\mathbf{L}$). In particular, ${\mathcal{I}}^{+}$ itself can serve as an index, and the absence

If $\phi$ is a $\mathcal{L}\left({\mathbf{Q}}^{*}\right)$ formula, then let

$$\begin{array}{ccc}\hfill \mathrm{NAM}\phi & =& \mathrm{the}\mathrm{set}\mathrm{of}\mathrm{all}\mathrm{names}\tau \mathrm{that}\mathrm{occur}\mathrm{in}\phi ;\hfill \\ \hfill \mathrm{IND}\phi & =& \mathrm{the}\mathrm{set}\mathrm{of}\mathrm{all}\mathrm{quantifier}\mathrm{indices}B\mathrm{which}\mathrm{occur}\mathrm{in}\phi ;\hfill \\ \hfill {\left|\phi \right|}^{+}& =& \bigcup _{\tau \in \mathrm{NAM}\phi }{\left|\tau \right|}^{+}(\mathrm{a}\mathrm{set}\mathrm{of}{\omega }_1-\mathrm{size});\hfill \\ \hfill \left|\right|\phi \left|\right|& =& {\left|\phi \right|}^{+}\cup \left(\bigcup \mathrm{ind}\phi \right)-\mathrm{so}\mathrm{that}{\left|\phi \right|}^{+}\subseteq \left|\right|\phi \left|\right|\subseteq {\mathcal{I}}^{+}.\hfill \end{array}$$

If a set $G\subseteq {\mathbf{Q}}^{*}$ is minimally $\phi$-generic(that is, minimally $\tau$-generic w. r. t. every name $\tau \in \mathrm{nam}\phi$, in the sense of Section 3.5), then the valuation $\phi \left[G\right]$ is the result of substitution of $\tau \left[G\right]$ for any name $\tau \in \mathrm{nam}\phi$, and changing each quantifier ${\exists }^{B}x$, ${\forall }^{B}x$ to resp. $\exists \left(\forall \right)x\in {\omega }^{\omega }\cap \mathbf{L}\left[G\upharpoonright B\right]$, while index-free type 1 quantifiers are relativized to ${\omega }^{\omega }$; $\phi \left[G\right]$ is a formula of $\mathcal{L}$ with real parameters, and some quantifiers of type 1 relativized to certain submodels of $\mathbf{L}\left[G\right]$.

An arithmetic formula in $\mathcal{L}\left(K\right)$ is a formula with no quantifiers of type 1 (names in ${\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$ are allowed). If $n<\omega$ then let a $\mathcal{L}{\Sigma }_n^1\left(K\right)$, resp., $\mathcal{L}{\Pi }_n^1\left(K\right)$ formulabe a formula of the form

$${\exists }^{\circ }{x}_1{\forall }^{\circ }{x}_2\dots {\forall }^{\circ }\left({\exists }^{\circ }\right)x_{n-1}\exists \left(\forall \right)x_n\psi ,{\forall }^{\circ }{x}_1{\exists }^{\circ }{x}_2\dots {\exists }^{\circ }\left({\forall }^{\circ }\right)x_{n-1}\forall \left(\exists \right)x_n\psi$$

respectively, where $\psi$ is an arithmetic formula in $\mathcal{L}\left(K\right)$, all variables $x_i$ are of type 1 (over ${\omega }^{\omega }$), the sign ${}^{\circ }$ means that this quantifier can have a bounding index as above, and it is required that the rightmost (closest to the kernel $\psi$) quantifier does not have a bounding index.

If in addition $M\vDash {\mathbf{ZFC}}^{-}$ is a transitive model and $K\subseteq {\mathbf{Q}}^{*}$ then define

$\mathcal{L}{\Sigma }_n^1(K,M)=$ all $\mathcal{L}{\Sigma }_n^1\left(K\right)$ formulas $\phi$ such that $\mathrm{NAM}\phi \subseteq {\mathbf{SN}}_{\omega }^{\omega }\left(K\right)\cap M$ and each index $B\in \mathrm{IND}\phi$ satisfies the requirement: either $B\in M$ or $\mathcal{I}\setminus B\in M$.

Define $\mathcal{L}{\Pi }_n^1(K,M)$ similarly.

5.2. Forcing Approximation

We introduce a convenient forcing-type relation $p{\mathbf{forc}}_U^M\phi$ for pairs $⟨M,U⟩$ in $\mathbf{sJS}$ and formulas $\phi$ in $\mathcal{L}\left(K\right)$, associated with the truth in $K$-generic extensions of $\mathbf{L}$, where $K=\mathbf{Q}\left[U\right]\subseteq {\mathbf{Q}}^{*}$ and $U\in \mathbf{L}$ is a system.

(F1)

First, writing $p{\mathbf{forc}}_U^M\phi$, it is assumed that:

(a)

$⟨M,U⟩\in \mathbf{sJS}$ and p belongs to $\mathbf{Q}\left[U\right]$,

(b)

$\phi$ is a closed formula in $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)\cup \mathcal{L}{\Sigma }_{k+1}^1(\mathbf{Q}\left[U\right],M)$ for some $k\ge 1$, and each name $\tau \in \mathrm{nam}\phi$ is $\mathbf{Q}\left[U\right]$-full below p.

Under these assumptions, the sets $U,\mathbf{Q}\left[U\right],p,\mathrm{nam}\phi$ belong to M.

The definition of forc goes on by induction on the complexity of formulas.

(F2)

If $⟨M,U⟩\in \mathbf{sJS},p\in \mathbf{Q}\left[U\right]$, and $\phi$ is a closed formula in $\mathcal{L}{\Pi }_1^1(\mathbf{Q}\left[U\right],M)$ (then by definition it has no quantifier indices), then: $p{\mathbf{forc}}_U^M\phi$ iff (F1) holds and p$\mathbf{Q}\left[U\right]$-forces $\phi \left[\underline{G}\right]$ over M in the usual sense. Please note that the forcing notion $\mathbf{Q}\left[U\right]$ belongs to M in this case by (F1).

(F3)

If $\phi \left(x\right)\in \mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M),k\ge 1$, then:

(a)

$p{\mathbf{forc}}_U^M{\exists }^{B}x\phi \left(x\right)$ iff there is a name $\tau \in M\cap {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)\upharpoonright B$, $\mathbf{Q}\left[U\right]$-full below p (by (F1)b) and such that $p{\mathbf{forc}}_U^M\phi \left(\tau \right)$.

(b)

$p{\mathbf{forc}}_U^M\exists x\phi \left(x\right)$ iff there is a name $\tau \in M\cap {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$, $\mathbf{Q}\left[U\right]$-full below p (by F1)b) and such that $p{\mathbf{forc}}_U^M\phi \left(\tau \right)$.

(F4)

If $k\ge 2$, $\phi$ is a closed $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)$ formula, $p\in \mathbf{Q}\left[U\right]$, and (F1) holds, then $p{\mathbf{forc}}_U^M\phi$ iff we have $\neg q{\mathbf{forc}}_{U^{\prime }}^{M^{\prime }}\phi {\phantom{)}}^{\neg }$ for every pair $⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$ extending $⟨M,U⟩$, and every condition $q\in \mathbf{Q}\left[U^{\prime }\right],q\le p$, where $\phi {\phantom{)}}^{\neg }$ is the result of canonical conversion of $\neg \phi$ to $\mathcal{L}{\Sigma }_k^1(\mathbf{Q}\left[U\right],M)$.

The next theorem classifies the complexity of forc in terms of projective hierarchy. Please note that if $⟨M,U⟩\in \mathbf{sJS}$ and $k\ge 1$ then any formula $\phi$ in $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)\cup \mathcal{L}{\Sigma }_{k+1}^1(\mathbf{Q}\left[U\right],M)$ belongs to M if we somehow “label” any large index $B\in \mathrm{IND}\phi$ (such that $\mathtt{card}(\mathcal{I}\setminus B)\le {\omega }_1$) by its small complement $\mathcal{I}\setminus B\in M$. Therefore, the sets

$$\begin{array}{ccc}\mathbf{Forc}\left({\Pi }_k^1\right)\hfill & =& \{⟨M,U,p,\phi ⟩:⟨M,U⟩\in \mathbf{sJS}\wedge p\in \mathbf{Q}[U]\wedge \hfill \\ & & \wedge \phi \mathrm{is}\mathrm{a}\mathrm{closed}\mathrm{formula}\mathrm{in}\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)\wedge p{\mathbf{forc}}_U^M\phi \},\hfill \end{array}$$

and $\mathbf{Forc}\left({\Sigma }_k^1\right)$ similarly defined, are subsets of $\mathrm{H}{\omega }_2$ (in $\mathbf{L}$).

Lemma 26 (in L).

The sets $\mathbf{Forc}\left({\Pi }_1^1\right)$ and $\mathbf{Forc}\left({\Sigma }_2^1\right)$ belong to ${\Delta }_1^{\mathrm{H}{\omega }_2}$.

If $k\ge 2$ then the sets $\mathbf{Forc}\left({\Pi }_k^1\right)$ and $\mathbf{Forc}\left({\Sigma }_{k+1}^1\right)$ belong to ${\Pi }_{k-1}^{\mathrm{H}{\omega }_2}$.

Proof 

(sketch) Suppose that $\phi$ is $\mathcal{L}{\Pi }_1^1$. Under the assumptions of the theorem, items (F1)a, (F1)b of (F1) are ${\Delta }_1^{\mathrm{H}{\omega }_2}$ relations, while (F2) is reducible to a forcing relation over M that we can relativize to M. The inductive step goes on straightforwardly using (F3), (F4). Please note that the quantifier over names in (F3) is a bounded quantifier (bounded by M), hence it does not add any extra complexity. □

5.3. Further Properties of Forcing Approximations

The notion of names $\nu ,\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$ being equivalent below some $p\in {\mathbf{Q}}^{*}$,is introduced in Section 3.5. We continue with a couple of routine lemmas.

Lemma 27.

Suppose that $⟨M,U⟩,p,\phi$ satisfy (F1) of Section 5.2, and $\mathrm{nam}\phi =\{{\tau }_1,\dots ,{\tau }_m\}$. Let ${\mu }_1,\dots ,{\mu }_m$ be another list of names in ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$, $\mathbf{Q}\left[U\right]$-full below p, and such that ${\tau }_j$ and ${\mu }_j$ are equivalent below p for each $j=1,\dots ,m$. Then $p{\mathbf{forc}}_U^M\phi ({\tau }_1,\dots ,{\tau }_m)$ iff $p{\mathbf{forc}}_U^M\phi ({\mu }_1,\dots ,{\mu }_m)$.

Proof. 

Suppose that $\phi$ is $\mathcal{L}{\Pi }_1^1$. Let $G\subseteq \mathbf{Q}\left[U\right]$ be a set $\mathbf{Q}\left[U\right]$-generic over M, and containing p. Then ${\tau }_{\ell }\left[G\right]={\mu }_{\ell }\left[G\right]$ for all ℓ by Lemma 12. This implies the result required, by (F2) of Section 5.2.

The induction steps $\mathcal{L}{\Pi }_k^1\to \mathcal{L}{\Sigma }_{k+1}^1$ and $\mathcal{L}{\Sigma }_k^1\to \mathcal{L}{\Pi }_k^1$ are carried out by an easy reduction to items (F3), (F4) of Section 5.2. □

Lemma 28 (in $\mathbf{L}$).

Let $⟨M,U⟩,p,\phi$ satisfy (F1) of Section 5.2. Then:

(i)

if $k\ge 2$, φ is $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)$, and $p{\mathbf{forc}}_U^M\phi$, then $p{\mathbf{forc}}_U^M\phi {\phantom{)}}^{\neg }$ fails;

(ii)

if $p{\mathbf{forc}}_U^M\phi$, $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$, and $q\in \mathbf{Q}\left[U^{\prime }\right],q\le p$, then $q{\mathbf{forc}}_{U^{\prime }}^{M^{\prime }}\phi .$

Proof. 

Claim (i) immediately follows from (F4) of Section 5.2.

To prove (ii) let $\phi =\phi ({\tau }_1,\dots ,{\tau }_m)$ be a closed formula in $\mathcal{L}{\Pi }_1^1(\mathbf{Q}\left[U\right],M)$, where all $\mathbf{Q}\left[U\right]$-names ${\tau }_j$ belong to M and are $\mathbf{Q}\left[U\right]$-full below p. Then all names ${\tau }_j$ remain $\mathbf{Q}\left[U^{\prime }\right]$-full below p by Corollary 3 in Section 4.2, therefore below q as well since $q\le p$. Consider a set $G^{\prime }\subseteq \mathbf{Q}\left[U^{\prime }\right]$, $\mathbf{Q}\left[U^{\prime }\right]$-generic over $M^{\prime }$ and containing q. We have to prove that $\phi \left[G^{\prime }\right]$ is true in $M^{\prime }\left[G^{\prime }\right]$. Please note that the set $G=G^{\prime }\cap \mathbf{Q}\left[U\right]$ is $\mathbf{Q}\left[U\right]$-generic over M by Corollary 2 in Section 4.2, and we have $p\in G$. Moreover, the valuation $\phi \left[G^{\prime }\right]$ coincides with $\phi \left[G\right]$ since all names in $\phi$ belong to ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$. And $\phi \left[G\right]$ is true in $M\left[G\right]$ as $p{\mathbf{forc}}_U^M\phi$. It remains to apply Mostowski’s absoluteness (see [10] (p. 484) or [11]) between the models $M\left[G\right]\subseteq M^{\prime }\left[G^{\prime }\right]$.

The induction steps related to (F3), (F4) of Section 5.2 are easy. □

5.4. Transformations and Invariance

To prove Theorem 4 of Section 4.4, we make use of the transformations considered in Section 3.6, Section 3.7 and Section 3.8. In addition to the definitions given there, define, in $\mathbf{L}$, the action of any transformation $\pi \in \mathbf{B}\mathbf{IJ}$ (permutation), $\lambda \in \mathbf{L}{\mathbf{IP}}^{\mathcal{I}}$ (multi-Lipschitz), or one of the form $H_{pq}$ (multisubstitution), on $\mathcal{L}$-formulas with quantifier indices and names in ${\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$ as parameters.

(I)

Assume that $\pi \in \mathbf{B}\mathbf{IJ}$. To get $\pi \phi$ replace each quantifier index B (in ${\exists }^B$ or ${\forall }^B$) by $\pi ·B$ and each name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$ by $\pi ·\tau$.

(II)

Assume that $\lambda \in \mathbf{L}{\mathbf{IP}}^{\mathcal{I}}$. To get $\lambda \phi$ replace each name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)$ in $\phi$ by $\alpha ·\tau$, but do not change quantifier indices.

(III)

Assume that $p,q\in {\mathbf{Q}}^{*}$ satisfy (6) of Section 3.8, and all names $\tau$ occurring in $\phi$ belong to ${{\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)}_{pq}$. To get $H_{pq}\phi$ replace each name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }{\left({\mathbf{Q}}^{*}\right)}_{pq}$ in $\phi$ by $H_{pq}·\tau \in {{\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)}_{qp}$, but do not change quantifier indices.

Lemma 29 (in L).

Suppose that $⟨M,U⟩\in \mathbf{sJS}$, $p\in \mathbf{Q}\left[U\right]$, $k\ge 1$, φ is a formula in $\mathcal{L}{\Sigma }_{k+1}^1(\mathbf{Q}\left[U\right],M)\cup \mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)$, and $\pi \in \mathbf{B}\mathbf{IJ}$ is coded in M in the sense that $\left|\pi \right|\in M$ and $\pi \upharpoonright \left|\pi \right|\in M$. Then: $p{\mathbf{forc}}_U^M\phi$ iff $\left(\pi ·p\right){\mathbf{forc}}_{\pi ·U}^M\pi \phi$. □

Proof. 

Under the conditions of the lemma, $\pi$ acts as an isomorphism on all relevant domains and preserves all relevant relations between the objects involved. Thus, $⟨M,\pi ·U⟩,\pi ·p,\pi \phi$ still satisfy (F1) in Section 5.2. This allows proof of the lemma by induction on the complexity of $\phi$.

Base. Suppose that $\phi$ is a closed formula in $\mathcal{L}{\Pi }_1^1(\mathbf{Q}\left[U\right],M)$. Then $\pi \phi$ is a closed formula in $\mathcal{L}{\Pi }_1^1(\mathbf{Q}\left[\pi ·U\right],M)$. Moreover, the map $p⟼\pi ·p$ is an order isomorphism (in M) $\mathbf{Q}\left[U\right]\stackrel{\mathrm{onto}}{⟶}\mathbf{Q}\left[\pi ·U\right]$ by Lemma 14. We conclude that a set $G\subseteq P$ is $\mathbf{Q}\left[U\right]$-generic over M iff $\pi ·G$ is, accordingly, $\mathbf{Q}\left[\pi ·U\right]$-generic over M, and the valuated formulas $\phi \left[G\right]$ and $\left(\pi \phi \right)\left[\pi ·G\right]$ coincide. Now the result for ${\Pi }_1^1$ formulas follows from in Section 5.2.

Step${\Pi }_n^1\to {\Sigma }_{n+1}^1,n\ge 1$. Let $\psi \left(x\right)$ be a $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)$ formula, and $\phi$ be $\exists x\psi \left(x\right)$. Assume $p{\mathbf{forc}}_U^M\phi$. By definition there is a name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)\cap M$, $\mathbf{Q}\left[U\right]$-full below the given $p\in \mathbf{Q}\left[U\right]$, such that $p{\mathbf{forc}}_U^M\psi \left(\tau \right)$. Then, by the inductive hypothesis, we have $\pi ·p{\mathbf{forc}}_{\pi ·U}^M\left(\pi \psi \right)\left(\pi ·\tau \right)$, and hence by definition $\pi ·p{\mathbf{forc}}_{\pi ·U}^M\pi \phi$.

The case of $\phi$ being ${\exists }^{B}x\psi \left(x\right)$ is similar.

Step${\Sigma }_n^1\to {\Pi }_n^1,n\ge 2$. This is somewhat less trivial. Assume that $\phi$ is a closed $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)$ formula; all names in $\phi$ belong to ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)\cap M$ and are $\mathbf{Q}\left[U\right]$-full below p. Then $\pi \phi$ is a closed $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[\pi ·U\right],M)$ formula, whose all names belong to ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[\pi ·U\right]\right)\cap M$ and are $\mathbf{Q}\left[\pi ·U\right]$-full below $\pi ·p$. Suppose that $p{\mathbf{forc}}_U^M\phi$ fails.

By definition there exist a pair $⟨M_1,U_1⟩\in \mathbf{sJS}$ with $⟨M,U⟩\preccurlyeq ⟨M_1,U_1⟩$, and a condition $q\in \mathbf{Q}\left[U_1\right],q\le p$, such that $q{\mathbf{forc}}_{U_1}^{M_1}\phi {\phantom{)}}^{\neg }$. Then $\left(\pi ·q\right){\mathbf{forc}}_{\pi ·U_1}^{M_1}\pi \phi {\phantom{)}}^{\neg }$ by the inductive hypothesis. Yet the pair $⟨M_1,\pi ·U_1⟩$ belongs to $\mathbf{sJS}$ and extends $⟨M,\pi ·U⟩$. (Recall that $U\in M$ and $\pi$ is coded in M.) In addition, $\pi ·q\in \mathbf{Q}\left[\pi ·U_1\right]$, and $\pi ·q\le \pi ·p$. Therefore, the statement $\left(\pi ·p\right){\mathbf{forc}}_{\pi ·U}^M\pi \phi$ fails, as required. □

Lemma 30 (in L).

Suppose that $⟨M,U⟩\in \mathbf{sJS},p\in \mathbf{Q}\left[U\right]$, $k\ge 1$, φ is a formula in $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)\cup \mathcal{L}{\Sigma }_{k+1}^1(\mathbf{Q}\left[U\right],M)$, and $\alpha \in \mathbf{L}{\mathbf{IP}}^{\mathcal{I}}\cap M$. Then: $p{\mathbf{forc}}_U^M\phi$ iff $\left(\alpha ·p\right){\mathbf{forc}}_{\alpha ·U}^M\alpha \phi$.

Proof. 

Similar to the previous one, but with a reference to Lemma 15 rather than Lemma 14. □

Lemma 31 (in L).

Assume that $⟨M,U⟩\in \mathbf{sJS}$, conditions $p,q\in \mathbf{Q}\left[U\right]$ satisfy (6) of Section 3.8, $k\ge 1$, φ is a closed formula in $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)\cup \mathcal{L}{\Sigma }_{k+1}^1(\mathbf{Q}\left[U\right],M)$ with all names in ${{\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)}_{pq}$ (see Section 3.8), and $r\in \mathbf{Q}\left[U\right],r\le p$. Then: $r{\mathbf{forc}}_U^M\phi$ iff $H_{pq}·r{\mathbf{forc}}_U^M{H}_{pq}\phi$.

Proof. 

Similar to the proof of Lemma 29, except for the step ${\Pi }_k^1\to {\Sigma }_{k+1}^1$, $k\ge 1$, where we need to take additional care to keep the names involved in ${{\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)}_{pq}$. Thus, let $\psi \left(x\right)$ be a $\mathcal{L}{\Pi }_k^1(\mathbf{Q}\left[U\right],M)$ formula, with names in ${{\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)}_{pq}$, and let $\phi$ be $\exists x\psi \left(x\right)$. Assume that $r{\mathbf{forc}}_U^M\phi$.

By definition there is a name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)\cap M$, $\mathbf{Q}\left[U\right]$-full below r, such that $r{\mathbf{forc}}_U^M\psi \left(\tau \right)$. Please note that $\tau$ does not necessarily belong to ${{\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)}_{pq}$. However, the restricted name ${\tau }^{\prime }={\tau }_{\le r}$ (see Lemma 13 in Section 3.8) is still a name in ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)$ because $r\in \mathbf{Q}\left[U\right]$, and we have $r^{\prime }\in \mathtt{dom}{\tau }^{\prime }⟹r^{\prime }\le r\le p$, so that ${\tau }^{\prime }\in {{\mathbf{SN}}_{\omega }^{\omega }\left(\mathbf{Q}\left[U\right]\right)}_{pq}$. Moreover, ${\tau }^{\prime }$ is equivalent to $\tau$ below r by Lemma 13. We conclude that $r{\mathbf{forc}}_U^M\psi \left({\tau }^{\prime }\right)$, by Lemma 27.

Then, by the inductive hypothesis, we have $H_{pq}·r{\mathbf{forc}}_U^M\left(H_{pq}\psi \right)\left(H_{pq}·{\tau }^{\prime }\right)$, and hence by definition $H_{pq}·r{\mathbf{forc}}_U^M{H}_{pq}\phi$ via $H_{pq}·{\tau }^{\prime }$. □

6. Elementary Equivalence Theorem

The goal of this section is to prove Theorem 4 of Section 4.4, and accomplish the proof of Theorem 1. We make use of the relation forc defined above, and exploit certain symmetries in forc studied in Section 5.4.

6.1. Hidden Invariance

To explain the idea, one may note first that elementary equivalence of subextensions of a given generic extension is usually a corollary of the fact that the forcing notion considered is enough homogeneous, or in different words, invariant w. r. t. a sufficiently large system of order-preserving transformations. The forcing notion $\mathbb{Q}=\mathbf{Q}\left[\mathbb{U}\right]$ we consider, as well as basically any $\mathbf{Q}\left[U\right]$, is invariant w. r. t. multi-substitutions by Lemma 17. However, for a straightaway proof of Theorem 4 we would naturally need the invariance under permutations of Section 3.6—to interchange the domains Z and $Z^{\prime }$, whereas $\mathbb{Q}$ is definitely not invariant w. r. t. permutations.

On the other hand, the relation $\mathbf{forc}$ is invariant w. r. t. both permutations (Lemma 29) and multi-Lipschitz (Lemma 30), as well as still w. r. t. multi-substitutions by Lemma 31. To bridge the gap between $\mathbf{forc}$ (not explicitly connected with $\mathbb{Q}$ in any way) and $\mathbb{Q}$-generic extensions, we prove Lemma 33, which ensures that ${\mathbf{forc}}_{}^{}$ admits a forcing-style association with the truth in $\mathbb{Q}$-generic extensions, bounded to formulas of type ${\Sigma }_{𝕟}^1$ and below. This key result will be based on the $𝕟$-completeness property (Definition 2 in Section 4.3). Speaking loosely, one may say that some transformations, i.e., permutations and multi-Lipschitz, are hidden in construction of $\mathbb{Q}$, so that they do not act per se, but their influence up to $𝕟$th level, is preserved.

This method of hidden invariance, i.e., invariance properties (of an auxiliary forcing-type relationship like $\mathbf{forc}$) hidden in $\mathbb{Q}$ by a suitable generic-style construction of $\mathbb{Q}$, was introduced in Harrington’s notes [3] in a somewhat different terminology. We may note that the hidden invariance technique is well known in some other fields of mathematics, including more applied fields, see e.g., [12,13].

6.2. Approximations of the $𝕟$-Complete Forcing Notion

We return to the forcing notion $\mathbb{Q}=\mathbf{Q}\left[\mathbb{U}\right]$ defined in $\mathbf{L}$ as in Definition 2 in Section 4.3 for a given number $𝕟\ge 2$ of Theorem 1. Arguing in $\mathbf{L}$, we let the pairs $⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩,\xi <{\omega }_2$, also be as in Definition 2. Let ${\displaystyle \mathbf{forc}{}_{\xi }}$ denote the relation ${\mathbf{forc}}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}$, and let $p{\displaystyle \mathbf{forc}{}_{\infty }}\phi$ mean: $\exists \xi <{\omega }_2\left(p{\displaystyle \mathbf{forc}{}_{\xi }}\phi \right)$.

Claims (i), (ii) of Lemma 28 take the form:

(I)

$p{\displaystyle \mathbf{forc}{}_{\xi }}\phi$ and $p{\displaystyle \mathbf{forc}{}_{\eta }}\phi {\phantom{)}}^{\neg }$ ($\xi ,\eta <{\omega }_2$) contradict to each other.

(II)

If $p{\displaystyle \mathbf{forc}{}_{\xi }}\phi$ and $\xi \le \zeta <{\omega }_2$, $q\in \mathbf{Q}\left[{\mathbb{U}}_{\zeta }\right],q\le p$, then $q{\displaystyle \mathbf{forc}{}_{\zeta }}\phi$.

The next lemma shows that ${\displaystyle \mathbf{forc}{}_{\infty }}$ satisfies a key property of forcing relations up to the level of ${\Pi }_{𝕟-1}^1$ formulas.

Lemma 32.

If φ is a closed formula in $\mathcal{L}{\Pi }_k^1\left(\mathbb{Q}\right),2\le k<𝕟$, $p\in \mathbb{Q}$, and all names in φ are $\mathbb{Q}$-full below p, then there is a condition $q\in \mathbb{Q},q\le p$, such that either $q{\displaystyle \mathbf{forc}{}_{\infty }}\phi$, or $q{\displaystyle \mathbf{forc}{}_{\infty }}\phi {\phantom{)}}^{\neg }$.

Proof. 

As the names considered are ${\omega }_1$-size objects, there is an ordinal $\eta <{\omega }_2$ such that $p\in {\mathbb{Q}}_{\eta }$, and all names in $\phi$ belong to ${\mathbb{M}}_{\eta }\cap {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbb{Q}}_{\eta }\right)$; then all names in $\phi$ are ${\mathbb{Q}}_{\eta }$-full below p, of course. As $k<𝕟$, the set D of all pairs $⟨M,U⟩\in \mathbf{sJS}$ that extend $⟨{\mathbb{M}}_{\eta },{\mathbb{U}}_{\eta }⟩$ and there is a condition $q\in \mathbf{Q}\left[U\right],q\le p$, satisfying $q{\mathbf{forc}}_U^M\phi {\phantom{)}}^{\neg }$, belongs to ${\Sigma }_{𝕟-2}^{\mathrm{HC}}$ by Lemma 26. Therefore, by the $𝕟$-completeness of the sequence ${\left\{⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩\right\}}_{\xi <{\omega }_1}$, there is an ordinal $\zeta ,\eta \le \zeta <{\omega }_1$, such that $⟨{\mathbb{M}}_{\zeta },{\mathbb{U}}_{\zeta }⟩\in D^{\mathrm{solv}}$.

We have two cases.

Case 1: $⟨{\mathbb{M}}_{\zeta },{\mathbb{U}}_{\zeta }⟩\in D$. Then there is a condition $q\in K\left[{\mathbb{U}}_{\zeta }\right],q\le p$, satisfying $q{\mathbf{forc}}_{{\mathbb{U}}_{\zeta }}^{{\mathbb{M}}_{\zeta }}\phi {\phantom{)}}^{\neg }$, that is, $q{\displaystyle \mathbf{forc}{}_{\infty }}\phi {\phantom{)}}^{\neg }$. However, obviously $q\in \mathbb{Q}$.

Case 2: there is no pair $⟨M,U⟩\in D$ extending $⟨{\mathbb{M}}_{\zeta },{\mathbb{U}}_{\zeta }⟩$. Prove $p{\displaystyle \mathbf{forc}{}_{\zeta }}\phi$. Suppose otherwise. Then by the choice of $\eta$ and (F4) in Section 5.2, there exist: a pair $⟨M,U⟩\in \mathbf{sJS}$ extending $⟨{\mathbb{M}}_{\zeta },{\mathbb{U}}_{\zeta }⟩$, and a condition $q\in \mathbf{Q}\left[U\right],q\le p$, such that $q{\mathbf{forc}}_U^M\phi {\phantom{)}}^{\neg }$. Then $⟨M,U⟩\in D$, a contradiction. □

Now we prove another key lemma which connects, in a forcing-style way, the relation ${\displaystyle \mathbf{forc}{}_{\infty }}$ and the truth in $\mathbb{Q}$-generic extensions of $\mathbf{L}$, up to the level of ${\Sigma }_{𝕟}^1$ formulas.

Lemma 33.

Suppose that φ is a formula in $\mathcal{L}{\Pi }_k^1\left(\mathbb{Q}\right)\cup \mathcal{L}{\Sigma }_{k+1}^1\left(\mathbb{Q}\right),1\le k<𝕟$, and all names in φ are $\mathbb{Q}$-full. Let $G\subseteq \mathbb{Q}$ be $\mathbb{Q}$-generic over $\mathbf{L}$. Then $\phi \left[G\right]$ is true in $\mathbf{L}\left[G\right]$ iff there is a condition $p\in G$ such that $p{\displaystyle \mathbf{forc}{}_{\infty }}\phi$.

Proof. 

We proceed by induction and begin with the case of $\mathcal{L}{\Pi }_1^1$ formulas. Consider a closed formula $\phi$ in $\mathcal{L}{\Pi }_1^1\left(\mathbb{Q}\right)$. As names in the formulas considered are ${\omega }_1$-size names in ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbb{Q}\right)$, there is an ordinal $\xi <{\omega }_2$ such that $\phi$ is a $\mathcal{L}{\Pi }_1^1\left({\mathbb{Q}}_{\xi }\right)$ formula. Please note that since $G\subseteq \mathbb{P}$ is $\mathbb{Q}$-generic over $\mathbf{L}$, the smaller set $G_{\xi }=G\cap {\mathbb{Q}}_{\xi }$ is ${\mathbb{Q}}_{\xi }$-generic over ${\mathbb{M}}_{\xi }$ by Corollary 2 in Section 4.2, and the formulas $\phi \left[G\right]$, $\phi \left[G_{\xi }\right]$ coincide by the choice of $\xi$. Therefore

iff $\phi \left[G\right]$ holds in $\mathbf{L}\left[G\right]$:

iff $\phi \left[G_{\xi }\right]$ holds in ${\mathbb{M}}_{\xi }\left[G_{\xi }\right]$ by the Mostowski absoluteness [10] (p. 484),

iff there is $p\in G_{\xi }$ which ${\mathbb{Q}}_{\xi }$-forces $\phi$ over ${\mathbb{M}}_{\xi }$,

iff $\exists p\in G_{\xi }\left(p{\displaystyle \mathbf{forc}{}_{\xi }}\phi \right)$ by (F2) in Section 5.2,

easily getting the result required since $\xi$ is arbitrary.

The step from$\mathcal{L}{\Sigma }_k^1$ to $\mathcal{L}{\Pi }_k^1$, $k\ge 2$. Prove the theorem for a $\mathcal{L}{\Pi }_k^1\left(\mathbb{Q}\right)$ formula $\phi$, assuming that the result holds for ${\phi }^{\neg }$. Suppose that $\phi \left[G\right]$ is false in $\mathbf{L}\left[G\right]$. Then $\phi {\phantom{)}}^{\neg }\left[G\right]$ is true, and hence by the inductive hypothesis, there is a condition $p\in G\upharpoonright c$ such that $p{\displaystyle \mathbf{forc}{}_{\infty }}\phi {\phantom{)}}^{\neg }$. Then it follows from (I) and (II) above that $q{\displaystyle \mathbf{forc}{}_{\infty }}\phi$ fails for all $q\in G$.

Conversely let $p{\displaystyle \mathbf{forc}{}_{\infty }}\phi$ fail for all $p\in G$. Then by Lemma 32 there exists $q\in G$ satisfying $q{\displaystyle \mathbf{forc}{}_{\infty }}\phi {\phantom{)}}^{\neg }$. It follows that $\phi {\phantom{)}}^{\neg }\left[G\right]$ is true by the inductive hypothesis, therefore $\phi \left[G\right]$ is false.

The step from$\mathcal{L}{\Pi }_k^1$ to $\mathcal{L}{\Sigma }_{k+1}^1$. Let $\phi \left(x\right)$ be a $\mathcal{L}{\Pi }_k^1\left(\mathbb{Q}\right)$ formula; prove the result for a formula ${\exists }^{B}x\phi \left(x\right)$. If $p\in G$ and $p{\displaystyle \mathbf{forc}{}_{\xi }}{\exists }^{B}x\phi \left(x\right)$ then by definition there is a name $\tau \in {\mathbb{M}}_{\xi }\cap {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbb{Q}}_{\xi }\right)\upharpoonright B$, ${\mathbb{Q}}_{\xi }$-full below p, and such that $p{\displaystyle \mathbf{forc}{}_{\xi }}\phi \left(\tau \right)$. Then $\phi \left(\tau \right)\left[G\right]$ holds by the inductive hypothesis, and this implies $\left({\exists }^{B}x\phi \left(x\right)\right)\left[G\right]$ since obviously $\tau \left[G\right]\in \mathbf{L}\left[G\upharpoonright B\right]$.

If conversely $\left({\exists }^{B}x\phi \left(x\right)\right)\left[G\right]$ is true, then by Lemma 11 there is a $\mathbb{Q}$-full name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbb{Q}\right)\upharpoonright B$ such that $\phi \left(\tau \right)\left[G\right]$ is true. Then, by the inductive hypothesis, there is a condition $p\in G$ such that $p{\displaystyle \mathbf{forc}{}_{\infty }}\phi \left(\tau \right)$. Therefore $p{\displaystyle \mathbf{forc}{}_{\infty }}{\exists }^{B}x\phi \left(x\right)$ by the choice of $\tau$.

The case of $\exists x\phi \left(x\right)$ is treated similarly. □

6.3. The Elementary Equivalence Theorem

We begin the proof of Theorem 4 of Section 4.4, so let $d,Z,Z^{\prime },x_0$ be as in the theorem.

Step 1. We assume w.l.o.g. that $x_0$ itself is the only parameter in the ${\Sigma }_{𝕟}^1$ formula $\Phi$ of Theorem 4. By Lemma 11, there exists, in $\mathbf{L}$, a $\mathbb{Q}$-full name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(\mathbb{Q}\right)$ such that $x_0=\tau \left[G\right]$ and ${\left|\tau \right|}^{+}\subseteq d$. Thus, $\Phi$ is $\phi \left(\tau \right[G\left]\right)$, where $\phi (·)$ is a parameter-free ${\Sigma }_{𝕟}^1$ formula with a single free variable. Then ${\left|\phi \left(\tau \right)\right|}^{+}={\left|\tau \right|}^{+}\subseteq d$.

We also assume w.l.o.g. that the sets $Z,Z^{\prime }$ satisfy the requirement that $Z\setminus Z^{\prime }$ and $Z^{\prime }\setminus Z$ are infinite (countable) sets. Indeed, otherwise, under the assumptions of Theorem 4, one easily defines a third set $Z^{\prime \prime }$ such that each of the pairs $Z,Z^{\prime \prime }$ and $Z^{\prime },Z^{\prime \prime }$ still satisfies the assumptions of the theorem, and in addition, all four sets $Z\setminus Z^{\prime \prime }$, $Z^{\prime \prime }\setminus Z$, $Z^{\prime \prime }\setminus Z^{\prime }$ and $Z^{\prime }\setminus Z^{\prime \prime }$ are infinite. Please note that this argument necessarily requires that the complementary set $\mathcal{I}\setminus (d\cup Z\cup Z^{\prime })$ is infinite.

Step 2. We are going to reorganize the quantifier prefix of $\phi$, in particular, by assigning the indices Z and $Z^{\prime }$ to certain quantifiers, to reflect the relativization to classes $\mathbf{L}[x_0,G\upharpoonright Z]$ and $\mathbf{L}[x_0,G\upharpoonright Z^{\prime }]$. This is not an easy task because generally speaking there is no set $Z_0\subseteq \mathcal{I}$ in $\mathbf{L}$ satisfying $\mathbf{L}\left[x_0\right]=\mathbf{L}\left[G\upharpoonright Z_0\right]$. However, nevertheless we will define an $\mathcal{L}{\Sigma }_{𝕟}^1$ formula, say ${\psi }^Z\left(v\right)$, and then ${\psi }^{Z^{\prime }}\left(v\right)$ by the substitution of $Z^{\prime }$ for Z, such that the following will hold:

(A)

For any set $G\subseteq \mathbb{Q}$, $\mathbb{Q}$-generic over $\mathbf{L}:$

$$\begin{array}{cccc}\phi \left(\tau \right[G\left]\right)\mathrm{is}\mathrm{true}\mathrm{in}\mathbf{L}\left[\tau \right[G],G\upharpoonright Z]\hfill & \mathrm{iff}& \hfill {\psi }^Z\left(\tau \right)\left[G\right]\mathrm{is}\mathrm{true}\mathrm{in}\mathbf{L}\left[G\right],& \mathrm{and}\\ \phi \left(\tau \right[G\left]\right)\mathrm{is}\mathrm{true}\mathrm{in}\mathbf{L}[\tau \left[G\right],G\upharpoonright Z^{\prime }]\hfill & \mathrm{iff}& \hfill {\psi }^{Z^{\prime }}\left(\tau \right)\left[G\right]\mathrm{is}\mathrm{true}\mathrm{in}\mathbf{L}\left[G\right].\end{array}$$

(See Section 5.1 on the interpretation $\psi \left[G\right]$ for any $\mathcal{L}$-formula $\psi$.)

To explain this transformation, assume that $𝕟=4$ for the sake of brevity, and hence $\phi \left(v\right)$ has the form $\exists x\forall y\vartheta (v,x,y)$, where $\vartheta$ is a ${\Sigma }_2^1$ formula. To begin with, we define

$${\psi }_1^Z\left(v\right):={\exists }^Z{x}^{\prime }\exists x\in \mathbf{L}[x^{\prime },v]{\forall }^Z{y}^{\prime }\forall y\in \mathbf{L}[v,y^{\prime }]\vartheta (v,x,y),$$

(17)

and define ${\psi }_1^{Z^{\prime }}\left(v\right)$ accordingly.

Lemma 34.

The formulas ${\psi }_1^Z$, ${\psi }_1^{Z^{\prime }}$ satisfy (A).

Proof. 

To prove the implication $⟹$, suppose that $\phi \left(\tau \right[G\left]\right)$ holds in $\mathbf{L}\left[\tau \right[G],G\upharpoonright Z]$, so that there is a real $x_1\in {\omega }^{\omega }\cap \mathbf{L}[\tau \left[G\right],G\upharpoonright Z]$ satisfying $\forall y\vartheta (\tau \left[G\right],x_1,y)$ in $\mathbf{L}\left[\tau \right[G],G\upharpoonright Z]$. By a standard argument there is a real $x^{\prime }\in {\omega }^{\omega }\cap \mathbf{L}\left[G\upharpoonright Z\right]$ with $x_1\in {\omega }^{\omega }\cap \mathbf{L}[\tau \left[G\right],x^{\prime }]$. We claim that these reals $x^{\prime }$ and $x_1$ witness that ${\psi }_1^Z\left(\tau \right)\left[G\right]$ holds in $\mathbf{L}\left[G\right]$, that is, we have ${\forall }^Z{y}^{\prime }\forall y\in \mathbf{L}[\tau \left[G\right],y^{\prime }]\vartheta (\tau \left[G\right],x_1,y)$ in $\mathbf{L}\left[G\right]$.

Indeed, suppose that $y^{\prime }\in {\omega }^{\omega }\cap \mathbf{L}\left[G\upharpoonright Z\right]$ and $y\in {\omega }^{\omega }\cap \mathbf{L}[\tau \left[G\right],y^{\prime }]$. Then $y\in \mathbf{L}\left[\tau \right[G],G\upharpoonright Z]$, of course. Therefore $\vartheta (\tau \left[G\right],x_1,y)$ is true in $\mathbf{L}\left[\tau \right[G],G\upharpoonright Z]$ by the choice of $x_1$. We conclude that $\vartheta (\tau \left[G\right],x_1,y)$ is true in $\mathbf{L}\left[G\right]$ as well by the Shoenfield absoluteness theorem, as $\vartheta$ is a ${\Sigma }_2^1$ formula.

The inverse implication is proved similarly.            (Lemma) □

Thus, the formulas ${\psi }_1^Z$, ${\psi }_1^{Z^{\prime }}$ do satisfy (A), but they are not $\mathcal{L}{\Sigma }_{𝕟}^1$ formulas as defined in Section 5.1, of course. It will take some effort to convert them to a $\mathcal{L}{\Sigma }_{𝕟}^1$ form. We must recall some instrumentarium known in Gödel’s theory of constructability of reals.

• If $x\in {\omega }^{\omega }$ then define reals ${\left(x\right)}_{\mathrm{ev}}$ and ${\left(x\right)}_{\mathrm{odd}}$ in ${\omega }^{\omega }$ by ${\left(x\right)}_{\mathrm{ev}}\left(k\right)=x\left(2k\right)$ and ${\left(x\right)}_{\mathrm{odd}}\left(k\right)=x(2k+1)$ for all k. If $y,z\in {\omega }^{\omega }$ then define $x*y\in {\omega }^{\omega }$ such that ${(x*y)}_{\mathrm{ev}}=x$, ${(x*y)}_{\mathrm{odd}}=y$.
• There is a ${\Pi }_1^1$ set $\mathbf{WO}=\left\{w\in {\omega }^{\omega }:\mathrm{wo}\left(x\right)\right\}$ of codes of countable ordinals, defined by a ${\Pi }_1^1$ formula $\mathrm{wo}$, so that $\left|w\right|$ is the ordinal coded by $w\in \mathbf{WO}$, and ${\omega }_1=\{\left|w\right|:w\in \mathbf{WO}\}$, see ([14] (1E))).

As a one more pre-requisite, we make use of a system of maps ${\mathbf{f}}_{\xi }:{\omega }^{\omega }\to {\omega }^{\omega }$, $\xi <{\omega }_1$, such that:

(a)

if $x\in {\omega }^{\omega }$ then $\mathbf{L}\left[x\right]\cap {\omega }^{\omega }=\{{\mathbf{f}}_{\xi }\left(x\right):\xi <{\omega }_1\}$, and

(b)

there exist a ${\Sigma }_1^1$ formula $S(x,y,w)$ and a ${\Pi }_1^1$ formula $P(x,y,w)$ such that if $w\in \mathbf{WO}$ then ${\mathbf{f}}_{\left|w\right|}\left(x\right)=y⟺S(x,y,w)⟺P(x,y,w)$ for all $x,y\in {\omega }^{\omega }$,

see e.g., ([14] (Theorem 2.6)). Recall that ${\omega }_1^{\mathbf{L}\left[G\right]}={\omega }_1^{\mathbf{L}\left[G\upharpoonright Z\right]}={{\omega }_2}^{\mathbf{L}}$ by Lemma 22.

Now consider the formula

$$\begin{array}{c}{\psi }_2^Z\left(v\right):={\exists }^{Z}x(\mathrm{wo}\left({\left(x\right)}_{\mathrm{ev}}\right)\wedge {\forall }^{Z}y[\mathrm{wo}\left({\left(y\right)}_{\mathrm{ev}}\right)⟹\hfill \\ ⟹\vartheta (v,{\mathbf{f}}_{{|\left(x\right)}_{\mathrm{ev}}|}(v*{\left(x\right)}_{\mathrm{odd}}),{\mathbf{f}}_{{|\left(y\right)}_{\mathrm{ev}}|}(v*{\left(y\right)}_{\mathrm{odd}}))\left]\right),\hfill \end{array}$$

(18)

and define ${\psi }_2^{Z^{\prime }}\left(v\right)$ similarly.

We keep the global understanding that the quantifiers ${\exists }^Z,{\forall }^Z$ are relativized to $\mathbf{L}\left[G\upharpoonright Z\right]\cap {\omega }^{\omega }$.

Lemma 35.

The formulas ${\psi }_1^Z\left(\tau \left[G\right]\right)$ and ${\psi }_2^Z\left(\tau \left[G\right]\right)$ are equivalent in $\mathbf{L}\left[G\right]$, and the same for ${\psi }_1^{Z^{\prime }}$ and ${\psi }_2^{Z^{\prime }}.$

Proof (Lemma).

To prove the implication $⟹$, assume that ${\psi }_1^Z\left(\tau \left[G\right]\right)$ holds in $\mathbf{L}\left[G\right]$, and this is witnessed by reals $x^{\prime }\in {\omega }^{\omega }\cap \mathbf{L}\left[G\upharpoonright Z\right]$ and $x_1\in {\omega }^{\omega }\cap \mathbf{L}[\tau \left[G\right],x^{\prime }]={\omega }^{\omega }\cap \mathbf{L}[\tau \left[G\right]*x^{\prime }]$ satisfying ${\forall }^Z{y}^{\prime }\forall y\in \mathbf{L}[\tau \left[G\right],y^{\prime }]\vartheta (\tau \left[G\right],x_1,y)$ in $\mathbf{L}\left[G\right]$. Please note that ${\omega }_1^{\mathbf{L}\left[G\upharpoonright Z\right]}={\omega }_1^{\mathbf{L}\left[G\right]}={\omega }_2^{\mathbf{L}}$ by Lemma 9 (ii). It follows by (a) that there is an ordinal $\xi <{\omega }_1^{\mathbf{L}\left[G\upharpoonright Z\right]}$ with $x_1={\mathbf{f}}_{\xi }(\tau \left[G\right]*x^{\prime })$, and then there is a real $w\in \mathbf{WO}\cap \mathbf{L}\left[G\upharpoonright Z\right]$ with $\xi =\left|w\right|$.

Now let $\tilde{x}=w*x^{\prime }$, so that $w={\left(\tilde{x}\right)}_{\mathrm{ev}}$, $x^{\prime }={\left(\tilde{x}\right)}_{\mathrm{odd}}$, and $x_1={\mathbf{f}}_{|{\left(\tilde{x}\right)}_{\mathrm{ev}}|}(\tau \left[G\right]*{\left(\tilde{x}\right)}_{\mathrm{odd}})$. We claim that $\tilde{x}$ witnesses ${\psi }_2^Z\left(\tau \left[G\right]\right)$ in $\mathbf{L}\left[G\right]$. Indeed, assume that $\tilde{y}\in {\omega }^{\omega }\cap \mathbf{L}\left[G\upharpoonright Z\right]$ and $w={\left(\tilde{y}\right)}_{\mathrm{ev}}\in \mathbf{WO}$, $\eta =|{\left(\tilde{y}\right)}_{\mathrm{ev}}|$, and $y_1={\mathbf{f}}_{\eta }(\tau \left[G\right]*{\left(\tilde{y}\right)}_{\mathrm{odd}})$; we must prove that $\vartheta (\tau \left[G\right],x_1,y_1)$ is true in $\mathbf{L}\left[G\right]$.

However, we have $y_1\in \mathbf{L}[\tau \left[G\right],y^{\prime }]$ by construction, where $y^{\prime }={\left(\tilde{y}\right)}_{\mathrm{odd}}\in \mathbf{L}\left[G\upharpoonright Z\right]$ by the choice of $\tilde{y}$. Now it follows by the choice of $x_1$ that $\vartheta (\tau \left[G\right],x_1,y_1)$ indeed holds, as required.

The proof of the inverse implication is similar.      (Lemma) □

Please note that the formula ${\psi }_2^Z\left(v\right)$ can be converted to the following logically equivalent form:

$$\begin{array}{c}{\psi }_3^Z\left(v\right):={\exists }^{Z}x{\forall }^{Z}y[\mathrm{wo}\left({\left(x\right)}_{\mathrm{ev}}\right)\wedge (\mathrm{wo}\left({\left(y\right)}_{\mathrm{ev}}\right)⟹\hfill \\ ⟹\vartheta (v,{\mathbf{f}}_{{|\left(x\right)}_{\mathrm{ev}}|}(v*{\left(x\right)}_{\mathrm{odd}}),{\mathbf{f}}_{{|\left(y\right)}_{\mathrm{ev}}|}(v*{\left(y\right)}_{\mathrm{odd}}))\left)\right].\hfill \end{array}$$

(19)

And here the kernel $\left[\dots \right]$ can be converted to a true ${\Sigma }_2^1$ form, say $\chi (v,x,y)$, with the help of the formulas S and P of (b), and because $\mathrm{wo}(·)$ is ${\Pi }_1^1$ and $\vartheta$ is ${\Sigma }_2^1$. This yields a $\mathcal{L}{\Sigma }_4^1$ formula ${\psi }^Z\left(v\right):={\exists }^{Z}x{\forall }^{Z}y\chi (v,x,y)$, equivalent to ${\psi }_1^Z$, and hence satisfying (A) by Lemmas 34 and 35, as required.

Step 3. Assuming that the formula $\Phi :=\phi \left(\tau \right[G\left]\right)$ is true in $\mathbf{L}[x_0,G\upharpoonright Z]$, the transformed formula ${\psi }^Z\left(\tau \right)\left[G\right]$ holds in $\mathbf{L}\left[G\right]$ by (A). By Lemma 33 there is a condition $p\in G$ such that $p{\displaystyle \mathbf{forc}{}_{\infty }}{\psi }^Z\left(\tau \right)$ that is, there is an ordinal $\xi <{\omega }_2$ such that $p{\displaystyle \mathbf{forc}{}_{\xi }}{\psi }^Z\left(\tau \right)$—then by definition $p\in \mathbf{Q}\left[{\mathbb{U}}_{\xi }\right]$. We w.l.o.g. assume that p and $\zeta$ satisfy the following two requirements:

(B)

$\mathtt{card}\left(\right|p|\cap (Z\setminus Z^{\prime }))=\mathtt{card}\left(\right|p|\cap (Z^{\prime }\setminus Z))$ (recall that $Z^{\prime }\setminus Z$, $Z\setminus Z^{\prime }$ are infinite, Step 1).

(C)

$-1\in {\left|p\right|}^{+}$, and if $\nu ,{\nu }^{\prime }\in \left|p\right|$ then $S_p\left(\nu \right)\subseteq F_p^{\vee }\left(\nu \right)$ and the sets $F_p^{\vee }\left(\nu \right)$ and $F_p^{\vee }\left({\nu }^{\prime }\right)$ are i-similar (see Section 2.3).

Please note that if $\xi <\eta <{\omega }_2$ then still $p{\displaystyle \mathbf{forc}{}_{\eta }}{\psi }^Z\left(\tau \right)$ by Lemma 28. Therefore, we can increase $\xi$ below ${\omega }_2$ so that the following holds:

(D)

the sets d, $Z\setminus Z^{\prime }$, $Z^{\prime }\setminus Z$ belong to ${\mathbb{M}}_{\xi }$ and are subsets of $|{\mathbb{U}}_{\xi }|$.

Step 4. Now, to finalize the proof of Theorem 4, it suffices (by Lemma 33) to prove:

Lemma 36.

We have $p{\displaystyle \mathbf{forc}{}_{\infty }}{\psi }^{Z^{\prime }}\left(\tau \right)$ as well.

Proof (Lemma).

Let $\delta =d\cup \left(Z\Delta Z^{\prime }\right)$; then $\delta \in {\mathbb{M}}_{\xi }$ by (D), and $\delta \subseteq |{\mathbb{U}}_{\xi }|$. There is a bijection $f\in M$, $f:\delta \stackrel{\mathrm{onto}}{⟶}\delta$, such that

(E)

$f\upharpoonright d$ is the identity, f maps $Z\setminus Z^{\prime }$ onto $Z^{\prime }\setminus Z$ and vice versa.

Then, by (B), f maps $\left|p\right|$ onto $\left|p\right|$. Let $\pi$ be the trivial extension of f onto $\mathcal{I}$: $\pi \left(\nu \right)=\nu$ for $\nu \notin \delta$. Thus, $\pi$ is coded in ${\mathbb{M}}_{\xi }$ in the sense of Lemma 29, and $\left|\pi \right|\subseteq \delta \subseteq |{\mathbb{U}}_{\xi }|$. We have $p{\mathbf{forc}}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}{\psi }^Z\left(\tau \right)$ by the choice of $\xi$, hence ${\mathbb{U}}_{\xi }\in {\mathbb{M}}_{\xi }$ and $p\in {\mathbb{P}}_{\xi }=\mathbf{Q}\left[{\mathbb{U}}_{\xi }\right]\in {\mathbb{M}}_{\xi }$. Moreover, $\pi ·\tau =\tau$ because ${\left|\tau \right|}^{+}\subseteq d$ and $\pi \upharpoonright d$ is the identity by (E). It follows that $p^{\prime }{\mathbf{forc}}_{U^{\prime }}^{{\mathbb{M}}_{\xi }}{\phi }^{Z^{\prime }}\left(\tau \right)$ by Lemma 29, where $U^{\prime }=\pi ·{\mathbb{U}}_{\xi }$, $p^{\prime }=\pi ·p$. Please note that $p^{\prime }\in \mathbf{Q}\left[U^{\prime }\right]$, $|p^{\prime }{|}^{+}={\left|p\right|}^{+}$, $|U^{\prime }|=|{\mathbb{U}}_{\xi }|$, $U^{\prime }\upharpoonright d={\mathbb{U}}_{\xi }\upharpoonright d$, $p^{\prime }\upharpoonright d=p\upharpoonright d$. Also note that

(F)

if $\nu \in |p^{\prime }|=|p|$ then the sets $F_p^{\vee }\left(\nu \right)$, $F_{p^{\prime }}^{\vee }\left(\nu \right)$ are i-similar by (C), (E).

We conclude, by Lemma 16, that there is a transformation $\lambda ={\left\{{\lambda }_{\nu }\right\}}_{\nu \in |{\mathbb{U}}_{\xi }|}\in \mathbf{L}{\mathbf{IP}}^{\mathcal{I}}\cap {\mathbb{M}}_{\xi }$, such that $\lambda ·U^{\prime }={\mathbb{U}}_{\xi }$, ${\lambda }_{\nu }=$ the identity for all $\nu \in d$, and $F_p^{\vee }\left(\nu \right)=F_q^{\vee }\left(\nu \right)$ for all $\nu \in \left|p\right|=|p^{\prime }|=|q|$, where $q=\lambda ·p^{\prime }\in \mathbf{Q}\left[{\mathbb{U}}_{\xi }\right]$. Then we have $q{\mathbf{forc}}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}{\psi }^{Z^{\prime }}\left(\tau \right)$ by Lemma 30. Here $\lambda ·{\psi }^{Z^{\prime }}\left(\tau \right)={\psi }^{Z^{\prime }}\left(\tau \right)$ by the choice of $\lambda$, because ${\left|\tau \right|}^{+}\subseteq d$. And $q\upharpoonright d=p\upharpoonright d$ holds by the same reason.

It remains to derive $p{\mathbf{forc}}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}{\psi }^{Z^{\prime }}\left(\tau \right)$ from $q{\mathbf{forc}}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}{\psi }^{Z^{\prime }}\left(\tau \right)$. Please note that $p,q$ satisfy (6) of Section 3.8 by construction, hence the transformation $H_{qp}$ is defined. Moreover, the only name $\tau$ occurring in ${\psi }^{Z^{\prime }}\left(\tau \right)$ satisfies ${\left|\tau \right|}^{+}\subseteq d$, and $\pi \upharpoonright d$ is the identity by (E). It follows that $\tau \in {{\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{Q}}^{*}\right)}_{qp}$, and $\pi ·\tau =\tau$. We conclude that Lemma 31 is applicable. This yields $p{\mathbf{forc}}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}{\psi }^{Z^{\prime }}\left(\tau \right)$, as required. (Lemma 36) □

                                            (Theorem 4 of Section 4.4) □

                                            (Theorem 1, see Section 4.5) □

7. Conclusions and Discussion

In this study, the method of almost-disjoint forcing was employed to the problem of getting a model of $\mathbf{ZFC}$ in which the constructible reals are precisely the ${\Delta }_n^1$ reals, for different values $n>2$. The problem appeared under no 87 in Harvey Friedman’s treatise One hundred and two problems in mathematical logic [1], and was generally known in the early years of forcing, see, e.g., problems 3110, 3111, 3112 in an early survey [2] by A. Mathias. The problem was solved by Leo Harrington, as mentioned in [1,2] and a sketch of the proof mainly related to the case $n=3$ in Harrington’s own handwritten notes [3].

From this study, it is concluded that the hidden invariance technique (as outlined in Section 6.1) allows the solution of the general case of the problem (an arbitrary $n\ge 3$), by providing a generic extension of $\mathbf{L}$ in which the constructible reals are precisely the ${\Delta }_n^1$ reals, for a chosen value $n\ge 3$, as sketched by Harrington. The hidden invariance technique has been applied in recent papers [7,15,16,17] for the problem of getting a set theoretic structure of this or another kind at a pre-selected projective level. We may note here that the hidden invariance technique, as a true mathematical technique, also has multiple applications both in the physical and engineering fields. In this regard, we cite works [18,19] that have exploited this technique (albeit simplified) for engineering applications.

We continue with a brief discussion with a few possible future research lines.

1. Harvey Friedman completes [1] with a modified version of the above problem, defined as Problem 87${}^{\prime }$: find a model of

$$\mathbf{ZFC}+"\mathrm{for}\mathrm{any}\mathrm{reals}x,y,\mathrm{we}\mathrm{have}:x\in \mathbf{L}\left[y\right]⟹x\mathrm{is}{\Delta }_3^1\mathrm{in}y".$$

(20)

This problem was also known in the early years of forcing, see, e.g., problem 3111 in [2]. Problem (20) was solved in the positive by René David [20], where the question is attributed to Harrington. So far it is unknown whether this result generalizes to higher classes ${\Delta }_n^1$, $n\ge 4$, or ${\Delta }_{\infty }^1$, and whether it can be strengthened towards $⟺$ instead of $⟹$. This is a very interesting and perhaps difficult question.

2. Another question to be mentioned here is the following. Please note that in any extension of $\mathbf{L}$ satisfying Theorem 1, it is true that every universal ${\Sigma }_{𝕟+1}^1$ set $u\subseteq \omega \times \omega$ is by necessity ${\Sigma }_{𝕟+1}^1$ but non-${\Delta }_{𝕟+1}^1$, and hence nonconstructible. This gives another proof of Theorem 3 in [7]. (It claims, for any $𝕟\ge 2$, the existence of a generic extension of $\mathbf{L}$ in which there is a nonconstructible ${\Sigma }_{𝕟+1}^1$ set $a\subseteq \omega$ whereas all ${\Delta }_{𝕟+1}^1$ sets are constructible.) And the problem is, given $𝕟\ge 2$, to find a model in which

all ${\Delta }_{𝕟+1}^1$ reals are constructible, but there exists a ${\Sigma }_{𝕟+1}^1$ nonconstructible real $u\subseteq \omega$, which satisfies $\mathbf{V}=\mathbf{L}\left[u\right]$.

Neither the model considered in Section 4.5 above, nor the model for ([7] (Theorem 3)), suffice to solve the problem, because these models in principle are incompatible with $\mathbf{V}=\mathbf{L}\left[u\right]$ for a real u.

3. For any $n<\omega$, let $D_{1n}$ be the set of all reals (here subsets of $\omega =\{0,1,2,\dots \}$), definable by a type-theoretic parameter-free formula whose quantifiers have types bounded by n from above. In particular, $D_{10}$= arithmetically definable reals and $D_{11}$= analytically definable reals. Alfred Tarski asked in [6] whether it is true that for a given $n\ge 1$, the set $D_{1n}$ belongs to $D_{2n}$, that is, is itself definable by a type-theoretic parameter-free formula whose quantifiers have types bounded by n. The axiom of constructibility $\mathbf{V}=\mathbf{L}$ implies that $D_{1n}\notin D_{2n}$, so the problem is to find a generic model in which $D_{1n}\in D_{2n}$ holds, and moreso the equality $D_{1n}=\mathbf{L}\cap \mathcal{P}\left(\omega \right)$ holds. We believe that such a model can be constructed by an appropriate modification of the methods developed in this paper.

4. It will be interesting to apply the hidden invariance technique to some other forcing notions and coding systems (those not of the almost-disjoint type), such as in [21,22].

5. This is a rather technical question. One may want to consider a smaller extension $\mathbf{L}\left[w^{+}\left[G\right]\right]$ instead of $\mathbf{L}[w^{+}\left[G\right],G\upharpoonright W]$ in Lemma 23. Claim (i) of Lemma 23 then holds for such a smaller model in virtue of the same argument as above. However, the proof of Claim (ii) of Lemma 23, as given above for $\mathbf{L}[w^{+}\left[G\right],G\upharpoonright W]$, does not go through for $\mathbf{L}\left[w^{+}\left[G\right]\right]$. The obstacle is that if we try to carry out the proof of Lemma 24 for $\mathbf{L}\left[w^{+}\left[G\right]\right]$, then it may well happen that say $Z^{\prime }=⌀$, and then Theorem 4 is not applicable. It is an interesting problem to figure out whether in fact Claim (ii) of Lemma 23 holds in $\mathbf{L}\left[w^{+}\left[G\right]\right]$.