Elephant Herding Optimization: Variants, Hybrids, and Applications
Abstract
1. Introduction
2. Historical Development of Elephant Herding Optimization
2.1. Elephant Herding Optimization Research Studies
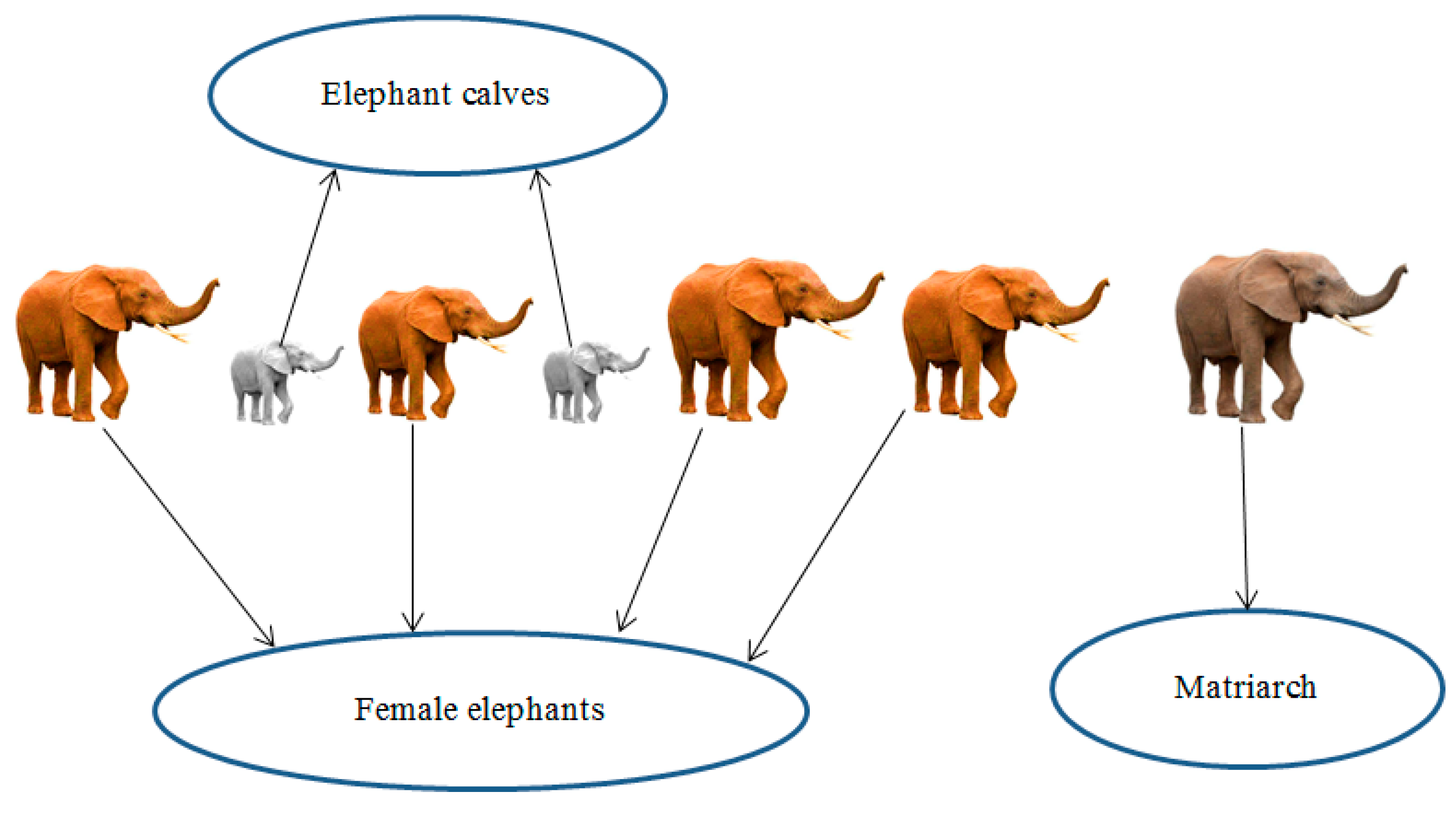
2.2. Basics of Elephant Herding Optimization
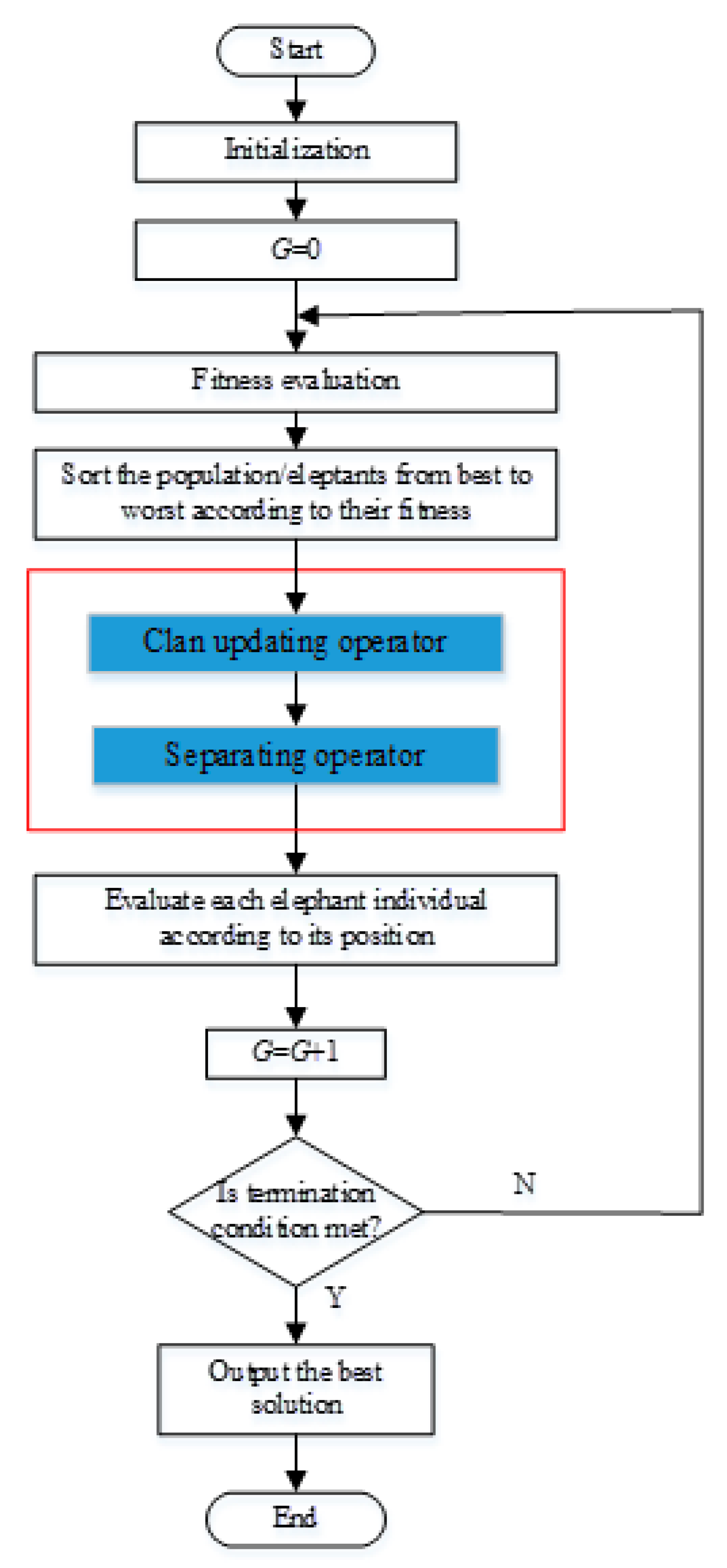
2.2.1. Clan-updating Operator
2.2.2. Separating Operator
| Algorithm 1. Elephant herding optimization |
| (1) Begin |
| (2) Initialization. Set the initialize iterations G = 1; initialize the population P randomly; set maximum generation MaxGen. |
| (3) While stopping criterion is not met do |
| (4) Sort the population according to fitness of individuals. |
| (5) For all clans ci do |
| (6) For elephant j in the clan ci do |
| (7) Generate xnew, ci,j and update xci,j by Equation (1). |
| (8) If xci,j = xbest,ci then |
| (9) Generate xnew, ci,j and update xci,j by Equation (2). |
| (10) End if |
| (11) End for |
| (12) End for |
| (13) For all clans ci do |
| (14) Replace the worst individual ci by Equation (4). |
| (15) End for |
| (16) Evaluate each elephant individual according to its position. |
| (17) T = T + 1. |
| (18) End while |
| (19) End. |
2.2.3. Analysis of Algorithm Complexity
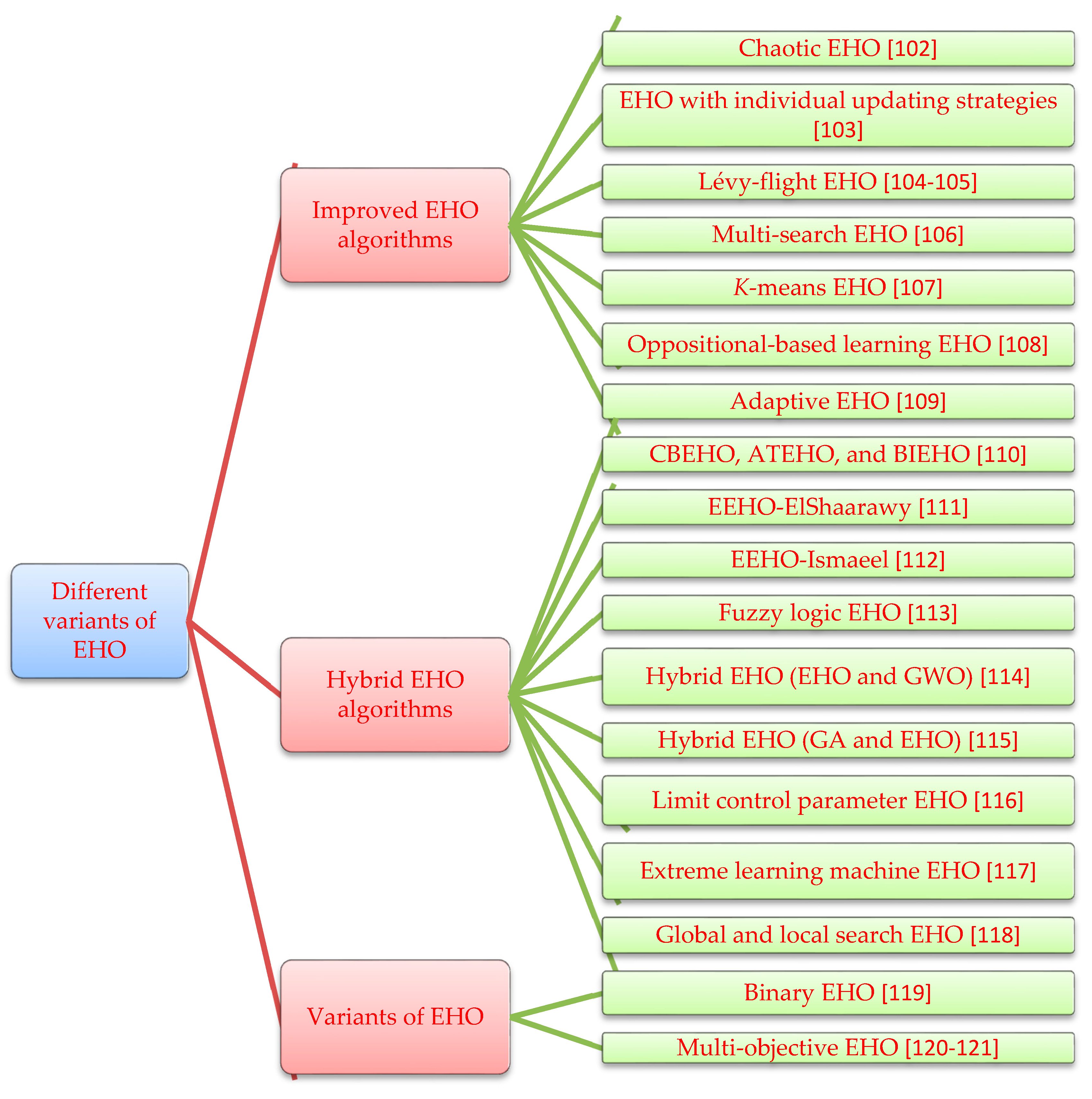
3. Different Variants of EHO
3.1. Improved EHO Algorithms
3.1.1. Chaotic EHO
3.1.2. EHO with Individual Updating Strategies
3.1.3. Lévy Flight EHO
3.1.4. Multi-Search EHO
3.1.5. k-Means EHO
3.1.6. Oppositional-Based Learning EHO
3.1.7. Adaptive Whale EHO
3.2. Hybrid EHO Algorithms
3.2.1. CBEHO, ATEHO, and BIEHO
3.2.2. EEHO-ElShaarawy
3.2.3. EEHO-Ismaeel
3.2.4. FEHO
3.2.5. EHGWO
3.2.6. GEHO
3.2.7. HEHO
3.2.8. ELM-EHO
3.2.9. Global and Local Search EHO
3.3. Variants of EHO
3.3.1. Binary EHO
3.3.2. Multi-Objective EHO
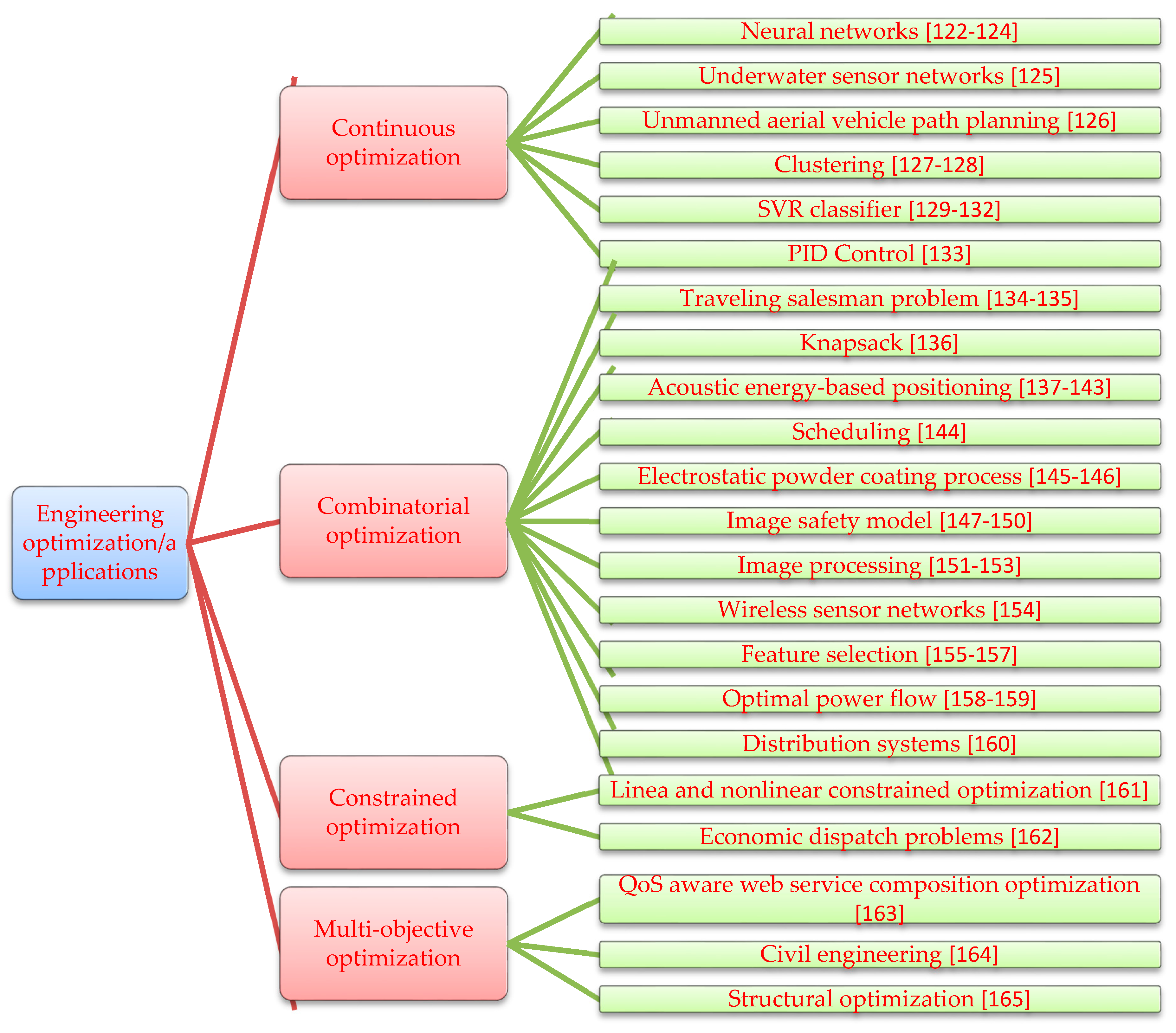
4. Engineering Optimization/Applications
4.1. Continuous Optimization
4.1.1. Neural Networks
4.1.2. Underwater Sensor Networks
4.1.3. Unmanned Aerial Vehicle Path Planning
4.1.4. Clustering
4.1.5. SVR Classifier
4.1.6. PID Control
4.2. Combinatorial Optimization
4.2.1. Traveling Salesman Problem
4.2.2. Knapsack
4.2.3. Acoustic Energy-Based Positioning
4.2.4. Scheduling
4.2.5. Electrostatic Powder Coating Process
4.2.6. Image Safety Model
4.2.7. Image Processing
4.2.8. Wireless Sensor Networks
4.2.9. Feature Selection
4.2.10. Optimal Power Flow
4.2.11. Distribution Systems
4.3. Constrained Optimization
4.3.1. Linear and Nonlinear Constrained Optimization
4.3.2. Economic Dispatch Problems
Economic-Based Dispatch Problem
Stochastic Inequality Constrained Optimization Problems
4.4. Multi-Objective Optimization
4.4.1. QoS Aware Web Service Composition Optimization
4.4.2. Civil Engineering
4.4.3. Structural optimization
5. Conclusions and Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Santucci, V.; Baioletti, M.; Milani, A. An algebraic framework for swarm and evolutionary algorithms in combinatorial optimization. Swarm Evol. Comput. 2020, 55, 100673. [Google Scholar] [CrossRef]
- Wang, G.-G.; Tan, Y. Improving metaheuristic algorithms with information feedback models. IEEE Trans. Cybern. 2019, 49, 542–555. [Google Scholar] [CrossRef] [PubMed]
- Valentino, S.; Alfredo, M.; Fabio, C. An optimisation-driven prediction method for automated diagnosis and prognosis. Mathematics 2019, 7, 1051. [Google Scholar] [CrossRef]
- Alfredo, M.; Valentino, S. Asynchronous differential evolution. IEEE Congr. Evol. Comput. 2010, 7, 18–23. [Google Scholar]
- Sang, H.-Y.; Pan, Q.-K.; Duan, P.-Y.; Li, J.-Q. An effective discrete invasive weed optimization algorithm for lot-streaming flowshop scheduling problems. J. Intell. Manuf. 2015, 29, 1337–1349. [Google Scholar] [CrossRef]
- Sang, H.-Y.; Pan, Q.-K.; Li, J.-Q.; Wang, P.; Han, Y.-Y.; Gao, K.-Z.; Duan, P. Effective invasive weed optimization algorithms for distributed assembly permutation flowshop problem with total flowtime criterion. Swarm Evol. Comput. 2019, 44, 64–73. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Sang, H.-Y.; Duan, J.-H.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl.-Based Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Gao, D.; Wang, G.-G.; Pedrycz, W. Solving fuzzy job-shop scheduling problem using de algorithm improved by a selection mechanism. IEEE Trans. Fuzzy Syst. 2020. [Google Scholar] [CrossRef]
- Santucci, V.; Baioletti, M.; Milani, A. Algebraic differential evolution algorithm for the permutation flowshop scheduling problem with total flowtime criterion. IEEE Trans. Evolut. Comput. 2016, 20, 682–694. [Google Scholar] [CrossRef]
- Li, M.; Xiao, D.; Zhang, Y.; Nan, H. Reversible data hiding in encrypted images using cross division and additive homomorphism. Signal Process. Image Commun. 2015, 39, 234–248. [Google Scholar] [CrossRef]
- Li, M.; Guo, Y.; Huang, J.; Li, Y. Cryptanalysis of a chaotic image encryption scheme based on permutation-diffusion structure. Signal Process. Image Commun. 2018, 62, 164–172. [Google Scholar] [CrossRef]
- Fan, H.; Li, M.; Liu, D.; Zhang, E. Cryptanalysis of a colour image encryption using chaotic apfm nonlinear adaptive filter. Signal Process. 2018, 143, 28–41. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.; Hu, Y.; Zhang, W. Feature selection algorithm based on bare bones particle swarm optimization. Neurocomputing 2015, 148, 150–157. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, X.-F.; Gong, D.-W. A return-cost-based binary firefly algorithm for feature selection. Inf. Sci. 2017, 418–419, 561–574. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Tang, J.; Li, Y. Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Jian, M.; Lam, K.-M.; Dong, J. Facial-feature detection and localization based on a hierarchical scheme. Inf. Sci. 2014, 262, 1–14. [Google Scholar] [CrossRef]
- Fan, L.; Xu, S.; Liu, D.; Ru, Y. Semi-supervised community detection based on distance dynamics. IEEE Access 2018, 6, 37261–37271. [Google Scholar] [CrossRef]
- Wang, G.-G.; Chu, H.E.; Mirjalili, S. Three-dimensional path planning for ucav using an improved bat algorithm. Aerosp. Sci. Technol. 2016, 49, 231–238. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H.; Shao, M. Path planning for uninhabited combat aerial vehicle using hybrid meta-heuristic de/bbo algorithm. Adv. Sci. Eng. Med. 2012, 4, 550–564. [Google Scholar] [CrossRef]
- Wang, G.-G.; Cai, X.; Cui, Z.; Min, G.; Chen, J. High performance computing for cyber physical social systems by using evolutionary multi-objective optimization algorithm. IEEE Trans. Emerg. Top. Comput. 2017. [Google Scholar] [CrossRef]
- Cui, Z.; Sun, B.; Wang, G.-G.; Xue, Y.; Chen, J. A novel oriented cuckoo search algorithm to improve dv-hop performance for cyber-physical systems. J. Parallel Distrib. Comput. 2017, 103, 42–52. [Google Scholar] [CrossRef]
- Jian, M.; Lam, K.-M.; Dong, J. Illumination-insensitive texture discrimination based on illumination compensation and enhancement. Inf. Sci. 2014, 269, 60–72. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. The model and algorithm for the target threat assessment based on elman_adaboost strong predictor. Acta Electron. Sin. 2012, 40, 901–906. [Google Scholar]
- Jian, M.; Lam, K.M.; Dong, J.; Shen, L. Visual-patch-attention-aware saliency detection. IEEE Trans. Cybern. 2015, 45, 1575–1586. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.-G.; Lu, M.; Dong, Y.-Q.; Zhao, X.-J. Self-adaptive extreme learning machine. Neural Comput. Appl. 2016, 27, 291–303. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.-X.; Tian, S.-S.; Xia, J.-L. An improved cuckoo search algorithm with self-adaptive knowledge learning. Neural Comput. Appl. 2019. [Google Scholar] [CrossRef]
- Liu, G.; Zou, J. Level set evolution with sparsity constraint for object extraction. IET Image Process. 2018, 12, 1413–1422. [Google Scholar] [CrossRef]
- Liu, K.; Gong, D.; Meng, F.; Chen, H.; Wang, G.-G. Gesture segmentation based on a two-phase estimation of distribution algorithm. Inf. Sci. 2017, 394–395, 88–105. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; El-Sehiemy, R.A.; Wang, G.-G. A novel parallel hurricane optimization algorithm for secure emission/economic load dispatch solution. Appl. Soft Comput. 2018, 63, 206–222. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; El-Sehiemy, R.A.; Deb, S.; Wang, G.-G. A novel fruit fly framework for multi-objective shape design of tubular linear synchronous motor. J. Supercomput. 2017, 73, 1235–1256. [Google Scholar] [CrossRef]
- Yi, J.-H.; Deb, S.; Dong, J.; Alavi, A.H.; Wang, G.-G. An improved nsga-iii algorithm with adaptive mutation operator for big data optimization problems. Future Gener. Comput. Syst. 2018, 88, 571–585. [Google Scholar] [CrossRef]
- Liu, G.; Deng, M. Parametric active contour based on sparse decomposition for multi-objects extraction. Signal Process. 2018, 148, 314–321. [Google Scholar] [CrossRef]
- Sun, J.; Miao, Z.; Gong, D.; Zeng, X.-J.; Li, J.; Wang, G.-G. Interval multi-objective optimization with memetic algorithms. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.-G.; Li, K.; Yeh, W.-C.; Jian, M.; Dong, J. Enhancing moea/d with information feedback models for large-scale many-objective optimization. Inf. Sci. 2020, 522, 1–16. [Google Scholar] [CrossRef]
- Gu, Z.-M.; Wang, G.-G. Improving NSGA-III algorithms with information feedback models for large-scale many-objective optimization. Future Gener. Comput. Syst. 2020, 107, 49–69. [Google Scholar] [CrossRef]
- Srikanth, K.; Panwar, L.K.; Panigrahi, B.K.; Herrera-Viedma, E.; Sangaiah, A.K.; Wang, G.-G. Meta-heuristic framework: Quantum inspired binary grey wolf optimizer for unit commitment problem. Comput. Electr. Eng. 2018, 70, 243–260. [Google Scholar] [CrossRef]
- Li, J.; Xiao, D.-D.; Lei, H.; Zhang, T.; Tian, T. Using cuckoo search algorithm with q-learning and genetic operation to solve the problem of logistics distribution center location. Mathematics (Basel) 2020, 8, 149. [Google Scholar] [CrossRef]
- Chen, S.; Chen, R.; Wang, G.-G.; Gao, J.; Sangaiah, A.K. An adaptive large neighborhood search heuristic for dynamic vehicle routing problems. Comput. Electr. Eng. 2018. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G. Binary moth search algorithm for discounted {0–1} knapsack problem. IEEE Access 2018, 6, 10708–10719. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G.; Wang, L. Solving randomized time-varying knapsack problems by a novel global firefly algorithm. Eng. Comput. 2018, 34, 621–635. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: New York, NY, USA, 1998. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Perth, Australia, 1995; pp. 1942–1948. [Google Scholar]
- Wang, G.-G.; Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. A novel improved accelerated particle swarm optimization algorithm for global numerical optimization. Eng. Comput. 2014, 31, 1198–1220. [Google Scholar] [CrossRef]
- Sun, J.; Feng, B.; Xu, W. Particle Swarm Optimization with Particles Having Quantum Behavior. In Proceedings of the Congress on Evolutionary Computation (CEC 2004), Portland, OR, USA, 19–23 June 2004; IEEE: Portland, OR, USA, 2004; pp. 325–331. [Google Scholar]
- Adewumi, A.O.; Arasomwan, M.A. On the performance of particle swarm optimisation with(out) some control parameters for global optimisation. Int. J. Bio-Inspir. Com. 2016, 8, 14–32. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Xu, Z.; Unveren, A.; Acan, A. Probability collectives hybridised with differential evolution for global optimisation. Int. J. Bio-Inspir. Com. 2016, 8, 133–153. [Google Scholar] [CrossRef]
- Wang, G.-G.; Zhao, X.; Deb, S. A Novel Monarch Butterfly Optimization with Greedy Strategy and Self-Adaptive Crossover Operator. In Proceedings of the 2015 IEEE 2nd Intl, Conference on Soft Computing & Machine Intelligence (ISCMI 2015), Hong Kong, China, 23–24 November 2015; pp. 45–50. [Google Scholar]
- Wang, G.-G.; Deb, S.; Zhao, X.; Cui, Z. A new monarch butterfly optimization with an improved crossover operator. Oper. Res. Int. J. 2018, 18, 731–755. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G.; Li, W.; Li, N. Multi-strategy monarch butterfly optimization algorithm for discounted {0–1} knapsack problem. Neural Comput. Appl. 2018, 30, 3019–3036. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G.; Deb, S.; Lu, M.; Zhao, X. Solving 0–1 knapsack problem by a novel binary monarch butterfly optimization. Neural Comput. Appl. 2017, 28, 1619–1634. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (abc) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Coelho, L.D.S. Earthworm optimization algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Int. J. Bio.-Inspir. Com. 2018, 12, 1–22. [Google Scholar] [CrossRef]
- Dorigo, M.; Stutzle, T. Ant Colony Optimization; MIT Press: Cambridge, UK, 2004. [Google Scholar]
- Li, J.; Xiao, D.-D.; Zhang, T.; Liu, C.; Li, Y.-X. Multi-swarm cuckoo search algorithm with q-learning model. Comput. J. 2020. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC 2009), Coimbatore, India, 9–11 December 2009; Abraham, A., Carvalho, A., Herrera, F., Pai, V., Eds.; IEEE Publications: Coimbatore, India, 2009; pp. 210–214. [Google Scholar]
- Li, X.; Wang, J.; Yin, M. Enhancing the performance of cuckoo search algorithm using orthogonal learning method. Neural Comput. Appl. 2013, 24, 1233–1247. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Modified cuckoo search algorithm with self adaptive parameter method. Inf. Sci. 2015, 298, 80–97. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Zhao, X.; Chu, H.E. Hybridizing harmony search algorithm with cuckoo search for global numerical optimization. Soft Comput. 2016, 20, 273–285. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Gandomi, A.H.; Zhang, Z.; Alavi, A.H. Chaotic cuckoo search. Soft Comput. 2016, 20, 3349–3362. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H.; Wang, J. A hybrid meta-heuristic de/cs algorithm for ucav path planning. J. Inform. Comput. Sci. 2012, 9, 4811–4818. [Google Scholar]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Yi, J.-H.; Wang, G.-G. A new swarm intelligence approach for clustering based on krill herd with elitism strategy. Algorithms 2015, 8, 951–964. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H.; Deb, S. A multi-stage krill herd algorithm for global numerical optimization. Int. J. Artif. Intell. Tools 2016, 25, 1550030. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H.; Gong, D. A comprehensive review of krill herd algorithm: Variants, hybrids and applications. Artif. Intell. Rev. 2019, 51, 119–148. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Mixed variable structural optimization using firefly algorithm. Comput. Struct. 2011, 89, 2325–2336. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspir. Com. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.; Duan, H.; Wang, H. A new improved firefly algorithm for global numerical optimization. J. Comput. Theor. Nanosci. 2014, 11, 477–485. [Google Scholar] [CrossRef]
- Gálvez, A.; Iglesias, A. New memetic self-adaptive firefly algorithm for continuous optimisation. Int. J. Bio-Inspir. Com. 2016, 8, 300–317. [Google Scholar] [CrossRef]
- Nasiri, B.; Meybodi, M.R. History-driven firefly algorithm for optimisation in dynamic and uncertain environments. Int. J. Bio.-Inspir. Com. 2016, 8, 326–339. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. A modified firefly algorithm for ucav path planning. Int. J. Hybrid Inf. Technol. 2012, 5, 123–144. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Shah-Hosseini, H. The intelligent water drops algorithm: A nature-inspired swarm-based optimization algorithm. Int. J. Bio-Inspir. Com. 2009, 1, 71–79. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Wang, G.-G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018, 10, 151–164. [Google Scholar] [CrossRef]
- Zhao, R.; Tang, W. Monkey algorithm for global numerical optimization. J. Uncertain Syst. 2008, 2, 165–176. [Google Scholar]
- Beyer, H. The Theory of Evolution Strategies; Springer: New York, NY, USA, 2001. [Google Scholar]
- Penev, K.; Littlefair, G. Free search-a comparative analysis. Inf. Sci. 2005, 172, 173–193. [Google Scholar] [CrossRef]
- Baluja, S. Population-Based Incremental Learning: A Method for Integrating Genetic Search Based Function Optimization and Competitive Learning; CMU-CS-94-163; Carnegie Mellon University: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Let a biogeography-based optimizer train your multi-layer perceptron. Inf. Sci. 2014, 269, 188–209. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, W.; Wang, G.; Feng, X. Test-sheet composition using analytic hierarchy process and hybrid metaheuristic algorithm ts/bbo. Math. Probl. Eng. 2012, 2012, 1–22. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. Dynamic deployment of wireless sensor networks by biogeography based optimization algorithm. J. Sens. Actuator Netw. 2012, 1, 86–96. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Gandomi, A.H. Interior search algorithm (ISA): A novel approach for global optimization. ISA Trans. 2014, 53, 1168–1183. [Google Scholar] [CrossRef]
- Shi, Y. An optimization algorithm based on brainstorming process. Int. J. Swarm Intell. Res. 2011, 2, 35–62. [Google Scholar] [CrossRef]
- Shi, Y.; Xue, J.; Wu, Y. Multi-objective optimization based on brain storm optimization algorithm. Int. J. Swarm Intell. Res. 2013, 4, 1–21. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H.; Talatahari, S. Bat algorithm for constrained optimization tasks. Neural Comput. Appl. 2013, 22, 1239–1255. [Google Scholar] [CrossRef]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.-S. Binary bat algorithm. Neural Comput. Appl. 2013, 25, 663–681. [Google Scholar] [CrossRef]
- Cai, X.; Gao, X.-Z.; Xue, Y. Improved bat algorithm with optimal forage strategy and random disturbance strategy. Int. J. Bio-Inspir. Com. 2016, 8, 205–214. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L. A novel hybrid bat algorithm with harmony search for global numerical optimization. J. Appl. Math. 2013, 2013, 1–21. [Google Scholar] [CrossRef]
- Wang, G.-G.; Chang, B.; Zhang, Z. A Multi-Swarm Bat Algorithm for Global Optimization. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC 2015), Sendai, Japan, 25–28 May 2015; IEEE: Sendai, Japan, 2015; pp. 480–485. [Google Scholar]
- Wang, G.-G.; Lu, M.; Zhao, X.-J. An improved bat algorithm with variable neighborhood search for global optimization. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (IEEE CEC 2016), Vancouver, BC, Canada, 24–29 July 2016; pp. 1773–1778. [Google Scholar]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms, 2nd ed.; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Khatib, W.; Fleming, P. The stud ga: A mini revolution? In Parallel Problem Solving from Nature-ppsn v; Eiben, A., Bäck, T., Schoenauer, M., Schwefel, H.-P., Eds.; Springer: Berlin/Heidelberg, Germany; London, UK, 1998; Volume 1498, pp. 683–691. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Wang, H.; Liu, L.; Shao, M. Hybridizing harmony search with biogeography based optimization for global numerical optimization. J. Comput. Theor. Nanosci. 2013, 10, 2318–2328. [Google Scholar] [CrossRef]
- Niknam, T.; Fard, A.K. Optimal energy management of smart renewable micro-grids in the reconfigurable systems using adaptive harmony search algorithm. Int. J. Bio-Inspir. Com. 2016, 8, 184–194. [Google Scholar] [CrossRef]
- Rezoug, A.; Boughaci, D. A self-adaptive harmony search combined with a stochastic local search for the 0–1 multidimensional knapsack problem. Int. J. Bio-Inspir. Com. 2016, 8, 234–239. [Google Scholar] [CrossRef]
- Tan, Y. Fireworks Algorithm-A Novel Swarm Intelligence Optimization Method; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A new bio-inspired algorithm: Chicken swarm optimization. In Proceedings of the Advances in Swarm Intelligence (ICSI 2014), Hefei, China, 17–20 October 2014; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8794, pp. 86–94. [Google Scholar]
- Wang, G.-G.; Deb, S.; Coelho, L.d.S. Elephant Herding Optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI 2015), Bali, Indonesia, 7–9 December 2015; IEEE: Bali, Indonesia, 2015; pp. 1–5. [Google Scholar]
- Tuba, E.; Capor-Hrosik, R.; Alihodzic, A.; Jovanovic, R.; Tuba, M. Chaotic Elephant Herding Optimization Algorithm. In Proceedings of the 2018 IEEE 16th World Symposium on Applied Machine Intelligence and Informatics (SAMI 2018), Kosice and Herlany, Slovakia, 7–10 February 2018; IEEE: Kosice and Herlany, Slovakia, 2018; pp. 213–216. [Google Scholar]
- Li, J.; Guo, L.; Li, Y.; Liu, C. Enhancing elephant herding optimization with novel individual updating strategies for large-scale optimization problems. Mathematics 2019, 7, 395. [Google Scholar] [CrossRef]
- Xu, H.; Cao, Q.; Fang, C.; Fu, Y.; Su, J.; Wei, S.; Bykovyy, P. Application of Elephant Herd Optimization Algorithm Based on Levy Flight Strategy in Intrusion Detection. In Proceedings of the 2018 IEEE 4th International Symposium on Wireless Systems within the International Conferences on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS-SWS), Lviv, Ukraine, 20–21 September 2018; IEEE: Lviv, Ukraine, 2018; pp. 16–20. [Google Scholar]
- Xu, H.; Cao, Q.; Fu, H.; Fu, C.; Chen, H.; Su, J. Application of Support Vector Machine Model Based on an Improved Elephant Herding Optimization Algorithm in Network Intrusion Detection; Springer: Singapore, 2019; pp. 283–295. [Google Scholar]
- Hakli, H. Elephant herding optimization using multi-search strategy for continuous optimization problems. Acad. Platf. J. Eng. Sci. 2019, 7, 261–268. [Google Scholar] [CrossRef]
- Tuba, E.; Dolicanin-Djekic, D.; Jovanovic, R.; Simian, D.; Tuba, M. Combined Elephant Herding Optimization Algorithm with k-Means for Data Clustering; Springer: Singapore, 2019; pp. 665–673. [Google Scholar]
- Chakraborty, F.; Roy, P.K.; Nandi, D. Oppositional elephant herding optimization with dynamic cauchy mutation for multilevel image thresholding. Evol. Intell. 2019, 12, 445–467. [Google Scholar] [CrossRef]
- Chowdary, K.U.; Prabhakara Rao, B. Performance improvement in mimo-ofdm systems based on adaptive whale elephant herd optimization algorithm. Int. J. Eng. Adv. Technol. 2019, 9, 6651–6657. [Google Scholar]
- Rashwan, Y.I.; Elhosseini, M.A.; El Sehiemy, R.A.; Gao, X.Z. On the performance improvement of elephant herding optimization algorithm. Knowl.-Based Syst. 2019, 166, 58–70. [Google Scholar]
- ElShaarawy, I.A.; Houssein, E.H.; Ismail, F.H.; Hassanien, A.E. An exploration-enhanced elephant herding optimization. Eng Comput. 2019, 36, 3029–3046. [Google Scholar] [CrossRef]
- Ismaeel, A.A.K.; Elshaarawy, I.A.; Houssein, E.H.; Ismail, F.H.; Hassanien, A.E. Enhanced elephant herding optimization for global optimization. IEEE Access 2019, 7, 34738–34752. [Google Scholar] [CrossRef]
- Veera manikandan, P.; Selvaperumal, S. A fuzzy-elephant herding optimization technique for maximum power point tracking in the hybrid wind-solar system. Int. Trans. Electr. Energy Syst. 2019. [Google Scholar] [CrossRef]
- Arora, P.; Dixit, A. The hybrid optimization algorithm for load balancing in cloud. Int. J. Eng. Adv. Technol. 2019, 8, 67–71. [Google Scholar]
- Bukhsh, R.; Javaid, N.; Iqbal, Z.; Ahmed, U.; Ahmad, Z.; Iqbal, M.N. Appliances Scheduling Using Hybrid Scheme of Genetic Algorithm and Elephant Herd Optimization for Residential Demand Response. In Proceedings of the 2018 32nd International Conference on Advanced Information Networking and Applications Workshops (WAINA 2018), Krakow, Poland, 16–18 May 2018; IEEE: Krakow, Poland, 2018; pp. 210–217. [Google Scholar]
- Strumberger, I.; Minovic, M.; Tuba, M.; Bacanin, N. Performance of elephant herding optimization and tree growth algorithm adapted for node localization in wireless sensor networks. Sensors 2019, 19, 2515. [Google Scholar] [CrossRef]
- Satapathy, P.; Pradhan, S.K.; Hota, S. Development of a novel neural network model for brain image classification. Int. J. Recent Technol. Eng. 2019, 8, 7230–7235. [Google Scholar]
- Hakli, H. A novel approach based on elephant herding optimization for constrained optimization problems. Selçuk Üniversitesi Mühendislik Bilim ve Teknoloji Dergisi 2019, 7, 405–419. [Google Scholar] [CrossRef]
- Hakli, H. Bineho: A new binary variant based on elephant herding optimization algorithm. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Jaiprakash, K.P.; Nanda, S.J. Classifying Physical Actions of Human Models Using Multi-Objective Clustering Based on Elephant Herding Algorithm. In Proceedings of the 1st International Conference on Pervasive Computing Advances and Applications (PerCAA 2019), Jaipur, India, 8–10 January 2019; Bundele, M., Dey, N., Madria, S.K., Eds.; Elsevier B.V.: Jaipur, India, 2019; pp. 84–91. [Google Scholar]
- Meena, N.K.; Parashar, S.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Improved elephant herding optimization for multiobjective der accommodation in distribution systems. IEEE Trans. Ind. Inform. 2018, 14, 1029–1039. [Google Scholar] [CrossRef]
- Moayedi, H.; Mu′azu, M.A.; Foong, L.K. Novel swarm-based approach for predicting the cooling load of residential buildings based on social behavior of elephant herds. Energy Build. 2020, 206, 109579. [Google Scholar] [CrossRef]
- Kowsalya, S.; Periasamy, P.S. Recognition of tamil handwritten character using modified neural network with aid of elephant herding optimization. Multimed Tools Appl. 2019, 78, 25043–25061. [Google Scholar] [CrossRef]
- Sahlol, A.T.; Ismail, F.H.; Abdeldaim, A.; Hassanien, A.E. Elephant Herd Optimization with Neural Networks: A Case Study on Acute Lymphoblastic Leukemia Diagnosis. In Proceedings of the 2017 12th International Conference on Computer Engineering and Systems (ICCES 2017), Cairo, Egypt, 19–20 December 2017; IEEE: Cairo, Egypt, 2017; pp. 657–662. [Google Scholar]
- Kaur, S. Energy optimization for underwater sensor network using nature inspired technique. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 161–164. [Google Scholar]
- Alihodzic, A.; Tuba, E.; Capor-Hrosik, R.; Dolicanin, E.; Tuba, M. Unmanned Aerial Vehicle Path Planning Problem by Adjusted Elephant Herding Optimization. In Proceedings of the 2017 25th Telecommunication Forum (TELFOR), Belgrade, Serbia, 21–22 November 2017; IEEE: Belgrade, Serbia, 2017; pp. 1–4. [Google Scholar]
- Rani, R.R.; Ramyachitra, D.; Brindhadevi, A. Detection of dynamic protein complexes through markov clustering based on elephant herd optimization approach. Sci. Rep. 2019, 9, 11106. [Google Scholar] [CrossRef]
- Jaiprakash, K.P.; Nanda, S.J. Elephant Herding Algorithm for Clustering; Springer: Singapore, 2019; pp. 317–325. [Google Scholar]
- Hassanien, A.E.; Kilany, M.; Houssein, E.H.; AlQaheri, H. Intelligent human emotion recognition based on elephant herding optimization tuned support vector regression. Biomed. Signal Process. Control 2018, 45, 182–191. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Kilany, M.; Houssein, E.H. Combining support vector machine and elephant herding optimization for cardiac arrhythmias. arXiv 2018, arXiv:1806.08242. [Google Scholar]
- Tuba, E.; Stanimirovic, Z. Elephant Herding Optimization Algorithm for Support Vector Machine Parameters Tuning. In Proceedings of the IEEE International Conference on Electronics, Computers and Artificial Intelligence (ECAI 2017), Targoviste, Romania, 29 June–1 July 2017; pp. 1–4. [Google Scholar]
- Tuba, E.; Ribic, I.; Capor-Hrosik, R.; Tuba, M. Support vector machine optimized by elephant herding algorithm for erythemato-squamous diseases detection. Procedia Comput. Sci. 2017, 122, 916–923. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Fagna, R. A Novel Elephant Herding Optimization Based pid Controller Design for Load Frequency Control in Power System. In Proceedings of the 2017 International Conference on Computer, Communications and Electronics (Comptelix), Jaipur, India, 1–2 July 2017; IEEE: Jaipur, India, 2017; pp. 595–600. [Google Scholar]
- Almufti, S.; Boya Marqas, R.; Asaad, R.R. Comparative study between elephant herding optimization (eho) and u-turning ant colony optimization (u-taco) in solving symmetric traveling salesman problem (stsp). J. Adv. Comput. Sci. Technol. 2019, 8. [Google Scholar] [CrossRef]
- Darmawan, H.; Rini, D.P.; Arsalan, O. Penerapan Algoritma Elephant Herding Optimization pada Permasalahan Knapsack 0-1. Undergraduate thesis, Sriwijaya University, Kota Palembang, Sumatera Selatan, 2019. Undergraduate Thesis, Sriwijaya University, Kota Palembang, Sumatera Selatan, 2019. [Google Scholar]
- Correia, S.D.; Beko, M.; Cruz, L.A.D.S.; Tomic, S. Implementation and Validation of Elephant Herding Optimization Algorithm for Acoustic Localization. In Proceedings of the 2018 26th Telecommunications Forum (TELFOR), Belgrade, Serbia, 20–21 November 2018; IEEE: Belgrade, Serbia, 2018; pp. 1–4. [Google Scholar]
- Parashar, S.; Swarnkar, A.; Niazi, K.R.; Gupta, N. Stochastic operational management of grid-connected microgrid under uncertainty of renewable resources and load demand. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2020; Volume 607, pp. 573–581. [Google Scholar]
- Cahig, C.; Villanueva, J.J.; Bersano, R.; Pacis, M. Optimal Virtual Power Plant Scheduling Using Elephant Herding Optimization. In Proceedings of the 10th IEEE International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management, HNICEM 2018, Baguio City, Philippines, 29 November–2 December 2018; IEEE: Baguio City, Philippines, 2019. [Google Scholar]
- Sarwar, M.A.; Amin, B.; Ayub, N.; Faraz, S.H.; Khan, S.U.R.; Javaid, N. Scheduling of appliances in home energy management system using elephant herding optimization and enhanced differential evolution. In Advances in Intelligent Networking and Collaborative Systems, Proceedings of the 9th International Conference on Intelligent Networking and Collaborative Systems (INCoS 2017), Ryerson Univ, Toronto, ON, Canada, 24–26 August 2017; Springer: Berlin, Germany, 2017; pp. 132–142. [Google Scholar]
- Parvez, K.; Aslam, S.; Saba, A.; Aimal, S.; Amjad, Z.; Asif, S.; Javaid, N. Scheduling of appliances in hems using elephant herding optimization and harmony search algorithm. In Advances on Broad-Band Wireless Computing, Communication and Applications, Proceedings of the 12th International Conference on Broad-Band Wireless Computing, Communication and Applications (BWCCA 2017), Barcelona, Spain, 8–10 November 2017; Springer: Berlin, Germany, 2017; pp. 62–72. [Google Scholar]
- Mohsin, S.M.; Javaid, N.; Madani, S.A.; Akber, S.M.A.; Manzoor, S.; Ahmad, J. Implementing Elephant Herding Optimization Algorithm with Different Operation Time Intervals for Appliance Scheduling in Smart Grid. In Proceedings of the 2018 32nd International Conference on Advanced Information Networking and Applications Workshops (WAINA), Krakow, Poland, 16–18 May 2018; IEEE: Krakow, Poland, 2018; pp. 240–249. [Google Scholar]
- Gholami, H.R.; Mehdizadeh, E.; Naderi, B. Mathematical models and an elephant herding optimization for multiprocessor-task flexible flow shop scheduling problems in the manufacturing resource planning (mrpii) system. Scientia Iranica 2018. [Google Scholar] [CrossRef]
- Fatima, I.; Asif, S.; Shafiq, S.; Fatima, I.; Rahim, M.H.; Javaid, N. Efficient Demand Side Management Using Hybridization of Elephant Herding Optimization and Firefly Optimization. In Proceedings of the 2018 IEEE 32nd International Conference on Advanced Information Networking and Applications (AINA), Krakow, Poland, 16–18 May 2018; IEEE: Krakow, Poland, 2018; pp. 839–845. [Google Scholar]
- Luangpaiboon, P. Variable tuning for electrostatic powder coating process via elephant herding optimisation algorithm on modified simplex method. Int. J. Mech. Eng. Robot. Res. 2019, 8, 807–812. [Google Scholar] [CrossRef]
- Shankar, K.; Elhoseny, M.; Perumal, E.; Ilayaraja, M.; Sathesh Kumar, K. An efficient image encryption scheme based on signcryption technique with adaptive elephant herding optimization. In Cybersecurity and Secure Information Systems: Challenges and Solutions in Smart Environments; Springer: Cham, Switzerland, 20 June 2019; pp. 31–42. [Google Scholar]
- Chibani, S.S.; Tari, A. Elephant herding optimization for service selection in qos-aware web service composition. Int. J. Comput. Electr. Autom. Control Inf. Eng. 2017, 11, 1045–1049. [Google Scholar]
- Tuba, E.; Alihodzic, A.; Tuba, M. Multilevel Image Thresholding Using Elephant Herding Optimization Algorithm. In Proceedings of the 2017 14th International Conference on Engineering of Modern Electric Systems (EMES), Oradea, Romania, 1–2 June 2017; IEEE: Oradea, Romania, 2017; pp. 240–243. [Google Scholar]
- Jino Ramson, S.R.; Lova Raju, K.; Vishnu, S.; Anagnostopoulos, T. Nature inspired optimization techniques for image processing-a short review. In Nature Inspired Optimization Techniques for Image Processing Applications; Springer: Cham, Switzerland, 20 September 2018; Volume 150, pp. 113–145. [Google Scholar]
- Jayanth, J.; Shalini, V.S.; Ashok Kumar, T.; Koliwad, S. Land-use/land-cover classification using elephant herding algorithm. J. Indian Soc. Remote 2019, 47, 223–232. [Google Scholar] [CrossRef]
- De Vasconcelos Cardoso, A.; Nedjah, N.; De Macedo Mourelle, L.; Tavares, Y.M. Co-Design System for Template Matching Using Dedicated co-Processor and Modified Elephant Herding Optimization. In Proceedings of the 2018 IEEE 9th Latin American Symposium on Circuits and Systems (LASCAS 2018), Puerto Vallarta, Mexico, 25–28 February 2018; pp. 1–4. [Google Scholar]
- Correia, S.; Beko, M.; Cruz, L.; Tomic, S. Elephant herding optimization for energy-based localization. Sensors 2018, 18, 2849. [Google Scholar] [CrossRef]
- Strumberger, I.; Beko, M.; Tuba, M.; Minovic, M.; Bacanin, N. Elephant Herding Optimization Algorithm for Wireless Sensor Network Localization Problem. In Proceedings of the Technological Innovation for Resilient Systems: 9th IFIP WG 5.5/SOCOLNET Advanced Doctoral Conference on Computing, Electrical and Industrial Systems (DoCEIS 2018), Costa de Caparica, Portugal, 2–4 May 2018; pp. 175–184. [Google Scholar]
- Kaur, K.; Randhawa, R. Energy efficient approach for underwater sensor network using elephant herd optimization. Res. Cell Int. J. Eng. Sci. 2018, 30, 148–160. [Google Scholar]
- Xu, H.; Cao, Q.; Fu, H.; Chen, H. Applying an improved elephant herding optimization algorithm with spark-based parallelization to feature selection for intrusion detection. Int. J. Perform. Eng. 2019, 15, 1600–1610. [Google Scholar] [CrossRef]
- Dhillon, S.S.; Agarwal, S.; Wang, G.-G.; Lather, J.S. Automatic generation control of interconnected power systems using elephant herding optimization. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2020; pp. 9–18. [Google Scholar]
- Kuchibhatla, S.M.; Padmavathi, D.; Rao, R.S. An elephant herding optimization algorithm-based static switched filter compensation scheme for power quality improvement in smart grid. J. Circuits Syst. Comput. 2019. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Fagna, R. A Robust Pid Controller for Load Frequency Control of Single Area re-heat Thermal Power Plant Using Elephant Herding Optimization Techniques. In Proceedings of the 2017 IEEE International Conference on Information, Communication, Instrumentation and Control, ICICIC 2017, Indore, India, 17–19 August 2017; pp. 1–6. [Google Scholar]
- Prasad, C.H.; Subbaramaiah, K.; Sujatha, P. Cost–benefit analysis for optimal dg placement in distribution systems by using elephant herding optimization algorithm. Renew. Wind Water Sol. 2019, 6. [Google Scholar] [CrossRef]
- Vijay, R.; Abhilash, M. Elephant herding optimization for optimum allocation of electrical distributed generation on distributed power networks. Asian J. Electr. Sci. 2018, 7, 70–76. [Google Scholar]
- Strumberger, I.; Bacanin, N.; Tuba, M. Hybridized Elephant Herding Optimization Algorithm for Constrained Optimization. In Proceedings of the 17th International Conference on Hybrid Intelligent Systems (HIS 2017), Delhi, India, 14–16 December 2017; Springer International Publishing: Delhi, India, 2017; pp. 158–166. [Google Scholar]
- Singh, N.; Kumar, M.P.; Kumar, B.S. Effect of valve loading on the thermal power economic load dispatch using new elephant herding optimization. Int. J. Recent Technol. Eng. 2019, 7, 345–349. [Google Scholar]
- Horng, S.-C.; Lin, S.-S. Coupling elephant herding with ordinal optimization for solving the stochastic inequality constrained optimization problems. Appl. Sci. 2020, 10, 2075. [Google Scholar] [CrossRef]
- Sadouki, S.C.; Tari, A. Multi-objective and discrete elephants herding optimization algorithm for qos aware web service composition. RAIRO-Oper. Res. 2019, 53, 445–459. [Google Scholar] [CrossRef]
- Adarsha, B.S.; Harish, N.; Janardhan, P.; Mandal, S. Elephant Herding Optimization Based Neural Network to Predict Elastic Modulus of Concrete; Soft Computing for Problem Solving; Das, K.N., Bansal, J.C., Deep, K., Nagar, A.K., Pathipooranam, P., Naidu, R.C., Eds.; Springer: Singapore, 2020; pp. 353–364. [Google Scholar]
- Jafari, M.; Salajegheh, E.; Salajegheh, J. An efficient hybrid of elephant herding optimization and cultural algorithm for optimal design of trusses. Eng. Comput. 2018, 35, 781–801. [Google Scholar] [CrossRef]
- Milani, A.; Santucci, V. Community of scientist optimization: An autonomy oriented approach to distributed optimization. AI Commun. 2012, 25, 16. [Google Scholar] [CrossRef]
| Name | Author | Reference |
|---|---|---|
| Chaotic elephant herding optimization (CEHO) | Tuba et al. | [106] |
| EHO with individual updating strategies | Li et al. | [107] |
| EHO with Lévy flight (LFEHO) | Xu et al. | [108] |
| Improved elephant herding optimization (IEHO) | Xu et al. | [109] |
| Multi-search elephant herding optimization (Multi-EHO) | Hakli et al. | [110] |
| k-means EHO | Tuba et al. | [111] |
| Dynamic Cauchy mutation EHO (EHO-DCM) | Chakraborty et al. | [112] |
| Adaptive whale elephant herding optimization (AWEHO) | Chowdary et al. | [113] |
| Name | Author | Reference |
|---|---|---|
| Cultural-based EHO, alpha-tuning EHO, and biased initialization EHO (CBEHO, ATEHO, and BIEHO) | Rashwan et al. | [114] |
| Enhanced elephant herding optimization (EEHO-ElShaarawy) | ElShaarawy et al. | [115] |
| Enhanced elephant herding optimization (EEHO-Ismaeel) | Ismaeel et al. | [116] |
| Fuzzy elephant herding optimization (FEHO) | Veera et al. | [117] |
| Elephant herding optimization and gray wolf optimization (EHGWO) | Arora et al. | [118] |
| Genetic algorithm and elephant herding optimization (GEHO) | Bukhsh et al. | [119] |
| Hybrid elephant herding optimization (HEHO) | Ivana et al. | [120] |
| Extreme learning machine and elephant herding optimization (ELM-EHO) | Satapathy et al. | [121] |
| Global and local search (GL-EHO) | Hakli et al. | [122] |
| Name | Author | Reference |
|---|---|---|
| Binary EHO algorithm (BinEHO) | Huseyin et al. | [123] |
| Multi-objective clustering EHO algorithm (MOEHO) | Jaiprakash et al. | [124] |
| Improved and multi-objective EHO (IMOEHO) | Meena et al. | [125] |
| Category | Problem/Application | Author | Ref. |
|---|---|---|---|
| Continuous optimization | Training artificial neural networks | Moayedi et al. | [126] |
| Selecting structure and weights for neural networks | Kowsalya et al. | [127] | |
| Training neural networks | Sahlol et al. | [128] | |
| Optimizing underwater sensor networks | Sukhman et al. | [129] | |
| Unmanned aerial vehicle path planning | Alihodzic et al. | [130] | |
| Clustering | Rani et al. | [131] | |
| Jaiprakash et al. | [132] | ||
| Support vector regression (SVR) classifier | Hassanien et al. | [133] | |
| Hassanien et al. | [134] | ||
| Tuba et al. | [135] | ||
| Tuba et al. | [136] | ||
| Control problem | Sambariya et al. | [137] |
| Category | Problem/Application | Author | Ref. |
|---|---|---|---|
| Combinatorial optimization | Traveling salesman problem | Almufti et al. | [138] |
| Knapsack | Darmawan et al. | [139] | |
| Acoustic energy-based positioning | Arora et al. | [140] | |
| Scheduling | Parasha et al. | [141] | |
| Cahig et al. | [142] | ||
| Sarwar et al. | [143] | ||
| Komal et al. | [144] | ||
| Mohsin et al. | [145] | ||
| Gholam et al. | [146] | ||
| Fatima et al. | [147] | ||
| Electrostatic powder coating process | Pongchanun et al. | [148] | |
| Image safety model | Shankar et al. | [149] | |
| Chibani et al. | [150] | ||
| Image processing | Tuba et al. | [151] | |
| Shankar et al. | [152] | ||
| Jayanth et al. | [153] | ||
| Cardoso et al. | [154] | ||
| Wireless sensor networks | Sérgio et al. | [155] | |
| Ivana et al. | [156] | ||
| Kaur et al. | [157] | ||
| Feature selection | Xu et al. | [158] | |
| Optimal power flow problem | Mukherjee et al. | [159] | |
| S. Mani et al. | [160] | ||
| Sambariya et al. | [161] | ||
| Distribution systems | Prasad et al. | [162] | |
| Vijay et al. | [163] | ||
| Constrained Optimization | Linear and nonlinear constrained optimization problems | Ivana e et al. | [164] |
| Economic dispatch problems | Singh et al. | [165] | |
| Stochastic inequality constrained optimization problems | Horng et al. | [166] | |
| Multi-objective optimization | Quality of service (QoS) aware web service composition optimization | Sadouki et al. | [167] |
| Civil engineering | Adarsha et al. | [168] | |
| Structural optimization | Malihe et al. | [169] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Lei, H.; Alavi, A.H.; Wang, G.-G. Elephant Herding Optimization: Variants, Hybrids, and Applications. Mathematics 2020, 8, 1415. https://doi.org/10.3390/math8091415
Li J, Lei H, Alavi AH, Wang G-G. Elephant Herding Optimization: Variants, Hybrids, and Applications. Mathematics. 2020; 8(9):1415. https://doi.org/10.3390/math8091415
Chicago/Turabian StyleLi, Juan, Hong Lei, Amir H. Alavi, and Gai-Ge Wang. 2020. "Elephant Herding Optimization: Variants, Hybrids, and Applications" Mathematics 8, no. 9: 1415. https://doi.org/10.3390/math8091415
APA StyleLi, J., Lei, H., Alavi, A. H., & Wang, G.-G. (2020). Elephant Herding Optimization: Variants, Hybrids, and Applications. Mathematics, 8(9), 1415. https://doi.org/10.3390/math8091415







