New Proof That the Sum of the Reciprocals of Primes Diverges

Abstract

In this paper, we give a new proof of the divergence of the sum of the reciprocals of primes using the number of distinct prime divisors of positive integer n, and the placement of lattice points on a hyperbola given by $n=pr$ with prime number p. We also offer both a new expression of the average sum of the number of distinct prime divisors, and a new proof of its divergence, which is very intriguing by its elementary approach.

1. Introduction

It has sometimes been mentioned that number theory is the theory of prime numbers. There are infinitely many prime numbers, a theorem proved by Euclid (ca. 300 BCE), but it was also proved by other different methods by Christian Goldbach, Leonhard Euler, Charles Hermite, and Thomas J. Stieltjes from the 18th to the 19th century, and in the 20th and 21st centuries by Paul Erdős, Hillel Furstenberg, Filip Saidak, Juan P. Pinasco, Junho P. Whang, and Alexander Shen, among several dozen existing proofs [1].

$\mathsf{\Pi }\left(x\right)$, the prime-counting function, gives a number of primes less than or equal to $x\in \mathbb{R}$. So, in terms of $\mathsf{\Pi }\left(x\right)$, Euclid’s theorem on the infinitude of prime numbers can be expressed as

$$\underset{x\to +\infty }{lim}\mathsf{\Pi }\left(x\right)=+\infty .$$

On the other hand, prime numbers show asymptotic distribution, formalizing that, as one progresses along the natural numbers, prime numbers are less common, something that we can simply express as

$$\underset{x\to +\infty }{lim}\frac{\mathsf{\Pi }\left(x\right)}{\frac{x}{logx}}=1.$$

Leonhard Euler proved in 1737 [2] that the sum of the reciprocals of all prime numbers diverges:

$$\sum _{\mathit{p}\in \mathit{P}}\frac{1}{p}=\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\dots =+\infty .$$

(1)

For this, he used the harmonic series, and the equality between it and its product formula

$$\sum _{n=1}^{\infty }\frac{1}{n}=\prod _{\mathit{p}\in \mathit{P}}\frac{1}{1-p^{-1}}$$

after applying logarithms and using the equality of the Taylor series of $log(1-x)$.

Euler also noticed that the value of this sum had a correspondence to $loglogx$, although he did not give a proof. Karl F. Gauss formulated the same result in [3].

In 1874, using some results of Pafnuti L. Chebyshev [4,5], Franz Mertens [6] found that $loglogx$ is the right order of magnitude, obtaining

$$\sum _{\mathit{p}\le x}\frac{1}{p}=loglogx+M+\mathcal{O}\left(\frac{1}{logx}\right).$$

(2)

Here, M is the Meissel–Mertens constant, defined by equation

$$M=\gamma +\sum _{\mathit{p}}\left(log\left(1-\frac{1}{p}\right)+\frac{1}{p}\right)\approx 0.2614972,$$

where $\gamma$ is the Euler–Mascheroni constant:

$$\gamma =\underset{n\to \infty }{lim}\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\dots +\frac{1}{n}-logn\right)\approx 0.5772156.$$

Mertens’ formula, although it was refined [7,8], is sufficient for our purposes here.

Following the proofs of the divergence of the sum of the reciprocals of prime numbers, two further ones are those of Paul Erdős [9], which were developed by reductio ad absurdum; assuming a partial sum less than $1/2$ (first proof) or $1/8$ (second proof) from a certain prime $p_i$ to infinity,

$$\sum _{\mathit{p}\in \mathit{P}}\frac{1}{p}=k<\infty .$$

With similar elements, we indicate a third proof by Seki Shin-ichiro [10] in 2018, which uses the Euler–Legendre theorem (“there are no length-three arithmetic progressions whose terms are cubes of positive integers”), and Szemerédi’s theorem (“let A be a set of positive integers that has positive upper density. Then, A contains an arithmetic progression of length k for every positive integer k”), proved for the case of $k=3$ by Klaus F. Roth in 1953 [11].

A fourth proof was obtained from the Pierre Dusart’s inequality [12], of 1999 for the i-th prime,

$$p_i<ilogi+iloglogi,\forall i\ge 6.$$

We show below a new proof of the same result.

2. A New Proof

A new proof shows the diversity of ways of solving the same problem by different techniques, and helps us to better understand the original problem, analyzing it from different points of view.

For our purposes, arithmetic functions are fundamental. A function f is called an arithmetic function whose domain is $\mathbb{N}$ and whose codomain is $\mathbb{R}$ or $\mathbb{C}$; in our case, typically, $\mathbb{R}$.

An arithmetic function f is said to be additive if $f\left(mn\right)=f\left(m\right)+f\left(n\right)$ with $gcd(m,n)=1$; and completely additive if $f\left(mn\right)=f\left(m\right)+f\left(n\right)$ for all $m,n\in \mathbb{N}$. An arithmetic function is also defined as multiplicative if $f\left(mn\right)=f\left(m\right)f\left(n\right)$ with $gcd(m,n)=1$, and completely multiplicative if $f\left(mn\right)=f\left(m\right)f\left(n\right)$ for all $m,n\in \mathbb{N}$.

A main element of our proof is function $\omega \left(n\right)$, which is defined as the number of distinct prime divisors of n, which is additive but not completely additive. A completely additive function is $\mathsf{\Omega }\left(n\right)$, defined as the number of prime divisors of n counting multiplicity. On the other hand, among multiplicative functions, we can mention $\phi \left(n\right)$, the number of positive integers less than n that are relatively prime to n, although not completely multiplicative. It is completely multiplicative, for example $id\left(n\right)=n$, the identity function.

In 1917, Godfrey H. Hardy and Srinivāsa A. Rāmānujan [13] proved that, if the number of distinct prime divisors of n, $\omega \left(n\right)$ is additively calculated up to a certain value,

$$\widetilde{\omega \left(x\right)}=\sum _{n\le x}\omega \left(n\right)=xloglogx+Mx+\mathcal{O}\left(\frac{x}{logx}\right),$$

the arithmetic mean or average value tends to infinity:

$$\underset{x\to \infty }{lim}\frac{\widetilde{\omega \left(x\right)}}{x}=+\infty .$$

The latter is specifically the result that we need for our proof of (1). However, in order not to fall into a circular argument, since it is based on the divergence of the sum of the reciprocals of the primes, on the basis of (2), we need a previous theorem, which we present below.

Theorem 1.

The average sum of the number of distinct prime divisors of n tends to infinity:

$$\underset{x\to \infty }{lim}\frac{\widetilde{\omega \left(x\right)}}{x}=+\infty .$$

(3)

Proof. 

We build the following series of paired intervals, set of i pairs of intervals, $\forall n\in \mathbb{N}$, $n>2$:

$$\left\{\left(0,\frac{n}{2}\right],\left(\frac{n}{2},n\right]\right\},\left\{\left(0,\frac{n}{4}\right],\left(\frac{n}{4},\frac{n}{2}\right]\right\},\left\{\left(0,\frac{n}{8}\right],\left(\frac{n}{8},\frac{n}{4}\right]\right\},\dots ,\left\{\left(0,\frac{n}{2^i}\right],\left(\frac{n}{2^i},\frac{n}{2^{i-1}}\right]\right\},$$

where $\frac{n}{2^i}<2$, a value from which we can count prime numbers.

Each element of each pair, with $j=1,\dots ,i$, $\left\{\left(0,\frac{n}{2^j}\right],\left(\frac{n}{2^j},\frac{n}{2^{j-1}}\right]\right\}$, has the same extension, which we call ${\lambda }_j=\frac{n}{2^j}$.

If we consider the new sequence of $i+1$ elements,

$$\left(0,\frac{n}{2^i}\right],\left(\frac{n}{2^i},\frac{n}{2^{i-1}}\right],\dots ,\left(\frac{n}{8},\frac{n}{4}\right],\left(\frac{n}{4},\frac{n}{2}\right],\left(\frac{n}{2},n\right],$$

(4)

we see that the two intervals of lesser length are of equal length with the following recurrence:

$$\begin{array}{c}\hfill \begin{array}{c}{\lambda }_i={\lambda }_{i+1},\\ {\lambda }_{i-1}={\lambda }_i+{\lambda }_i,\\ {\lambda }_{i-2}={\lambda }_{i-1}+{\lambda }_i+{\lambda }_i,\\ \dots ,\\ {\lambda }_{i-r}={\lambda }_i+\sum _{t=0}^{r-1}{\lambda }_{i-t}\\ \dots ,\end{array}\end{array}$$

(5)

with $n={\lambda }_i+{\sum }_{j=1}^i{\lambda }_j$, and ${\lambda }_1=2^{i-1}{\lambda }_{i+1}$.

In each interval $\left(a,b\right]$ of length ${\lambda }_j$, there is a number of different prime factors for each number of the interval, of value $\tilde{\omega }\left(b\right)-\tilde{\omega }\left(a\right)$, which we call ${\mathsf{\Omega }}_j$ and calculate. So, from there, we analyze the convergence or divergence of the average sum of the number of distinct prime divisors of n.

In (4), we consider how many primes there are and, from them, how many prime factors appear. We do this from prime $p_i$ Considering values $p_i$, $p_i+p_i$, $p_i+p_i+p_i$, … that appear and so on.

We see that prime $p_i\in \left(\frac{n}{2k},\frac{n}{2\left(k-1\right)}\right]$, with $k\in \mathbb{N}$, $k\ge 2$, that appears in $\left(0,\frac{n}{2}\right]$, appears $k-1$ times in $\left(0,\frac{n}{2}\right]$. Prime numbers $p_i\in \left(\frac{n}{2k},\frac{n}{2k-1}\right]$, with $k\ge 2$, that appear in $\left(0,\frac{n}{2}\right]$, appear one more time in the interval $\left(\frac{n}{2},n\right]$.

Thus, given a value n, primes in $\left(\frac{n}{4},\frac{n}{2}\right]$ are $\mathsf{\Pi }\left(\frac{n}{2}\right)-\mathsf{\Pi }\left(\frac{n}{4}\right)$, and appear only once in this interval, and therefore only once in $\left(0,\frac{n}{2}\right]$. Prime numbers in $\left(\frac{n}{6},\frac{n}{4}\right]$ are $\mathsf{\Pi }\left(\frac{n}{4}\right)-\mathsf{\Pi }\left(\frac{n}{6}\right)$, and appear only once in this interval, and $2\left(\mathsf{\Pi }\left(\frac{n}{4}\right)-\mathsf{\Pi }\left(\frac{n}{6}\right)\right)$ in $\left(0,\frac{n}{2}\right]$. Primes in $\left(\frac{n}{8},\frac{n}{6}\right]$ are $\mathsf{\Pi }\left(\frac{n}{6}\right)-\mathsf{\Pi }\left(\frac{n}{8}\right)$, and appear only once in this interval, and $3\left(\mathsf{\Pi }\left(\frac{n}{6}\right)-\mathsf{\Pi }\left(\frac{n}{8}\right)\right)$ in $\left(0,\frac{n}{2}\right]$, and so on. Hence, adding, we have as a result, in $\left(0,\frac{n}{2}\right]$, the total

$$\mathsf{\Pi }\left(\frac{n}{2}\right)+\mathsf{\Pi }\left(\frac{n}{4}\right)+\mathsf{\Pi }\left(\frac{n}{6}\right)+\mathsf{\Pi }\left(\frac{n}{8}\right)+\dots +\mathsf{\Pi }\left(\frac{n}{2k}\right),$$

as long as $\frac{n}{2k}\ge 2$, $k\in \mathbb{N}$ that we can bound by $\mathsf{\Pi }\left(2\right)$, so

$$\tilde{\omega }\left(\frac{n}{2}\right)-\tilde{\omega }\left(0\right)=\tilde{\omega }\left(\frac{n}{2}\right)=\sum _{k=1}^{⌊\frac{n}{4}⌋}\mathsf{\Pi }\left(\frac{n}{2k}\right).$$

(6)

Considering values $p_i$, $p_i+p_i$, $p_i+p_i+p_i+\dots$ that appear in $\left(\frac{n}{2},n\right]$, they are more than those in $\left(0,\frac{n}{2}\right]$. We have all those mentioned before, $\mathsf{\Pi }\left(\frac{n}{2}\right)+\mathsf{\Pi }\left(\frac{n}{4}\right)+\mathsf{\Pi }\left(\frac{n}{6}\right)+\mathsf{\Pi }\left(\frac{n}{8}\right)+\dots$, and also those that in their intervals that we saw that added one more, $\left(\mathsf{\Pi }\left(\frac{n}{3}\right)-\mathsf{\Pi }\left(\frac{n}{4}\right)\right)+\left(\mathsf{\Pi }\left(\frac{n}{5}\right)-\mathsf{\Pi }\left(\frac{n}{6}\right)\right)+\left(\mathsf{\Pi }\left(\frac{n}{7}\right)-\mathsf{\Pi }\left(\frac{n}{8}\right)\right)+\dots$, as well as all the new primes that appear in this interval, $\mathsf{\Pi }\left(n\right)-\mathsf{\Pi }\left(\frac{n}{2}\right)$; so, by adding, we get the total

$$\mathsf{\Pi }\left(n\right)+\mathsf{\Pi }\left(\frac{n}{3}\right)+\mathsf{\Pi }\left(\frac{n}{5}\right)+\mathsf{\Pi }\left(\frac{n}{7}\right)+\dots$$

that we can bound by $\mathsf{\Pi }\left(2\right)$, which is the number of different factors in the interval $\left(\frac{n}{2},n\right]$:

$$\tilde{\omega }\left(n\right)-\tilde{\omega }\left(\frac{n}{2}\right)=\mathsf{\Pi }\left(n\right)+\sum _{k=1}^{⌊\frac{n-2}{4}⌋}\mathsf{\Pi }\left(\frac{n}{2k+1}\right).$$

(7)

In this way, for any value $n\in \mathbb{N}$, if we consider the first half (6) versus the second half (7) of the interval, we have that the difference between the number of different factors shows that in the interval $\left(\frac{n}{2},n\right]$ is greater in an amount

$$\left(\mathsf{\Pi }\left(n\right)-\mathsf{\Pi }\left(\frac{n}{2}\right)\right)+\left(\mathsf{\Pi }\left(\frac{n}{3}\right)-\mathsf{\Pi }\left(\frac{n}{4}\right)\right)+\left(\mathsf{\Pi }\left(\frac{n}{5}\right)-\mathsf{\Pi }\left(\frac{n}{6}\right)\right)+\dots ,$$

versus the amount in $\left(0,\frac{n}{2}\right]$.

So, for different ${\mathsf{\Omega }}_j$, with $j=1,\dots ,i+1$, we have that

$$\begin{array}{c}{\mathsf{\Omega }}_{i+1}\le {\mathsf{\Omega }}_i,\\ {\mathsf{\Omega }}_{i+1}+{\mathsf{\Omega }}_i\le {\mathsf{\Omega }}_{i-1},\\ {\mathsf{\Omega }}_{i+1}+{\mathsf{\Omega }}_i+{\mathsf{\Omega }}_{i-1}\le {\mathsf{\Omega }}_{i-2},\\ \dots ,\\ {\mathsf{\Omega }}_{i+1}+{\mathsf{\Omega }}_i+{\mathsf{\Omega }}_{i-1}+\dots +{\mathsf{\Omega }}_2\le {\mathsf{\Omega }}_1.\end{array}$$

(8)

From ${\mathsf{\Omega }}_j$ and ${\lambda }_j$, with $j=1,\dots ,i+1$, we build sequence

$$\begin{array}{c}{a}_1=\frac{{\mathsf{\Omega }}_{i+1}}{{\lambda }_{i+1}},\\ a_2=\frac{{\mathsf{\Omega }}_{i+1}+{\mathsf{\Omega }}_i}{{\lambda }_{i+1}+{\lambda }_i},\\ a_3=\frac{{\mathsf{\Omega }}_{i+1}+{\mathsf{\Omega }}_i+{\mathsf{\Omega }}_{i-1}}{{\lambda }_{i+1}+{\lambda }_i+{\lambda }_{i-1}},\\ \dots \\ a_{i+1}=\frac{{\sum }_{j=1}^{i+1}{\mathsf{\Omega }}_j}{{\sum }_{j=1}^{i+1}{\lambda }_j}=\frac{{\sum }_{j=1}^{i+1}{\mathsf{\Omega }}_j}{n},\end{array}$$

which is a monotonically increasing succession, by (5) and (8).

The value of term $a_{i+1}$, developing the numerator, where

$$\begin{array}{c}{\mathsf{\Omega }}_1=\mathsf{\Pi }\left(n\right)+\mathsf{\Pi }\left(\frac{n}{3}\right)+\mathsf{\Pi }\left(\frac{n}{5}\right)+\mathsf{\Pi }\left(\frac{n}{7}\right)+\dots ,\\ {\mathsf{\Omega }}_2=\mathsf{\Pi }\left(\frac{n}{2}\right)+\mathsf{\Pi }\left(\frac{n}{6}\right)+\mathsf{\Pi }\left(\frac{n}{10}\right)+\mathsf{\Pi }\left(\frac{n}{14}\right)+\dots ,\\ {\mathsf{\Omega }}_3=\mathsf{\Pi }\left(\frac{n}{4}\right)+\mathsf{\Pi }\left(\frac{n}{12}\right)+\mathsf{\Pi }\left(\frac{n}{20}\right)+\mathsf{\Pi }\left(\frac{n}{28}\right)+\dots ,\\ {\mathsf{\Omega }}_4=\mathsf{\Pi }\left(\frac{n}{8}\right)+\mathsf{\Pi }\left(\frac{n}{24}\right)+\mathsf{\Pi }\left(\frac{n}{40}\right)+\mathsf{\Pi }\left(\frac{n}{56}\right)+\dots ,\\ \dots \end{array}$$

until ${\mathsf{\Omega }}_{i+1}$, is

$$\begin{array}{c}{a}_{i+1}=\frac{{\sum }_{j=1}^{i+1}{\mathsf{\Omega }}_j}{n}=\frac{\mathsf{\Pi }\left(n\right)+\mathsf{\Pi }\left(\frac{n}{2}\right)+\mathsf{\Pi }\left(\frac{n}{3}\right)+\mathsf{\Pi }\left(\frac{n}{4}\right)+\mathsf{\Pi }\left(\frac{n}{5}\right)+\dots }{n}=\frac{{\sum }_{k=1}^{⌊\frac{n}{2}⌋}\mathsf{\Pi }\left(\frac{n}{k}\right)}{n}.\end{array}$$

It turns out to be so that the numerator value of $a_{i+1}$ is another way to calculate $\widetilde{\omega \left(x\right)}={\sum }_{n\le x}\omega \left(n\right)$, and $a_{i+1}$ another expression of $\frac{\widetilde{\omega \left(x\right)}}{x}$. With our choice of variables

$$\frac{\widetilde{\omega \left(x\right)}}{x}=\frac{{\sum }_{k=1}^{⌊\frac{x}{2}⌋}\mathsf{\Pi }\left(\frac{x}{k}\right)}{x}.$$

(9)

To study its convergence or divergence, because it is not a typical sequence or a typical numerical series of addends under a single index in the sum, we apply the following method:

Taking $n=10$, the sum of terms is:

$$S_1=\frac{\mathsf{\Pi }\left(\frac{10}{1}\right)}{10}+\frac{\mathsf{\Pi }\left(\frac{10}{2}\right)}{10}+\dots +\frac{\mathsf{\Pi }\left(\frac{10}{5}\right)}{10}=a_1^{}+a_2^{}+a_3^{}+a_4^{}+a_5^{}.$$

With $n=20$:

$$S_2=\frac{\mathsf{\Pi }\left(\frac{20}{1}\right)}{20}+\frac{\mathsf{\Pi }\left(\frac{20}{2}\right)}{20}+\dots +\frac{\mathsf{\Pi }\left(\frac{20}{10}\right)}{20}=a_1^{{}^{\prime }}+a_2^{{}^{\prime }}+\dots +a_{10}^{{}^{\prime }}.$$

With $n=40$:

$$S_3=\frac{\mathsf{\Pi }\left(\frac{40}{1}\right)}{40}+\frac{\mathsf{\Pi }\left(\frac{40}{2}\right)}{40}+\dots +\frac{\mathsf{\Pi }\left(\frac{40}{20}\right)}{40}=a_1^{{}^{″}}+a_2^{{}^{″}}+\dots +a_{20}^{{}^{″}},$$

and so on.

We can put many of the terms of the sequence $S_j$, with $j>1$, as values already present in the previous sequence $S_{j-1}$. For example, for $S_2$ and $S_3$:

$$\begin{array}{c}{S}_2=a_1^{{}^{\prime }}+a_2^{{}^{\prime }}+a_3^{{}^{\prime }}+a_4^{{}^{\prime }}+a_5^{{}^{\prime }}+a_6^{{}^{\prime }}+a_7^{{}^{\prime }}+a_8^{{}^{\prime }}+a_9^{{}^{\prime }}+a_{10}^{{}^{\prime }}=\\ =a_1^{{}^{\prime }}+\left(a_2^{{}^{\prime }}+a_4^{{}^{\prime }}+a_6^{{}^{\prime }}+a_8^{{}^{\prime }}+a_{10}^{{}^{\prime }}\right)+\left(a_3^{{}^{\prime }}+a_5^{{}^{\prime }}+a_7^{{}^{\prime }}+a_9^{{}^{\prime }}\right)=\\ =a_1^{{}^{\prime }}+\frac{1}{2}{S}_1+\left(a_3^{{}^{\prime }}+a_5^{{}^{\prime }}+a_7^{{}^{\prime }}+a_9^{{}^{\prime }}\right)>\\ >a_1^{{}^{\prime }}+\frac{1}{2}{S}_1+\left(a_4^{{}^{\prime }}+a_6^{{}^{\prime }}+a_8^{{}^{\prime }}+a_{10}^{{}^{\prime }}\right)=\\ =a_1^{{}^{\prime }}+\frac{1}{2}{S}_1+\frac{1}{2}{S}_1-a_2^{{}^{\prime }}=\left(a_1^{{}^{\prime }}-a_2^{{}^{\prime }}\right)+S_1.\end{array}$$

$$\begin{array}{c}{S}_3=a_1^{{}^{″}}+a_2^{{}^{″}}+a_3^{{}^{″}}+a_4^{{}^{″}}+\dots +a_{20}^{{}^{″}}>\\ >\left(a_1^{{}^{″}}-a_2^{{}^{″}}\right)+S_2>\left(a_1^{{}^{″}}-a_2^{{}^{″}}\right)+\left(a_1^{{}^{\prime }}-a_2^{{}^{\prime }}\right)+S_1.\end{array}$$

Thus,

$$\begin{array}{c}{S}_2>\left(a_1^{{}^{\prime }}-a_2^{{}^{\prime }}\right)+S_1,\\ S_3>\left(a_1^{{}^{″}}-a_2^{{}^{″}}\right)+\left(a_1^{{}^{\prime }}-a_2^{{}^{\prime }}\right)+S_1,\\ S_4>\left(a_1^{{}^{‴}}-a_2^{{}^{‴}}\right)+\left(a_1^{{}^{″}}-a_2^{{}^{″}}\right)+\left(a_1^{{}^{\prime }}-a_2^{{}^{\prime }}\right)+S_1,\\ S_5>\left(a_1^{{}^{⁗}}-a_2^{{}^{⁗}}\right)+\left(a_1^{{}^{‴}}-a_2^{{}^{‴}}\right)+\left(a_1^{{}^{″}}-a_2^{{}^{″}}\right)+\left(a_1^{{}^{\prime }}-a_2^{{}^{\prime }}\right)+S_1,\\ \dots \end{array}$$

an expression that we can put as

$$S_t>S_1+\sum _{\delta =1}^{t-1}\left(\frac{\mathsf{\Pi }\left(20·2^{\delta -1}\right)}{20·2^{\delta -1}}-\frac{\mathsf{\Pi }\left(10·2^{\delta -1}\right)}{20·2^{\delta -1}}\right).$$

Approximating

$$\mathsf{\Pi }\left(x\right)\sim \frac{x}{lnx},$$

(10)

we have

$$\begin{array}{c}{S}_1+\sum _{\delta =1}^{t-1}\left(\frac{\mathsf{\Pi }\left(20·2^{\delta -1}\right)}{20·2^{\delta -1}}-\frac{\mathsf{\Pi }\left(10·2^{\delta -1}\right)}{20·2^{\delta -1}}\right)=\\ =S_1+\sum _{\delta =1}^{t-1}\left(\frac{1}{ln(10·2^{\delta })}-\frac{1}{2ln(5·2^{\delta })}\right)=\\ =S_1+\sum _{\delta =1}^{t-1}\frac{ln(5·2^{\delta })-ln2}{2ln(5·2^{\delta })(ln2+ln(5·2^{\delta }))}.\end{array}$$

(11)

If we consider that

$$\begin{array}{c}\frac{ln(5·2^{\delta })-ln2}{2ln(5·2^{\delta })(ln2+ln(5·2^{\delta }))}=\frac{\delta ln2+ln5-ln2}{2\left(ln5+\delta ln2\right)\left(ln2+ln5+\delta ln2\right)}>\\ >\frac{\delta ln2}{2\left(2+\delta \right)\left(3+\delta \right)}>\frac{\frac{1}{2}\delta }{2{\delta }^2+10\delta +12}=\frac{1}{4}\frac{\delta }{{\delta }^2+5\delta +6}>\frac{1}{4}\frac{\delta }{{\left(\delta +3\right)}^2}=\frac{1}{4}\left(\frac{1}{\delta +3}-\frac{3}{{\left(\delta +3\right)}^2}\right),\end{array}$$

to know ${lim}_{t\to \infty }{S}_t$, it is enough to calculate the limit to infinity of the summation of the last expression,

$$\underset{t\to \infty }{lim}\left(\frac{1}{4}\sum _{\delta =1}^{t-1}\frac{1}{\delta +3}-\frac{3}{4}\sum _{\delta =1}^{t-1}\frac{1}{{\left(\delta +3\right)}^2}\right),$$

which is the subtraction between a divergent series and a convergent (of value $\frac{3}{4}\left({\pi }^{2}6-4936\right)$) series, so the total diverges; hence, ${lim}_{t\to \infty }{S}_t$ tends to infinity and also (9), and this completes the proof of (3).

However, as a precaution, and avoiding the use of (10), the result of such a deep theorem, mathematically broad in its methodological development, as is the prime-number theorem (whatever its proof [14,15,16,17,18,19,20,21]), and thus not fall into a possible implicit use of the result that we want to prove, we use a much more modest result and without so many implications, such as Chebyshev’s bound theorem [4,5]:

$$c_1\frac{x}{lnx}<\mathsf{\Pi }\left(x\right)<c_2\frac{x}{lnx},$$

with $c_1=0.92$ and $c_2=1.11$ positive constants, for all sufficiently large numbers x.

With this, (11) becomes

$$\begin{array}{c}{S}_1+\sum _{\delta =1}^{t-1}\left(\frac{\mathsf{\Pi }\left(20·2^{\delta -1}\right)}{20·2^{\delta -1}}-\frac{\mathsf{\Pi }\left(10·2^{\delta -1}\right)}{20·2^{\delta -1}}\right)=S_1+\sum _{\delta =1}^{t-1}\left(\frac{c_1}{ln(10·2^{\delta })}-\frac{c_2}{2ln(5·2^{\delta })}\right),\end{array}$$

and considering

$$\begin{array}{c}\frac{c_1}{ln(10·2^{\delta })}-\frac{c_2}{2ln(5·2^{\delta })}>\frac{2·0.9·ln(5·2^{\delta })-1.2·ln(10·2^{\delta })}{2ln(5·2^{\delta })(ln(10·2^{\delta }))}=\\ =\frac{0.6·ln(5·2^{\delta })-1.2·ln2}{2ln(5·2^{\delta })(ln(10·2^{\delta }))}=\frac{0.6·(ln5+\delta ·ln2)-1.2·ln2}{2(ln5+\delta ·ln2)(ln2+ln5+\delta ·ln2)}>\\ >\frac{0.6·ln5+\delta ·0.6·ln2-1.2·ln2}{2(2+\delta )(3+\delta )}>\frac{0.1+0.4\delta }{2{\delta }^2+10\delta +12}>\frac{0.25\delta }{2{\delta }^2+10\delta +12}=\frac{1}{8}\frac{\delta }{{\delta }^2+5\delta +6}>\frac{1}{8}\frac{\delta }{{(\delta +3)}^2},\end{array}$$

the result of the final value (9) is the same in terms of divergence. This proves (3). □

Theorem 2.

The sum of the reciprocals of all prime numbers diverges:

$$\sum _{\mathit{p}\in \mathit{P}}\frac{1}{p}=+\infty .$$

Proof. 

We have

$$\widetilde{\omega \left(x\right)}=\sum _{n\le x}\omega \left(n\right)=\omega \left(1\right)+\omega \left(2\right)+\dots +\omega \left(x\right)=\sum _{n\le x}\sum _{p|n}1=\underset{p\in P}{\sum _{n=pr\le x}}1.$$

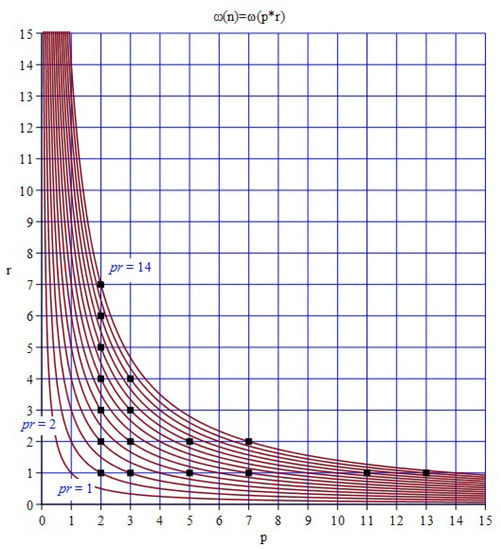
We can interpret this result as a sum extended over certain lattice points in the $pr$ plane, lying on a hyperbola, with $n,p,r\in \mathbb{N}$ and p prime (Figure 1).

If we put the lattice points for all $n=pr$ values on the hyperbolas, and we select those points in the graph, always taking the p values of the columns, it is clear that $\widetilde{\omega \left(n\right)}$ corresponds to the number of lattice points of the graph. Each hyperbola corresponds to a different number n, without intersections between them. They must pass, among others, through all the lattice points $n=\left(n_1,n_2\right)/n,n_1,n_2\in \mathbb{N}$. For each value n, expressed as $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\dots p_i^{{\alpha }_i}\dots p_m^{{\alpha }_m}$, each of these $p_i$ values on the abscissa axis has a lattice point $\left(p_i,p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\dots p_i^{{\alpha }_i-1}\dots p_m^{{\alpha }_m}\right)$ on its own curve, neither more nor less than the number of its different primes.

Counting the number of lattice points from $p=2$, $p=3$, $p=5$, onwards, partial sums are $⌊\frac{x}{2}⌋$, $⌊\frac{x}{3}⌋$, $⌊\frac{x}{5}⌋$, respectively. So,

$$\widetilde{\omega \left(x\right)}=\sum _{n\le x}\omega \left(n\right)=\underset{p\in P}{\sum _{n=pr\le x}}1=\underset{p\in P}{\sum _{p\le n\le x}}⌊\frac{x}{p}⌋\le \underset{p\in P}{\sum _{p\le n\le x}}\frac{x}{p}$$

and extending the rightmost sum beyond x

$$\frac{\widetilde{\omega \left(x\right)}}{x}\le \sum _{\mathit{p}\in \mathit{P}}\frac{1}{p},$$

which, with (3), completes the proof. □