Hybrid Annealing Krill Herd and Quantum-Behaved Particle Swarm Optimization
Abstract
1. Introduction
2. Related Work
2.1. KH
2.2. PSO
2.3. 100-Digit Challenge
3. KH and PSO
3.1. KH
| Algorithm 1. KH [49] |
| 1. Begin |
| 2. Step 1: Initialization. Initialize the generation counter G, the population P, Vf, Dmax, and Nmax. |
| 3. Step 2: Fitness calculation. Calculate fitness for each krill according to its initial position. |
| 4. Step 3: WhileG < MaxGeneration do |
| 5. Sort the population according to their fitness. |
| 6. for i = 1:N (all krill) do |
| 7. Perform the following motion calculation. |
| 8. Motion induced by other individuals |
| 9. Foraging motion |
| 10. Physical diffusion |
| 11. Implement the genetic operators. |
| 12. Update the krill position in the search space. |
| 13. Calculate fitness for each krill according to its new position |
| 14. end for i |
| 15. G = G + 1. |
| 16. Step 4: end while. |
| 17. End. |
3.2. PSO
| Algorithm 2. PSO [46] |
| Begin |
| Step 1: Initialization. |
| 1. Initial position: the initial position of each particle obeys uniform distribution, that is . |
| 2. Initialize its own optimal solution and the overall optimal solution: the initial position is its own optimal solution pi = xi, and then calculating the corresponding value of each particle according to the defined utility function f, and find the global optimal solution gbest. |
| 3. Initial speed: the speed also obeys the uniform distribution. |
| Step 2: Update. |
| According to Equations (7) and (8), the velocity and position of particles are updated, and the current fitness of particles is calculated according to the utility function f of the problem. If it is better than its own historical optimal solution, it will update its own historical optimal solution pbest, otherwise it will not update. If the particle’s own optimal solution pbest is better than the global optimal solution g, then the global optimal solution g is updated, otherwise it is not updated. |
| Step 3: Determine whether to terminate: |
| Determine whether the best solution meets the termination conditions, if yes, stop. |
| Otherwise, return to Step 2. |
| End. |
- Particles have memory. Each iteration of particles will transfer the optimal solution of the population to each other, and update the database of all particles. If the particles deviate, the direction and velocity can be corrected by self-cognition and group-cognition.
- PSO algorithm has fewer parameters, so it is easy to adjust, and the structure is simple, so it is easy to implement.
- The operation is simple, and it only searches for the optimal solution in the solution space according to the flight of particles.
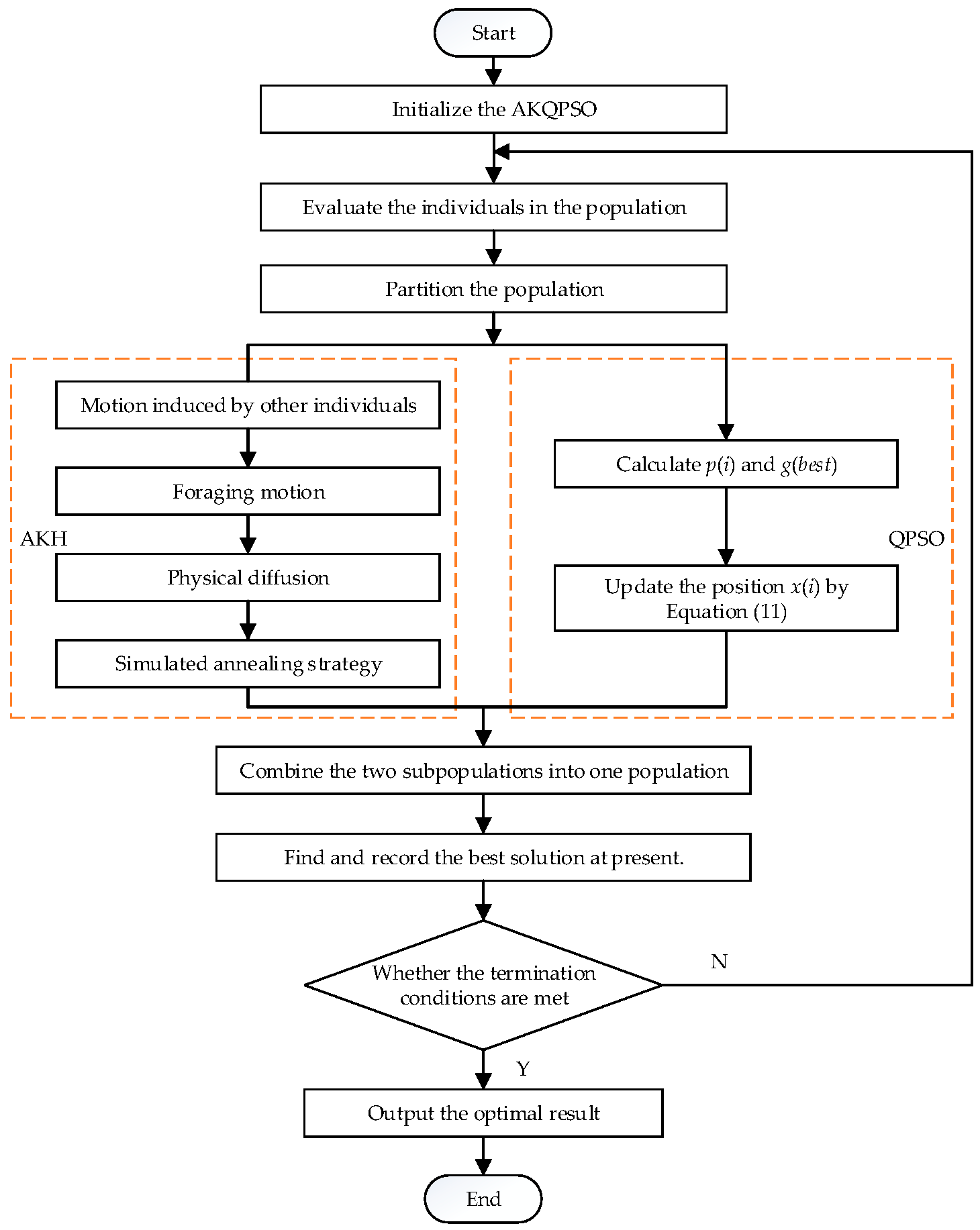
4. AKQPSO
| Algorithm 3 AKQPSO |
| Initialization: |
| N random individuals were generated. |
| Set initialization parameters of AKH and QPSO. |
| Evaluation: |
| Evaluate all individuals based on location. |
| Partition: |
| The whole population was divided into subpopulation-AKH and subpopulation-QPSO. |
| AKH process: |
| Subpopulation-AKH individuals were optimized by AKH. |
| Update through these three actions of the influence of other krill individuals, behavior of getting food and random diffusion. |
| The simulated annealing strategy is used to deal with the above behaviors. |
| Update the individual position according to the above behavior. |
| QPSO process: |
| Subpopulation-QPSO individuals were optimized by QPSO. |
| Update the particle’s local best point Pi and global best point Pbest. |
| Update the position by Equation (10). |
| Combination: |
| The population optimized by AKH and QPSO was reconstituted into a new population. |
| Finding the best solution: |
| The fitness of all individuals was calculated, and the best solution was found in the newly-combined population. |
| Determine whether to terminate: |
| Determine whether the best solution meets the termination conditions, if yes, stop. |
| Otherwise, return to step Evaluation. |
5. Simulation Results
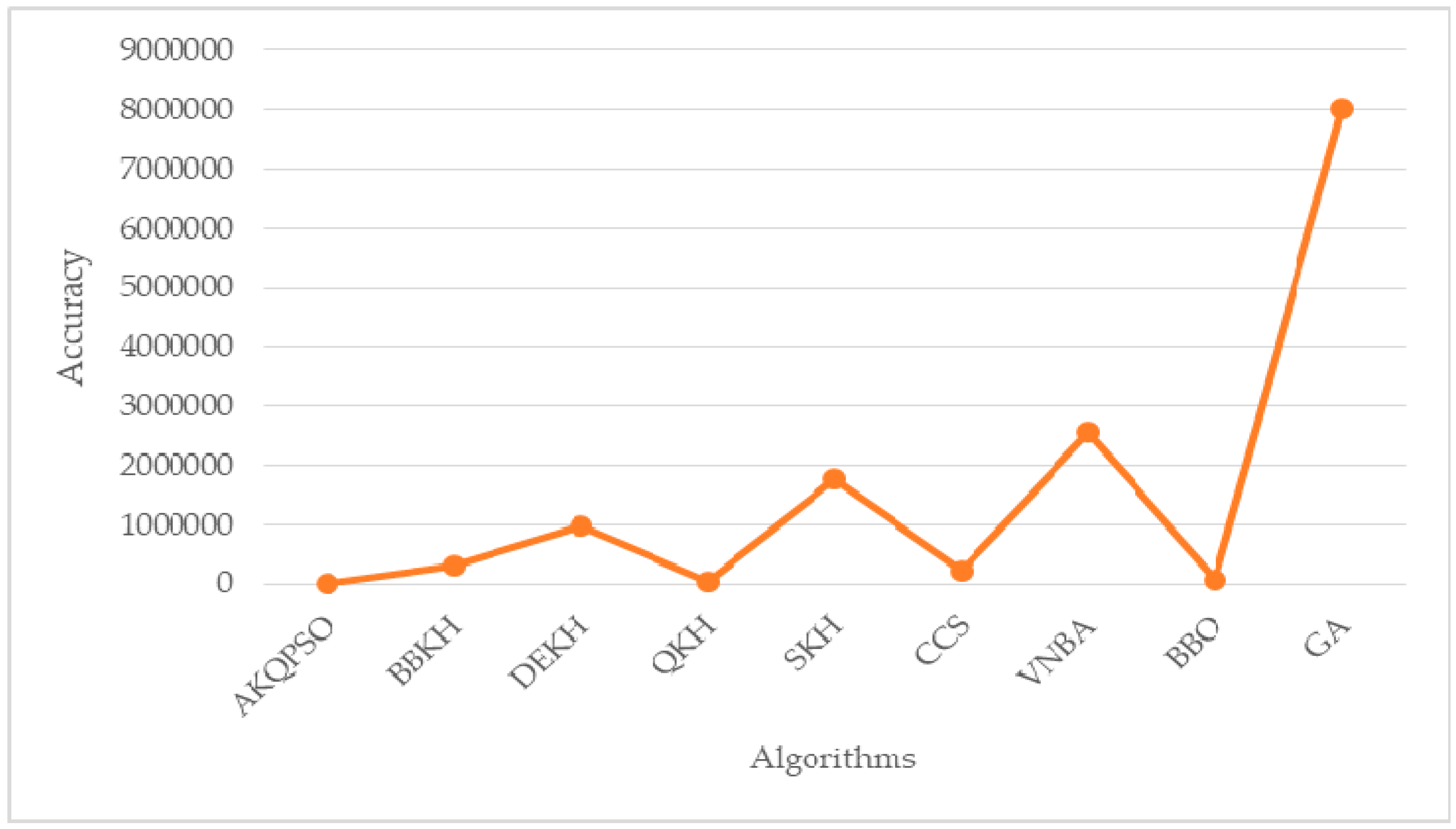
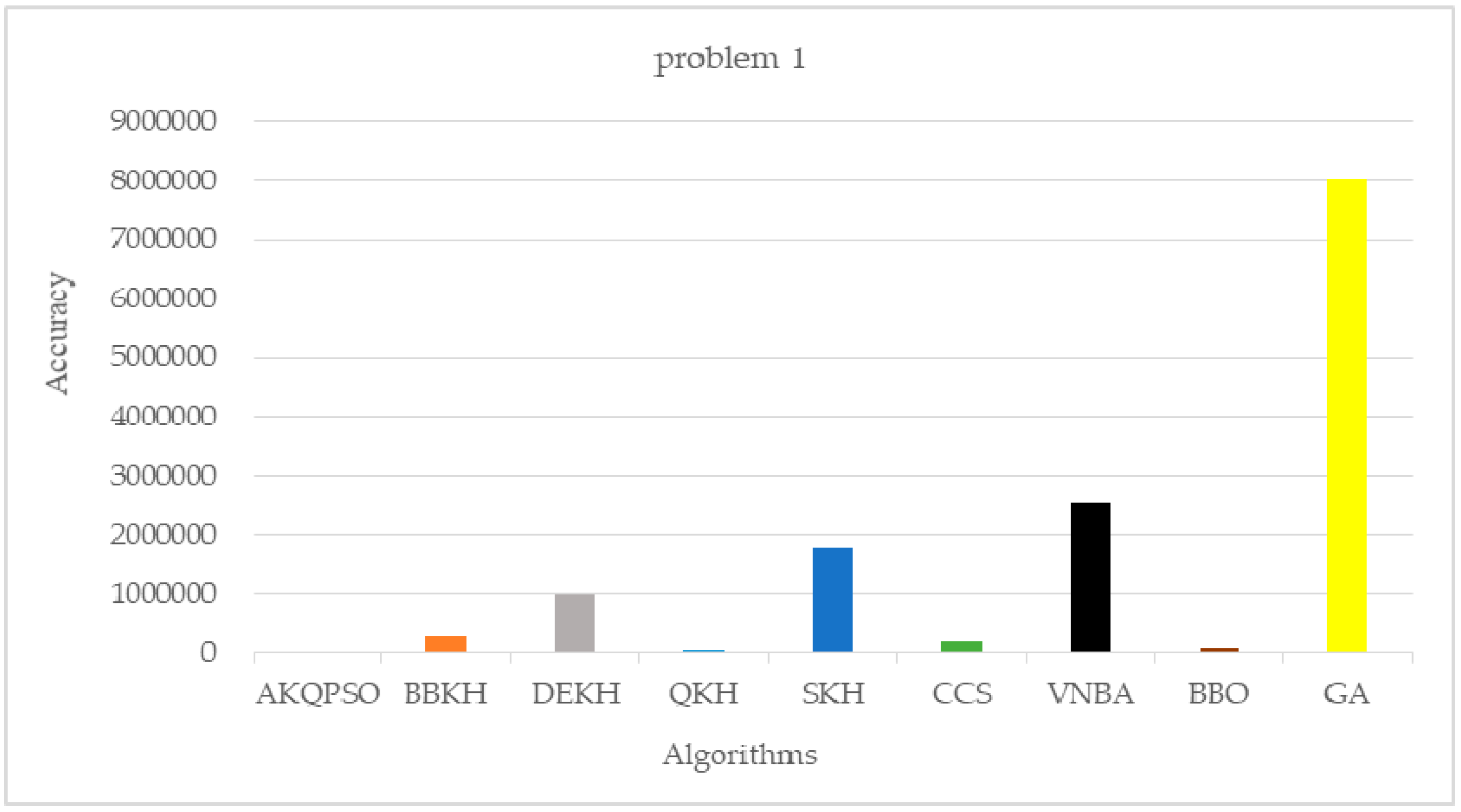
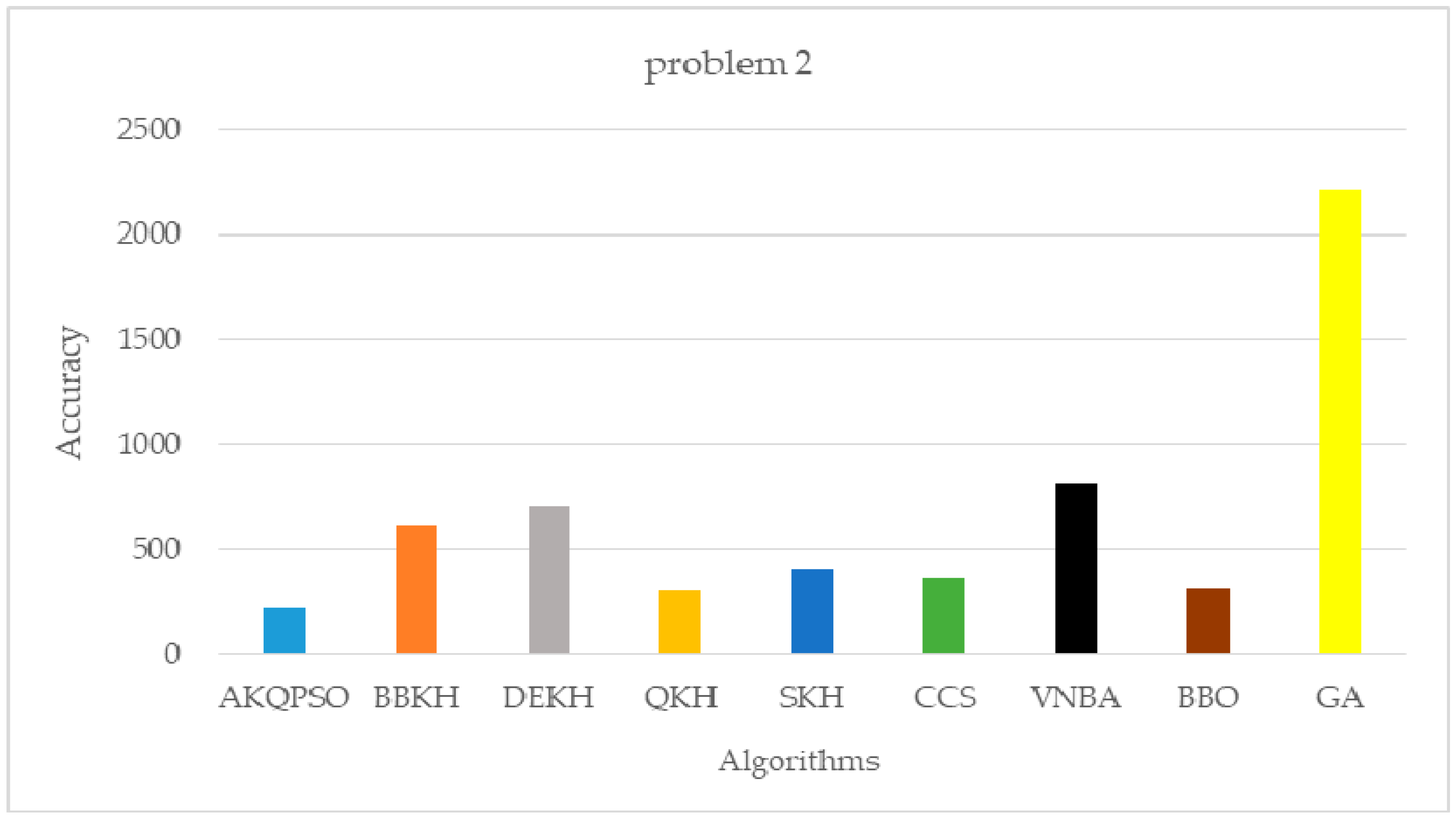
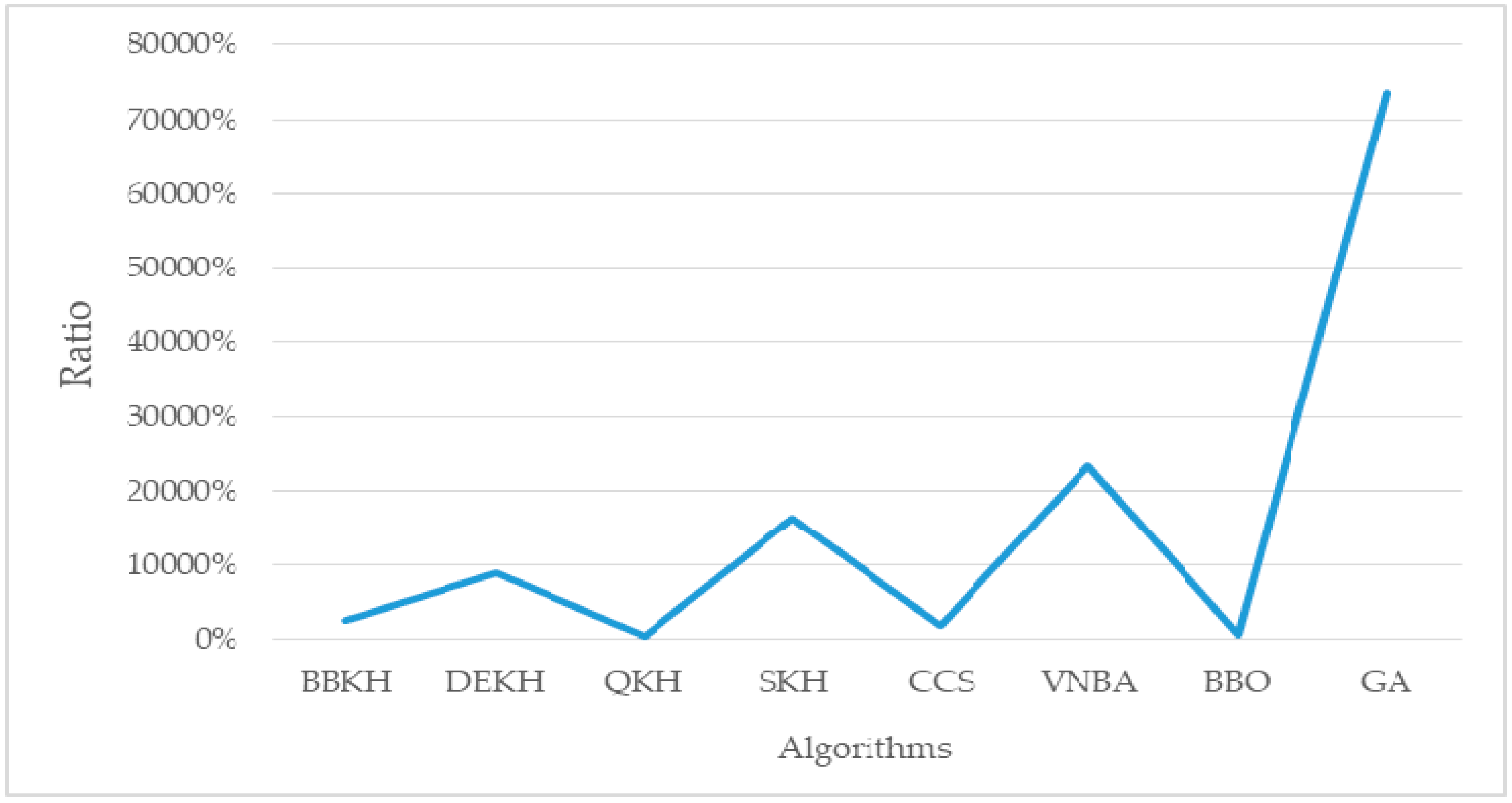
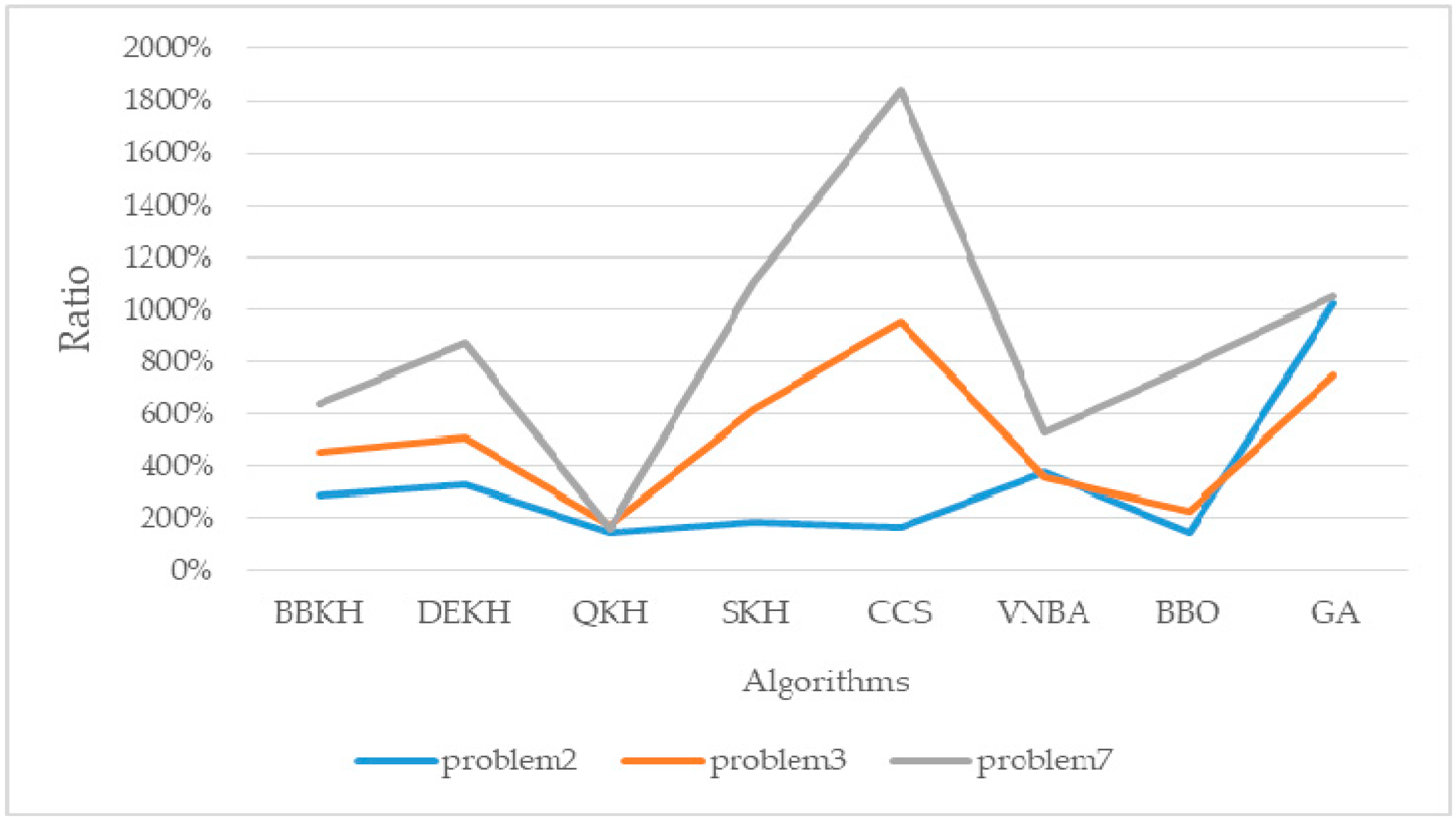
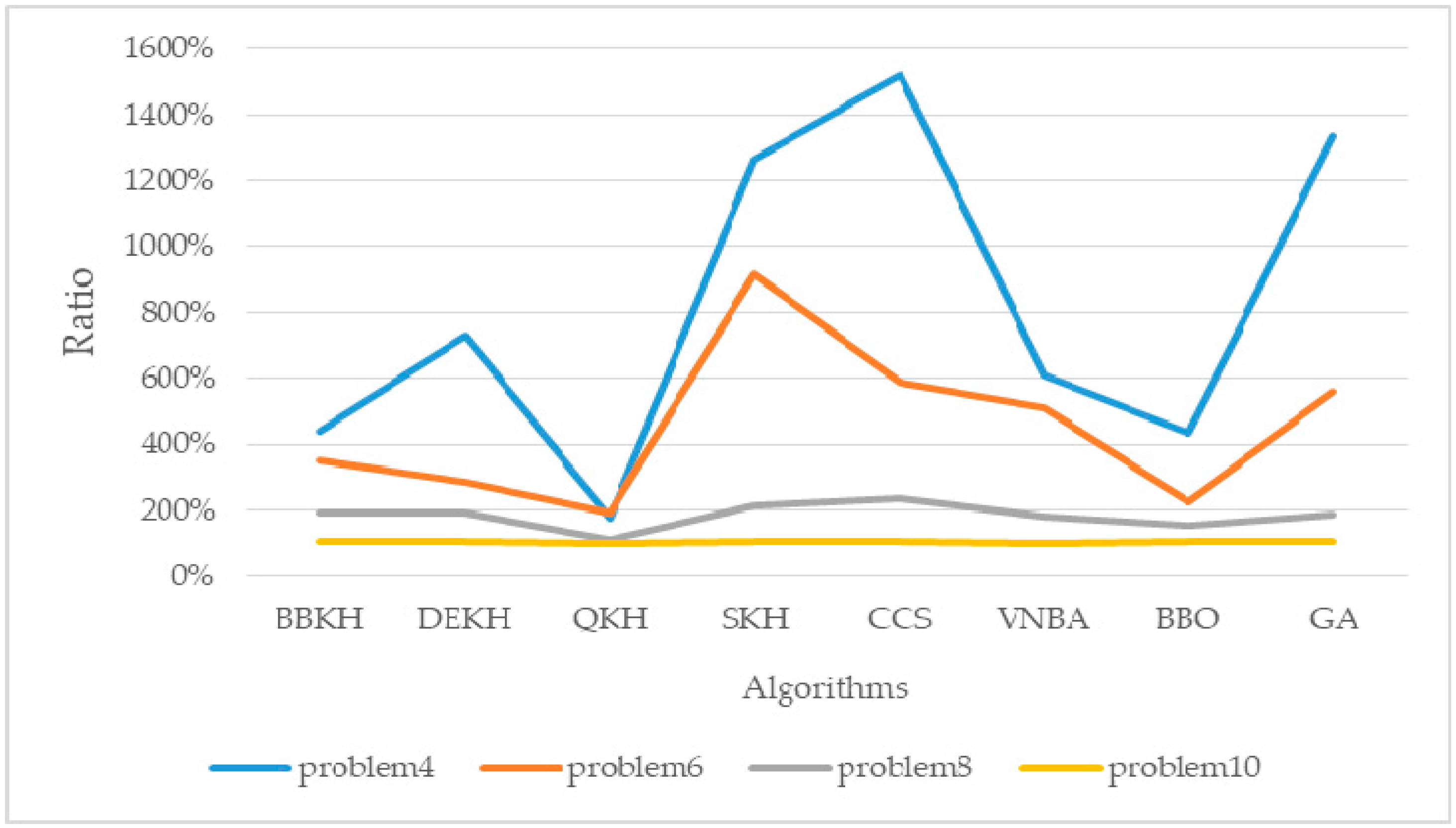
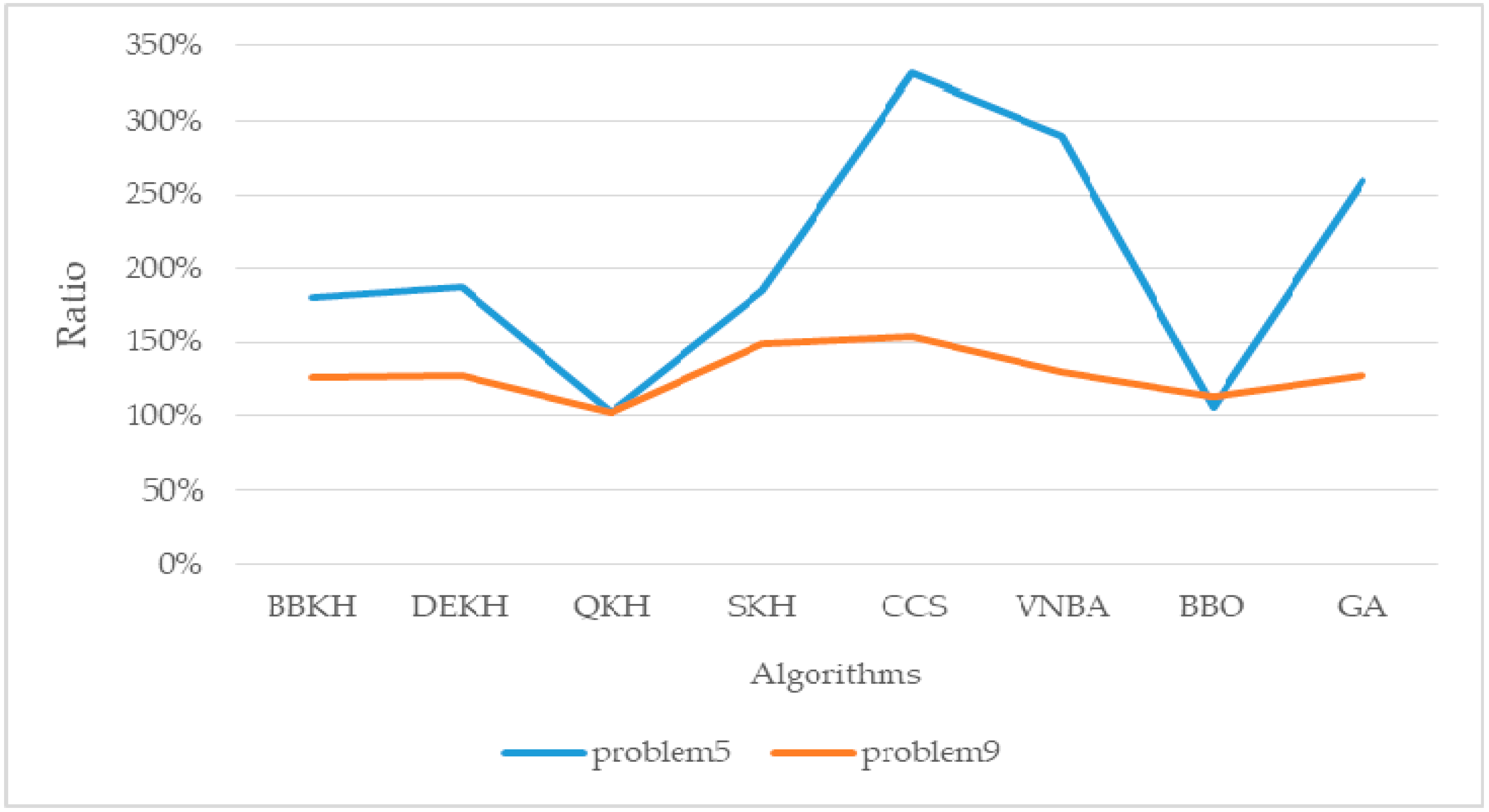
5.1. The Comparison of AKQPSO and Other Algorithms
- By improving krill migration operator, biogeography-based KH (BBKH) [51] was proposed.
- By adding a new hybrid differential evolution operator, the efficiency of the updating process is improved, and differential evolution KH (DEKH) [80] was proposed.
- By quantum behavior to optimize KH, quantum-behaved KH (QKH) [65] was proposed.
- By adding the stud selection and crossover operator, the efficiency was improved and stud krill herd (SKH) [81] was proposed.
- By adding chaos map to optimize cuckoo search (CS), the chaotic CS (CCS) [82] was proposed.
- By adding variable neighborhood (VN) search to bat algorithm (BA), VNBA [83] was proposed.
- By discussing physical biogeography and its mathematics, biogeography-based optimization (BBO) [84] was proposed.
- Genetic algorithm (GA) [45] is basic algorithm of evolutionary computing.
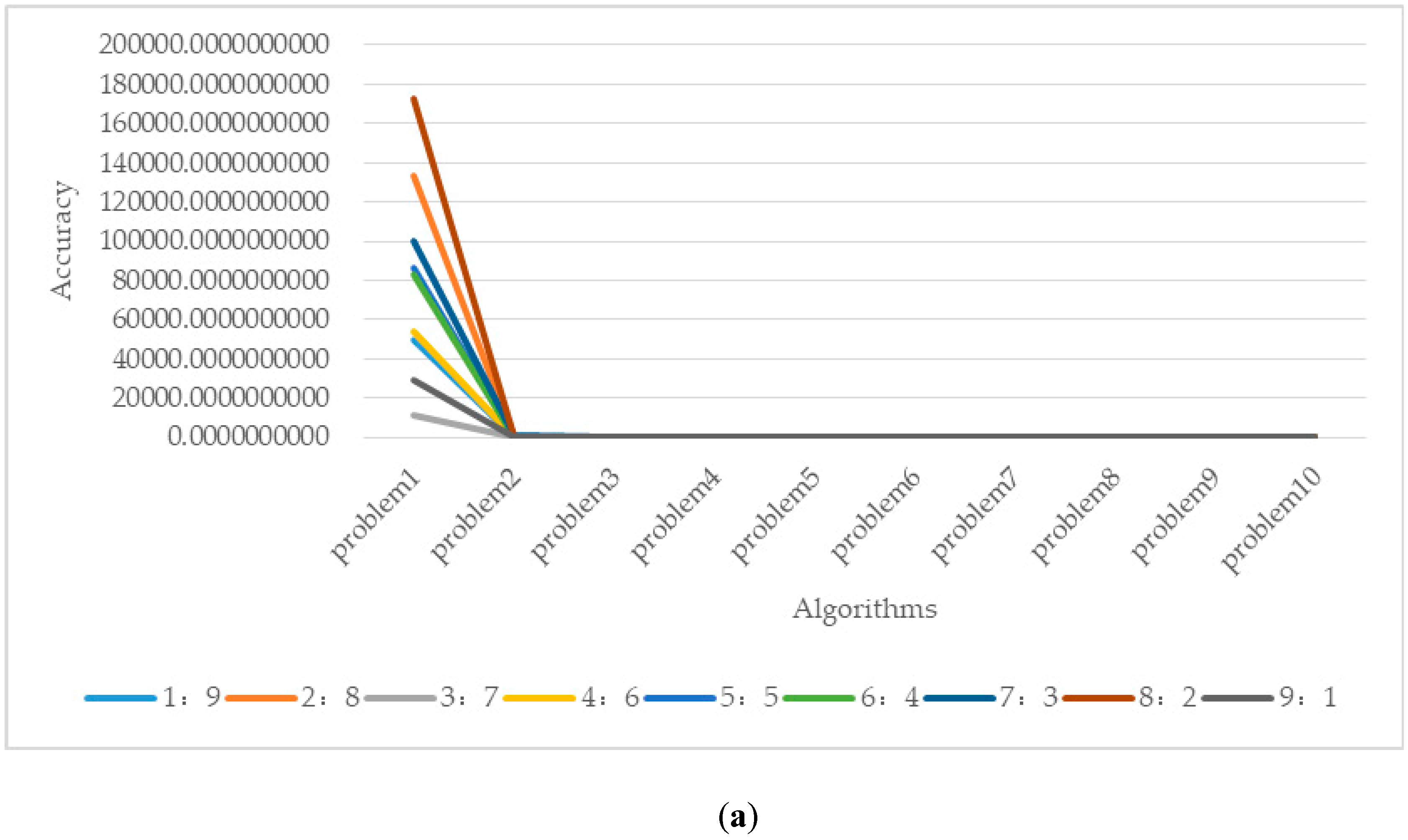
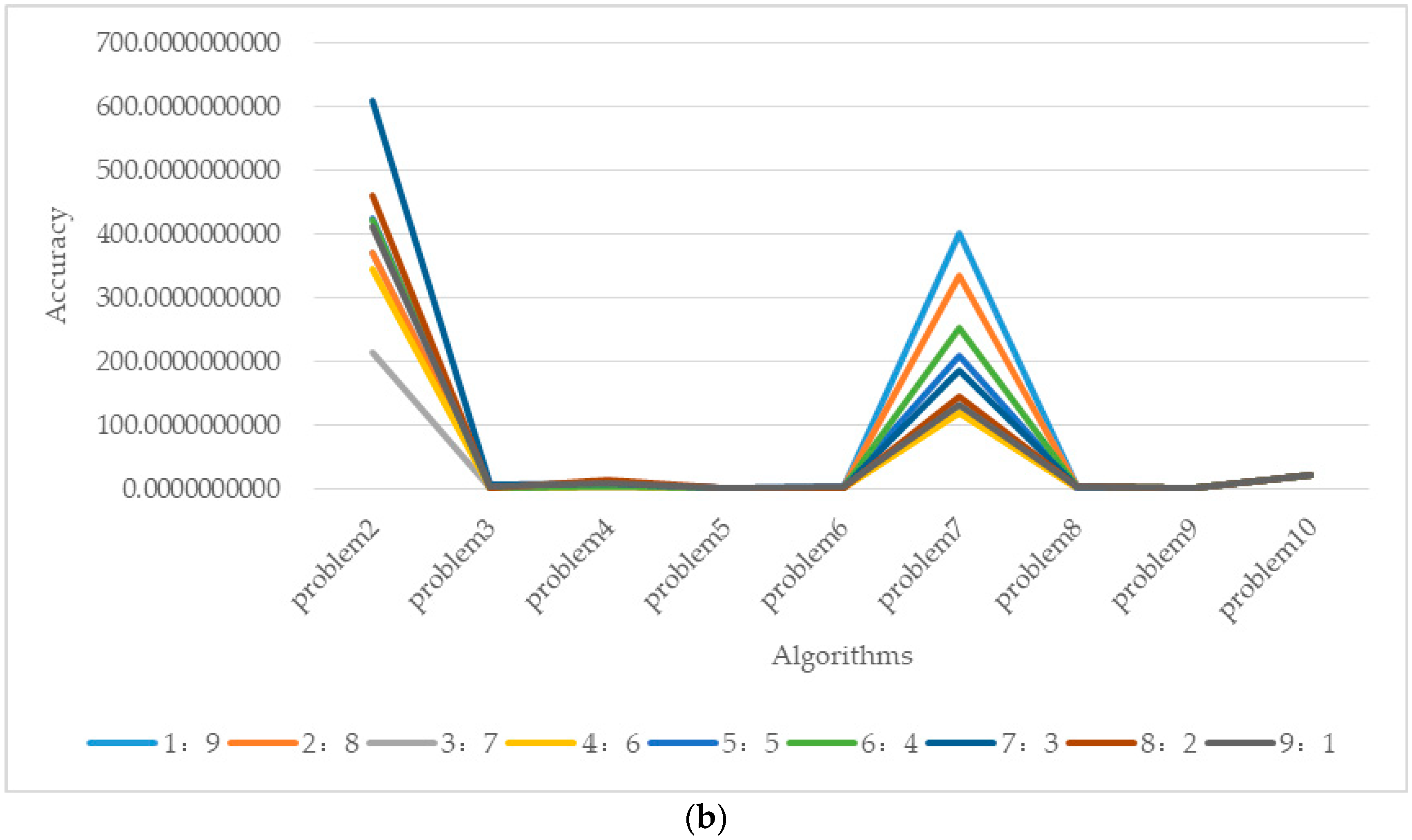
5.2. Evaluation Parameter λ
5.3. Complexity Analysis of AKQPSO
- Step “Partition”: This step accounts for the main computational overhead, so we focus on this step.
- Step “AKH process”: The computational complexity of this step mainly includes “Subpopulation-AKH individuals were optimized by AKH”, “Update through these three actions of the influence of other krill individuals, behavior of getting food and random diffusion”, “The simulated annealing strategy is used to deal with the above behaviors”, and “Update the individual position according to the above behavior”, and their complexities are O(N), O(N2), O(N), and O(N), respectively.
- Step “QPSO process”: The computational complexity of this step mainly includes “Subpopulation-QPSO individuals were optimized by QPSO”, “Update the particle’s local best point Pi and global best point Pbest”, and “Update the position by Equation (10)”, and their complexities are all O(N).
- Other step.
- The computational complexity of Step “Initialization”, Step “Evaluation”, Step “Combination”, and Step “Finding the best solution” are all O(N).
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, X.; Wang, C.; Su, J.; Wang, J. Research and application based on the swarm intelligence algorithm and artificial intelligence for wind farm decision system. Renew. Energy 2019, 134, 681–697. [Google Scholar] [CrossRef]
- Anandakumar, H.; Umamaheswari, K. A bio-inspired swarm intelligence technique for social aware cognitive radio handovers. Comput. Electr. Eng. 2018, 71, 925–937. [Google Scholar] [CrossRef]
- Shang, K.; Ishibuchi, H. A New Hypervolume-based Evolutionary Algorithm for Many-objective Optimization. IEEE Trans. Evol. Comput. 2020, 1. [Google Scholar] [CrossRef]
- Sang, H.-Y.; Pan, Q.-K.; Duan, P.-Y.; Li, J.-Q. An effective discrete invasive weed optimization algorithm for lot-streaming flowshop scheduling problems. J. Intell. Manuf. 2015, 29, 1337–1349. [Google Scholar] [CrossRef]
- Sang, H.-Y.; Pan, Q.-K.; Li, J.-Q.; Wang, P.; Han, Y.-Y.; Gao, K.-Z.; Duan, P. Effective invasive weed optimization algorithms for distributed assembly permutation flowshop problem with total flowtime criterion. Swarm Evol. Comput. 2019, 44, 64–73. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Sang, H.-Y.; Duan, J.-H.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl. Based Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Gao, D.; Wang, G.-G.; Pedrycz, W. Solving Fuzzy Job-shop Scheduling Problem Using DE Algorithm Improved by a Selection Mechanism. IEEE Trans. Fuzzy Syst. 2020, 1. [Google Scholar] [CrossRef]
- Li, M.; Xiao, D.; Zhang, Y.; Nan, H. Reversible data hiding in encrypted images using cross division and additive homomorphism. Signal Process. Image Commun. 2015, 39, 234–248. [Google Scholar] [CrossRef]
- Li, M.; Guo, Y.; Huang, J.; Li, Y. Cryptanalysis of a chaotic image encryption scheme based on permutation-diffusion structure. Signal Process. Image Commun. 2018, 62, 164–172. [Google Scholar] [CrossRef]
- Fan, H.; Li, M.; Liu, N.; Zhang, E. Cryptanalysis of a colour image encryption using chaotic APFM nonlinear adaptive filter. Signal Process. 2018, 143, 28–41. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.-W.; Hu, Y.; Zhang, W. Feature selection algorithm based on bare bones particle swarm optimization. Neurocomputing 2015, 148, 150–157. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, X.-F.; Gong, D.-W. A return-cost-based binary firefly algorithm for feature selection. Inf. Sci. 2017, 418, 561–574. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Tang, J.; Li, Y. Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network. Adv. Mech. Eng. 2018, 10, 10. [Google Scholar] [CrossRef]
- Jian, M.; Lam, K.M.; Dong, J. Facial-feature detection and localization based on a hierarchical scheme. Inf. Sci. 2014, 262, 1–14. [Google Scholar] [CrossRef]
- Fan, L.; Xu, S.; Liu, D.; Ru, Y. Semi-Supervised Community Detection Based on Distance Dynamics. IEEE Access 2018, 6, 37261–37271. [Google Scholar] [CrossRef]
- Wang, G.; Chu, H.E.; Mirjalili, S. Three-dimensional path planning for UCAV using an improved bat algorithm. Aerosp. Sci. Technol. 2016, 49, 231–238. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H.; Shao, M. Path Planning for Uninhabited Combat Aerial Vehicle Using Hybrid Meta-Heuristic DE/BBO Algorithm. Adv. Sci. Eng. Med. 2012, 4, 550–564. [Google Scholar] [CrossRef]
- Wang, G.; Cai, X.; Cui, Z.; Min, G.; Chen, J. High Performance Computing for Cyber Physical Social Systems by Using Evolutionary Multi-Objective Optimization Algorithm. IEEE Trans. Emerg. Top. Comput. 2017, 8, 1. [Google Scholar] [CrossRef]
- Cui, Z.; Sun, B.; Wang, G.; Xue, Y.; Chen, J. A novel oriented cuckoo search algorithm to improve DV-Hop performance for cyber-physical systems. J. Parallel Distrib. Comput. 2017, 103, 42–52. [Google Scholar] [CrossRef]
- Jian, M.; Lam, K.M.; Dong, J. Illumination-insensitive texture discrimination based on illumination compensation and enhancement. Inf. Sci. 2014, 269, 60–72. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. The model and algorithm for the target threat assessment based on elman_adaboost strong predictor. Acta Electron. Sin. 2012, 40, 901–906. [Google Scholar]
- Jian, M.; Lam, K.M.; Dong, J.; Shen, L. Visual-Patch-Attention-Aware Saliency Detection. IEEE Trans. Cybern. 2014, 45, 1575–1586. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Lu, M.; Dong, Y.-Q.; Zhao, X.-J. Self-adaptive extreme learning machine. Neural Comput. Appl. 2015, 27, 291–303. [Google Scholar] [CrossRef]
- Mao, W.; Zheng, Y.; Mu, X.; Zhao, J. Uncertainty evaluation and model selection of extreme learning machine based on Riemannian metric. Neural Comput. Appl. 2013, 24, 1613–1625. [Google Scholar] [CrossRef]
- Liu, G.; Zou, J. Level set evolution with sparsity constraint for object extraction. IET Image Process. 2018, 12, 1413–1422. [Google Scholar] [CrossRef]
- Liu, K.; Gong, D.; Meng, F.; Chen, H.; Wang, G. Gesture segmentation based on a two-phase estimation of distribution algorithm. Inf. Sci. 2017, 88–105. [Google Scholar] [CrossRef]
- Parouha, R.P.; Das, K.N. Economic load dispatch using memory based differential evolution. Int. J. Bio-Inspired Comput. 2018, 11, 159–170. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; El-Sehiemy, R.A.; Wang, G. A novel parallel hurricane optimization algorithm for secure emission/economic load dispatch solution. Appl. Soft Comput. 2018, 63, 206–222. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; El-Sehiemy, R.A.; Deb, S.; Wang, G. A novel fruit fly framework for multi-objective shape design of tubular linear synchronous motor. J. Supercomput. 2017, 73, 1235–1256. [Google Scholar] [CrossRef]
- Yi, J.-H.; Xing, L.; Wang, G.; Dong, J.; Vasilakos, A.V.; Alavi, A.H.; Wang, L. Behavior of crossover operators in NSGA-III for large-scale optimization problems. Inf. Sci. 2020, 509, 470–487. [Google Scholar] [CrossRef]
- Yi, J.-H.; Deb, S.; Dong, J.; Alavi, A.H.; Wang, G. An improved NSGA-III algorithm with adaptive mutation operator for Big Data optimization problems. Future Gener. Comput. Syst. 2018, 88, 571–585. [Google Scholar] [CrossRef]
- Liu, G.; Deng, M. Parametric active contour based on sparse decomposition for multi-objects extraction. Signal Process. 2018, 148, 314–321. [Google Scholar] [CrossRef]
- Sun, J.; Miao, Z.; Gong, D.; Zeng, X.-J.; Li, J.; Wang, G.-G. Interval multi-objective optimization with memetic algorithms. IEEE Trans. Cybern. 2020, 50, 3444–3457. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, G.; Li, K.; Yeh, W.-C.; Jian, M.; Dong, J. Enhancing MOEA/D with information feedback models for large-scale many-objective optimization. Inf. Sci. 2020, 522, 1–16. [Google Scholar] [CrossRef]
- Srikanth, K.; Panwar, L.K.; Panigrahi, B.; Herrera-Viedma, E.; Sangaiah, A.K.; Wang, G. Meta-heuristic framework: Quantum inspired binary grey wolf optimizer for unit commitment problem. Comput. Electr. Eng. 2018, 70, 243–260. [Google Scholar] [CrossRef]
- Chen, S.; Chen, R.; Wang, G.; Gao, J.; Sangaiah, A.K. An adaptive large neighborhood search heuristic for dynamic vehicle routing problems. Comput. Electr. Eng. 2018, 67, 596–607. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G. Binary moth search algorithm for discounted {0–1} knapsack problem. IEEE Access 2018, 6, 10708–10719. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.; Wang, L. Solving randomized time-varying knapsack problems by a novel global firefly algorithm. Eng. Comput. 2018, 34, 621–635. [Google Scholar] [CrossRef]
- Abdel-Basst, M.; Zhou, Y. An elite opposition-flower pollination algorithm for a 0–1 knapsack problem. Int. J. Bio-Inspired Comput. 2018, 11, 46–53. [Google Scholar] [CrossRef]
- Yi, J.-H.; Wang, J.; Wang, G. Improved probabilistic neural networks with self-adaptive strategies for transformer fault diagnosis problem. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Li, Y.; Yan, Y. Bearing fault diagnosis with auto-encoder extreme learning machine: A comparative study. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 1560–1578. [Google Scholar] [CrossRef]
- Mao, W.; Feng, W.; Liang, X. A novel deep output kernel learning method for bearing fault structural diagnosis. Mech. Syst. Signal Process. 2019, 117, 293–318. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, W.; Wang, G.; Feng, X. Test-Sheet Composition Using Analytic Hierarchy Process and Hybrid Metaheuristic Algorithm TS/BBO. Math. Probl. Eng. 2012, 2012, 1–22. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic algorithms in search. In Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Mistry, K.; Zhang, L.; Neoh, S.C.; Lim, C.P.; Fielding, B. A Micro-GA Embedded PSO Feature Selection Approach to Intelligent Facial Emotion Recognition. IEEE Trans. Cybern. 2017, 47, 1496–1509. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Song, X.-F.; Zhang, Y.; Guo, Y.-N.; Sun, X.-Y.; Wang, Y.-L. Variable-size Cooperative Coevolutionary Particle Swarm Optimization for Feature Selection on High-dimensional Data. IEEE Trans. Evol. Comput. 2020, 1. [Google Scholar] [CrossRef]
- Sun, Y.; Jiao, L.; Deng, X.; Wang, R. Dynamic network structured immune particle swarm optimisation with small-world topology. Int. J. Bio-Inspired Comput. 2017, 9, 93–105. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Abualigah, L.M.; Khader, A.T.; Hanandeh, E.S.; Gandomi, A.H. A novel hybridization strategy for krill herd algorithm applied to clustering techniques. Appl. Soft Comput. 2017, 60, 423–435. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model. 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H.; Deb, S. A Multi-Stage Krill Herd Algorithm for Global Numerical Optimization. Int. J. Artif. Intell. Tools 2016, 25, 1550030. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H.; Gong, D. A comprehensive review of krill herd algorithm: Variants, hybrids and applications. Artif. Intell. Rev. 2019, 51, 119–148. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Gandomi, A.H.; Hao, G.-S.; Wang, H. Chaotic Krill Herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man. Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Zheng, F.; Zecchin, A.C.; Newman, J.P.; Maier, H.R.; Dandy, G.C. An Adaptive Convergence-Trajectory Controlled Ant Colony Optimization Algorithm With Application to Water Distribution System Design Problems. IEEE Trans. Evol. Comput. 2017, 21, 773–791. [Google Scholar] [CrossRef]
- Dorigo, M.; Stutzle, T. Ant Colony Optimization; MIT Press: Cambridge, UK, 2004. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Gao, S.; Yu, Y.; Wang, Y.; Wang, J.; Cheng, J.; Zhou, M. Chaotic Local Search-Based Differential Evolution Algorithms for Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2019, 1–14. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An Adaptive Island Evolutionary Algorithm for the berth scheduling problem. Memetic Comput. 2020, 12, 51–72. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Delayed Start Parallel Evolutionary Algorithm for just-in-time truck scheduling at a cross-docking facility. Int. J. Prod. Econ. 2019, 212, 236–258. [Google Scholar] [CrossRef]
- Agapitos, A.; Loughran, R.; Nicolau, M.; Lucas, S.; OrNeill, M.; Brabazon, A. A Survey of Statistical Machine Learning Elements in Genetic Programming. IEEE Trans. Evol. Comput. 2019, 23, 1029–1048. [Google Scholar] [CrossRef]
- Back, T. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Kashan, A.H.; Keshmiry, M.; Dahooie, J.H.; Abbasi-Pooya, A. A simple yet effective grouping evolutionary strategy (GES) algorithm for scheduling parallel machines. Neural Comput. Appl. 2016, 30, 1925–1938. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H.; Deb, S. A hybrid method based on krill herd and quantum-behaved particle swarm optimization. Neural Comput. Appl. 2015, 27, 989–1006. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Wang, H.; Duan, H.; Liu, L.; Li, J. Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural Comput. Appl. 2012, 24, 853–871. [Google Scholar] [CrossRef]
- Abualigah, L.M.; Khader, A.T.; Hanandeh, E.S. A combination of objective functions and hybrid Krill herd algorithm for text document clustering analysis. Eng. Appl. Artif. Intell. 2018, 73, 111–125. [Google Scholar] [CrossRef]
- Niu, P.; Chen, K.; Ma, Y.; Li, X.; Liu, A.; Li, G. Model turbine heat rate by fast learning network with tuning based on ameliorated krill herd algorithm. Knowl. Based Syst. 2017, 118, 80–92. [Google Scholar] [CrossRef]
- Slowik, A.; Kwasnicka, H. Nature Inspired Methods and Their Industry Applications—Swarm Intelligence Algorithms. IEEE Trans. Ind. Inform. 2018, 14, 1004–1015. [Google Scholar] [CrossRef]
- Brezočnik, L.; Fister, J.I.; Podgorelec, V. Swarm Intelligence Algorithms for Feature Selection: A Review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef]
- Sun, C.; Jin, Y.; Cheng, R.; Ding, J.; Zeng, J. Surrogate-Assisted Cooperative Swarm Optimization of High-Dimensional Expensive Problems. IEEE Trans. Evol. Comput. 2017, 21, 644–660. [Google Scholar] [CrossRef]
- Tran, B.N.; Xue, B.; Zhang, M. Variable-Length Particle Swarm Optimization for Feature Selection on High-Dimensional Classification. IEEE Trans. Evol. Comput. 2019, 23, 473–487. [Google Scholar] [CrossRef]
- Tran, B.N.; Xue, B.; Zhang, M. A New Representation in PSO for Discretization-Based Feature Selection. IEEE Trans. Cybern. 2018, 48, 1733–1746. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, X.; Wang, Y.; Zhou, M. Dual-Environmental Particle Swarm Optimizer in Noisy and Noise-Free Environments. IEEE Trans. Cybern. 2019, 49, 2011–2021. [Google Scholar] [CrossRef]
- Bornemann, F.; Laurie, D.; Wagon, S.; Waldvogel, J. The siam 100-digit challenge: A study in high-accuracy numerical computing. SIAM Rev. 2005, 1, 47. [Google Scholar]
- Epstein, A.; Ergezer, M.; Marshall, I.; Shue, W. Gade with fitness-based opposition and tidal mutation for solving ieee cec2019 100-digit challenge. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 395–402. [Google Scholar]
- Brest, J.; Maučec, M.S.; Bošković, B. The 100-digit challenge: Algorithm jde100. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 19–26. [Google Scholar]
- Zhang, S.X.; Chan, W.S.; Tang, K.S.; Zheng, S.Y. Restart based collective information powered differential evolution for solving the 100-digit challenge on single objective numerical optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 14–18. [Google Scholar]
- Jun, S.; Bin, F.; Wenbo, X. Particle swarm optimization with particles having quantum behavior. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; Volume 321, pp. 325–331. [Google Scholar]
- Wang, G.; Gandomi, A.H.; Alavi, A.H.; Hao, G.-S. Hybrid krill herd algorithm with differential evolution for global numerical optimization. Neural Comput. Appl. 2014, 25, 297–308. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H. Stud krill herd algorithm. Neurocomputing 2014, 128, 363–370. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Gandomi, A.H.; Zhang, Z.; Alavi, A.H. Chaotic cuckoo search. Soft Comput. 2016, 20, 3349–3362. [Google Scholar] [CrossRef]
- Wang, G.; Lu, M.; Zhao, X. An improved bat algorithm with variable neighborhood search for global optimization. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 1773–1778. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Wang, G.; Tan, Y. Improving Metaheuristic Algorithms With Information Feedback Models. IEEE Trans. Cybern. 2017, 49, 542–555. [Google Scholar] [CrossRef]
- Yang, X.-S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L. A Novel Hybrid Bat Algorithm with Harmony Search for Global Numerical Optimization. J. Appl. Math. 2013, 2013, 1–21. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. Dynamic Deployment of Wireless Sensor Networks by Biogeography Based Optimization Algorithm. J. Sens. Actuator Netw. 2012, 1, 86–96. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.-X.; Tian, S.-S.; Zou, J. Dynamic cuckoo search algorithm based on taguchi opposition-based search. Int. J. Bio-Inspired Comput. 2019, 13, 59–69. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Zhao, X.; Chu, H.C.E. Hybridizing harmony search algorithm with cuckoo search for global numerical optimization. Soft Comput. 2016, 20, 273–285. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Coelho, L.D.S. Earthworm optimization algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Int. J. Bio-Inspired Comput. 2018, 12, 1–22. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Coelho, L.D.S. Elephant herding optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI 2015), Bali, Indonesia, 7–9 December 2015; pp. 1–5. [Google Scholar]
- Wang, G.-G.; Deb, S.; Gao, X.-Z.; Coelho, L.d.S. A new metaheuristic optimization algorithm motivated by elephant herding behavior. Int. J. Bio-Inspired Comput. 2016, 8, 394–409. [Google Scholar] [CrossRef]
- Wang, G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018, 10, 151–164. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspired Comput. 2010, 2, 78. [Google Scholar] [CrossRef]
- Wang, H.; Yi, J.-H. An improved optimization method based on krill herd and artificial bee colony with information exchange. Memetic Comput. 2018, 10, 177–198. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Liu, F.; Sun, Y.; Wang, G.-G.; Wu, T. An artificial bee colony algorithm based on dynamic penalty and chaos search for constrained optimization problems. Arab. J. Sci. Eng. 2018, 43, 7189–7208. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Zhao, X.; Cui, Z. A new monarch butterfly optimization with an improved crossover operator. Oper. Res. 2018, 18, 731–755. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Multi-stage genetic programming: A new strategy to nonlinear system modeling. Inf. Sci. 2011, 181, 5227–5239. [Google Scholar] [CrossRef]


| No. | Functions | D | Search Range | |
|---|---|---|---|---|
| 1 | Storn’s Chebyshev Polynomial Fitting Problem | 1 | 9 | (−8192–8192) |
| 2 | Inverse Hilbert Matrix Problem | 1 | 16 | (−16,384–16,384) |
| 3 | Lennard–Jones Minimum Energy Cluster | 1 | 18 | (−4–4) |
| 4 | Rastrigin’s Function | 1 | 10 | (−100–100) |
| 5 | Griewangk’s Function | 1 | 10 | (−100–100) |
| 6 | Weierstrass Function | 1 | 10 | (−100–100) |
| 7 | Modified Schwefel’s Function | 1 | 10 | (−100–100) |
| 8 | Expanded Schaffer’s F6 Function | 1 | 10 | (−100–100) |
| 9 | Happy Cat Function | 1 | 10 | (−100–100) |
| 10 | Ackley Function | 1 | 10 | (−100–100) |
| Parameters | N | max_gen | max_run |
|---|---|---|---|
| Value | 50 | 7500 | 100 |
| Algorithm | Problem 1 | Problem 2 | Problem 3 |
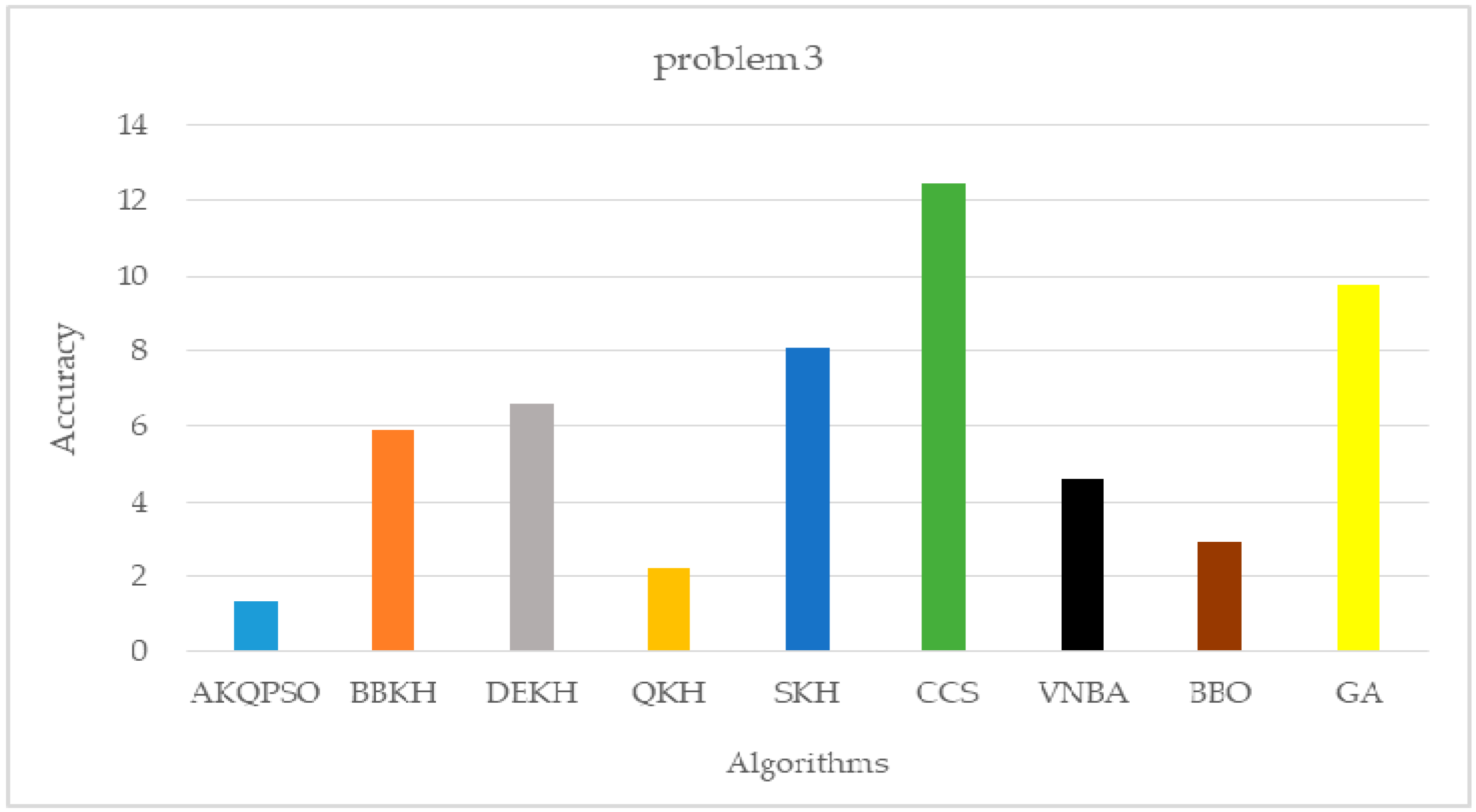
| AKQPSO (Algorithm 3) | 10,893.3861385383 | 215.6832766302 | 1.3068652046 |
| BBKH | 291,803.2852933580 | 613.7135086878 | 5.9027057769 |
| DEKH | 975,339.7308122220 | 708.0601338156 | 6.5872946609 |
| QKH | 47,583.9014728552 | 404.4416682185 | 2.1853645745 |
| SKH | 1,773,168.4809322700 | 402.7243166556 | 8.0692567398 |
| CCS | 211,411.5538712060 | 358.9175375272 | 12.4818284785 |
| VNBA | 2,550,944.5550316900 | 816.8071391350 | 4.6163144446 |
| BBO | 72,287.9373622652 | 311.8124377894 | 2.9209583205 |
| GA | 8,009,879.0206872900 | 2209.1904660292 | 9.7547945042 |
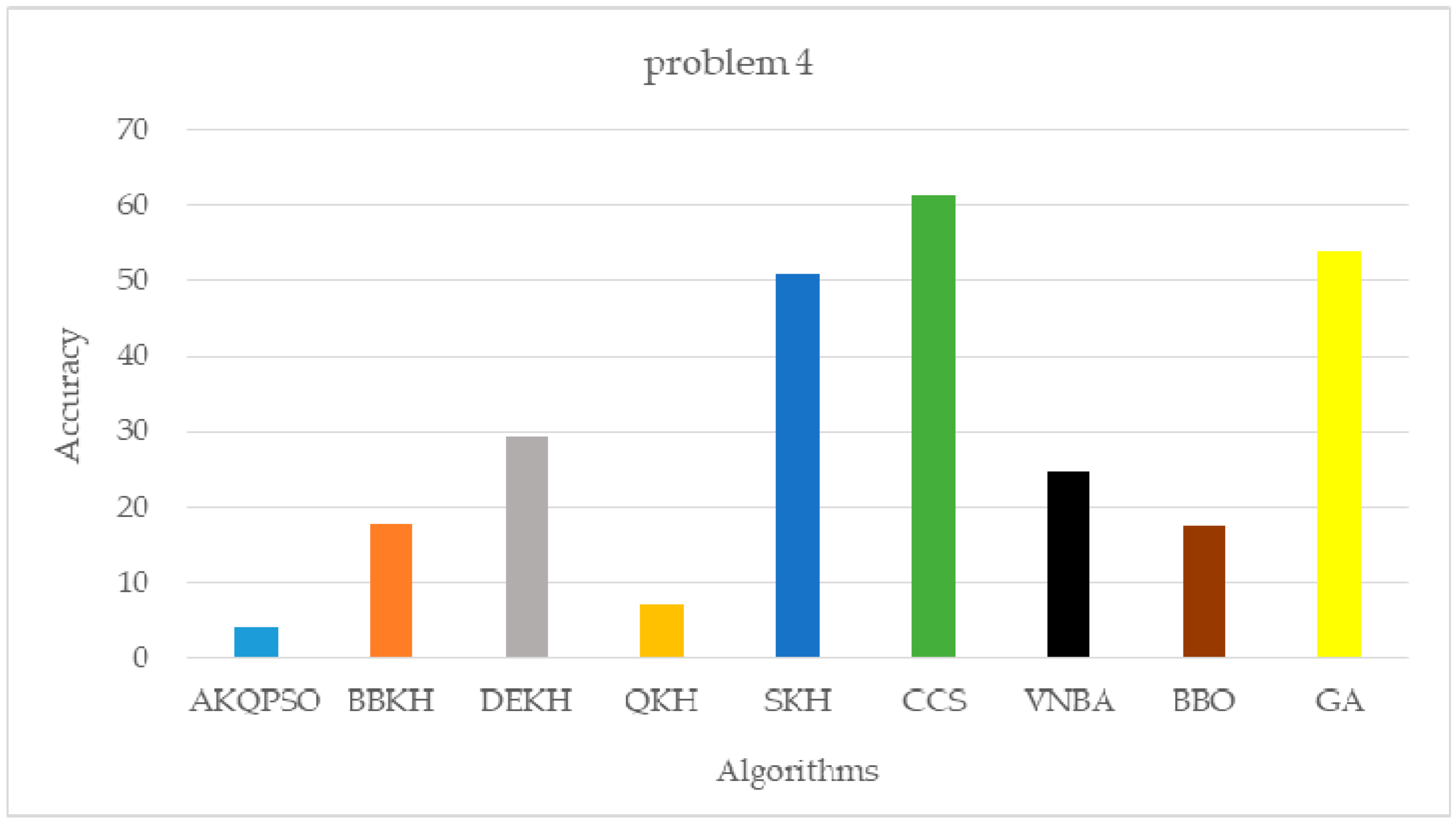
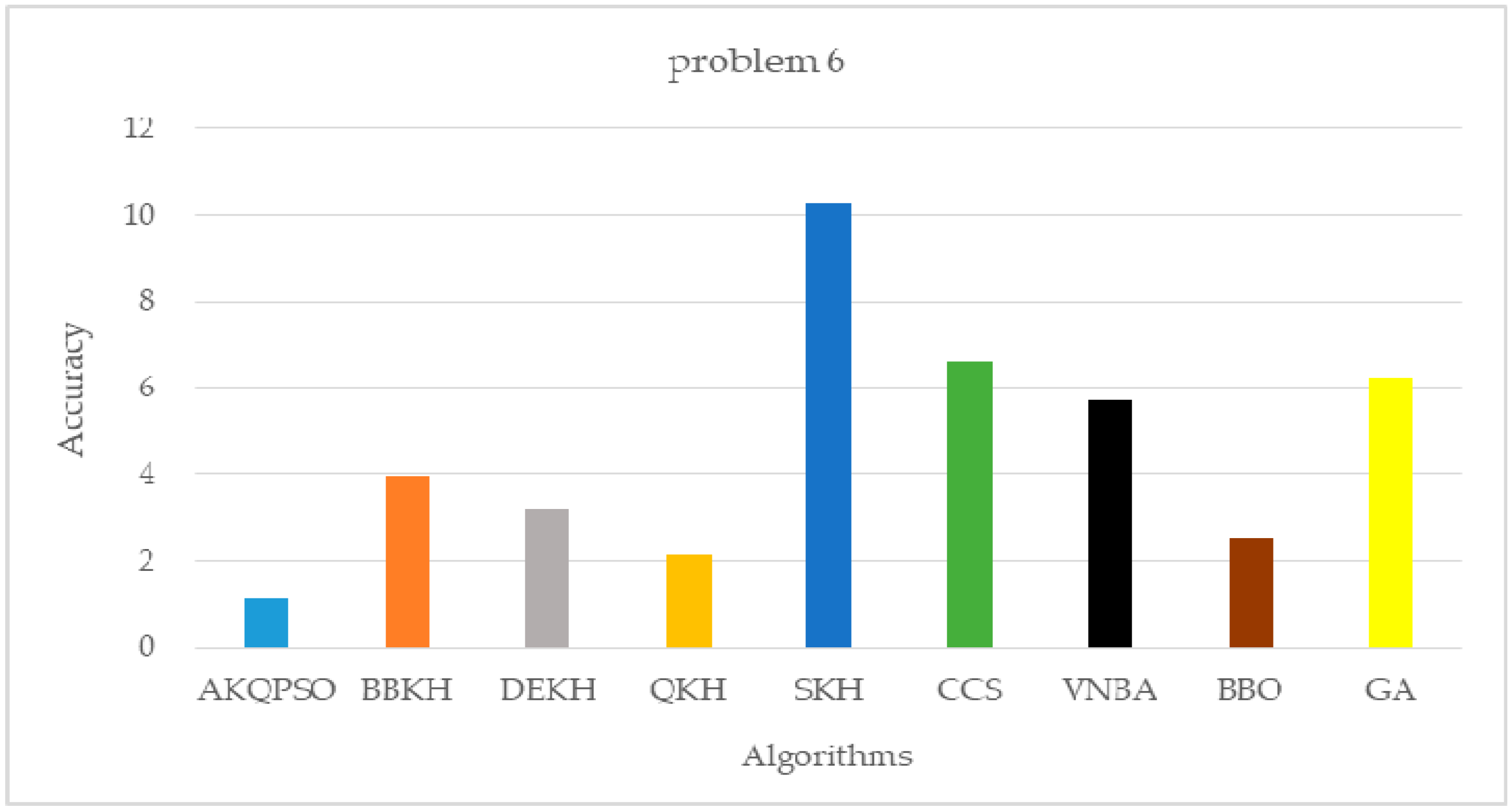
| Algorithm | Problem 4 | Problem 5 | Problem 6 |
| AKQPSO (Algorithm 3) | 4.0398322695 | 1.0434696313 | 1.1185826442 |
| BBKH | 17.7900443880 | 1.8852367864 | 3.9551854227 |
| DEKH | 29.4088567232 | 1.9507021960 | 3.1953451545 |
| QKH | 7.1133424631 | 2.0695362381 | 3.1213610789 |
| SKH | 50.9548872356 | 1.9350825919 | 10.2543233489 |
| CCS | 61.4604530135 | 3.4583111771 | 6.6010211976 |
| VNBA | 24.7278199397 | 3.0251295691 | 5.7134938818 |
| BBO | 17.4206259198 | 1.0971964590 | 2.5154932374 |
| GA | 53.9444360765 | 2.7126573212 | 6.2420012291 |
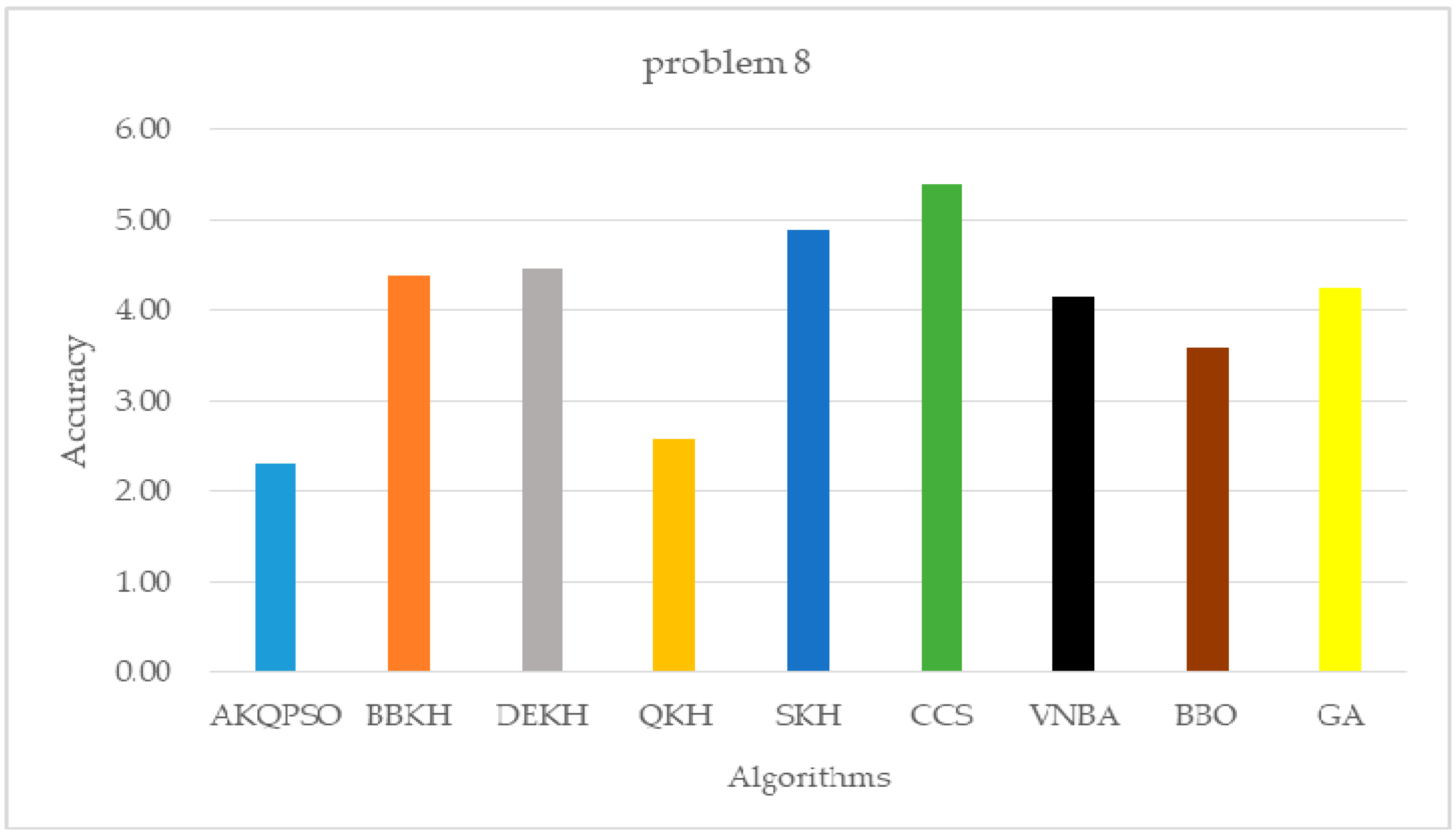
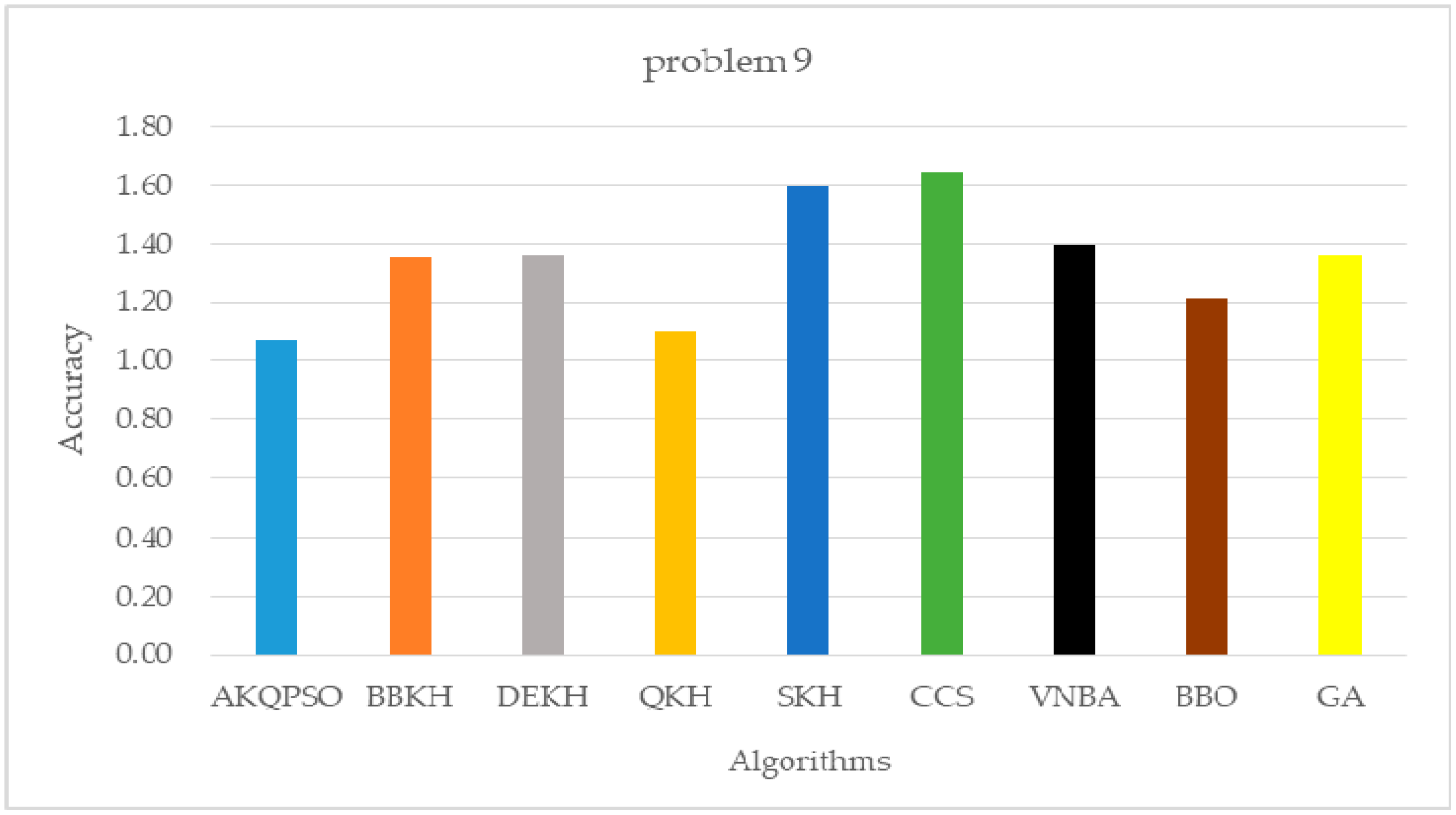
| Algorithm | Problem 7 | Problem 8 | Problem 9 |
| AKQPSO (Algorithm 3) | 121.8932375270 | 2.3131324015 | 1.0715438957 |
| BBKH | 779.4066229661 | 4.3846591727 | 1.3554069744 |
| DEKH | 1060.0387128932 | 4.4509969471 | 1.3614909209 |
| QKH | 195.0770363640 | 2.5711387868 | 1.2989726797 |
| SKH | 1348.8213407547 | 4.8795287164 | 1.5980935412 |
| CCS | 2247.4406602539 | 5.4002626350 | 1.6453371395 |
| VNBA | 644.6334455535 | 4.1477932707 | 1.3950038682 |
| BBO | 950.8018632939 | 3.5941524656 | 1.2098037868 |
| GA | 1276.4565372145 | 4.2393160129 | 1.3580083289 |
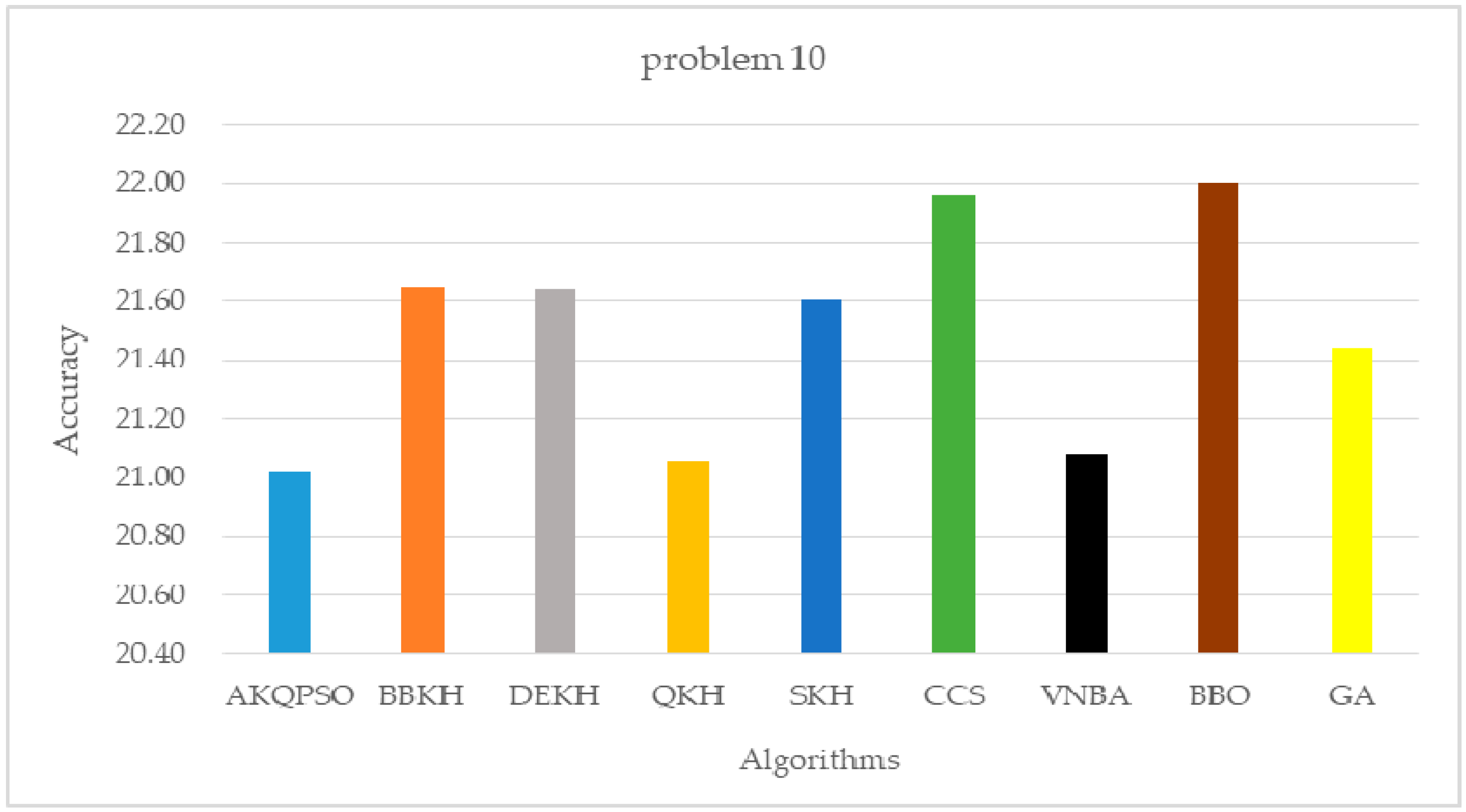
| Algorithm | Problem 10 | - | - |
| AKQPSO (Algorithm 3) | 21.0237707978 | - | - |
| BBKH | 21.6420368754 | - | - |
| DEKH | 21.6383024320 | - | - |
| QKH | 21.1582649016 | - | - |
| SKH | 21.6017549654 | - | - |
| CCS | 21.9603961872 | - | - |
| VNBA | 21.0799825759 | - | - |
| BBO | 21.9988888954 | - | - |
| GA | 21.4392031521 | - | - |
| λ | Problem 1 | Problem 2 | Problem 3 | Problem 4 | Problem 5 |
| 0.1 | 49,649.1118923043 | 371.5625700159 | 1.4091799599 | 6.9697543426 | 1.1082189445 |
| 0.2 | 133,608.1106469210 | 370.0473039979 | 1.4091358439 | 3.9848771713 | 1.0983396055 |
| 0.3 | 10,893.3861385383 | 215.6832766302 | 1.3068652046 | 4.0398322695 | 1.0434696313 |
| 0.4 | 53,539.2035950009 | 346.1060025716 | 1.4091347288 | 4.9798362284 | 1.0588561989 |
| 0.5 | 86,346.3589566716 | 424.4795442904 | 1.4091497973 | 5.9747952855 | 1.0564120753 |
| 0.6 | 82,979.4098834243 | 422.2483723507 | 1.4094790359 | 5.0457481023 | 1.0861547616 |
| 0.7 | 99,948.7393233432 | 609.3844384539 | 7.7057897580 | 7.9647083618 | 1.0885926731 |
| 0.8 | 172,794.7224327620 | 462.1482898652 | 1.4091546130 | 13.9344627044 | 1.0689273036 |
| 0.9 | 29,013.1541012323 | 412.4776865757 | 3.9404220234 | 8.9597299262 | 1.0642761100 |
| λ | Problem 6 | Problem 7 | Problem 8 | Problem 9 | Problem 10 |
| 0.1 | 1.4704093392 | 401.1855067018 | 3.0118025092 | 1.0958187632 | 21.1048204811 |
| 0.2 | 1.2289194470 | 336.4312675492 | 2.7987816724 | 1.0968167661 | 21.0708288643 |
| 0.3 | 1.1185826442 | 121.8932375270 | 2.3131324015 | 1.0715438957 | 21.0237707978 |
| 0.4 | 2.6943320338 | 119.5337169812 | 2.3299026264 | 1.1010758378 | 21.0389405345 |
| 0.5 | 2.9771884111 | 209.5578114314 | 2.5217968033 | 1.1257275250 | 21.0587530353 |
| 0.6 | 2.5706601162 | 253.1211550958 | 3.5227629532 | 1.1353127271 | 21.0976573470 |
| 0.7 | 1.4737157145 | 187.5895821815 | 3.0884949525 | 1.1344605652 | 21.1144506567 |
| 0.8 | 1.5487741806 | 144.3502633617 | 3.1612574448 | 1.1553497252 | 21.0835644844 |
| 0.9 | 4.0000000000 | 131.2707035329 | 4.0209018951 | 1.1615503990 | 21.0768903380 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.-L.; Wang, G.-G. Hybrid Annealing Krill Herd and Quantum-Behaved Particle Swarm Optimization. Mathematics 2020, 8, 1403. https://doi.org/10.3390/math8091403
Wei C-L, Wang G-G. Hybrid Annealing Krill Herd and Quantum-Behaved Particle Swarm Optimization. Mathematics. 2020; 8(9):1403. https://doi.org/10.3390/math8091403
Chicago/Turabian StyleWei, Cheng-Long, and Gai-Ge Wang. 2020. "Hybrid Annealing Krill Herd and Quantum-Behaved Particle Swarm Optimization" Mathematics 8, no. 9: 1403. https://doi.org/10.3390/math8091403
APA StyleWei, C.-L., & Wang, G.-G. (2020). Hybrid Annealing Krill Herd and Quantum-Behaved Particle Swarm Optimization. Mathematics, 8(9), 1403. https://doi.org/10.3390/math8091403






