Abstract
Electoral systems are modified by individuals who have incentives to bias the rules for their political advantage (i.e., gerrymandering). To prevent gerrymandering, legislative institutions can rely on mathematical tools to guarantee democratic fairness and territorial contiguity. These tools have been successfully used in the past; however, there is a need to accommodate additional meanings of the term fairness within the electoral systems of modern democracies. In this paper, we present an optimization framework that considers multiple criteria for drawing districts and assigning the number of representatives. Besides some typical districting criteria (malapportionment and contiguity), we introduce novel criteria for ensuring territorial equilibrium and incentives for candidates to deploy their representation efforts fairly during their campaign and period in office. We test the method, which we denote as Multi-criteria Pen, in a recent and a forthcoming reform of the Chilean electoral system. The results show the potential of our tool to improve the current territorial design and offers insights on the motivations, objectives, and deficiencies of both reform plans.
1. Introduction and Motivation
The reform of an electoral system typically includes the design of districts (by grouping elementary territorial units to define a political territory) and the assignment of representatives to them. Because an unequal representation of the population is seen as nondemocratic, electoral reforms must ensure an adequate equilibrium in the distribution of political power among districts [1,2,3]. Otherwise, some voters are better represented than others, a phenomenon known as malapportionment, and it is considered as a “pathology of electoral systems” (see [4]). Formally, malapportionment is defined as the difference between the number of representatives of a territory and the fraction of representatives that would correspond to its population if representatives were evenly distributed [5]; the smaller the difference, the closer the system is to the equity principle of representative democracies, namely “one person, one vote” [6].
Despite its importance, reforms do not always satisfy this principle. One of the major reasons is that countries have geo-administrative divisions that burden the possibility of defining politically fair districts [7]. These limitations introduce unavoidable malapportionment, and some districts will be over-represented (i.e., the number of assigned seats (or representatives) will be larger than what it should be according to its population) while others will be sub-represented. The actual issue arises when distortions result from deliberate actions taken by political institutions that want to change the current districting plan. Malapportionment becomes a problem when decision-makers design districts to benefit their own interests (see [8,9] for recent case analysis on the issue), specially because of its self-perpetuating nature (the distortion facilitates advantageous conditions for those in power when peforming future modifications). This phenomenon is known as gerrymandering (see [10] for an early reference on this topic). In a gerrymandering situation, redistricting becomes a matter of reorganizing districts to benefit incumbent representatives, a specific party, or a special interest group (see [11]). Evidently, such misuse of institutional power affects how citizens view democracy and alter the distribution of resources from the central administration to the districts (see [12,13] for an in-depth analysis on the U.S. case).
Even when gerrymandering is not a part of the decision-making process, the suspicion of gerrymandering is still a threat to the acceptance of the plan. This work tries to address this problem or, more precisely, it tries to answer the questions on how to draw districts without political bias and how to reach a generalized consensus among stake-holders when designing and implementing a political reform. Because answers to these questions are difficult, reforms to electoral systems are not common (we refer the reader to [1,14,15,16] and the references therein, for fundamental textbooks discussing this issue). The resistance of political systems to undergo electoral reforms is strong in well-established democracies (see [17,18]). However, when the political parties of incumbents overcome this resistance and support an electoral reform, there are two main issues discussed: (i) the electoral formula that will transform votes into seats and (ii) the design of the districts and how they approximate to the ideal of “one person, one vote”.
Furthermore, the legitimacy of democracy and effectiveness of representation are increasingly being questioned; we refer the reader to [19,20,21,22] for theoretical and empirical discussions on these phenomena. As a result, electoral systems must account for broader expressions of democratic and demographic fairness. As shown in [23,24], the structure of the districts plays a relevant role in the democratic representation that exceeds the quest for a minimum level of malapportionment. Moreover, the authors in [3,5] stress the need for electoral systems that increase electoral competition and political engagement among candidates and parties during their campaign and mandates. In other words, the democratic value of an electoral system shall be measured not only by malapportionment, but also by other expressions of democratic and demographic fairness.
In this paper, we present a multi-criteria mathematical optimization framework that we refer to as Multi-Criteria Pen. It is utilized for drawing districts and assigning seats to procure districting policies that embody a broader sense of political fairness rather than minimizing a single malapportionment function. On the one hand, it tackles malapportionment not only locally, but systemically. On the other hand, it seeks solutions that incorporate other features of territorial fairness within and among districts. Specifically, it tries to encourage candidates, parties, and coalitions to diversify their efforts to expand the number of voters that see their needs being represented by the candidates. The five considered criteria are (i) global equity, expressed by minimizing of the sum of the malapportionment of all districts; (ii) balancedness, encoded by minimizing of the maximum malapportionment among all districts to avoid the democratic inequity being concentrated in a single district; (iii) compactness, addressed by the minimization of territorial dispersion among districts; (iv) global demographic fairness, expressed by maximizing the assignment balance of the most populated cities among the different districts; and, (v) local demographic fairness, approached by seeking districts in which the distance between the two most populated cities is maximized. While the first three criteria encompass measures of democratic equity and compactness, the fourth and fifth criteria, introduced here for the first time, try to avoid territorial concentration, ensure territorial equilibrium among districts and provide incentives for candidates to deploy representation efforts (during the election, and later during office) across the whole district. While our experiments only consider these five criteria, the method is general enough to consider other fairness criteria, such as the representation of minorities or ethnic groups among others.
Consider the following example to illustrate the demographic fairness criteria: Let us suppose that we want to define two territories; assume that there are three major territorial units (i.e., cities) A, B and C, that concentrate, respectively, the 30%, 30%, and 20% of the total population, while the remaining 20% of the population is uniformly distributed among 10 other territorial units. Likewise, assume that the pairwise distance among the cities is (A,B) = 40 km, (A,C) = 50 km, and (B,C) = 90 km. Given this demographic structure, the global demographic fairness criterion would prefer a districting setting in which cities A and B belong to different districts, say X and Y. As city C must be part of either district, the local demographic fairness criterion would prefer city C to be part of Y (as B is further from C than A). Evidently, a districting plan where A and B belong to the same district induces an unbalanced distribution of power as no less than 60% of the population of the region would be part of a single district. Likewise, by including city C in the same district of B we will ensure that the candidate (and later the elected representative) will deploy more efforts to represent the territorial diversity of the district. We would create more incentives for the candidates of district X to invest efforts into seeking the electoral support of voters from small towns and including their needs in their political program.
The method proposed to tackle this problem is a hybrid algorithm comprising two phases. In the first phase, we solve a mixed integer linear programming (MILP) model. In the second phase, we use a multiobjective local-search procedure to explore the Pareto frontier and return a pool of non-dominated solutions (i.e., districting plans) with different trade-offs among the considered criteria. Decision-makers would then choose among non-dominated solutions according to hard-to-formalize criteria that are common in political systems. Finally, the method is tested on recent redistricting plans in Chile as well as on a recent presidential effort to further modify the districting plan.
Our contribution and paper outline: Our framework extends the previous work on districting from the political science, applied mathematics, and operational research communities (see [25,26,27,28]), in several directions. First, and to the best of our knowledge, our approach is the first one to include demographic fairness criteria in the systematic design of districts. Second, it optimizes the five criteria simultaneously by constructing the so-called Pareto frontier; therefore, it provides a pool of efficient solutions to the decision-makers. This feature is crucial, since it helps decision-makers to make more informed decisions. Third, we implemented the proposed framework and tested the performance of a recent electoral law reform in Chile and the recent suggestion of the president of Chile to further change the electoral system. In both cases, the comparison between the results of the framework and the implemented and suggested changes shed some light on the interests and gerrymandering issues from each proposal, enabled us to audit the performance and criteria behind the decisions-makers that propel such changes. The results also show that our tool can design electoral systems that considerably improve the current system, both in classical measures of fairness as well in the newly introduced ones. The results that were associated with the suggestion of the Chilean president were published on the main online news portal in Chile on 16th June 2019 [29]. Furthermore, following this publication, a more complete report was delivered to governmental authorities as input for redrawing the current electoral system as part of the constitutional reform project.
2. Literature Review
2.1. Malapportionment
Malapportionment is a pathology of electoral systems that corresponds to a distortion in political representation because of a disproportional assignment of seats to electoral districts [5] or (see [30] for a thorough review on this phenomenon); in other words, “malapportionment is the disjuncture between the share of population in an electoral district and its share of seats” (see [31] for a recent reference). Although there are some researchers that consider that malapportionment may be a desirable attribute in countries with strong cultural and historical division [7], there is a wide consensus that over- and sub-represented districts should be avoided [1,15]. Deliberate malapportionment can be seen as an elaborate mechanism to rig an election, even when it may not be seen as such (see [5]). Notwithstanding, the distortion that is induced by over- or sub-representing a territory has a significant impact on the political distribution of power [32].
Frequently, electoral systems that are characterized by high degrees of malapportionment respond to partisan-biased designs [33,34,35]. The incumbents in charge of reforming electoral systems tailor districts (and the assignment of seats) to favor their political interests, hence maximizing their chances of electoral success. This practice is known as gerrymandering [36]. A similar situation occurs when authoritarian regimes transition to democracies, and the authorities design districts to maximize the potential electoral success of political parties that share their ideology. In [5], the authors argued that “malapportionment appears to be a key component of electoral systems in many newly-democratic countries”. In Latin America, for example, studies suggest that malapportionment favors politically-conservative rural districts at the expense of politically-progressive urban districts. Furthermore, according to [37], “beyond efforts to screen and split their competitors, authoritarian incumbents often institute self-serving electoral rules that give them a decisive edge at the moment of translating votes into seats. They design biased rules of representation to prevent an eventual loss of votes from translating into a loss of power”. In [31], the authors established that there is a curvilinear relationship between democracy and malapportionment, i.e., “[malapportionment] exists at relatively low levels in consolidated democracies and highly authoritarian countries and at relatively high levels in countries in the middle of the democratic-authoritarian spectrum”.
There is a large body of literature devoted to studing malapportionment in different countries, see examples regarding Chile [38,39], Romania [8], India [40], Turkey [41], France [36], Brazil [42,43], Argentina [44], the United States [45,46,47,48], and African countries [49]. In Africa, a so-called “rural bias” is suggested in [49], a phenomenon that also occurs in other democracies that are emerging from authoritarian regimes. Chile is/was one of most representative cases of this phenomenon. The authoritarian regime that ruled the country from 1973 to 1990 knew that they had firm support in rural areas. Therefore, when designing the electoral system, they arbitrarily over-represented rural areas at the expense of sub-representing urban areas where opposition had tronger support [38,39]. This rural bias has other political consequences; according to [5], “in new democracies, overrepresentation of rural districts can contribute to the maintenance, and even the proliferation, of nondemocratic enclaves at the subnational level”.
2.2. Political Districting: An Optimization Perspective
The design of political districts has been approached as an optimization problem for decades, and the so-called Political Districting Problem (PDP) is a fundamental combinatorial optimization problem (see [50] for one of the earliest references on mathematical optimization developments for the PDP). The PDP corresponds to the problem of aggregating territorial units (like municipalities or counties) to maximize a measure of (electoral) fairness or to minimize a measure of unfairness (malapportionment) while ensuring a set of topological and functional requirements. From a modeling point of view, the PDP typically enforces three conditions (or constraints).
The first of these conditions is integrity, i.e., each territorial unit must belong to exactly one district (see [26,51]). The second condition is compactness and it imposes conditions on the shape of the territories. Compactness is a guarantee against political interference, gerrymandering.
A common strategy for modeling compactness is to use the moment of inertia. This concept is defined as the product sum amongst the total population of each territorial unit and the squared distance between the unit and the center of its district (see [27,52,53]). Another common strategy for ensuring compactness is to impose a limit on the diameter of the district [54]. We refer the reader to [26] for a detailed review of compactness measures in political districting optimization. A third condition is contiguity or connectivity, i.e., each district should comprise a geographically connected set of territorial units. In the earliest references of electoral districts design (see [50]), every feasible territory should be connected.
The above conditions are common in most of the related literature (see [55]); however, there are specific PDP variants that seek additional conditions, such as geographical considerations [55,56,57], socio-economic homogeneity [58], compliance with existing administrative subdivisions [59,60], or representation of ethnic minorities [54,61]. In [58,62,63,64,65], the authors seek PDP solutions that perform well with respect to socio-economic homogeneity and similarity to the current electoral districts, among other criteria, by combining these measures into a single weighted objective function, and solving the resulting optimization problem with a general purpose algorithm.
From an algorithmic point of view, the literature reports different strategies to solve PDPs from classical exact approaches to modern heuristics (we refer the reader to [66] for a relatively recent review on algorithmic aspects of the PDP). It is worth mentioning that, from an algorithmic point of view, imposing connectivity typically leads to difficult to solve optimization problems. Connectivity is, by far, the main computational bottleneck of many approaches for solving PDPs. Therefore, several strategies for ensuring connectivity have been used over the decades, according the algorithmic strategy in use. Ad-hoc algorithms (see [67,68]), metaheuristics (see [63,69,70]), or MILP-based approaches (see [71]) use different modelling decision to impose contiguity. For a complementary discussion on the PDP, we refer the reader to [66,72,73] and recommend the literature reviews on the PDP available in [66,74,75,76].
3. The Multi-Criteria Pen for FAIR Districting
In this section, we present the methodological framework devised for the design or reform of an electoral system. Given the particularities of different electoral systems, we first give a basic description of the system for which we designed the method, i.e., the Chilean electoral system, and then give an overall description of the solution strategy. In addition, and before giving details of the resolution method, we discuss how to apply the framework to other electoral systems.
The Chilean electoral system divides the country into regions and considers the municipalities as the elementary territorial units. Each region is divided into one or more electoral districts, each selecting a variable number of representatives. The number of electoral districts, the total number of representatives, and the minimum and the maximum number of representatives allotted to each district are fixed by electoral law. This system naturally leads to a two-phase approach in which we first assign the number of electoral districts and representatives to each region, and then we assign municipalities in each region to the different districts.
Schematically, our strategy is comprised by the following phases:
- Phase I: formulate and solve a MILP model that minimizes the total malapportionment of the system by optimally grouping territorial units (i.e., municipalities) and assigning the number of representatives to these groups. Following Chilean regulations, we ensure that electoral districts comply with the regional boundaries (i.e., a district only contains municipalities of a given territory). In this phase, we do not enforce contiguity or compactness and aim to find a fair distribution of districts to regions, and representatives to districts.
- Phase II: the second phase is only required when a region contains two or more districts.
- Step 1: the solution from Phase I is repaired to obtain a solution that satisfies connectivity constraints. The resulting design corresponds to a feasible design for the electoral system.
- Step 2: a pool of efficient solutions, i.e., alternative districting plans, is sought by exploring the set of feasible solutions using a multi-objective optimization approach.
Some electoral systems may not require each of these phases and steps. For instance, if the electoral system does not consider regions, or the country does not have an internal division as such, Step I is omitted. Similarly, electoral systems where each district assigns a single representative should define the minimum and maximum number of representatives for each district to one or remove the condition for Phase I.
Notation and preliminaries: Let be the set of elementary territorial units (the municipalities in our case study), so that corresponds to the population or a measure of the population of the territorial unit , e.g., could correspond to the electoral roll of that unit (we will use this definition), and let . Likewise, let be the Cartesian coordinates of the geographical centroid of territorial unit ; and let : be the distance function, so that , , correspond to the distance between unit i and j. The proposed method considers the number of districts and the number of seats as input for the PDP, as these values are usually obtained through political discussions. Let be the desired number of districts, and let be the total number of seats. Complementary, let and be the minimum number and maximum number of seats to be assigned to any district, respectively.
Let be a vector of binary variables, such that if unit j is selected as district root (these variables are used within the model and criterion objective functions to ease calculation and can be see as auxiliary variables). Let be a vector of binary variables, such that if unit i is assigned to a district rooted at unit j if units belong to different regions variable and may be removed from the model. Finally, let be a vector of variables so that corresponds to the number of seats assigned to a district rooted at unit j.
3.1. The Criteria of Democratic and Demographic Fairness
A districting plan is encoded by a particular realization of the variables, say , which satisfy the conditions of integrity ensured by the domain of the variables and the contiguity condition discussed below.
Democratic fairness criteria: For any given solution, the malapportionment of each district, say the district rooted at unit j, is given by
i.e., the malapportionment is the difference between the fraction of the electoral roll (or population) represented by the district () with respect to the fraction of seats assigned to the district (). If , district j is over-represented, while if , district j is sub-represented; in an ideal case, . When considering this definition of malapportionment per district, the malapportionment of a complete districting plan corresponds to
this is one of the most common ways of measuring malapportionment in the political science literature, and it is based on the well-known Loosemore-Hanby index [77]. We refer the reader to [2,5] for thorough studies on the use of this measure. As pointed out by [5] and others, Equation (1) establishes that the malapportionment of the electoral system is measured by half of the sum of the absolute values of the malapportionment of its districts (note that over-representing part of a population implies under-representing the same amount of population; hence, there is no need to account both times for the same distortion). Given this notation, our first criterion, global equity, corresponds to finding a districting policy so that the value of is minimum.
As explained above, the Equation (1) gives the total malapportionment of the electoral system. As the malapportionment of the districts is accumulated, a low value of may be achieved at the expense of concentrating all of the malapportionment in one or a few districts. The worst malapportionment among the districts of any given districting plan corresponds to
where is the district with the largest malapportionment. Our second criterion, balancedness, corresponds to finding a districting policy so that the value of is minimum.
Demographic fairness criteria: One assumes that districts are territorially compact, i.e., to be geographically smooth. There are several alternatives to enforce such a behavior within districting plans. One approach is to seek territorial aggregations that are centered with respect to their geographical centroid (see [26,53,78,79,80] and the references therein).
This work follows this scheme. Let us consider a districting design encoded by , and, for such a solution, let j be a district. Hence, the coordinates and , of the centroid of the district rooted at unit j are
so the territorial dispersion of a district rooted at j is given by
that corresponds to the sum of the Euclidean distance between the territorial units and the centroids of their districts. Therefore, the total dispersion of the districting design if given by the sum of , , i.e.,
Given this definition of total dispersion, our third criterion, compactness, corresponds to the search for a districting design that minimizes .
Our fourth criterion, global demographic fairness, corresponds to the maximization of the assignment balance of the most populated cities among the different districts (in an ideal case, each of the n most populated territorial units shall be assigned to a different district). To illustrate the evaluation of the criteria, consider two districts, rooted at units j and k. The demographic difference between the most populated units of these districts is given by
i.e., the absolute difference between the population of their most populated territorial units. This function is minimized if the most populated units are assigned to different districts. With this definition, the total demographic difference of the districting design encoded by is expressed as
and by minimizing , we attempt to satisfy the global demographic fairness criterion.
The global demographic fairness criterion addresses the following situation. If a district has two very large territorial units and several (proportionally) small surrounding units, political parties and candidates are likely to focus their campaigns only in the larger territorial units, ignoring other voters. Evidently, this would lead to a biased representation, since the political programs of the candidates are likely to focus only on the demands of voters from more populated units (larger cities). The criterion encoded by (4) discourages the problem by distributing the largest cities among districts.
Finally, we consider the local demographic fairness criterion. Let us consider a given district rooted at ; for this district, territorial units
are the most populated and the second most populated territorial units in the district, respectively. Denote the distance between them as . The total sum of these values is given by
thus, the local demographic fairness criterion aims at minimizing .
For a better understanding of the local demographic fairness criterion, consider the following situation. Suppose that any feasible electoral design is such that at least one district is inevitably comprised by two large territorial units (in terms of population). If that is the case, then we would prefer that this district be one where the two most populated units are as far as possible. Seeking electoral systems that fulfill this criterion is justified by similar arguments for the global demographic fairness criterion, i.e., ensure that the territorial composition will create incentives for a better representation of the territories in the design of the political program and during the electoral campaign. If the distances between the major sources of voters are far from one another in a given district, it is more likely that the electoral campaigns would cover smaller territorial units in between. Therefore, the political programs of successful candidates would cover the demands and needs of a more diverse number of voters from the district.
3.2. First Phase: An MILP Model for Minimum Malapportionment
We now present the MILP model to assign districts and seats to regions while minimizing the total malapportionment, i.e., a model that addresses global equity without imposing connectivity among districts. The second step will address the remaining criteria as well as the connectivity requirements, as discussed in Section 3.3. The solution of the MILP model provides the input for the second phase method, which repairs the solution to ensure connectivity, and then explores the Pareto frontier of the five criteria presented above.
Let be a matrix, such that indicates that territorial unit i can be part of the same district as territorial unit j; otherwise, . This matrix allows us to impose that a district contains units of a single region or province by setting for every pair of units that do not belong to the same region or province. Additionally, this matrix may impose historical or geographical conditions that decision-makers may favor.
Besides the sets of variables , , and defined above, we will use two sets of auxiliary variables. Let be the variable encoding the difference between the portion of population of a district rooted at j and the fraction of seats assigned to a district rooted at j, and let be an auxiliary variable that allows modeling the absolute values of , i.e., , . The MILP model for finding the minimum total malapportionment is stated as (6)–(16)
Objective function (6) encodes the minimization of malapportionment, and it is equivalent to (1). Constraint (7) ensures that every territorial unit is assigned to exactly one district. The fact that districts should be defined is modeled by constraint (8); similarly, constraint (9) ensures that seats are assigned. Constraint (10) evaluates the difference between the portion of population of a district rooted at j and the fraction of seats assigned to the said district (i.e., the value of ), while constraints (11) and (12), together, ensure that variables take the absolute value of , (and can, therefore, be used in the objective function). Constraint (13) ensures that a territorial unit i can be assigned to a district rooted at j if, and only if, the corresponding value of is one. The minimum and maximum number of seats that can be assigned to a given district is imposed by constraints (14) and (15), respectively. Finally, the nature of the variables is imposed by constraint (16).
The solution of (6)–(16) does not correspond to a districting plan that does not ensure contiguity, i.e., the districts do not necessarily comprise connected clusters. Hence, the attained value of malapportionment, , is an ideal value and only serves as a reference. Moreover, solution will serve as input for the process that searches for finding a feasible districting plan.
3.3. Second Phase: An Algorithm to Explore Pareto-Efficient Districting Plans
Given the multi-objective nature of the problem in hand, the second phase aims to compute a set of efficient solutions using an algorithm that is based on the Pareto local search scheme [81]. To describe this procedure, let us first consider the following concepts.
First, recall that a feasible solution, i.e., a feasible districting plan, corresponds to a particular realization of variable sets , , and that satisfies the characteristics encoded by constraints (7)–(16), as well as the contiguity feature (i.e., the resulting districts are territorially connected). Contiguity can be verified by computing strongly connected components in an auxiliary adjacency graph among territorial units, such as the algorithm proposed in [82].
The second concept corresponds to dominance and Pareto optimality, which, in our setting, is defined as:
Definition 1.
(see [83]) A feasible solution is Pareto optimal if, and only if, there is no other feasible solution , such that , , , , , and holds and at least one of the inequalities is strict. A feasible solution is weakly Pareto optimal, if and only if there is no solution , where any inequality is strict.
A feasible solution is said to dominate a feasible solution if the above inequalities hold with at least one strict inequality (if no inequality is strict, then the first solution weakly dominates the second solution).
In other words, a districting design encoded by a solution is Pareto optimal if, and only if, attaining a better value for any of the five criteria necessary implies a sacrifice to the performance of any other criteria (i.e., no other solution dominates the districting design). Note that given the heuristic nature of the proposed method, we do not ensure finding the set of Pareto optimal solutions. Consequently, the Pareto optimality of any given solution is limited to comparison with the set of feasible solutions found during the search and not to the complete set of feasible solutions.
The third concept that we need to introduce is the concept of a local operator, which corresponds to any procedure that receives a feasible solution as input and modifies it by rearranging territorial units among districts to produce a new feasible solution, along with the corresponding assignment of seats. Such an exchange procedure ensures that the resulting solutions complies with constraints (7)–(15) and connectivity requirements. In our approach, we consider two types of local operators: transfer (a territorial unit is transferred from one district to another) and exchange (two territorial units are transferred to the original territory of the other unit). For a given feasible solution, say , the set of all feasible solutions obtained by the local operators is referred to as the neighborhood.
Finally, we introduce the concept of an archive. An archive is a set of non-dominated solutions with two additional operations, add and join. The add operation adds a solution to the archive if it is non-dominated by any solution in the archive and removes any solution from the archive dominated by the said solution. The join operation joins archive B with archive A. The join operation involves the following steps: (1) remove all solutions from archive B that belong to archive A; (2) remove all solutions from archive A dominated by a solution from archive B; (3) remove all solutions from archive B dominated by a solution from archive A; and, (4) perform a traditional set union operation between sets and store its result in archive A.
As in a traditional local search, the Pareto local search method starts from an initial solution, known as the incumbent, and explores its neighborhood. If the method finds a solution with better objective value for any of the criteria, it becomes the incumbent at a later stage, and we repeat the exploration procedure from the new incumbent until no further improvements are possible (i.e., a local optimum is found). The major difference between the Pareto local search and a traditional local search is that multiple solutions are maintained and explored concurrently.
The initial solution corresponds to the modified solution to (6)–(16), where the connectivity has been obtained as follows. First, define an auxiliary connectivity graph in which the set of vertices corresponds to the set of territorial units and the set of edges contains an edge between vertices i and if the territorial units are adjacent in the map and belong to the same district (i.e., for some ) in the solution to (6)–(16). Subsequently, find the set of connected components in the auxiliary connectivity graph and identify the connected components that do not include a root (i.e., for each unit i, holds). If the previous step reports no components without a root, we have an initial feasible solution. Otherwise, randomly select a component with a root and an adjacent component with no root (two components are adjacent if two of its territorial units share a common border) and add an edge in the auxiliary graph between arbitrary vertices from each of the two components. This edge removes a component with no root from the solution, and to obtain a feasible solution, we apply the above procedure until all connected components have a root.
Once an initial solution is available, the local search starts there and explores its neighborhood and adds any solution into an archive of neighbor solutions. This archive becomes both the best known archive and the initial archive for a second iteration of the Pareto local search. Each subsequent iteration operates as follows: (1) builds an archive from the neighbors of each solution in the initial archive; (2) performs a join operation among archives until a single archive is obtained. This archive is denoted as the iteration archive. (3), the iteration performs a join operation from the iteration archive into the best known archive. Save the state of the iteration archive after the third step of the join operation, as it will become the initial archive of the following iteration. The previous process is repeated until the initial archive for an iteration is an empty set.
The resulting best known archive corresponds to a locally optimal solution archive and becomes the pool of solutions reported by the algorithm. Given that the initial solution as well as all generated solutions are feasible districting plans, the solution archive contains a set of viable districting plans for the decision-maker to choose from, each providing a different trade-off between the five criteria without completely dominated solutions.
Finally, the procedure may report different archives if different initial solutions are considered. The previous steps are run with ten different random seeds (each providing a different set of decisions during the construction of the initial solution) and the best known archives from each run are combined into a single solution archive through join operations in order to improve the overall performance of the algorithm.
Besides the method described above, there are additional algorithmic alternatives for solving multicriteria or multiobjective (combinatorial) optimization problems. The reader is referred to [84,85,86], and the references therein, for literature revisions on metaheuristic approaches specially devised for addressing multiobjective combinatorial optimization problems.
4. Results and Discussion: The Chilean Case
In this section, we present the results from applying our methodology to the Chilean Chamber of Deputies. We first describe the, recently modified, rules of the system and then present and discuss the solutions, emphasizing the differences, capabilities, and benefits from our Multi Criteria Pen for drawing electoral districts. We also detail a recently proposed, still under debate, modification to the system.
4.1. Brief Description of the Recent Electoral Reform in the Chilean Parliament
After the defeat of the dictatorship of General Augusto Pinochet (1973–1990) in the 1988 plebiscite to return to democracy, the political leaders of the totalitarian regime designed and established an electoral system that suffered from severe cases of malapportionment and gerrymandering. The system also featured a special case of the D’Hondt (or Jefferson) method to assign seats to political parties, known as the binominal system. In a binominal system, each district elects two representatives, and a seat if given to each of the two most-voted lists unless the most-voted list receives twice as many votes as the second most-voted list. In the later case, both representatives are assigned to the most voted list.
This system ruled the elections from 1989 to 2013, for both cameras, the Senate and the Chamber of Deputies. The system led to two anomalies; first, it perpetuated a political system comprised only by two large coalitions, and second, large majorities, as the ones that were needed to change the rules of the electoral system, were nearly impossible to reach. The led to problems in representativity, diversity, and self-regulatory control.
In 2015, and after several attempts to reform the electoral system, a consensus was reached to create a new and more proportional system. The district layout associated to both chambers changed by merging old districts into larger ones. Moreover, the new system assigned a number of representatives that could vary between districts between a minimum of three and a maximum of eight for the Chamber of Deputies, and from two to five for the Senate. Gerrymandering may still be an issue in the districting plan as the final decision was made in a deliberation of parliament where the current representatives could have argued in favor of a distribution perceived as favorable for them in future elections.
Table 1 summarizes the differences between the old and new system. The new system includes more representatives and the number of seats varies in each district depending on the corresponding population. These changes should improve demographic representation (i.e., a larger number of representatives should lead to smaller malapportionment differences).

Table 1.
Comparison of the main characteristics of the electoral system valid from 1990 until 2015 and the reformed electoral system established in 2015 (see [39]). M stands for the number of representatives under election for the district.
The system simplified the territorial design used to elect the Senate but not for the Chamber of Deputies. Each region of the Chilean administrative divisions corresponds to one district to elect senators, but to elect deputies, the regions are divided into one or more electoral districts, creating an opportunity for gerrymandering. Table 2 provides the details of the new districting plan. The content of each column is as follows: Region, is the name the administrative unit; New district (j), corresponds to the unique identifier of each of the 28 districts; Previous District, provides the id of the previous districts merged to define the new district; # seats, provides the number of seats assigned to the district; % electoral roll, is the fraction of the total electoral roll corresponding to the district; % district seats, corresponds to the fraction of the chamber seats assigned to the district; MAL, provides the malapportionment value of the district; and, (1), provides the total malapportionment of each region. The values of (1) are computed according to the expression (1); for instance, for the Metropolitana region, the malapportionment is given by

Table 2.
Summary of the Chamber of Deputies electoral system defined in the 2015 reform.
The following are additional reported values (2), the worst-case malapportionment among the different districts of the corresponding region; (3), the value of the territorial dispersion among districts, (4), the value of total demographic difference (sum of the absolute differences between the population of the most populated territorial units among districts)r; and, (5), the sum, among all districts, of the weighted distance between the two most populated territorial units within the district. The latter four columns are computed only for those regions comprising more than one district.
The last row reports the total number of seats (155) and the malapportionment of the complete electoral system (or country-wise malapportionment), which is 9.96 (i.e., the sum of the MAL values of each region); therefore, any change to the system must be assessed, at least from the point of view of democratic equity, by measuring how the induced systematic malapportionment compares to 9.96.
The values reported in column MAL show that the most populated regions (Valparaíso, Metropolitana, and Bío-Bío) are sub-represented, while the less populated regions (Arica, Aysén, and Magallanes) are over-represented. Evidently, the most notable case corresponds to the Metropolitana region; although almost 40% of the electoral roll inhabit this region, only 30% of the representantives correspond to the region. This result is common in countries with a hyper-concentration of the population in the capital area (see [1]). On the one hand, assigning more seats to the capital area is unpopular and, on the other, it might perpetuate structural inequalities that are produced by such demographic unbalance. The current districting design of the Metropolitana region is displayed in Figure 1a; but, even in this situation, Table 2 shows that there are different degrees of unbalancedness within the region.
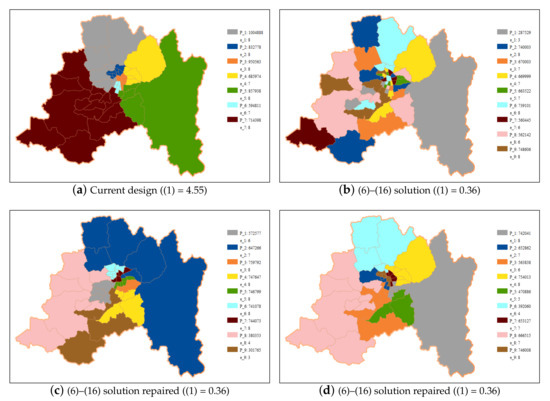
Figure 1.
Comparison of districting designs for Region Metropolitana.
4.2. Computing (First-Phase): Results and Discussion
As explained in Section 3, the first step of our methodological framework corresponds to the resolution of the MILP model (6)–(16). We solve the model for the Chamber of Deputies using ILOG CPLEX 12.8, an off-the-shelf, state-of-the-art software for MILP and other related optimization problems. Following the notation that is presented in Section 3, the set V corresponds to the territorial units (in Chile, the municipalities). Their electoral roll corresponds to the values of , for every territorial unit , and the administrative divisions (i.e., regions in this case) are encoded by matrix . Besides this demographic data, the information provided in Table 1 indicates that (number of districts), (number of seats), (minimum number of seats per district), and (maximum number of seats per district).
Table 3 reports the results that were obtained by solving the resulting instance of the MILP model (6)–(16). The attained value of country-wise malapportionment is 3.29, a third of the value of the current design (9.96, as shown in Table 2). Consequently, it is not possible to group cities, assign seats, and produce a country-wise malapportionment lower than 3.29, but this value may be unattainable due to the contiguity requirements being ignored.

Table 3.
Summary of the Chamber of Deputies electoral system obtained by solving (6)–(16).
One interesting finding is that the O’Higgins and Los Lagos regions are better represented by a single district, with eight and seven seats, respectively, than by two districts. In the current system, the malapportionment of these regions is 0.33 and 0.44, respectively (see Table 2), and each of them is assigned 9 seats; while the districting design produced by model (6)–(16) has malapportionments equal to 0.00 and 0.21. The assignment of these districts to the Metropolitana region also allows for a better allocation in this region. This result hints that incumbents divided these regions according to criteria other than representativity (these regions were formerly divided into four districts as shown in Table 1) and to increase their chances of re-election.
Despite the attained results, as model (6)–(16) does not guarantee connectivity, the solution of the regions with two or more districts (Valparaíso, Metropolitana, Maule, Bío-Bío, and Araucanía) may not be feasible. This can be seen in Figure 1b, where we show the districting design for the Metropolitana region. Territorial units are grouped into nine scattered districts, assigning 60 seats, and inducing a malapportionment equal to 0.36. The values of malapportionment for single-district regions are optimal as no better spatial distribution can be achieved. The methodology proceeds to Phase II for regions with two or more districts.
4.3. Exploring the Efficient Solutions (Second-Phase): Results and Discussion
For the case under study, we apply the second phase of the algorithmic framework to Valparaíso, Metropolitana, Maule, Bío-Bío and Araucanía regions. The goals of this phase are: (1) to draw connected districts for these regions without a significant worsening of the attained district and country-wise malapportionment and (2) to explore the different trade-offs between alternative metrics of fairness.
In Figure 1c, we show some districting plans provided by this phase. Among the different districting plans, we replicate the arrangement with minimum malapportionment that maximizes the number of territorial units that remain in the same district as in the disconnected design. As shown in the caption, these solutions have the same malapportionment than the solution from the first phase, i.e., no degradation of the solution is required to obtain connectivity. In Figure 1d, we show another solution from the second phase with minimum malapportionment that maximizes the common surface between districts in each solution. As in the previous case, this districting plan is not only feasible, but also achieves the minimum possible malapportionment. These two figures reveal that there are feasible districting designs for the Metropolitana region with a malapportionment almost 13 times lower than the current one. The same situation holds for Valparaíso, Maule, Bío-Bío, and Araucanía regions, i.e., it is possible to repair the MILP-based solutions and to obtain feasible districting plans with the same malapportionment values as the corresponding scattered one. Therefore, one could reform the whole electoral system of the Chamber of Deputies with a new territorial organization that has the same number of districts, assigns the same number of seats, and induces a global demographic equity level equal to 3.29 (a third of the level of the current system).
If we analyze the pool of efficient solutions provided by the method for each region, we find the set of efficient solution contains 14 feasible solutions for the Valaparíso region. In the case of the Metropolitana, Maule, Bío-Bío and Araucanía regions, the set of efficient solution contain 915, 12, 23, and 13 feasible solutions, respectively. Notice that the differences between the Metropolitana region and the other regions is a direct result of the larger number of possible territorial designs provided by the larger number of districts and territorial units of the Metropolitana region.
We consider the best solution found for each of the criteria and compare it to the solution provided by the districting plan in use in order to expose the ability of the approach to obtain better solutions than the current approach. The comparison is made in terms of the relative differences between our proposal and the current design. For instance, in the case of Metropolitana region, the best possible value of the global equity criteria is MAL, and the global equity of the current system is MAL; therefore, the relative difference of the global equity criteria is given by
i.e., the best performance that we can obtain for the global equity criteria is 92% better than the performance of the current system. If we replicate this for the other four criteria, we obtained the following results
These values reveal that our approach is capable of producing solutions that largely improve the current system in all criteria, with the exception of the global demographic fairness criterion, measured by (4), where we get a performance that is 54% inferior than the one of the current system. This result is attributed to the differences between the current design (with seven districts) and our design (with nine districts) as function (4) will increase its value if more districts are considered.
We replicated this analysis for the other four regions and the results are shown in Table 4. In the column #dist, we report the number of districts; in the column #seats, we report the number of assigned seats; and in the rest of the columns, we report the relative differences in the performance of the different criteria when comparing the best possible values with the values associated to the current design. The values reported in this table show that our approach is capable of producing districting decisions that largely outperform the current design in basically all criteria for all regions comprising two or more districts.

Table 4.
Current system v/s Our method: Relative differences (in %) in the performance of the five criteria.
We now display how the trade-offs among the different criteria influence the territorial deployment of the districting design. In Figure 2a, we show the districting design that corresponds to the solution obtained by the following procedure. First, we limit our analysis to all of the solutions that minimize the balancedness criterion () and, second, among these solutions, we found the solutions with the minimum value of the global demographic fairness criterion (). In this case, we observe that achieving the best possible performance for the balancedness criterion does not imply worsening the global equity criterion. However, attaining the best performance for the compactness criterion () implies trade-offs in terms of the global demographic fairness criterion (1), as seen in Figure 2b. For the performance of the compactness criterion, the is 14.79, which is considerably worse than 0.36. Figure 2c,d are equivalent to the other two figures, but address the global and local demographic fairness criteria, respectively. The information provided in the caption of these figures show that the best possible performance of global demographic fairness () does not yield an important worsening of the global demographic fairness (); while for local demographic fairness, achieving its best performance () does imply a considerable deterioration of global democratic fairness ().
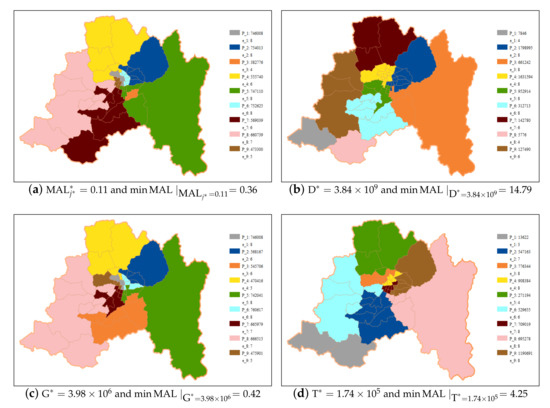
Figure 2.
Districting designs for the Metropolitana region: Pursuing the best performance for each criterion.
As described in Section 2, along with democratic fairness (measured by (1)), compactness is one the most important criteria when reforming an electoral system. In Figure 3, we show two districting plans from the Metropolitana region with opposite performance with respect to compactness. In Figure 3a, we show the districting design with the best performance of the compactness criterion () among the solutions that achieverd, the minimum malapportionment (); while, Figure 3b shows the districting plan with the worst performance of the compactness criterion ( = ) among the solutions that achieve the minimum malapportionment (). In terms of compactness, the solution shown in Figure 3b is 40% worse than the solution shown in Figure 3a. A visual inspection reveals that districts 1, 4, 5, and 8 in Figure 3b have odd shapes; while only districts 2 and 3 present odd shapes in the design shown in Figure 3a.
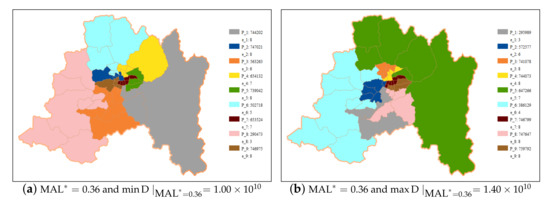
Figure 3.
Districting designs for the Metropolitana region: Opposite performances of compactness for .
To complement the results that are presented in Figure 2, we provide in Table 5 a more complete analysis regarding the trade-offs of global democratic fairness to compactness, global demographic fairness and local demographic fairness. The first column, , reports the relative difference between the best performance of the global democratic fairness criterion ( in the case of the Metropolitana region) and the best performance of the same criterion when achieving the best performance for the compactness criterion ( in the case of the same region), i.e.,

Table 5.
Trade-offs of global democratic fairness (in %): Differences when pursuing compactness, global demographic fairness, and local demographic fairness.
Complementary, in , we report the relative difference between the best performance of the compactness criterion ( for the Metropolitana region) and the best performance of the same criterion when achieving the best performance for the global democratic fairness criterion ( in the case of the same region), i.e.,
The rest of the entries in the table are computed in an equivalent manner for the other criteria. The reported values lead us to the following observations: (i) when pursuing the best performance for compactness and global demographic fairness criteria (columns 2 and 3), we sacrifice the performance of the global democratic fairness criterion, especially for the compactness criterion; (ii) seeking the best performance of the local demographic fairness criterion (column 4), implies a deterioration of the global democratic fairness criterion only for the Metropolitana region, most likely due to the considerably larger number of districts with respect to two or three district regions; (iii) seeking an optimal performance of the global democratic fairness criterion implies a deterioration of the performance of the compactness criterion (column 5); and, (iv) pursuing an optimal performance of the global democratic fairness criterion does not necessarily lead to a deterioration of the global and local demographic fairness criteria (columns 6 and 7), with the exception of the Valparaíso region where the local demographic fairness criterion worsens its performance when compared to the best known performance.
The attained results show the potential of the proposed tool to produce a wide range of solutions with different performance trade-offs. Furthermore, even if malapportionment (measured by (1)) is the pivoting criterion, there are several alternatives featuring an optimal value of malapportionment and different values for the remaining criteria. This represents a unique opportunity for decision-makers, who are now capable of including further considerations in the design process (e.g., socioeconomic characteristics, ethnicity composition, etc.), to tip the balance in favor of designs that embody a broader notion of democratic fairness.
Finally, Figure 4 provides a graphical representation of the efficiency sets provided by the method. As we have five different criteria, we consider pairwise comparisons and do not include , as there is a high correlation between and , leading to near-identical efficient sets. Each figure shows all of the Pareto-efficient solutions and the lines join Pareto-efficient solutions according to the two criteria objectives under consideration. While the figures show a degree of correlation among some of these metrics, it highlights the ability of the method to explore the relations between criteria when there is a trade-off between them.
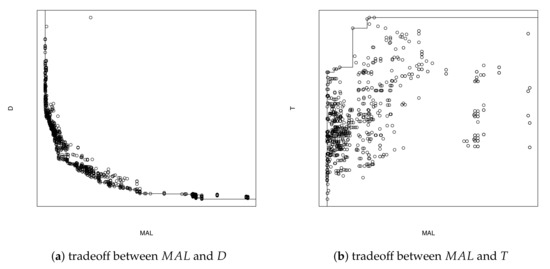
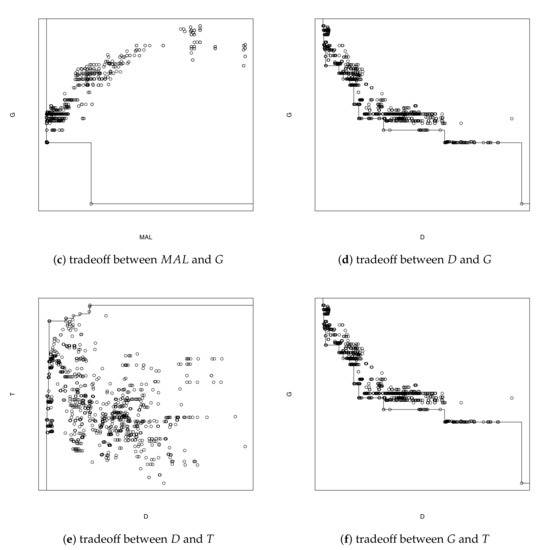
Figure 4.
Pareto fronts for the “Metropolitana” region.
4.4. A New Redistricting Plan
In the 2019 annual report to the nation by the President of Chile, the President suggested a new reform of the system. The reform tries to palliate the general malcontent from the population with the current democratic system and reduce the costs that are associated to the system itself. While the details were unclear, the idea that circulated through the press was that the new system would increase “the quality of the political system” while reducing the number of representatives from 155 to 120 changing the minimum and maximum representatives per district in unspecified ways.
If we run the framework under similar conditions, we find results that do not greatly differ from the ones that are discussed above, at least in terms of malapportionment; see detailed results are reported in the Appendix A section. First, it is still possible to improve upon the current districting plan by redistributing districts and, especially, representatives, even if fewer representatives are considered. As reported in Table A1, we are able to produce a districting design for a 120 seats chamber with malapportionment equal to 2.39, which is better than the malapportionment of the current 155 seats design (9.96) and considerably better than the malapportionment of the previous 120 seats design (16.1). Second, the new system needs to reduce the lower and upper limits on the number of seats per district in order to obtain representative solutions. Otherwise, the minimum number of representatives per district introduce a large level of malapportionment. Third, the reduction in the number of representatives should affect mostly the less populated regions. Unsurprisingly, the number of seats in metropolitana region is held almost constant from the current plan with 155 representatives to the new plan with only 120 representatives. Fourth, and most importantly, the resulting system tends towards the binominal system with the exception of the Metropolitana region and other heavily populated regions.
To conclude, while the proposed approach may, in fact, improve upon the current plan, other features of the resulting plan make it less than desirable (e.g., it could be seen as a return to the binominal system) and difficult to pass as a bill in the parliament.
The results that were associated with this proposal by the Chilean president were published on the main online news portal in Chile on 16th June 2019 [29]. Furthermore, following this publication, a more complete report was delivered to governmental authorities as input for the constitutional reform project in which it is necessary to redraw the current electoral system.
5. Conclusions and Future Work
Electoral reforms are especially challenging when they encompass the design of new districts. Such a problem involves a combinatorial problem that tries to find a solution complying with the “one person, one vote” democratic equity principle. In other words, the goal of electoral policymakers should be to ensure the fairness and representativity of the electoral system, while preserving additional conditions like territorial connectivity and complying with other administrative divisions. Nonetheless, if decisions-makers are only guided by specific fairness definitions, the resulting electoral system may still suffer from representation anomalies associated with different expressions of malapportionment or the demographic composition of the designed districts. The resulting designs would fail to ensure democratic and demographic fairness and immunity to future interventions that could benefit incumbents over challengers (i.e., to be immune to gerrymandering).
In this paper, we provide a multi-criteria optimization framework, i.e., a Multi-Criteria Pen, for drawing districts and for assigning seats, that seeks fairer electoral systems according to five criteria: global equity, balancedness, compactness, global demographic fairness, and local demographic fairness. While the first and third criteria are common in most electoral reform processes (as shown in the reviewed literature), the other three criteria address more complex expressions of democratic and demographic representation. As we have pointed out, these additional criteria focus on the composition of districts, and they target two important characteristics: better representation of territories in the political programs, and more competitive electoral campaigns within and among political parties and alliances. Therefore, including all of them within the same decision support system should produce a considerably better performance of the designed system from a territorial and democratic fairness point of view.
Methodologically, our framework is divided into two optimization phases. The first phase solves an MILP formulation of a districting model, while the second phase solves a multi-objective method through local search and provides a set of Pareto-efficient solutions among them (i.e., solutions that ensure trade-offs among different criteria). Therefore, as the devised tool provides not one but a pool of solutions, decision-makers can choose the electoral design that best fits the social and political challenges and expectations imposed not only by voters, but by the electoral system itself.
The proposed methodology was then tested in the last districting process that was conducted in Chile and in a recently proposed change in the previous redistricting plans. When we analyze the results, the framework is shown to be capable of improving considerably the current system in terms of the classical measure of malapportionment: it is almost three times better (3.29 compared to a 9.96) in terms of malapportionment. Likewise, the performance of the other criteria is also considerably improved. More importantly, we provide several alternatives for the electoral redesign, each with its different trade-offs. These alternatives, although may sacrifice performance in some criteria, are capable of addressing the other considered criteria. Therefore, those in charge of the political reform have the opportunity to choose among multiple options, each with different advantages, leaving the decision-maker to choose the districting design that accomplishes the best balance among the different criteria. The results obtained for a recently proposed plan also provide an illustration on the possible results and consequences of the proposed reform (and specifically issues like the return to the binominal system and malapportionment concerns derived from the ratio of population between the most populated and the less populated areas of Chile). This is especially relevant, as the proposed optimization approach may be seen as a simulation method among decision-makers or as a validation approach to audit the performance of the decision-makers.
The method can use other factors to evaluate the performance of the proposed solutions (like socioeconomic characteristics, ethnicity composition, etc.). These could be relevant for decision-makers to include in a later stage to tip the balance in favor of specially desirable properties.
In summary, our approach incorporates deeper political and electoral dimensions to the decision-making process to improve the legitimacy and representation of electoral systems under a reform. Our finding suggest that although malapportionment is, and will be, a fundamental issue of electoral systems, the resulting designs might still present considerable demographic and territorial issues at a global and local scale. This means they may also ultimately lead to imperfect representation, biased political programs, and perverse incentives for political parties and alliances. Tackling these unbalances is an obligation for decision-makers if their aim is to enhance democratic fairness and representation while legitimizing the representativity of a system.
When considering the results, we believe that possible venues for future work should focus on two three issues. First, on extending our tool to different, and eventually more complex, electoral systems and types of elections in order enhance its capabilities and flexibility. For instance, countries using the so-called “Block vote” and “Party Block vote” systems (e.g., Chad, Cotê d’Ivoire, Djibouti, and Lebanon, among others), instead of Proportional Representation, as the case considered in this paper, it is necessary to consider non-standard constitutional arrangements; evidently, measures, such as malapportionment, might not suit directly to these contexts. Second, on including further criteria in our framework so as to address the need of fair representation of the interests of minorities; in this case, a population-based measure, such as malapportionment, might not be effective for this purpose. This could be addressed by exploiting the natural connection between political districting and territorial clustering (see, e.g., [64,87,88,89,90]). Therefore, clustering methods, such as those presented in [91,92], might be also used for district design. Additionally, third, on embedding a simulation approach for measuring the electoral results that different districting designs might produce to predict the political configuration of the chamber(s).
Author Contributions
Conceptualization, E.Á.-M., J.P. and M.M.Q.; Data curation, C.C.-V., M.M.-F. and M.M.Q.; Funding acquisition, E.Á.-M.; Investigation, C.C.-V., E.Á.-M., J.P. and M.M.-F.; Methodology, C.C.-V., E.Á.-M., J.P. and M.M.-F.; Visualization, J.P. and M.M.-F.; Writing–original draft, E.Á.-M. and J.P.; Writing–review and editing, J.P. All authors have read and agreed to the published version of the manuscript.
Funding
E. Álvarez-Miranda acknowledges the support of the National Agency of Research and Development ANID, Chile, through the grant FONDECYT N.1180670 and through the Complex Engineering Systems Institute ANID PIA/BASAL AFB180003.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Summary of the results obtained when optimizing the (1) criterion for a Chamber of Deputies comprising 120 seats. Further analysis is presented in Section 4.4.

Table A1.
Summary of the malapportionment levels obtained for the districting design of a Chamber of Deputies considering 120 seats.
Table A1.
Summary of the malapportionment levels obtained for the districting design of a Chamber of Deputies considering 120 seats.
| Region District (j) | MILP | # Seats | % Electoral Roll | % District Seats | MAL | (1) | (2) |
|---|---|---|---|---|---|---|---|
| Arica y Parinacota | 1 | 2 | 1.29 | 1.67 | 0.37 | 0.19 | |
| Tarapacá | 2 | 2 | 1.70 | 1.67 | −0.03 | 0.02 | |
| Antofagasta | 3 | 3 | 3.14 | 2.50 | −0.64 | 0.32 | |
| Atacama | 4 | 2 | 1.63 | 1.67 | 0.04 | 0.02 | |
| Coquimbo | 5 | 5 | 4.03 | 4.17 | 0.14 | 0.07 | |
| Valparaíso | 6 | 2 | 1.63 | 1.67 | 0.04 | 0.05 | 0.04 |
| 7 | 8 | 6.63 | 6.67 | 0.04 | |||
| 8 | 3 | 2.49 | 2.50 | 0.01 | |||
| Metropolitana | 9 | 8 | 6.68 | 6.67 | −0.01 | 0.10 | 0.07 |
| 10 | 8 | 6.74 | 6.67 | −0.07 | |||
| 11 | 8 | 6.69 | 6.67 | −0.02 | |||
| 12 | 7 | 5.88 | 5.83 | −0.05 | |||
| 13 | 8 | 6.70 | 6.67 | −0.03 | |||
| 14 | 8 | 6.66 | 6.67 | 0.01 | |||
| O’Higgins | 15 | 2 | 1.77 | 1.67 | −0.11 | 0.09 | 0.11 |
| 16 | 4 | 3.39 | 3.33 | −0.06 | |||
| Maule | 17 | 3 | 2.50 | 2.50 | 0.00 | 0.05 | 0.10 |
| 18 | 4 | 3.43 | 3.33 | −0.10 | |||
| Bío-Bío | 19 | 3 | 2.88 | 2.50 | −0.38 | 0.25 | 0.38 |
| 20 | 2 | 1.61 | 1.67 | 0.06 | |||
| 21 | 7 | 5.80 | 5.83 | 0.03 | |||
| 22 | 2 | 1.65 | 1.67 | 0.02 | |||
| Araucanía | 23 | 3 | 2.52 | 2.50 | −0.02 | 0.05 | 0.08 |
| 24 | 4 | 3.41 | 3.33 | −0.08 | |||
| Los Ríos | 25 | 3 | 2.36 | 1.67 | −0.69 | 0.35 | |
| Los Lagos | 26 | 6 | 4.93 | 5.00 | 0.07 | 0.04 | |
| Aysén | 27 | 2 | 0.66 | 1.67 | 1.01 | 0.51 | |
| Magallanes | 28 | 2 | 1.11 | 1.67 | 0.56 | 0.28 | |
| 120 | 100 | 100 | 2.39 |
References
- Gallagher, M.; Mitchell, P. The Politics of Electoral Systems; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Monroe, B. Disproportionality and malapportionment: Measuring electoral inequity. Elect. Stud. 1994, 13, 132–149. [Google Scholar] [CrossRef]
- Snyder, R.; Samuels, D. Legislative Malapportionment in Latin America: Historical and Comparative Perspectives. In Federalism and Democracy in Latin America; Gibson, E., Ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 2004; pp. 131–172. [Google Scholar]
- Taagepera, R.; Shugart, M. Seats and Votes: The Effects and Determinants of Electoral Systems; Yale University: New Haven, CT, USA, 1989. [Google Scholar]
- Samuels, D.; Snyder, R. The value of a vote: Malapportionment in comparative perspective. Br. J. Political Sci. 2001, 31, 651–671. [Google Scholar] [CrossRef]
- Dahl, R. Democracy and Its Critics; Yale University Press: New Haven, CT, USA, 1989. [Google Scholar]
- Reynoso, D. Las consecuencias políticas de la sobre-representación distrital. Política Gobierno 2002, IX, 325–359. [Google Scholar]
- Giugăl, A.; Johnston, R.; Chiru, M.; Ciobanu, I.; Gavriș, A. Gerrymandering and Malapportionment, Romanian Style: The 2008 Electoral System. East Eur. Politics Soc. 2017, 31, 683–703. [Google Scholar] [CrossRef]
- Wong, S. Gerrymandering in Electoral Autocracies: Evidence from Hong Kong. Br. J. Political Sci. 2019, 49, 579–610. [Google Scholar] [CrossRef]
- Vickrey, W. On the prevention of gerrymandering. Political Sci. Q. 1961, 76, 105–110. [Google Scholar] [CrossRef]
- Helbig, R.; Orr, P.; Roediger, R. Political redistricting by computer. Commun. ACM 1972, 15, 735–741. [Google Scholar] [CrossRef]
- Lee, F. Representation and public policy: The consequences of senate apportionment for the geographic distribution of federal funds. J. Politics 1998, 60, 34–62. [Google Scholar] [CrossRef]
- Lee, F. Senate representation and coalition building in distributive politics. Am. Political Sci. Rev. 2000, 94, 59–72. [Google Scholar] [CrossRef]
- Ahmed, A. Democracy and the Politics of Electoral System Choice: Engineering Electoral Dominance; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Farrell, D. Electoral Systems: A Comparative Introduction; Macmillan International Higher Education: London, UK, 2011. [Google Scholar]
- Renwick, A. The Politics of Electoral Reform: Changing the Rules of Democracy; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bowler, S.; Donovan, T.; Karp, J. Why politicians like electoral institutions: Self-interest, values, or ideology? J. Politics 2006, 68, 434–446. [Google Scholar] [CrossRef]
- Colomer, J. It’s parties that choose electoral systems (or, Duverger’s laws upside down). Political Stud. 2005, 53, 1–21. [Google Scholar] [CrossRef]
- Buchanan, A. Political legitimacy and democracy. Ethics 2002, 112, 689–719. [Google Scholar] [CrossRef]
- Fuchs, D.; Klingemann, H. Globalization, Populism and Legitimacy in Contemporary Democracy. In Democracy under Threat; Springer: Berlin/Heidelberg, Germany, 2019; pp. 3–21. [Google Scholar]
- Parkinson, J. Legitimacy problems in deliberative democracy. Political Stud. 2003, 51, 180–196. [Google Scholar] [CrossRef]
- Widmaier, U. Tendencies toward an Erosion of Legitimacy. In Comparing Pluralist Democracies; Routledge: Abingdon, UK, 2019; pp. 143–167. [Google Scholar]
- Jones, D.; Walsh, R. How do voters matter? Evidence from US congressional redistricting. J. Public Econ. 2018, 158, 25–47. [Google Scholar] [CrossRef]
- Stephanopoulos, N. Our electoral exceptionalism. Univ. Chic. Law Rev. 2013, 80, 769–858. [Google Scholar]
- Chambers, C.; Miller, A. Measuring legislative boundaries. Math. Soc. Sci. 2013, 66, 268–275. [Google Scholar] [CrossRef]
- Fryer, R.; Holden, R. Measuring the compactness of political districting plans. J. Law Econ. 2011, 54, 493–535. [Google Scholar] [CrossRef]
- Hess, S.; Weaver, J.; Siegfeldt, H.; Whelan, J.; Zitlau, P. Nonpartisan political redistricting by computer. Oper. Res. 1965, 13, 998–1006. [Google Scholar] [CrossRef]
- Weaver, J.; Hess, S. A Procedure for Nonpartisan Districting: Development of Computer Techiques. Yale LJ 1963, 73, 288. [Google Scholar] [CrossRef]
- El Mercurio, Online Version. Nuevo diseño de Distritos y Regreso al Binominal en Regiones: La fórmula Matemática Para Reducir el Número de Parlamentarios. Published 16 June 2019. Available online: https://www.emol.com/noticias/Nacional/2019/06/16/951370/Nuevo-diseno-de-distritos-y-regreso-al-binominal-en-regiones-La-formula-matematica-para-reducir-el-numero-de-parlamentarios.html (accessed on 25 June 2019).
- Cox, G. Making Votes Count: Strategic Coordination in the World’s Electoral Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Ong, K.; Kasuya, Y.; Mori, K. Malapportionment and democracy: A curvilinear relationship. Elect. Stud. 2017, 49, 118–127. [Google Scholar] [CrossRef]
- Altman, M.; McDonald, M. BARD: Better Automated ReDistricting. J. Stat. Softw. Forthcom. 2011, 42, 1–28. [Google Scholar] [CrossRef]
- Benoit, K. Electoral laws as political consequences: Explaining the origins and change of electoral institutions. Ann. Rev. Political Sci. 2007, 10, 363–390. [Google Scholar] [CrossRef]
- Boix, C. Setting the rules of the game: The choice of electoral systems in advanced democracies. Am. Political Sci. Rev. 1999, 93, 609–624. [Google Scholar] [CrossRef]
- Grofman, B.; Koetzle, W.; Brunell, T. An integrated perspective on the three potential sources of partisan bias: Malapportionment, turnout differences, and the geographic distribution of party vote shares. Elect. Stud. 1997, 16, 457–470. [Google Scholar] [CrossRef]
- Sauger, N.; Grofman, B. Partisan bias and redistricting in France. Elect. Stud. 2016, 44, 388–396. [Google Scholar] [CrossRef]
- Schedler, A. The nested game of democratization by elections. Int. Political Sci. Rev. 2002, 23, 103–122. [Google Scholar] [CrossRef]
- Carey, J. Malapportionment and ideological bias in Chilean electoral districts. Lat. Am. Politics Soc. 2016, 58, 123–133. [Google Scholar] [CrossRef]
- Gamboa, R.; Morales, M. Chile’s 2015 Electoral Reform: Changing the Rules of the Game. Lat. Am. Politics Soc. 2016, 58, 126–144. [Google Scholar] [CrossRef]
- Bhavnani, R. The effects of malapportionment on cabinet inclusion: Subnational evidence from India. Br. J. Political Sci. 2018, 48, 69–89. [Google Scholar] [CrossRef]
- Çarkoğlu, A.; Aksen, D. Partisan and apportionment bias in creating a predominant party system. Political Geogr. 2019, 69, 43–53. [Google Scholar] [CrossRef]
- Hiroi, T. Paradox of Redistribution: Legislative Overrepresentation and Regional Development in Brazil. Publius J. Fed. 2019, 49, 642–670. [Google Scholar] [CrossRef]
- Hiroi, T.; Neiva, P. Malapportionment and geographical bases of electoral support in the Brazilian Senate. J. Politics Lat. Am. 2013, 5, 127–150. [Google Scholar] [CrossRef]
- Gibson, E.; Calvo, E. Federalism and low-maintenance constituencies: Territorial dimensions of economic reform in Argentina. Stud. Comp. Int. Dev. 2000, 35, 32–55. [Google Scholar] [CrossRef]
- Cho, Y.; Frederickson, H. Measuring the Effects of Reapportionment in the American States; National Municipal League: New York, NY, USA, 1976. [Google Scholar]
- Cowan, S. Periodic Discordance Between Vote Equality and Representational Equality in the United States. Sociol. Sci. 2015, 2, 442–453. [Google Scholar] [CrossRef][Green Version]
- Erikson, R. Malapportionment, gerrymandering, and party fortunes in congressional elections. Am. Political Sci. Rev. 1972, 66, 1234–1245. [Google Scholar] [CrossRef]
- Zagarri, R. The Politics of Size: Representation in the United States, 1776–1850; Cornell University Press: Ithaca, NY, USA, 1987. [Google Scholar]
- Boone, C.; Wahman, M. Rural bias in African electoral systems: Legacies of unequal representation in African democracies. Elect. Stud. 2015, 40, 335–346. [Google Scholar] [CrossRef]
- Garfinkel, R.; Nemhauser, G. Optimal Political Districting by Implicit Enumeration Techniques. Manag. Sci. 1970, 16, B495–B508. [Google Scholar] [CrossRef]
- Ricca, F.; Simeone, B. Local search algorithms for political districting. Eur. J. Oper. Res. 2008, 189, 1409–1426. [Google Scholar] [CrossRef]
- Hojati, M. Optimal political districting. Comput. Oper. Res. 1996, 23, 1147–1161. [Google Scholar] [CrossRef]
- Horn, D.; Hampton, C.; Vandenberg, A. Practical application of district compactness. Political Geogr. 1993, 12, 103–120. [Google Scholar] [CrossRef]
- Mehrotra, A.; Johnson, E.; Nemhauser, G. An optimization based heuristic for political districting. Manag. Sci. 1998, 44, 1100–1114. [Google Scholar] [CrossRef]
- Gopalan, R.; Kimbrough, S.; Murphy, F.; Quintus, N. The Philadelphia districting contest: Designing territories for city council based upon the 2010 census. Interfaces 2013, 43, 477–489. [Google Scholar] [CrossRef][Green Version]
- George, J.; Lamar, B.; Wallace, C. Political district determination using large-scale network optimization. Socio-Econ. Plan. Sci. 1997, 31, 11–28. [Google Scholar] [CrossRef]
- Ricca, F.; Scozzari, A.; Simeone, B. Weighted Voronoi region algorithms for political districting. Math. Comput. Model. 2008, 48, 1468–1477. [Google Scholar] [CrossRef]
- Bozkaya, B.; Erkut, E.; Haight, D.; Laporte, G. Designing new electoral districts for the city of edmonton. Interfaces 2011, 41, 534–547. [Google Scholar] [CrossRef]
- Chou, C.; Li, S. Spin systems and political districting problem. J. Magn. Magn. Mater. 2007, 310, 2889–2891. [Google Scholar] [CrossRef]
- Cirincione, C.; Darling, T.; O’Rourke, T. Assessing South Carolina’s 1990s congressional districting. Political Geogr. 2000, 19, 189–211. [Google Scholar] [CrossRef]
- Rincón-García, E.; Gutiérrez-Andrade, M.; de-los Cobos-Silva, S.; Mora-Gutiérrez, R.; Ponsich, A.; Lara-Velázquez, P. A system for political districting in the State of Mexico. Lect. Notes Comput. Sci. 2015, 9413, 248–259. [Google Scholar]
- Alawadhi, S.; Mahalla, R. The political districting of Kuwait: Heuristic approaches. Kuwait J. Sci. 2015, 42, 160–188. [Google Scholar]
- Bozkaya, B.; Erkut, E.; Laporte, G. A tabu search heuristic and adaptive memory procedure for political districting. Eur. J. Oper. Res. 2003, 144, 12–26. [Google Scholar] [CrossRef]
- Fragoso, R.; Rego, C.; Bushenkov, V. Clustering of territorial areas: A multi-criteria districting problem. J. Quant. Econ. 2016, 14, 179–198. [Google Scholar] [CrossRef]
- Kong, Y.; Zhu, Y.; Wang, Y. A center-based modeling approach to solve the districting problem. Int. J. Geogr. Inf. Sci. 2018, 33, 1–17. [Google Scholar] [CrossRef]
- Ricca, F.; Scozzari, A.; Simeone, B. Political Districting: From classical models to recent approaches. Ann. Oper. Res. 2013, 204, 271–299. [Google Scholar] [CrossRef]
- Bodin, L. A districting experiment with a clustering algorithm. Ann. N. Y. Acad. Sci. 1973, 219, 209–214. [Google Scholar] [CrossRef] [PubMed]
- King, D.; Jacobson, S.; Sewell, E.; Cho, W. Geo-graphs: An efficient model for enforcing contiguity and hole constraints in planar graph partitioning. Oper. Res. 2012, 60, 1213–1228. [Google Scholar] [CrossRef]
- Chou, C.; Li, S. Taming the Gerrymander-Statistical physics approach to Political Districting Problem. Phys. A Stat. Mech. Appl. 2006, 369, 799–808. [Google Scholar] [CrossRef][Green Version]
- Rincón-García, E.; Gutiérrez-Andrade, M.; de-los Cobos-Silva, S.; Mora-Gutiérrez, R.; Ponsich, A.; Lara-Velázquez, P. A comparative study of population-based algorithms for a political districting problem. Kybernetes 2017, 46, 172–190. [Google Scholar] [CrossRef]
- Shirabe, T. Districting modeling with exact contiguity constraints. Environ. Plan. B Plan. Des. 2009, 36, 1053–1066. [Google Scholar] [CrossRef]
- Bruno, G.; Genovese, A.; Piccolo, C. Territorial amalgamation decisions in local government: Models and a case study from Italy. Socio-Econ. Plan. Sci. 2017, 57, 61–72. [Google Scholar] [CrossRef][Green Version]
- Kalcsics, J.; Nickel, S.; Schröder, M. Towards a unified territorial design approach—Applications, algorithms and GIS integration. TOP 2005, 13, 1–56. [Google Scholar] [CrossRef]
- Arrington, T. Redistricting in the U.S.: A review of scholarship and plan for future research. Forum 2010, 8, 1–49. [Google Scholar] [CrossRef]
- Tasnadi, A. The political districting problem: A survey. Soc. Econ. 2011, 33, 543–554. [Google Scholar] [CrossRef]
- Williams, J. Political redistricting: A review. Pap. Reg. Sci. 1995, 74, 13–40. [Google Scholar] [CrossRef]
- Loosemore, J.; Hanby, V. The theoretical limits of maximum distortion: Some analytic expressions for electoral systems. Br. J. Political Sci. 1971, 1, 467–477. [Google Scholar] [CrossRef]
- Altman, M. Modeling the effect of mandatory district compactness on partisan gerrymanders. Political Geogr. 1998, 17, 989–1012. [Google Scholar] [CrossRef]
- Polsby, D.D.; Popper, R.D. The third criterion: Compactness as a procedural safeguard against partisan gerrymandering. Yale L. Pol’y Rev. 1991, 9, 301. [Google Scholar] [CrossRef]
- Young, H. Measuring the compactness of legislative districts. Legis. Stud. Q. 1988, 13, 105–115. [Google Scholar] [CrossRef]
- Dubois-Lacoste, J.; López-Ibáñez, M.; Stützle, T. Anytime pareto local search. Eur. J. Oper. Res. 2015, 243, 369–385. [Google Scholar] [CrossRef]
- Hopcroft, J.; Tarjan, R. Algorithm 447: Efficient algorithms for graph manipulation. Commun. ACM 1973, 16, 372–378. [Google Scholar] [CrossRef]
- Censor, Y. Pareto optimality in multiobjective problems. Appl. Math. Optim. 1977, 4, 41–59. [Google Scholar] [CrossRef]
- Blot, A.; Kessaci, M.; Jourdan, L. Survey and unification of local search techniques in metaheuristics for multi-objective combinatorial optimisation. J. Heuristics 2018, 24, 853–877. [Google Scholar] [CrossRef]
- Gandibleux, X.; Sevaux, M.; Sörensen, K.; Tkindt, V. (Eds.) Metaheuristics for Multiobjective Optimisation; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 2004; Volume 535. [Google Scholar]
- Talbi, E. Hybrid metaheuristics for multi-objective optimization. J. Algorithms Comput. Technol. 2015, 9, 41–63. [Google Scholar] [CrossRef]
- Belussi, F. In search of a useful theory of spatial clustering. In Clusters and Regional Development; Routledge: Abingdon, UK, 2006; pp. 69–89. [Google Scholar]
- Gibler, D.; Tir, J. Territorial peace and democratic clustering. J. Politics 2014, 76, 27–40. [Google Scholar] [CrossRef]
- Laghi, A.; Luppi, G.; Mazzocchetti, A. Detecting homogeneus areas in a sub-regional demographic analisys. In Atti della XLIII Riunione Scientifica della Società Italiana di Statistica; Università di Torino: Torino, Italy, 2006; pp. 14–16. [Google Scholar]
- Sobolewski, M.; Markowska, M. Hierarchical clustering methods with territorial integrity criterion. Acta Univ. Lodz. Folia Oeconomica 2017, 4, 99–109. [Google Scholar] [CrossRef][Green Version]
- Kropat, E.; Weber, G.; Alparslan-Gök, S.; Özmen, A. Inverse problems in complex multi-modal regulatory networks based on uncertain clustered data. In Modeling, Dynamics, Optimization and Bioeconomics I; Springer Proceedings in Mathematics & Statistics; Pinto, A., Zilberman, D., Eds.; Springer: Cham, Switzerland, 2014; Volume 73, pp. 437–451. [Google Scholar]
- Volkovich, Z.; Toledano-Kitai, D.; Weber, G. Self-learning K-means clustering: A global optimization approach. J. Glob. Optim. 2013, 56, 219–232. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).