A New ECDLP-Based PoW Model ^†

Abstract

Blockchain technology has attracted a lot of research interest in the last few years. Originally, their consensus algorithm was Hashcash, which is an instance of the so-called Proof-of-Work. Nowadays, there are several competing consensus algorithms, not necessarily PoW. In this paper, we propose an alternative proof of work algorithm which is based on the solution of consecutive discrete logarithm problems over the point group of elliptic curves. At the same time, we sketch a blockchain scheme, whose consensus is reached via our algorithm. In the considered architecture, the curves are pseudorandomly determined by block creators, chosen to be cryptographically secure and changed every epoch. Given the current state of the chain and a prescribed set of transactions, the curve selection is fully rigid, therefore trust is needed neither in miners nor in the scheme proposers.

1. Introduction

A proof of work (PoW) is a procedure that allows a prover to demonstrate that he is very likely to have performed a specific amount of computational work within a prescribed interval of time [1].

This concept has been formalized in 1999 [2], although previous instances of delaying functions conceived for similar purposes had appeared earlier [3,4,5,6,7,8,9].

Since 2008, PoW-methods have been attracting a considerable interest as Bitcoin [10] introduced a PoW-based consensus algorithm, which puts miners in competition for solving a cryptographic challenge. Bitcoin’s consensus relies on a hashcash system [11,12], whose workload may be easily adjusted with a fastly verifiable output. Despite their high efficiency and easy implementation, all the hashcash-based protocols share a common limitation: the huge amount of computations employed by nodes becomes useless after the consensus is reached. This aspect has been raising environmental concerns and many solutions have been proposed to reduce these energy-intensive computer calculations.

A promising countermeasure to this issue is the adoption of bread pudding protocols [2]. They face the aforementioned problem by performing a computational work that is reusable either for practical [13,14,15,16], cryptographical [2,17], or mathematical [18] reasons. Moreover, the latter class of systems encloses several protocols that are meant to be research propellants [19], namely designed to boost the commitment upon the solution of difficult mathematical problems. A notable example is PrimeCoin [18], which appeared in 2013 and is a cryptocurrency whose Proof-of-Work consensus is based on searching for prime numbers.

Along the same line, we have proposed [20], a blockchain architecture with a PoW-consensus algorithm based on the solution of the Discrete Logarithm Problem over the point groups of elliptic curves (ECDLP). The idea of basing a PoW on ECDLP has already appeared in other works [21,22], as this problem is widely studied and applied in cryptographic protocols. In particular, the PoW consensus algorithm proposed in [21] is based on solving the ECDLP on a fixed elliptic curve. Although we do appreciate their approach for the novelty of using ellptic curves in their PoW constructions, the choice of a specific fixed curve may look suspicious. In fact, in these previous approaches, the considered curves do not usually fulfill the standard security criteria [23], especially for what concerns the fully rigidity: the network has to initially trust an authority that is providing the curve parameters.

In this work, we radically solve this issue by designing a PoW-system based on elliptic curves that are changing over the time. Since the curves are pseudo-randomly constructed and satisfy general security conditions, a malicious user wanting to attack the chain shall efficiently break the ECDLP over an immense class of elliptic curves, a task that may be fairly considered infeasible. We provide the aforementioned scheme [20] with precise mathematical foundations and further implementation details. Concrete choices of the involved parameters are exhibited, and the security of the system is debated in a formal manner.

The paper is organized as follows: a quick summary of the ECDLP is given in Section 2, while the main blockchain architecture is proposed in Section 3, whose block construction is detailed in Section 3.1 and Section 3.2. The strong points of this system are discussed in Section 4, where its security is also debated, while, in Section 5, future work directions are presented.

2. ECDLP

The ECDLP is a renowned problem that consists, given two points P and Q of an elliptic curve E, of finding (if existent) an integer $N\in \mathbb{N}$ such that the N-th multiple of P (usually called the base point) equals Q, i.e., $Q=N·P$.

Here, we are only interested in elliptic curves over prime fields ${\mathbb{F}}_p$ and determined by their short Weierstrass equation $y^2=x^3+Ax+B$. Solving ECDLP on curves E over large prime fields is considered to be a difficult challenge except for degenerate cases.

2.1. The General Case

The most efficient currently known general attacks are Baby-Step Giant-Step [24] and Pollard’s Rho—Kangaroo algorithms [25], which have an asymptotic complexity of $O\left(\sqrt{\left|E\right|}\right)$, where $\left|E\right|$ is the size of E. These are general parallel collision-finding algorithms, which work over any groups, i.e., no properties of the underlying structure, but the operation definitions are used.

The introduction of Semaev’s polynomials [26] has suggested the existence of subexponential algorithms to solve ECDLP; however, no clear evidence has emerged. Pairings-based attacks [27,28], Index calculus [29,30,31], and Xedni calculus [32] have been recently being studied, but none of them seem to significantly reduce the problem complexity of the general case so far.

2.2. Special Cases

There are some families of curves whose ECDLP is known to be easier than the general case, as there are algorithms for efficiently solving it. Consequently, such curves have to be carefully avoided for designing a ECDLP-based protocol. A concise summary of those particular attacks, the curve on which they may be efficiently applied, and how we avoid them are drawn in

Table 1. Attacks on ECDLP over special curves.

Attack	It Applies on Curves	To Avoid It: Use	Ref.
Weil-descent	over composite fields	prime fields	[33,34]
Pohlig–Hellman	of composite orders	prime orders	[35]
Semaev, Satoh–Araki, Smart	anomalous	non-anomalous curves	[36,37,38]
Menezes–Okamoto–Vanstone	low embedding degree	high embedding degree	[28]
Frey–Rück	low embedding degree	high embedding degree	[27]
Wiener–Zuccherato	low CM discriminant	high CM discriminant	[39]

.

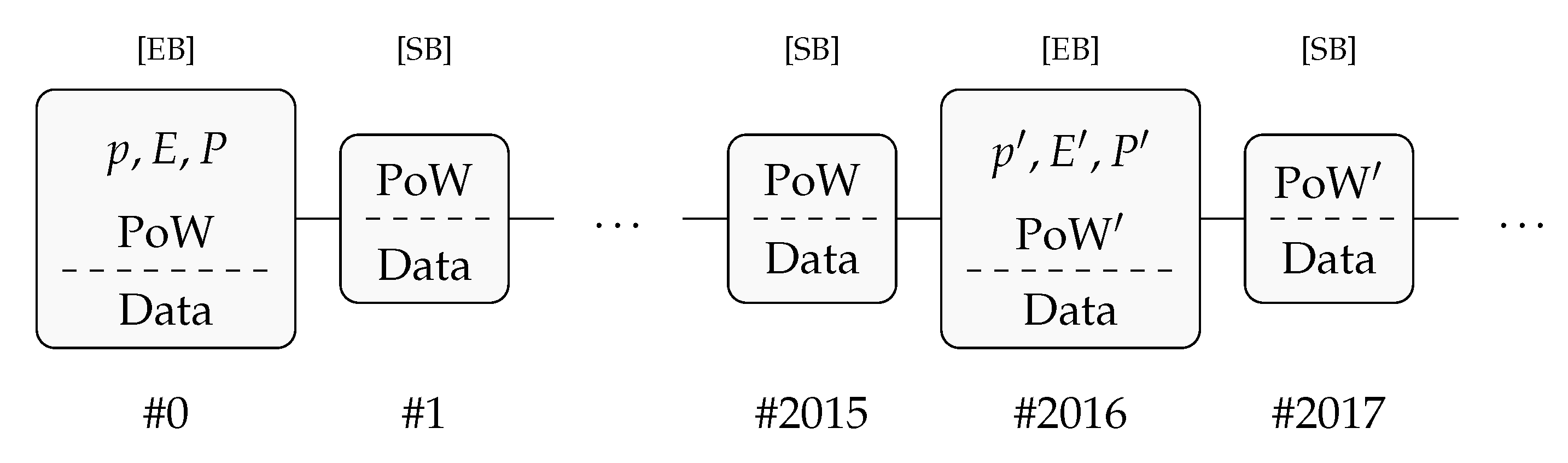
3. A Sample Blockchain Architecture

To show how our PoW-proposal works, we introduce a schematic sample ledger architecture, but the same idea may easily be adapted for other similar architectures. The consensus of our ledger is based on solving ECDLP on non-suspicious curves, hence it needs to address two radically-different closely-linked tasks: finding a strong pseudo-random curve and producing generic instances of ECDLP on it. Therefore, we have chosen a blockchain scheme based on two types of blocks, the standard ones and those defining the involved parameters. Other approaches are still viable, provided they solve the two aforementioned connected tasks.

[EB]

An Epoch Block contains, aside from the header and a list of transactions, a prime number p, an elliptic curve E defined over ${\mathbb{F}}_p$, and a base point P of E, all to be determined by the proposing miner via rigid algorithms with a pseudorandom set of input parameters.

Moreover, it encloses as PoW a pair of integers $(N_1,N_2)$ to be discovered by the proposing miner, such that $N_i·P$ are points of E deterministically determined from the block contents and the current chain status.

The frequency of the EBs determines the number of changes in the ECDLP-parameters with respect to the network block construction speed. In the current proposal, we arbitrarily set these EBs to occur once every 2016 blocks, emulating the bitcoin difficulty adjustment rate.

[SB]

The Standard Blocks are just a light version of the EB blocks; they are constructed in the same way except for p, E, P, which are inherited from the last EB block of the chain.

SBs constitute the vast majority of the blocks of the chain, as portrayed in Figure 1.

EBs basically define the setting (curves and base points) on which the discrete logarithm PoWs will have to be solved in the following epoch. They are slightly heavier to be produced and verified but occur rarely (roughly once every two weeks with the proposed frequency and assuming a BTC-like network computational power).

In order to give the specifications of our blocks, we need a deterministic function P_Gen, used for constructing a point on a given elliptic curve E from a prescribed hash digest h, which we treat as an integer for simplicity. The following is a concrete example of such a function:

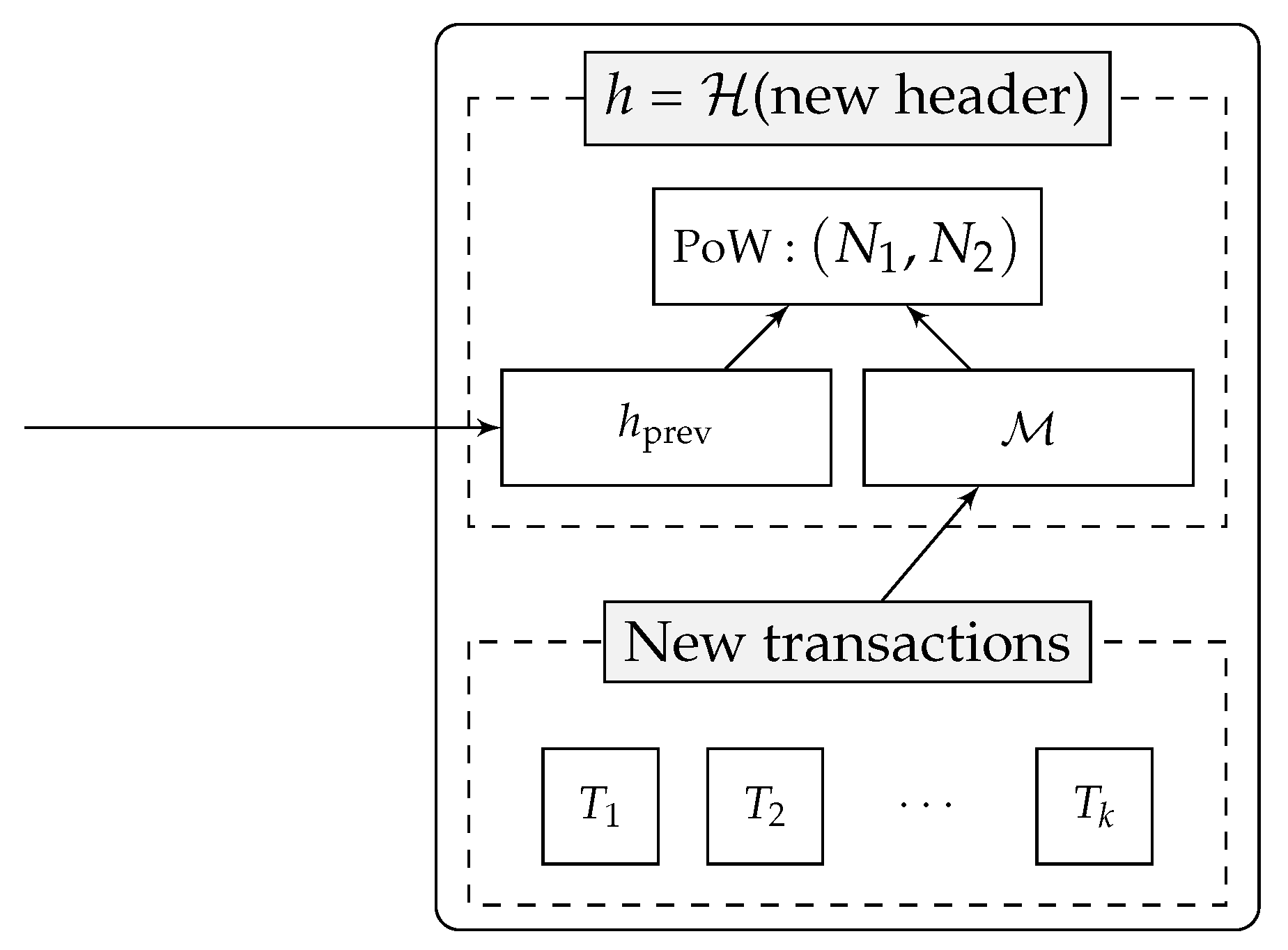
• function P_Gen (h,E)
•   i = 0
•   while #{points of E with x-coord = h + i} = 0:
•     i = i + 1
•   P = (h + i, *) point of E with 0 ≤ * < p/2
•   return P

We notice that the points determined by the above function are affine by construction. The hash $\mathscr{H}$ that we propose to use in the following is SHA3-512 [40], which provides a satisfying collision resistance even against post-quantum attacks, but one might conceivably replace it with another properly constructed one.

We also assume that all proposing miners use prescribed signature algorithms and we denote with ${\sigma }_k\left(m\right)$ the signature of the string m obtained by the miner with signing key k.

3.1. Standard Blocks

A minimal model of a SB consists of a list of valid transactions and a header, which comprises their Merkel root $\mathcal{M}$, the hash of the previous header $h_{\mathrm{prev}}$ and a pair of integers $(N_1,N_2)$ solving

$$PoW:\left\{\begin{array}{c}\mathtt{P}\_\mathtt{G}\mathtt{e}\mathtt{n}(\mathscr{H}\left(h_{\mathrm{prev}}\right),E)=N_1·P,\hfill \\ \mathtt{P}\_\mathtt{G}\mathtt{e}\mathtt{n}(\mathscr{H}\left(\mathcal{M}\right),E)=N_2·P,\hfill \end{array}\right.$$

where E and P have been defined in the last EB. A model of the proposed SB is given in Figure 2.

3.2. Epoch Blocks

An EB is a thick version of a SB, namely it is constructed in a similar fashion, but it encodes three additional pieces of data: the prime p, the elliptic curve E over ${\mathbb{F}}_p$, and the base point P of E.

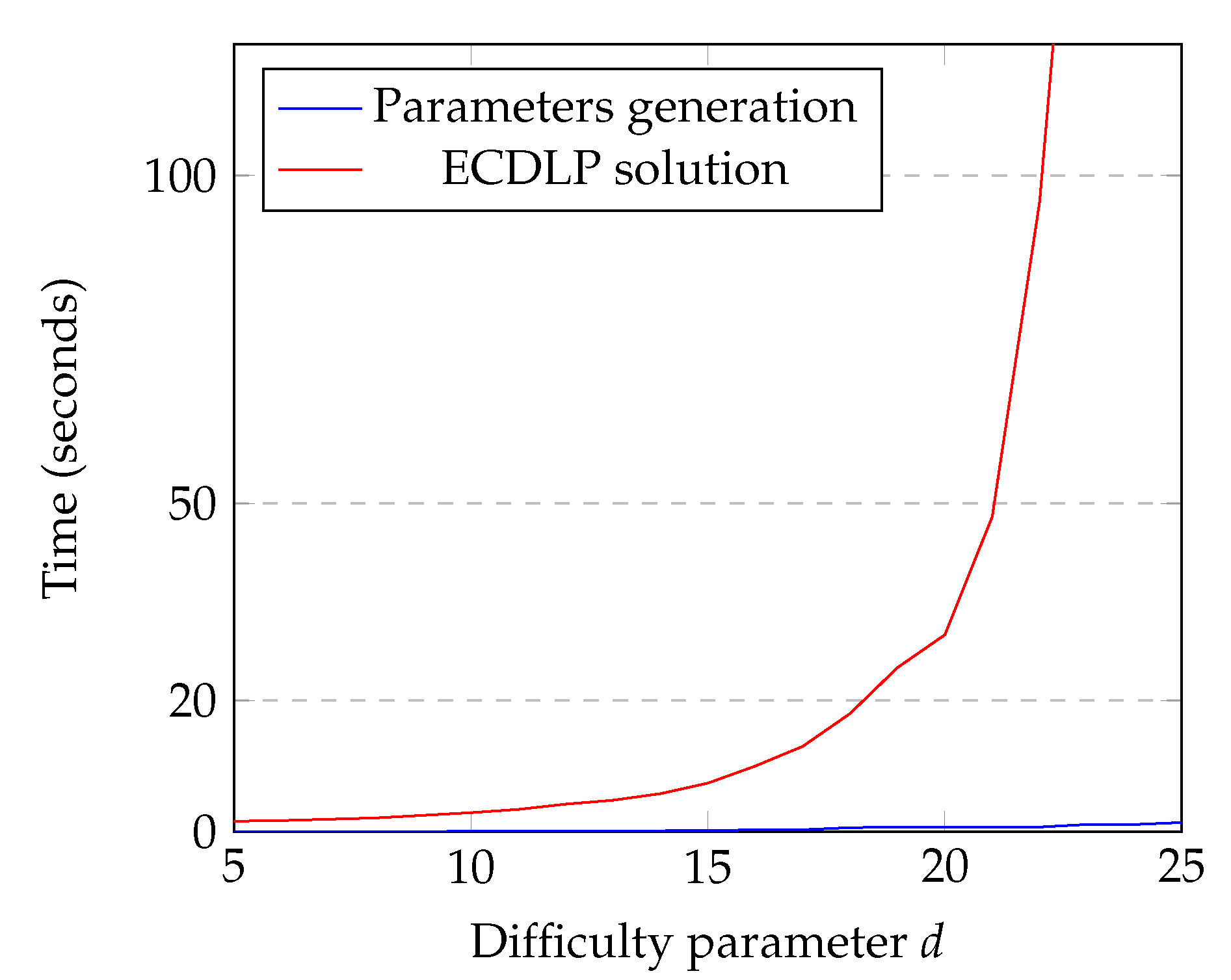
• Generating p
  The prime number p is the responsibility of the expected runtime of the PoW. Its size is determined by the difficulty parameter d, whose tuning depends on the block production ratio that a designer wants to obtain. Therefore, we do not discuss the choice of d, but we refer to the BTC implementation [41] or to more structured models such as personalized difficulty adjustments [42]. Our goal is to produce a prime number of the prescribed size and which does not allow fast arithmetic for the known cases, i.e. we pick it satisfying the following properties.
  Exceptionality properties
  • p is not a Crandall prime [43], i.e., not of the from $2^k-c$ for a relatively small and positive integer c.
  • p is neither a Generalized Mersenne prime [44] nor a More Generalized Mersenne prime [45], i.e., it may not be written as $p\left(m\right)$ for some integer m and polynomial p with very small coefficients and number of monomials.
  • p is not Montgomery-friendly [46,47,48], i.e., it may not be obtained as $2^{\alpha }(2^{\beta }-\gamma )-1$ for small positive integers $\alpha ,\beta ,\gamma$.
  Given the difficulty parameter d and the hash of the previous header h, we propose the generation of such a prime number p as follows.
  • function p_Gen(d, h)
  •   repeat
  •     h = $\mathscr{H}$ (h)
  •     p = Next, Prime (h mod 2^2d)
  •   until p satisfies exceptionality properties
  •   return p
• Generating E
  We aim at generating pseudorandom elliptic curves for which no efficient attacks are currently known, i.e., satisfying the following properties:
  Security properties
  • The number of points of E is prime and different from p.
  • The embedding degree B is greater than 20, i.e., $\left|E\right|\nmid p^B-1$ for every $1\le B\le 20$.
  • Let D be the CM field discriminant, defined as

    $$D=\left\{\begin{array}{cc}\Delta \hfill & \mathrm{if}\Delta \equiv 1mod4,\hfill \\ 4\Delta \hfill & \mathrm{otherwise},\hfill \end{array}\right.\Delta =\mathrm{SquareFreePart}(t^2-4p),$$

    where t is the trace of E. Then, we require $D>2^{40}$.
  Let h be the previous block header; we suggest generating the curve as follows:
  • function E_Gen (p, h)
  •   i = 0
  •   repeat
  •     i = i + 1
  •     A_E = $\mathscr{H}$ (h + i)
  •     B_E =  $\mathscr{H}$(A_E)
  •     E defined by y² = x³ + A_E x + B_E over 𝔽_p
  •   until E is an EC satisfying security properties
  •   return E
• Generating P
  The base point we prescribe for an EB and its subsequent epoch is

  $$P=\mathtt{P}\_\mathtt{G}\mathtt{e}\mathtt{n}(\mathscr{H}(p\left|\right|A_E\left|\right|B_E),E),$$

  where $x\left|\right|y$ denotes the concatenation of the bit representations of x and y.

We remark that the new epoch parameters are manufactured before the PoW production, which therefore depends on them. A schematic epoch block is sketched in Figure 3.

Despite the verification of SBs being extremely fast, EBs are slower to be checked since verifiers need to test that all the curve parameters involved have been properly constructed, running several types of mathematical algorithms such as primality testing, finite fields operations, and elliptic curve points counting.

4. Method Discussion

Here, we discuss motivation and advantages of the presented choices.

First, this PoW model involves many different mathematical algorithms of wide interest, for which this blockchain may represent a concrete research propellant. Furthermore, it might also provide a public collection of cryptographically secure elliptic curves of moderate size.

Apart from its scientific usefulness, it conveys many desirable security properties. The challenges involved do not rely on a given curve of questionable provenance but on the generic difficulty of the ECDLP, which is much more fair to be trusted. Thus, we find it aims at embracing the decentralization ideals that lead to cryptocurrencies creation: even the mathematical objects involved are publicly manufactured, and no trust is required even in the authors or the proposing entities. For example, in the Bitcoin case, everybody must trust the strength of the given curve Secp256k1.

The existence of different types of blocks in blockchains has become common, as it is considered suitable for tackling the problem of scalability [49]. Here, we pursue this idea by designing a scheme with two different types of blocks, but possibly more sophisticated solutions may be taken under consideration for obtaining further worthwhile properties.

As for blocks forgery, we point out that both SBs and EBs comprise a PoW which depends on the entire block, together with the previous one. This means that any counterfeit in any position of the chain results into an incorrect final block, which may be easily detected from the network.

Moreover, it is hard to conceive shortcuts for the PoW production: for a given difficulty parameter d, we expect a d-bits secutity of the general ECDPL by using $p\approx 2^{2d}$, unless attacks outperforming Pollard’s rho are discovered. Moreover, common base field operations speed ups are avoided by making use of not-exceptional primes, ensuring a fair and general problem to be solved equally for every miner. In fact, neither specific algorithms nor dedicated hardware may be used for solving such a general problem, of which easy cases are carefully avoided. In addition, the constructed curves fulfill the known security criteria [23]:

• working over prime fields avoids Weil-descent attacks;
• searching for curves of prime order prevents from Pohlig–Hellman attacks;
• since $p\ne \left|E\right|$ the curves are not anomalous so Smart, Semaev, Satoh–Araki attacks do not apply;
• the embedding degree we suggest is greater than 20 as required by SEC1 [50], which prevents pairing attacks such as Menezes–Okamoto–Vanstone (based on Weil Pairing) and Frey–Rück (based on Tate–Lichtenbaum Pairing);
• attacks to curves with low CM discriminant are prevented by requiring it higher than $2^{40}$, as for Brainpool Standard Curves [51].

The following theorem shows that, whatever the difficulty of the considered ECDLP is, when the cryptographic primitives are well-constructed, solving an instance of this problem is inescapable for proposing a new valid block.

Theorem 1.

Let us assume that the current epoch is endowed with the curve E and its base-point P, and let $h_{\mathit{prev}}$ be the hash of the previous header’s block. Let σ be a uniform and deterministic digital signature algorithm and $\mathbb{M}$ be a proposing miner with fixed signing key k. If $\mathscr{H}$ is uniform and $\mathbb{M}$ exhibits a valid block, then $\mathbb{M}$ has solved at least one generic instance of ECDLP on E.

Proof. 

By definition of our PoW, the given block is valid if and only if it contains $(N_1,N_2)$ such that

$$\left\{\begin{array}{c}{Q}_1=\mathtt{P}\_\mathtt{G}\mathtt{e}\mathtt{n}(\mathscr{H}\left({\sigma }_k\left(h_{\mathrm{prev}}\right)\right),E)=N_1·P,\hfill \\ Q_2=\mathtt{P}\_\mathtt{G}\mathtt{e}\mathtt{n}(\mathscr{H}\left(\mathcal{M}\right),E)=N_2·P.\hfill \end{array}\right.$$

Since E and P are determined by the epoch and $h_{\mathrm{prev}}$ is determined by the previous block, the proposing miner has no control on them. Moreover, $\sigma$ is deterministic and k is fixed, so that $Q_1=\mathtt{P}\_\mathtt{G}\mathtt{e}\mathtt{n}(\mathscr{H}\left({\sigma }_k\left(h_{\mathrm{prev}}\right)\right),E)$ cannot be influenced by the miner. Therefore, if $\mathbb{M}$ has proposed a valid block, it must have solved $Q_1=N_1·P$. Since both ${\sigma }_k$ and $\mathscr{H}$ are uniform, then also $\mathtt{P}\_\mathtt{G}\mathtt{e}\mathtt{n}(\mathscr{H}\left({\sigma }_k(*)\right),E)$ is, so the instance of the ECDLP that $\mathbb{M}$ has solved was generic. □

We notice that the hypotheses of Theorem 1 are satisfied whenever $\sigma$ and $\mathscr{H}$ are cryptographically well-designed, e.g., in a random oracle model [52]. Moreover, in such model, a solution of the equation $Q_2=N_2·P$, which ensures transactions integrity but is not directly employed in the previous proof, may only be discovered by solving another generic instance of ECDLP. Indeed, if $\mathscr{H}$ behaves as a random oracle, then finding a pair of integers $(X,Y)$ that solves

$$\mathtt{P}\_\mathtt{G}\mathtt{e}\mathtt{n}(\mathscr{H}(X),E)=Y·P$$

is as difficult as computing a generic discrete logarithm on E. However, the same argument might hold under much weaker assumptions (e.g., $\mathscr{H}$ to be preimage resistant).

Besides security, the curves we propose are fully rigid as defined in [23]: their construction is entirely explained in terms of the previous block, which cannot be controlled by a malicious actor since there is no room for miner choices (such as nonces). Even assuming that the transactions of the previous block might be chosen ad hoc, an attacker who wants to impose a particular curve during the next epoch has to brute-force invert the hash $\mathscr{H}$ at the cost of one ECDLP solution for each attempt, until a desired hash digest is obtained, within the time needed for the entire network to solve a single ECDLP. We consider this scenario unachievable under realistic assumptions.

As regards the difference between EBs and SBs, we point out that the bulk of miner’s work consists of the ECDLP solution: we expect good parameters to be generated in EBs in a time that is linear in the difficulty parameter [53], whereas the asymptotic difficulty of ECDLP solution is exponential in it. This difference in complexity is concretely presented in Figure 4, where with a Magma [54] test we have compared the time used for generating the parameters $p,E,P$ and the time needed for solving a generic ECDLP on them.

Since the curve creation appears not to be computationally demanding when compared to the actual PoW, then lazy miners do not have any substantial advantage in skipping it.

Remark 1.

As regards forks, they may occur if two miners find at nearly the same time a valid solution. This is possible, but unlikely, for two reasons. The first is that each miner is trying to solve a distinct ECDLP mathematical problem (since its input data include the miner’s digital signature), so the difficulty of these problems may differ in practice, although they have the same average complexity. The second is that all known efficient algorithms to solve ECDLP on a generic strong curve are randomized algorithms, so that, even if two miners had the same identical initial data, their running time would be different. In any case, if the computational power of the miner network grows significantly before the parameter d is adjusted, then forks will be more likely to occur, exactly as it happens with Bitcoin. In conclusion, we cannot exclude the event of forks, but its probability will be about the same as forks in Bitcoin, and, when they happen, the chain that survives is the one that is supported by the majority of the network computational power (again, as it happens for Bitcoin).

5. Conclusions

We have proposed a new PoW-based blockchain model based on general ECDLP, highlighting the desirable properties that such a scheme provides in terms of scientific relevance, security, and pure decentralization ideals. In particular, even though the scheme employs a well-known underlying mathematical problem, it does not rely on specific choices of curve parameters, so that its security depends on the average complexity of the ECDLP solution. This removes possible suspects on the security of a given fixed curve.

It may be interesting to produce an actual implementation of the proposed scheme, obtaining practical time measurements and efficiency considerations. A subsequent engaging project might address the resistance of such a protocol to the known attacks under real-world assumptions, comparing the obtained results with outcomes of existing cryptocurrencies. Other types of curve models may be also considered for such schemes, such as Edwards or Montgomery curves, which may have faster point arithmetic. More generally, every family of groups on which the DLP is considered hard may be exploited to conceive a similarly fair PoW-schemes. The choice of basing our proposal on elliptic curves that are considered secure is motivated by their intrinsic interest and worldwide adoption.

Finally, different types of PoW might be conceived in a similar fashion, possibly employing problems that are thought to be resistant even to quantum attacks.