Cokriging Prediction Using as Secondary Variable a Functional Random Field with Application in Environmental Pollution
Abstract
1. Introduction and Bibliographical Review
2. Cokriging Using as Secondary Variable a Functional Random Field
2.1. Ordinary Cokriging Predictor
- (i)
- , for .
- (ii)
- .
- (iii)
2.2. Cokriging Predictor Using Functional Secondary Variables
3. Real Data Analysis
3.1. Definition of the Problem upon Study
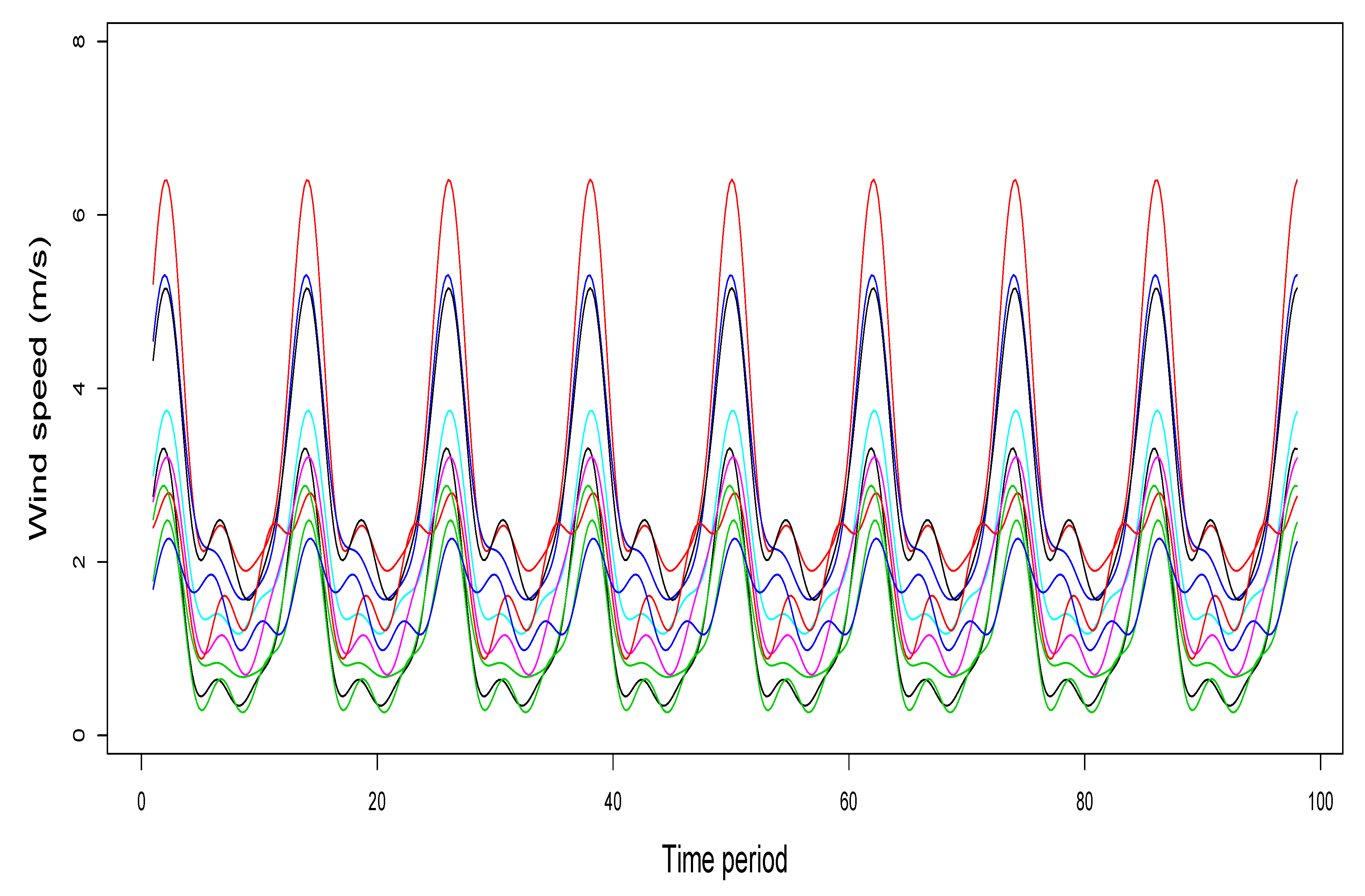
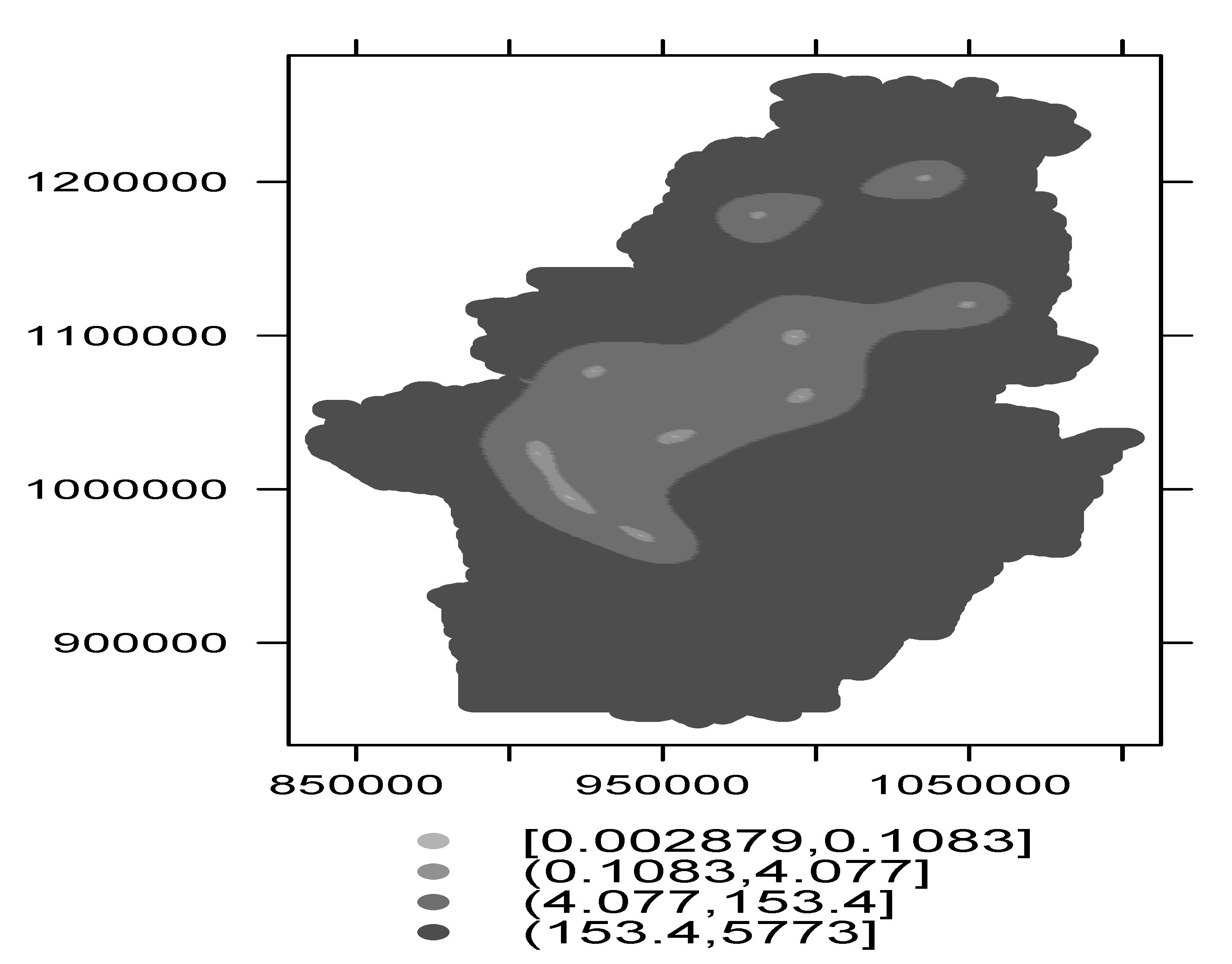
3.2. Cokriging Prediction of PM10 Using WS Curves
4. Concluding Remarks, Discussion, and Future Research
4.1. Conclusions and Discussion
- (i)
- A cokriging predictor considering a functional secondary variable was proposed.
- (ii)
- After smoothing by using basis functions, an ordinary cokriging was defined by means of several secondary variables (as many as basis functions are used for smoothing the data).
- (iii)
- Cokriging was considered to be a better option than kriging, because including one or more secondary variables in the prediction process reduces uncertainty.
- (iv)
- It was showed how to use the proposed methodology when there are many measurements of a secondary variable over time.
- (v)
- An illustration with a real data set was considered to predict PM10 values in Bogotá city by using a cokriging predictor with wind speed as functional secondary variable.
4.2. Further Work
- (i)
- A cokriging predictor with functional variables can be studied upon non-stationarity [21].
- (ii)
- Extensions to the multivariate case is also of practical relevance [41].
- (iii)
- (iv)
- (v)
- The applications of the new methodology proposed in this investigation can be of interest in diverse areas, where the functional data analysis is considered [29].
- (vi)
- (vii)
- Autoregressive model-based fuzzy clustering can be used for detecting information redundancy in air pollution monitoring networks [49].
- (viii)
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Cokriging System of Equations
Appendix A.2. Coefficients of Basis Functions
References
- Diggle, P.; Ribeiro, P. Model-Based Geoestatistics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Ver Hoef, J.; Barry, R. Constructing and fitting models for cokriging and multivariable spatial prediction. J. Stat. Plan. Inference 1998, 69, 275–294. [Google Scholar] [CrossRef]
- Chiles, J.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Marchant, C.; Leiva, V.; Cavieres, M.F.; Sanhueza, A. Air contaminant statistical distributions with application to PM10 in Santiago, Chile. Rev. Environ. Contam. Toxicol. 2013, 223, 1–31. [Google Scholar]
- Cappelli, C.; D’Urso, P.; De Giovanni, L.; Massari, R. Regime change analysis of interval-valued time series with an application to PM10. Chemom. Intell. Lab. Syst. 2015, 146, 337–346. [Google Scholar] [CrossRef]
- Leiva, V.; Marchant, C.; Ruggeri, F.; Saulo, H. Monitoring urban environmental pollution by bivariate control charts: New methodology and case study in Santiago, Chile. Environmetrics 2015, 30, e2551. [Google Scholar]
- D’Urso, P.; Cappelli, C.; De Giovanni, L.; Massari, R. Autoregressive metric-based trimmed fuzzy clustering with an application to PM10 time series. Chemom. Intell. Lab. Syst. 2017, 161, 15–26. [Google Scholar] [CrossRef]
- Marchant, C.; Leiva, V.; Christakos, G.; Cavieres, M.F. A criterion for environmental assessment using Birnbaum-Saunders attribute control charts. Environmetrics 2019, 26, 463–476. [Google Scholar]
- Cavieres, M.F.; Leiva, V.; Marchant, C.; Rojas, F. A methodology for data-driven decision making in the monitoring of particulate matter environmental contamination in Santiago of Chile. Rev. Environ. Contam. Toxicol. 2020. [Google Scholar] [CrossRef]
- Leiva, V.; Saulo, H.; Souza, R.; Aykroyd, R.G.; Vila, R. A new BISARMA time series model for forecasting mortality using weather and particulate matter data. J. Forecast. 2020. [Google Scholar] [CrossRef]
- Le, N.; Zidek, J. Statistical Analysis of Environmental Space-Time Processes; Springer: New York, NY, USA, 2006. [Google Scholar]
- Garcia-Papani, F.; Leiva, V.; Ruggeri, F.; Uribe-Opazo, M.A. Kriging with external drift in a Birnbaum-Saunders geostatistical model. Stoch. Environ. Res. Risk Assess. 2018, 32, 1517–1530. [Google Scholar] [CrossRef]
- Wackernagel, H. Cokriging versus kriging in regionalized multivariate data analysis. Geoderma 1994, 62, 83–92. [Google Scholar] [CrossRef]
- Helterbrand, J.; Cressie, N. Universal cokriging under intrinsic coregionalization. Math. Geol. 1994, 26, 205–226. [Google Scholar] [CrossRef]
- Rivoirard, J. Which models for collocated cokriging? Math. Geol. 2001, 33, 117–131. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Dowd, P. Multiple indicator cokriging with application to optimal sampling for environmental monitoring. Comput. Geosci. 2005, 31, 1–13. [Google Scholar] [CrossRef]
- Isaaks, E.; Srivastava, M. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Delicado, P.; Giraldo, R.; Comas, C.; Mateu, J. Geostatistics for spatial functional data: Some recent contributions. Environmetrics 2010, 21, 224–239. [Google Scholar] [CrossRef]
- Giraldo, R. Geostatistics for Functional Data. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2009. [Google Scholar]
- Martinez, S.; Giraldo, R.; Leiva, V. Birnbaum-Saunders functional regression models for spatial data. Stoch. Environ. Res. Risk Assess. 2019, 33, 1765–1780. [Google Scholar] [CrossRef]
- Goulard, M.; Voltz, M. Geostatistical interpolation of curves: A case study in soil science. In Geostatistics Tróia’92; Soares, A., Ed.; Kluwer Academc Press: Dordrecht, The Netherlands, 1993; Volume 2, pp. 805–816. [Google Scholar]
- Nerini, D.; Monestiez, P.; Manté, C. Cokriging for spatial functional data. J. Multivar. Anal. 2010, 101, 409–418. [Google Scholar] [CrossRef]
- Giraldo, R.; Delicado, P.; Mateu, J. Ordinary kriging for function-valued spatial data. Environ. Ecol. Stat. 2011, 18, 411–426. [Google Scholar] [CrossRef]
- Menafoglio, A.; Petris, G. Kriging for Hilbert-space valued random fields. The operational point of view. J. Multivar. Anal. 2016, 146, 84–94. [Google Scholar] [CrossRef]
- Caballero, W.; Giraldo, R.; Mateu, J. A universal kriging approach for spatial functional data. Stoch. Environ. Res. Risk Assess. 2013, 27, 1553–1563. [Google Scholar] [CrossRef]
- Ignaccolo, R.; Mateu, J.; Giraldo, R. Kriging with external drift for functional data for air quality monitoring. Stoch. Environ. Res. Risk Assess. 2014, 28, 1171–1186. [Google Scholar] [CrossRef]
- Reyes, A.; Giraldo, R.; Mateu, J. Residual kriging for functional prediction of salinity curves. Commun. Stat. Theory Methods 2005, 44, 798–809. [Google Scholar] [CrossRef]
- Ramsay, J.; Silverman, B. Functional Data Analysis; Springer: New York, NY, USA, 2005. [Google Scholar]
- Hooyberghsa, J.; Mensinka, C.; Dumontb, G.; Fierensb, F.; Brasseurc, O. A neural network forecast for daily average PM10 concentrations in Belgium. Atmos. Environ. 2005, 39, 3279–3289. [Google Scholar] [CrossRef]
- Pérez, P.; Reyes, J. Prediction of maximum of 24-h average of PM10 concentrations 30 h in advance in Santiago, Chile. Atmos. Environ. 2002, 36, 4555–4561. [Google Scholar] [CrossRef]
- Giri, D.; Krishna-Murthy, V.; Adhiraky, P. The influence of meteorological conditions on PM10 concentrations in Kathmandu valley. Int. J. Environ. Res. 2008, 2, 49–60. [Google Scholar]
- Emery, X. Iterative algorithms for fitting a linear model of coregionalization. Comput. Geosci. 2010, 36, 1150–1160. [Google Scholar] [CrossRef]
- Giraldo, R. Propuesta de un indicador como variable auxiliar en el análisis cokriging. Rev. Colomb. Estadística 2001, 24, 1–12. [Google Scholar]
- Rodríguez-Camargo, L.; Sierra-Parada, R.; Blanco-Becerra, L. Análisis espacial de las concentraciones de PM2.5 en Bogotá según los valores de las guías de la calidad del aire de la Organización Mundial de la Salud para enfermedades cardiopulmonares, 2014–2015. Biomédica 2020, 40, 137–152. [Google Scholar] [CrossRef]
- Myers, D. Matrix formulation of cokriging. Math. Geol. 1982, 14, 249–257. [Google Scholar] [CrossRef]
- Bogaert, P. Comparison of kriging techniques in a space-time context. Math. Geol. 1996, 28, 73–86. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Pebesma, E. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- R Code. Available online: https://sites.google.com/a/unal.edu.co/ramon-giraldo-webpage/r-code (accessed on 20 July 2020).
- Sánchez, L.; Leiva, V.; Galea, M.; Saulo, H. Birnbaum-Saunders quantile regression models with application to spatial data. Mathematics 2020, 8, 1000. [Google Scholar] [CrossRef]
- Huerta, M.; Leiva, V.; Rodriguez, M.; Villegas, D. On a partial least squares regression model for asymmetric data with a chemical application in mining. Chemom. Intell. Lab. Syst. 2019, 190, 55–68. [Google Scholar] [CrossRef]
- Saulo, H.; Leão, J.; Leiva, V.; Aykroyd, R.G. Birnbaum-Saunders autoregressive conditional duration models applied to high-frequency financial data. Stat. Pap. 2019, 60, 1605–1629. [Google Scholar] [CrossRef]
- Carrasco, J.M.F.; Figueroa-Zuniga, J.I.; Leiva, V.; Riquelme, M.; Aykroyd, R.G. An errors-in-variables model based on the Birnbaum-Saunders and its diagnostics with an application to earthquake data. Stoch. Environ. Res. Risk Assess. 2020, 34, 369–380. [Google Scholar] [CrossRef]
- Sánchez, L.; Leiva, V.; Galea, M.; Saulo, H. Birnbaum-Saunders quantile regression and its diagnostics with application to economic data. Appl. Stoch. Model. Bus. Ind. 2020. [Google Scholar] [CrossRef]
- Garcia-Papani, F.; Leiva, V.; Uribe-Opazo, M.A.; Aykroyd, R.G. Birnbaum-Saunders spatial regression models: Diagnostics and application to chemical data. Chemom. Intell. Lab. Syst. 2018, 177, 114–128. [Google Scholar] [CrossRef]
- Liu, Y.; Mao, G.; Leiva, V.; Liu, S.; Tapia, A. Diagnostic analytics for an autoregressive model under the skew-normal distribution. Mathematics 2020, 8, 693. [Google Scholar] [CrossRef]
- Genton, M.G.; Zhang, H. Identifiability problems in some non-Gaussian spatial random fields. Chilean J. Stat. 2012, 3, 171–179. [Google Scholar]
- D’Urso, P.; Di Lallo, D.; Maharaj, E.A. Autoregressive model-based fuzzy clustering and its application for detecting information redundancy in air pollution monitoring networks. Soft Comput. 2013, 17, 83–131. [Google Scholar] [CrossRef]
- D’Urso, P.; De Giovanni, L.; Massari, R. Time series clustering by a robust autoregressive metric with application to air pollution. Chemom. Intell. Lab. Syst. 2015, 141, 107–124. [Google Scholar] [CrossRef]
- Velasco, H.; Laniado, H.; Toro, M.; Leiva, V.; Lio, Y. Robust three-step regression based on comedian and its performance in cell-wise and case-wise outliers. Mathematics 2020, 8, 1259. [Google Scholar] [CrossRef]
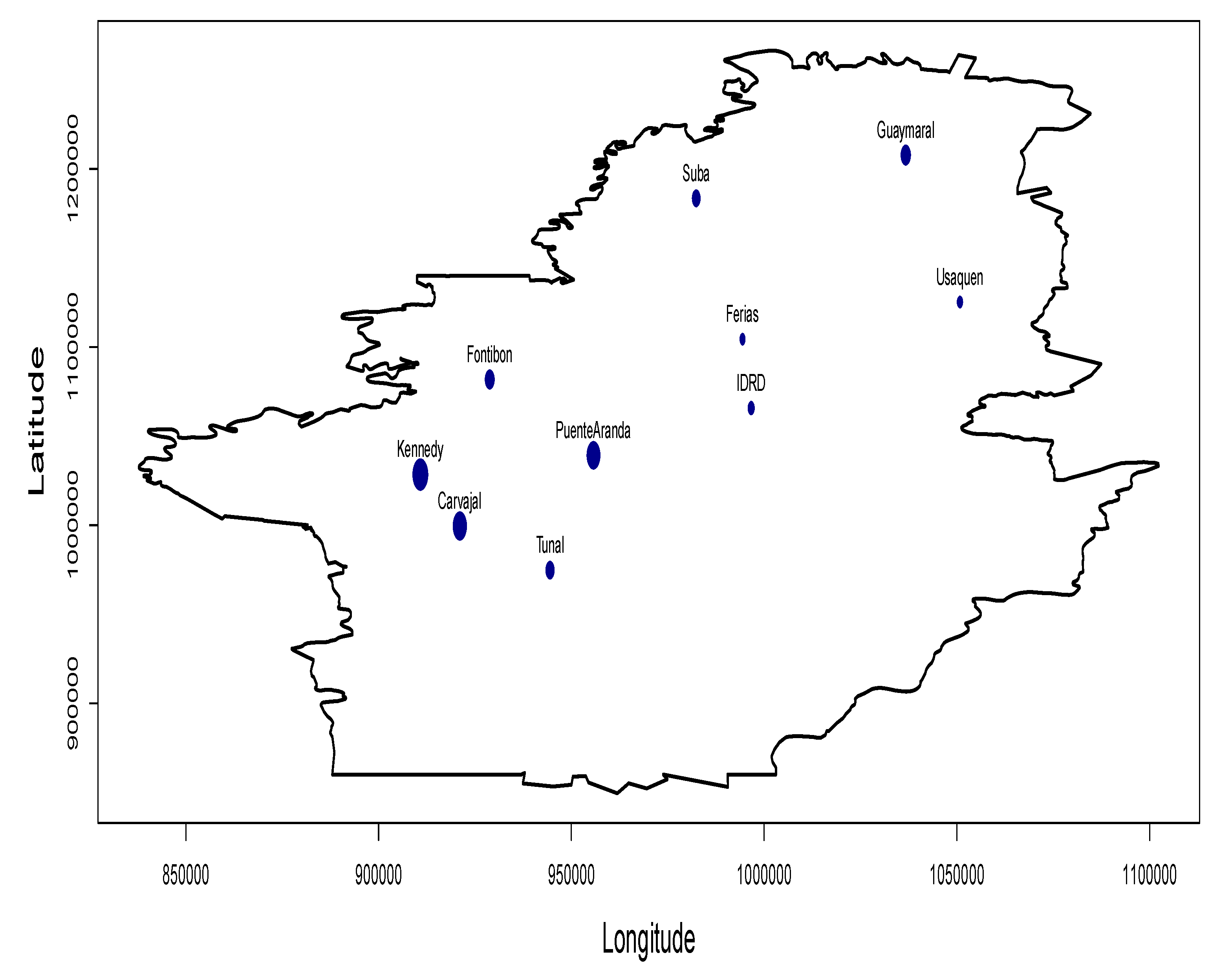


| Station ID | Monitoring Station | PM10 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | Carvajal | 242 | 4.35 | 2.31 | 1.87 | 1.40 | –0.40 | –0.10 | –0.67 |
| 2 | Fontibon | 174 | 11.24 | 3.97 | 2.12 | 2.17 | –1.05 | –0.37 | –0.83 |
| 3 | Guaymaral | 179 | 3.49 | 1.67 | 1.26 | 0.85 | –0.48 | –0.51 | –0.50 |
| 4 | Kennedy | 265 | 9.76 | 3.52 | 1.72 | 1.54 | –0.55 | –0.05 | –0.60 |
| 5 | Las Ferias | 116 | 6.90 | 2.17 | 1.37 | 0.91 | –0.69 | –0.26 | –0.56 |
| 6 | Simón Bolivar | 130 | 5.77 | 2.13 | 1.52 | 0.88 | –0.27 | –0.48 | –0.24 |
| 7 | Puente Aranda | 237 | 9.80 | 3.00 | 1.49 | 1.77 | –0.37 | –0.48 | –0.63 |
| 8 | Suba | 157 | 6.41 | 0.76 | 1.63 | 0.51 | –0.13 | –0.83 | –0.23 |
| 9 | Tunal | 162 | 4.64 | 1.94 | 1.27 | 1.07 | –0.33 | –0.01 | –0.35 |
| 10 | Usaquen | 118 | 5.39 | 1.12 | -0.22 | 0.19 | –0.07 | –0.17 | –0.59 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giraldo, R.; Herrera, L.; Leiva, V. Cokriging Prediction Using as Secondary Variable a Functional Random Field with Application in Environmental Pollution. Mathematics 2020, 8, 1305. https://doi.org/10.3390/math8081305
Giraldo R, Herrera L, Leiva V. Cokriging Prediction Using as Secondary Variable a Functional Random Field with Application in Environmental Pollution. Mathematics. 2020; 8(8):1305. https://doi.org/10.3390/math8081305
Chicago/Turabian StyleGiraldo, Ramón, Luis Herrera, and Víctor Leiva. 2020. "Cokriging Prediction Using as Secondary Variable a Functional Random Field with Application in Environmental Pollution" Mathematics 8, no. 8: 1305. https://doi.org/10.3390/math8081305
APA StyleGiraldo, R., Herrera, L., & Leiva, V. (2020). Cokriging Prediction Using as Secondary Variable a Functional Random Field with Application in Environmental Pollution. Mathematics, 8(8), 1305. https://doi.org/10.3390/math8081305







