Coordination in Coupled Arrays of Stiff Filaments—Modelling and Simulation
Abstract
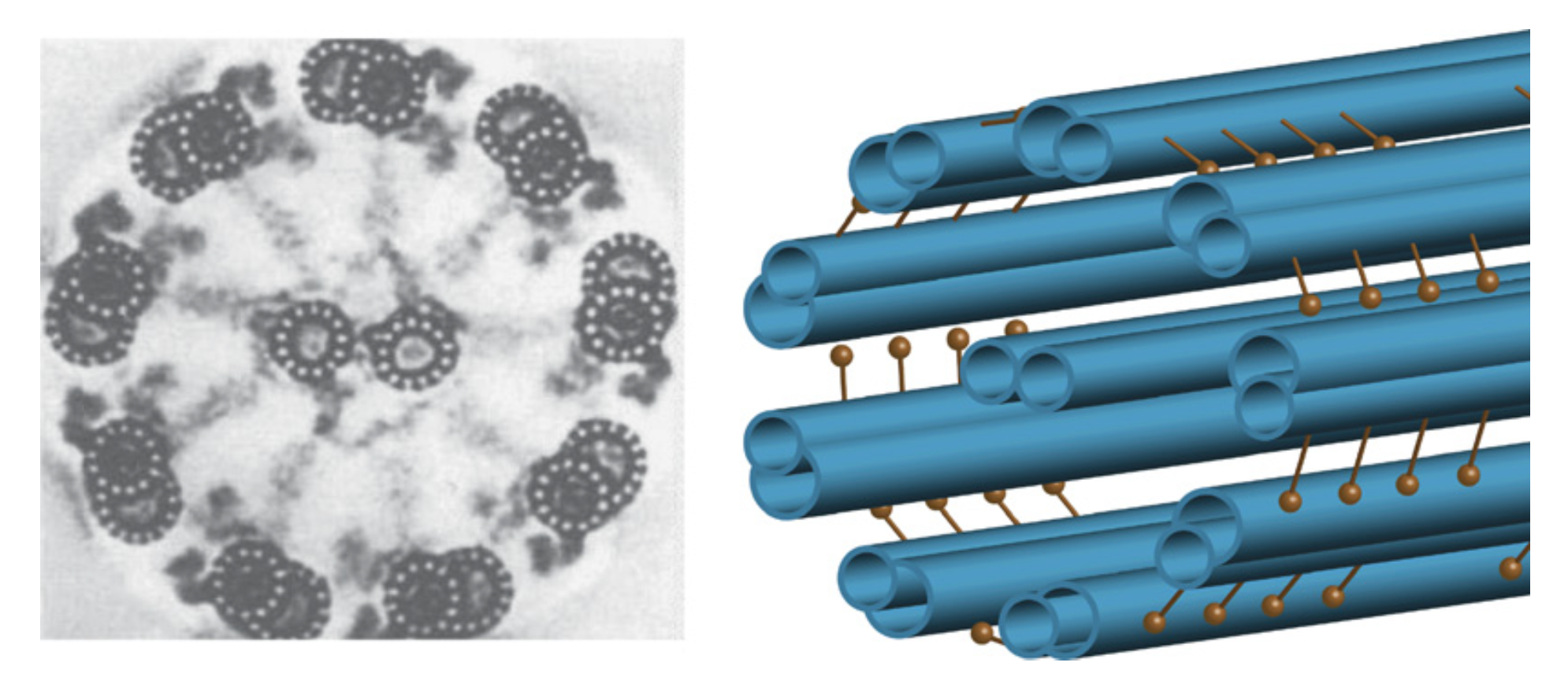
:1. Introduction
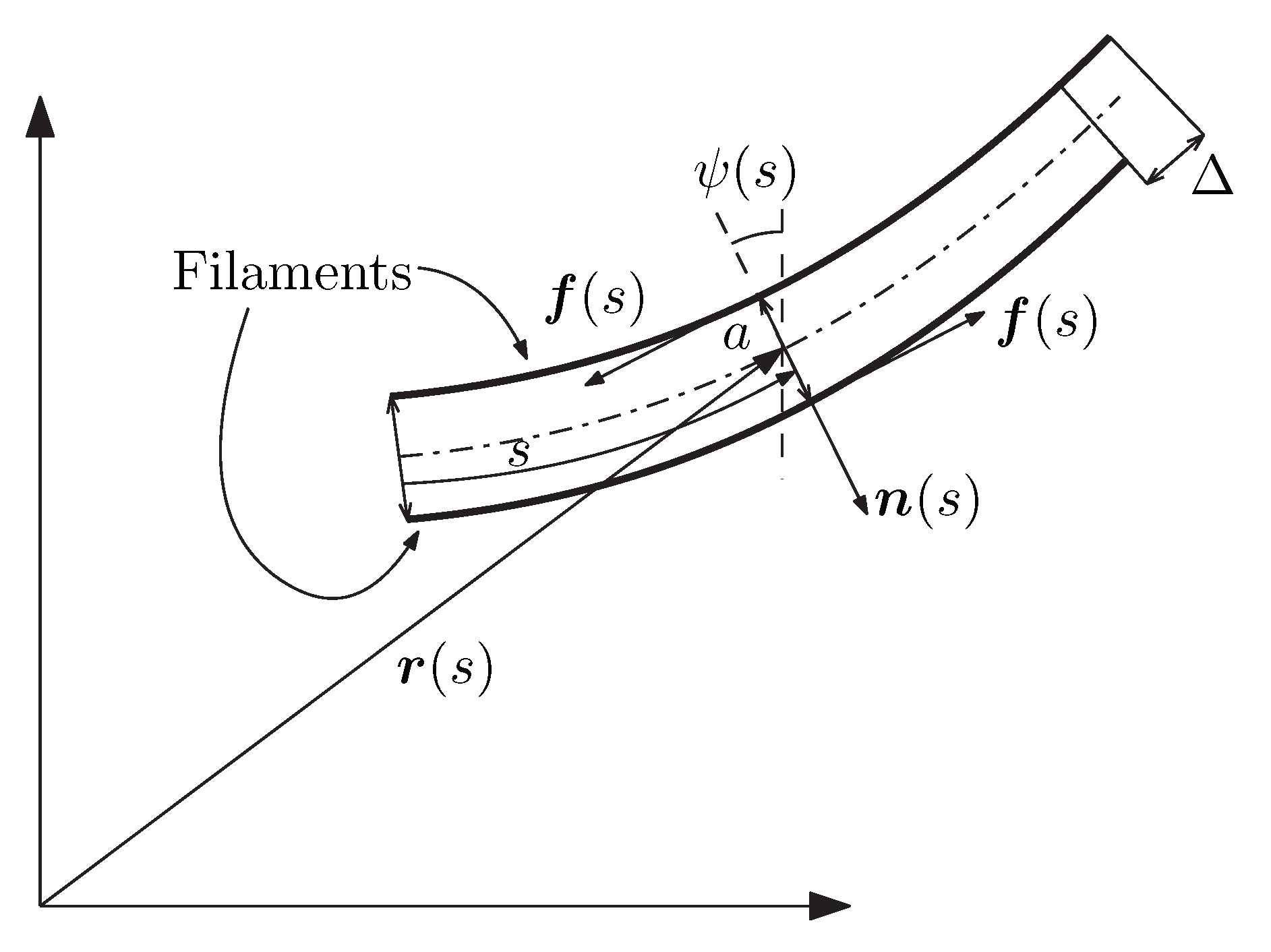
2. Stiff Filaments with Internal Action
3. Weak Form and Finite Element Formulation
3.1. Boundary Conditions and Coupling
3.2. Finite Element Discretization
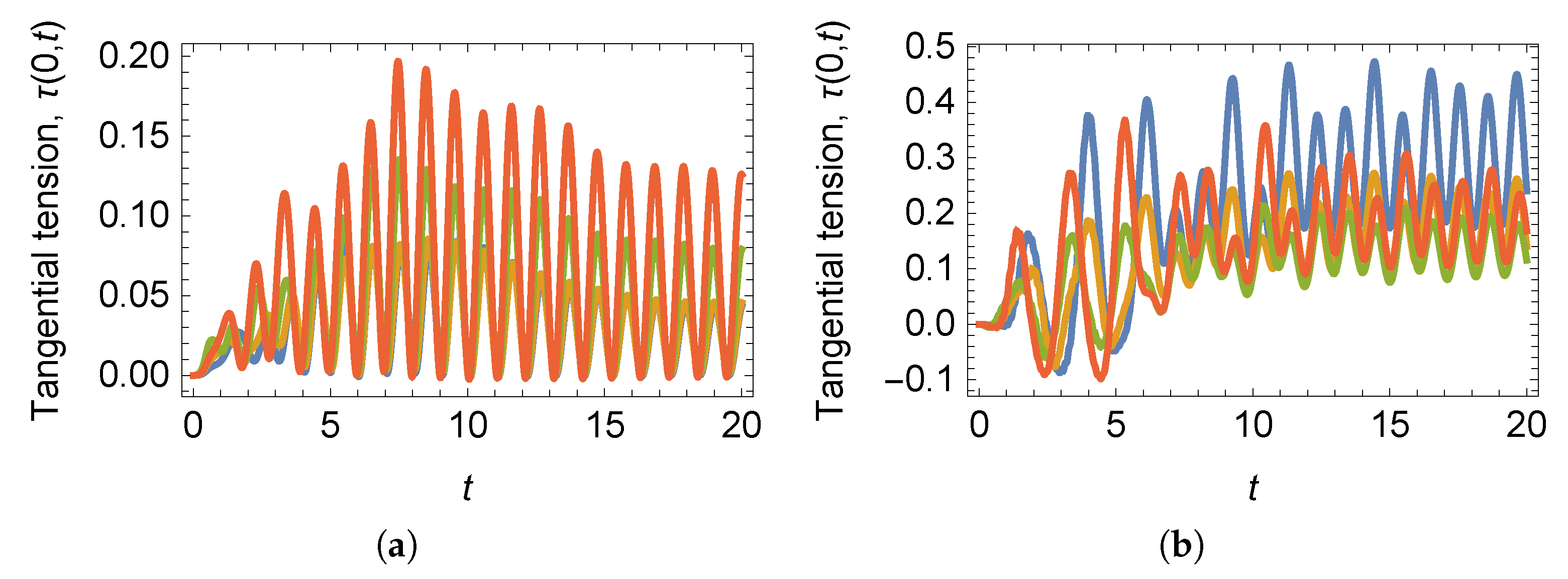
4. Simulation Results and Discussion
5. Conclusions
Funding
Conflicts of Interest
Appendix A
Appendix B
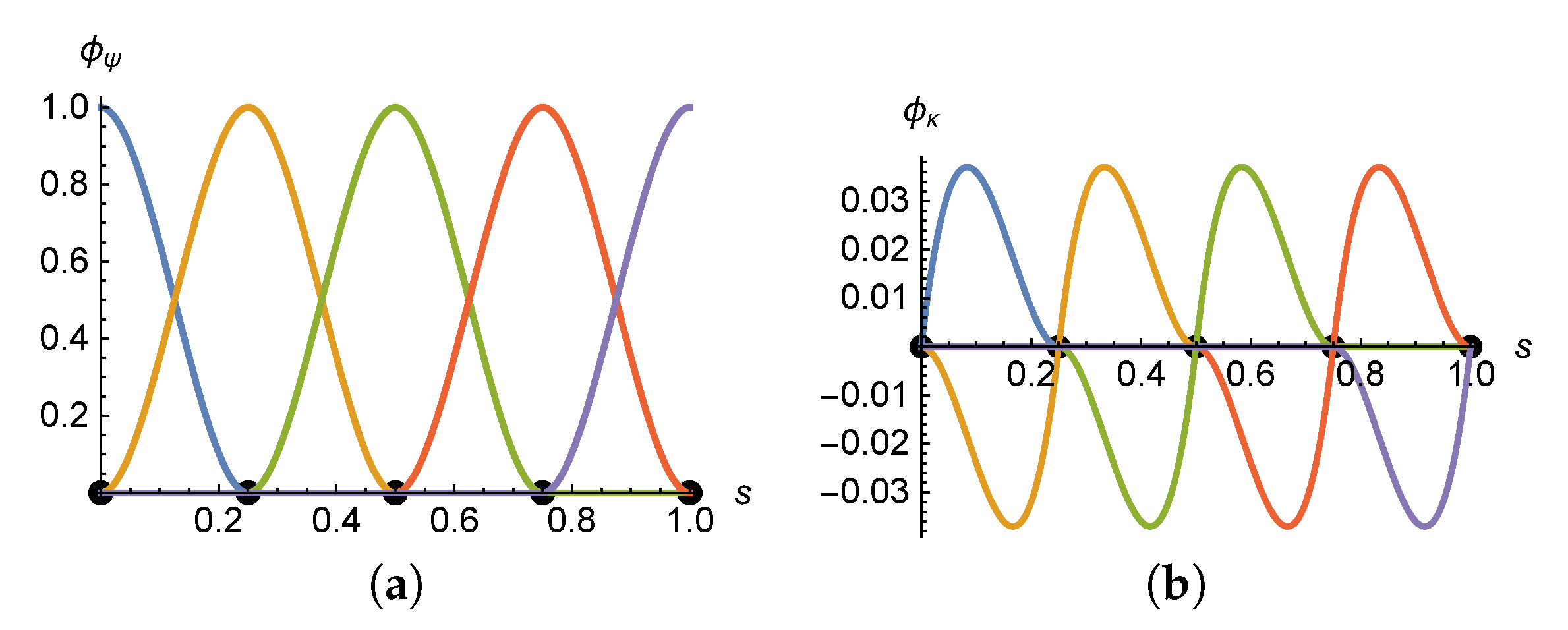
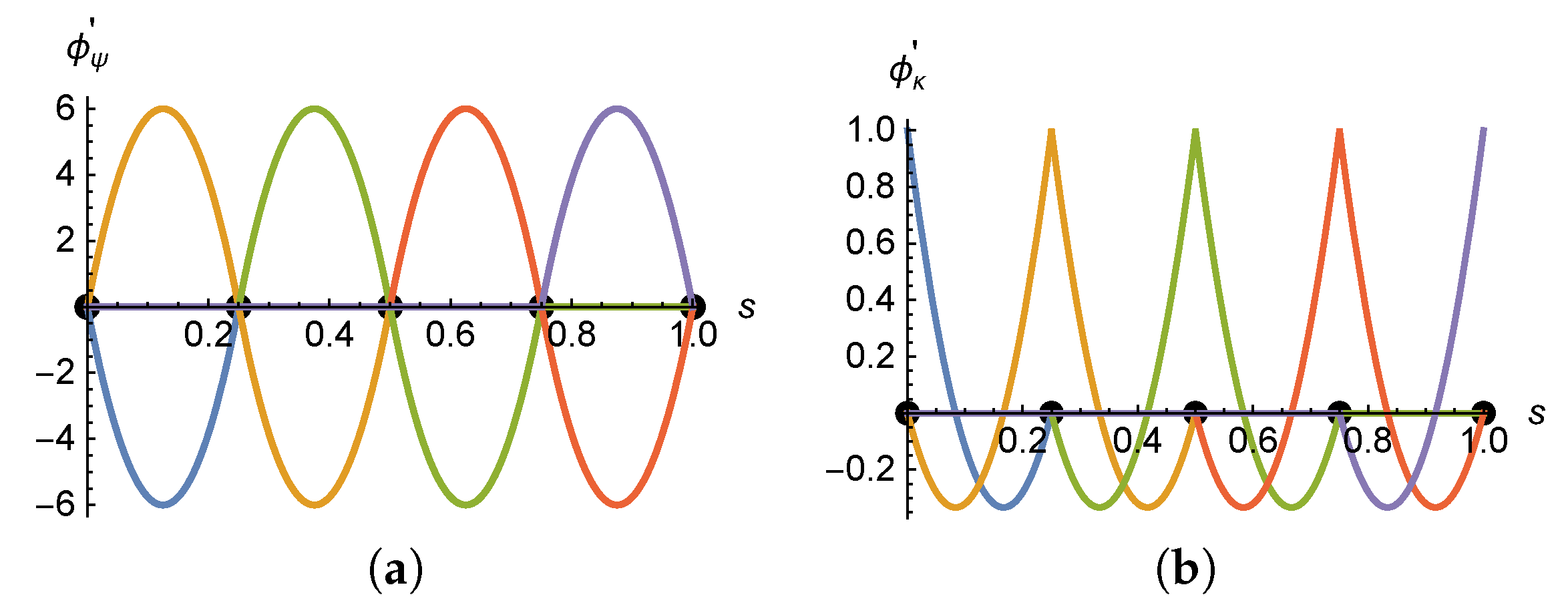
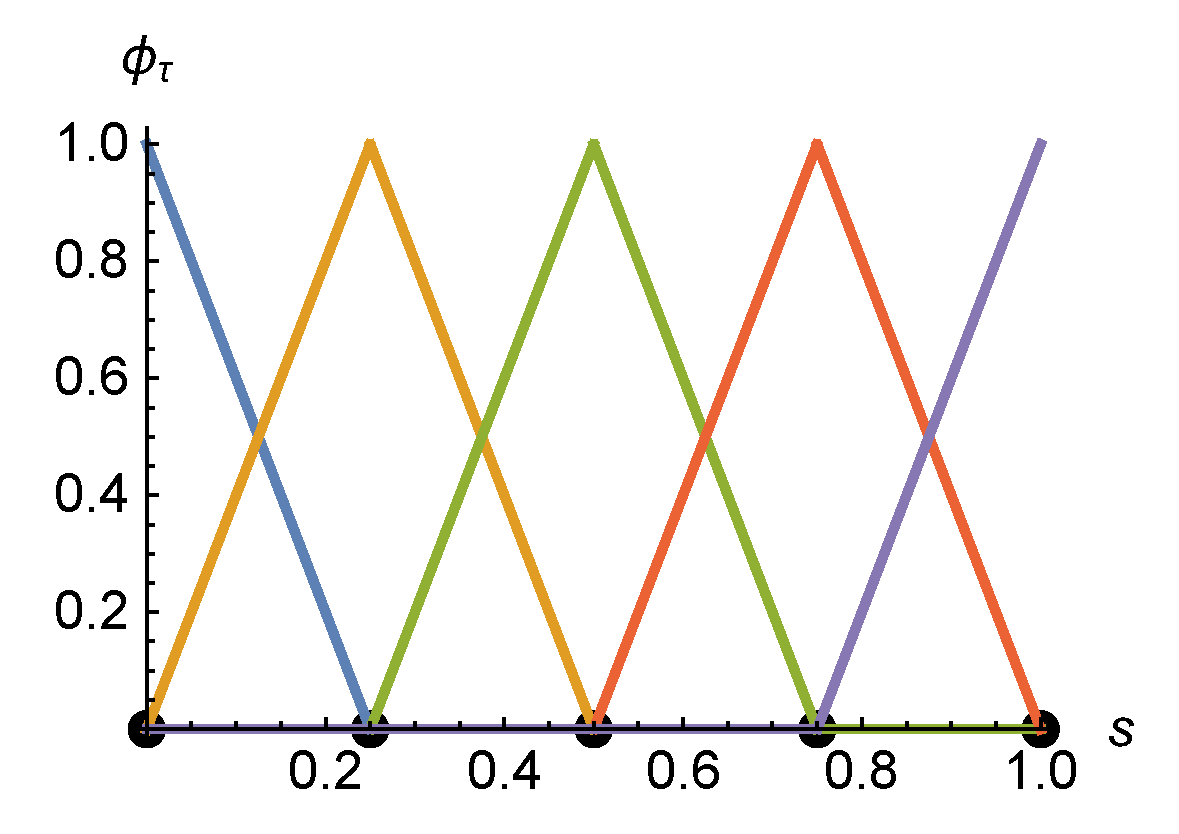
Appendix C
References
- Camalet, S.; Jülicher, F. Generic Aspects of Axonemal Beating. New J. Phys. 2000, 2, 24. [Google Scholar] [CrossRef]
- Srigiriraju, S.V.; Powers, T.R. Model for Polymorphic Transitions in Bacterial Flagella. Phys. Rev. E 2006, 73, 011902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dillon, R.H.; Fauci, L.J.; Omoto, C. Mathematical Modeling of Axoneme Mechanics and Fluid Dynamics in Ciliary and Sperm Motility. Dyn. Contin. Discret. Impuls. Syst. Ser. A Math. Anal. 2003, 10, 745–757. [Google Scholar]
- Riedel-Kruse, I.H.; Hilfinger, A.; Howard, J.; Juelicher, F. How Molecular Motors Shape the Flagellar Beat. HFSP J. 2007, 1, 192–208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pellicciotta, N.; Hamilton, E.; Kotar, J.; Faucourt, M.; Delgehyr, N.; Spassky, N.; Cicuta, P. Entrainment of Mammalian Motile Cilia in the Brain with Hydrodynamic Forces. Proc. Natl. Acad. Sci. USA 2020, 117, 8315–8325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saleem, N.; Munawar, S. Entropy Analysis in Cilia Driven Pumping Flow of Hyperbolic Tangent Fluid with Magnetic Field Effects. Fluid Dyn. Res. 2020, 52, 025503. [Google Scholar] [CrossRef]
- Hall, J.; Clarke, N. The Mechanics of Cilium Beating: Quantifying the Relationship between Metachronal Wavelength and Fluid Flow Rate. J. Fluid Mech. 2020, 891, A20. [Google Scholar] [CrossRef]
- Oldenburg, A.L.; Chhetri, R.K.; Hill, D.B.; Button, B. Monitoring Airway Mucus Flow and Ciliary Activity with Optical Coherence Tomography. Biomed. Opt. Express 2012, 3, 1978–1992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dasgupta, A.; Amack, J.D. Cilia in Vertebrate Left–Right Patterning. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niedermayer, T.; Eckhardt, B.; Lenz, P. Synchronization, Phase Locking, and Metachronal Wave Formation in Ciliary Chains. Chaos 2008, 18, 037128. [Google Scholar] [CrossRef] [PubMed]
- Elgeti, J.; Gompper, G. Emergence of Metachronal Waves in Cilia Arrays. Proc. Natl. Acad. Sci. USA 2013, 110, 4470–4475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elshalakani, M.; Bruecker, C. Simulation of Self-Coordination in a Row of Beating Flexible Flaplets for Micro-Swimmer Applications: Model and Experiment Study. J. Fluids Struct. 2020, 94, 102923. [Google Scholar] [CrossRef]
- Wan, K.Y.; Goldstein, R.E. Coordinated Beating of Algal Flagella Is Mediated by Basal Coupling. Proc. Natl. Acad. Sci. USA 2016, 113, E2784–E2793. [Google Scholar] [CrossRef] [Green Version]
- Bogue, R. Robots for Monitoring the Environment. Ind. Robot Int. J. 2011, 38, 560–566. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, H.; Reddy, H.A.; Kalyan, B.; Murthy, C.S.N. Mine Rescue Robot System—A Review. Procedia Earth Planet. Sci. 2015, 11, 457–462. [Google Scholar] [CrossRef] [Green Version]
- Bangalkar, Y.V.; Kharad, S.M. Review Paper on Search and Rescue Robot for Victims of Earthquake and Natural Calamities. Int. J. Recent Innov. Trends Comput. Commun. 2015, 3, 2037–2040. [Google Scholar] [CrossRef]
- Thavasi, P.T.; Suriyakala, C.D. Sensors and Tracking Methods Used in Wireless Sensor Network Based Unmanned Search and Rescue System—A Review. Procedia Eng. 2012, 38, 1935–1945. [Google Scholar] [CrossRef] [Green Version]
- Trevelyan, J.P.; Kang, S.C.; Hamel, W.R. Robotics in Hazardous Applications. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1101–1126. [Google Scholar]
- Hilfinger, A.; Jülicher, F. The Chirality of Ciliary Beats. Phys. Biol. 2008, 5, 016003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldstein, R.E.; Langer, S.A. Nonlinear Dynamics of Stiff Polymers. Phys. Rev. Lett. 1995, 75, 1094–1097. [Google Scholar] [CrossRef] [Green Version]
- Hughes, T.J. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: Mineola, NY, USA, 2000. [Google Scholar]
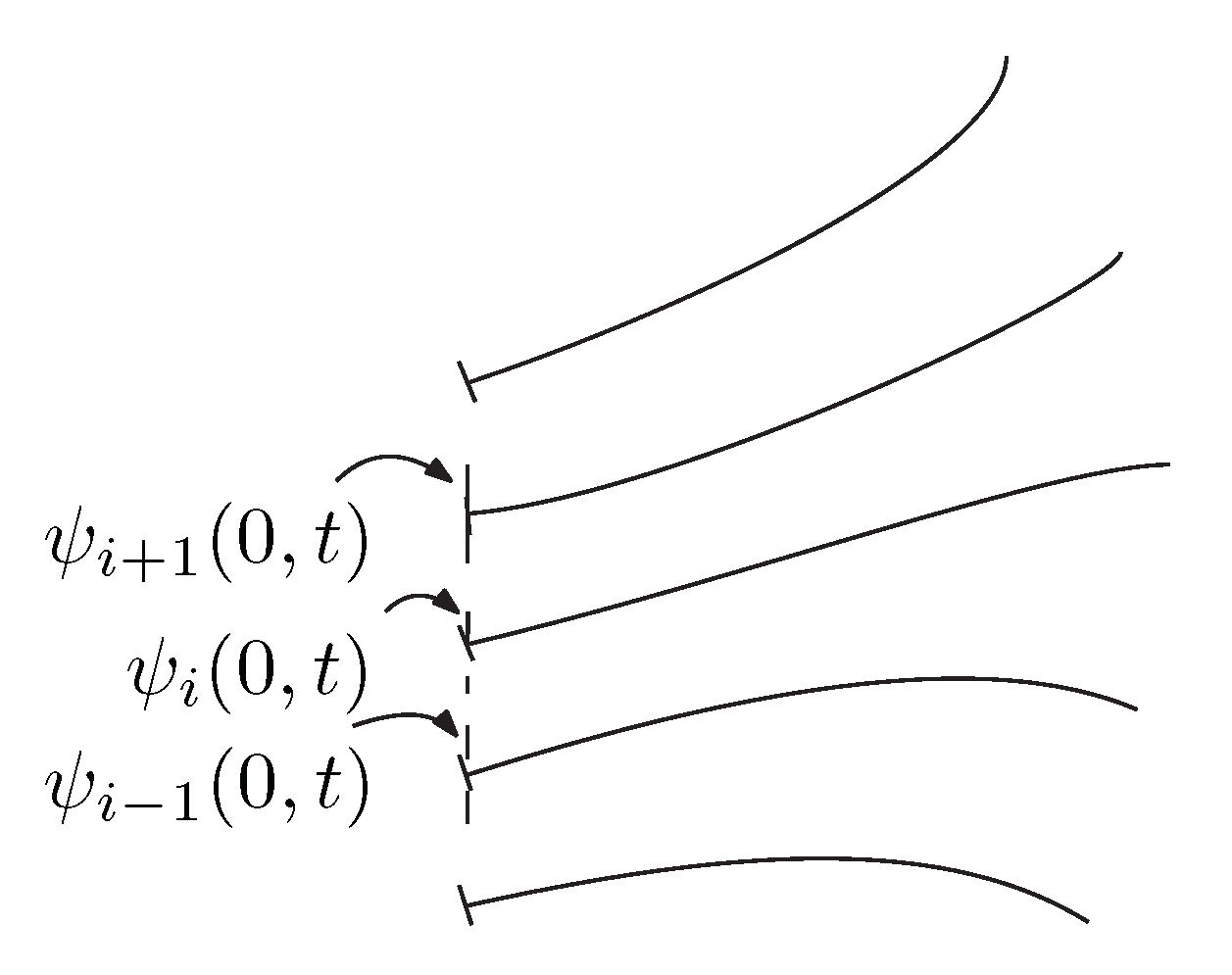

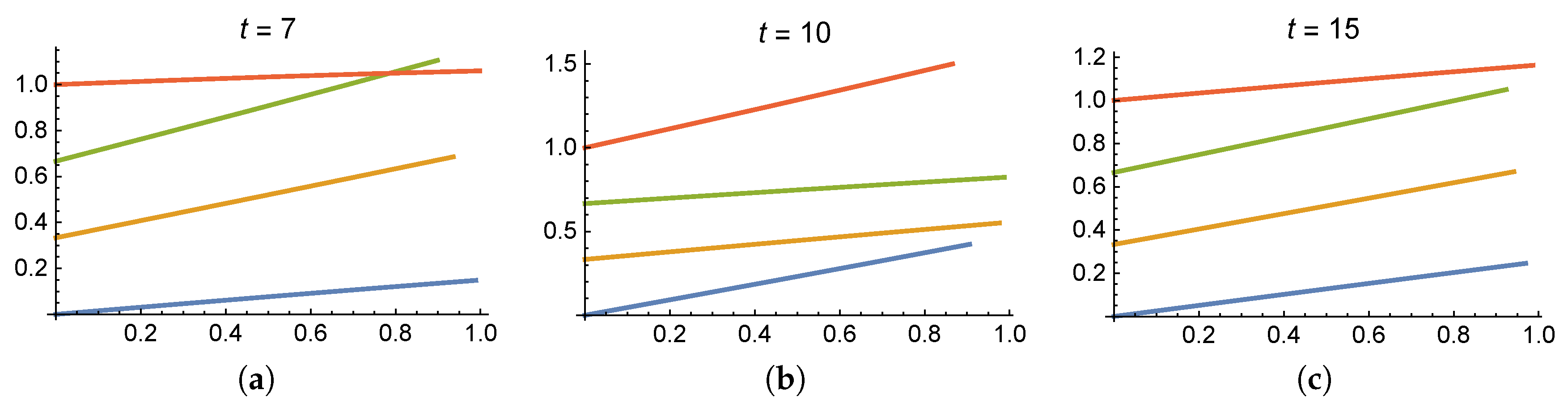
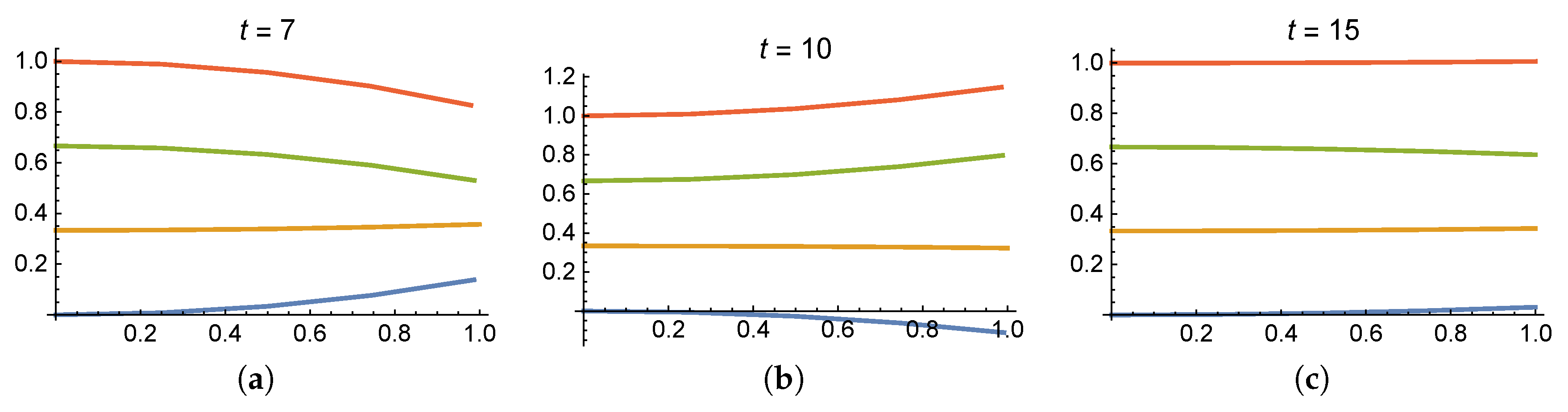
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spinello, D. Coordination in Coupled Arrays of Stiff Filaments—Modelling and Simulation. Mathematics 2020, 8, 1282. https://doi.org/10.3390/math8081282
Spinello D. Coordination in Coupled Arrays of Stiff Filaments—Modelling and Simulation. Mathematics. 2020; 8(8):1282. https://doi.org/10.3390/math8081282
Chicago/Turabian StyleSpinello, Davide. 2020. "Coordination in Coupled Arrays of Stiff Filaments—Modelling and Simulation" Mathematics 8, no. 8: 1282. https://doi.org/10.3390/math8081282




