Dynamic Behaviors of a Single Species Stage Structure Model with Michaelis–Menten-TypeJuvenile Population Harvesting

Abstract

A single species stage structure model with Michaelis–Menten-type juvenile population harvesting is proposed and investigated. The existence and local stability of the model equilibria are studied. It shows that for the model, two cases of bistability may exist. Some conditions for the global asymptotic stability of the boundary equilibrium are derived by constructing some suitable Lyapunov functions. After that, based on the Bendixson–Dulac discriminant, we obtain the sufficient conditions for the global asymptotic stability of the internal equilibrium. Our study shows that nonlinear harvesting can make the dynamics of the system more complex than linear harvesting; for example, the system may admit the bistable stability property. Numeric simulations support our theoretical results.

1. Introduction

It is well known that many species go through two stages, juvenile and adult, and that there are significant differences in the characteristics of species at different stages, so the stage structure model can better show the real-world phenomena.

In recent years, many scholars have considered the stage structure model [1,2,3,4,5,6,7,8,9,10,11,12,13], and they have achieved many excellent results in the extinction, permanence, and global attractivity of the model. For example, Lei [5] considered a two species stage-structured commensalism model:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{x}_1}{dt}}& =& \alpha x_2-\beta x_1-{\delta }_1{x}_1,\hfill \\ \hfill {\displaystyle \frac{d{x}_2}{dt}}& =& \beta x_1-{\delta }_2{x}_2-\gamma x_2^2+d{x}_{2}y,\hfill \\ \hfill {\displaystyle \frac{dy}{dt}}& =& y(b_2-a_{2}y),\hfill \end{array}$$

(1)

where $\alpha ,\beta ,{\delta }_1,{\delta }_2,\gamma ,d,a_2$, and $b_2$ are all positive constants; $x_1$ and $x_2$ describe the juvenile and adult of the first species densities at time t, respectively; y describes the second species densities at time t. The stability of the equilibria is investigated. Their study shows that increasing the intensity of cooperation between species is one of the most effective ways to prevent the extinction of endangered species.

After that, considering that the juvenile species needs time to grow up, Ma, Li, et al. [4], Chen, Xie, et al. [7], Chen, Chen, et al. [8], and Chen, Wang, et al. [9] proposed the stage-structure predator-prey model; the main model takes the following:

$$\begin{array}{ccc}\hfill {\dot{x}}_1(t)& =& r_1(t)x_2(t)-d_{11}{x}_1(t)-r_1(t-{\tau }_1)e^{-d_{11}{\tau }_1}{x}_2(t-{\tau }_1),\hfill \\ \hfill {\dot{x}}_2(t)& =& r_1(t-{\tau }_1)e^{-d_{11}{\tau }_1}{x}_2(t-{\tau }_1)-d_{12}{x}_2(t)\hfill \\ & & -b_1(t)x_2^2(t)-c_1(t)x_2(t)y_2(t),\hfill \\ \hfill {\dot{y}}_1(t)& =& r_2(t)y_2(t)-d_{22}{y}_1(t)-r_2(t-{\tau }_2)e^{-d_{22}{\tau }_2}{y}_2(t-{\tau }_2),\hfill \\ \hfill {\dot{y}}_2(t)& =& r_2(t-{\tau }_2)e^{-d_{22}{\tau }_2}{y}_2(t-{\tau }_2)-d_{21}{y}_2(t)\hfill \\ & & -b_2(t)y_2^2(t)+c_2(t)y_2(t)x_2(t),\hfill \end{array}$$

(2)

where $x_1(t)$, $x_2(t)$ denote the juvenile and adult of the prey species densities at time t, respectively; $y_1(t)$, $y_2(t)$ describe the juvenile and adult of the predator species densities at time t, respectively. The persistent, extinction and stability of the model are discussed. The results show that under appropriate conditions, the system is persistent, and when the prey population is extinct, the predator is not necessarily extinct.

In addition, in order to meet their own needs, human beings develop and utilize natural resources. Therefore, to ensure the sustainable development of the ecosystem and maximize the economic benefits, the harvest model has attracted the attention of many scholars [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. There are two types of harvesting proposed by May et al. [34]: constant [14]: it is a constant independent of the number of harvested populations; and linear harvesting [15,16,17,18,19,20,21,22,23,24]: it is proportional to the number of harvested populations, namely its expression is $h=qEx$. With constant harvesting, we cannot harvest a fixed number of species each year. With linear harvesting, if x is fixed, $E\to \infty$ or E is fixed, and $x\to \infty$, then we have $h\to \infty$; this is contrary to the facts. In order to overcome this shortcoming, nonlinear harvesting [25,26,27,28,29,30,31,32,33] was proposed by Clark [35]. Among them, the nonlinear harvesting, which is also called Michaelis–Menten-type harvesting, can be expressed as $h=\frac{qEx}{mE+nx}$. If $E\to \infty$, then ${\displaystyle h\to \frac{qx}{m}}$; or if $x\to \infty$, then ${\displaystyle h\to \frac{qE}{n}}$. However, the fact is that the number of species and the ability to harvest are limited, that is to say, the number of species that can be harvested is limited, so from the biological and economic point of view, it is more realistic [29].

This brings to our attention that for linear harvesting systems, generally speaking, the dynamic behavior is relatively simple. For example, Xiao and Lei [15] discussed the impact of harvesting on the dynamics of a single species stage structure model; the main model is as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{x}_1}{dt}}& =& \alpha x_2-\beta x_1-{\delta }_1{x}_1-q_{1}Em{x}_1,\hfill \\ \hfill {\displaystyle \frac{d{x}_2}{dt}}& =& \beta x_1-{\delta }_2{x}_2-\gamma x_2^2-q_{2}Em{x}_2,\hfill \end{array}$$

(3)

in which $x_1$, $x_2$ describe the juvenile and adult species densities at time t, respectively. The authors showed that if ${\displaystyle \alpha <({\delta }_2+q_{2}Em)(1+\frac{{\delta }_1+q_{1}Em}{\beta })}$, then the system has a globally asymptotically stable boundary equilibrium $O(0,0)$. Moreover, if $\alpha >({\delta }_2+q_{2}Em)(1+\frac{{\delta }_1+q_{1}Em}{\beta })$, the positive equilibrium $A(x_1^{*},x_2^{*})$ of the system is globally asymptotically stable. The dynamic behaviors of the system (3) are very simple, since only two cases exist.

Compared to linear harvesting, Michaelis–Menten-type harvesting has a greater impact on the model dynamics, which makes the model dynamics becomes more complicated. Therefore, it is necessary to consider the influence of Michaelis–Menten-type harvesting on the dynamic behavior of the system. Moreover, it can reflect the harvest process more truly, so it has attracted the attention of many scholars. For example, Liu, Huang, Deng, et al. [29] considered the influence of Michaelis–Menten-type harvesting on the dynamics of the amensalism model with cover; the modified model is as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dx}{dt}}& =& {\displaystyle a_{1}x-b_1{x}^2-c_1(1-k)xy-\frac{qE(1-k)x}{m_{1}E+m_2(1-k)x},}\hfill \\ \hfill {\displaystyle \frac{dy}{dt}}& =& a_{2}y-b_2{y}^2.\hfill \end{array}$$

(4)

The authors showed that the system has bifurcation phenomena (saddle bifurcation and transcritical bifurcation) when the parameters meet certain conditions, and then, they obtained the threshold of maximum sustainable harvest. Hu and Cao [30] also investigated the effect of Michaelis–Menten-type harvesting on the dynamic behaviors of the predator-prey model, and the dynamic behaviors of the model are more complicated, showing very rich bifurcation phenomena.

From the perspective of fishery production, etc., we basically harvest the adult fish and keep the juvenile fish. Therefore, Yu, Zhu, Lai, et al. [33] proposed the single species stage structure system with Michaelis–Menten-type adult species harvesting. They obtained sufficient conditions for the global asymptotic stability of the unique boundary equilibrium and positive equilibrium of the model. In addition, their results also indicated that the system has bifurcation phenomena; more specifically, within the proper harvesting range, the two species can coexist; over harvesting will lead to species extinction. At the same time, their research showed that the model has at most two positive steady states.

To our knowledge, up to now, no scholars have considered the dynamic behaviors of the stage structure model of single species with Michaelis–Menten-type juvenile population harvesting. Therefore, in this paper, we propose the following models:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dx}{dt}}& =& {\displaystyle \alpha y-\beta x-{\delta }_{1}x-\frac{hEx}{mE+nx},}\hfill \\ \hfill {\displaystyle \frac{dy}{dt}}& =& \beta x-{\delta }_{2}y-\gamma y^2,\hfill \end{array}$$

(5)

where x, y describe the juvenile and adult population densities at time t, respectively; $\alpha ,\beta ,{\delta }_1,{\delta }_2,\gamma ,h,E,m$, and n are all positive constants, in which: $\alpha$ describes the per capita birth rate of the juvenile population; $\beta$ indicates the surviving rate of the juvenile to reach adulthood; ${\delta }_1,{\delta }_2$ indicate the death rate of the juvenile and adult population, respectively; $\gamma$ represents the intraspecific competition of the adult population; h represents the catchability coefficient of the adult population; E represents the external effort devoted to harvesting of the juvenile population. Here, we only assume that the immature species is harvested. A typical example is bamboo shoot and bamboo: in China, peasants may pick bamboo shoots as their food resources.

For the sake of simplicity, we first make the following transformations:

$${\displaystyle \overline{x}=\frac{\gamma }{\alpha }x,\overline{y}=\frac{\gamma }{{\delta }_2}y,\overline{t}={\delta }_{2}t.}$$

Dropping the bars, we can obtain the following system:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dx}{dt}}& =& {\displaystyle y-ax-\frac{bx}{c+x},}\hfill \\ \hfill {\displaystyle \frac{dy}{dt}}& =& ex-y(1+y),\hfill \end{array}$$

(6)

in which:

$${\displaystyle a=\frac{\beta +{\delta }_1}{{\delta }_2},b=\frac{hE\gamma }{\alpha {\delta }_{2}n},c=\frac{mE\gamma }{n\alpha },e=\frac{\alpha \beta }{{\delta }_2^2},}$$

and the initial conditions

$$x(0)=x_0>0,y(0)=y_0>0.$$

By the biological implications, we only consider the model in the first quadrant.

The layout of this paper is as follows: The existence and local stability of the equilibria of the model (6) are discussed and show that the model may exhibit two types of bistability in Section 2. In Section 3, the global asymptotic stability of the boundary equilibrium and the positive equilibrium of the model (6) are investigated, respectively. The paper ends with some numeric simulations and a brief discussion.

2. Existence and The Types of Equilibria

Notice that the model always has a unique boundary equilibrium $E_0(0,0)$. The Jacobian matrix of Model (6) can be written as follows:

$$J(E)=\left(\begin{array}{cc}{\displaystyle -a-\frac{bc}{{(c+x)}^2}}& {\displaystyle 1}\hfill \\ e& {\displaystyle -1-2y}\hfill \end{array}\right).$$

(7)

and:

$${\displaystyle DetJ(E)=(1+2y)(a+\frac{bc}{{(c+x)}^2})-e,}$$

(8)

$${\displaystyle trJ(E)=-(a+1+2y+\frac{bc}{{(c+x)}^2})<0.}$$

(9)

It is clear that when $DetJ(E)\ne 0$, it is an elementary equilibrium; when $DetJ(E)<0$, then it is a saddle; when $DetJ(E)=0$, then it is a degenerate equilibrium.

2.1. The Boundary Equilibrium

Lemma 1.

[36] Suppose that $O(0,0)$ is the isolated singularity of system:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dx}{dt}}& =& P_2(x,y),\hfill \\ \hfill {\displaystyle \frac{dy}{dt}}& =& y+Q_2(x,y),\hfill \end{array}$$

and $P_2$ and $Q_2$ are analytic functions whose degree is no less than two in $S_{\delta }(O)$, so when δ is sufficiently small, there exists an analytic function $\varphi (x)$, which satisfies:

$$\varphi (x)+P_2(x,\varphi (x))\equiv 0,-\delta <x<\delta .$$

Let

$$\psi (x)=P_2(x,\varphi (x))=a_m{x}^m+{\left[x\right]}_{m+1},$$

where $a_m\ne 0,m\ge 2$, then:

(i) 

If m is odd and $a_m>0$, $O(0,0)$ is the unstable node.

(ii) 

If m is odd and $a_m<0$, $O(0,0)$ is the saddle.

(iii) 

If m is even, $O(0,0)$ is the saddle node.

  From the Jacobian matrix of Model (6) at $E_0$, one could get the following theorem:

Theorem 1.

Model (6) always has a unique boundary equilibrium $E_0(0,0)$ for all positive parameters, then we have:

(1) 

$E_0$ is a saddle if $b<c(e-a)$.

(2) 

$E_0$ is a stable node if $b>c(e-a)$.

(3) 

$E_0$ is a saddle node if $b=c(e-a)$ and $c{e}^2+a-e\ne 0$; $E_0$ is a saddle if $b=c(e-a)$, $c{e}^2+a-e=0$, and ${\displaystyle ce>\frac{1}{2}}$; $E_0$ is a stable node if $b=c(e-a)$, $c{e}^2+a-e=0$, and ${\displaystyle ce<\frac{1}{2}}$.

Proof. 

From (8), one could get:

$${\displaystyle DetJ(E_0)=\frac{b}{c}+a-e,}$$

so if $DetJ(E_0)<0$, i.e., $b<c(e-a)$, $E_0$ is a saddle; if $DetJ(E_0)>0$, i.e., $b>c(e-a)$, $E_0$ is a stable node and if $DetJ(E_0)=0$, $E_0$ is a degenerate equilibrium, to discuss the property of $E_0$, we introduce a new time scale transformation ${\displaystyle d\tau =\frac{dt}{c+x}}$, and we have:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dx}{d\tau }}& =& -cex+cy+xy-a{x}^2,\hfill \\ \hfill {\displaystyle \frac{dy}{d\tau }}& =& cex-cy+e{x}^2-c{y}^2-xy-x{y}^2.\hfill \end{array}$$

(10)

Then, make a transformation as follows:

$$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{cc}c& -ce\\ ce& ce\end{array}\right)\left(\begin{array}{c}u\\ v\end{array}\right),$$

(11)

and let $ds=-c(e+1)d\tau$. System (10) becomes:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{du}{ds}}& =& a_{01}{u}^2+a_{02}{v}^2+a_{03}uv+a_{04}{u}^3+P_1(u,v),\hfill \\ \hfill {\displaystyle \frac{dv}{ds}}& =& v+b_{01}{u}^2+b_{02}{v}^2+b_{03}uv+b_{04}{u}^3+P_2(u,v):=P(u,v),\hfill \end{array}$$

(12)

where

• ${\displaystyle a_{01}=\frac{c{e}^2+a-e}{{(e+1)}^2},a_{02}=\frac{e^2(a+c-e)}{{(e+1)}^2},a_{03}=\frac{2e(ce+e-a)}{{(e+1)}^2},a_{04}=\frac{c{e}^2}{{(e+1)}^2},b_{01}=\frac{ce+e-a}{{(e+1)}^2},}$
• ${\displaystyle b_{02}=\frac{-e(ae+2e+1-c)}{{(e+1)}^2},b_{03}=\frac{2ae+2ce+2e+1-e^2}{{(e+1)}^2},b_{04}=\frac{ce}{{(e+1)}^2},}$ and $P_1(u,v)$ and $P_2(u,v)$ are power series in $(u,v)$ with terms $u^i{v}^j$ satisfying $i+j\ge 3$.

By the implicit function theorem, one could get an implicit function $v=\omega (u)$, in which $\omega (0)=0$ and $P(u,\omega (u))=0$. According to the second equation of (12), one could obtain:

$$v=\omega (u)=-b_{01}{u}^2+(b_{01}{b}_{03}-b_{04})u^3.$$

(13)

Substitute (13) into the first equation of (12), one could get:

$${\displaystyle \frac{du}{ds}=a_{01}{u}^2+(a_{04}-b_{01}{a}_{03})u^3+\dots }$$

From Lemma 1, when $a_{01}\ne 0$, i.e., $c{e}^2+a-e\ne 0$, we have $m=2$, and $E_0$ is a saddle node. On the contrary, when $a_{01}=0$, i.e., $c{e}^2+a-e=0$, we have $m=3$ and ${\displaystyle a_m=\frac{c{e}^2(1-2ce)}{{(e+1)}^2}}$, so $E_0$ is a saddle if ${\displaystyle ce>\frac{1}{2}}$. $E_0$ is an unstable node if ${\displaystyle ce<\frac{1}{2}}$; however, due to the transformation $ds=-c(e+1)d\tau$, the orbit goes in the opposite direction of time, then $E_0$ is a stable node.

This completes the proof. □

2.2. The Internal Equilibria

Next, we consider the internal equilibria of System (6), and it is given by the following equations:

$$\begin{array}{ccc}\hfill {\displaystyle y-ax-\frac{bx}{c+x}}& =& 0,\hfill \\ \hfill ex-y(1+y)& =& 0.\hfill \end{array}$$

(14)

By the second equation of (14), one could get ${\displaystyle x=\frac{y(1+y)}{e}}$, and y satisfies:

$$a{y}^3+(2a-e)y^2+(e(ac+b)+a-e)y+e(ac+b)-c{e}^2=0.$$

(15)

To investigate the properties of internal equilibria, we firstly let:

$$f(y)=a{y}^3+(2a-e)y^2+(e(ac+b)+a-e)y+e(ac+b)-c{e}^2,$$

$$f^{{}^{\prime }}(y)=3a{y}^2+2(2a-e)y+e(ac+b)+a-e.$$

From $f(y)=0$, we can get:

$${\displaystyle b=-\frac{a{y}^3+(2a-e)y^2+(ace+a-e)y+ce(a-e)}{e(1+y)}.}$$

(16)

Substituting (15) into $(8)$, we have:

$$\begin{array}{ccc}\hfill DetJ(E)& =& {\displaystyle \frac{y(y^2+y+ce)(2a{y}^3+(5a-e)y^2+(4a-2e)y+c{e}^2+a-e)}{1+y}}\hfill \\ & =& (y^2+y+ce)(y{f}^{{}^{\prime }}(y)-f(y))\hfill \\ & =& y(y^2+y+ce)f^{{}^{\prime }}(y).\hfill \end{array}$$

(17)

By the root formula of the cubic equation of one variable, suppose that:

$$\tilde{A}={(2a-e)}^2-3a(e(ac+b)+a-e),$$

$${\displaystyle \Delta (b)=\frac{1}{9a^2}(-4{\tilde{A}}^3+{(3(a+e)\tilde{A}-{(a+e)}^3+27a^2{e}^{2}c)}^2).}$$

In order to investigate the maximum number of roots of (15), let us consider its constant terms; next, we discuss it in two cases: $b<c(e-a)$ and $b\ge c(e-a)$. Similar to the discussion of Lemma $2.5$ in [37], we have the following results.

(I) The case $b<c(e-a)$:

Theorem 2.

If $b<c(e-a)$, Model (6) has one to three distinct internal equilibria. Furthermore,

(1) 

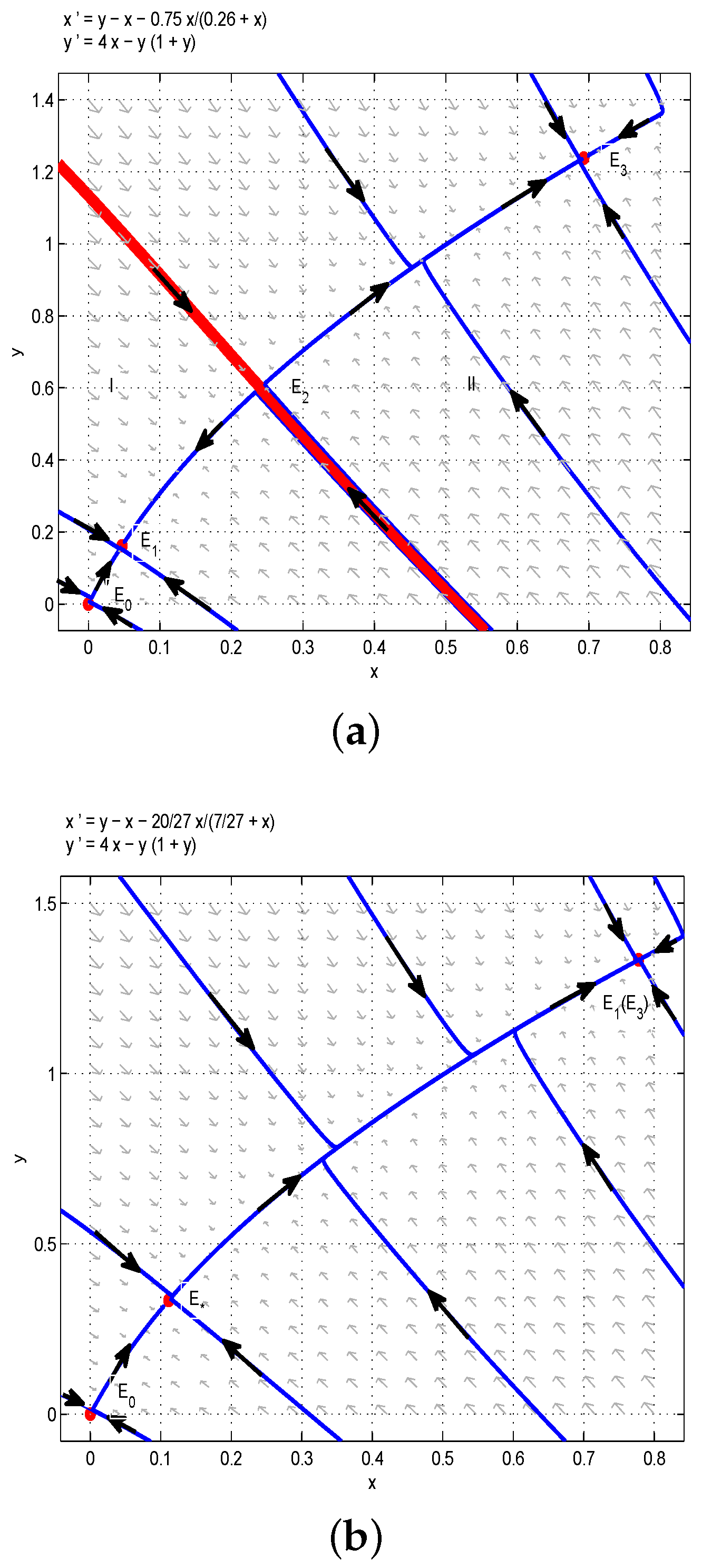
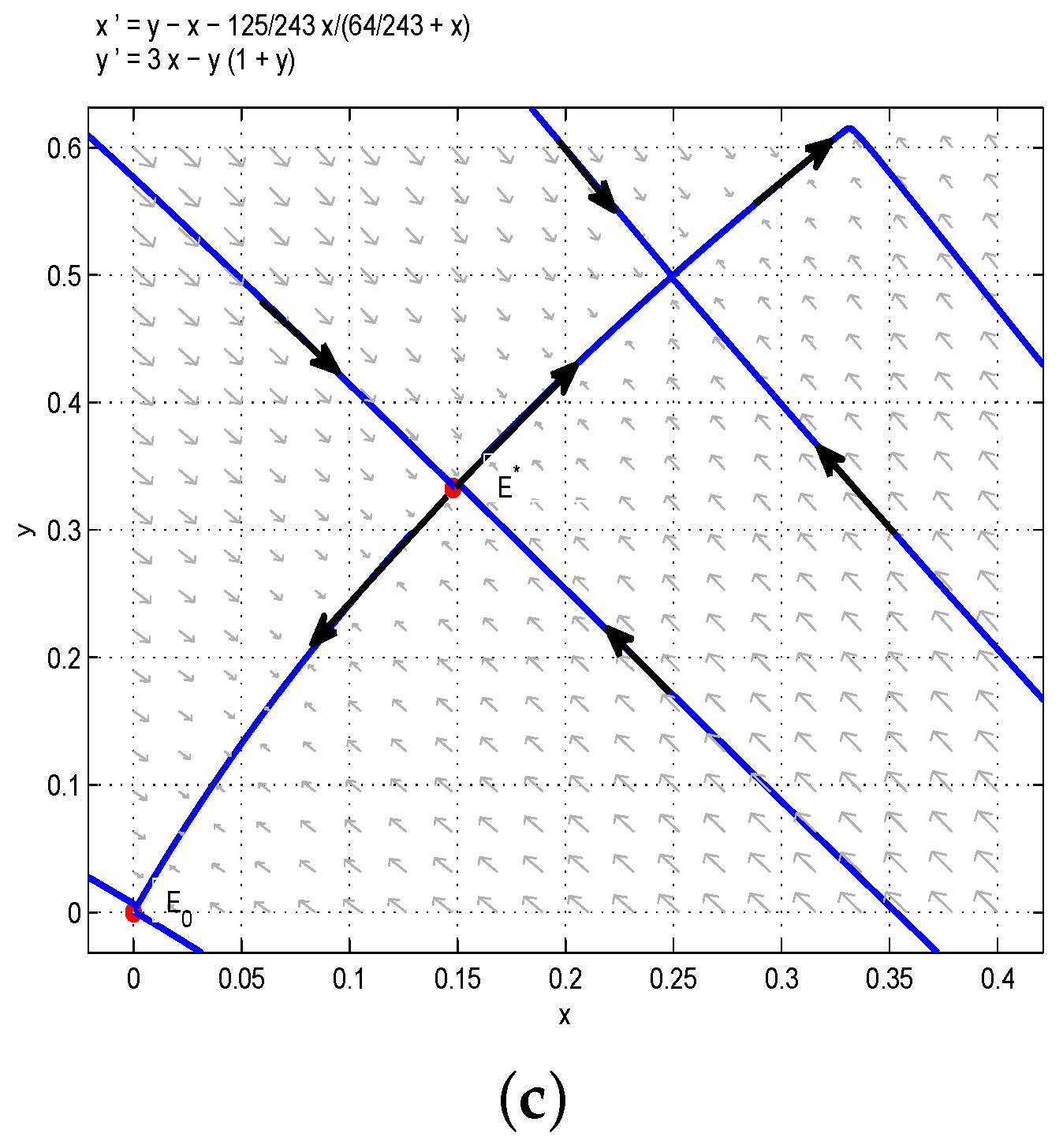
when $\Delta (b)<0$, there are three distinct internal equilibria: $E_2$ is a saddle, and $E_i,(i=1,3)$ is a stable node, in which $0<y_1<y_2<y_3$.

(2) 

when $\Delta (b)=0$:

(i) 

when $\tilde{A}>0$, there are two distinct internal equilibria: $E_{*}$ is the degenerate equilibrium, and $E_1$ (or $E_3$) is a stable node that is an elementary equilibrium, in which $y_1<y_{*}<y_3$.

(ii) 

when $\tilde{A}=0$, there is only one internal equilibrium $E^{*}$, and it is a degenerate equilibrium.

(3) 

when $\Delta (b)>0$, there is a unique internal equilibrium $E_3$, and it is a stable node.

Proof. 

From Equations (9) and (17) and the property of the derivative of $f(y)$, one could easily get $Det(E_i)>0,(i=1,3)$, $Det(E_2)<0$, $Det(E^{*})=0$, and $Det(E_{*})=0$, so $E_i,(i=1,2,3)$ are elementary equilibria, in which $E_1$ and $E_3$ are stable nodes and $E_2$ is a saddle, while $E_{*}$ and $E^{*}$ are degenerate equilibria.

Next, we study the stability of $E_{*}$. We first let $(X,Y)=(x-x_{*},y-y_{*})$ move $E_{*}$ to the origin and make the Taylor expansion. System (6) becomes:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dX}{dt}}& =& a_{01}X+Y+a_{02}{X}^2+a_{03}{X}^3+a_{04}{X}^4+a_{05}{X}^5,\hfill \\ \hfill {\displaystyle \frac{dY}{dt}}& =& eX+b_{01}Y-Y^2,\hfill \end{array}$$

(18)

where

• ${\displaystyle a_{01}=-(a+\frac{bc}{{(c+x_{*})}^2}),a_{02}=\frac{bc}{{(c+x_{*})}^3},a_{03}=\frac{-bc}{{(c+x_{*})}^4},a_{04}=\frac{bc}{{(c+x_{*})}^5},a_{05}=\frac{-bc}{{(c+x_{*})}^6},}$
• $b_{01}=-1-2y_{*}.$

Making the transformations as follows:

$$\left(\begin{array}{c}X\\ Y\end{array}\right)=\left(\begin{array}{cc}{\displaystyle \frac{b_{01}}{e}}& a_{01}\\ -1& e\end{array}\right)\left(\begin{array}{c}u\\ v\end{array}\right),$$

(19)

and letting ${\displaystyle d\tau =\frac{dt}{a_{01}+b_{01}}}$, System (18) can be rewritten as:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{du}{d\tau }}& =& c_{01}{u}^2+c_{02}{v}^2+c_{03}uv+c_{04}{u}^3+P_3(u,v),\hfill \\ \hfill {\displaystyle \frac{dv}{d\tau }}& =& v+d_{01}{u}^2+d_{02}{v}^2+d_{03}uv+d_{04}{u}^3+P_4(u,v):=Q(u,v),\hfill \end{array}$$

(20)

where

• ${\displaystyle c_{01}=\frac{e{a}_{01}+a_{02}{b}_{01}^2}{e{(a_{01}+b_{01})}^2},}$${\displaystyle c_{02}=\frac{e{a}_{01}(e+a_{01}{a}_{02})}{{(a_{01}+b_{01})}^2},}$${\displaystyle c_{03}=\frac{2a_{01}(a_{01}{a}_{02}-e)}{{(a_{01}+b_{01})}^2},}$${\displaystyle c_{04}=\frac{a_{03}{b}_{01}^3}{{(a_{01}+b_{01})}^2},}$
• ${\displaystyle d_{01}=\frac{b_{01}(a_{02}{b}_{01}-e)}{e^2{(a_{01}+b_{01})}^2},d_{02}=\frac{a_{01}^2{a}_{02}-e{b}_{01}}{a_{01}+b_{01}},d_{03}=\frac{2b_{01}(e+a_{01}{a}_{02})}{e{(a_{01}+b_{01})}^2},d_{04}=\frac{a_{03}{b}_{01}^3}{e^3(a_{01}+b_{01})},}$

and $P_3(u,v)$ and $P_4(u,v)$ are power series in $(u,v)$ with terms $u^i{v}^j$ satisfying $i+j\ge 3$.

From the implicit function theorem, we have an implicit function $v=\varphi (u)$, in which $\varphi (0)=0$, $Q(u,\varphi (u))=0$. According to the second equation of System (20), then:

$$v=\varphi (u)=-d_{01}{u}^2+\dots$$

(21)

If we take (21) into the first equation of System (20), we can get:

$${\displaystyle \frac{du}{d\tau }=c_{01}{u}^2+\dots }$$

Based on Lemma 1, one could obtain $m=2$, $a_m=c_{01}>0$, so $E_{*}$ is the saddle node.

In the same way, $E^{*}$ is also a saddle node; here, we omit its proof.

Through the above analysis and Figure 1, one could obtain that if $b<c(e-a)$, i.e., ${\displaystyle \alpha >{\delta }_2(1+\frac{{\delta }_1}{\beta })+\frac{h}{\beta m}}$, the boundary equilibrium $E_0$ of Model (6) is unstable, and there are multiple stable states in the first quadrant. More precisely, if the birth rate of the juvenile species is much greater than the threshold ${\displaystyle {\delta }_2(1+\frac{{\delta }_1}{\beta })+\frac{h}{\beta m}}$, then two species can always coexist stably. In order to verify the above results, we take $a=1,b=0.75,c=0.26,e=4$, then we have $c(e-a)=0.78>b,\Delta (b)=-0.272832<0$, $E_1(0.04689,0.16148)$ and $E_3(0.69311,1.2385)$ are stable nodes, and $E_0(0,0)$ and $E_2(0.24,0.6)$ are saddles. According to Figure 1a, the red line divides the first quadrant into two parts, denoted as I (left one) and II (right one). If the initial conditions lie in Region I, then all solutions tend to $E_1(0.04689,0.16148)$, which is a stable manifold, and both $E_0(0,0)$ and $E_2(0.24,0.6)$ are unstable manifolds. From the biological point of view, the juvenile and adult species will coexist if the initial conditions lie in Region I. Similarly, the juvenile and adult species will also coexist if the initial conditions lie in Region II. This is the first case of bistability phenomena, as shown in Figure 1a. If we take $a=1$, ${\displaystyle b=\frac{20}{27}}$, ${\displaystyle c=\frac{7}{20},e=4}$, then we have $c(e-a)>b,\Delta (b)=0,\tilde{A}=1>0$. Obviously, the model has two positive equilibria $E_{*}$ and $E_1$ (or $E_3$) and one unstable boundary equilibrium $E_0$. Therefore, the model has two positive steady states, as shown in Figure 1b. Moreover, if we let $a=1$, ${\displaystyle b=\frac{125}{243}}$,${\displaystyle c=\frac{64}{243},e=3}$, then one could get $c(e-a)>b,\Delta (b)=0,\tilde{A}=0$, and the model has a positive equilibrium $E^{*}$ and an unstable boundary equilibrium $E_0$, so the model has a positive steady state, as shown in Figure 1c.

This completes the proof. □

(II) The case $b\ge c(e-a)$:

Theorem 3.

If $b\ge c(e-a)$, Model (6) has no more than two internal equilibria. Furthermore,

(1) 

when $\Delta (b)<0$, Model (6) has two distinct internal equilibria: $E_2$ is a saddle, and $E_3$ is a stable node; in this case, $0<y_2<y_3$.

(2) 

when $\Delta (b)=0$, $\tilde{A}>0$, there is only one internal equilibrium $E_{*}$, which is an elementary equilibrium.

(3) 

when $\Delta (b)>0$ or $\Delta (b)=\tilde{A}=0$, Model (6) has no internal equilibrium.

Proof. 

From Equations (9) and (17) and the property of the derivative of $f(y)$, one could easily get $Det(E_3)>0$, $Det(E_2)<0$, and $Det(E_{*})=0$, so $E_2$ is a saddle, $E_3$ is a stable node, and $E_{*}$ is a degenerate equilibrium, in which $E_{*}$ is a saddle node; the proof of the above conclusion is similar to Theorem 2, so here, we omit it.

Based on the above analysis and Figure 2, one could obtain that the model has a positive steady state. Two species will coexist permanently with some initial conditions, and under some initial conditions, two species will be extinct. In order to verify the above results, we choose $a=1$, $b=0.125$, $c=0.03125,e=2$, then we can obtain $c(e-a)=0.03125<b,\Delta (b)=-1.0518<0$, $E_0(0,0)$ and $E_3(0.50321,0.6209)$ are stable nodes, and $E_2(0.21178,0.32071)$ is a saddle. According to Figure 2a, the red line divides the first quadrant into two parts, denoted as I (left one) and II (right one). If the initial conditions lie in Region I, then all solutions tend to $E_0(0,0)$, which is a stable manifold, and $E_2(0.21178,0.32071)$ is an unstable manifold. From the biological point of view, the juvenile and adult species will be driven to extinction if the initial conditions lie in Region I. However, if the initial conditions lie in Region II, then all solutions tend to $E_3(0.50321,0.6209)$, which is a stable manifold, and $E_2(0.21178,0.32071)$ is an unstable manifold. From the biological point of view, the juvenile and adult species will coexist if the initial conditions lie in Region II. This is the second case of bistability phenomena, as shown in Figure 2a. In addition, when we take $a=0.125,b=6.5915,c=1,e=0.25$, then $c(e-a)=0.125<b,\Delta (b)=0,\tilde{A}=0.155>0$. It is easy to get that the model has a positive equilibrium $E_{*}$, and the model has a positive steady state, as shown in Figure 2b.

This completes the proof. □

3. Global Stability of Equilibria

Theorem 4.

When $e<a$ holds, $E_0(0,0)$ is globally asymptotically stable.

Proof. 

By constructing a suitable Lyapunov function to prove Theorem 4, let:

$${\displaystyle V(x,y)=\frac{e}{a}x+y.}$$

It is obvious that the function $V(x,y)$ is zero at $E_0(0,0)$, and V is positive if $x>0,y>0$. We have:

$$\begin{array}{ccc}\hfill D^{+}V(t)& =& {\displaystyle \frac{e}{a}(y-ax-\frac{bx}{c+x})+ex-y(1+y)}\hfill \\ & =& {\displaystyle (\frac{e}{a}-1)y-\frac{ebx}{a(c+x)}-y^2.}\hfill \end{array}$$

Since $e<a$, we have $D^{+}V(t)\le 0$ and $D^{+}V(t)=0$ if and only if $(x,y)=(0,0)$. Then, $V(x,y)$ satisfies Lyapunov’s asymptotic stability theorem, and we have that $E_0(0,0)$ is globally asymptotically stable (see Figure 3).

This completes the proof of Theorem 4. □

Theorem 5.

When $b<c(e-a)$ and $\Delta (b)>0$ hold, $E_3(x_3,y_3)$ is globally asymptotically stable.

Proof. 

To prove Theorem 5, taking the Dulac function $D(x,y)=1$, we have:

$${\displaystyle \frac{\partial (DP)}{\partial x}+\frac{\partial (DQ)}{\partial y}=-a-1-2y-\frac{bc}{{(c+x)}^2}<0,}$$

where:

$$\begin{array}{c}{\displaystyle P(x,y)=y-ax-\frac{bx}{c+x},}\hfill \\ Q(x,y)=ex-y(1+y).\hfill \end{array}$$

By the Bendixson–Dulac discriminant, one could show that the model (6) has no limit cycle when $x>0$, $y>0$. On the other hand, When $b<c(e-a)$, $E_0(0,0)$ is the unique boundary equilibrium of the model (6) and is a saddle. Therefore, according to the Poincaré–Bendixson theorem, $E_3(x_3,y_3)$ is globally asymptotically stable (see Figure 4).

The proof of Theorem 5 is finished. □

4. Numerical Simulations

Example 1.

Consider the following single species stage structure model with Michaelis–Menten-type juvenile population harvesting:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dx}{dt}}& =& {\displaystyle y-x-\frac{bx}{c+x},}\hfill \\ \hfill {\displaystyle \frac{dy}{dt}}& =& ex-y(1+y);\hfill \end{array}$$

(22)

here, we choose $a=1$.

(1) 

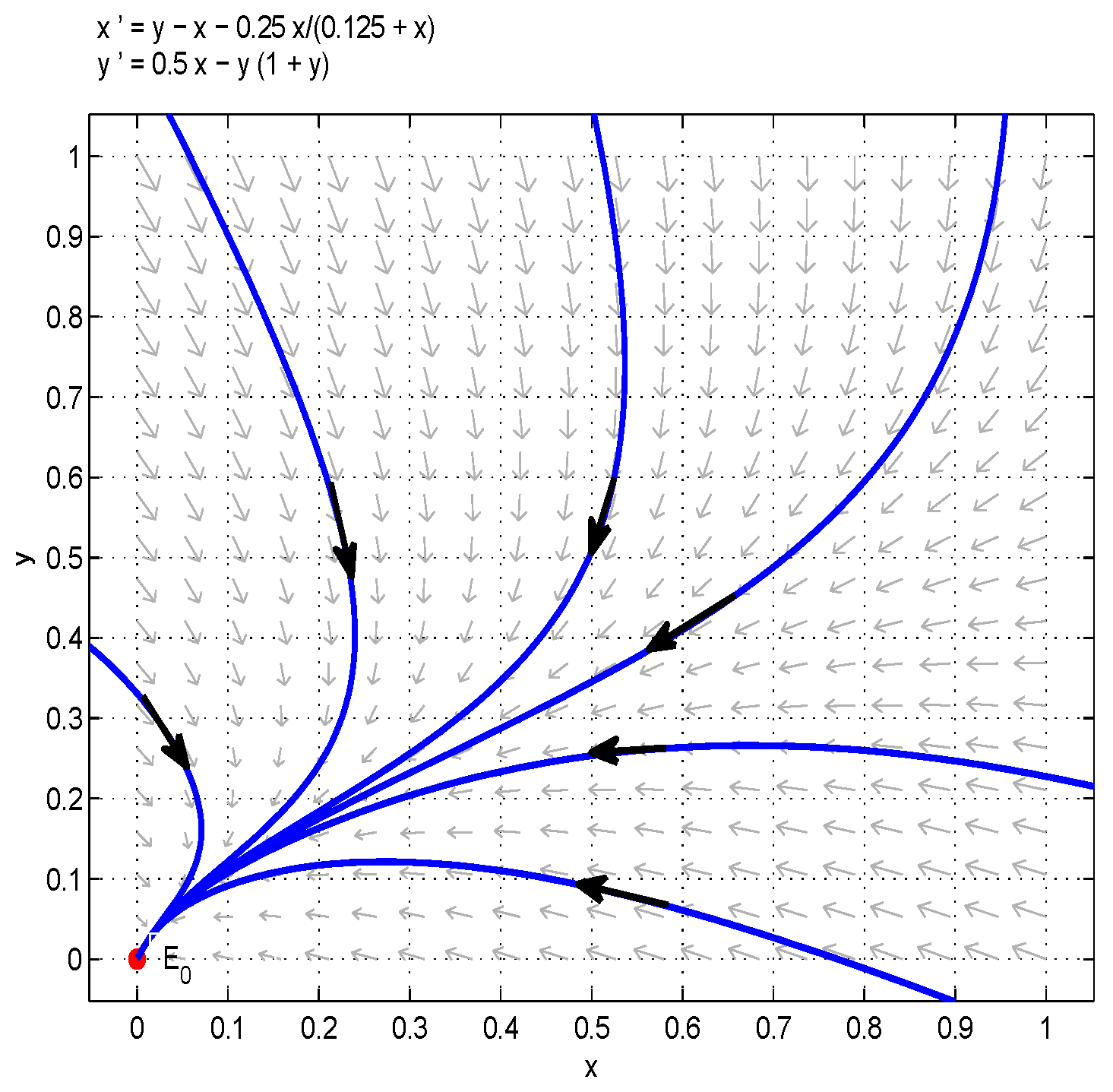
Let $b=0.25,c=0.125,e=0.5$; we have $b>c(e-a)$ and $e<a$, i.e., ${\displaystyle \alpha <{\delta }_2(1+\frac{{\delta }_1}{\beta })}$, then $E_0$ is globally asymptotically stable (see Figure 3). More precisely, when the birth rate of the juvenile species is much less than the threshold ${\displaystyle {\delta }_2(1+\frac{{\delta }_1}{\beta })}$, both species will be driven to extinction.

(2) 

Let $b=1,c=12,e=2$; by simple computation, we have $\Delta (b)=226704>0$ and $b>c(e-a)$, i.e., ${\displaystyle \alpha <{\delta }_2(1+\frac{{\delta }_1}{\beta })+\frac{h}{\beta m}}$, then $E_3$ is globally asymptotically stable (see Figure 4). That is to say, when when the birth rate of the juvenile species is much less than the threshold ${\displaystyle {\delta }_2(1+\frac{{\delta }_1}{\beta })+\frac{h}{\beta m}}$ and if b satisfies $\Delta (b)>0$, both species will coexist.

(3) 

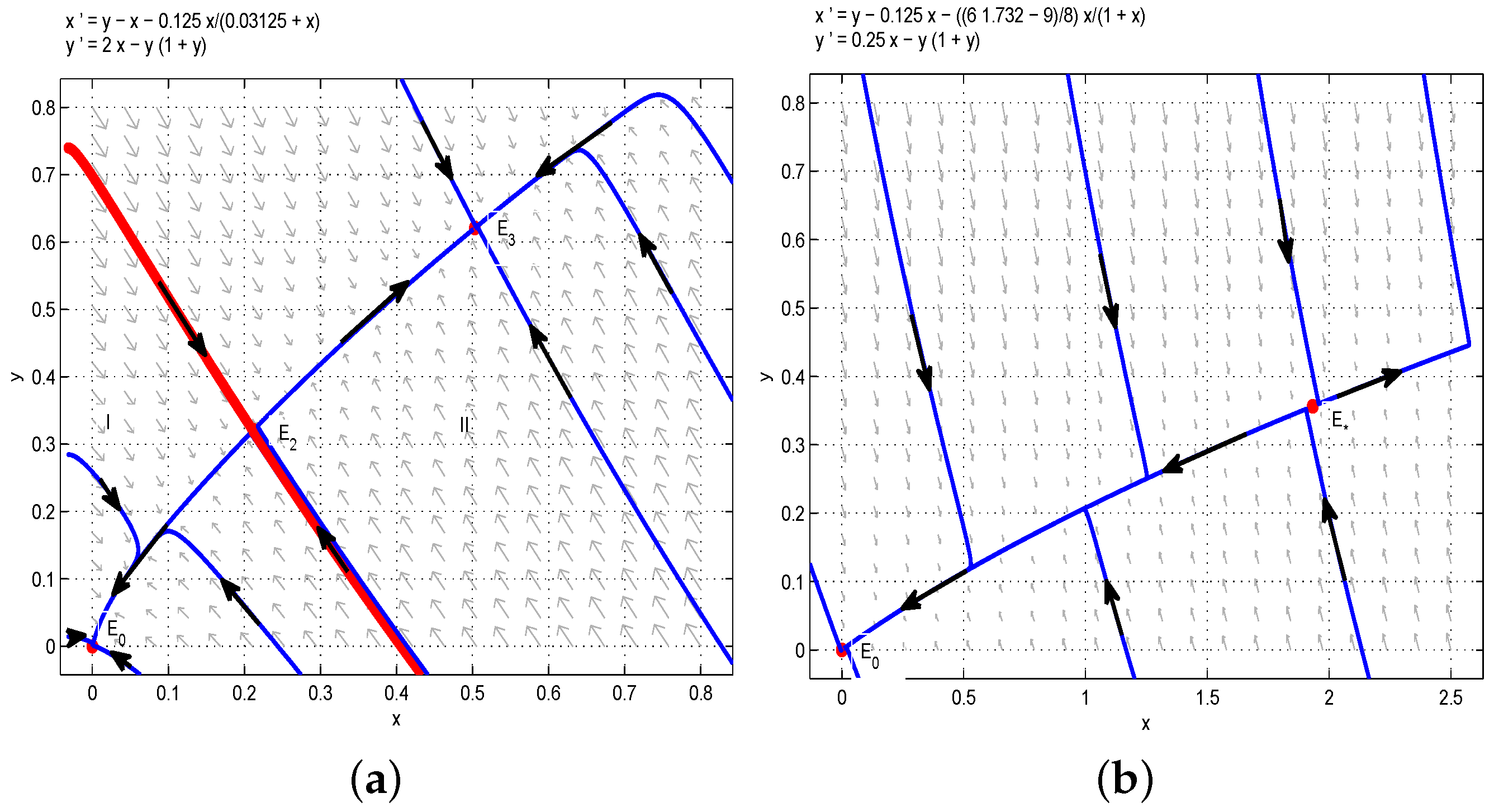
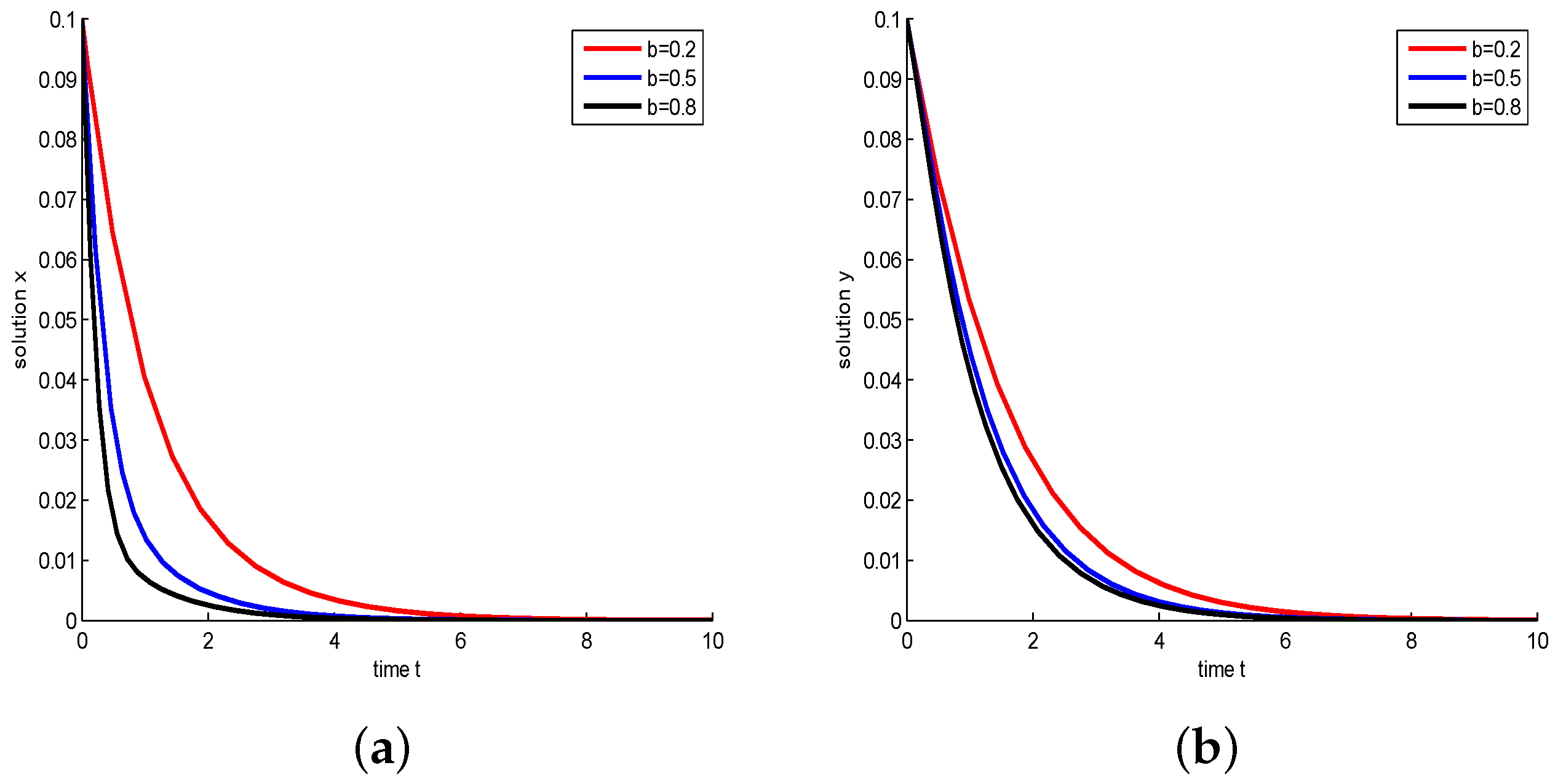
Let $c=0.125,e=0.5$, and take $b=0.2,b=0.5,b=0.8$, respectively, and $(x(0),y(0))=(0.1,0.1)$. We have $b>c(e-a)$ and $e<a$, then both species will be driven to extinction. The influence of Michaelis–Menten-type harvesting on the model is shown in Figure 5. It shows that with b increasing, species will become extinct in a much shorter time; in other words, increasing the harvest area will accelerate the extinction of species.

(4) 

Let $c=12,e=2$, and take $b=0.2,b=0.5,b=0.8$, respectively, and $(x(0),y(0))=(0.1,0.1)$. We have $b<c(e-a)=12$ and $\Delta (b)=81{(2b-24)}^2+12{(23+2b)}^3>0$, then the model has a global asymptotically stable positive equilibrium $E_3$. The influence of Michaelis–Menten-type harvesting on the model is shown in Figure 6. It shows that with b increasing, the density of species decreases; in other words, increasing the harvest area will reduce the species density.

5. Conclusions

A single species stage structure model with Michaelis–Menten-type juvenile population harvesting is discussed. The properties of the possible equilibria of the model are studied. Our results indicate that the Michaelis–Menten-type harvesting is more sensitive to the impact of model dynamics. It can not only reflect the harvesting process more realistically, but also make the dynamic behaviors of the model more complex than the linear harvesting in [15].

According to the analysis, we can get, compared with [33], that the model exhibits rich dynamic behaviors, and there are many kinds of positive steady states. The first type of bistability phenomenon shows that if $b<c(e-a),\Delta (b)<0$, then the model is persistent when the initial value lies in the first quadrant. From the biological point of view, juvenile and adult species can coexist steadily. The second type of bistability phenomenon indicates that both species will coexist with some conditions, and under some conditions, both species will be extinct. Moreover, if $e<a$ i.e., $\alpha <{\delta }_2(\beta +\frac{{\delta }_1}{\beta })$, the boundary equilibrium $E_0(0,0)$ is globally asymptotically stable; in other words, when the birth rate of the juvenile population is low enough, and the species will be driven to extinction. At the same time, our research also shows that increasing the harvest area will accelerate the rate of species extinction. In addition, if $b>c(e-a)$ and $\Delta (b)>0$, the system has a unique globally asymptotically stable internal equilibrium $E_3(x_3,y_3)$. That is to say, when the parameters meet certain conditions, harvesting does not affect the persistence of the model. However, increasing the harvest area will reduce the density of species. Our research is of great significance for decision makers in resource management of fisheries, forestry, and wildlife management. In other words, making a reasonable harvesting plan can not only ensure the maximization of economic benefits, but also maintain the sustainable development of resources.