A Simple Parallel Solution Method for the Navier–Stokes Cahn–Hilliard Equations
Abstract
:1. Introduction
2. Navier–Stokes Cahn–Hilliard Equations for Two-Phase Flow
3. Time Discretization
3.1. Time Discretization of the Navier–Stokes Equations
3.2. Time Discretization of the Cahn–Hilliard Equations
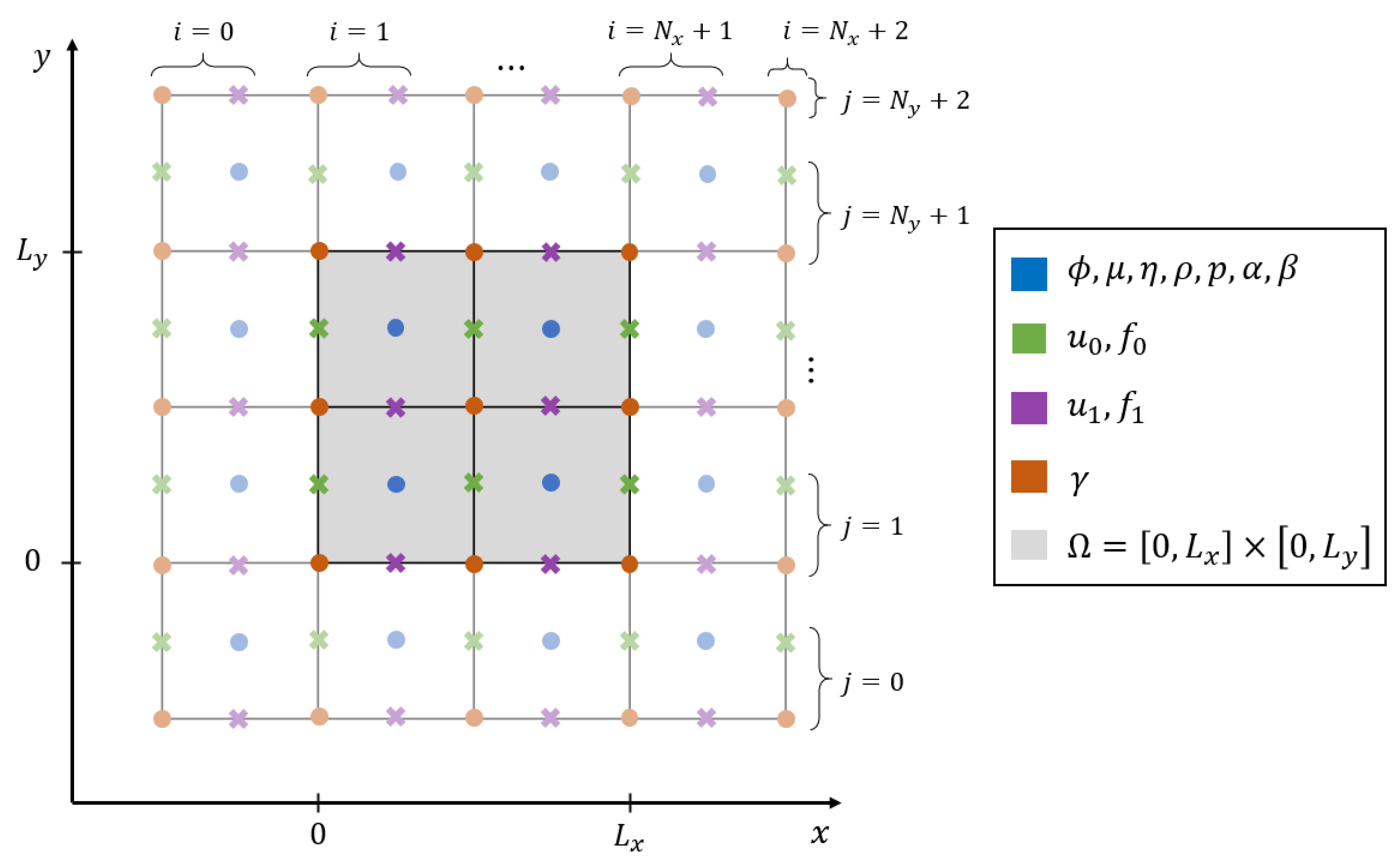
4. Space Discretization
4.1. Matched Densities and Viscosities
4.2. Non-Matched Density and Viscosity
5. Benchmark Test Results
5.1. Test Scenario
5.2. Measured Quantities
5.3. Results
5.3.1. Bubble Shape
5.3.2. Benchmark Quantities
5.3.3. Error Norms
5.3.4. Parallelization
6. Implementation
- helpers.h—handles output and data structure of 2 dimensional arrays.
- config.conf—self explanatory file defining all constants and simulation parameters.
- main.cc—contains core code of the numerical algorithm, but most of the lines are needed for reading parameters and managing output.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Boundary Conditions
References
- Aland, S.; Chen, F. An efficient and energy stable scheme for a phase-field model for the moving contact line problem. Int. J. Numer. Methods Fluids 2016, 81, 657–671. [Google Scholar] [CrossRef]
- Kim, J. Phase-Field Models for Multi-Component Fluid Flows. Commun. Comput. Phys. 2012, 12, 613–661. [Google Scholar] [CrossRef]
- Lee, H.G.; Kim, J. An efficient numerical method for simulating multiphase flows using a diffuse interface model. Phys. A Stat. Mech. Appl. 2015, 423, 33–50. [Google Scholar] [CrossRef]
- Aland, S. Phase field models for two-phase flow with surfactants and biomembranes. In Transport Processes at Fluidic Interfaces; Springer: Cham, Switzerland, 2017; pp. 271–290. [Google Scholar]
- Aland, S. Time integration for diffuse interface models for two-phase flow. J. Comput. Phys. 2014, 262, 58–71. [Google Scholar] [CrossRef] [Green Version]
- Aland, S.; Voigt, A. Benchmark computations of diffuse interface models for two-dimensional bubble dynamics. Int. J. Numer. Methods Fluids 2012, 69, 747–761. [Google Scholar] [CrossRef]
- Aland, S.; Boden, S.; Hahn, A.; Klingbeil, F.; Weismann, M.; Weller, S. Quantitative comparison of Taylor flow simulations based on sharp-interface and diffuse-interface models. Int. J. Numer. Methods Fluids 2013, 73, 344–361. [Google Scholar] [CrossRef]
- Kay, D.; Welford, R. Efficient Numerical Solution of Cahn-Hilliard-Navier-Stokes Fluids in 2D. SIAM J. Sci. Comput. 2007, 29, 2241–2257. [Google Scholar] [CrossRef]
- Han, D.; Wang, X. A second order in time, uniquely solvable, unconditionally stable numerical scheme for Cahn–Hilliard–Navier–Stokes equation. J. Comput. Phys. 2015, 290, 139–156. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.; Yang, X. Decoupled, energy stable schemes for phase-field models of two-phase incompressible flows. SIAM J. Numer. Anal. 2015, 53, 279–296. [Google Scholar] [CrossRef]
- Guo, Z.; Lin, P.; Lowengrub, J.; Wise, S.M. Mass conservative and energy stable finite difference methods for the quasi-incompressible Navier–Stokes–Cahn–Hilliard system: Primitive variable and projection-type schemes. Comput. Methods Appl. Mech. Eng. 2017, 326, 144–174. [Google Scholar] [CrossRef] [Green Version]
- Anderson, D.; McFadden, G.; Wheeler, A. Diffuse interface methods in fluid mechanics. Ann. Rev. Fluid Mech. 1998, 30, 139–165. [Google Scholar] [CrossRef] [Green Version]
- Emmerich, H. Advances of and by phase-field modeling in condensed-matter physics. Adv. Phys. 2008, 57, 1–87. [Google Scholar] [CrossRef]
- Singer-Loginova, I.; Singer, H. The phase field technique for modeling multiphase materials. Rep. Prog. Phys. 2008, 71, 106501. [Google Scholar] [CrossRef] [Green Version]
- Jaqmin, D. Calculation of two-phase Navier-Stokes flows using phase-field modelling. J. Comput. Phys. 1999, 155, 96–127. [Google Scholar] [CrossRef]
- Feng, X. Fully Discrete Finite Element Approximations of the Navier–Stokes–Cahn-Hilliard Diffuse Interface Model for Two-Phase Fluid Flows. SIAM J. Numer. Anal. 2006, 44, 1049–1072. [Google Scholar] [CrossRef]
- Ding, H.; Spelt, P.; Shu, C. Diffuse interface model for incompressible two-phase flows with large density ratios. J. Comput. Phys. 2007, 226, 2078–2095. [Google Scholar] [CrossRef]
- Boyer, F. A theoretical and numerical model for the study of incompressible mixture flows. Comput. Fluids 2002, 31, 41–68. [Google Scholar] [CrossRef] [Green Version]
- Lowengrub, J.; Truskinovsky, L. Quasi-incompressible Cahn-Hilliard fluids and topological changes. Proc. Roy. Soc. Lond. A 1998, 454, 2617–2654. [Google Scholar] [CrossRef]
- Abels, H.; Garcke, H.; Grün, G. Thermodynamically consistent, frame indifferent diffuse interface models for incompressible two-phase flows with different densities. Math. Model. Methods Appl. Sci. 2012, 22, 1150013. [Google Scholar] [CrossRef]
- Aland, S. Modelling of Two-Phase Flow with Surface Active Particles. Ph.D. Dissertation, TU Dresden, Dresden, Germany, 2012. [Google Scholar]
- Shen, J.; Yang, X. A phase-field model and its numerical approximation for two-phase incompressible flows with different densities and viscosities. SIAM J. Sci. Comput. 2010, 32, 1159–1179. [Google Scholar] [CrossRef]
- Shang, Y. Resilient multiscale coordination control against adversarial nodes. Energies 2018, 11, 1844. [Google Scholar] [CrossRef] [Green Version]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Temam, R. Navier-Stokes Equations: Theory and Numerical Analysis; American Mathematical Society: Providence, RI, USA, 2001; Volume 343. [Google Scholar]
- Guermond, J.L.; Minev, P.; Shen, J. An overview of projection methods for incompressible flows. Comput. Methods Appl. Mech. Eng. 2006, 195, 6011–6045. [Google Scholar] [CrossRef] [Green Version]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Hysing, S.; Turek, S.; Kuzmin, D.; Parlini, N.; Burman, E.; Ganesan, S.; Tobiska, L. Quantitative benchmark computations of two-dimensional bubble dynamics. Int. J. Numer. Meth. Fluids 2009, 60, 1259–1288, Raw Data. Available online: http://www.featflow.de/en/benchmarks/cfdbenchmarking/bubble.html (accessed on 24 July 2020). [CrossRef]
- Aland, S.; Lowengrub, J.; Voigt, A. Two-phase flow in complex geometries: A diffuse domain approach. CMES-Comput. Model. Eng. Sci. 2010, 57, 77–107. [Google Scholar]
- Mokbel, D.; Abels, H.; Aland, S. A Phase-Field Model for Fluid-Structure-Interaction. J. Comput. Phys. 2018, 372, 823–840. [Google Scholar] [CrossRef] [Green Version]



| h | NDOF | CPU Time [s] | ||
|---|---|---|---|---|
| 1/32 | 0.04 | 64 × 10−5 | 10,240 | 37.18 |
| 1/64 | 0.02 | 16 × 10−5 | 40,960 | 132.93 |
| 1/128 | 0.01 | 4 × 10−5 | 163,840 | 717.62 |
| 1/256 | 0.005 | 1 × 10−5 | 655,360 | 5904.87 |
| (h) | |||
|---|---|---|---|
| 1/32 | 0.2081 | 1.0630 | 1.0329 |
| 1/64 | 0.2295 | 0.9730 | 1.0654 |
| 1/128 | 0.2372 | 0.9420 | 1.0753 |
| 1/256 | 0.2395 | 0.9270 | 1.0776 |
| ref | 0.2417 | 0.9213 | 1.0813 |
| h | ||||||
|---|---|---|---|---|---|---|
| Center of mass | ||||||
| 1/32 | 0.0387 | 0.0423 | 0.0415 | |||
| 1/64 | 0.0116 | 1.7435 | 0.0125 | 1.7525 | 0.0119 | 1.8090 |
| 1/128 | 0.0025 | 2.1930 | 0.0027 | 2.2039 | 0.0025 | 2.2164 |
| Rise velocity | ||||||
| 1/32 | 0.1121 | 0.1173 | 0.1609 | |||
| 1/64 | 0.0351 | 1.6765 | 0.0370 | 1.6655 | 0.0531 | 1.5998 |
| 1/128 | 0.0081 | 2.1143 | 0.0087 | 2.0940 | 0.0130 | 2.0256 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adam, N.; Franke, F.; Aland, S. A Simple Parallel Solution Method for the Navier–Stokes Cahn–Hilliard Equations. Mathematics 2020, 8, 1224. https://doi.org/10.3390/math8081224
Adam N, Franke F, Aland S. A Simple Parallel Solution Method for the Navier–Stokes Cahn–Hilliard Equations. Mathematics. 2020; 8(8):1224. https://doi.org/10.3390/math8081224
Chicago/Turabian StyleAdam, Nadja, Florian Franke, and Sebastian Aland. 2020. "A Simple Parallel Solution Method for the Navier–Stokes Cahn–Hilliard Equations" Mathematics 8, no. 8: 1224. https://doi.org/10.3390/math8081224
APA StyleAdam, N., Franke, F., & Aland, S. (2020). A Simple Parallel Solution Method for the Navier–Stokes Cahn–Hilliard Equations. Mathematics, 8(8), 1224. https://doi.org/10.3390/math8081224





