1. Introduction
The well-known Black–Scholes (BS) partial differential equation (PDE) [
1,
2] is an accurate and efficient mathematical model for option pricing. The pioneers F. Black, M. Scholes, and R. Merton made a great breakthrough in the option pricing; and M. Scholes and R. Merton received in 1997 the Nobel Prize for their discovery of the BS equation. A European call option is a contract that gives the owner the right to buy an asset with a strike price
K at an expiration date
T. Let
be the value of the option, where
is the underlying
i-th asset value. We consider the following generalized
n-asset BS equation [
3,
4]:
for
The final condition is
Here, r is an interest rate, is a constant volatility of the i-th asset, and is the correlation coefficient between i-th and j-th underling assets.
The finite difference method (FDM) has been used for numerically solving the BS equations. In FDM, a PDE is replaced by discrete equations by using the Taylor series approximations to the partial derivatives. Then, we solve the resulting discrete equations by using various numerical methods [
5]. Jeong et al. [
6] developed the FDM without the far-field boundary condition. Hout and Valkov [
7] obtained the European two-asset options by the FDM based numerical method considering non-uniform grids. For high-order option pricing schemes, there are the Crandall–Douglas method [
8], the Crank–Nicolson method [
9,
10], and second-order in time and fourth-order in space method [
11]. In [
12], Zhao and Tian investigated FDMs for solving the fractional BS equation, and studied the stability and convergence of the proposed first- and second-order implicit numerical schemes. Chen and Wang [
13] presented a second-order Crank–Nicolson alternating direction implicit (ADI) scheme for solving a 2D spatial fractional BS equation. Sawangtong et al. [
14] proposed the BS equation with two assets based on the Liouville–Caputo fractional derivative. In [
15], Zhan et al. developed numerical methods for the time fractional BS equation. Hu and Gan [
16] developed a fourth-order scheme for the BS PDE. In [
17], Hendricks et al. combined high-order FDM with an ADI scheme for the BS equation in a sparse grid setting. In [
18], Rao proposed an FDM for a generalized BS equation (non-constant interest rate and volatility) and proved that the scheme is second-order accurate spatially and temporally. In [
19], Ullah presented numerical solution of three dimensional Heston–Hull–White (HHW) model using a high order FDM. The HHW model applies to pricing options arising from the probabilistic nature of asset prices, volatility, and risk-free interest rates. In [
9], Ankudinova and Ehrhardt presented numerical methods for the nonlinear BS equation [
20].
The main contribution of this paper is to present the detailed FDM for the BS equations for pricing derivative securities and provide the MATLAB codes for the one-, two-, and three-dimensional numerical implementation so that the beginners can use the provided codes for their research projects without wasting time for debugging the implementation [
21].
The outline of this paper is as follows. The numerical solutions of the one-, two-, and three-dimensional BS equation are briefly described in
Section 2. In
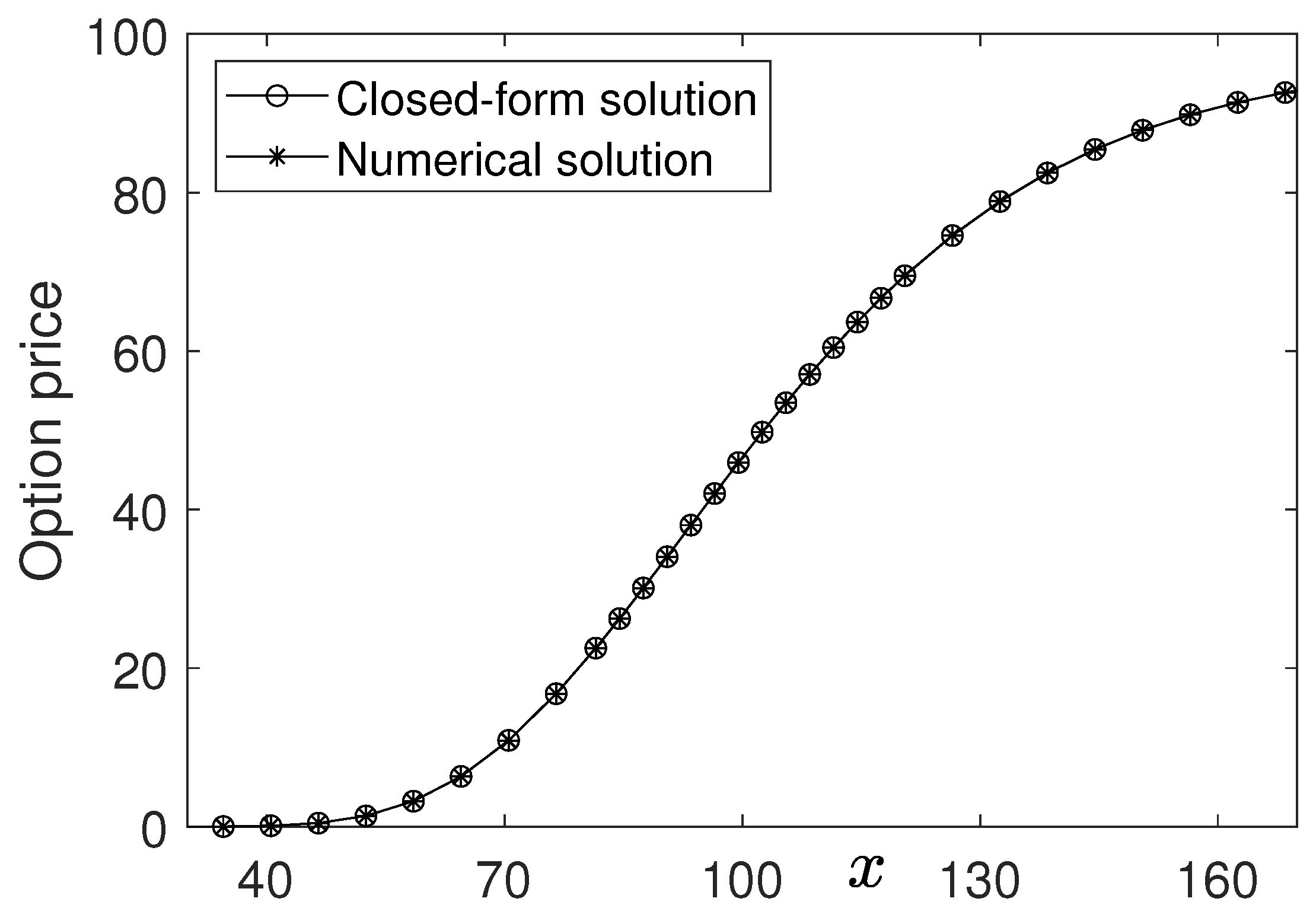
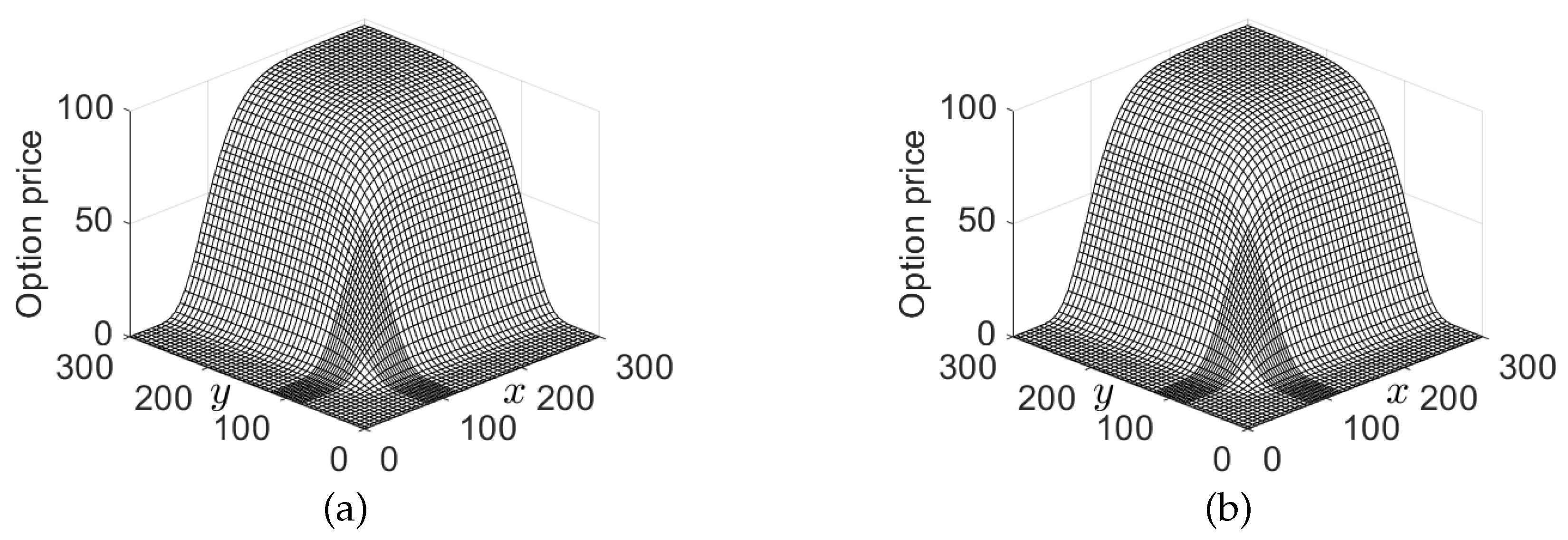
Section 3, we present the numerical results of cash-or-nothing options in order to show the accuracy and efficiency. We finalize the paper with the conclusion in
Section 4. In the
Appendix A, we provide the MATLAB codes for the numerical implementation for one-, two-, and three-dimensions.
2. Numerical Solutions
By changing the variable with
, Equation (
1) becomes
The initial condition is
. Let us consider the numerical solution algorithm for the three-dimensional BS equation. The algorithms for the one- and two-dimensional BS equations are similarly defined. Let
,
, and
. Let
be the following operator:
Then, the BS equation can be written as
where
. We truncate the original infinite domain into a finite domain
. We discretize
with a non-uniform space step
for
,
, and
. Here,
, and
. A time step is
.
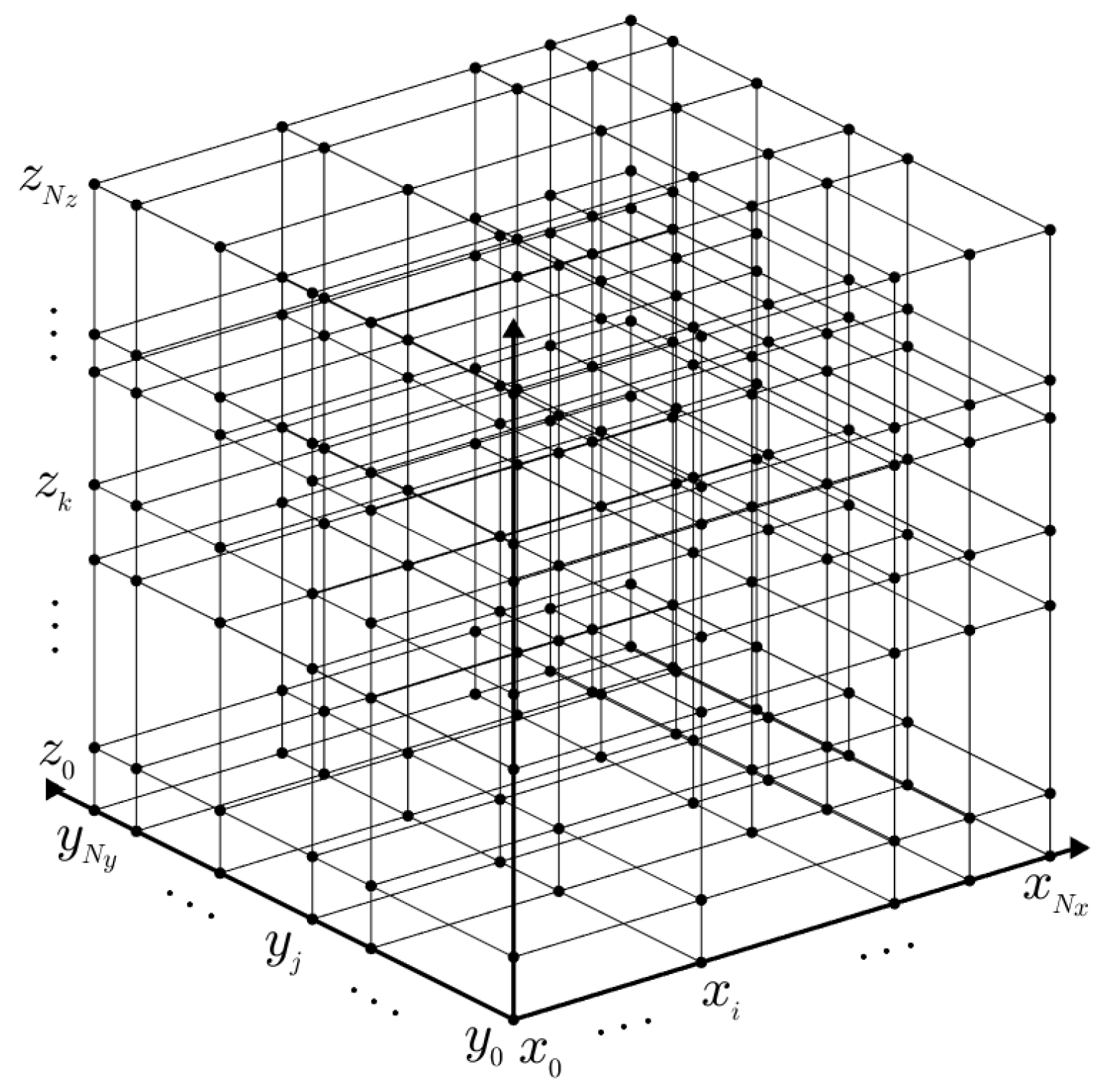
Figure 1 is an example of 3D non-uniform grid.
Let where , and . We use the zero Dirichlet boundary condition: for , i.e., for , for , and for ; and the homogeneous Neumann boundary condition: , that is, for , for , and for .
Now, we apply the operator splitting (OS) method [
22,
23] to solve Equation (
5). We consider the following three discrete equations:
for
. Here, the discrete difference operators
,
, and
are defined by
where the first and second derivatives are defined in [
24] as
Now, we describe the numerical algorithm for Equations (
6)–(8). Given
, Equation (
6) is rewritten as follows:
where
For fixed indices
j and
k; and
, the solution vector
can be found by solving the tridiagonal system
where
is a matrix obtained from Equation (
21) with the zero Dirichlet (i.e.,
at
) and the one-sided difference for the homogeneous Neumann (i.e.,
at
) boundary conditions, that is,
To generate a tridiagonal matrix
of Equation (
26) in MATLAB, see Listing 1, we use the
diag function which returns a square matrix with the elements of input vector
V on the
n-th diagonal. For example, option
and
place the elements of input vector
V on the main-, first super-, and first sub-diagonal, respectively.
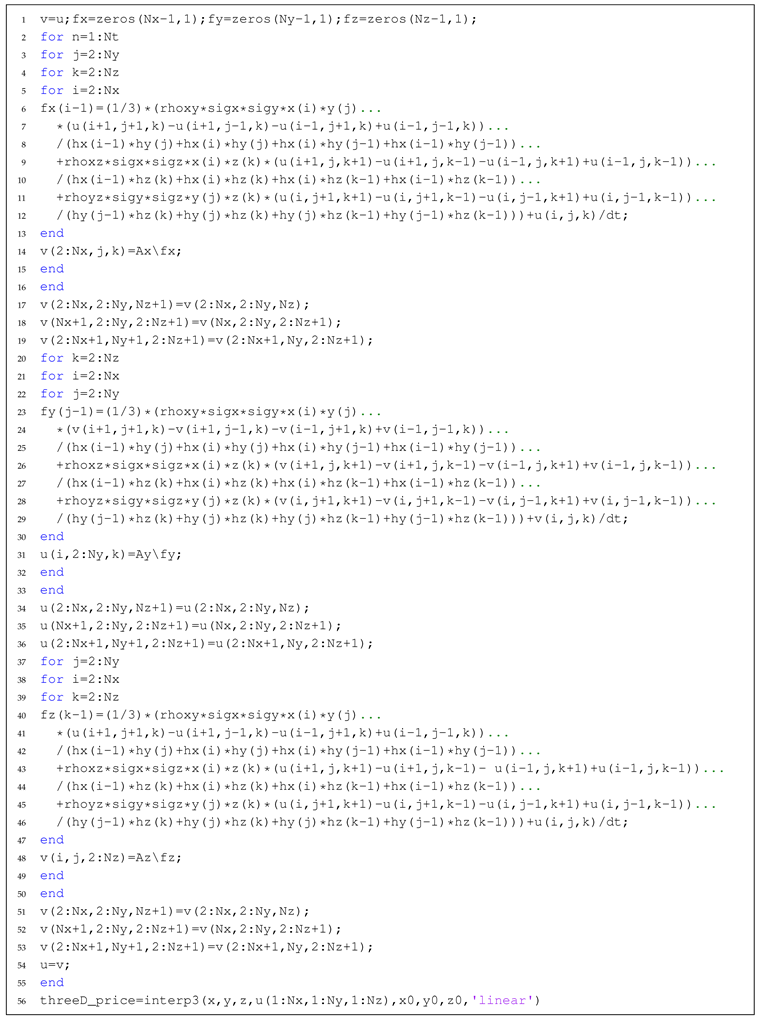
| Listing 1: Generating a tridiagonal matrix . |
![Mathematics 08 00391 i001 Mathematics 08 00391 i001]() |
Similarly, Equation (7) is rewritten as matrix form:
where
For fixed indices
i and
k; and
, the solution vector
can be obtained by
where
is a matrix obtained from Equation (
27) with the zero Dirichlet (i.e.,
at
) and the one-sided difference for the homogeneous Neumann (i.e.,
at
) boundary conditions, that is,
The process of generating a tridiagonal matrix is similar to that of generating and the code is as follows Listing 2.
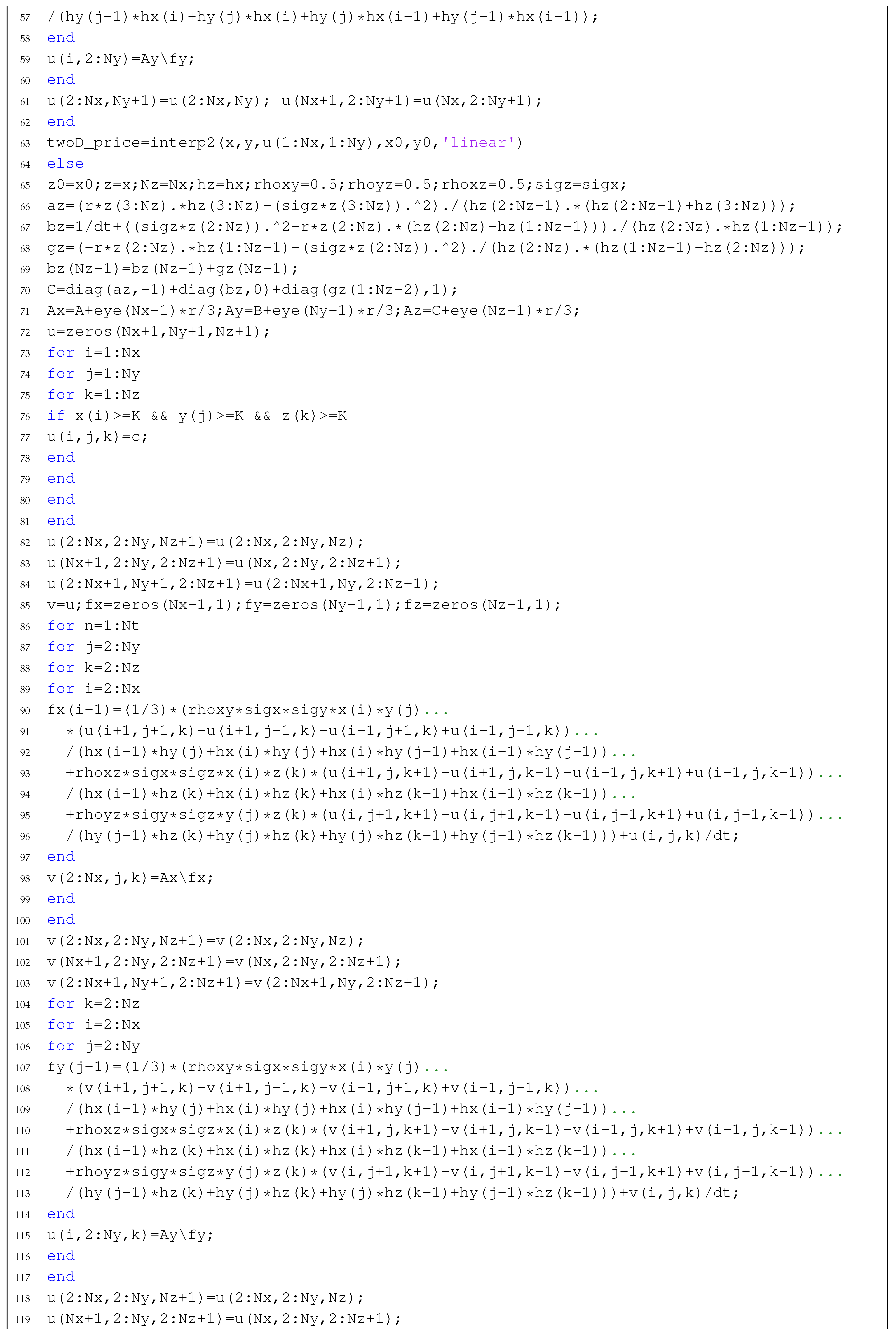
| Listing 2: Generating a tridiagonal matrix . |
![Mathematics 08 00391 i002 Mathematics 08 00391 i002]() |
Finally, Equation (8) is rewritten as matrix form:
where
For fixed indices
i and
j; and
, the solution vector
can be found by solving the tridiagonal system
where
is a matrix obtained from Equation (
33) with the zero Dirichlet (i.e.,
at
) and the one-sided difference for the homogeneous Neumann (i.e.,
at
) boundary conditions, that is,
The code for generating a tridiagonal matrix
is as follows, Listing 3.
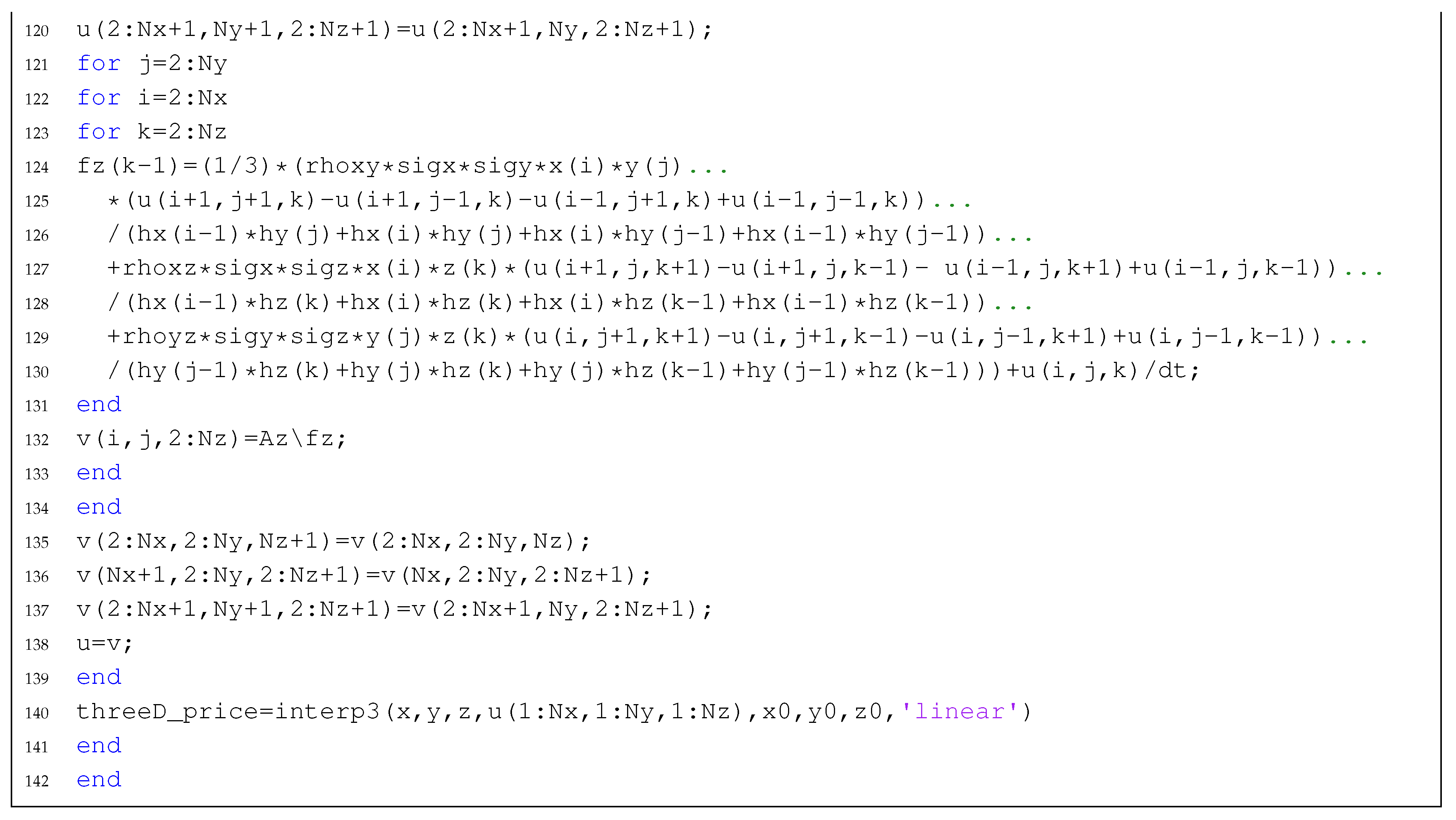
| Listing 3: Generating a tridiagonal matrix . |
![Mathematics 08 00391 i003 Mathematics 08 00391 i003]() |
Then, Equations (
6)–(8) are implemented with the following Algorithm 1.
| Algorithm 1 Implicit scheme and OSM for three-dimensional Black–Scholes (BS) equation. |
Require: Previous data . procedure F ind the solution for Equation ( 6) for do for do for do Generate and set by using Equations ( 22)–(24) end for Solve end for end for end procedure procedure Find the solution for Equation (7) for do for do for do Generate and set by using Equations ( 28)–(30) end for Solve end for end for end procedure procedure Find the solution for Equation (8) for do for do for do Generate and set by using Equations ( 34)–(36) end for Solve end for end for end procedure
|
To solve the tridiagonal systems found in Equations (
25), (
31), and (
37), we used the backslash operator in MATLAB. Also,
interp3() function, which returns interpolated value from a function of three variables at the query points, is used to determine the value at specific query point using the calculated
u. The code for Algorithm 1 is as follows, Listing 4:
| Listing 4: Code for Algorithm 1. |
![Mathematics 08 00391 i004 Mathematics 08 00391 i004]() |