Backward Reasoning and Epistemic Actions in Discovering Processes of Strategic Games Problems
Abstract
:1. Introduction
2. Theoretical Elements
2.1. Backward Reasoning
- Direction vs. cause–effect: In Pappus’ definition, the backward direction of reasoning is highlighted. By applying the method, the premises of a certain idea are sought. In the 17th and 18th centuries, authors such as Arnauld and Nicole interpreted the method as a backward search for cause–effect relationships between ideas. By these, the connection between the notions in background and the problem can be identified [11,17].
- Breakdown: According to Plato and Pappus, this kind of reasoning allows for the reduction of the problem to its simplest components. The properties that define the assignment and the relationships between the objects involved in it are identified by extracting and investigating the principles that are at the base of the task. Aristotle, for example, underlined the fact that “sometimes, to solve a geometrical problem, you can only analyze a figure,” breaking it down into its basic components and understanding the different parts of it [17].
- Introduction of auxiliary elements: Kant, Polya, and Hintikka focused their attention on a fundamental part of the process: the introduction of new elements (a well know practice in geometry with the auxiliary constructions). In progressive and deductive processes, all the bases are given, and from these, consequences are elaborated. Instead, in backward reasoning new notions appear and develop throughout the resolution according to the needs of the solver [1,17].
2.2. Epistemic Actions
- The actions that correspond to backward reasoning features from the mathematical point of view. These actions are not only cognitive but also involve the qualification provided by mathematical knowledge (Section 2.1).
- The actions identify as problem-solving heuristics that are inherent to strategy games [18].
- The actions as defined in AiC theory, the RBC model. These actions give priority of cognitive processes involved in thinking processes (Section 2.3).
2.3. RBC Model
- Recognizing: Recognizing some previously learned knowledge as relevant for the resolution of the problem.
- Building-with: Combining a set of knowledge with the aim to implement a strategy, to meet a conjecture or justification, or to find a solution to the problem.
- Constructing: Assembling and integrating the previous knowledge with the aim to produce a new construct.
3. Research Objective and Methodology
3.1. Objective
- What epistemic actions, in terms of heuristics use and backward reasoning features, are involved solving the strategy game?
- What epistemic actions, in terms of chain of thought, are implied in the abstract process of mathematical formula development?
- How do epistemic actions generate a recurring model in discovering processes following the RBC model?
3.2. Study Group and Presentation of the Task
3.3. Methodology and Data Analysis
3.4. Reliability and Validation of Data Analysis
4. Results
4.1. Heuristics and Background Mathematical Knowledge in the Group
- Analyzing geometric properties of winning lines.
- Studying the geometric positions in which most of the lines pass through.
- Searching for the final geometric configuration that leads a player to win the game: This consisted of the configuration in which the winner had two half-finished winning lines at the same time. This forced the opponent to put a token in a specific position, blocking only one of the two lines.
- Studying the opponent’s configuration of winning lines and predicting his/her possible movements.
- Developing the mathematical formula.
4.2. Patterns of Epistemic Actions
- They did an exploration/manipulation of the elements/data/concepts given by the problem.
- They recognize an element/concept useful for the resolution.
- They manipulated the objects that appeared in previous point in order to build a new concept.
- They did an exploration/manipulation of the elements/data/concepts given by the problem.
- They manipulated the objects given by the problem in order to build a new concept.
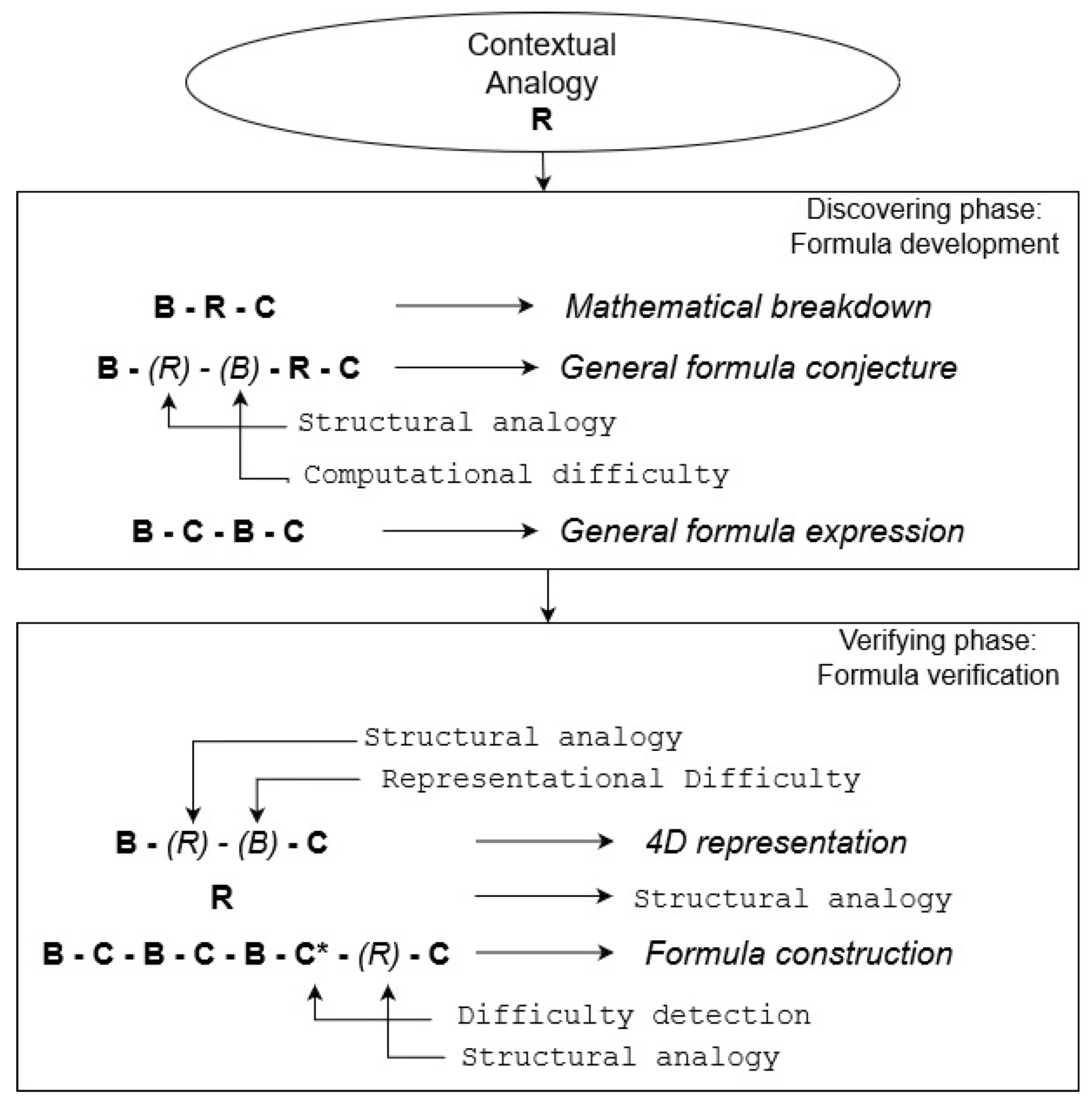
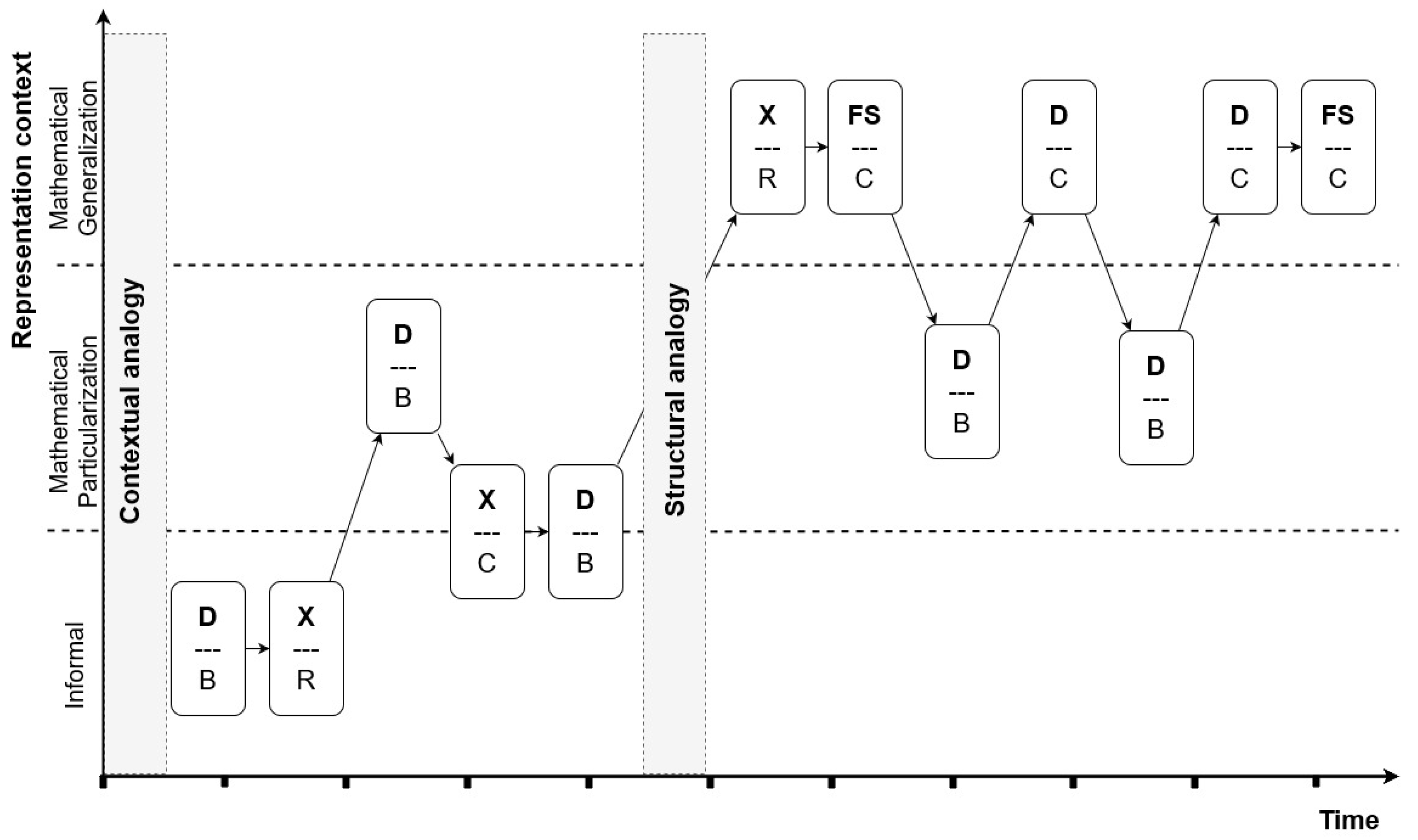
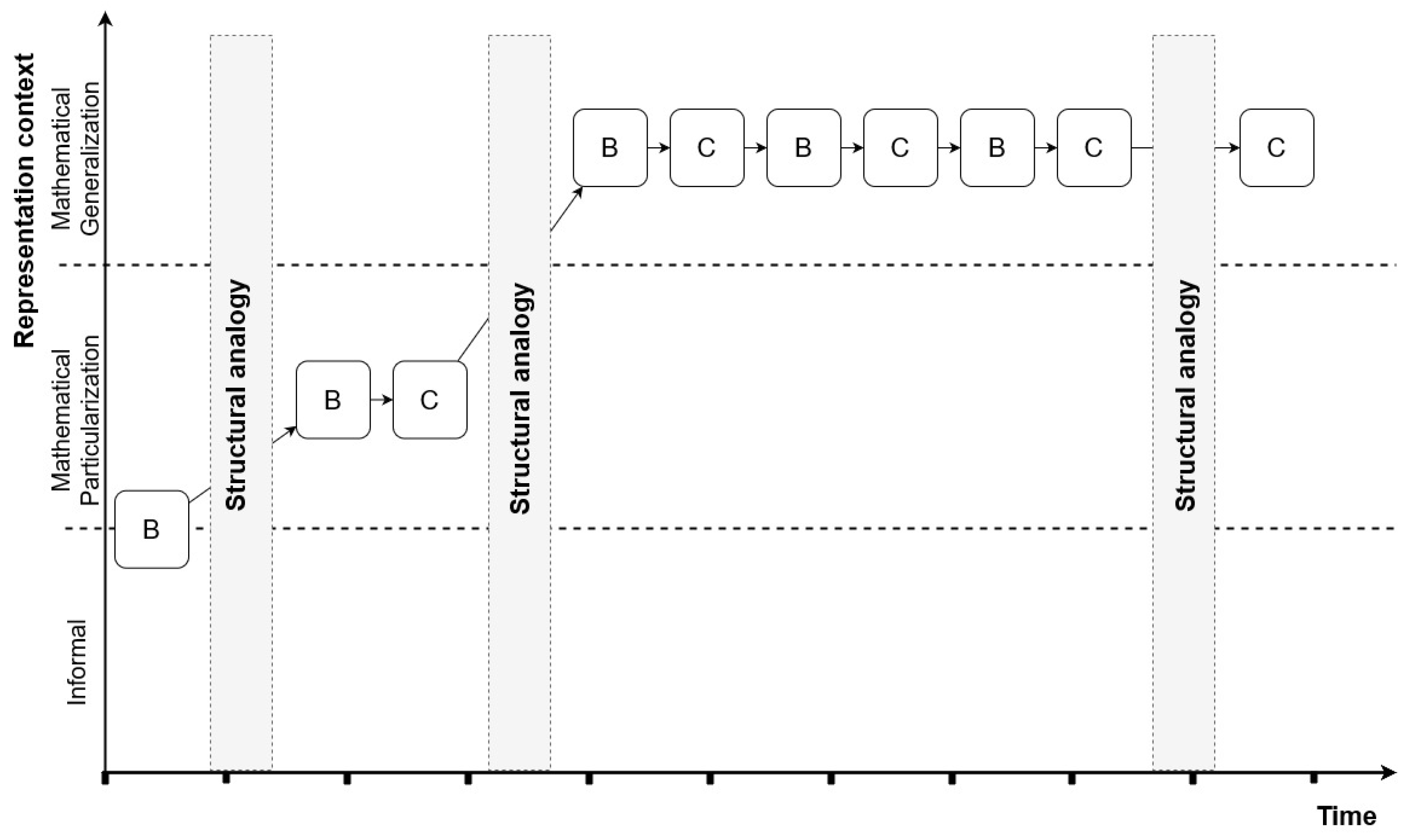
4.3. Epistemic Actions Model: Case Study
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hintikka, J.; Remes, U. The Method of Analysis: Its Geometrical Origin and Its General Significance; Reidel: Dodrecht, The Netherlands, 1974. [Google Scholar]
- Lakatos, I. Mathematics, Science and Epistemology; Worrall, J., Currie, G., Eds.; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Hintikka, J. Inquiry as Inquiry: A logic of Scientific Discovery; Springer Science & Business Media: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Grabczewski, K. Meta-Learning in Decision Tree Induction; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Dias, J.; Paiva, A. Feeling and reasoning: A computational model for emotional characters. In Portuguese Conference on Artificial Intelligence; Springer: Heidelberg, Germany, 2005; pp. 127–140. [Google Scholar]
- Marsella, S.C.; Gratch, J. EMA: A process model of appraisal dynamics. Cogn. Syst. Res. 2009, 10, 70–90. [Google Scholar] [CrossRef]
- Picard, R.W. Affective Computing; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Trivino, G.; Alvarez-Alvarez, A.; Bailador, G. Application of the computational theory of perceptions to human gait pattern recognition. Pattern Recognit. 2010, 43, 2572–2581. [Google Scholar] [CrossRef]
- Hintikka, J.; Halonen, I.; Mutanen, A. Interrogative logic as a general theory of reasoning. In Handbook of Practical Reasoning; Johnson, R.H., Woods, J., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 2002; pp. 295–337. [Google Scholar]
- Antonini, S. Generating examples: Focus on processes. ZDM Math. Educ. 2011, 43, 205–217. [Google Scholar] [CrossRef]
- Peckhaus, V. Regressive Analysis. Hist. Philos. Log. Anal. 2002, 5, 97–110. [Google Scholar]
- Barbero, M.; Gómez-Chacón, I.M. Analyzing Regressive reasoning at university level. In Proceedings of the Second Conference of the International Network for Didactic Research in University Mathematics (INDRUM), Kristiansand, Norway, 5–7 April 2018; Durand-Guerrier, V., Hochmuth, R., Goodchild, S., Hogstad, N.M., Eds.; University of Agder & INDRUM: Kristiansand, Norway, 2018; pp. 204–213. [Google Scholar]
- Gómez-Chacón, I.M.; Barbero, M. Situation Specific-Skills Working Backward Reasoning: The Student’s Perceptions and Affect Dimension. In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education (CERME11), Utrecht, The Netherlands, 6–10 February 2019; Jankvist, U.T., Van den Heuvel-Panhuizen, M., Veldhuis, M., Eds.; Freudenthal Group & Freudenthal Institute, Utrecht University and ERME: Utrecht, The Netherlands, 2019; pp. 1427–1434. [Google Scholar]
- Gómez-Chacón, I.M. Emotions and heuristics: The state of perplexity in mathematics. ZDM Math. Educ. 2017, 49, 323–338. [Google Scholar] [CrossRef]
- Hilbert, D.; Cohn-Vossen, S. Geometry and the Imagination; Translation from the German original of 1932; AMS Chelsea: New York, NY, USA, 1952. [Google Scholar]
- Dreyfus, T.; Kydron, I. Introduction to Abstraction in Context (AiC). In Networking of Theories as a Research Practice in Mathematics Education; Bikner-Ahsbahs, A., Prediger, S., Eds.; Springer: Heidelberg, Germany, 2014; pp. 85–96. [Google Scholar]
- Beaney, M. Analysis. The Stanford Encyclopedia of Philosophy. In Metaphysics Research; Zalta, E.N., Ed.; Stanford University Lab: Stanford, CA, USA, 2018. [Google Scholar]
- Polya, G. How to Solve It: A New Aspect of Mathematical Method; Doubleday: New York, NY, USA, 1945. [Google Scholar]
- Kirsh, D.; Maglio, P. On distinguishing epistemic from pragmatic action. Cogn. Sci. 1994, 18, 513–549. [Google Scholar] [CrossRef]
- Hershkowitz, R.; Schwarz, B.B.; Dreyfus, T. Abstraction in context: Epistemic actions. J. Res. Math. Educ. 2001, 32, 195–222. [Google Scholar] [CrossRef]
- Pontecorvo, C.; Girardet, H. Arguing and reasoning in understanding historical topics. Cogn. Instr. 1993, 11, 365–395. [Google Scholar] [CrossRef]
- Golomb, S.W.; Hales, A.W. Hypercube Tic-Tac-Toe. In More Games of No Chance, Proceeding of the MSRI Workshop on Combinatorial Games, Berkeley, CA, USA, 24–28 July 2000; Nowakowski, R.J., Ed.; MSRI Publications, Cambridge University Press: Cambridge, UK, 2002; Volume 42, pp. 167–182. [Google Scholar]
- Patashnik, O. Qubic: 4 × 4 × 4 Tic-Tac-Toe. Math. Mag. 1980, 53, 202–216. [Google Scholar]
- Bassey, M. Case Study Research in Educational Settings; Open University Press: Buckingham, UK, 1999. [Google Scholar]
- Gliner, J.A.; Morgan, G.A.; Leech, N.L. Sampling and Introduction to External Validity. In Research Methods in Applied Setting: An Integrated Approach to Design and Analysis; Gliner, J.A., Morgan, G.A., Leech, N.L., Eds.; Routledge Taylor & Francis Group: New York, NY, USA, 2009; pp. 115–133. [Google Scholar]
- Lincoln, Y.S.; Guba, E.G. Naturalistic Inquiry; Sage Publications: Newbury Park, CA, USA, 1985. [Google Scholar]
- Gómez-Chacón, I.M.; Romero Albaladejo, I.M.; del Mar García López, M. Zig-zagging in geometrical reasoning in technological collaborative environments: A Mathematical Working Space-framed study concerning cognition and affect. ZDM Math. Educ. 2016, 48, 909–924. [Google Scholar] [CrossRef]
- Tall, D. Advanced Mathematical Thinking; Springer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Chou, S.C. Mechanical Geometry Theorem Proving; Reidel: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Cox, D.; Little, J.; O’Shea, D. Ideals, Varieties and Algorithms; Springer: Berlin, Germany, 1992. [Google Scholar]
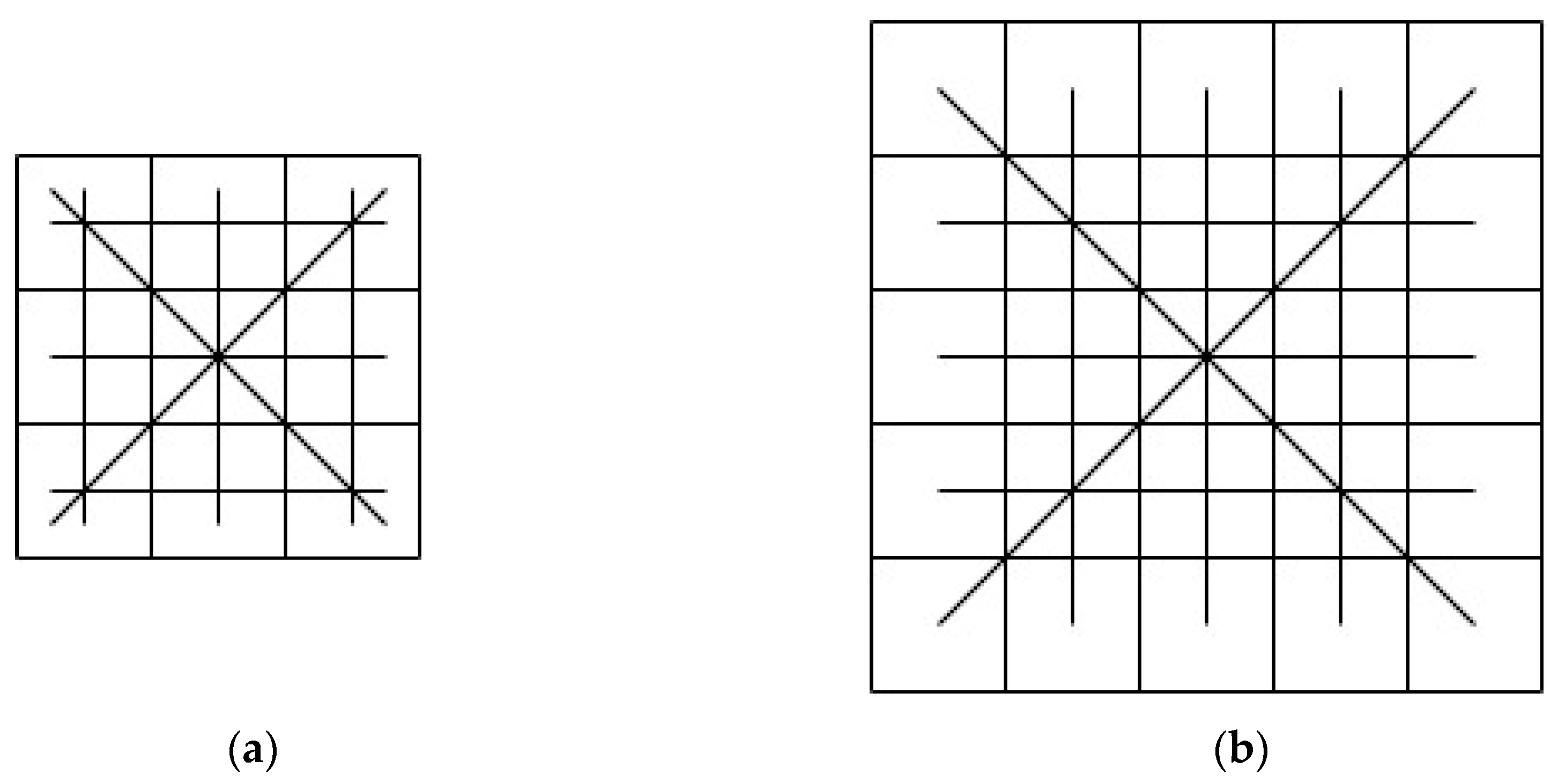



| BR | Whole Group | Group 1 | Group 2 | |
|---|---|---|---|---|
| Analyzing winning lines | D and X | 55% | 44% | 67% |
| Studying favorable positions | D and X | 81% | 72% | 91% |
| Searching for the final movements | E and X | 56% | 58% | 53% |
| Blocking the opponent | E and X | 75% | 71% | 79% |
| Developing a mathematical formula | D and X | 34% | 10% | 62% |
| Heuristics | Whole Group | Group 1 | Group 2 |
|---|---|---|---|
| Making a systematic study of all geometric positions | 81% | 70% | 93% |
| Using a mathematical language | 56% | 31% | 85% |
| Visualizing the geometrical properties of 3D board | 43% | 29% | 58% |
| Reducing geometrically the board size | 56% | 55% | 58% |
| Making diagrams, drawings, graphic representations | 73% | 67% | 80% |
| Using backtracking heuristics | 80% | 76% | 85% |
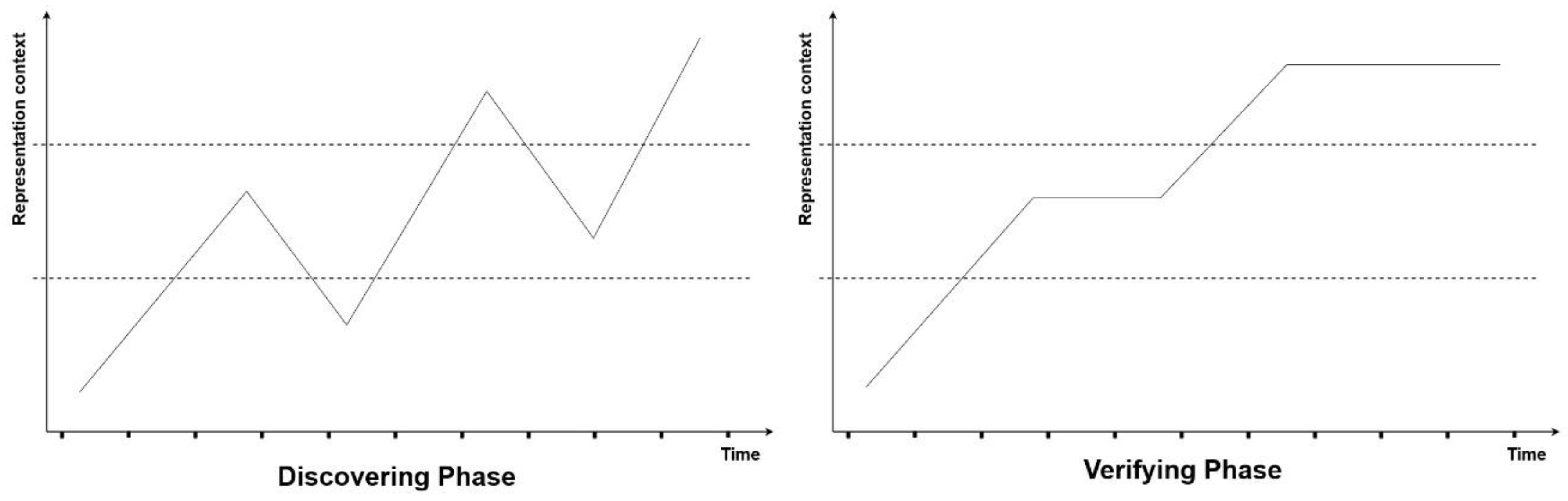
| Whole Group | Discovering Phase | Verifying Phase | |
|---|---|---|---|
| Analyzing winning lines | 55% | B–R–C | - |
| Studying favorable positions | 81% | B–R–C | - |
| Searching for the final movements | 56% | B–R–C | - |
| Blocking the opponent | 75% | B–R–C | - |
| Developing a mathematical formula | 34% | B–R–C and B–C | B–C |
| Protocols | Epistemic Action | BR | RBC |
|---|---|---|---|
| 12 | Splitting the board into planes | D | B |
| Counting the winning lines in each plan | D | B | |
| Grouping winning lines into a scheme | X | R | |
| 13 | Mathematically breaking down a number | D | B |
| Identifying each element of the decomposition | X | C | |
| 14 | Mathematically breaking down a number | D | B |
| 15 | Analogy/break motion | - | R–B |
| 16 | Introducing a recursive pattern | X | R |
| Conjecturing: general recursive formula | FS | C | |
| 17 | Breaking down the formula into its elements | D | B |
| Analyzing the factor element | D | B | |
| Representing the factor in relation to the board dimensions | D | C | |
| 18 | Analyzing the diagonal element | D | B |
| 19 | Representing the diagonals in relation to the vertices of the hypercube | D | C |
| Expressing the general formula | FS | C |
| Protocols | Epistemic Action | BR | RBC |
|---|---|---|---|
| 20 | Checking the formula | - | B |
| Identifying possible proof path | - | R | |
| 21 | Checking the formula in 4D case | - | B |
| Representing the 4D case | - | C | |
| 22 | Identifying a structural analogy with analytical representation | - | R |
| Reasoning about possible coordinates | - | B | |
| 23 | Identifying the direction vector | - | C |
| 24 | Analyzing cases Introducing a recursive pattern | - | B |
| Justifying “” | - | C | |
| 25 | Analyzing cases | - | B |
| Constructing diagonals value: | - | C | |
| 26 | Identifying an action of | - | R |
| Constructing diagonals value: | - | C |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbero, M.; Gómez-Chacón, I.M.; Arzarello, F. Backward Reasoning and Epistemic Actions in Discovering Processes of Strategic Games Problems. Mathematics 2020, 8, 989. https://doi.org/10.3390/math8060989
Barbero M, Gómez-Chacón IM, Arzarello F. Backward Reasoning and Epistemic Actions in Discovering Processes of Strategic Games Problems. Mathematics. 2020; 8(6):989. https://doi.org/10.3390/math8060989
Chicago/Turabian StyleBarbero, Marta, Inés M. Gómez-Chacón, and Ferdinando Arzarello. 2020. "Backward Reasoning and Epistemic Actions in Discovering Processes of Strategic Games Problems" Mathematics 8, no. 6: 989. https://doi.org/10.3390/math8060989
APA StyleBarbero, M., Gómez-Chacón, I. M., & Arzarello, F. (2020). Backward Reasoning and Epistemic Actions in Discovering Processes of Strategic Games Problems. Mathematics, 8(6), 989. https://doi.org/10.3390/math8060989





