Averaging Methods for Second-Order Differential Equations and Their Application for Impact Systems
Abstract
1. Introduction
2. Preliminaries
- —the inner product of vectors ;
- —the Euclidean norm of ;
- —the distance of nonempty sets ;
- ()—the first (second) derivative of function x at time t;
- ()—the right (left) derivative of function x at time t.
3. Results and Proofs
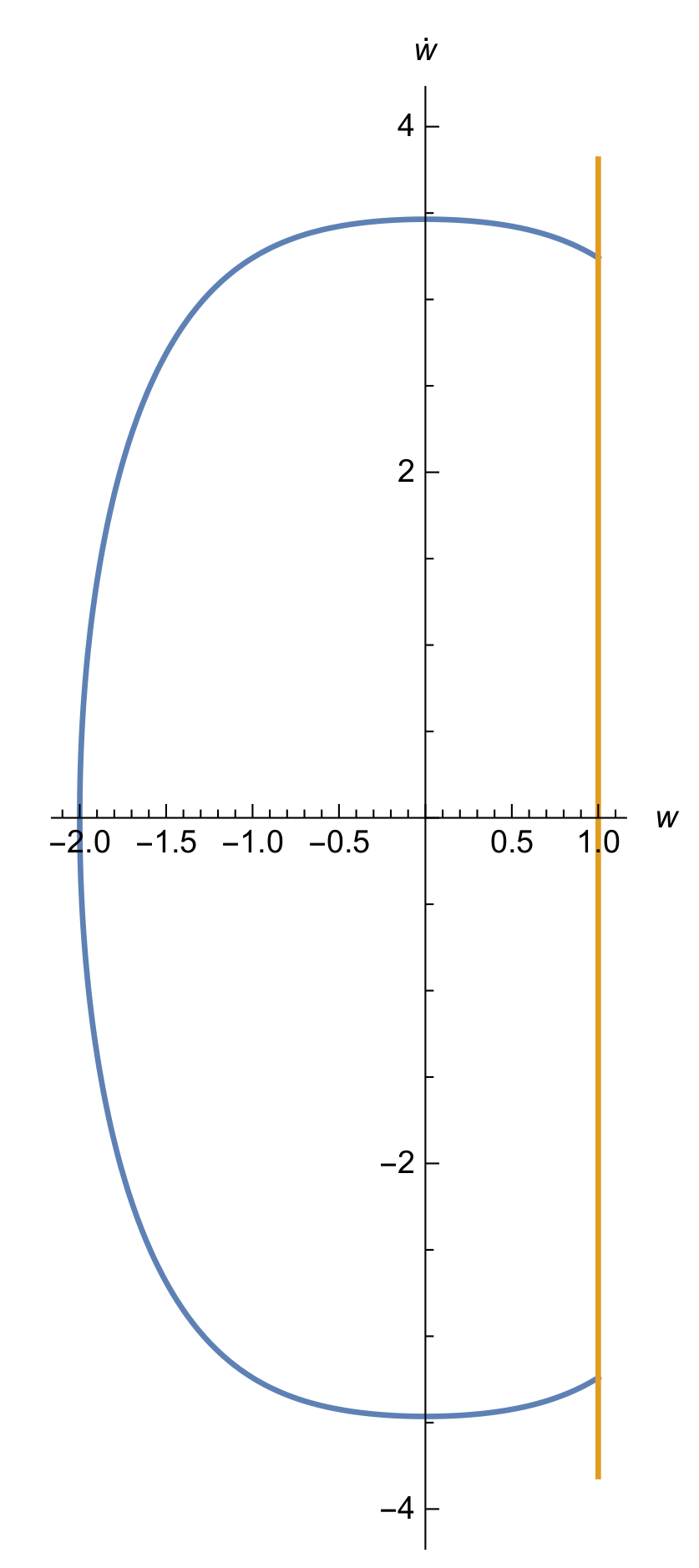
4. Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fiedler, B.; Scheurle, J. Discretization of Homoclinic Orbits, Rapid Forcing and “Invisible” Chaos. Mem. Am. Math. Soc. 1996, 119, 570. [Google Scholar] [CrossRef]
- Lombardi, E. Oscillatory Integrals and Phenomena Beyond all Algebraic Orders; Lecture Notes in Mathematics 1741; Springer: Berlin, Germany, 2000. [Google Scholar]
- Chicone, C. Ordinary Differential Equations with Applications, 2nd ed.; Texts in Applied Mathematics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Hale, J.K. Ordinary Differential Equations; Wiley-Interscience: New York, NY, USA, 1969. [Google Scholar]
- Ricceri, B. A class of equations with three solutions. Mathematics 2020, 8, 478. [Google Scholar] [CrossRef]
- Treanţă, S. Gradient structures associated with a polynomial differential equation. Mathematics 2020, 8, 535. [Google Scholar] [CrossRef]
- Chow, S.N.; Hale, J.K. Methods of Bifurcation Theory; Springer: Berlin, Germany, 1982. [Google Scholar]
- Gao, P. Averaging principle for stochastic Korteweg-de Vries equation. J. Differ. Equ. 2019, 267, 6872–6909. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P.J. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields; Applied Mathematical Sciences; Springer: New York, NY, USA, 1983. [Google Scholar]
- Lehman, B.; Weibel, S.P. Fundamental theorems of averaging for functional differential equations. J. Differ. Equ. 1999, 152, 160–190. [Google Scholar] [CrossRef]
- Liu, W.; Röckner, M.; Sun, X.B.; Xie, Y.C. Averaging principle for slow-fast stochastic differential equations with time dependent locally Lipschitz coefficients. J. Differ. Equ. 2020, 268, 2910–2948. [Google Scholar] [CrossRef]
- Maslov, V.P. An averaging method for the quantum many-body problem. Funct. Anal. Its Appl. 1999, 33, 280–291. [Google Scholar] [CrossRef]
- Murdock, J.A.; Sanders, J.A.; Verhulst, F. Averaging Methods in Nonlinear Dynamical Systems; Applied Mathematical Sciences; Springer Science+Business Media, LLC: New York, NY, USA, 2007. [Google Scholar]
- Zgliczyński, P. Hyperbolicity and averaging for the Srzednicki–Wójcik equation. J. Differ. Equ. 2017, 262, 1931–1955. [Google Scholar] [CrossRef]
- Bernardo, M.; Budd, C.; Champneys, A.R.; Kowalczyk, P. Piecewise-Smooth Dynamical Systems: Theory and Applications; Applied Mathematical Sciences; Springer: London, UK, 2008. [Google Scholar]
- Battelli, F.; Fečkan, M. Chaos in forced impact systems. Disc. Cont. Dyn. Syst. S 2013, 6, 861–890. [Google Scholar] [CrossRef]
- Fečkan, M.; Pačuta, J.; Pospíšil, M.; Vidlička, P. Averaging methods for piecewise-smooth ordinary differential equations. AIMS Math. 2019, 4, 1466–1487. [Google Scholar]
- Liu, K.; Fečkan, M.; Wang, J.R. A fixed point approach to the Hyers-Ulam stability of Caputo-Fabrizio fractional differential equations. Mathematics 2020, 8, 647. [Google Scholar] [CrossRef]
- Lawden, D.F. Elliptic Functions and Applications; Springer: New York, NY, USA, 1989. [Google Scholar]
- Battelli, F.; Fečkan, M. On the Poincaré-Adronov-Melnikov method for the existence of grazing impact periodic solutions of differential equations. J. Differ. Equ. 2020, 268, 3725–3748. [Google Scholar] [CrossRef]
- Shen, J.; Du, Z.D. Double impact periodic orbits for an inverted pendulum. Int. J. Non Linear Mech. 2011, 46, 1177–1190. [Google Scholar] [CrossRef]
- Belan, V.G. Averaging method for difference equations. Ukr. Mat. Zhurnal 1976, 28, 78–82. [Google Scholar]
- Brännström, N. Averaging in weakly coupled discrete dynamical systems. J. Nonlinear Math. Phys. 2009, 16, 465–487. [Google Scholar] [CrossRef]
- Martynyuk, D.I.; Danilov, V.Y.; Panikov, V.G. On the second Bogolyubov theorem for a system of difference equations. Ukr. Mat. Zhurnal 1988, 40, 110–120. [Google Scholar] [CrossRef]
- Griffiths, D.F.; Higham, D.J. Numerical Methods for Ordinary Differential Equations; Springer: London, UK, 2010. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fečkan, M.; Pačuta, J. Averaging Methods for Second-Order Differential Equations and Their Application for Impact Systems. Mathematics 2020, 8, 916. https://doi.org/10.3390/math8060916
Fečkan M, Pačuta J. Averaging Methods for Second-Order Differential Equations and Their Application for Impact Systems. Mathematics. 2020; 8(6):916. https://doi.org/10.3390/math8060916
Chicago/Turabian StyleFečkan, Michal, and Július Pačuta. 2020. "Averaging Methods for Second-Order Differential Equations and Their Application for Impact Systems" Mathematics 8, no. 6: 916. https://doi.org/10.3390/math8060916
APA StyleFečkan, M., & Pačuta, J. (2020). Averaging Methods for Second-Order Differential Equations and Their Application for Impact Systems. Mathematics, 8(6), 916. https://doi.org/10.3390/math8060916